Global dynamics of a delayed diffusive virus infection model with cell-mediated immunity and cell-to-cell transmission

1.   Introduction

Viral dynamics is a field of applied mathematics which employs mathematical models to describe the changes over time of infected cells and the viral load. Nowak et al. ^[1] and Nowak and May ^[2] proposed the following basic viral dynamic model,

where $u(t)$, $w(t)$, and $v(t)$ are the numbers of uninfected cells, productively infected cells, and virus particles at time $t$, respectively. See the references for the biological meanings of the parameters. This basic model has been modified to study different viral infections, which include hepatitis C virus (HCV) ^[3,4], human immunodeficiency virus (HIV) ^[5,6,7,8], human T-cell leukemia virus (HTLV) ^[9,10,11], and so on.

During the process of viral infection, specific immune response plays an important role. Specific immune response includes cell-mediated immunity (which depends on cytotoxic T lymphocytes response (CTLs)) and humoral immunity (which depends on antibody response). Since the work of Nowak and Bangham ^[12], much has been done on mathematical models on immune response against infected cells ^{[13,14,15,16]}.

Nowadays, time delays have been taken into account in order to better understand viral dynamics. Usually, distributed time delays ^[17,18,19] and discrete time delays ^[20,21,22] have been incorporated into viral dynamic models. In particular, based on (1.1), Zhu and Zou ^[20] proposed the following viral dynamic model with time delay and CTL immune response,

where $z(t)$ denotes the density of immune effectors at time $t$. Here the delay $\hat{\tau}$ represents the time from a virus entering a target cell to the production of new free virus particles. We refer to ^[20] for the meanings of the other parameters.

Note that both models (1.1) and (1.2) and most existing ones are described by ordinary differential equations. The cells and free virus particles are assumed to be uniform in location. In other words, the effect of spatial heterogeneity is ignored. For example, the lymphoid tissues are among the primary sites of HIV infection and replication. The lymphoid tissues consist of many lymph nodes with different sizes. The different tissue architecture and composition and biophysical parameters can influence the spread and replication of the virus ^[23]. To understand the viral pathogenesis better, it is necessary to consider the spatial aspects of the tissues. In ^[24], Wang and Wang proposed the following mathematical model of HBV infection with spatial dependence,

where $u(x, t)$, $w(x, t)$, and $v(x, t)$ are the densities of uninfected cells, productively infected cells, and free virus particles at spatial position $x$ and time $t$, respectively. $D$ is the diffusion coefficient and $\Delta$ is the Laplace operator. Using the geometric singular perturbation method, they studied the existence of traveling waves. Since then a lot of works have followed in this direction (see, for example, ^{[25,26,27,28,29]}).

In (1.1), (1.2), and (1.3), only the cell-free transmission (newly released free virus particles infect uninfected cells ^[2]) is considered. Recent experimental studies ^[30,31] prove that a healthy cell can be infected when it comes with close contact of an infected cell (cell-to-cell transmission ^[32,33]). Sigal et al. ^[34] found that the cell-to-cell spread of HIV can still permit ongoing replication even with an antiretroviral therapy. Consequently, viral dynamic models incorporating both transmission modes have been formulated and studied (to name a few, see ^{[35,36,37,38,39]}). We should mention that the incidences in these works are bilinear. Incidence is the number of new infections per unit of time. It depends on the infectivity of viruses and behavior of cells. Thus it is reasonable to be nonlinear in general. For example, the saturated incidence rate $\frac{\beta uv}{1+\alpha v}$ is used in ^[40] and the Beddington-DeAngelis incidence function is used in ^[41]. In a recent work, Sun and Wang ^[42] also used a general incidence $f(u, v)$ in a diffusive viral dynamic model.

Based on the above discussion, in this paper, we propose and study the following delayed diffusive viral dynamic model with cell-mediated immunity, cell-to-cell transmission, and general incidences,

where $z(x, t)$ denotes the densities of immune effectors at spatial position $x$ and time $t$. $\Omega$ is a general open bounded domain in $\mathbb{R}^n$ with smooth boundary $\partial\Omega$. We consider model (1.4) with the homogeneous Neumann boundary conditions

where $\frac{\partial }{\partial \vec{n}}$ denotes the outward normal derivative on $\partial\Omega$. We also assume the initial conditions

where $\phi_i$'s ($i = 1$, $2$, $3$, $4$) are bounded and uniformly continuous functions on $\overline{\Omega}\times[-\tau, 0]$.

In (1.4), intracellular delays for both transmission modes are assumed to be the same. In general, the intracellular delay in the cell-to-cell transmission is less than that in the cell-free infection ^[30,39]. However, the difference is not large enough. As for some existing studies (for example, ^[35,38]), for simplicity of presentation, we make the above assumption on the delays.

In (1.4), the incidences due to the cell-free transmission and the cell-to-cell transmission are given by the nonlinear functions $f(u, v)$ and $g(u, w)$, respectively. As in ^[26], we always make the following assumption on them in the sequel.

$\bf(A1)$ The nonlinear incidence functions $f$ and $g$ satisfy the following properties.

${\rm (i)}$ $f(u, v)\ge 0$ and $g(u, w)\ge 0$ for $u\ge0$, $v\ge 0$, and $w\ge0$, and the equalities hold if and only if $uv = 0$ and $uw = 0$;

${\rm (ii)}$ There exists $\eta_1 > 0$ and $\eta_2 > 0$ such that $f(u, v)\leq\eta_1u$ and $g(u, w)\leq\eta_2u$ for $u\ge0$, $v\ge 0$, and $w\geq 0$;

${\rm (iii)}$ $\frac{\partial f(u, v)}{\partial u}$ and $\frac{\partial g(u, w)}{\partial u}$ are continuous with $\frac{\partial f(u, v)}{\partial u} > 0$ and $\frac{\partial g(u, w)}{\partial u} > 0$ for $u\ge0$, $v > 0$, and $w > 0$;

${\rm (iv)}$ $\frac{\partial f(u, v)}{\partial v}$ and $\frac{\partial g(u, w)}{\partial w}$ are continuous with $\frac{\partial f(u, v)}{\partial v}\ge0$ and $\frac{\partial g(u, w)}{\partial w}\geq0$ for $u\ge0$, $v\ge0$, and $w\geq 0$;

${\rm (v)}$ $v\frac{\partial f(u, v)}{\partial v}-f(u, v)\leq0$ and $w\frac{\partial g(u, w)}{\partial w}-g(u, w)\leq0$ for $u\ge0$, $v\ge 0$, and $w\geq 0$.

Note that, by Assumption (A1), for any $u > 0$,

which implies that $\frac{f(u, v)}{v}$ is decreasing on $(0, \infty)$. In particular, for any $u > 0$ and $v > 0$,

An analog also holds for $g$. Thus we have

The rest of the paper is organized as follows. In section 2, we consider the existence, uniqueness, positivity, and boundedness of solutions to system (1.4)–(1.6). Then we study the existence of homogeneous steady states in section 3, which depend on the basic reproduction number of infection and the basic reproduction number of immunity. The main part is section 4, where we discuss the local and global dynamics of system (1.4)–(1.6) by analyzing the characteristic equations and constructing suitable Lyapunov functionals. These results are supported with numerical simulations in section 5. The paper ends with a brief conclusion.

2.   Well-posedness

Let $\bf{X}: = \mathcal{C}(\overline{\Omega}, \mathbb{R}^4)$ be the Banach space equipped with the supremum norm $\| \cdot \|_{\bf{X}}$. For $\tau\geq0$, define $\mathcal{C} = \mathcal{C}([-\tau, 0], \bf{X})$, which is a Banach space equipped with the norm $\| \phi \| = \max_{\theta\in[-\tau, 0]}\| \phi(\theta) \|_{\bf{X}}$. If $\sigma > 0$ and $U: [-\tau, \sigma)\to \bf{X}$, then for $t\in [0, \sigma)$, $U_t\in \mathcal{C}$ is defined by $U_t(\theta) = U(t+\theta)$ for $\theta\in [-\tau, 0]$. Denote $\bf{X}^+ = \mathcal{C}(\overline{\Omega}, \mathbb{R}^4_+)$ and $\mathcal{C^+} = \mathcal{C}([-\tau, 0], \bf{X}^+)$. Then both $(\bf{X}, \bf{X}^+)$ and $(\mathcal{C}, \mathcal{C}^+)$ are strongly ordered spaces. According to Corollary 4 in ^[43], we have the following result on the well-posedness. The arguments are standard and hence are omitted here. Interested readers can refer to, for example, a recent paper by Gao and Wang ^[44].

Theorem 2.1. For each $\phi = (\phi_1, \phi_2, \phi_3, \phi_4)\in\mathcal{C}^+$, system (1.4)–(1.6) has a unique solution $U(\cdot, t, \phi) = (u(\cdot, t, \phi), w(\cdot, t, \phi), v(\cdot, t, \phi), z(\cdot, t, \phi))$ on $[0, \infty)$ with $U_0(\cdot, \phi) = \phi$. Moreover, $U_t(\cdot, \phi)\in\mathcal{C}^+$ for $t\ge 0$ and $U(\cdot, t, \phi)$ is a classical solution.

Let $\Phi(t): \mathcal{C}^+\to \mathcal{C}^+$ be the solution semiflow associated with (1.4)–(1.6), that is, $\Phi(t, \phi) = U_t(\cdot, \phi)$, where $U(\cdot, t, \phi)$ is the solution of (1.4)–(1.6) with the initial condition $\phi\in \mathcal{C}^+$.

The following result gives some properties of solutions.

Lemma 2.2. For $\phi\in \mathcal{C}^+$, the following statements hold for the solution $U(\cdot, t, \phi)$ of (1.4)–(1.6).

${\rm(i)}$ $\limsup\limits_{t\to\infty}u(x, t, \phi)\le \frac{s}{d}$, $\limsup\limits_{t\to\infty}w(x, t, \phi)\le \frac{e^{-m\tau}(\eta_1+\eta_2)s}{d\delta}$, $\limsup\limits_{t\to\infty}v(x, t, \phi)\le \frac{Ne^{-m\tau}(\eta_1+\eta_2)s}{dc}$, and $\limsup\limits_{t\to\infty}z(x, t, \phi)\le \frac {e^{-m\tau}(\eta_1+\eta_2)s}{d\min\{\delta, b\}}$ uniformly for all $x\in \Omega$.

${\rm (ii)}$ $u(\cdot, t, \phi) > 0$ for $t > 0$ and $\liminf\limits_{t\to\infty}u(x, t, \phi)\geq\frac{s}{d+\eta_1+\eta_2}$ uniformly for all $x\in \Omega$.

${\rm(iii)}$ If $w(\cdot, t_0, \phi)\not\equiv0$ or $v(\cdot, t_0, \phi)\not\equiv0$ for some $t_0\geq0$, then $w(x, t, \phi) > 0$ and $v(x, t, \phi) > 0$ for all $x\in\Omega$ and $t > t_0+\tau$.

${\rm(iv)}$ If $z(\cdot, t_0, \phi)\not\equiv0$ for some $t_0\geq0$, then $z(x, t, \phi) > 0$ for all $x\in\Omega$ and $t > t_0$.

Proof. For simplicity of notation, in the proof here we omit $\phi$ from the expressions of the solution.

(ⅰ) First, we have

which implies that $\limsup\limits_{t\to\infty}u(x, t)\le \frac{s}{d}$ uniformly for all $x\in \Omega$. Next, by Assumption (A1) and the second equation in (1.4), we have

Then $\limsup\limits_{t\to\infty}w(x, t)\le \frac{e^{-m\tau}(\eta_1+\eta_2)s}{d\delta}$ uniformly for $x\in \Omega$ follows easily from this and $\limsup\limits_{t\to\infty}u(x, t)\le \frac{s}{d}$ uniformly for $x\in \Omega$. Similarly, adding the second and fourth equations of (1.4) yields

It follows that $\limsup\limits_{t\to\infty}(w(x, t)+z(x, t))\le \frac {e^{-m\tau}(\eta_1+\eta_2)s}{d\min\{\delta, b\}}$ uniformly for $x\in\Omega$ and hence $\limsup\limits_{t\to\infty}z(x, t)\le \frac {e^{-m\tau}(\eta_1+\eta_2)s}{d\min\{\delta, b\}}$ uniformly for $x\in\Omega$. Now, $\limsup\limits_{t\to\infty}w(x, t)\le \frac{e^{-m\tau}(\eta_1+\eta_2)s}{d\delta}$ uniformly for $x\in \Omega$ together with the third equation of (1.4) (Lemma 1 in ^[45]), and comparison theorem, gives $\limsup\limits_{t\to\infty}v(x, t)\le \frac{Ne^{-m\tau}(\eta_1+\eta_2)s}{dc}$ uniformly for $x\in\Omega$.

(ⅱ) Noting that $\frac{\partial u(x, t)}{\partial t} \geq s-(d+\eta_1+\eta_2)u(x, t)$, one can easily get

for $x\in \Omega$ and $t\ge 0$. Then (ⅱ) follows immediately.

(ⅲ) Note that the operator $D_1\Delta -c\mathrm {Id}$ generates a positive semigroup on $C(\overline{\Omega}, \mathbb{R})$, where $\mathrm {Id}$ is the identity operator. Thus if $w(\cdot, t_0)\not\equiv0$, then from the third equation of (1.4), we see that $v(\cdot, t)\not\equiv 0$ for $t > t_0$. Without loss of generality, we assume that $v(\cdot, t_0)\not\equiv 0$. We first show that $v(\cdot, t) > 0$ for $t > t_0$. By Theorem 2.1, $v(x, t)$ satisfies

Let $\bar{v}(x, t)$ be the solution of

Then $\bar{v}(x, t) > 0$ for $x\in\Omega$ and $t > t_0$. In fact, suppose, by contradiction, there exist $x_0\in\Omega$ and $\hat{t} > t_0$ such that $\bar{v}(x_0, \hat{t}) = 0$. Then, according to the strong maximum principle ^[46], $\bar{v}(x, t)\equiv0$ for each $t\geq t_0$, contradicting with $\bar{v}(\cdot, t_0)\not\equiv0$. Applying the comparison theorem, we know that $v(x, t)\ge\bar{v}(x, t) > 0$ for $t > t_0$ and $x\in \Omega$. We now prove that $w(x, t) > 0$ for $x\in \Omega$ and $t > t_0+\tau$. Otherwise, there exist $\bar{x}\in\Omega$ and $\bar{t} > t_0+\tau$ such that $w(\bar{x}, \bar{t}) = 0$. As $w(x, t)\ge 0$, we have $\frac{\partial w(\bar{x}, \bar{t})}{\partial t} = 0$. This is impossible since

by Assumption (A1) (ⅱ) due to $u(\bar{x}, \bar{t}-\tau) > 0$ and $v(\bar{x}, \bar{t}-\tau) > 0$. This proves statement (ⅲ).

(ⅳ) The proof is similar to that of (ⅲ) on $v(x, t) > 0$ for $x\in \Omega$ and $t > t_0$ and hence we omit it here. This completes the proof.

Lemma 2.2 tells us that $\Phi$ is point dissipative. Then it follows from Theorem 2.1.8 in ^[47] that $\Phi(t)$ is compact for all $t > \tau$. This, together with Theorem 3.4.8 in ^[48], gives the following result.

Theorem 2.3. The semiflow $\Phi$ has a global compact attractor $\mathcal{A}$ in $\mathcal{C}^+$. Moreover, $u(x, t, \phi)\le \frac{s}{d}$ for all $x\in \overline{\Omega}$, $t\ge 0$, and $\phi\in \mathcal{A}$.

3.   Steady states and basic reproduction numbers

System (1.4) with (1.5) always has a unique infection-free steady state $P_0 = (u_0, 0, 0, 0)$, where $u_0 = s/d$. Applying the result of Wang and Zhao (Theorem 3.4 in ^[49]), we can obtain the expression of the basic reproduction number of infection, $R_0$, which is given by

Denote

Then $R_{01}$ is the number of secondly infected cells through the cell-free transmission and it is referred to as the basic reproduction number from the cell-free transmission; while $R_{02}$ is the number of secondly infected cells through the cell-to-cell transmission and it is referred to as the basic reproduction number from the cell-to-cell transmission ^[38].

In the following, we discuss the existence of homogeneous steady states for (1.4) (the stability results in section 4 indicate that they are the only possible steady states). Clearly, a homogeneous steady state $P = (u, w, v, z)$ satisfies

It follows from (3.1d) that $z = 0$ (which corresponds to the immunity-free infected steady states) or $w = \frac{b}{q}$ (which, when $z\neq 0$, corresponds to the infected-immune steady states).

We firstly consider the case where $z = 0$. It follows from (3.1c) that $v = \frac{N\delta w}{c}$. Multiplying both sides of (3.1b) by $e^{m\tau}$ and then adding up the resultant and (3.1a) to get $u = \frac{s-\delta w e^{m\tau}}{d}$. It is necessary that $w\in(0, \frac{s}{\delta e^{m\tau}})$. Substituting $u = \frac{s-\delta w e^{m\tau}}{d}$ and $v = \frac{N\delta w}{c}$ into (3.1a), we see that $w$ is a positive zero of $H_1$, where

According to Assumption (A1), we have $H_1(0) = 0$, $H_1 (\frac{s}{\delta e^{m\tau}})-s < 0$, and

If $R_0 > 1$, then $H_1'(0) > 0$. This, together with $H_1(0) = 0$, implies that $H_1(w)$ is positive for all sufficiently small $w > 0$. By the Intermediate Value Theorem, $H_1$ has at least one zero in $(0, \frac{s}{\delta e^{m\tau}})$ and hence (1.4) has at least one immunity-free infected steady state. In fact, there is only one such steady state by the claim that $H_1'(w_1) < 0$ for any immunity-free infected steady state, which is proved as follows. Note that $\delta e^{m\tau} = \frac{f(u_1, v_1)}{w_1}+\frac{g(u_1, w_1)}{w_1}$ and $w_1 = \frac{cv_1}{N\delta}$. By Assumption (A1),

This proves the claim. Next, we assume that $R_0 < 1$. Then $H_1^{\prime}(0) = \delta e^{m\tau}(R_0-1) < 0$, which combined with $H_1(0) = 0$ implies that $H_1(w) < 0$ for $w > 0$ sufficiently small. Using the above claim, we can easily see that there is no immunity-free infected steady state when $R_0 < 1$. Moreover, $H_1(w) < 0$ for $w\in (0, \frac{s}{\delta e^{m\tau}}]$. Finally, we assume that $R_0 = 1$. We use contradictive arguments to show that there is no immunity-free infected steady state in this case. Otherwise, assume that $H_1(w)$ has a positive zero say $w^*$. Then from the above claim $H_1(w) > 0$ for $w < w^*$ and closely enough to $w^*$. Note that $H_1(w)$ depends continuously on the parameters and $H_1(w) < 0$ for $w\in (0, \frac{s}{\delta e^{m\tau}}]$ when $R_0 < 1$. Fix $w\in (0, w^*)$. Choose a sequence of parameters such that the basic reproduction number $R_0 < 1$ and tends to $1$. Then $H_1(w)$ tends to $H_1(w^*) > 0$, a contradiction to the fact that the limit is less than or equal to 0. This proves that there is no immunity-free infected steady state when $R_0 = 1$.

Now we study the case where $w = \frac{b}{q}$. This, together with (3.1c), yields $v = \frac{N\delta b}{cq}$. As before, add up (3.1a) and (3.1b) multiplied by $e^{m\tau}$ to get $z = \frac{s-du-\delta e^{m\tau}w}{pe^{m\tau}w}$, which necessarily requires $u\in(0, \frac{s}{d}-\frac{\delta b}{dq}e^{m\tau})$. Substituting $w = \frac{b}{q}$ and $z = \frac{s-du-\delta e^{m\tau}w}{pe^{m\tau}w}$ into (3.1a), we see that $u$ is a positive zero of $H_2$, where

With Assumption (A1), we have $H_2(0) = -s < 0$ and

Therefore, in order for model (1.4) to have an infected-immune steady state (if exists there is a unique one), it is necessary and sufficient that $H_2(\frac{s}{d}-\frac{\delta b}{d q}e^{m\tau}) = H_1(\frac{b}{q}) > 0.$ Recall that when $R_0 \leq 1, \ H_1(w) < 0$ for $w \in (0, \frac{s}{\delta e^{m\tau}}]$; while when $R_0 > 1, \ H_1(w) > 0$ for $w\in (0, w_1)$ and $H_1(w) < 0$ for $w\in(w_1, \frac{s}{\delta e^{m\tau}})$. It follows that $H_1(\frac{b}{q}) > 0$ if and only if $R_0 > 1$ and $\frac{b}{q} < w_1$. Denote,

As $q$ is the average number of immune effectors produced from contacting with a productively infected cell and $\frac{1}{b}$ is the average life of an immune effector, it follows that $R_1$ is the total number of immune effectors produced at the immunity-free infected steady state. Thus $R_1$ is called the basic reproduction number of immunity.

Summarizing the above discussion, we have obtained the following result on the existence of homogeneous steady states.

Theorem 3.1. For model (1.4) with (1.5), the following statements on the existence of homogeneous steady states are true.

${\rm(i)}$ If $R_0\le1$, then there is only the infection-free steady state $P_0$.

${\rm (ii)}$ If $R_1\leq1 < R_0$, then besides $P_0$, there is also a unique immunity-free infected steady state $P_1 = (u_1, w_1, v_1, 0)$, where $w_1$ is the only positive zero of $H_1$ defined by (3.2), $u_1 = \frac{s-\delta w_1 e^{m\tau}}{d}$ and $v_1 = \frac{N\delta w_1}{c}$.

${\rm (iii)}$ If $R_1 > 1$ (it is necessary that $R_0 > 1$), then in addition to $P_0$ and $P_1$, there is also a unique infected-immune steady state $P_2 = (u_2, w_2, v_2, z_2)$, where $u_2$ is the only positive zero of $H_2$ defined by (3.3), $w_2 = \frac{b}{q}$, $v_2 = \frac{N\delta b}{cq}$, and $z_2 = \frac{s-du_2-\delta w_2 e^{m\tau}}{pw_2e^{m\tau}}$.

4.   Stability analysis

In the main part of this paper, we establish the stability of each steady state obtained in Theorem 3.1.

Let $P^* = (u^*, w^*, v^*, z^*)$ be an arbitrary homogeneous steady state. The linearization of (1.4) at $P^*$ is

where

Denote $0 = \mu_0 < \mu_1 < \mu_2 < \cdots < \mu_n < \cdots$ to be all the eigenvalues of the operator $-\Delta$ on $\Omega$ with the homogeneous Neumann boundary condition. Then $P^*$ is locally asymptotically stable if, for any $i\in \mathbb{N} = \{0, 1, 2, \dots\}$, every solution of the characteristic equation

has a negative real part and $P^*$ is unstable if there exists $i_0\in \mathbb{N}$ such that (4.2) has a solution with a positive real part.

4.1.   Stability of the infection-free steady state $P_0$

We first study the local stability of $P_0$.

Proposition 4.1. The infection-free steady state $P_0$ of (1.4) is locally asymptotically stable if $R_0 < 1$ and unstable if $R_0 > 1$.

Proof. By (4.2), the characteristic equation at $P_0$ is

Obviously, the stability of $P_0$ is determined by

Firstly, suppose that $R_0 < 1$. We claim that all roots of (4.3) have negative real parts. Otherwise, there exists $i_0\in \mathbb{N}$ such that (4.3) has a root $\lambda_0$ with $\mathrm{Re}(\lambda_0)\ge 0$. Then

It follows that

a contradiction to $R_0 < 1$. This proves the claim and hence $P_0$ is locally asymptotically stable when $R_0 < 1$.

Secondly, assume $R_0 > 1$. For $i\in \mathbb{N}$, denote

Recall that $\mu_0 = 0$. We have

and

By the Intermediate Value Theorem, $F(\lambda, 0)$ has a positive zero and hence (4.3) has at least one positive zero for $i = 0$. This means that $P_0$ is unstable when $R_0 > 1$.

In fact, $P_0$ is globally stable if it is locally stable.

Theorem 4.2. If $R_0\leq1$, then the infection-free steady state $P_0$ of (1.4) is globally attractive. In particular, $P_0$ is globally asymptotically stable when $R_0 < 1$.

Proof. It suffices to show that $P_0$ is globally attractive in $\mathcal{A}$. For this purpose, we consider the Lyapunov functional

Calculating the time derivative of $W(t)$ along solutions of model (1.4), we have

It follows from the homogeneous Neumann boundary condition (1.5) and the Divergence Theorem that

Moreover, by Theorem 2.3, $u(x, t)\le \frac{s}{d}$ for $x\in \Omega$ and $t\ge 0$. With the help of (1.7), for $v(x, t) > 0$, we have

The above inequality holds automatically for $v(x, t) = 0$ and also observe that the inequality is strict for $u(x, t) < \frac{s}{d}$ and $v(x, t) > 0$. Therefore,

Moreover, $\frac{\mathrm{d} W(t)}{\mathrm{d} t} = 0$ if and only if $v(x, t) = 0$ and $z(x, t) = 0$. In fact, if $v(x_0, t_0)\neq 0$, then there exists a neighborhood $N_{(x_0, t_0)}$ of $(x_0, t_0)$ such that $v(x, t)\neq0$ for $(x, t)\in N_{(x_0, t_0)}$. Then by the observation, $u(x, t) = \frac{s}{d}$ for $(x, t)\in N_{(x_0, t_0)}$. This, together with the first equation of (1.4) and Assumption (A1), implies that $v(x, t) = 0$ for $(x, t)\in N_{(x_0, t_0)}$, a contradiction. Then it is easy to see that the largest invariant subset of $\frac{\mathrm{d} W(t)}{\mathrm{d} t} = 0$ is $\{P_0\}$. By LaSalle's Invariance Principle (see Theorem 5.3.1 in ^[50] or Theorem 3.4.7 in ^[51]), the infection-free steady state $P_0$ is globally attractive. In particular, this together with Proposition 4.1, tells us that $P_0$ is globally asymptotically stable when $R_0 < 1$.

4.2.   Stability of the immunity-free infected steady state $P_1$

Next we consider the stability of the immunity-free infected steady state $P_1$. For convenience of notations, denote

Theorem 4.3. Suppose $R_0 > 1$. Then the immunity-free infected steady state $P_1$ of (1.4) is locally asymptotically stable if $R_1 < 1$ and unstable if $R_1 > 1$.

Proof. From (4.2), we know that the characteristic equation at $P_1$ is given by

where

Clearly, the eigenvalue $\lambda = b(R_1-1)-\mu_iD_2 < 0$ for $i\in \mathbb{N}$ when $R_1 < 1$ but when $R_1 > 1$, with $i = 0$, we have a positive eigenvalue $\lambda = b(R_1-1)$. Thus $P_1$ is unstable if $R_1 > 1$. Now, we assume that $R_1 < 1$. Then the stability of $P_1$ is determined by the roots of $\rho_i(\lambda) = 0$, which is equivalent to

We claim that all solutions of (4.4) have negative real parts. Otherwise, suppose that there exists $i_{1}\in \mathbb{N}$ such that (4.4) has a solution $\lambda_1$ with $\mathrm{Re}(\lambda_{1})\geq0$. Then

However, from the steady state Eqs (3.1b) and (3.1c), we have

This and Assumption (A1) (v) together give us

which is a contradiction with (4.5). This proves the claim and hence $P_1$ is locally asymptotically stable when $R_1 < 1 < R_0$.

Before studying the global stability of $P_1$, we establish the persistence of infection.

From the linearized system at $P_0$ (see (4.1)), we have the following cooperative system for $(w, v)$,

With similar arguments as those for Lemma 3 and Lemma 4 in Lou and Zhao ^[45], we can obtain the following results.

Lemma 4.4. There exists a principal eigenvalue $\bar{\lambda}(u_0, \tau)\triangleq \bar{\lambda}(P_0, \tau)$ of (4.6) associated with a strongly positive eigenvector. Moreover, $\bar{\lambda}(u_0, \tau)$ has the same sign as $\lambda(u_0)\triangleq \bar{\lambda}(u_0, 0)$.

Lemma 4.5. $R_0-1$ and $\lambda(u_0)$ have the same sign.

Theorem 4.6. Suppose $R_1\le 1 < R_0$. Then the infection is persistent, that is, there exists $\varepsilon > 0$ such that

uniformly for all $x\in\overline{\Omega}$, where $\phi\in \mathcal{W}_1: = \left\{\phi\in\mathcal{C}^+ : w(\cdot, 0)\not\equiv0\ \mathit{\text{and}}\ v(\cdot, 0)\not\equiv0 \right\}$.

Proof. Define

By Lemma 2.2 and the second equation of (1.4), we know that $\Phi(t)\mathcal{W}_1\subseteq\mathcal{W}_1$ for all $t\geq0$. Denote

Claim 1. $\omega(\phi) = \{(u_0, 0, 0, 0)\}$ for $\phi\in\mathcal{M}_{\partial}$, where $\omega(\phi)$ is the omega limit set of the orbit $\mathcal{O}^+(\phi): = \{\Phi(t)\phi:t\geq0\}$.

Since $\phi\in\mathcal{M}_{\partial}$, for all $t\ge 0$, either $w(x, t, \phi)\equiv0$ or $v(x, t, \phi)\equiv0$. If $w(x, t, \phi)\equiv0$ for all $t\geq0$, then $\lim\limits_{t\to\infty}v(x, t, \phi) = 0$ uniformly for $x\in\overline{\Omega}$ from the third equation of (1.4). Now, suppose that $w(x, t_1, \phi)\not\equiv0$ for some $t_1\geq0$. Then by Lemma 2.2, $w(x, t, \phi) > 0$ for all $t\geq t_1+\tau$ and $x\in \Omega$. Thus $v(x, t, \phi)\equiv0$ for all $t\geq t_1+\tau$. This, combined with the third equation of (1.4), implies that $w(x, t, \phi)\equiv 0$ for $x\in \overline{\Omega}$ and $t\ge t_1+\tau$. Then, in either case, $\lim\limits_{t\to\infty}v(x, t, \phi) = \lim\limits_{t\to\infty}w(x, t, \phi) = 0$ uniformly for $x\in \overline {\Omega}$. Thus $u$ is asymptotic to

By Corollary 4.3 in ^[52], we get $\lim\limits_{t\to\infty}u(x, t, \phi) = u_0$ uniformly for $x\in\overline{\Omega}$. The above discussion tells us that $w(x, t, \phi)\equiv 0$ for all $t$ large enough. Then we can easily see from the fourth equation of (1.4) that $\lim\limits_{t\to\infty}z(x, t, \phi) = 0$ uniformly for $x\in\overline{\Omega}$. This proves $\omega(\phi) = \{(u_0, 0, 0, 0)\}$.

Since $R_1\leq1 < R_0$, by Lemma 4.4 and Lemma 4.5, there exists a sufficiently small $\varepsilon_0 > 0$ such that the following linear system

has a positive principal eigenvalue $\bar{\lambda}(u_0-\varepsilon_0)$ with positive eigenfunction $(w_{\varepsilon_0}, v_{\varepsilon_0})$. By the continuity in Assumption (A1), there exists $\delta_0\in (0, \varepsilon_0]$ such that

for all $u_0-\delta_0\le u\le u_0+\delta_0$, $0\le v\le \delta_0$, and $0\le w\le \delta_0$.

Claim 2. $\{(u_0, 0, 0, 0)\}$ is a uniform weak repeller for $\mathcal{W}_1$ in the sense that

Suppose, by contradiction, there exists $\phi_1^*\in\mathcal{W}_1$ such that $\limsup\limits_{t\to\infty}\|\Phi(t)\phi_1^*-(u_0, 0, 0, 0)\| < \delta_0$. Then there exists $t_2 > 0$ such that $u(x, t, \phi_1^*) > u_0-\delta_0\ge u_0-\varepsilon_0$, $w(x, t, \phi_1^*)\le \delta_0$, and $v(x, t, \phi_1^*)\le \delta_0$ for $t\geq t_2$ and $x\in\overline{\Omega}$. It follows from Assumption (A1) and the choice of $\delta_0$ that $w$ and $v$ satisfy

Due to $w(x, t, \phi_1^*) > 0$ and $v(x, t, \phi_1^*) > 0$ for $t > 0$ and $x\in \Omega$, there exists $\kappa_1 > 0$ such that $(w(x, t_2+\theta, \phi_1^*), v(x, t_2+\theta, \phi_1^*))\ge \kappa_1 e^{\bar{\lambda}(u_0-\varepsilon_0)(t_2+\theta)}(w_{\varepsilon_0}(x), v_{\varepsilon_0}(x))$ for all $x\in \Omega$ and $\theta\in [-\tau, 0]$. Then it follows from the comparison principle that $w(x, t, \phi_1^*)\ge \kappa_1 e^{\bar{\lambda}(u_0-\varepsilon_0)t}w_{\varepsilon_0}(x)$ and $v(x, t, \phi_1^*)\ge \kappa_1 e^{\bar{\lambda}(u_0-\varepsilon_0)t}v_{\varepsilon_0}(x)$ for all $x\in \Omega$ and $t\ge t_2$, a contradiction to the fact that both $w(x, t, \phi_1^*)$ and $v(x, t, \phi_1^*)$ are bounded. This proves Claim 2.

Define a continuous function $\mathcal{P}_1 : \mathcal{C}^+\rightarrow[0, \infty)$ by

Clearly, $\mathcal{P}_1^{-1}(0, \infty)\subset\mathcal{W}_1$, and $\mathcal{P}_1$ has the property that if $\mathcal{P}_1(\phi) = 0$ and $\phi\in\mathcal{W}_1$ or $\mathcal{P}_1(\phi) > 0$, then $\mathcal{P}_1(\Phi(t)\phi) > 0$ for all $t > 0$. Hence, $\mathcal{P}_1$ is a generalized distance function for the semiflow $\Phi(t)$ ^[53]. According to the above discussions, we obtain that any forward orbit of $\Phi(t)$ in $\mathcal{M}_{\partial}$ converges to $(u_0, 0, 0, 0)$, which is isolated in $\mathcal{C}^+$ and $\mathcal{W}^s(u_0, 0, 0, 0)\cap \mathcal{W}_1 = \varnothing$, where $\mathcal{W}^s(u_0, 0, 0, 0)$ is the stable manifold of $(u_0, 0, 0, 0)$. Moreover, there is no cycle in $\partial\mathcal{W}_1$ from $(u_0, 0, 0, 0)$ to $(u_0, 0, 0, 0)$. Applying Theorem 3 in ^[53], we know that there exists an $\bar{\varepsilon} > 0$ such that $\min\{\mathcal{P}_1(\phi)\} > \bar{\varepsilon}$ for any $\phi\in\mathcal{W}_1$. It follows that

This combined with Lemma 2.2 finishes the proof with $\varepsilon = \min\{\bar{\varepsilon}, \frac{s}{d+\eta_1+\eta_2}\}$.

In order to study the global stability of $P_1$, define $G:(0, \infty)\ni x\to x-1-\ln x$. Obviously, $G(x) > 0$ for $x\in (0, \infty)$ and $G$ attains its global minimum only at $x = 1$. We also need the following assumption.

$\bf(A2)$ The nonlinear incidence functions $f(u, v)$ and $g(u, w)$ satisfy the following conditions.

${\rm (i)}$ For any $u > 0$,

${\rm (ii)}$ For any $u > 0$,

Theorem 4.7. Suppose that $R_1\leq1 < R_0$ and Assumption (A2) are satisfied. Then the immunity-free infected steady state $P_1$ is globally attractive in

In particular, it is globally asymptotically stable in $\mathcal{C}_1^+$ if further $R_1 < 1$.

Proof. According to Lemma 2.2 and Theorem 4.6, we know that there exists $\varepsilon > 0$ such that $\liminf\limits_{t\to\infty}u(x, t, \phi)\geq\varepsilon$, $\liminf\limits_{t\to\infty}w(x, t, \phi)\geq\varepsilon$, and $\liminf\limits_{t\to\infty}v(x, t, \phi)\geq\varepsilon$ for $\phi\in\mathcal{C}_1^+$. Without loss of generality, we define a Lyapunov functional

where

Calculating the time derivative of $L(x, t)$ along solutions of (1.4) yields

With

we have

Clearly,

and

Using the Divergence Theorem and the homogeneous Neumann boundary conditions of (1.5), we have

and

The latter gives

and hence

To summarize, we have obtained

Note that the monotonicity of $G(x)$ on each side of $x = 1$ and Assumption (A2) give us

Thus

Moreover, $\frac{\mathrm {d} L(t)}{\mathrm {d} t} = 0$ if and only if $u(x, t) = u_1$, $w(x, t) = w_1$, $v(x, t) = v_1$, and $z(x, t) = 0$. Then the largest invariant subset of $\frac{\mathrm{d} L(t)}{\mathrm {d} t} = 0$ is $\{P_1\}$. By LaSalle's Invariance Principle (see Theorem 5.3.1 in ^[50] or Theorem 3.4.7 in ^[51]), the immunity-free infected steady state $P_1$ is globally attractive in $\mathcal{C}_1^+$ when $R_1\leq1 < R_0$. This, together with Theorem 4.3, implies that $P_1$ is globally asymptotically stable in $\mathcal{C}_1^+$ if further $R_1 < 1$.

4.3.   The stability of the infected-immune steady state $P_2$

For convenience of notations, denote

Theorem 4.8. If $R_1 > 1$, then the infected-immune steady state $P_2$ is locally asymptotically stable.

Proof. According to (4.2), the characteristic equation at $P_2$ is

We claim that all roots of (4.8) have negative real parts. Otherwise, suppose for some $i_2\in \mathbb{N}$, it has a root $\lambda_2$ with $\mathrm {Re}(\lambda_2)\ge 0$. Since $w_2 = \frac {b}{q}$, we have

which implies

With similar arguments as those in the proof of Theorem 4.3, we can obtain

Thus we have arrived at

which is impossible as one can check that $|(\lambda_2+\mu_{i_2}D_2)(\lambda_2+\delta+pz_2)+pbz_2| > |(\lambda_2+\mu_{i_2}D_2)(\delta+pz_2)|$.

This completes the proof.

To establish the global stability of $P_2$, we need the persistence of immunity.

From the linearized system at $P_1$ (see (4.1)), we have the following cooperative system for $(w, v, z)$,

With similar arguments as those for Lemma 3 and Lemma 4 in Lou and Zhao ^[45], we can obtain the following results.

Lemma 4.9. There exists a principal eigenvalue $\hat{\lambda}(P_1, \tau)$ of (4.9) associated with a strongly positive eigenvector. Moreover, $\hat{\lambda}(P_1, \tau)$ has the same sign as $\hat{\lambda}(P_1, 0)$.

Lemma 4.10. $R_1-1$ and $\hat{\lambda}(P_1, 0)$ have the same sign.

Theorem 4.11. Suppose that $R_1 > 1$ (it is necessary that $R_0 > 1$) and (A2) holds. Then the immunity is persistent, that is, there exists $\epsilon > 0$ such that

uniformly for all $x\in\overline{\Omega}$, where $\phi\in \mathcal{W}_2: = \left\{\phi\in\mathcal{C}^+ : w(\cdot, 0)\not\equiv0, \ v(\cdot, 0)\not\equiv0, \ { and}\ z(\cdot, 0)\not\equiv0 \right\}$.

Proof. The proof is quite similar to that of Theorem 4.6. Denote

Set $M_0 = \{P_0\}$ and $M_1 = \{P_1\}$.

According to Lemma 2.2, we know that $w(x, t, \phi) > 0$, $v(x, t, \phi) > 0$, and $z(x, t, \phi) > 0$ for all $t > 0$ and $x\in\Omega$, $\phi\in\mathcal{W}_2$, which implies that $\Phi(t)\mathcal{W}_2\subseteq\mathcal{W}_2$ for all $t\geq0$. Define

Claim 3. Let $\phi\in \mathcal{M}^*_{\partial}$. Then $\omega(\phi) = M_0$ or $M_1$.

Sine $\phi\in \mathcal{M}^*_{\partial}$, for any $t\ge 0$, we have either $w(x, t, \phi) \equiv 0$, or $v(x, t, \phi)\equiv 0$, or $z(x, t, \phi)\equiv 0$. If $z(x, t_4, \phi)\not\equiv0$ for some $t_4\ge 0$, then by Lemma 2.2, $z(x, t, \phi) > 0$ for $t > t_4$ and $x\in \Omega$. Then either $w(x, t, \phi)\equiv0$ or $v(x, t, \phi)\equiv 0$ for each $t > t_4$. By the proof of Claim 1, we know that $\omega(\phi) = M_0$. Now, suppose that $z(x, t, \phi)\equiv 0$ for all $t\ge 0$. If for each $t\ge 0$, either $w(x, t, \phi)\equiv0$ or $v(x, t, \phi)\equiv 0$, then by Claim 1, $\omega(\phi) = M_0$. If there exists $\tilde{t}\ge 0$ such that $w(x, \tilde{t}, \phi)\not \equiv 0$ and $v(x, \tilde{t}, \phi)\not\equiv 0$. Then by Theorem 4.6, there exists $\xi > 0$ such that

Now consider the reduced system of (1.4) with $z = 0$. Modifying the Lyapunov functional $L(t)$ in the proof of Theorem 4.7 by ignoring the term $\frac{p}{q}e^{m\tau}z(x, t)$ in $L(x, t)$, we can show that the solution of the reduced system converges to $(u_1, w_1, v_1)$ and hence $\omega(\phi) = M_1$. This proves Claim 3.

Claim 4. Both $M_0$ and $M_1$ are uniform weak repellers for $\mathcal{W}_2$. Since $\mathcal{W}_2\subset \mathcal{W}_1$, by Claim 2, $M_0$ is a uniform repeller for $\mathcal{W}_2$. The proof of $M_1$ being a uniform repeller of $\mathcal{W}_2$ is similar as that of Claim 2 by using Lemma 4.9 and Lemma 4.10. Therefore, we omit the detail here.

Define a continuous function $\mathcal{P}_2 : \mathcal{C}^+\rightarrow[0, \infty)$ by

It is easy to see that $\mathcal{P}_2^{-1}(0, \infty)\subset\mathcal{W}_2$, and $\mathcal{P}_2$ has the property that if $\mathcal{P}_2(\phi) = 0$ and $\phi\in\mathcal{W}_2$ or $\mathcal{P}_2(\phi) > 0$, then $\mathcal{P}_2(\Phi(t)\phi) > 0$ for all $t > 0$. Thus $\mathcal{P}_2$ is a generalized distance function for the semiflow $\Phi(t)$. As $M_0$ and $M_1$ are repellers, we know that both $M_0$ and $M_1$ are isolated, and $\mathcal{W}^s(M_i)\cap \mathcal{W}_2 = \emptyset$ for $i = 0$ and $1$. Moreover, no subset of $\{M_0, M_1\}$ forms a cycle in $\partial \mathcal{W}_2$. By Smith and Zhao [53,Theorem 3], there exists a $\bar{\epsilon} > 0$ such that $\min\{\mathcal{P}_2(\phi)\} > \bar{\epsilon}$ for any $\phi\in\mathcal{W}_2$. Then as for Theorem 4.6, with $\varepsilon = \min\{\bar{\epsilon}, \frac {s}{d+\eta_1+\eta_2}\}$ finishes the proof.

As for the global stability of $P_2$, we make the following assumption to establish the global stability of $P_2$.

$\bf(A3)$ The nonlinear incidence functions $f(u, v)$ and $g(u, w)$ satisfy the following conditions.

${\rm (i)}$ For any $u > 0$,

${\rm (ii)}$ For any $u > 0$,

Theorem 4.12. Suppose that $R_1 > 1$ and Assumptions (A2) and (A3) are satisfied. Then the infected-immune steady state $P_2$ is globally asymptotically stable in

Proof. It follows from Lemma 2.2 and Theorem 4.11 that there exists an $\varepsilon > 0$ such that

unfiormly in $\overline{\Omega}$ and $\phi\in \mathcal{C}_2^+$. Without loss of generality, we define a Lyapunov functional

where

Calculate the time derivative of $I(x, t)$ along the solutions of (1.4) to get

With the following relations,

we get

Then

Similarly as in the proof of Theorem 4.7, we can show

Therefore, we have $\frac{\mathrm{d}I(t)}{\mathrm {d}t}\le 0$. Moreover, $\frac{\mathrm{d} I(t)}{\mathrm{d} t} = 0$ if and only if $u(x, t) = u_2$, $w(x, t) = w_2$, $v(x, t) = v_2$, $z(x, t) = z_2$. Then the largest invariant subset of $\frac{\mathrm{d} I(t)}{\mathrm{d} t} = 0$ is $\{P_2\}$. By LaSalle's Invariance Principle (see Theorem 5.3.1 in ^[50] or Theorem 3.4.7 in ^[51]), the infected-immune steady state $P_2$ is globally attractive in $\mathcal{C}_2^+$. This, together with Theorem 4.8, implies the global asymptotic stability of $P_2$ in $\mathcal{C}_2^+$.

5.   Numerical simulations

In this section, we perform some numerical simulations to illustrate the results obtained in section 4. Let $f(u, v) = \frac{\beta_1 uv}{1+\alpha_1v}$ and $g(u, w) = \frac{\beta_2 uw}{1+\alpha_2w}$. One can easily verify that $f$ and $g$ satisfy (A1)–(A3). Then the model (1.4) becomes

subject to the homogeneous Neumann boundary conditions

For (5.1), the basic reproduction number of infection is given by

and the basic reproduction number of immunity is given by

where

For simulations, we take $\alpha_1 = 0.01, \ \alpha_2 = 0.01$, $D_1 = 0.0017$, $D_2 = 0.0001$, and the values of the other parameters are summarized in Table 1. Moreover, $\Omega = [0, 4]$ and the initial condition used is

for $x\in[0, 4]$ and $\theta\in[-0.5, 0]$.

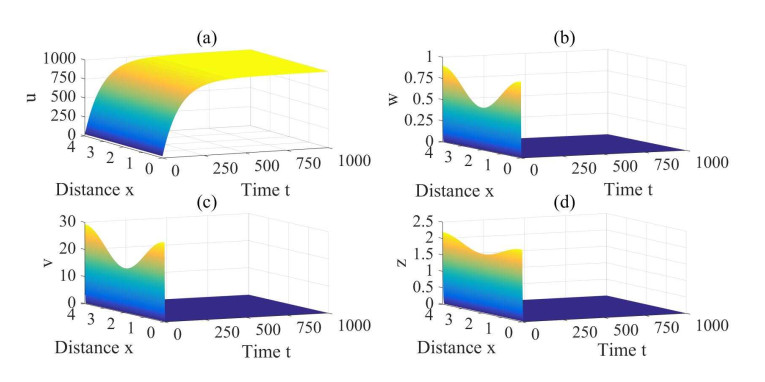
Firstly, we take $\beta_1 = 1\times10^{-5}$. Then $R_0 = 0.8715 < 1$. By Theorem 4.2, the infection-free steady state $P_0 = (1000, 0, 0, 0)$ is globally asymptotically stable (see Figure 1).

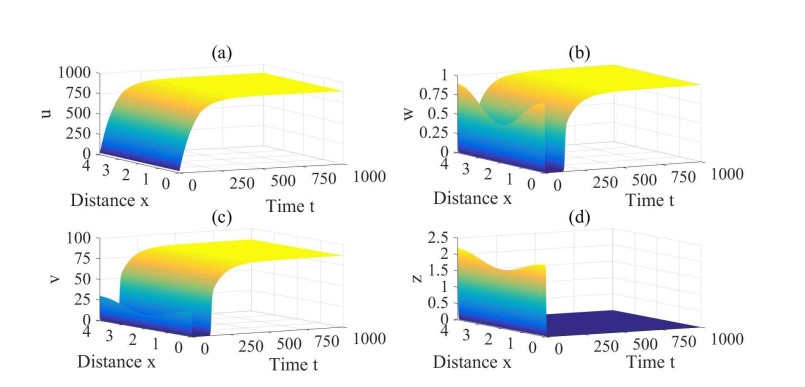
Next, we choose $\beta_1 = 2.4\times10^{-5}$. Then $R_0 = 2.0588 > 1$ and $R_1 = 0.2989 < 1$. From Theorem 4.7, the immunity-free infected steady state $P_1 = (897.8483, 0.9963, 86.6344, 0)$ is globally asymptotically stable (see Figure 2).

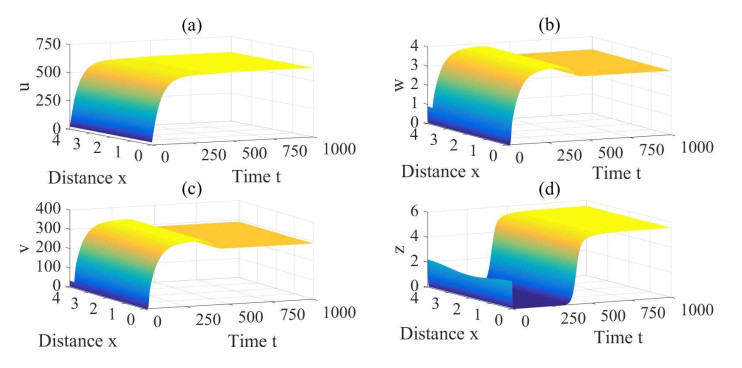
Finally, with $\beta_1 = 8.4\times10^{-5}$, we get $R_0 = 7.1474 > 1$ and $R_1 = 1.1594 > 1$. By Theorem 4.12, the infected-immune steady state $P_2 = (609.8631, 3.3333,289.8550, 5.8964)$ is globally asymptotically stable (see Figure 3).

6.   Conclusions

In this paper, we have proposed and studied a reaction-diffusion virus infection model by incorporating time delays, general incidence functions, and cell-to-cell transmission.

We have proved that the global dynamics of system (1.4)–(1.6) is determined by the basic reproduction number of infection $R_0$ and the basic reproduction number of immunity $R_1$. By analyzing the characteristic equations and constructing Lyapunov functionals, we have obtained the following conclusions: if $R_0 < 1$, then the infected-free steady state $P_0$ is globally asymptotically stable; if $R_1\leq1 < R_0$, then the immunity-free infected steady state $P_1$ is globally asymptotically stable under additional Assumption (A2); if $R_1 > 1$, then the infected-immune steady state $P_2$ is globally asymptotically stable under additional Assumptions (A2) and (A3). We mention that most commonly used incidences satisfy (A1)–(A3). Some examples are the Holling type Ⅱ incidence $f(u, v) = \frac{\beta u v}{1+\alpha v}$ ^[40], Beddington-DeAnglis incidence ^[41], and $f(u, v) = ku\ln(1+\frac{\beta v}{k})$ ^[56].

Acknowledgements

Chen is supported by NSERC of Canada. Wang is supported by the NSFC (No. 11771374), the Nanhu Scholars Program for Young Scholars of Xinyang Normal University.

Conflict of interests

The authors declare that there is no conflict of interest.