Dynamics analysis of Mackey-Glass model with two variable delays

1.   Introduction

The complex characterization of delay dynamic model has been the hot topic in diverse applications of physics, mathematical biology, economic finance and networks systems, etc. ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14]}. As early as 1977, for the sake of investigating the regulation and control mechanisms of human diseases, Mackey and Glass ^[15] put forward the following famous delay differential equation:

to describe hematopoiesis with a single-humped production rate, which is now called as Mackey-Glass model. Biologically, $P(t)$ is the density of mature circulating cells, $n > 0$, $\gamma, \beta_0, \theta$ are positive constants and denote the destruction rate, maximal production rate, shape parameter respectively, $\tau$ represents the time delay from immature to mature cells produced by bone marrow in the circulations. The simple mathematical model of physiological system (1.1) can reproduce certain qualitative features of normal and abnormal respiration, and the existence of positive solutions, bifurcation, permanence, boundedness, oscillation, and local stability of such equation and similar models have greatly attracted the attention of both theoretical and empirical communities (for example ^{[16,17,18,19,20,21]}).

In order to analyze the effects of maturity time and incubation time on system dynamics, system (1.1) was generalized to the following nonautonomous delay differential equation form ^[20]

in which $g(t)$ represents the developmental or maturation time, $h(t)$ represents the incubation time. It should be assumed that $\beta, g, \ h:[ t_{0}, \ +\infty)\rightarrow (0, \ +\infty)$ are continuous functions with

and

where

Just as shown in ^[20], the introduction of two different time delays ($g(t)$ and $h(t)$) in the model shows more complex dynamic behavior than the previous single delay ($\tau$). For instance, practical examples with two delays instead of single delay can produce sustained oscillations or even chaotic phenomenon ^{[22,23,24,25,26,27,28,29]}. Dynamics on the famous Mackey-Glass model have not been further explored yet in two variable delays case, which was first proposed by Berezansky and Braverman as open problems ^[20]. In fact, when two delays occur in system (1.2), the delayed feedback function can only be treated as a binary function, which brings many essential research difficulties. Up to now, the investigation on the global stability of the model (1.2) is still a challenging open problem, and the research results are very rare, we only find ^[20] in the existing work, however, the authors of ^[20] assume that $a > 1$ and put some additional technical conditions on the delay terms. More precisely, one of the main results of ^[20] is established as follows.

Theorem 1.1 (see Theorem 2.1 in ^[20]) Suppose that $a > 1$, $\int^{\infty}_{0} \beta(t)dt = +\infty$, and $x(t)$ is a positive global solution of system (1.2). Then system (1.2) has the unique positive equilibrium $N^{*} = (a-1)^{\frac{1}{\nu}}$. Moreover,

(ⅰ) $x(t) > N^{*}, t\geq t_{0}$, implies $N^{*} = \liminf\limits_{t\rightarrow\infty}x(t)$;

(ⅱ) $x(t)\in(0, N^{*}), t\geq t_{0}$ yields that $N^{*} = \limsup\limits_{t\rightarrow\infty}x(t)$.

Now, a natural question is: whether the non-oscillatory solutions mentioned in Theorem 1.1 converge to $N^{*}$. Sparked by the above reason and discussion, we try to give a satisfying answer and establish the global asymptotical stability of the Mackey-Glass model (1.2) with two different delays $h \not\equiv g$, $a > 1$ or $0 < a\leq 1$.

The rest of the proposed work is furnished as follows: In section 2, some necessary symbols and preliminary results are introduced. Two delay-independent criteria based on the fluctuation lemma and techniques of differential inequality are established in section 3. One numerical example and its computer simulations are provided to illustrate the effectiveness of the acquired results in section 4. At last, section 5 contains conclusions.

2.   Preliminary results

Before stating our results, we present some symbols. Let $C = C([-\tau, \ 0], \mathbb{R})$ be the Banach space of the set of all continuous functions from $[-\tau, \ 0]$ to $\mathbb{R}$ equipped with the supremun norm $||\cdot||$ and $C_{+} = \{\varphi\in C|$ $\varphi(\theta)\ge 0$ for $\theta\in [-\tau, \ 0]\}$. Define $x_t\in C$ by $x_t(\theta) = x(t+\theta)$ for $\theta\in [-\tau, \ 0]$, where $x$ is a continuous function defined on $[ -\tau, \ \sigma)$ with $0\leq t < \sigma$. The initial condition with respect to system (1.2) is as below

Lemma 2.1. For $\varphi\in C_+$, the solution of system (1.2) with respect to $\varphi$ can be denoted by $x(t; t_{0}, \varphi)$, then $x(t; t_{0}, \varphi)$ is nonnegative, unique and exists on $[t_{0}, \ +\infty)$. Moreover, for $\varphi\in C_+ \ \mbox{and} \ \varphi(0) > 0$, $x(t; t_{0}, \varphi) > 0$ for all $t\in [t_{0}, \ +\infty)$.

Proof. By using the method of step by step, one can show that $x(t) = x(t; t_{0}, \varphi)$ is unique and exists on $[t_{0}, \ +\infty)$. As $\varphi\in C_+$, according to systems (1.2) and (1.4), we obtain

By the method of steps, we have $x(t)\geq0$ on $[t_{0}+r, \ t_{0}+2r], [t_{0}+2r, \ t_{0}+3r]\cdots, [t_{0}+nr, \ t_{0}+(n+1)r], \cdots$. Thus, $x(t)\geq 0$ for all $t\geq t_{0}$.

Moreover, if $\varphi\in C_+ \ \mbox{and} \ \varphi(0) > 0$, then

for all $t\in[t_{0}, \ +\infty)$. This ends the proof.

Lemma 2.2. Let $0 < a\leq 1$ and $x(t) = x(t; t_{0}, \varphi)$, if $\varphi\in C_+$, then for all $t\in [t_{0}, \ +\infty)$, we have $x(t)\leq \|\varphi\|$.

Proof. For $\varphi\in C_+$, we state that $x(t) = x(t; \varphi)\leq \|\varphi\|$ for all $t\in[t_{0}, \ t_{0}+r]$. Otherwise, there is $t_{1}\in(t_{0}, \ t_{0}+r]$ obeying

Furthermore, systems (1.2) and (2.2) lead to

This is a clear contradiction and reveals the above statement. Then, $x (t)\leq \|\varphi\|$ holds on $[t_{0}, \ +\infty)$ by induction. The proof of Lemma 2.2 is now completed.

Remark 2.1. Suppose that $0 < a\leq 1$ is satisfied. For any $\epsilon > 0$, we can choose $\widetilde{\delta}\in [0, \ \epsilon)$. Then, for any $\varphi\in C_+ \mbox{ with } \ \|\varphi\| < \widetilde{\delta}$, from Lemma 2.2, we can show that

This suggests that $0$ is locally stable for Eq (1.2) with $0 < a\leq 1$.

3.   Main results

First, we establish two delay-independent criteria to show the attractivity of all non-oscillating solutions about the positive equilibrium point.

Theorem 3.1. Let $a > 1$, $x(t) = x(t; t_{0}, \varphi)$ with $\varphi\in C_+ \ \mbox{and} \ \varphi(0) > 0$, and there exists $T_{1} > t_{0}$ such that $x (t)\leq N^{*} \ \mbox{for all} \ t\geq T_{1}$. Then $\lim\limits_{t\rightarrow +\infty}x (t) = N^{*}$.

Proof. From Lemma 2.1, it is obvious that $0 < x (t)\leq N^{*} \ \mbox{for all} \ t\geq T_{1}+\tau.$ We claim that $l: = \liminf\limits_{t\rightarrow +\infty} x (t) > 0$. Otherwise, by the definition of $l$, we have $l = 0$. For each $t\geq T_{1}+\tau$, we define

It follows from $l = 0$ that $\lim\limits_{t\to+\infty}m(t) = +\infty, \ \ \lim\limits_{t\to+\infty}x (m(t)) = 0,$ and

which, together with (1.2), implies that

This is a contradiction and suggests that $l > 0$.

By the fluctuation lemma (see Lemma A.1 in ^[30]), one can pick a sequence $\{t_k \} _{k\geq 1}$ agreeing with

From the boundedness on $\beta(\cdot)$, we can select a subsequence of $\{\beta(t_k)\}_{k\geq 1}$, still denoted by $\{\beta(t_k)\}_{k\geq 1}$, such that $\lim\limits_{k\to+\infty}\beta(t_k)$ exists and $\lim\limits_{k\to+\infty}\beta(t_k)\geq \beta^{-} > 0$. This follows that

and then $\limsup\limits_{k\to+\infty}x(t_k-g (t_k)) = N^{*}$, which, implies that $\limsup\limits_{t\to+\infty} x (t) = N^{*}$ since $\limsup\limits_{t\to+\infty} x (t)\leq N^{*}$.

For any $\varepsilon\in(0, \ \liminf\limits_{t\to+\infty} x (t)),$ we select $\widetilde{T} > T_{1}+2\tau$, such that for all $t\geq \widetilde{T}$, we have

Consequently, for all$\ t\geq \widetilde{T}+\tau$, one have

Take $k_{0} > 0$ satisfying $k_{0}\tau_{1}\geq \widetilde{T}+\tau$ for all $k\geq k_{0}$. Given a positive integer $k\geq k_{0}$, we denote

Now, we state that $\{x(s_{k})\}_{k\geq k_{0}}$ is nondecreasing. Suppose the contrary and choose a positive integer $n_{0}\geq k_{0}$ with $x(s_{n_{0}}) > x(s_{n_{0}+1}).$ Then, $s_{n_{0}+1}\in ((n_{0}+1)\tau_{1}, (n_{0}+2)\tau_{1}]$, and there is $s^{*} = \inf\{\omega\in ((n_{0}+1)\tau_{1}, (n_{0}+2)\tau_{1}]:x(\omega) = x(s_{n_{0}+1}) \}$ agreeing with

Subsequently, system (1.2) gives us that

is a contradiction. This validates the above statement, which implies that

Take a subsequence $\{ k_{j} \}_{ j \geq1}$ of $\{k\}_{k\geq k_{0}}$ such that

With the aid of the boundedness of $\{ \int_{s_{k +1}}^{S_{k }} \beta(v)dv \}_{k\geq k_{0}}$, we can select its subsequence, still labeled by $\{ \int_{s_{k +1}}^{S_{k }} \beta(v)dv \}_{k\geq k_{0}}$, such that $\lim\limits_{j\to+\infty}\int_{s_{k_{j}+1}}^{S_{k_{j}}} \beta(v)dv$ exists and

With the help of an integration of system (3.1) on $[S_{k_{j}}, \ s_{k_{j}+1}]$, we see that

and

According to Eqs (3.3)–(3.5) and inequality (3.6), setting $j\rightarrow +\infty$ produces

It follows from the arbitrariness of $\varepsilon$ that $\liminf\limits_{t\to+\infty} x (t) = N^{*}$, and proves Theorem 3.1.

Theorem 3.2. Let $a > 1$, $x(t) = x(t; t_{0}, \varphi)$ with $\varphi\in C_+$, and there exists $T_{2} > t_{0}$ such that $x(t)\geq N^{*} \ \mbox{for all} \ t\geq T_{2}.$ Then $\lim\limits_{t\rightarrow +\infty}x (t) = N^{*}.$

Proof. We state that $\limsup\limits_{t\rightarrow +\infty} x (t) < +\infty.$ Otherwise, $\limsup\limits_{t\rightarrow +\infty} x (t) = +\infty.$ For each $t\geq T_{2}+\tau$, we label

It follows from $\limsup\limits_{t\rightarrow +\infty} x (t) = +\infty$ that $\lim\limits_{t\to+\infty}\widetilde{M}(t) = +\infty$, $\lim\limits_{t\to+\infty}x (\widetilde{M}(t)) = +\infty,$ and

According to the definition of $\widetilde{M}(t)$, we know that

This is a contradiction and suggests that $\limsup\limits_{t\rightarrow +\infty} x (t) < +\infty$. Using the fluctuation lemma (see Lemma A.1 in ^[30]), and considering the boundedness of $\beta(t)$, one can find a sequence $\{t_{k}^{*} \} _{k\geq 1}$ obeying that

and $\lim\limits_{k\to+\infty}\beta(t_{k}^{*})\geq \beta^{-} > 0$. This entails that

and then $\liminf\limits_{k\to+\infty}x(t_{k}^{*}-g(t_{k}^{*})) = N^{*}.$ This and the fact that $\liminf\limits_{t\to+\infty} x (t)\geq N^{*}$ produce $\liminf\limits_{t\to+\infty} x (t) = N^{*}.$

For any $\varepsilon > 0,$ one can pick $\widetilde{T}_{1} > T_{2}$ agreeing with

Furthermore, for all $t\geq \widetilde{T}_{1}+\tau$, we gain

Set $k_{0}^{*} > 0$ with $k_{0}^{*}\tau_{1}\geq \widetilde{T}_{1}+\tau$ for all $k\geq k_{0}^{*}$. Given a positive integer $k$ obeying $k\geq k_{0}^{*}$, we denote

where $\ s_{k}^{*}, \ S_{k}^{*}\in[k\tau_{1}, (k+1)\tau_{1}]$. Hereafter, we assert that $\{x(S_{k}^{*})\}_{k\geq k_{0}^{*}}$ is non-increasing. Suppose that, on the contrary, there is a positive integer $n_{0}^{*}\geq k_{0}^{*}$ obeying $x(S_{n_{0}^{*}}^{*}) < x(S_{n_{0}^{*}+1}^{*}).$ Then, $S_{n_{0}^{*}+1}\in ((n_{0}^{*}+1)\tau_{1}, (n_{0}^{*}+2)\tau_{1}]$, and we can find $S^{* } = \inf\{\omega\in ((n_{0}^{*}+1)\tau_{1}, (n_{0}^{*}+2)\tau_{1}]:x(\omega) = x(S_{n_{0}^{*}+1}^{*}) \}$ agreeing with

It follows from system (1.2) that

which is a contradiction. This furnishes the above assertion and results that

Now, from the definition of $\{s_{k }^{*} \}_{k\geq k_{0}^{*}}$ and the boundedness of $\{\int_{S_{k +1}^{*}}^{s_{k }^{*}} \beta(v)dv \}_{k\geq k_{0}^{*}}$, we can pick a subsequence $\{ k_{j} \}_{ j \geq1}$ of $\{k\}_{k\geq k_{0}^{*}}$ such that

and

Computing the integration of (3.7) on $[s_{k_{j}} ^{*}, \ S_{k_{j}+1}^{*}]$ yields

and

In view of (3.9), (3.10), (3.11) and (3.12), we gain

which produces that $\limsup\limits_{t\to+\infty} x (t) = N^{*}$ and reveals Theorem 3.2.

Next, we establish the global asymptotical stability on the zero equilibrium point. More precisely,

Theorem 3.3. If $0 < a\leq 1$, then for system (1.2), the trivial solution $0$ is globally asymptotically stable with respect to $C_+$.

Proof. From Lemma 2.2 and Remark 2.1, it is obvious that $x(t) = x(t; t_{0}, \varphi)$ with $\varphi\in C_+$ is bounded, and $0$ is a local stable. In order to prove Theorem 3.3, it is sufficient to show that $\limsup\limits_{t\rightarrow +\infty} x(t) = 0$. Suppose the contrary and let

Using the fluctuation lemma (see Lemma A.1 in ^[30]), and considering the boundedness of $\beta(t)$, one can find a sequence $\{T_{k}^{*}\} _{k\geq 1}$ with

and $\lim\limits_{k\to+\infty}\beta(T_{k}^{*})\geq \beta^{-} > 0$. This leads to

and then

Given $\varepsilon > 0,$ we can take $\widehat{T} > t_{0}+\tau$ agreeing with

Then, $0 < a\leq 1$ produces

Choose $k_{0}^{**} > 0$ satisfying $k_{0}^{*}\tau_{1}\geq \widehat{T}+\tau$ for all $k\geq k_{0}^{**}$, for $k\geq k_{0}^{**}$, we denote

where $\ q_{k}, \ Q_{k} \in[k\tau_{1}, (k+1)\tau_{1}]$. Furthermore, we state that $\{x(Q_{k})\}_{k\geq k_{0}^{*}}$ is non-increasing. If the statement is not true, then we can choose a positive integer $n_{0}^{**}\geq k_{0}^{**}$, such that $x(Q_{n_{0}^{**}}) < x(Q_{n_{0}^{**}+1})$. Consequently, we get $Q_{n_{0}^{**}+1}\in ((n_{0}^{**}+1)\tau_{1}, (n_{0}^{**}+2)\tau_{1}]$, and there exists $Q^{* } = \inf\{\omega\in((n_{0}^{**}+1)\tau_{1}, (n_{0}^{**}+2)\tau_{1}]:x(Q_{n_{0}^{**}+1}) = x(\omega)\}$ satisfying

However, system (1.2) entails that

which is a contradiction. This results the above statement and implies that

Now, making use of the definition of $\{q_{k } \}_{k\geq k_{0}^{**}}$ and by employing the boundedness of $\{e^{\int_{Q_{k +1} }^{q_{k } } \beta(v)dv}\}_{k\geq k_{0}^{**}}$, it is easy to see that there is a subsequence $\{ k_{j} \}_{ j \geq1}$ of $\{k\}_{k\geq k_{0}^{**}}$ such that

From inequality (3.14), we obtain

and

With the aid of Eqs (3.16) and (3.17) and inequality (3.18), setting $j\rightarrow +\infty$ yields

which entails that $\limsup\limits_{t\to+\infty} x (t) = L = 0$. This contradicts Eq (3.13) and proves Theorem 3.3.

Remark 3.1. Clearly, under assumption (1.4), all results in Theorem 1.1 are special ones of Theorems 3.1 and 3.2 in this present paper. In particular, we can show that the two different time-varying delays $h(t)$ and $g(t)$ do not yield the effect on the asymptotic behavior on the non-oscillating solutions about the positive equilibrium point of Mackey-Glass equation. Also, Theorem 3.3 implies that, for $0 < a\leq 1$, the global stability of non-autonomous Mackey-Glass equation is independent of the two different time-varying delays $h(t)$ and $g(t)$.

4.   Numerical examples

In this section, we present two examples with graphical illustration to show the theoretical findings in this paper. Consider the following delay Mackey-Glass equations:

and

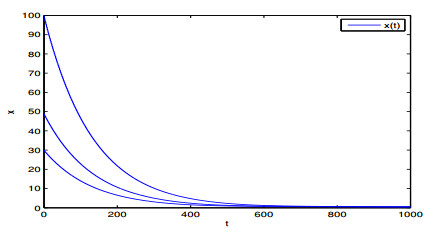
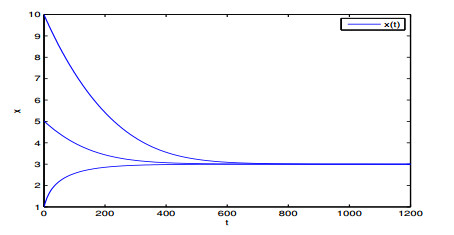
From Theorems 3.1 and 3.2, one can see that all non-oscillating solutions about the positive equilibrium point $N^{*} = 3$ of Eq (4.1) are convergent to $N^{*}$. Moreover, Theorem 3.3 suggests that Eq (4.2) is globally asymptotically stable. Computer simulations of the two numerical examples are arranged in Figures 1 and 2 to illustrate the correctness and effectiveness of the presented convergence results.

Remark 4.1. We should point out that the delay-independent criteria for the asymptotic behavior of the non-autonomous Mackey-Glass equation with two different delays have not been established in the previous literature. Most recently, the authors in ^[31] used the classical approach of "decomposing + embedding" to investigate the global attraction for the autonomous equation

in the case that $\beta, \sigma, \tau \in [0, \ +\infty)$ are constants and $\sigma\leq \tau$. On the other hand, I. Győri, et al. ^[32] studied the permanence of the below system

Obviously, all results in ^{[17,18,19,20,31,32,33,34]} cannot be applicable to show convergence of the solutions of Eqs (4.1) and (4.2).

5.   Conclusions

In this paper, we mainly investigate the attractivity and the global asymptotical stability for a class of non-autonomous Mackey-Glass model with two variable delays. Firstly, in the case of a unique positive equilibrium point, we prove that two different variable delays appearing in Mackey-Glass equation do not yield the effect on the asymptotic behavior of the non-oscillating solutions about the positive equilibrium point. Then two delay-independent criteria based on the fluctuation lemma and techniques of differential inequality are established. The obtained results improve and complement some published results, and partly answer the open problem proposed by Berezansky and Braverman ^[20]. By the way, the approach proposed in this article furnishes a possible method for studying the asymptotic behavior on the other population dynamic models involving the different reproductive function delays.

Acknowledgements

The author would like to express the sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper. This work was supported by the National Natural Science Foundation of China (No. 11971076), Research Promotion Program of Changsha University of Science and Technology (No. 2019QJCZ050).

Conflict of interest

The author confirms that he has no conflict of interest.