Numerical study of discretization algorithms for stable estimation of disease parameters and epidemic forecasting

1.   Introduction

Stable estimation of system parameters for infectious disease outbreaks is of paramount importance to the design of adequate forecasting algorithms ^[1,2,3]. Oftentimes parameter estimation procedures are cast as ODE-constrained nonlinear least squares problems, where infinite dimensional time dependent disease parameters need to be recovered from finite dimensional data sets. As the result, the Jacobian of the corresponding parameter-to-data operator is generally ill-conditioned and may be numerically singular. When such an operator is fitted to noise-contaminated epidemiological data, the estimated parameters tend to be entirely unreliable due to severe error propagation into the approximate solution. The sources of noise in the reported incidence data vary for different types of diseases and can be attributed to possible under or over reporting owing to, for instance, a large proportion of asymptomatic cases or false diagnostics.

Noisy data coupled with modeling, discretization, and computational errors necessitate the use of special mathematical tools known as regularization ^[4,5]. It amounts to solving some "nearby" auxiliary problem in place of the initial one. The auxiliary problem has to be formulated in such a way that its solution is less sensitive to noise propagation as opposed to the solution of the original problem.

A time dependent transmission rate of an infectious disease is an important parameter, which can be defined as the effective contact rate, that is, the probability of infection given contact between an infectious and susceptible individual multiplied by the average rate of contacts between these groups. Generally the transmission rate cannot be pre-estimated since it depends on multiple environmental, genetic, social, and other factors. Hence one has to recover cause form effect using epidemiological data for an emerging outbreak together with a suitable compartmental model governing the disease. Once recovered and extrapolated, the transmission rate can be used to project future incidence cases. That, in turn, may be helpful in the design of effective control measures and optimal resource allocation.

In what follows, we use Matlab built-in implementation of the Levenberg-Marquardt algorithm ^[6,7] to reconstruct a variable transmission rate. The regularization provided by this optimization scheme, which is a penalized version of the Gauss-Newton procedure ^[8], is enforced by the appropriate problem-oriented discretization tools. Specifically, we compare what we call parametric and non-parametric discretization routines. By parametric discretization we mean that the transmission rate is modeled by a pre-defined function that involves only a few parameters. The rationale behind this approach is simple: if one is given some a priori information about the outbreak, one can reasonably choose an appropriate expression to describe changes in the transmission coefficient. For example, in case of a single cycle outbreak with the incorporation of control measures at the beginning stages, it is reasonable to assume a declining transmission rate defined, say, by a hyperbolic, harmonic, or exponential function. While parametric discretization may not capture all aspects of the actual transmission rate, it may capture enough crucial information to provide a useful forecasting tool. Our main expectation is that recovering fewer parameters helps mitigate instability caused by noise and the lack of data without, we hope, a significant loss in accuracy.

At the same time, even for a single-cycle outbreak, the transmission rate of an infectious disease may vary depending on the type of a disease, population group, characteristics of a region, and the efficiency of control measures. So, realistically we cannot expect transmission rates to always exhibit a simple decline pattern and therefore parametric discretization inevitably leads to a loss of information. In order to better capture the shape of the time dependent transmission rate, one has to use non-parametric discretization schemes. In such schemes, the transmission rate is projected onto a subspace spanned by a finite set of orthogonal polynomials or spline functions. Again, depending on the nature of the transmission, one may use Legendre or Chebyshev polynomials, B-splines, wavelets, or other base functions.

The main goal of our numerical study is to see how parametric and non-parametric discretization schemes compare in terms of accuracy of parameter estimation and in terms of their ability to provide a reliable forecasting tool. The paper is organized as follows. In Section 2, the governing SEIR model and the regularized inversion procedure are outlined, followed by the discussion of parametric and non-parametric discretization algorithms. In Section 3, numerical experiments with synthetic data are presented. Simulation results with real data for the 1918 influenza outbreak in San Francisco are given in Section 4. Future plans are summarized in Section 5.

2.   Problem formulation and mathematical preliminaries

Consider a well-mixed population of size $N$, where individuals have the same probability of being in contact with each other. The population is sorted into four classes: susceptible ($S$), exposed ($E$), infectious ($I$) and removed ($R$) ^[9] as shown in Figure 2.

It is assumed that susceptible humans (category $S$) infected with a virus enter the latent period (category $E$) at the rate $\beta(t) I(t)/N$, where $\beta(t)$ is the mean transmission rate per day (week). Latent humans progress to the infectious class (category $I$) at the rate $\kappa$ ($1/\kappa$ is the mean latent period). Infected individuals are assumed to recover and acquire protective immunity for the duration of the entire epidemic period at rate $\gamma$, where $1/\gamma$ is the average time from symptoms onset to recovery. Recovered humans move back to the susceptible class at the rate $\sigma$ ($1/\sigma$ is the duration of immunity). For simplicity, we let the host birth and death rates have the same value, which means that the total population size remains constant for the duration of the outbreak. The overall transmission dynamics can be mathematically described by the following set of nonlinear differential equations for $t\in [a, b]$

with initial conditions

and the system parameters listed in Table 1 below.

In our numerical experiments all parameters of the model, except for the transmission rate $\beta(t)$, are pre-estimated for each particular disease, while $\beta(t)$ is fitted to the incidence data given by the following expression:

where $C(t)$ and $\frac{dC}{dt}$ are the cumulative and incidence data, respectively. A primary limitation of (2.1)-(2.5) is that we assume a completely susceptible population at the beginning of the epidemic, and let the transmission rate capture the baseline susceptibilty of the population. A more detailed model could also account for age-specific transmission rates because for diseases like measles, for example, there are significant differences in transmission rates between children and adults. Our goal is to recover $\beta(t)$ by solving a nonlinear ODE-constrained least-squares minimization problem with limited data for an emerging outbreak and then to forecast future disease incidence cases. Given finite incident data at each point in time, $D = [D_1, D_2, ..., D_m]$, the reconstruction of $\beta(t)$ can be formulated as follows:

Here $u$ stands for $[S, E, I, R]$, $p$ denotes the unknown parameter vector, and the operator equation $F(p, u) = 0$ is given by (2.1)-(2.5).

Let $u = u(p)$ be a (numerical) solution to the SEIR system (2.1)-(2.5). Introduce a parameter-to-observation map

One then obtains the unconstrained least squares problem:

where $m$ is the number of data points and $n$ the number of unknowns for each particular discretization algorithm. The least squares problem is solved with the Levenberg-Marquardt numerical optimization procedure (Matlab's built in implementation), where $\psi'(p_k)$ is the Frećhet derivative of the nonlinear operator $\psi$ evaluated at the point $p_k$, $\psi'^*(p_k)$ is the adjoint of $\psi'(p_k)$, and $\mathcal{I}$ is the identity operator,

At each step of the iterative process, the ODE system is solved with Matlab's ode23s stiff solver.

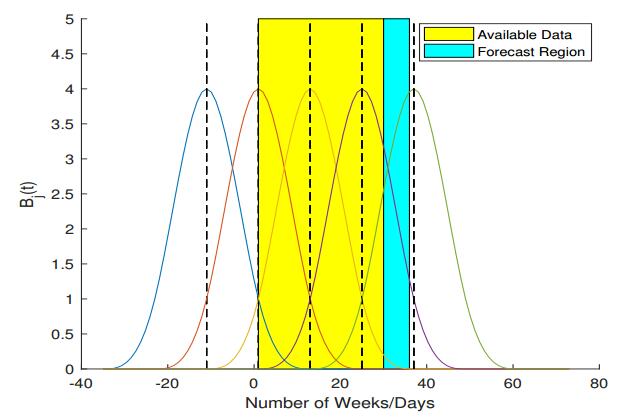
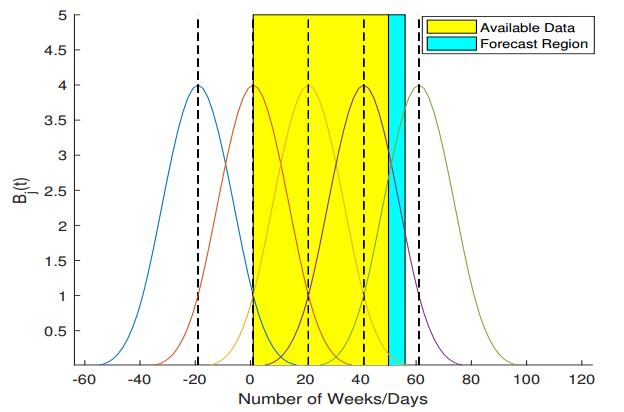
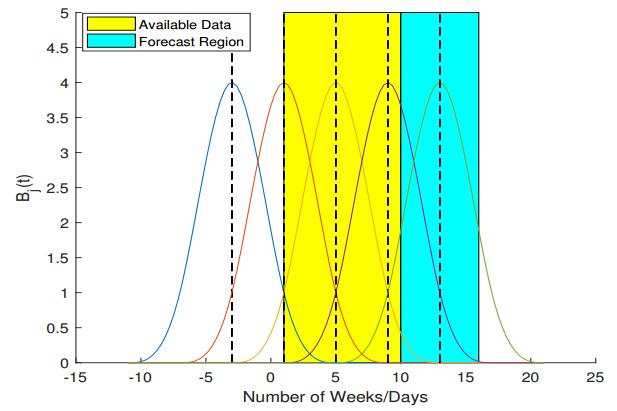
Let $[a, b]$ and $(b, b+c]$ be the regions where the incident cases are given and where they are forecasted, respectively. In case of a nonparametric discretization, $\beta(t)$ is projected onto the finite dimensional space spanned by a set of base functions

Here $B(t)$ is the cubic B-spline ^[10,8], $h = t_j-t_{j-1}$, $j = 0, 1, ..., l+1$, and the vertices of the splines are located at the grid points

for some $T > a$ such that $T+3h\ge b+c$. Thus the base functions, $B_j(t)$, are defined on the overlapping subintervals, whose union covers the entire region, $[a, b+c]$, as illustrated in Figures 1, 3, and 4. The domains for B-splines are selected in such a way that they all intersect with the interval $[a, b]$, and at least some of the domains also intersect with $(b, b+c]$. Once the least squares problem is solved on $[a, b]$ for the set of unknown expansion parameters, $A_j$, $j = 1, ..., n,$ $n = l+3$, one approximates the transmission rate, $\beta(t)$, as a linear combination,

and extrapolates it to the interval $[a, b+c]$ in order to solve the forward problem and to obtain the forecasting incidence values.

For a parametric discretization approach, the transmission rate is modeled as a predefined function with few parameters to enforce stability. We choose a four parametric hyperbolic decline with initial transmission rate $\beta_0$, decline rate $q$, curvature degree $\nu$, and a chosen asymptotic value of the transmission rate $\phi$:

where $\beta_0 > 0$, $0\leq q \leq 1$, $0\leq \nu \leq 1$, and $\phi \geq0$. This monotonically decreasing transmission rate is assumed based on a priori information that appropriate intervention and control measures have been introduced at the early stages of the outbreak, and they continue to remain effective for the entire duration of the epidemic.

To compare the two discretization approaches, which also serve as an important regularization tool complementing the regularization introduced by the damping parameter in the Levenberg-Marquardt procedure, we start by considering numerical examples with synthetic data.

3.   Numerical experiments with synthetic data

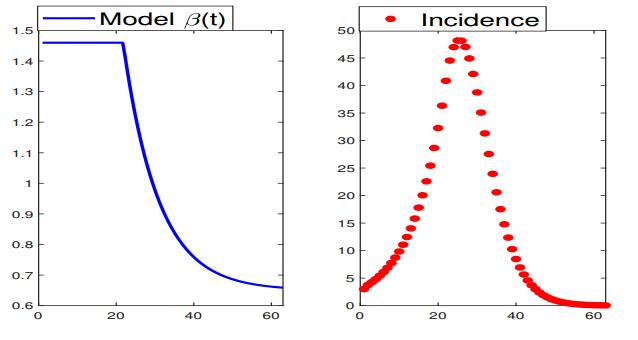
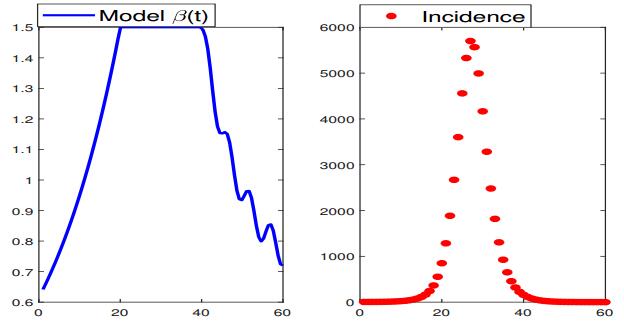
For our first experiment, we choose a model transmission rate in such a way that it could be approximated by a four parametric hyperbolic decline function (2.11) with a reasonable accuracy. To that end, we introduce the following piece-wise defined function

shown in the left picture of Figure 5. By solving the corresponding forward problem, i.e., the SEIR system with given $\beta(t)$ and given values of $\kappa$ and $\gamma$ presented in Table 2, we generate synthetic incidence data (the right picture in Figure 5).

To quantify uncertainty in the recovered transmission rate, $\beta(t)$, and in our estimates of future incidence cases, we use the bootstrapping strategy proposed in ^[11,12]. For the selected model function, $\beta_m(t)$, the corresponding incidence data is perturbed $10$ times by adding a simulated error structure with Poisson mean for the number of new case notifications between week $j-1$ and week $j$ being equal to the "true" incidence, $D_j$, $j = 2, ..., m$. As the result, a different noisy incidence curve is generated for each parameter estimation step, which enables us to use the mean value forecasts as our best estimates for the short-term projections of future incidence cases and the mean value of $\beta(t)$ as the most accurate approximation of the disease transmission rate.

To start the iterative process (2.10), we take initial guesses of $\beta(t)$ to be constants that are uniformly distributed in the interval $[0.5, 2]$, though in case of parametric discretization for some data sets this interval has to be slightly reduced. Since there would be no prior knowledge of the transmission rate in case of real epidemiological data, we randomly select $10$ initial values of $\beta_0$ for every partial noise contaminated incidence data set to avoid any bias towards any particular starting point and to confirm that there is a broad range of initial guesses for which convergence can be expected.

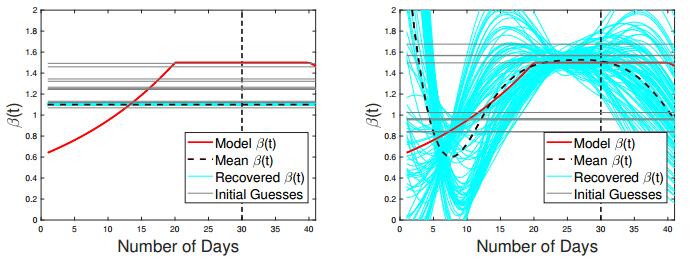
In case of non-parametric discretization the two regularization parameters, the initial damping factor, $\tau_0$, in (2.10) and the step size, $h$, for the base spline functions, are selected to provide the best possible fit for the "given" partial data set (close but without over-fitting) and to ensure the most agammaessive convergence rate for the Levenberg-Marquardt iterative scheme, which is terminated at $p$-tolerance and $\psi$-tolerance equal to $10^{-5}$ or when the maximum number of function evaluations is exhausted. In the course of our numerical simulations, we have tried multiple values of $h$ for B-spline discretization in order to analyze how it affects parameter estimation and forecasting. The values $h = 4$, $h = 12$, and $h = 20$ have emerged as near optimal for $10$, $30$, and $50$ data points, respectively. These choices of $h$ give the same size of the solution space for the above three data sets, see Figures 1, 3, and 4.

For parametric discretization, the size of the solution space is fixed, and one has no control as to how much regularization it provides. Thus the initial damping coefficient, $\tau_0$, in (2.10) is the only regularization parameter one can vary to balance accuracy and stability. For parametric and non-parametric discretization routines, we used $\tau_0$ between $10^{5}$ and $10^{13}$. The over-damping at the start of the iterative process promotes stability. As iterations progress, $\{\tau_k\}$ goes down, which guarantees convergence of $\{p_k\}$ as long as the stopping rule does not result in over-fitting.

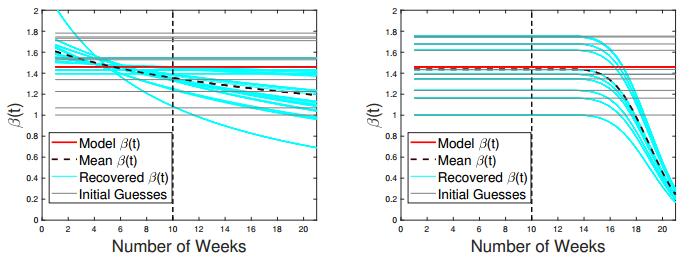
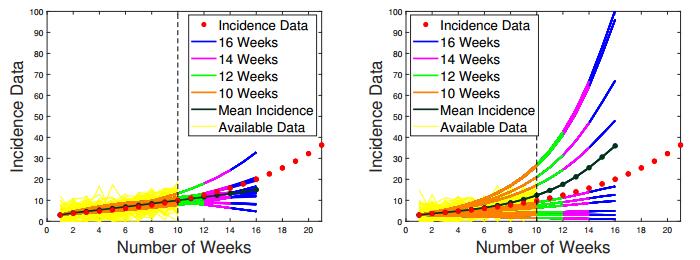
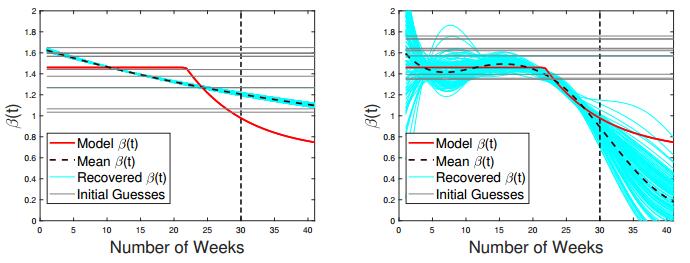
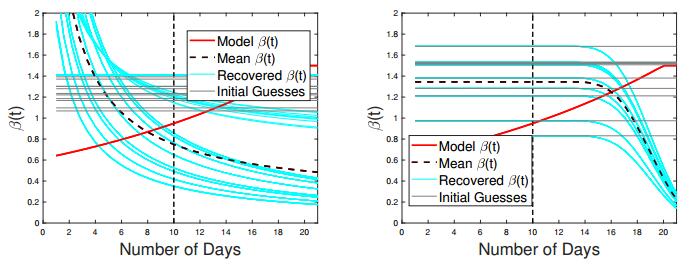
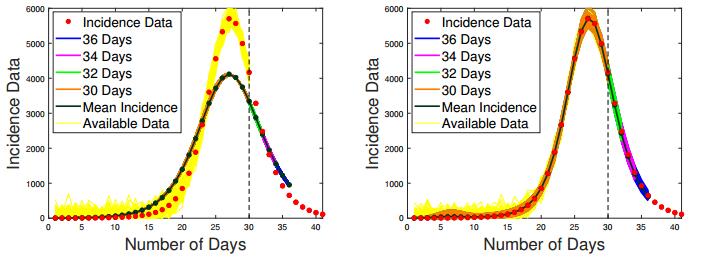
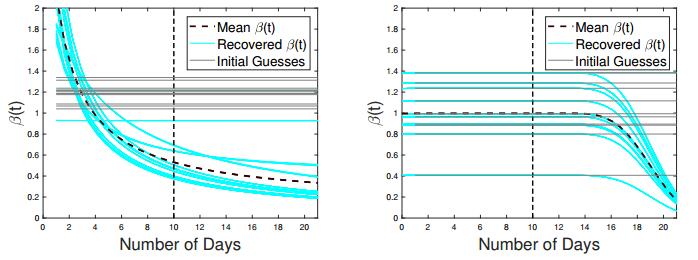
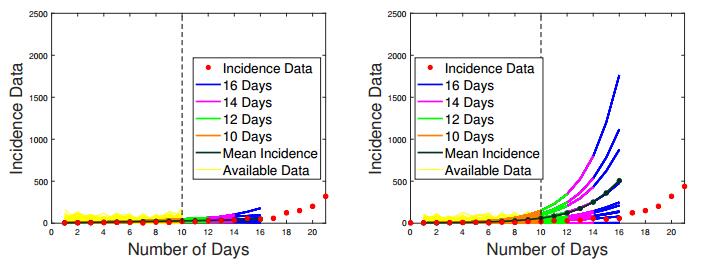
As one can see in Figures 6 and 7, for the highly unstable scenario when only $10$ weeks of data are available, parametric discretization provides the amount of regularization that is "just right". Despite of a drastic reduction in the size of the solution space, the reconstruction process does not seem to be over-regularized. It generates the forecasting bundle with the mean value that slightly under-estimates the actual incidence curve. All forecasts are close together, which points to the stability of the inversion algorithm. On the other hand, the non-parametric discretization, while much harder to implement due to the need to adjust two regularization parameters $\tau$ and $h$, generates less stable (and less accurate) results. Its mean value shows almost twice the actual number of cases at the end of week $16$. Individual forecasting curves for B-spline discretization deviate from the model data by quite a lot, some under-estimating and some considerably over-estimating the actual case count. This indicates that the reconstruction with B-spline functions is less stable as compared to parametric discretization for early stages of an emerging outbreak, when the transmission rate is constant and, therefore, close in its structure to a four-parametric hyperbolic function (2.11) in the interval $[a, b+c]$.

For $30$ weeks of data (half-way through the outbreak, Figures 8 and 9) forecasting with parametric discretization method is much less accurate. It over-estimates future incidence cases showing more than double the actual number at the end of week $36$. It cuts through the "real" incidence curve between weeks $19$ and $28$ showing the wrong inflection point around week $33$ for the cumulative data as illustrated in Figure 9. That happens because even though the reconstructed hyperbolic transmission rate (see Figure 8) is close to the model $\beta(t)$, it does not capture the steep exponential decline that begins at week $22$. The recovered $\beta(t)$ shows a much less agammaessive decent hence resulting in an over-estimate of future incidence cases. None of that happens when the transmission rate is approximated with B-spline functions. For a non-parametric discretization scheme, $\beta(t)$ is no longer tied to any particular shape and, though erratically, is capable of mimicking the actual model $\beta(t)$. As the result, the mean forecasting curve follows the model incidence data remarkably well, with only two (out of $100$) individual forecasting curves being slightly "off" and the rest of the curves being close together in the forecasting bundle. Thus, even though the B-spline discretization is less stable, for $30$ weeks of data it does a much better job forecasting future incidence cases and recovering the model transmission rate as compared to parametric discretization with hyperbolic function.

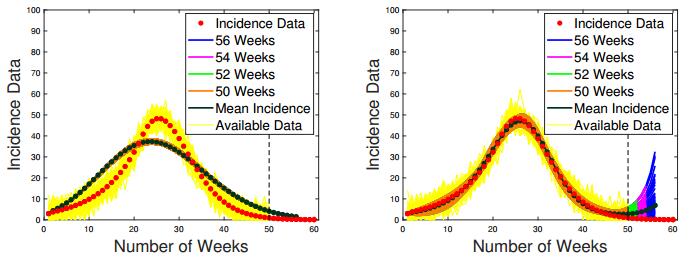
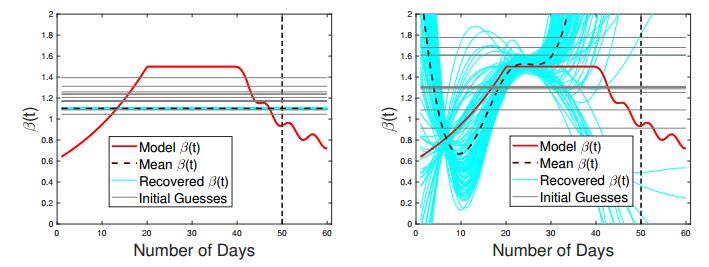
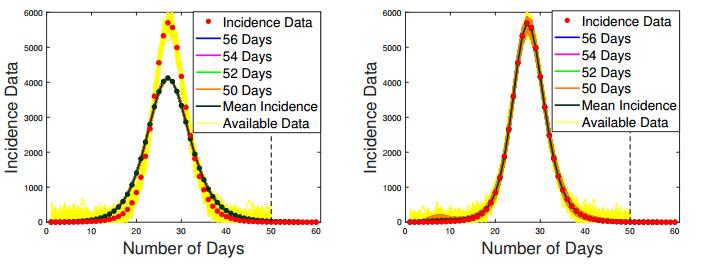
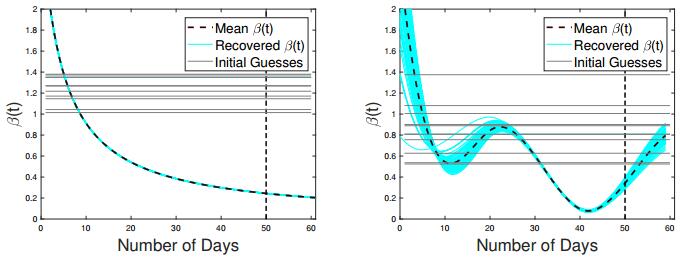
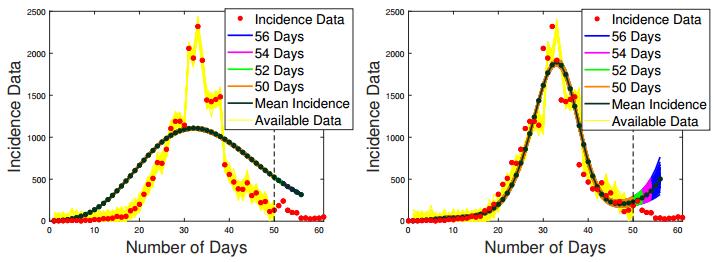
Finally, for $50$ weeks of data what we see in Figures 10 and 11 is essentially the reconstruction from full data set, since the outbreak practically comes to an end between weeks $50$ and $60$. While parametric method correctly shows the conclusion of the epidemic at this stage, the B-spline approximation erroneously hints at the beginning of a new cycle with the recovered $\beta(t)$ unexpectedly exhibiting an uphill behavior after $40$ weeks of the outbreak. Thus, due to instability and the lack of data between weeks $40$ and $50$, the B-spline discretization does not succeed in making accurate future projections. On the other hand, the parametric discretization, where hyperbolic decline is built-in, gives rise to more accurate forecasting curves.

There is also a major difference in how the true incidence data is followed for the first $50$ weeks by the incidence curves recovered with two competing discretization algorithms. The incidence curve recovered with B-splines is very accurate and follows the "real" data in a very stable manner. At the same time, the incidence curve recovered with hyperbolic parametrization once again cuts through the "real" data over-estimating the number of cases for the first $20$ weeks and from week $33$ on, while under-estimating between weeks $20$ and $33$ and shifting the cumulative turning point to the left. This is the exact consequence of the transmission rate being over-estimated in the beginning of the outbreak as well as in its second phase and under-estimated in the middle due to the special nature of the discretization method. For spline base functions the recovered transmission rate is accurate though, again, unstable. So, in fitting data that is available, the non-parametric discretization is the winner.

We now turn our attention to the second experiment with synthetic data. This time the model transmission rate takes the form that is entirely different from a hyperbolic decline as seen in Figure 12 and defined by equation (3.2). We set $\beta_m(t)$ to be exponentially increasing for the first $20$ weeks before it stabilizes at a constant level and then goes down with some minor oscillations after week $40$:

It is worth mentioning that the corresponding incidence data has very similar shape as compared to the first example, but it picks at almost $6,000$ as opposed to $49$ in case of the previous model. Thus, the shape of the incidence curve is not always indicative of the behavior of the disease transmission rate, and any a priori assumption regarding the nature of $\beta(t)$ based on the shape of the incidence curve may easily turn out to be wrong. We also assume that the disease is different in case of the second experiment, which is reflected in the new values of the parameters $\kappa$ and $\gamma$ as shown in Table 2.

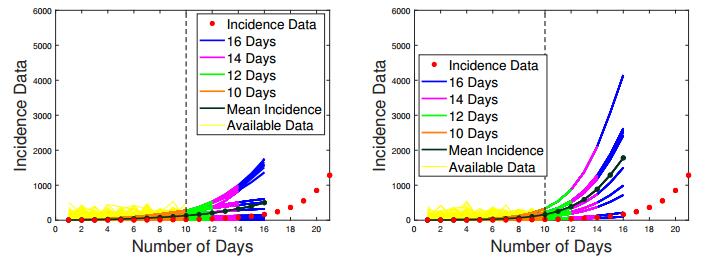
As one can see from the incidence curve, the effect of the increasing transmission rate at the early stage of the outbreak is delayed and in the first $18$ days the number of new cases is very low, until the incidence curve goes up almost vertically and reaches its pick in the next $10$ days. The hyperbolic model is not designed to capture this kind of increase in $\beta(t)$, and even the B-spline discretization does not succeed in recovering the right shape of the transmission rate from the limited data set (see Figures 13 and 14). From $10$ days of data, parametric discretization projects steady near-horizontal pattern for days $11$ through $16$. The B-spline discretization over-estimates the true $\beta(t)$ and, as the results, forecasts the future uphill behavior too early. Thus, even though parametric discretization recovers a less accurate $\beta(t)$, it gives a better short-term projection. The B-spline discretization succeeds in predicting a steep rise in new incidence cases, but it shows it sooner than it actually happens. To summarize, in case of the second experiment, from the first $10$ days of data one simply does not have enough information to ascertain the true structure of $\beta(t)$ that would enable us to generate an accurate forecasting curve.

For $30$ and $50$ days of data (see Figures 15–16 and 17–18, respectively), the B-spline discretization method provides very stable and accurate forecasting information with little to no deviations from the model incidence curve. It captures the right shape of $\beta(t)$ in the middle of the outbreak and shows the right pick for the incidence curve with the right inflection point for the cumulative number of cases. The B-spline discretization fails, however, to recover the right shape of the transmission rate at the early and late stages of the epidemic. Interestingly, that does not makes the recovered incidence curves any less accurate. The parametric discretization does the best it possibly can: approximates true $\beta(t)$ by a constant. This kind of approximation suggests that the outbreak picks with $4,000$ incidence cases rather than $6,000$. It also results in slight over-estimate of the actual number of cases between days $10$ and $22$ as well as days $33$ and $45$.

Overall, the two discretization methods both have their pros and cons. The comparison highlights the importance of using a priori information about the structure of the solution in the regularization algorithm. When this information is relevant, it helps to reinforce stability without considerable loss in accuracy. At the bottom of ill-posedness is always the lack of information. Thus, when the structure of the true solution is incorporated in the numerical algorithm, the algorithm becomes much more efficient. At the same time, the similarity of the incidence curves in the two experiments shows that it is hard to draw a reliable conclusion about the structure of the solution from the shape of the incidence data. And when the wrong structure is incorporated, the forecasting curve based on that structure may turn out to be misleading.

4.   Simulations with real data

We now move to recovering the disease transmission rate from real data. The real data set illustrates daily incidence cases of influenza in San Francisco during the 1918 "Spanish Flu" pandemic. The influenza pandemic of 1918-19 was a major public health challenge. The virus was extremely contagious and virulent. According to CDC, it killed an estimated $20$ to $50$ million people worldwide. The data we consider includes $63$ days of this epidemic in San Francisco, one of the most affected cities in the Unacted States. We assume a population of 550,000 individuals with infectious rate $\kappa = 1/2$ (days$^{-1}$) and recovery rate $\gamma = 1/3$ (days$^{-1}$).

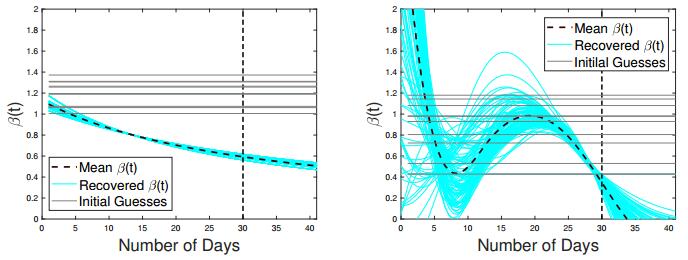
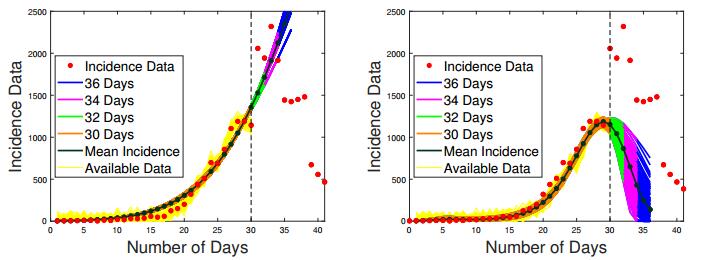
For the case of limited data with just $10$ points available (see Figures 19 and 20), the parametric discretization generates a perfect forecasting bundle, and its mean value passes through all real data points. For the B-spline discretization, all transmission rates are stuck at their initial values. The corresponding forecasting curves (for the most part) grossly over-estimate the actual number of future incidence cases.

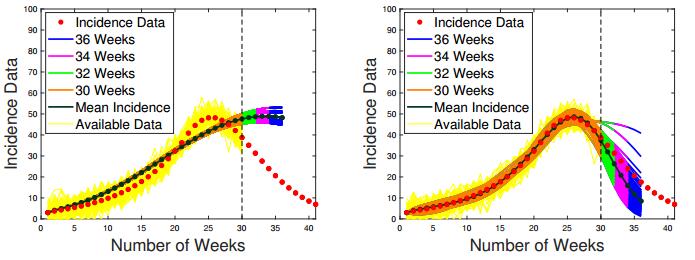
Half way through the outbreak, for $30$ data points, the situation is very different as illustrated in Figures 21 and 22. The B-spline discretization does an excellent job by showing the right turning point for the cumulative number of cases and the future downhill behavior of the incidence curve. It fails, however, in predicting the right number of new cases between weeks $30$ and $36$. The method seems to recover the right shape of $\beta(t)$, which reflects the dynamics of the outbreak without being over-regularized. At the same time, the epidemic curve obtained with parametric discretization algorithm mistakenly shows an exponential increase in new incidence cases, suggesting that the number of cases will continue to grow until the city runs out of susceptible population. Nevertheless, the parametric discretization covers the real data between weeks $30$ and $36$ much better as compared to the non-parametric one.

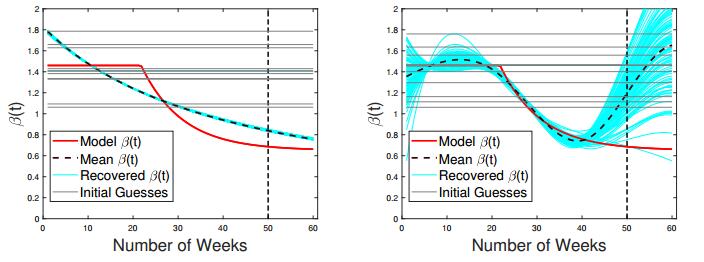
With $50$ data points (see Figures 23 and 24), the parametric incidence curve cuts through the real data right in the middle showing less than half the actual number of cases at the pick of the epidemic and over-estimating the actual number of cases for the first $27$ days and from day $39$ on. It does, however, correctly predict that the outbreak will come to an end not long after day $56$ (the last day of forecasting). Contrary to that, the non-parametric incidence curve follows the real data very closely for the entire $50$ day time period, leaving out only $3$ data points at the top of the epidemic. The non-parametric incidence curve hints at the beginning of the new cycle after day $50$ considerably over-estimating the actual number of cases reported between day $52$ and $56$. It is important to mention that, unlike the case of the first experiment, where the same kind of erroneous forecasting can only be attributed to noise and instability, in case of real data this false alarm is completely justified by the uphill behavior of the actual data between days $48$ and $51$. The data for this time period does suggest that a new cycle is about to begin, but the data afterwards shows that this is a "false positive". The reconstruction of $\beta(t)$ for the non-parametric case looks very stable and very reasonable.

Overall, we tend to declare the B-spline discretization a winner in case of the real influenza outbreak, since it correctly predicts the turning point of the epidemic based on $30$ days of data. This kind of reliable estimate is crucial for optimal resource allocation and for an adequate design of control measures in the affected area.

5.   Conclusions and discussion

Forecasting the trajectory of naturally occurring processes involving social dynamics in real time requires a sensible combination of mathematical and statistical methods together with reliable data sets at different spatial and temporal scales. Their importance can be investigated in different contexts using numerical simulation studies such as the type that we carried out in this paper. More specifically, we have explored the role of parametric and non-parametric discretization methods for both calibration and forecasting of epidemics that are shaped by time-dependent variation in the transmission rate using a simple SEIR compartmental model. Our findings highlight the limitations imposed by insufficient amount of information in time series data about the spread of infectious diseases. However, such limitations can often be handled or remedied through an appropriate balance of model complexity and state-of-the-art numerical methods, particularly regularization methods ^[5,4,13].

In our simulation study of parametric and nonparametric discretization algorithms using synthetic and real data we have observed that at the early stage (the first $10$ weeks/days of the outbreak), parametric discretization consistently provides more accurate (and stable) forecasting results as compared to B-spline approximation. At the same time, half way through the outbreak the nonparametric discretization is superior, while parametric discretization happens to be less reliable and often misses the turning point. This can be explained by the fact that even if the transmission rate is on the rise at the early stage, its impact on the dynamics of the incidence data is delayed. Therefore, the restrictions on the shape of $\beta(t)$, incorporated in the parametric discretization scheme, are not hurting the forecasting results, which greatly benefit from the stability imposed by a priori information enforced through the parametric approach. With more data, however, the restrictions on the shape of $\beta(t)$ become a liability keeping the algorithm from recovering a more accurate transmission rate and using it as a more reliable forecasting tool.

To summarize, one of the most challenging aspects in the applications of inverse problem is the need to develop techniques that handle parameter identifiability issues, which often arise owing to over-parameterized models or lack of information in available data. Fortunately, regularization techniques are one way in which scientists can still draw useful conclusions about model parameters and in turn generate potentially helpful forecast that policy makers could use to guide investments in particular control strategies ^[14]. In our study we found that lack of information in limited time series data is often the main challenge in generating useful parameter estimates and forecasts. This suggests that the incorporation of additional data about the epidemic dynamics in the regularization algorithm could prove useful for better constraining parameters and generating more accurate short-term forecasts of epidemic outbreaks. One such additional data could include social media streams which are being generated by Google Search Trends, Twitter, and Facebook. The hope is that capturing the right signals from these data sources could rapidly inform how the disease process is changing in real time. This is potentially a fruitful area for future research ^{[15,16,17,18,19]}.

Acknowledgments

This work is supported by NSF Grant 1818886. DMS Computational Mathematics.

Conflict of interest

All authors declare no conflict of interest in this paper.