Computing human to human Avian influenza $\mathcal{R}_0$ via transmission chains and parameter estimation

1.   Introduction

In the Netherlands, there was a report of an isolated incident of highly pathogenic avian influenza (HPAI H7N7) emerging from a poultry farm on February 28th 2003. As a result, 225 farms were culled in the affected area which meant that approximately 30 million chickens were killed. Weeks after the first case was reported, H7N7 was diagnosed in 89 humans who had visited the poultry farms; however, 3 of these individuals did not have any contact with the infected poultry farms suggesting human to human transmission of avian influenza ^[1]. During 10 months in 2004, highly pathogenic avian influenza H5N1 was reported to infect eight countries in Asia. During this time period, there were 44 human cases that were documented, and 32 of them passed away from avian influenza ^[2]. In 2005, there was evidence that three clusters of HPAI H5N1 infections occurred in Indonesia resulting in several human cases, and limited human to human H5N1 transmission could not be ruled out among the clusters ^[3]. While there isn't sustained human-to-human transmission of avian influenza, these outbreaks are alarming and suggest the possibility that more effective transmission could occur in the future if the virus mutates ^[4].

It is rare for the avian influenza A virus to infect humans and sustain an effective human to human transmission. Avian strains that transmit to humans require genetic assortment in some sort of mammalian intermediary; however, there have been cases where the highly pathogenic H5N1 did not need such genetic assortment ^[5,6]. Currently, the known human HPAI strains found in the outbreaks are H5N1, H7N3 or H7N7 ^[6]. In the human population, avian influenza virus causes flu like symptoms along with pneumonia. As with poultry, the low pathogenic human influenza A virus has a low mortality rate, but the high pathogenic human influenza A (namely, H5N1) has a mortality rate of up to 60 percent ^[7]. However, the current intra-species transmissions rate for humans is low. There have only been a few clusters of human to human transmissions and these have been among blood relatives who had close contacts, without any preliminary precautions, with an infected person ^[8]. Considering the high mortality rate of HPAI in humans, it is imperative that the process of transmission be better understood ^[5,9].

The first step in our investigation is to construct a suitable model that describes the biological situation for transmission of avian influenza in the chicken and human population. Certain biological systems can be represented by a set of mathematical equations. Thus if a given biological system's data fits a particular model then that data can be used (in conjunction with the models' predetermined mathematical equations) to determine some of the system's descriptive values such as transmission rates and the critical threshold referred to as the basic reproduction number ^[10]. The reproduction number for an infectious disease gives us insight into the disease's ability to cause an epidemic by serving as a threshold value. The basic reproduction number of a disease is defined as the number of secondary cases an infectious individual causes in a fully susceptible population until the individual is no longer infectious ^[11].

The objective of this article is to explore the traditional methodology of computing the human to human H5N1 avian influenza basic reproduction $\mathcal{R}_{0}$ through parameter estimation based on differential equations versus calculating $\mathcal{R}_{0}$ using transmission chains. There have been several papers that have estimated the human to human reproduction number by estimating parameters from data ^[12,13]. Xiao et al. developed a model with the intent of replicating the transmission dynamics of avian influenza H7N9. Using confirmed human cases in China, they fitted their model to data to obtain estimates for the transmission rate and estimated that the human to human reproduction number to be 0.467 ^[12]. Other approaches have been used to estimate $\mathcal{R}_{0}$. Chowell et al. used a Bayesian technique coupled with an SEIR model to find the reproduction number of H7N9 for the May 2013 China outbreak, and Boven et al. used final size distributions and household final size data to estimate parameters relevant to the reproduction number by maximum likelihood calculations. The reproduction number Chowell estimated was 0.1 while Boven concluded the secondary human to human transmission to be 0.21 ^[14,15].

While the differential equation-based approach is a more common method of estimating $\mathcal{R}_{0}$, the approach of inferring $\mathcal{R}_{0}$ from transmission chains provides in addition avenue for estimating the reproduction number. Some zoonotic diseases (Monkeypox, Nipah virus, Measles) display subcritical transmission ($0 < \mathcal{R}_{0} < 1$) such that infection happens as self contained chains that are too weak to cause an epidemic. H5N1 avian influenza is known to occur in small isolated pockets due to relatively weak transmissibility, and has the characteristics of subcritical transmission ^[16]. Being able to estimate $\mathcal{R}_{0}$ from transmission chain data is important for determining whether a disease that has $\mathcal{R}_{0}$ close to 1 would cause an epidemic, and it provides valuable insight on primary infections and secondary transmissions. Blumberg et al. used measles data from the United States and Canada to analyze what the impact of varying assumptions on chain size data would cause on $\mathcal{R}_{0}$ estimation ^[17].

This article is structured in the following fashion. In Section 2.1, we estimate $\mathcal{R}_{0}$ by using transmission chain size data and various maximum likelihood calculations. In Section 2.2, we establish an ordinary differential equation model describing the dynamics of avian influenza in chickens and humans. We use this model to derive the reproduction number and estimate the essential values represented in $\mathcal{R}_{0}$ by fitting to data. In Section 2.3 and Section 2.4, we explore the question of structural and practical identifiability of model. Finally, we conclude the manuscript by summarizing and discussing the results that we established.

2.   Methods

In this section, we describe two methodologies in which we compute the basic reproductive number. The first method deals with computing $\mathcal{R}_{0}$ through methods described in ^[17,18,19]. This will be the primary method used to calculate the reproductive number for the family cluster data presented in ^[20]. In the second methodology, we will construct a system of differential equations and find the reproduction number via the next generation method ^[13].

2.1.   Estimating $\mathcal{R}_{0}$ through transmission chains

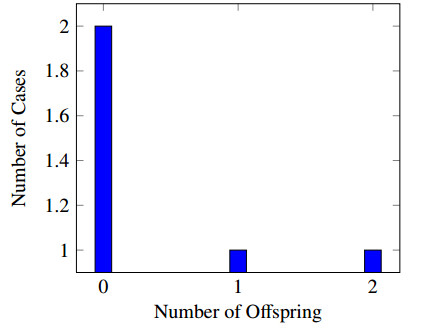
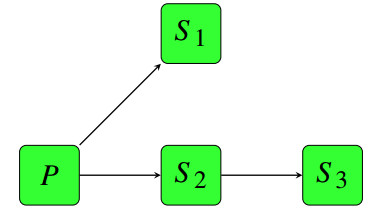
To calculate $\mathcal{R}_{0}$, we will use avian influenza (H5N1) transmission chain data gathered from ^[20,21], and a subfield in probability theory called branching process theory ^[22]. We define a transmission chain as a set for which all secondary infections can be traced back to a primary infection, and the number of cases found in a transmission chain is referred to as the chain size of a transmission chain. An example of a transmission chain can be found in Figure 1. This single transmission chain has size four. From Figure 2, there are two cases which produce zero offsprings ($S_{1}$ and $S_{3}$), one case that produces one offspring ($S_{2}$), and one case that produces two offsprings ($P$). Note that a primary infection without secondary cases is considered as a transmission chain of size 1.

The growth of a population for which an individual generates offsprings can be described mathematically by the Galton-Watson branching process. This method starts with a single primary individual who produces a random number of offsprings for which each of those offsprings produces a random number of offsprings ^[23]. This mechanism can be characterized by the probability generating function $Q(s) = \sum\limits_{i = 0}^{\infty} q_{i}s^{i}$ of the offspring distribution. $Q(s)$ defines the probability distribution of the new offspring in the population that are produced by each individual in the population. In the context of this paper, $Q(s)$ can be used to calculate the probability distribution for the number of secondary cases generated by each infected case. $q_{i}$ describes the probability that an infected individual produces $i$ infections. Selecting the proper offspring distribution is critical to this analysis since we want to determine the link between heterogeneity and spread of the disease. Therefore, we employ the same assumption as in ^[17] by using a negative binomial distribution with mean $\mathcal{R}_{0}$ and dispersion parameter $\kappa$, which helps explain the degree of transmission heterogeneity in transmission chains. So, we have the following generating function derived from ^[24].

Now, let $p_{i}(\mathcal{R}_{0}, \kappa)$ be the probability of a transmission chain having total size $i$ and define

Equation 2.2 is interpreted as the average probability of generating $n$ infections caused by $i$ individuals. From Theorem 1 in ^[25] and differentiating (2.1) with respect to $s$, we have

From equation (2.1), we have the $j$th derivative of $T_{i}(s)$ is

Substituting equation (2.4) into equation (2.3),

Recall the following special properties of the gamma function $\Gamma(x)$: $x \Gamma(x) = \Gamma(x+1)$ and $x! = \Gamma(x+1)$. Note from equation (2.5) that

Thus, the probability of a transmission chain having total size $i$ for a negative binomial offspring distribution is:

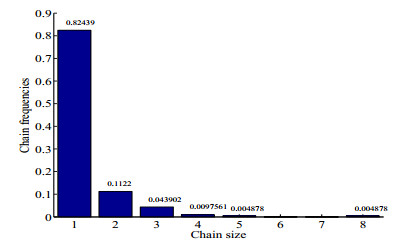
It is important to know how many transmission chains of a certain size are found in data since they play an integral part in computing the likelihood. In Figure 3, we see the distribution of the chain size for the avian influenza data set. From the data set, there are 94 cases presented of which 36 are primary cases and 58 are secondary cases. From December 2003 to December 2006, there were a total of 263 cases of H5N1 ^[26]. From here, we observe that there are 169 transmission chains of size 1, 23 transmission chains of size 2, 9 transmission chains of size 3, two transmission chains of size 4, one transmission chain of size 5, and one transmission chain of size 8. We notice skewness to the right in the chain size distribution which suggest that there is a high degree of transmission heterogeneity. Therefore, it is imperative for us to understand how the number of isolated cases and the degree of transmission heterogeneity affects the estimation of $\mathcal{R}_{0}$.

The probability defined in equation (2.9) is the basis for which we will estimate $\mathcal{R}_{0}$. When imperfections are ignored in the data and no assumptions are made in regarding the data at hand ^[19], the likelihood for a given chain size distribution with probability $p_{i}(\mathcal{R}_{0}, \kappa)$ is defined as

where $n_{i}$ is the number of transmission chains of size $i$. We maximize the likelihood function with respect to $\mathcal{R}_{0}$ and $\kappa$ to find the maximum likelihood estimate for these two parameters.

Let $\mathcal{C}(i, \alpha) = \alpha \cdot i$ denote the number of transmission chains of size $i$. Then we define the average observed chain size, $\hat{\mu}$, by $\hat{\mu} = \frac{1}{\hat{N}}\sum\limits_{k = 1}^{\hat{N}} \mathcal{C}_{k}(i, \alpha)$, where $\hat{N}$ is the number of transmission chains in the data. When perfect observation is assumed and we have the entire chain size distribution ^[19], the estimation of $\mathcal{R}_{0}$ is

We express the maximum likelihood estimation of $\mathcal{R}_{0}$ for this method by $\mathcal{R}_{0, MLE}$.

In order to account for various structures in the data, Equation (2.10) can be modified in two ways to represent a truncated likelihood and agammaegated likelihood. When computing the truncated likelihood, we only take a look at the chains in the data that are of size 2 or greater to avoid any discrepancy in the number of isolated cases ^[19]. Thus, we define the truncated likelihood as:

For the truncated estimate, we may alter the assumption of transmission heterogeneity to obtain three estimators for $\mathcal{R}_{0}$. By setting $\kappa = 1$, the negative binomial distribution simplifies to geometric offspring distribution, and by letting $\kappa\rightarrow\infty$, the negative binomial distribution simplifies to a Poisson offspring distribution for each of our estimators ^[19,18]. We can produce a third estimator $\mathcal{R}_{0, \kappa = ?}$ by letting $\kappa$ be a free parameter and assume that no prior information is provided for $\kappa$. This will allow us to determine the influence $\kappa$ has on the $\mathcal{R}_{0}$ estimator.

In the agammaegated likelihood calculation, intermediate sized chains found in the data are agammaegated to account for small chains that may not be observed. The likelihood is constructed by considering the number of isolated cases, the total number of stuttering chains, the size of the largest stuttering chain, and the number of chains having largest size ^[19]. We define the agammaegated likelihood as:

where $M$ denotes the largest chain size. Note that $p_{1}(\mathcal{R}_{0}, \kappa)^{n_{1}}$ denotes the probability of observing $n_{1}$ isolated cases and $p_{M}(\mathcal{R}_{0}, \kappa)^{n_{M}}$ denotes probability of observing $n_{M}$ chains of size $M$. As in the truncated estimator, the agammaegate likelihood formula provides us with three estimators for $\mathcal{R}_{0}$. Note that the truncated likelihood $\mathcal{R}_{0, \kappa}^{T}$ and the agammaegated likelihood $\mathcal{R}_{0, \kappa}^{A}$ are maximized over a single parameter $\mathcal{R}_{0}$ while $\mathcal{R}_{0, MLE}$ and $\mathcal{R}_{0, \kappa = ?}$ are maximized over two parameters $\mathcal{R}_{0}$ and $\kappa$.

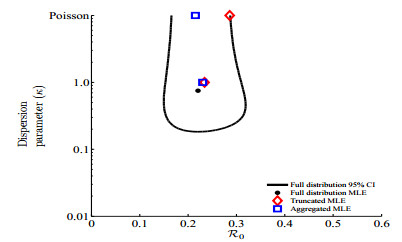
Figure 4 represents the estimates for $\mathcal{R}_{0}$ and $\kappa$ with respect to the likelihood calculation for the original data, truncated data, and agammaegated data. The results of this analysis are summarized in Table 1. The confidence intervals were computed by using likelihood profiling. $\mathcal{R}_{0, \kappa = 1}^{T}$ and $\mathcal{R}_{0, \kappa\rightarrow\infty}^{T}$ produce higher estimates than $\mathcal{R}_{0, MLE}$ which is expected since the truncated method assumes the chains of size 1 are under-represented in the data set. $\mathcal{R}_{0, \kappa = 1}^{A}$ and $\mathcal{R}_{0, \kappa\rightarrow\infty}^{A}$ produce the lower $\mathcal{R}_{0}$ estimates when compared to the truncated method since this method relies on isolated cases which make up about 82% of transmission chain data. In contrast to the truncated method, the agammaegated method assumes its transmission chains are homogeneous implying there will be fewer isolated cases which results in smaller $\mathcal{R}_{0}$ estimates. Observe that all likelihood estimates fall within 95% confidence interval of the full distribution maximum likelihood estimate $\mathcal{R}_{0, MLE}$. The optimized dispersion parameter for the maximum likelihood estimate was $\kappa = 0.751$.

In order to distinguish what method formulates the best likelihood estimate when compared to the initial data set, we compute the likelihood scores. Table 2 gives us the relative log likelihood scores for the avian influenza data. The likelihood scores are computed by taking the $\mathcal{R}_{0}$ estimates from Table 1 and computing the likelihood using the full data set and the truncated data set for each of the approaches. This is done to observe the variation between each of the estimation methods. As a reference point, we used $\mathcal{R}_{0, MLE}$ for $\Delta L$ and $\mathcal{R}_{0, \kappa = ?}^{T}$ for $\Delta L^{T}$ since these estimates produced the smallest likelihood scores for their respective methods. When we consider all chain size data in the likelihood calculation $L$, $\mathcal{R}_{0, MLE}$ gives the best likelihood score. This result makes sense because the $\mathcal{R}_{0, MLE}$ method is the only metric that takes into account all the information of the chain size distribution. The agammaegate likelihood $\mathcal{R}_{0, \kappa = 1}^{A}$ is the other estimator that is close to the likelihood score of $\mathcal{R}_{0, MLE}$ with -0.09 in relative log likelihood difference. From this analysis, we observe the models that assume a Poisson offspring distribution produce the lowest likelihood scores. When comparing the truncated method versus the agammaegated method, we observe that the agammaegated method produces better estimates than the truncated method. Since the likelihood calculation considers all the chain size data, and the truncated method ignores the isolated cases, this helps explain why the agammaegated methods would yield better $\mathcal{R}_{0}$ estimates.

If we remove the isolated cases from the likelihood calculation, we notice that the differences between the likelihood scores in the $L^{T}$ calculation are smaller compared to the $L$ calculation. Recall that the $L^{T}$ calculation doesn't consider the isolated cases which means that there are less data points in the calculation. Hence, this leads to the smaller differences in the likelihood scores. In this scenario, the agammaegated estimators perform worse than the truncated estimators due to the isolated cases being removed from the likelihood calculation. While the assumption of Poisson offspring distribution provides the best likelihood score for the truncated estimator when compared to $\mathcal{R}_{0, \kappa = ?}^{T}$, the Poisson distribution assumption gives the worst likelihood score for the agammaegated estimator when compared to $\mathcal{R}_{0, \kappa = ?}^{T}$.

2.2.   Estimating $\mathcal{R}_{0}$ through Differential Equations

We begin by defining the system of differential equations that describes the interaction between the human and the poultry population. The primary objective of our model is to capture the epidemiological dynamics of chicken-human interactions, and derive the basic reproduction number from the system.

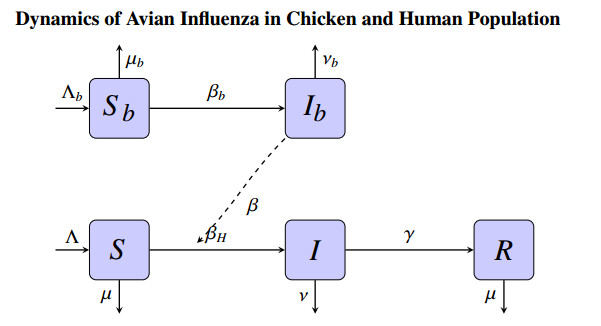
We introduce the model characterizing the dynamics of H5N1 in the chicken and human populations. For the chicken population, we use a simple $SI$ model since the disease kills the chickens or the infected chickens are culled to prevent the spread of avian influenza. $S$ denotes the number of susceptible humans at time $t$, $I$ denotes the number of infected humans with H5N1 at time $t$, and $R$ denotes the number of humans who have recovered from H5N1 at time $t$. $S_{b}$ and $I_{b}$ defines the susceptible chickens and the chickens infected with avian influenza, respectively. The description of each parameter in the model can be found in Table 3. The demographic parameters for humans and chickens and the duration of the infectious period are pre-estimated from the literature.

To find the total population size for the system, $N$, we use the population size from the countries from which the family cluster data and the WHO data are derived. The countries that are represented in the data sets are Vietnam, Thailand, Cambodia, Indonesia, China, Turkey, Iraq, Egypt, and Azerbaijan ^[20,26]. We estimated that the total population of the region is $N = 19225$ (in units of 10$^5$) individuals. Since the China is the largest country in the data sets, we use their average lifespan which is 75 years ^[27]. Thus, we define the natural death rate for humans as $\mu = \frac{1}{(75*365)}$ days$^{-1}$.

The total human population size in the model is $N = S+I+R$ which satisfies the differential equation $N^{\prime} = \Lambda-\mu N-\nu I$. Observe that the total human population size satisfies

This tells us that $\limsup\limits_{t\rightarrow \infty} N\leq \frac{\Lambda}{\mu}$. We will use this approximation for the total human population size to estimate the parameter $\Lambda$. An analogous argument can be constructed to estimate the parameter $\Lambda_{b}$.

The parameter $\Lambda$ represents the recruitment rate of humans, and as noted above, we define as $\Lambda = N*\mu$. Given $\mu$, we have that $\Lambda = \frac{19225}{(75*365)}$. The mean duration of infection in humans of the bird-to-human transmission estimated to be 6-7 days ^[27,28] hence $\gamma = 0.15$ days$^{-1}$. The total chicken population in these region is about $N_{b} = 63505$ in units of $10^5$ ^[29]. The lifespan for commercial poultry is about 2 years which means that $\mu_{b} = \frac{1}{(2*365)}$ days$^{-1}$. Thus, $\Lambda_{b} = \frac{63505}{(2*365)}$. The duration of infection in domestic birds is 10 days which means that $\nu_{b} = 0.1$ days$^{-1}$ ^[13].

Studies have shown that seasonality has played a factor in the transmissibility of avian influenza between birds ^[30]. To incorporate that factor into the model, we assume the transmission rate among chickens $\beta_{b}(t)$ to be periodically forced. This transmission rate is assumed to have sinusoidal behavior. Therefore, we define the transmission rate for chickens as:

This transmission rate assumes a 365 day periodicity. The first parameter in $\beta_{b}(t)$, $\kappa_{1}$, defines the amplitude, $\kappa_{2}$ represents the vertical shift, and $\omega$ the phase shift. All of these parameters in the transmissions rate $\beta_{b}(t)$ are fitted using the computer algebra program Matlab R2018a. Since the bird-to-human and human-to-human transmission events are sporadic and rare, we kept these transmission constant ^[31,32].

The human reproduction number for this model can be explicitly computed and is given by

Similarly, the poultry reproduction number for this model can be explicitly computed by ^[17,25]. Although our interest lies at estimating the reproduction number for humans, we nevertheless find the reproduction number for the chickens,

which simplifies to

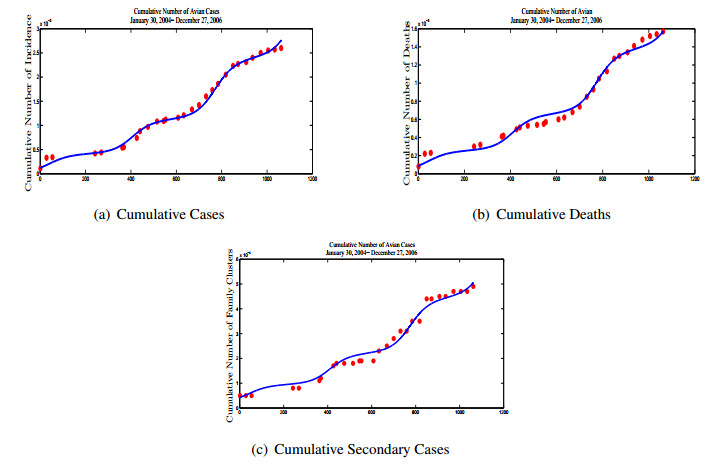
Figure 6 represents the cumulative number of human cases of H5N1 infections $C(t)$, the cumulative number of human deaths from H5N1 infections $D(t)$, and the cumulative number of secondary H5N1 human cases $F(t)$. The cumulative number of human cases and deaths is obtained from the World Health Organization (WHO) database, and the cumulative number of secondary cases are obtained from the family cluster data set ^[20,26]. The time span of the data set is from December 25, 2003 to December 27, 2006 and each data set consists of 29 data points. We used this time frame since the family cluster data set is limited to this period.

We fitted our model to the data using initial guess values for $\nu$, $\beta_{H}$, $\beta$, $\kappa_{1}$, $\kappa_{2}$, and $\omega$ to acquire the best estimates for these parameters. The blue curve denotes the model fit to each respective data set. Since the data are given as cumulative number of cases, deaths, and secondary cases, we fit the cumulative number of human cases, deaths, and secondary cases defined as:

We determined the goodness of fit for the model by using the ordinary least squares method. Since we want to measure how well our model fits to the observed data, we examine the model output for the number of cases, deaths, and secondary cases. In the optimization process, we minimized the least square distance

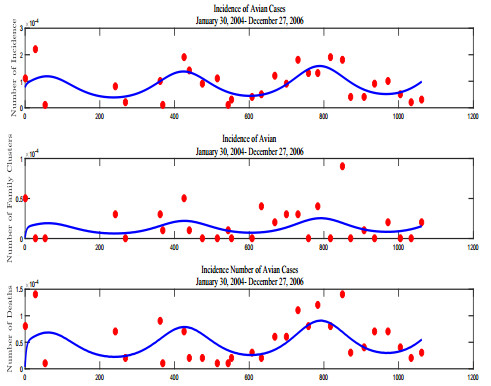
where $y_{ij}$ denotes the observed data points for each data set, $y_{1j}$ is the cumulative number of human cases at time $t_{j}$, $y_{2j}$ is the cumulative number of human deaths at time $t_{j}$, and $y_{3j}$ is the cumulative number of secondary at time $t_{j}$. We used an ODE solver (ode45) in Matlab to solve numerically our system of differential equations and the built-in nonlinear solver fminsearch for the numerical optimization. Since the optimization method relies heavily on the initial values for each parameter, we started off by manual fitting using Mathematica 9 and the Manipulate feature to give us a good starting point. We then used these parameter values in Matlab and minimized the SSR. We repeated this procedure until we obtained the smallest value for SSR and no further improvements in the SSR were observed. The results for the optimization procedure were very sensitive to the initial conditions for $S(t)$ and $S_{b}(t)$. Therefore the estimated parameters that we obtained are solely dependent on these initial conditions, and are not a set of unique parameter values. In addition, if the initial conditions for $\nu$, $\beta_{H}$, $\beta$, $\kappa_{1}$, $\kappa_{2}$, and $\omega$ were marginally changed from the initial guess, the recovered parameters and the reproduction numbers would change slightly from what we estimated. As King et. al. indicated, the use of a deterministic model to fit to cumulative data could result in the violation of the independent errors assumption needed for the least square procedure ^[33]. Thus in Figure 7, we fitted the model to incidence data which yielded a reasonable fit.

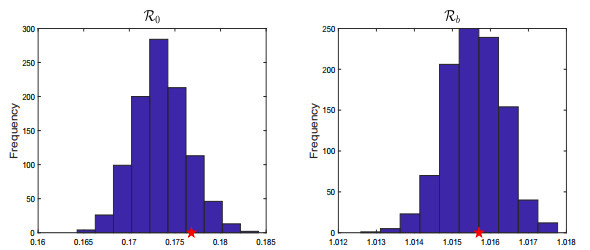
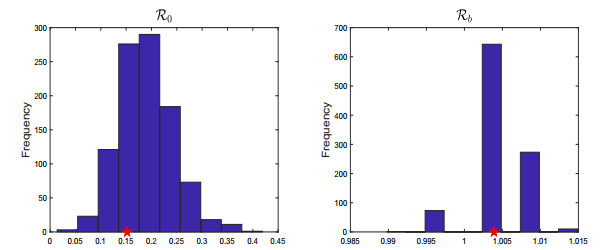
According to our simulations, we obtain the following values for the estimated parameters for the cumulative data: $\nu$ = 0.194, $\beta = 1.767\times10^{-7}$, $\beta_{H} = 3.168\times10^{-6}$, $\kappa_{1} = 2.409\times10^{-7}$, $\kappa_{2} = 1.621\times10^{-6}$, and $\omega$ = 147.634. With these fitted parameters, we observe that the human and chicken reproduction numbers are $\mathcal{R}_{0} = 0.1768$ and $\mathcal{R}_{b} = 1.0156$, respectively. Note that this human reproduction number differs slightly from the human reproduction number calculated in Section 2.1. From the incidence data fitting, the estimated parameters produced reproduction numbers ($\mathcal{R}_{0} = 0.1520$ and $\mathcal{R}_{b} = 1.0039$) that are relatively identical to the reproduction numbers generated from the estimated parameters of the cumulative data fitting. The transmission chains and the next generation operator methods cannot be compared directly with each other due to the fact that the data are treated differentially in each scenario. In the differential equations scenario, we took into account all the cases, deaths, and secondary infections that occurred during December 2003 to December 2006; while in the likelihood approach, the transmission chain contained only information about primary and secondary cases.

2.3.   Structural Identifiability

Determining whether the inverse problem is well posed for a given model and data set is the first step in parameter estimation. Since many parameters in a model are unmeasurable in practice, associating epidemic models with data to produce predicative results requires a plethora of parameter estimation and identifiability techniques. Structural identifiability analysis allows us to investigate whether the model parameters can be identified, provided that we have noise free data ^[34,35]. Identifiability analysis provides an avenue for which the model can be reconstructed to determine which combinations of parameters can be estimated even when single parameters were deemed unidentifiable ^[36,37]. If the ODE system is not structurally identifiable then the parameters estimated by a numerical optimization technique might yield unreliable results. On the other hand, a mathematical model which is structurally identifiable may not be practically identifiable. We note that in our model, all of the parameters are constants except for $\beta_{b}(t)$ which may cause an issue in this analysis. However, Kelejian states that structural identifiability in a system with random parameters is identical to the constant coefficient version of the model ^[38]. Therefore, we may treat $\beta_{b}(t)$ as a constant, and proceed to conduct the identifiability analysis.

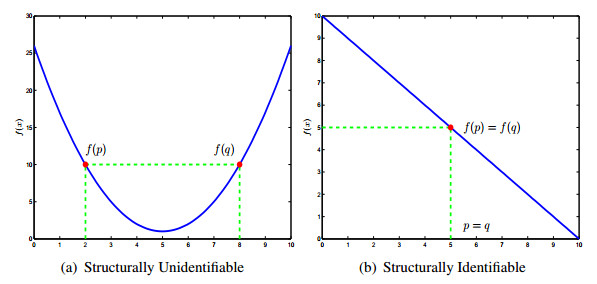
Mathematically, we say a parameter set ${ θ}$ is structurally globally identifiable if for every ${ { θ}_{0}}$ in the parameter space, if $f({\bf{x}}(t), { θ}) = f({\bf{x}}(t), { { θ}_{0}})$ implies ${ θ} = { { θ}_{0}}$.

For our model, if

implies ${ { θ}} = { { θ}_{0}}$ then the model is structurally identifiable. Figure 8 illustrates how a parameter set is structurally identifiable. Figure 8 A is unidentifiable since $f(2) = f(8) = 10$, but 2. Figure 8 B is identifiable since $f$ is injective i.e. $f(5) = f(5) = 5$ implies $5 = 5$. It is important for us to verify the structural identifiability of the model since parameter estimation results rely on the predictive capability of the model, and there are several methods constructed to undertake this assignment. The general methods used are Taylor Series expansion, differential algebra, exact arithmetic rank (EAR), and implicit function theorem among others ^[39]. For our analysis, we will use the differential algebra approach and EAR to test the model. One of the strengths of the differential algebra approach method is that if the model is unidentifiable, the identifiable parameter combinations can be obtained. Using the identifiable parameter combinations, the model can be re-parameterized to obtain a structurally identifiable model ^[35].

The differential algebra approach builds upon deriving the input-output function which contains all structural identifiability information of the model. Using Ritt's algorithm, the input-output equations are determined from the characteristic sets ^[40]. To derive an input-output equation for the model, we used the Differential Algebra for Identifiability of Systems (DAISY) software ^[41]. The results from DAISY tell us that $\Lambda_{b}$, $\beta_{b}$, and $\beta$ are unidentifiable. DAISY yields the following key parameter combinations that cause the model to be unindentifiable:

These combinations give us information about how we can reparameterize the model so that it can be identifiable. If we fix $\Lambda_{b}$, the parameter combination from DAISY informs us that the model becomes identifiable.

The EAR approach uses the inverse function theorem to the system of algebraic differential equations. The solvability of the system can be determined by examining the rank of the Jacobian matrix for this system of equations. If it's a rank-deficient matrix, the Jacobian would grant us insight into what parameters have an association with each other resulting in a non-identifiable model. The EAR method takes care of any rank scenario by efficiently computing a generic rank of the Jacobian matrix which allows a conclusive result about the identifiability ^[42]. We used the Mathematica package 'IdentifiabilityAnalysis' created by Karlsson et al. to perform this procedure. The EAR approach concluded that $\Lambda_{b}$, $\beta_{b}$, and $\beta$ are unidentifiable, which is consistent with the results from DAISY. Again if we fix $\Lambda_{b}$, the EAR approach tells us that our system is identifiable.

2.4.   Practical Identifiability

In the previous section, we examine the structural identifiability of the model. This analysis deals with the design of the model itself, and is independent of empirical data. This potentially poses a problem in practice since a parameter that is deemed structurally identifiable can potentially be practically unidentifiable. There may be several underlying reasons why a parameter is unidentifiable, but knowing that a parameter is structurally identifiable will provide us the insight of why a parameter is not practically identifiable. Noisy data and the inability for the numerical optimization algorithm to locate the minimum SSE are the two possible causes of loss of practical identifiability from that scenario. In this section, we will undertake the issue of practical identifiability by performing a bootstrap algorithm and creating a profile likelihood of the fitted parameters.

The parameter estimates obtained in Section 2.2 are most likely an inaccurate description of the true parameter values, due to the small sample size and noise in the data. However, we will construct the confidence intervals for our parameters estimates. We will use a bootstrapping algorithm which provides a way to construct a confidence interval with small sample size ^[43]. The algorithm will proceed as follows:

1. Begin by estimating the parameter set $\theta_{0}$ from the data sets ${y_{ij}}$ using the ordinary least squares method for $i = 1, 2, 3$ and $j = 1\ldots29$.

2. Define the standardized residuals from $\theta_{0}$ for each data set: $r_{ij} = \sqrt{\frac{n}{n-p}} (y_{ij}-f(t_{j}, \theta_{0}))$, where $n$ is the number of data points and $p$ is the number of parameters in $\theta_{0}$.

3. Create a bootstrap sample size using random samples with replacement from the residual set in step 2 to form a bootstrap sample of residuals ${r^{k}_{ij}}$.

4. Create new data sets from the residuals by adding the residuals to the model output. In this step, we must use the estimate $\theta_{0}$ to evaluate the model: $y_{ij}^{k} = f(t_{j}, \theta_{0})+r^{k}_{ij}$ where $k$ is the iteration index.

5. Using the new data sets, find a new estimate $\theta$.

6. Store values of $\theta$ into a matrix and repeat the algorithm 1000 times.

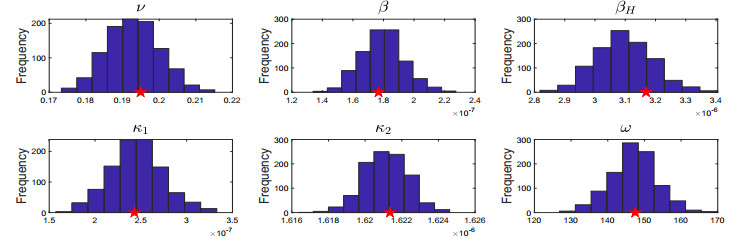
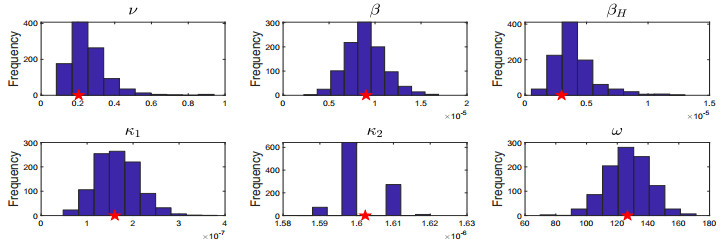
Figure 9 represents the distribution of the parameter estimates using the bootstrapping algorithm on the cumulative data. Figure 11 represents the distribution of the parameter estimates using the bootstrapping algorithm on the incidence data. The red star in each figure represents the parameter estimate obtained using the optimization method. We see that the majority of the distributions for the parameters resemble a normal distribution with the exception of the distribution for $\beta_{H}$, $\kappa_{2}$, and $\nu$ in the incidence case. Although the histograms for these three parameters do not display a normal distribution and the histogram of $\kappa_{2}$ is erratic, the largest frequencies for $\beta_{H}$, $\kappa_{2}$, and $\nu$ center near the optimized value. In the case for the cumulative data, we notice that all of the true parameters fall on or near the mean of the distribution except for $\beta_{H}$. Obtaining these type of results reveals the underlying distribution for our parameter space. Using the values for the parameters in the human and chicken reproduction number, we plotted the histogram for each respective reproduction number, and note that they too approximate a normal distribution (Figure 10 and Figure 12) with the exception of $\mathcal{R}_{b}$ in the incidence case. The distribution for $\mathcal{R}_{b}$ is attributed to the distribution of $\kappa_{2}$ and equation (2.16). The bootstrap results tell us that the data is noisy as excepted, but it isn't too noisy to obtain reliable parameter estimates.

In Tables 5 and 6, we see the 95% confidence intervals for each of the parameters that were estimated along with their relative error. We define the relative error as

where $\theta_{estimate}$ is the mean value for the estimated parameter in the bootstrap algorithm. In the cumulative case, $\beta$ and $\beta_{H}$ yield the largest relative errors while the $\nu$, $\kappa_{1}$, $\kappa_{2}$, and $\omega$ have low relative errors. In the incidence case, all the parameters had a small relative error with the exception of $\beta_{H}$. These results tell us that the parameters with low relative error can be practically identified while $\beta_{H}$ is practically unidentifiable using the bootstrap algorithm due to the high relative error in both cases.

Another method of testing the practical identifiability of the model is to calculate the profile likelihood of each fitted parameters (${\bf{p}}$ = [$\nu$, $\beta$, $\beta_{H}$, $\kappa_{1}$, $\kappa_{2}$, $\omega$]). We define the profile likelihood of the fitted parameters $p\in {\bf{p}}$ is

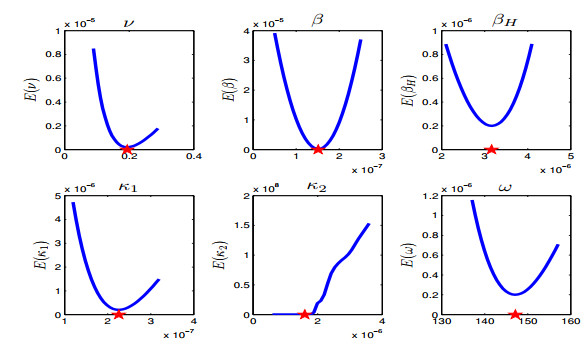
The purpose of this method is to determine whether a given parameter yields a unique profile likelihood value. If the graph of the profile likelihood is constant on a certain interval or stays below a fixed threshold, we classify that parameter to be practically unidentifiable ^[44]. For this simulation, ${\bf{p}} = [0.1949, 1.767\times10^{-7}, 3.169\times10^{-6}, 2.429\times10^{-7}, 1.621\times10^{-6}, 147.483]$, and the local minimum is $E(p_{i}) = 1.99561\times10^{-7}$. In Figure 13, we see the profile likelihood of the parameters ${\bf{p}}$. Notice that the minimum of the profile likelihood is achieved at the fitted values for $\nu$, $\beta$, $\beta_{H}$, $\kappa_{1}$, $\omega$, but the profile likelihood for the parameter $\kappa_{2}$ is horizontal at the minimum. Therefore, this simulation suggests that $\kappa_{2}$ is practically unidentifiable while the rest of the fitted parameters are practically identifiable.

3.   Discussion and conclusion

Constructing models that adequately describe the data from an outbreak is vital for public health. In this regard, parameter estimation plays a key role in developing such models. Testing the structural and practical identifiability for a model is imperative when it comes to estimating the basic reproduction number $\mathcal{R}_{0}$. In this article, we explored techniques that estimated $\mathcal{R}_{0}$ for human to human transmission from transmission chain data and parameter estimation via data fitting for avian influenza.

Incorporating transmission chain data and the likelihood function provides another mathematical process for estimating $\mathcal{R}_{0}$ instead of using the traditional differential equations procedure. Lloyd-Smith et al. considered a negative binomial distribution to be a more flexible method to employ when dealing with transmission data since it can describe a degree of transmission heterogeneity, and can be adjusted to a variety of infectious diseases ^[24]. The two parameters in the negative binomial distribution are $\mathcal{R}_{0}$ and the dispersion parameter $\kappa$. These two parameters are critical to understanding how a disease spreads since $\mathcal{R}_{0}$ represents the average secondary cases produced by an infectious individual in a susceptible population, and $\kappa$ describes the variation in the levels of infectiousness in an individual. We implemented three likelihood methods that incorporate varying assumptions: the standard likelihood $L$, the truncated likelihood $L^{T}$, and the agammaegated likelihood $L^{A}$. We found that the estimates for $\mathcal{R}_{0}$ were not equivalent under varying assumptions. When a data set has information about the full distribution chain size, it's better to use the $L$ likelihood method over the truncated and agammaegated method. However, if the data are lacking isolated cases, the truncated likelihood method performs the best in this scenario. The full distribution likelihood approach produced an estimate $\mathcal{R}_{0} = 0.2205$. Ferguson and Fraser established $\mathcal{R}_{0} = \frac{P_{c}}{1-P_{c}}$, where $P_{c}$ is the proportion of avian to human cases generating secondary cases. Out of the 263 cases that occurred between December 2003 to December 2006, 36 primary cases are known to produce secondary cases. Therefore, $\mathcal{R}_{0} = 0.1586$ from Ferguson and Fraser's formula for $\mathcal{R}_{0}$ ^[45]. By the epidemiological definition of $\mathcal{R}_{0}$, we have that $\mathcal{R}_{0}$ should approximately equal the number of secondary cases divided by the number of primary cases which produces $\mathcal{R}_{0}\approx 0.2829$.

We developed a system of differential equations to describe the dynamics of transmission of avian influenza from chickens to humans. Once we established the model, we computed the basic reproduction number $\mathcal{R}_{0}$ for the humans and $\mathcal{R}_{b}$ for the chickens. We saw that the human basic reproduction number was composed of the parameters $\Lambda$, $\mu$, $\gamma$, $\nu$, and $\kappa_{2}$. In order to gain a proper estimate for $\mathcal{R}_{0}$, we estimated $\nu$ and $\kappa_{2}$ along with $\beta$ and $\beta_{H}$ from the cumulative number of H5N1 cases, the cumulative number of H5N1 deaths and the cumulative number of secondary H5N1 cases data set. The other parameters in $\mathcal{R}_{0}$ were pre-estimated from the literature. The bird to human transmission rate we estimated was within two orders of magnitude of what Hsieh et al. found for the H7N9 avian influenza outbreak in China. They determined that the mean bird to human transmission parameter to be 3.15$\times10^{-5}$ ^[46]. After finding the optimal parameter set, we discovered that the reproduction number with the best fitted parameters is $\mathcal{R}_{0} = 0.1768$. When compared to reproduction estimates for H5N1 in poultry, we notice that our value for $\mathcal R_b = 1.016$ is smaller than the previously estimated reproduction numbers for in-poultry transmission. For instance, in the H5N1 outbreak in Thailand, the in-poultry reproduction number was estimated to be 1.27 ^[47]. We further note that our optimization procedure was highly sensitive to the initial conditions for the human and chicken populations. Thus, we fixed the initial conditions for the human and chicken populations as $S(0) = 19220$ and $S_{b}(0) = 63505$ (units $10^5$). We assumed that the entire population where the data was obtain to be susceptible to the H5N1 avian influenza virus. If we considered the susceptible population to be just the farmers (or poultry handlers) that may have resulted in a higher $\mathcal{R}_{0}$ estimate with this framework. Therefore, this approach appears to underestimate $\mathcal{R}_{0}$.

Although our estimate is inconsistent with the estimates found the literature, we must acknowledge that the data used related to several different countries while most studies use data from a single country. We must be cautious when using fitting to the cumulative data and applying the sum of square errors to test the goodness of fit. Since the sum of squares relies on the assumption of independent and identically distributed errors, our deterministic model may lead to an over estimation of precision. To satisfy these assumptions i.i.d., we fitted the model to the incidence data (Figure 7) and obtained parameter values that are similar to the fitted parameters for the cumulative data. We may consider a stochastic model in the future since they account for real variability and they can handle uncertainty more easily than deterministic models ^[33].

As described in this study, it is important to know what type of data are available when estimating the reproduction number for H5N1. We observed about $20\%$ difference among the reproduction values when using transmission chain data versus when we had cumulative number of cases, deaths, and secondary cases data. Given what is known about each method to under or over estimate, we can conclude that $\mathcal{R}_{0}\approx 0.2$. The likelihood analysis pertained more to isolated clusters and transmission chain sizes for data accumulated in different regions while data fitting approach relied on cumulative data. Therefore, there exist more bias in one of the estimates due to the type of data being used. We must be aware when it is appropriate to apply these methodologies because the wrong application could lead to a severe over/under estimation of the value of $\mathcal{R}_{0}$. While collecting data for H5N1 presents a challenge, the understanding of the mechanics behind the potential human to human transmission, and the estimation of $\mathcal{R}_{0}$ play a vital role in understanding the risk of an H5N1 epidemic.

Acknowledgments

The authors are grateful for the contributions Dr. Juliet Pulliam made to the formulation of the transmission chains research, and for putting us in touch with Dr. Seth Blumberg whose code was fundamental in the transmission chains analysis. The authors are thankful for the code provided by Dr. Johan Karlsson that was instrumental with the identifiability analysis. The authors would like to thank the anonymous referee for their insightful and constructive comments. This research has been supported in part by the Mathematical Biosciences Institute and the National Science Foundation under grant DMS 1440386

Conflict of interest

All authors declare no conflicts of interest in this paper.