Near-optimal control and threshold behavior of an avian influenza model with spatial diffusion on complex networks

1.   Introduction

Avian influenza is an animal disease, it caused by avian influenza A virus. Avian influenza generally targets specific species, but the virus can infect humans by crossing species barriers in rare cases. For example, avian influenza virus AH5N1 and AH5N7. Since the first outbreak of avian influenza AH5N1 in Hong Kong in 1997, the virus has infected more than 400 people worldwide, with a mortality rate close to 60% ^[1]. In 2013, the avian influenza AH7N9 crossed the species barrier for the first outbreak in mainland China. More than 400 people have been infected, and the mortality rate is close to 40% ^[1]. Avian influenza has not only brought serious threat to human health, but also caused human psychological panic. And it caused a huge blow to the national economy. Therefore, to provide effective control and prevention strategies, mathematical models and methods have been widely adopted to study the epidemiological characteristics of infectious diseases.

The mathematical dynamics method can describe the internal mechanism of infectious disease transmission by establishing a mathematical model. Kermack and McKendrick ^[2,3,4] established the famous compartmental model, a "threshold theory" was proposed to distinguish the prevalence of the disease. Liu and Ruan ^[5] constructed two bird-to-human avian influenza models with different growth laws of the avian population, and proved the globally asymptotic stability. Gourley et al. ^[6] established a patch model with delay to investigate the role of migratory birds in the spread of H5N1 avian influenza, they proved globally asymptotic stability of the disease-free equilibrium. Bourouiba et al. ^[6] established a delayed avian influenza model to investigate the role of migrating birds in the spread of avian influenza. S. Iwami et al. ^[7] constructed a mathematical model to explain the spread of avian influenza and mutant avian influenza. Tuncer and Martcheva ^[8] addressed the question of modeling the periodicity in cumulative number of human cases of H5N1. Three potential drivers of influenza seasonality were investigated. Hu ^[9] constructed an avian influenza model with nonlinear incidence and analyzed the stability of the model, as follows:

in model (1.1), $S_{a}$ and $I_{a}$ denote the sizes of susceptible poultry and infectious poultry. $S_{h}$, $I_{h}$, and $R_{h}$ denote the sizes of susceptible human, infectious human, recovery human, respectively. $\frac{1}{1+\alpha_{1}I_{a}}$ ^[10] describes the saturation due to the protection measures of the poultry farmers when the number of infective poultry increases. Similarly, as the number of the infective human individuals increases, the susceptible human population may tend to reduce the number of contacts with infective infective avian population per unit time due to the psychological effect, so we use a nonmonotone incidence function to describe the transmission of the virus from infective poultry to susceptible human; that is, $\frac{\beta_{h}S_{h}I_{a}}{1+\alpha_{2}I^{2}_{h}}$ ^[11,12]. All parameters are assumed non-negative and their meanings are described as follows: $\Lambda_{a}$ and $\Lambda_{h}$ denote the recruitment rate of poultry and human population, respectively; $\lambda_{a}$ and $\lambda_{h}$ represent the infected rate of poultry and human population, respectively; $\mu_{a}$ and $\mu_{h}$ represent the natural mortality rate of poultry and human population, respectively; $\delta_{a}$ and $\delta_{h}$ represent the mortality due to disease in poultry and human population, respectively; $\gamma_{h}$ denotes recovery rate of infected human population.

The model (1.1) is a time-dependent ordinary differential system. But in fact, the spread of infectious diseases are significantly affected by the spatial heterogeneity, for example, spatial position, water resource availability and other factors. There is increasing evidence that the spatial diffusion has significant impact on the spread of infectious diseases. Tang ^[13] investigated an avian influenza epidemic model with diffusion and nonlocal delay, this model describes the transmission of avian influenza among birds and human; especially the asymptomatic individuals in the latent period have infectious force. Lin ^[14] introduce two moving boundaries, which are called free boundaries, to describe the avian influenza virus transmitting in the habitat.

However, all the above models are obtained under the assumption that all individuals are uniformly mixed, which means they have the same contact rate with other individuals in the region. That is, the mixture between individuals are homogeneous, but, the contact between poultry-to-poultry, and poultry-to-human are obviously heterogeneous ^[15] in reality. In order to reflect the heterogeneity of contacting between individuals, it is of great significance to explore the spread of avian influenza on coupled networks. Zhan ^[16] had studied the coupling dynamics between epidemic spreading and relevant information diffusion.

On the other hand, as is known to all that avian influenza has posed huge economic burden which primarily includes opportunity loss, health care related expenditures, loss of employment and so on. Because of resource limitations, it is very necessary to formulate optimal control strategies which can prevent wide spreading of infectious diseases at minimum cost. Therefore, we introduce the slaughtering for poultry and treatment for humans as control variables, and establish an optimal control problem to decrease the number infected poultry and humans. Mathematically, the optimal control is obtained by solving the state equation and adjoint equation or the Hamilton-Jacobi-Bellman equation. In fact, for a complex system, such equations have difficulties giving analytic solutions. Optimal controls may not even exist in many situations, while near-optimal controls always exist. Many more near-optimal controls are available than optimal ones. Therefore, in this paper, we explore the near-optimal controls, aiming to slaughter poultry and treat infected humans while keeping the loss and cost to a minimum. The main contributions of this paper are as follows:

● An avian influenza model with spatial diffusion on complex networks is established.

● We define the basic reproduction number of virus and show that it is a threshold for viral persistence or extinction.

● The necessary and sufficient conditions of near-optimal control are presented.

The rest of this paper is organized as follows. In section 2, we construct an avian influenza model with spatial diffusion on complex networks, In section 3, we discuss the well-posedness of the system. We compute the basic reproduction number of the avian influenza model in section 4. In section 5, we analyze the sufficient and necessary conditions for the near optimal control. In section 6, several numerical simulations are given to demonstrate the theory results. Finally, we give a brief conclusion and future work in section 7.

2.   Model formulation

We will use the following notations in this paper:

● $\mid\cdot\mid$: the norm of an Euclidean space;

● $f_{x}$: the partial derivation of $f$ with respect to $x$;

● $\chi_{S}$: the indicator function of a set $S$;

● $C$: generally refers to all arbitary normal numbers.

Considering the heterogeneity of the contact between poultry-to-poultry and poultry-to-human, we introduce one-way-coupled networks into avian influenza model. There are two separate networks, $\mathcal{A}$ and $\mathcal{H}$. Network $\mathcal{H}$ consists of humanity, where each node represents an individual, and each connection between two individuals represents direct contact between them. Network $\mathcal{A}$ is composed of poultry population. And there is a connection from subnetwork $\mathcal{A}$ to subnetwork $\mathcal{H}$. We express in degrees $(i, j)$ that there are $i$ edges connected to subnetwork $\mathcal{A}$ and $j$ edges connected to subnetwork $\mathcal{H}$. And it is expressed in degrees $(i, \cdot)$ that $i$ edges are connected to subnetwork $\mathcal{A}$, and any edges are connected to subnetwork $\mathcal{H}$. The same degree $(\cdot, j)$ indicates that any edge is connected to the subnetwork $\mathcal{A}$ and $j$ edges are connected to the sub-network $\mathcal{H}$. Then, model (1.1) can be written as

$\Theta_{a}(t)$ denotes the infection probability of susceptible poultry nodes with the degree $i$ in contact with the infected poultry nodes. $\Theta_{ah}(t)$ denotes the infection probability of susceptible human nodes with the degree $j$ in contact with the infected poultry nodes. In the uncorrelated networks, $\Theta_{a}(t)$, $\Theta_{ah}(t)$ can be written as

where $\langle k\rangle_{a}$ = $\sum_{i = 1}^{n}ip_{a}(i, \cdot)$, $\langle k\rangle_{ah}$ = $\sum_{j = 1}^{n}jp_{a}(\cdot, j)$, $p_{a}(i, \cdot)$ = $\sum_{j = 1}^{n}p_{a}(i, j)$, $p_{a}(\cdot, j)$ = $\sum_{i = 1}^{n}p_{a}(i, j)$, $p_{a}(i, j)$ = $\frac{N^{a}_{i, j}}{N^{a}}$, $N^{a}$ = $\sum_{i = 1}^{n} \sum_{j = 1}^{n}S^{a}_{i, j}+\sum_{i = 1}^{n} \sum_{j = 1}^{n}I^{a}_{i, j}$. The stability of equilibrium points is often governed by a threshold called the basic reproduction number $\mathcal{R}_{0}$. The basic reproduction number $\mathcal{R}_{0}$ of model (2.1) is obtained by using the method in the reference ^[17], where

where $\langle i^{2}\rangle = \sum_{i = 1}^{n}i^{2}p_{a}(i, \cdot)$. The parameters of the coupling network are described in Table 1.

In general, the individual disperses randomly in the habitat. Therefore, we consider not only the individuals activity in temporal dimension, but also the distribution of the individual in the spatial and the dynamic characteristic of the avian influenza. Considering spatial spreading, Kim et al.^[18] investigated a diffusive epidemic model, this model describes the transmission of avian influenza among birds and humans. (We assume that susceptible individuals, infectious individuals and recovered individuals move spatially randomly.) In view of the fact that the spatial diffusion and environmental heterogeneity are important factors in modeling the spread of many diseases, with reference ^[19], an extended version of the avian-human model can be described by

because the removed population has no effect on the dynamics of $S^{h}_{i, j}$ and $I^{h}_{i, j}$, model (2.2) can be decoupled to the following model

where $S^{a}_{i, j}: = S^{a}_{i, j}(t, x)$, $I^{a}_{i, j}: = I^{a}_{i, j}(t, x)$, $S^{h}_{i, j}: = S^{h}_{i, j}(t, x)$, $I^{h}_{i, j}: = I^{h}_{i, j}(t, x)$, $x = (x_{1}, x_{2}, \cdots, x_{l})^{T}\in\Omega\subset \mathbb{R}^{l}$, $\Omega$ is the spatial habitat in $\mathbb{R}^{l}$ with smooth boundary $\partial\Omega$, $\Omega = \{x||x_{k}|\leq L_{k}\}$, $L_{k}$ is constant, $k = 1, 2, \cdots, l$; $D_{ik}: = D_{ik}(t, x) > 0$, $G_{kj}: = G_{kj}(t, x) > 0$ denote the transmission diffusion operator, $\Lambda_{a}: = \Lambda_{a}(x)$, $\Lambda_{h}: = \Lambda_{h}(x)$, $\lambda_{a}(i): = \lambda_{a}(i)(x)$, $\lambda_{ah}(j): = \lambda_{ah}(j)(x)$, $\mu_{a}: = \mu_{a}(x)$, $\mu_{h}: = \mu_{h}(x)$, $\delta_{a}: = \delta_{a}(x)$, $\delta_{h}: = \delta_{h}(x)$, and $\gamma_{h}: = \gamma_{h}(x)$ are positive Hölder continuous functions on $\overline{\Omega}$.

the initial conditions are given by $S^{a}_{i, j}(0, x) = \phi_{1i}$, $I^{a}_{i, j}(0, x) = \phi_{2i}$, $S^{h}_{i, j}(0, x) = \phi_{3j}$, $I^{h}_{i, j}(0, x) = \phi_{4j}$, $\phi\in\mathbb{R_{+}}$, $x\in\overline{\Omega}, i, j = 1, 2, \cdots, n$, where $\mathbb{R_{+}} = \{x\in\mathbb{R}:x\geq0\}$. For $x\in\Omega$, with homogeneous Neumann boundary conditions

where $\Omega$ is a bounded smooth domain in $\mathbb{R}^{l}$, $\partial\Omega$ and $\overline{\Omega}$ are the boundary and the closure of $\Omega$, $n$ is the outer normal vector of $\partial\Omega$. Let $\mathbb{X}: = C(\overline{\Omega}, \mathbb{R}^{4n})$ be the Banach space with the supremum norm $\|\cdot\|$. Define $\mathbb{X}^{+}: = C(\overline{\Omega}, \mathbb{R}_{+}^{4n})$. The symbol $\nabla$ is the gradient operator.

3.   Well-posedness of the system

In this section, we will focus on the existence and uniqueness of the global solutions of model (2.3).

Lemma 3.1. For every initial value function $\phi: = (\phi_{1i}, \phi_{2i}, \phi_{3j}, \phi_{4j})\in\mathbb{X}^{+}$, the solution $U(t, x;\phi) = (S^{a}_{i, j}(t, x;\phi_{1i}), I^{a}_{i, j}(t, x;\phi_{2i}), S^{h}_{i, j}(t, x;\phi_{3j}), I^{h}_{i, j}(t, x;\phi_{4j}))$ of model (2.3), satisfies that

where C is a normal constant.

Proof. Let

where $|\Omega|$ represents the volume of $\Omega$, we can obtain

In other words, there is a positive constant $C$ such that $\lim_{t\rightarrow \infty}W(t) < C$. This proof is complete. Next, we will focus on the existence and uniqueness of the global solutions of model (2.3) by semigroup.

Theorem 3.2. For every initial value function $\phi: = (\phi_{1i}, \phi_{2i}, \phi_{3j}, \phi_{4j}) \in\mathbb{X}^{+}$, model (2.3) has a unique solution $U(t, x;\phi) = (S^{a}_{i, j}(t, x;\phi_{1i}), I^{a}_{i, j}(t, x;\phi_{2i}), S^{h}_{i, j} (t, x;\phi_{3j}), I^{h}_{i, j}(t, x;\phi_{4j}))$ with $U(0, x;\phi) = \phi$ and the semiflow $\Psi_{t}:\mathbb{X}^{+}\longrightarrow\mathbb{X}^{+}$ generated by (2.3) is defined by

Furthermore, the semiflow $\Psi_{t}:\mathbb{X}^{+}\rightarrow \mathbb{X}^{+}$ is point dissipative and the positive orbits of bounded subsets of $\mathbb{X}^{+}$ for $\Psi_{t}$ are bounded.

Proof. Suppose $\mathcal{T}_{1i}(t)$, $\mathcal{T}_{2i}(t)$, $\mathcal{T}_{3j}(t)$, $\mathcal{T}_{4j}(t)$: $C(\overline{\Omega}, \mathbb{R})\longrightarrow C(\overline{\Omega}, \mathbb{R})$ be the $C_{0}$ semigroups associated with $\sum_{k = 1}^{l}\frac{\partial}{\partial x_{k}}(D_{ik}\frac{\partial}{\partial x_{k}})-\mu_{a}$, $\sum_{k = 1}^{l}\frac{\partial}{\partial x_{k}}(D_{ik}\frac{\partial}{\partial x_{k}})-(\mu_{a}+\delta_{a})$, $\sum_{k = 1}^{l}\frac{\partial}{\partial x_{k}}(G_{kj}\frac{\partial}{\partial x_{k}})-\mu_{h}$, $\sum_{k = 1}^{l}\frac{\partial}{\partial x_{k}}(G_{kj}\frac{\partial}{\partial x_{k}})-(\mu_{h}+\delta_{h}+\gamma_{h})$ subject to the Neumann boundary condition, respectively. It then follows that $\mathcal{T}(t)$: = ($\mathcal{T}_{1i}(t)$, $\mathcal{T}_{2i}(t)$, $\mathcal{T}_{3j}(t)$, $\mathcal{T}_{4j}(t)$), it is strongly positive and compact for each $t > 0$ ^[20]. For every initial value functions $\phi$ = ($\phi_{1i}(x)$, $\phi_{2i}(x)$, $\phi_{3j}(x)$, $\phi_{4j}(x)$)$\in\mathbb{X}^{+}$, we define $F$ = ($F_{1i}$, $F_{2i}$, $F_{3j}$, $F_{4j}$): $\mathbb{X}^{+}\longrightarrow\mathbb{X}$ by $F_{1i}(\phi)(x) = \Lambda_{a}-\lambda_{a}(i)\phi_{1i}(x)\frac{\Theta_{a}(t, x, \phi_{2i})} {1+\alpha_{1}\Theta_{a}(t, x, \phi_{2i})}$, $F_{2i}(\phi)(x) = \lambda_{a}(i)\phi_{1i}(x) \frac{\Theta_{a}(t, x, \phi_{2i})} {1+\alpha_{1}\Theta_{a}(t, x, \phi_{2i})}$, $F_{3j}(\phi)(x) = \Lambda_{h} -\lambda_{ah}(j)\phi_{3j}(x) \Theta_{ah}(t, x, \phi_{2i})$, $F_{4j}(\phi)(x) = \lambda_{ah}(j)\phi_{3j}(x) \Theta_{ah}(t, x, \phi_{2i})$. The model (2.3) can be rewritten as the integral equation

where $U(t) = (S^{a}_{i, j}, I^{a}_{i, j}, S^{h}_{i, j}, I^{h}_{i, j})^{T}$. It is easy to show that $\lim_{h\longrightarrow0^{+}}\; dist(\phi+hF(\phi), \mathbb{X}^{+}) = 0, \forall\phi\in\mathbb{X}^{+}$. By in ^[21], model (2.3) has a unique positive solution $(S^{a}_{i, j}(t, x;\phi_{1i}), I^{a}_{i, j}(t, x;\phi_{2i}), S^{h}_{i, j}(t, x;\phi_{3j}), I^{h}_{i, j}(t, x;\phi_{4j}))$ on $[0, \tau_{e})\times\Omega$, where $0 < \tau_{e}\leq\infty$. In what follows, we prove that the local solution can be extended to a global one, that is $\tau_{e} = \infty$. For this purpose, by a standard argument, we only need to prove that the solution is bounded in $[0, \tau_{e})\times\Omega$. To this end, we let $N^{a}_{i, j}(t, x) = S^{a}_{i, j}(t, x) +I^{a}_{i, j}(t, x)$, $N^{h}_{i, j}(t, x) = S^{h}_{i, j}(t, x)+I^{h}_{i, j}(t, x) +R^{h}_{i, j}(t, x)$. Then $N^{a}_{i, j}(t, x)$, and $N^{h}_{i, j}(t, x)$ satisfy the following system

Thank to ^[22], model (3.1) admits a unique positive steady state $E^{0}$ which is globally asymptotically stable in $C(\Omega, \mathbb{R})$. It follows that $U(t, x;\phi) = (S^{a}_{i, j}(t, x;\phi), I^{a}_{i, j}(t, x;\phi), S^{h}_{i, j}(t, x;\phi), I^{h}_{i, j}(t, x;\phi))$ is bounded on $[0, \tau_{e})\times\Omega$, which implies the Theorem.

4.   Threshold dynamics

In the rest of this subsection, we first define the basic reproduction number of virus and show that it is a threshold for viral persistence or extinction.

It follows from Theorem 3.2 model (2.3) with (2.4) admits a unique disease free steady state, $E^{0} = (S^{a0}_{1, j}, S^{a0}_{2, j}, \cdots, S^{a0}_{n, j}, 0, 0, \cdots, 0, S^{h0}_{i, 1}, S^{h0}_{i, 2}, \cdots, S^{h0}_{i, n}, 0, 0, \cdots, 0)$, linearizing (2.3) with (2.4) at $E^{0}$, we get the following linear cooperative system for $I^{a}_{i, j}$, and $I^{h}_{i, j}$, component

Substituting $I^{a}_{i, j} = e^{\xi_{i} t}\psi_{i}(x), \; I^{h}_{i, j} = e^{\xi_{j}t}\varphi_{j}(x),$ into (4.1), $\psi_{i}(x)\in C(\overline{\Omega}, \mathbb{R}^{2n})$, $\varphi_{j}(x)\in C(\overline{\Omega}, \mathbb{R}^{2n})$, we obtain the following eigenvalue problem,

which is a cooperation system. By a similar argument in ^[39], it follows that (4.2) admits a unique principal eigenvalue $\xi_{0}(E^{0})$ with a strongly positive eigenfunction $(\psi_{i}(x), \varphi_{j}(x))$. Denote by $\Gamma(t)$ the solution semigroup of (4.1) on $C(\overline{\Omega}, \mathbb{R}^{2n})$ with generator $\mathcal{B}: = B+F$,

where $\omega_{a} = -\mu_{a}-\delta_{a}$, $\omega_{h} = -\mu_{h} -\delta_{h}$, $f(i) = \frac{ip_{a}(i, \cdot)} {\langle k\rangle_{a}}$, $g(j) = \frac{jp_{a}(\cdot, j)}{\langle k\rangle_{ah}}$, $\triangle^{a}_{i} = \Sigma_{k = 1}^{l}\frac{\partial}{\partial x_{k}}D_{ik}\frac{\partial}{\partial x_{k}}$, $\triangle^{h}_{j} = \Sigma_{k = 1}^{l}\frac{\partial} {\partial x_{k}}G_{kj}\frac{\partial}{\partial x_{k}}$, $B = diag(\omega_{a}+\triangle^{a}_{1}, \cdots, \omega_{a}+\triangle^{a}_{n}, \omega_{h}+\triangle^{h}_{1}, \cdots, \omega_{h}+\triangle^{h}_{n})^{T} = diag(\triangle^{a}_{1}, \cdots, \triangle^{a}_{n}, \triangle^{h}_{1}, \cdots, \triangle^{h}_{n})^{T}-V$,

We further let $\overline{\Gamma}(t):C(\overline{\Omega}, \mathbb{R}^{2n})\rightarrow C(\overline{\Omega}, \mathbb{R}^{2n})$ be the $C_{0}$-semigroup generated by operator $B$, we know that both $B$ and $-V$ are cooperative for any $x\in\Omega$, which implies that $\overline{\Gamma}(t)$ is a positive semigroup in the sense that $\overline{\Gamma}(t)C(\overline{\Omega}, \mathbb{R}^{2n}_{+})\subseteq C(\overline{\Omega}, \mathbb{R}^{2n}_{+})$. Further from ^[27] and the fact that both $\mathcal{B}$ and $B$ are resolvent-operators, it then follows that the next generation operator is $\mathcal{L}: = -FB^{-1}$, given by $\mathcal{L}(\phi) = \int_{0}^{\infty}F(x) \overline{\Gamma}(t)\phi(x)dt, \phi\in C(\overline{\Omega}, \mathbb{R}^{2n}), x\in\overline{\Omega}$. Then $\mathcal{L}$ is well-defined, continuous, and positive operator on $C(\overline{\Omega}, \mathbb{R}^{2n})$, which maps the initial infection distribution $\phi$ to the distribution of the total new infections produced during the infection period. We follow the procedure in ^[28] to define the spectral radius of $\mathcal{L}$ as the basic reproduction number

Lemma 4.1. $\mathcal{R}_{0}-1$ and $\xi_{0}(E^{0})$ have the same sign. The steady state $E^{0}$ is asymptotically stable if $\mathcal{R}_{0} < 1$, and it is unstable $\mathcal{R}_{0} > 1$.

Proof. The method was the same as that in reference ^[26,27].

Theorem 4.2. (i)If $\mathcal{R}_{0} < 1$ then the disease-free equilibrium $E^{0}$ is globally asymptotically stable.

(ii) If $\mathcal{R}_{0} > 1$, then there exists $\epsilon_{0}$ such that any positive solution of model (2.3) satisfies

Proof. The method was the same as that in reference ^[29,30].

5.   Near-optimal control

In this section, we will establish an near-optimal control of model (2.3) and get an optimal control strategy in theory. We introduce control variables $u(t, x)$ = $(u^{a}_{i}(t, x)$, $u^{h}_{j}(t, x))^{T}\in\mathcal {U}([0, T]\times\Omega)$ = $\{u^{a}_{i}(t, x)$ and $u^{h}_{j}(t, x)$ measurable: $0\leq u^{a}_{i}(t, x)\leq1$, $0 \leq u^{h}_{j}(t, x)\leq1$, $i, j = 1, 2, \cdots, n\}$. Assume the control set ${U}([0, T]\times\Omega)$ is convex. $u^{a}_{i}(t, x)$ denotes the proportion of slaughtered susceptible poultry and infected poultry, $u^{h}_{j}(t, x)$ denotes the proportion of treatment for infected humans. Now, we obtain an optimal control system as follows,

we take saturated treatment rate $\frac{cu^{h}_{j}I^{h}_{i, j}} {1+\alpha_{2}I^{h}_{i, j}}\; (\alpha_{2}$ denotes saturation constant) because of the medical resources are limited. We intend to get an near-optimal pair of slaughter and treatment, which seeks to minimize the number of infected poultry, the number of infected humans, and the cost during the implementing these $2n$ control strategies. Therefore, we establish the following objective function

where $A_{1i}, \; A_{2i}, \; A_{3j}, \; A_{4j}$ are regarded as a tradeoff factor. The meaning of the objective functional $J(u^{a}_{i}(t, x), u^{h}_{j}(t, x))$ is described as follows:

(1) The term $\int_{0}^{T}\int_{\Omega}\sum_{i = 1}^{n}A_{1i} I^{a}_{i, j}(t, x)dxdt +\int_{0}^{T}\int_{\Omega}\sum_{j = 1}^{n}A_{3j}I^{h}_{i, j}(t, x)dxdt$ gives the total number of infected poultry infected with avian influenza virus and the total number of infected human over the time period $T$.

(2) The term $\int_{0}^{T}\int_{\Omega}\sum_{i = 1}^{n}A_{2i}u^{a}_{i}(t, x)(S^{a}_{i, j}(t, x)+I^{a}_{i, j}(t, x)) +\frac{1}{2}\varsigma_{i}(u^{a}_{i})^{2}(t, x)dxdt$ gives the total cost of slaughtering for susceptible and infected avian.

(3) The term $\int_{0}^{T}\int_{\Omega}\sum_{j = 1}^{n}A_{4j}u^{h}_{j}(t, x)I^{h}_{i, j}(t, x) +\frac{1}{2}\varrho_{j}(u^{h}_{j})^{2}(t, x)dxdt$ gives the total cost of treatment for infected humans.

The objective of the optimal control problem is to minimize the cost function $J(u^{a}_{i}(t, x), u^{h}_{j}(t, x))$ over all $u(t, x) = (u^{a}_{i}(t, x), u^{h}_{j}(t, x))^{T}\in\mathcal{U}([0, T]\times\Omega)$. The value function is defined as

Definition 5.1. (Near-optimal Control)^[24] Both a family of admissible pairs $\{(u^{a\varepsilon}_{i}(t, x), u^{h\varepsilon}_{j}(t, x)\}$ parameterized by $\varepsilon > 0$ and any element $(u^{a\varepsilon}_{i}(t, x), u^{h\varepsilon}_{j}(t, x))$ in the family are called near-optimal if

holds for sufficiently small $\varepsilon$, where $r$ is a function of $\varepsilon$ satisfying $r(\varepsilon)\rightarrow 0$ as $\varepsilon\rightarrow 0$. The estimate $r(\varepsilon)$ is called an error bound. If $r(\varepsilon) = c\varepsilon^{\kappa}$ for some $\kappa$ independent of the constant $c$, then $u^{a\varepsilon}_{i}(t), \; u^{h\varepsilon}_{j}(t)$ are called near-optimal with order $\varepsilon^{\kappa}$.

Lemma 5.2. (Ekeland's Principle, ^[25]). Let (S, d) be a complete metrix space, and let $\rho(\cdot):S\rightarrow R^{1}$ be lower semicontinuous and bounded from below. For $\epsilon\geq0$, suppose that $u^{\epsilon}(t, x)\in S$ satisfies

then, for any $\iota > 0$, there exists $u^{\iota}(\cdot)\in S$ such that $\rho(u^{\iota}(\cdot))\leq\rho(u^{\epsilon}(\cdot), \; d(u^{\iota}(\cdot), u^{\epsilon}(\cdot))\leq\iota, \; \rho(u^{\iota}(\cdot))\leq\rho(u(\cdot)) +\frac{\epsilon}{\iota}d(u(\cdot), u^{\iota}(\cdot))$.

5.1.   Adjoint equation and some prior estimates

In this section, we will first show a few lemmas, which will be used to establish the sufficient and necessary condition for the near-optimal control of model (5.1). As is well known, the study of adjoint equations plays a key role in deriving the necessary and sufficient conditions of optimality. Next, we introduce the adjoint equation:

The following Lemma 5.3 shows that the solution of model model (5.1) is bounded.

Lemma 5.3. For any $\eta\geq0$, and $(u^{a}_{i}(t, x), \; u^{h}_{j}(t, x))\in\mathcal{U}([0, T]\times\Omega)$, we have

where $C$ is a constant that depends only on $\eta$.

Proof. The method was the same as that the Lemma 3.1, we get the almost surely positively invariant set of model model (5.1), which means that the inequality (5.4) holds.

Lemma 5.4. For any $(u^{a}_{i}(t, x), \; u^{h}_{j}(t, x))\in\mathcal{U}([0, T]\times\Omega)$, we have

where $C$ is a constant.

The proof is shown in Appendix A.

For any $u(t, x), \; \widetilde{u}(t, x)\in\mathcal{U}([0, T]\times\Omega)$, define a metric on $\mathcal{U}([0, T]\times\Omega)$ as follows

by a similar way as Lemma 6.4 in ^[32], we know that $\mathcal{U}([0, T]\times\Omega)$ is a complete space under $d$.

The following Lemma will show the continuity of the state process $(S^{a}_{i, j}(t, x)$, $I^{a}_{i, j}(t, x)$, $S^{h}_{i, j}(t, x)$, $I^{h}_{i, j}(t, x))$ under metric $d$.

Lemma 5.5. For any $\eta\geq0$, and $0 < \kappa < 1$ satisfying $\kappa\eta < 1$, there exists a constant $C_{\kappa\eta}$ such that $u(t, x), \widetilde{u}(t, x)\in\mathcal{U}([0, T]\times\Omega)$ along with the corresponding trajectory $(S^{a}_{i, j}(t, x)$, $I^{a}_{i, j}(t, x)$, $S^{h}_{i, j}(t, x)$, $I^{h}_{i, j}(t, x))$, $(\widetilde{S}^{a}_{i, j}(t, x)$, $\widetilde{S}^{a}_{i, j}(t, x)$, $\widetilde{S}^{h}_{i, j}(t, x)$, $\widetilde{S}^{h}_{i, j}(t, x))$, we have

The proof is shown in Appendix B.

The next lemma will show that the $pth$ moment continuity of the solutions to the adjoint Eq (5.3) under metric $d$.

Lemma 5.6. For any $1 < \eta < 2$, and $0 < \kappa < 1$ satisfying $(1+\kappa)\eta < 2$, there exists a constant $C_{\kappa\eta}$ such that $u(t, x), \; \widetilde{u}(t, x) \in\mathcal{U}([0, T]\times\Omega)$ along with the corresponding trajectory $(S^{a}_{i, j}(t, x)$, $I^{a}_{i, j}(t, x)$, $S^{h}_{i, j}(t, x)$, $I^{h}_{i, j}(t, x))$, $(\widetilde{S}^{a}_{i, j}(t, x)$, $\widetilde{S}^{a}_{i, j}(t, x)$, $\widetilde{S}^{h}_{i, j}(t, x)$, $\widetilde{S}^{h}_{i, j}(t, x))$, and the solution of corresponding adjoint equation, we have

The proof is shown in Appendix C.

5.2.   Sufficient conditions for near optimal control

To obtain the sufficient conditions, we define the Hamiltonian function $H$ as follows:

We can test the Hamiltonian function $H$ is convex, a.s. Next, the sufficient conditions for the approximate optimal controls of model model (5.1) are proposed.

Theorem 5.7. Let $(S^{a\varepsilon}_{i, j}(t, x)$, $I^{a\varepsilon}_{i, j}(t, x)$, $S^{h\varepsilon}_{i, j}(t, x)$, $I^{h\varepsilon}_{i, j}(t, x)$ , $u^{a\varepsilon}_{i}(t, x)$, $u^{h\varepsilon}_{j}(t, x))$ be an admissible pair and $(p^{\varepsilon}_{1i}(t, x)$, $p^{\varepsilon}_{2i}(t, x)$, $p^{\varepsilon}_{3j}(t, x)$, $p^{\varepsilon}_{4j}(t, x))$ be the solution of (5.3) corresponding to $(S^{a\varepsilon}_{i, j}(t, x)$, $I^{a\varepsilon}_{i, j}(t, x)$, $S^{h\varepsilon}_{i, j}(t, x)$, $I^{h\varepsilon}_{i, j}(t, x)$ , $u^{a\varepsilon}_{i}(t, x)$, $u^{h\varepsilon}_{j}(t, x))$. Assume the control set $\mathcal{U}([0, T]\times\Omega)$ is convex.a.s. Then for any $\varepsilon > 0$, if

we have

Proof. In order to prove that $H_{u}$ can be estimated by $\varepsilon$, we define a new metric $d$ on $\mathcal{U}([0, T]\times\Omega)$. Since the control region is closed, $\mathcal{U}([0, T]\times\Omega)$ becomes a complete matric space when endowed with the metric

where $v^{\varepsilon}(t, x) = 1+|S^{a\varepsilon}_{i, j}| +|I^{a\varepsilon}_{i, j}|+ |S^{h\varepsilon}_{i, j}|+|I^{h\varepsilon}_{i, j}|$. Next, we will estimate $J(0, \phi(0, x);u^{a\varepsilon}_{i}(t, x), u^{h\varepsilon}_{j}(t, x)) -J(0, \phi(0, x);u^{a}_{i}(t, x), u^{h}_{j}(t, x))$. From the Hamiltonian function (5.5) and the objective function (5.2), we have

Next, we will focus on the estimation of $H_{u}$. Firstly, we define a new functional $M(\cdot):\mathcal{U}([0, T]\times\Omega)\rightarrow \mathbb{R}$,

we show that

Thus, $M(u)$ is continuous on $\mathcal{U}([0, T]\times\Omega)$ with respect to $d$. According to the conditions of Theorem (4.2) and Lemma 5.2, we can see that there exists $\widetilde{u}^{\varepsilon}\in\mathcal{U}([0, T]\times\Omega)$ such that

This show that

According to ^[23], we have

Because the Hamiltonian function $H$ is differentiable in $u$, it follows from (5.8) that there exists a $\vartheta^{\varepsilon}\in [-\varepsilon^{\frac{1}{2}}v^{\varepsilon}, \varepsilon^{\frac{1}{2}}v^{\varepsilon}]$ such that

From (5.9), we have

This proof is complete.

From the Lemma 5.4 and definition of $d$, we can achieve the desired conclusion from (5.6) and (5.10) by Hölder's inequality. Furthermore, according to the ideas in Lenhart and Workman ^[34], the optimal control $(u^{a\ast}_{i}, u^{h\ast}_{j})$, which minimizes the objective function $J(u^{a}_{i}(t, x), u^{h}_{j}(t, x))$, is obtained and represented by

5.3.   The necessary conditions for near optimal control

In this suction, we will derive the necessary conditions for near optimal control of model (5.1).

Theorem 5.8. Let $(S^{a\varepsilon}_{i, j}(t, x)$, $I^{a\varepsilon}_{i, j}(t, x)$, $S^{h\varepsilon}_{i, j}(t, x)$, $I^{h\varepsilon}_{i, j}(t, x)$ , $u^{a\varepsilon}_{i}(t, x)$, $u^{h\varepsilon}_{j}(t, x))$ be an admissible pair. There exists a constant C such that any $\eta\in[0, 1), \varepsilon > 0$ and any $\varepsilon$-optimal pair $(S^{a\varepsilon}_{i, j}(t, x)$, $I^{a\varepsilon}_{i, j}(t, x)$, $S^{h\varepsilon}_{i, j}(t, x)$, $I^{h\varepsilon}_{i, j}(t, x),$ $u^{a\varepsilon}_{i}(t, x)$, $u^{h\varepsilon}_{j}(t, x))$, the following condition holds:

Proof. We have that $J(0, \phi(0, x);u^{a}_{i}(t, x), u^{h}_{j}(t, x))$:$\mathcal{U}([0, T]\times\Omega) \rightarrow \mathbb{R}$ is continuous under the metric $d$, therefore, by using Ekeland's Principle 5.2, we can choose $\iota = \varepsilon^{\frac{2}{3}}$, there exists an admissible pair ($S^{a\varepsilon}_{i, j}$, $I^{a\varepsilon}_{i, j}$, $S^{h\varepsilon}_{i, j}$, $I^{h\varepsilon}_{i, j}$, $u^{a\varepsilon}_{i}$, $u^{h\varepsilon}_{j}$) such that $d(u^{\varepsilon}, \widetilde{u}^{\varepsilon}) < \varepsilon^{\frac{2}{3}}$, and $\widetilde{J}(0, \phi(0, x); \widetilde{u}^{\varepsilon}) \leq\widetilde{J}(0, \phi(0, x); u), \forall u\in\mathcal{U}([0, T]\times\Omega)$, where $\widetilde{J}(0, \phi(0, x); u(t, x)) = J(0, \phi(0, x); u(t, x))+\varepsilon^{\frac{1}{3}} d(u^{\varepsilon}, \widetilde{u}^{\varepsilon})$. This show that $(S^{a\varepsilon}_{i, j}, I^{a\varepsilon}_{i, j}, S^{h\varepsilon}_{i, j}, I^{h\varepsilon}_{i, j}, u^{a\varepsilon}_{i}, u^{h\varepsilon}_{j})$ is an optimal pair for the objective function $\widetilde{J}(0, \phi(0, x); u(t, x))$. Next, we will use the spike variation technique to derive a "maximum principle" for $(S^{a\varepsilon}_{i, j}, I^{a\varepsilon}_{i, j}, S^{h\varepsilon}_{i, j}, I^{h\varepsilon}_{i, j}, u^{a\varepsilon}_{i}, u^{h\varepsilon}_{j})$. Let $\overline{t}\in[0, T], \; \delta > 0$, and $u(t, x))\in\mathcal{U}([0, T]\times\Omega)$, we define $u^{\delta}(t, x)\in\mathcal{U}([0, T]\times\Omega)$ as follows

Then, we have

Thus $J(0, \phi(0, x);\widetilde{u}^{\varepsilon}(t, x)) = \widetilde{J}(0, \phi(0, x); \widetilde{u}^{\varepsilon}(t, x))\leq\widetilde{J}(0, \phi(0, x); u^{\delta}(t, x)) = J(0, \phi(0, x); u^{\delta}(t, x))+\delta\varepsilon^{\frac{1}{3}}$. It follows from (5.12), Lemma 5.5 and Taylor's expansion, we can obtain that

Using the Itô's formula to $Q(t, x) = \widetilde{p}^{\varepsilon}_{1i} (S^{a\delta}_{i, j} -\widetilde{S}^{a\varepsilon}_{i, j}) + \widetilde{p}^{\varepsilon}_{2i} (I^{a\delta}_{i, j} -\widetilde{I}^{a\varepsilon}_{i, j}) + \widetilde{p}^{\varepsilon}_{3j} (S^{h\delta}_{i, j} -\widetilde{S}^{h\varepsilon}_{i, j})+ \widetilde{p}^{\varepsilon}_{4j} (I^{h\delta}_{i, j} -\widetilde{I}^{h\varepsilon}_{i, j})$, and from Lemmas 5.3 and 5.4, we can obtain that

Substituting (5.14) into (5.13), we have

Dividing (5.15) by $\delta$ and letting $\delta\rightarrow0$, we can get

Now, we will derive an estimate for the right side of (5.16) with all the $(\widetilde{S}^{a\varepsilon}_{i, j}, \widetilde{I}^{a\varepsilon}_{i, j}, \widetilde{S}^{h\varepsilon}_{i, j}, \widetilde{I}^{h\varepsilon}_{i, j}, \widetilde{u}^{a\varepsilon}_{i}, \widetilde{u}^{h\varepsilon}_{j})$ replaced by $(S^{a\varepsilon}_{i, j}, I^{a\varepsilon}_{i, j}, S^{h\varepsilon}_{i, j}, I^{h\varepsilon}_{i, j}, u^{a\varepsilon}_{i}, u^{h\varepsilon}_{j})$. To achieve this goal, we first estimate the following difference:

From Lemma 5.6 and due to $d(u^{\varepsilon}, \widetilde{u}^{\varepsilon}) < \varepsilon^{\frac{2}{3}}$, we have that for any $1 < \eta < 2$, and $0 < \kappa < 1$ satisfying $(1+\kappa)\eta < 2$, and

similarly, we have

Thus

By analogous calculation as (5.17), we have

Combine the expression of Hamiltonian function (5.5), we can immediately obtain the conclusion.

6.   Numerical simulations

In this section, we present numerical simulations to demonstrate the results. Let $[0, T]\times\Omega$ be the admissible control domain. We consider a near-optimal problem with the following objective function, simulations are based on a scale-free network with $p(k) = (r-1)m^{(r-1)}k^{-r}$, where $m$ represents the smallest degree on a scale-free network nodes, $r$ is power exponent. Let $m = 1, r = 3$, the number of nodes on a scale-free network is $N = 100$, and we add each new node with 3 new edges. We choose degree $k$ as $k_{1} = 1, k_{2} = 2, k_{3} = 3, k_{4} = 4, k_{5} = 5, k_{6} = 6, k_{7} = 7, k_{8} = 8, k_{9} = 9$. We get the average degree of complex network structure $\langle k\rangle_{a}(\langle k^{2}\rangle_{a}) = 3.27(9.04)$ through simple calculation. The parameter values are chosen as follows:

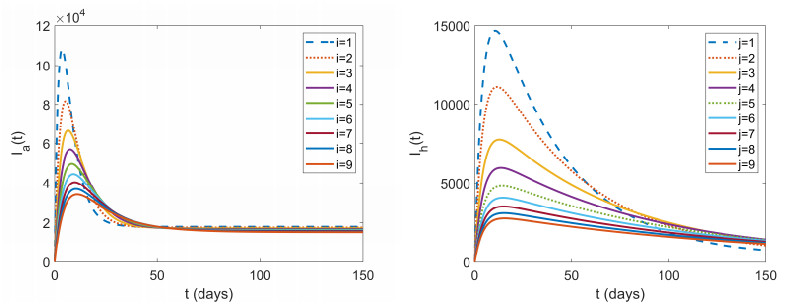
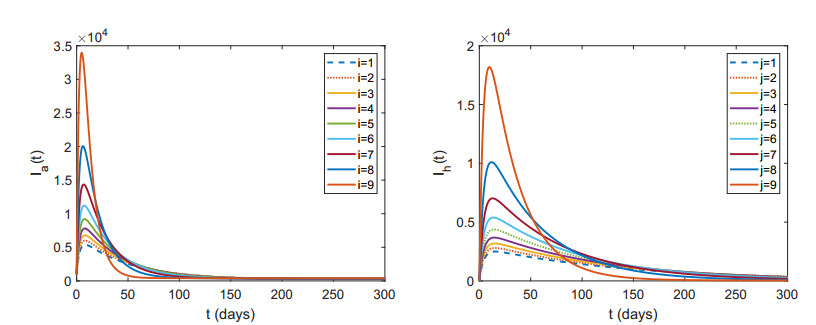
Example 6.1. For model (2.3) all parameters are positive constants, we choose degree $k$ as $k_{1} = 1, k_{2} = 2, k_{3} = 3, k_{4} = 4, k_{5} = 5, k_{6} = 6, k_{7} = 7, k_{8} = 8, k_{9} = 9$. We get the average degree of complex network structure $\langle k\rangle_{a}(\langle k^{2}\rangle_{a}) = 3.27(9.04)$ through simple calculation, when we choose $\lambda_{a} = 7\times10^{-4}$, $\mathcal{R}_{0} = 1.5246 > 1$; when we choose $\lambda_{a} = 3\times10^{-4}$, $\mathcal{R}_{0} = 0.3689 < 1$.

Figure 1 shows the unique endemic equilibrium point is globally asymptotically stable, and the virus will persist. Figure 2 shows the unique disease-free equilibrium point $E^{0}$ is globally asymptotically stable, and the virus will die out in the long run. Furthmore, we can obtain that the density of infected nodes increase with the degree k increase in Example 6.1. In other words, the lager the degree k is, the higher the density of infected nodes is, which indicates that the nodes having lots of relative neighbors are more likely to be infected by contacting frequently.

Example 6.2. We analyzed the effects of slaughter rate and curative ratio on avian influenza control. Let's take a one-dimensional spatial variable, $\Omega = [0, L]$. The control $u^{a}_{i}(t, x), \; u^{h}_{j}(t, x)$ are measurable and for any $(t, x)\in[0, T]\times[0, L], \; 0\leq u^{a}_{i}(t, x), \; u^{h}_{j}(t, x)\leq1$. Without the loss of generality, for any fixes time $T$, we give step size $\Delta t\in(0, 1)$ and for any fixes space $L$, we give step size $\Delta x\in(0, 1)$, we denote $t_{m} = m\Delta t, \; x_{n} = n\Delta t$, $m = 0, 1, \cdots, [\frac{T}{\Delta t}], \; n = 0, 1, \cdots, [\frac{L}{\Delta x}$]. For the numerical simulations of model (5.1) and adjoint Eq (5.3), we use the Milstein's method ^[33]. Thus, model (5.1) and (5.3) can be rewritten as the following discrete equations:

in order to find the optimal control of $u^{a}_{i}$, $u^{h}_{j}$, we give the nonlinear conjugate gradient algorithm ^[40] as follows:

Step 1: Choose an initial $u^{a}_{i0}$, $u^{h}_{j0}$, an initial step size $s_{0}$ and stopping tolerances $Tol_{1}$ and $Tol_{2}$, initial states $(S^{a}_{i, j}(0)$, $I^{a}_{i, j}(0)$, $S^{h}_{i, j}(0)$, $I^{h}_{i, j}(0))$ by solving Eq (6.1), initial adjoints $p_{0}$ = ($p_{1i}(0)$, $p_{2i}(0)$, $p_{3j}(0)$, $p_{4j}(0))$ by solving Eq (6.2), gradient of $J$, i.e., $g_{i, 0} = \varsigma_{i} u^{a}_{i0} + (p_{1i}(0)-A_{2i})S^{a\ast}_{i, j}(0) +p_{2i}(0)I^{a\ast}_{i, j}(0)$, $h_{j, 0} = (1+\alpha_{2}I^{h\ast}_{i, j}(0) u^{h}_{j0} + cp_{4j}(0)I^{h\ast}_{i, j}(0) -A_{4j}I^{h\ast}_{i, j}(0) (1+\alpha_{2}I^{h\ast}_{i, j}(0))$, anti-gradient of $J$, i.e., $d^{*}_{0} = -g_{i, 0}$, $d_{0} = -h_{j, 0}$.

Step 2: control, i.e., $u_{k+1} = u_{k} + s_{k}d_{k}$, states $(S^{a}_{i, \cdot, k+1}$, $I^{a}_{i, \cdot, k+1}$, $S^{h}_{\cdot, j, k+1}$, $I^{h}_{\cdot, j, k+1})$ = ($S^{a}_{i, \cdot, u_{k+1}}$, $I^{a}_{i, \cdot, u_{k+1}}$, $S^{h}_{\cdot, j, u_{k+1}}$, $I^{h}_{\cdot, j, u_{k+1}})$ by solving Eq (6.1) $(p_{1i, k+1}$, $p_{2i, k+1}$, $p_{3j, k+1}$, $p_{4j, k+1})$ = $(p_{1i, S^{a}_{i, \cdot, k+1}}$, $p_{2i, I^{a}_{i, \cdot, k+1}}$, $p_{3j, S^{h}_{\cdot, j, k+1}}$, $p_{4j, I^{h}_{\cdot, j, u_{k+1}}})$ by solving Eq (6.2), gradient of $J$, i.e., $g_{i, k+1} = \varsigma_{i} u^{a}_{i, k+1} + (p_{1i, k+1}-A_{2i})S^{a\ast}_{i, \cdot, k+1} +p_{2i, k+1}I^{a\ast}_{i, \cdot, k+1}$, $h_{j, k+1} = (1+\alpha_{2}I^{h\ast}_{\cdot, j, k+1} u^{h}_{j, k+1} + cp_{4j, k+1}I^{h\ast}_{\cdot, j, k+1} -A_{4j}I^{h\ast}_{\cdot, j, k+1} (1+\alpha_{2}I^{h\ast}_{\cdot, j, k+1})$.

Step 3: Stop if $\|g_{i, k+1}\| < Tol_{1}$, $\|h_{j, k+1}\| < Tol_{1}$ or $\|J_{k+1} - J_{k}\| \leq Tol_{2}$.

Compute the conjugate direction $\varpi_{k+1}$ according to one of the updated formulas ^[41].

$d_{k+1} = -g_{i, k+1} + \varpi_{k+1}d_{k}$. aselect step size $s_{k+1}$ in terms of some standard options.

Set $k: = k+1$ and go to Step 1.

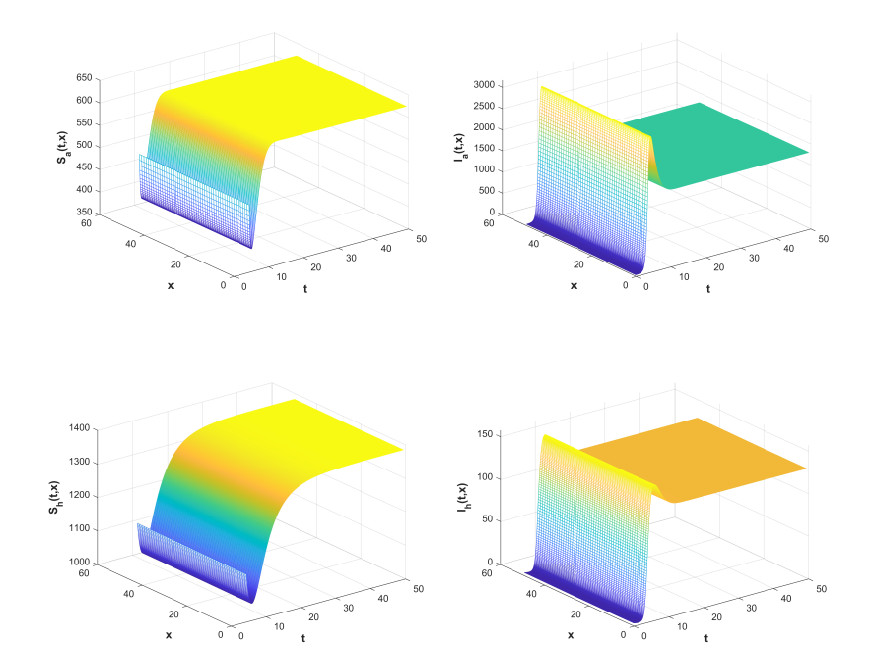
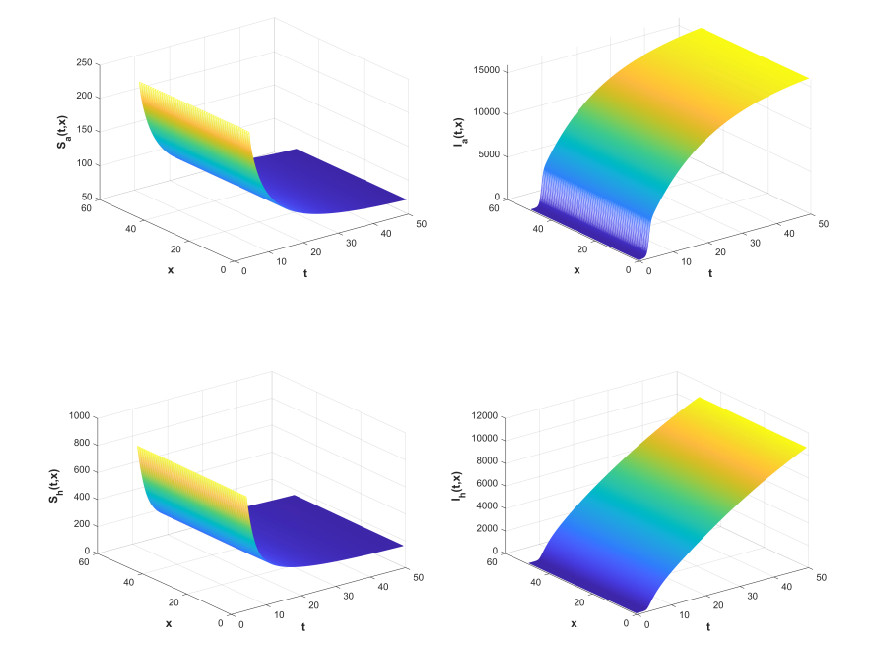
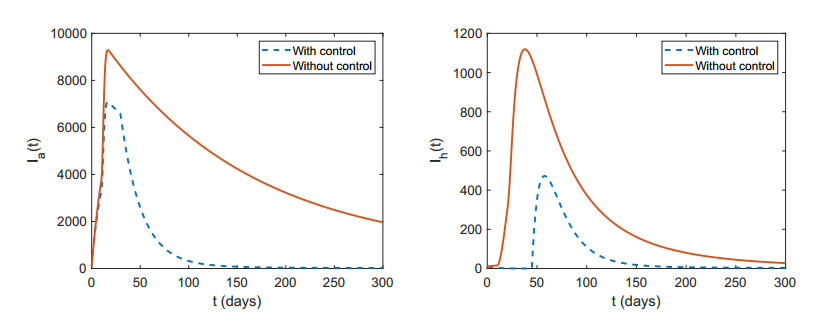
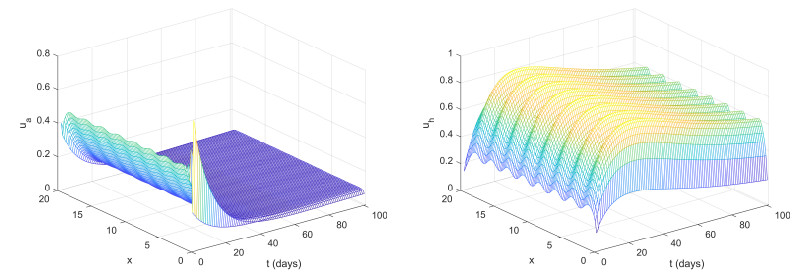
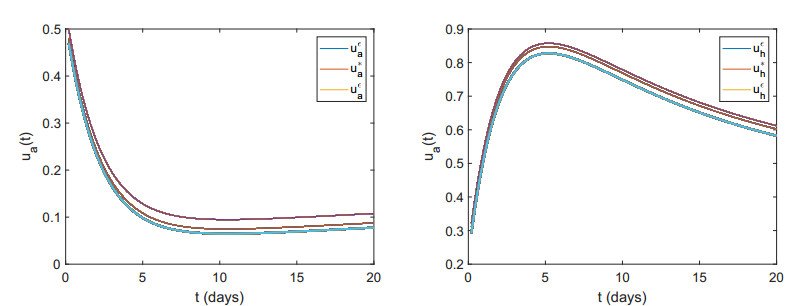
Figure 3 shows the solution of model (2.3) curves representing the variation of populations for susceptible poultry, infected poultry, susceptible human, infected human. Figure 4 shows the solution of model (5.1) curves representing the variation of populations for susceptible poultry, infected poultry, susceptible human, infected human. The comparison between Figure 4 and Figure 3 shows that the proportion of slaughtered susceptible poultry and infected poultry can effectively prevent the outbreak of avian influenza; With limited medical resources, treatment of infected humans can reduce the spread of avian influenza among humans. Figure 6, we can see that in order to prevent the spread of avian influenza and reduce the economic loss it brings, the slaughter rate of poultry should be gradually reduced over time. In order to reduce the risk of the spread of avian influenza, the proportion of treatment for infected humans should be gradually increased over time. However, because of limited medical resources, after the treatment rate reaches a peak for infected humans, it will gradually decrease. Figure 7 shows the optimal control $u^{a\ast}_{i}, u^{h\ast}_{j}$ and the near-optimal control $u^{a\varepsilon}_{i}, u^{h\varepsilon}_{j}$, respectively. The optimal control $u^{a\ast}_{i}$ indicates that the optimal slaughter rate for the poultry gradually decreases; the optimal control $u^{h\ast}_{j}$ denotes that the optimal treatment rate of the human is different in different times. The results show that the error of numerical simulation results of optimal control and near-optimal control is less than 0.2.

7.   Conclusions

The optimal control problem is usually composed of a group of state equations and adjoint equations, but these equations have difficulties obtaining an exact solution. Therefore, we concerned the near-optimal control and threshold behavior of an avian influenza model with saturation on heterogenous complex networks in this paper. We first give the basic reproduction number $\mathcal{R}_{0}$, which can be used to govern the threshold dynamics of influenza disease. In addition, we obtained the sufficient and necessary conditions for the near-optimality. Lastly, numerical simulations were performed to illustrate the results and confirm that the treatment control resulted in a substantial reduction in the level of infected population while the treatment cost was minimized. In this paper, we assumed that the parameters are all precisely known, however, they may not be true due to the unavoidable errors and the lack of sufficient information in the measurement process and so on. How uncertain parameter values and Lévy noise affect the near-optimality of this epidemic model remains unclear and deserves further investigation. We will study the near optimal control of the avian influenza model on complex network with Lévy noise and imprecise parameters in the future work. Firstly, we give the method of parameter estimates of the avian influenza model. According to the Lévy-It$\hat{o}$'s decomposition theorem, we have $\widetilde{L}(t) = \sigma B(t)+\int_{Y}\nu \widetilde{N}(t, d\nu)$. Then, by using Ekeland's principle and Hamiltonian function, we obtain the sufficient and necessary conditions of near optimal of the avian influenza model with Lévy noise and imprecise parameters.

Acknowledgements

The research was supported by the Ningxia Natural Science Foundation Project (2020AAC03048) and by the Graduate Innovation Project of North Minzu University, China (No.YCX21164).

Conflict of interest

This work does not have any conflict of interest.

Appendix

Appendix A: The proof of lemma 5.4

Proof. Integrating both sides of the first equation of (5.3) from $t$ to $T$, we get

By squaring the sides of the above equation, we have

similarly, we have

It follows from (A1)-(A4) that

where $t\in[T-\epsilon, T]$ with $\epsilon = \frac{1}{C}$. Using Gronwall's inequality ^[31], we derive from (A5) that

We apply the same method to (A1)–(A2) in $[T-\epsilon, T]$, and we can see that for any $t\in[T-2\epsilon, T]$, (A6) holds. Repeating a finite number of steps, we know that for any $t\in[0, T]$, the estimate (A6) holds.

Appendix B: The proof of lemma 5.5

Proof. If $\eta\geq1$. For any $r > 0$, an estimate of $|S^{a}_{i, j}-\widetilde{S}^{a}_{i, j}|^{2\eta}$ can be obtained as follows:

so, we have

We have the result using Gronwall's inequality. Next considering $0\leq\eta < 1$, by using Cauchy-Schwartz's inequality, we have

This proof is complete.

Appendix C: The proof of lemma 5.6

Proof. We let $\widehat{p}_{1i} = p_{1i} -\widetilde{p}_{1i}, \; \widehat{p}_{2i} = p_{2i} -\widetilde{p}_{2i}, \; \widehat{p}_{3j} = p_{3j} -\widetilde{p}_{3j}$, $\widehat{p}_{4j} = p_{4j} -\widetilde{p}_{4j}$. Then according to adjoint Eq (5.3), we can see

where

We assume that $\varphi = (\varphi_{1i}, \; \varphi_{2i}, \; \varphi_{3j}, \; \varphi_{4j})^{T}$ is the following linear differential equation:

where $sgn(\cdot)$ is a symbolic function. According to assumption and Lemma 5.5, the existence and uniqueness of solution of (C1) can be verified, and we have

Because $1 < \eta < 2$, thus there exist $\eta_{1} > 2$ such that $\frac{1}{\eta_{1}}+\frac{1}{\eta} = 1$. So, using Cauchy-Schwartz's inequality, we have

Using Cauchy-Schwartz's inequality, we have

Note that $\frac{2\eta}{1-\eta} < 1, \; 1-\frac{\eta}{2} > \frac{\kappa\eta}{2}$ and $d(u, \widetilde{u}) < 1$. It follows from $\int_{0}^{T}\int_{\Omega}|\widehat{f}_{1i}|^{\eta}dxdt\leq Cd(u^{a}_{i}, \widetilde{u}^{a}_{i})^ {\frac{\kappa\eta}{2}}$. In the same way, we get $\int_{0}^{T}\int_{\Omega}| \widehat{f}_{2i}|^{\eta}dxdt\leq Cd(u^{a}_{i}, \widetilde{u}^{a}_{i})^ {\frac{\kappa\eta}{2}}$, $\int_{0}^{T}\int_{\Omega}|\widehat{f}_{3j}|^{\eta}dxdt\leq Cd(u^{h}_{j}, \widetilde{u}^{h}_{j})^ {\frac{\kappa\eta}{2}}$, $\int_{0}^{T}\int_{\Omega}|\widehat{f}_{4j}|^{\eta}dxdt\leq Cd(u^{h}_{j}, \widetilde{u}^{h}_{j})^ {\frac{\kappa\eta}{2}}$. So, we have

This completes the proof.