Law of the single logarithm for randomly weighted sums of dependent sequences and an application

1.   Introduction

Let $\{X, X_n, n\geq1\}$ be a sequence of independent and identically distributed (i.i.d., for short) random variables and set $S_{n} = \sum_{i = 1}^{n}X_{i}$. Hsu and Robbins ^[1] proved that if $EX^{2} < \infty$ and $EX = \mu$, then for all $\epsilon > 0$,

The aforementioned result is the well-known complete convergence, which can derive that $S_{n}/n\rightarrow0$ almost surely ($a.s.$, for short) by the Borel-Cantelli lemma. For a sequence $\{X, X_n, n\geq1\}$ of i.i.d. random variables with zero mean, Baum and Katz ^[2] proved that for all $\epsilon > 0$,

if, and only if, $E|X|^{rp} < \infty$, where $r > 1$ and $1\leq p < 2$. For $p = 2$, Lai ^[3] proved that for any $\varepsilon > \sqrt{r-1}$,

if $EX = 0$, $EX^{2} = 1$ and $E(X^{2}/\log|X|)^{r} < \infty$. This result is called the law of the single logarithm. Chen and Wang ^[4] showed that the series is divergent if $\varepsilon < \sqrt{r-1}$ and, recently, Chen and Sung ^[5] proved the sufficiency part for negatively orthant dependent (NOD) random variables by applying a Bernstein type inequality for unbounded NOD random variables.

It is known that many useful linear statistics, such as least squares estimator, nonparametric regression function estimator, and jackknife estimator, are the form of weighted sums, i.e., $\sum_{i = 1}^{n}a_{ni}X_{i}$, where $a_{ni}, 1\leq i\leq n, n\geq1$ are called the weights and $\{X_{n}, n\geq1\}$ is a sequence of random variables. Therefore, it is of great interest to extend the law of the single logarithm for partial sums to weighted sums. Bai et al. ^[6] proved that

where $\{X, X_n, n\geq1\}$ is a sequence of i.i.d. random variables with $EX = 0$, $E|X|^{\beta} < \infty$, and $\{a_{ni}, 1\leq i\leq n, n\geq1\}$ is an array of constants satisfying $\sum_{i = 1}^{n}|a_{ni}|^{\alpha} = O(n)$ for $\alpha > 0$, $\beta > 0$, and $1/\alpha+1/\beta = 1/2$. Chen and Gan ^[7] pointed out that the moment condition in Bai et al. ^[6] is nonoptimal and they proved that the necessary condition is $E(|X|/\log^{1/2}|X|)^{\beta} < \infty$. Sung ^[8] extended the result of Chen and Gan ^[7] from classical probability space to Banach space. Chen et al. ^[9] extended the result of Chen and Gan ^[7] to a more general case. More recently, Liu et al. ^[10] also extended the result of Lai ^[3] for partial sums to weighted sums.

The randomly weighted sums also play an essential role in various theoretical problems and practical applications. For example, in the field of queueing theory, the randomly weighted sum $\sum_{i = 1}^{n}A_{ni}X_{i}$ represents the total output for a customer being served by $n$ machines, where the $A_{ni}$ is the service time in the $i$-th machine and $X_{i}$ is the output from the $i$-th machine. In a linear-time-invariant system, the convergence analysis of the state observers will reduce to the persistent excitation condition and the randomly weighted sums if the sampling time sequence is a random process; In statistics, the random weighting estimate of sample mean, bootstrap sample mean, and the least squares estimators in a simple linear regression model with random design are all the form of randomly weighted sums. The nonrandomly weighted sums can be regarded as a special case of randomly weighted sums, but not vice versa. The study on randomly weighted sums seems much more meaningful, but what followed is the increase in the difficulty of proofs. In comparison to the study on nonrandomly weighted sums, there are not so many investigations on the law of the single logarithm for randomly weighted sums. Cuzick ^[11] proved the law of single logarithm

for randomly weighted sums providing that $A_{ni}, 1\leq i\leq n, n\geq1$ is an array of independent Rademacher random variables, and $EX^2 = 1$. Chen et al. ^[12] investigated the law of single logarithm in the sense of almost sure convergence for randomly weighted sums of NOD random variables.

In this paper, we will further investigate the law of single logarithm in the sense of complete convergence for randomly weighted sums of widely orthant dependent (WOD) random variables, while the weights are also assumed to be WOD.

Let us recall the concept of WOD random variables, which was raised by Wang et al. ^[13] as follows.

Definition 1.1. A sequence $\{X_n, n\geq 1\}$ of random variables is said to be widely upper orthant dependent (WUOD) if there exists a finite sequence $\{g_{U}(n), n\geq 1\}$ of positive numbers such that for each $n\geq 1$ and for all $x_{i}\in(-\infty, \infty)$, $1\leq i\leq n$,

A sequence $\{X_n, n\geq 1\}$ of random variables is said to be widely lower orthant dependent (WLOD) if there exists a finite sequence $\{g_{L}(n), n\geq 1\}$ of positive numbers such that for each $n\geq 1$ and for all $x_{i}\in(-\infty, \infty)$, $1\leq i\leq n$,

If $\{X_n, n\geq 1\}$ is both WUOD and WLOD, then it is said to be WOD with dominating coefficients $g(n) = \max\{g_{U}(n), g_{L}(n)\}$.

By letting $x_{i}\rightarrow -\infty$ in the former inequality or $x_{i}\rightarrow \infty$ in the latter one above, for all $1\leq i\leq n$, it is easy to see that $g(n)\geq1$. Wang et al. ^[13] gave some examples to show that WOD random variables contain negatively associated (NA) random variables, negatively supper-additive dependent (NSD) random variables, NOD random variables, and extended negatively dependent (END) random variables, the concepts of which were introduced by Alam and Saxena ^[14], Hu ^[15], Lehmann ^[16], and Liu ^[17], respectively. Wang et al. ^[13] further presented examples to show that WOD random variables also include some positively dependent random variables. Therefore, it is of interest to investigate the limiting behaviors of random variables processing this dependence structure.

In this paper, the law of the single logarithm for randomly weighted sums of WOD random variables is studied. The result improves and generalizes some corresponding ones in the literature. As an application, the rate of complete convergence for random weighting estimation with WOD samples is obtained under general assumptions. We also carry out some numerical simulations to support the theoretical results.

Throughout the paper, let $C$ be a positive constant, which may vary in different places. Let $\log x = \ln\max(x, e)$. Define $x^{+} = xI(x\geq0)$ and $x^{-} = -xI(x < 0)$, where $I(A)$ is the indicator function of event $A$. $a_{n} = O(b_{n})$ stands for $a_{n}\leq Cb_{n}$, and $a_{n} = o(b_{n})$ means $a_{n}/b_{n}\rightarrow0$ as $n\rightarrow \infty$, where $\{a_{n}, n\geq1\}$ and $\{b_{n}, n\geq1\}$ are two sequences of positive numbers. Let $\{\xi_{n}, n\geq1\}$ be a sequence of random variables. If $\sum_{n = 1}^{\infty}P(|\xi_{n}|/a_{n} > M) < \infty$ for some $M > 0$, we abbreviate it to $|\xi_{n}| = O_{a.c.}(a_{n})$.

2.   Main results and an application

2.1.   Main results

For an array $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ of random variables, denote

It follows that if $\sum_{i = 1}^{n}E|A_{ni}|^{2} = O(n)$, then

and

if the limit above exists. Particularly, we have $\rho = r+\tau_{1}+\tau_{2}$ if $A_{ni}\equiv1$ for each $1\leq i\leq n$.

We now state our main result as follows.

Theorem 2.1. Let $r > 0$. Let $\{X; X_{n}, n\geq1\}$ be a sequence of identically distributed WOD random variables with $g_{1}(n) = O(n^{\tau_{1}})$ for some $\tau_{1}\geq0$, and let $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ be an array of WOD random variables with $g_{2}(n) = O(n^{\tau_{2}})$ for some $\tau_{2}\geq0$. Suppose that $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ is independent of $\{X; X_{n}, n\geq1\}$ and

for some $\alpha\geq2(r+1+\tau_{1}+\tau_{2})$. If $EX = 0$ and

then for any $\varepsilon > \sqrt{2\rho EX^{2}}$,

Remark 2.1. We point out that if $\{X; X_{n}, n\geq1\}$ is a sequence of i.i.d. random variables and $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ is an array of independent random variables, then (2.4) can be replaced with

If we further take $EX^{2} = 1$ and replace $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ with an array $\{a_{ni}, 1\leq i\leq n, n\geq1\}$ of constants, Theorem 2.1 degenerates to the convergence part of Theorem 1.1 in Liu et al. ^[10] when $\alpha\geq2(r+1)$. Furthermore, for $\alpha = 2(r+1)$, the moment condition $E|X|^{2(r+1)} < \infty$ in Liu et al. ^[10] is weakened to $E(|X|/\log^{1/2}|X|)^{2(r+1)}\log|X| < \infty$.

By taking $r = 1$ in Theorem 2.1, we can obtain the following result.

Corollary 2.1. Let $\{X; X_{n}, n\geq1\}$ be a sequence of identically distributed WOD random variables with $g_{1}(n) = O(n^{\tau_{1}})$ for some $\tau_{1}\geq0$, and let $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ be an array of WOD random variables with $g_{2}(n) = O(n^{\tau_{2}})$ for some $\tau_{2}\geq0$. Suppose that $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ is independent of $\{X; X_{n}, n\geq1\}$ and satisfies (2.2) for some $\alpha\geq2(2+\tau_{1}+\tau_{2})$. If $EX = 0$ and

then for any $\varepsilon > \sqrt{2\rho EX^{2}}$,

and thus

Remark 2.2. If $\{X; X_{n}, n\geq1\}$ is a sequence of identically distributed NOD random variables and $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ is an array of NOD random variables, Corollary 2.1 exhibits the same rate as Theorem 2 in Chen et al. ^[12] for $\alpha > 4$. Under this circumstance, $g_{1}(n) = g_{2}(n) = 1$. Moreover, the case $\alpha = 4$ was not considered in Chen et al. ^[12]. Note that the complete convergence in Corollary 2.1 is stronger than almost sure convergence in Chen et al. ^[12]. Therefore, our result improves and extends the corresponding one in Chen et al. ^[12] from the NOD setting to the WOD setting.

2.2.   Application to the random weighting estimation of sample mean

Random weighting is an emerging computational method which pocesses many advantages such as the simplicity in computation, the suitability for large samples, and there is no need to know the distribution function. Assume that $X_{1}, X_{2}, \cdots, X_{n}$ are identically distributed random variables, and the corresponding sample mean is defined as $\bar{X}_{n} = n^{-1}\sum_{i = 1}^{n}X_{i}$. The random weighting estimation (RWE) of $\bar{X}_{n}$ can be defined as

where $W_{ni}$'s are independent of $X_{i}$'s and the random vector $\boldsymbol{W} = (W_{n1}, \cdots, W_{nn})$ obeys the Dirichlet distribution. In general, $(W_{n1}, \cdots, W_{nn})\sim D(1, \cdots, 1)$, namely, $\sum_{i = 1}^{n}W_{ni} = 1$ and the joint density of $\boldsymbol{W}$ is $f_{\boldsymbol{W}}(w_{n1}, \cdots, w_{nn}) = \Gamma(n)$, where $(W_{n1}, \cdots, W_{nn})\in D_{n-1}$ and $D_{n-1} = \{(W_{n1}, \cdots, W_{nn}):W_{ni}\geq0, i = 1, \cdots, n-1, \sum_{i = 1}^{n-1}W_{ni}\leq1\}$. The asymptotic behavior of RWE has been investigated by some authors. Since the RWE was introduced by Zheng ^[18], some meaningful results have been investigated. For more details, we refer to Gao et al. ^[19], Xue and Zhu ^[20], Gao and Zhong ^[21], Roozegar and Soltani ^[22], and the references therein.

As an application of our main result, we obtain the rate of complete convergence for the RWE of the WOD sample mean as follows.

Theorem 2.2. Let $\{X; X_{n}, n\geq1\}$ be a sequence of identically distributed WOD random variables with $g_{1}(n) = O(n^{\tau_{1}})$ for some $\tau_{1}\geq0$ and $E\left(\frac{|X|}{\log^{1/2}|X|}\right)^{2(2+\tau_{1})} < \infty$, then

Remark 2.3. For i.i.d. samples, Gao et al. ^[19] obtained that

i.e., $H_{n}-\bar{X}_{n}\rightarrow0\; a.s., \; as\; n\rightarrow \infty$ under the moment condition $E|X|^{1+\theta} < \infty$, where $0 < \theta < 1$. The result of Gao et al. ^[19] does not reveal the convergence rate. Hence, Theorem 2.2 complements and improves the corresponding result of Gao et al. ^[19] from an independent setting to a WOD setting.

2.3.   Numerical simulation

In this subsection, we will carry out some simulations to study the numerical performance of the RWE of the WOD sample mean. For fixed $n$, we generate $X_{i}, 1\leq i\leq n$ under the following two cases.

Case 1: WOD sample. The marginal distributions of $X_1, \cdots, X_n$ are the uniform distribution on $[0, 1]$, while $(X_1, X_2)$, $(X_3, X_4)$, $\cdots$, $(X_{2m-1}, X_{2m})$, $\cdots$ respectively follow a joint distribution of the Farlie-Gumbel-Morgenstern (FGM) copula

with the parameter $\theta_n = n^{-1}$. It follows from Wang et al. ^[13] that $\{X_{n}, n\geq1\}$ is a sequence of identically distributed WOD random variables with the dominating coefficients $g(n) = O(n)$.

Case 2: NA sample. For any fixed $n\geq3$, let $(X_{1}, X_{2}, \cdots, X_{n})\sim N(\boldsymbol{0}, \boldsymbol{\Sigma})$, where $\boldsymbol{0}$ represents zero vector and

where $0 < \nu < 1$. In this paper, without specified, we will take $\nu = 0.1, 0.5, 0.8$ to show how this parameter will affect the performance. By Joag-Dev and Proschan ^[23], it can be seen that $(X_{1}, X_{2}, \cdots, X_{n})$ is an NA vector and is thus WOD.

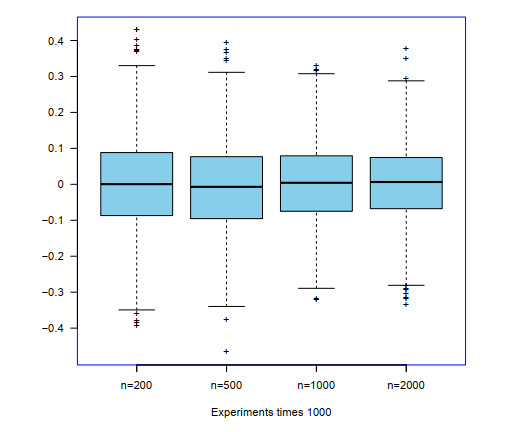
We carry out a simulation to confirm the consistency for RWE of the WOD sample mean that we established in Theorem 2.2. The random weights satisfy that $(W_{n1}, \cdots, W_{nn})\sim D(1, \ldots, 1)$. For the two cases above, by choosing the sample size $n = 200$, $500$, $1000$, $2000$, respectively, we adopt the R software to compute $\sqrt{n/\log n}(H_{n}-\bar{X}_{n})$ for $1000$ times and present the boxplots in Figure 1 to Figure 4.

From Figure 1 to Figure 4, we can see that the values of $\sqrt{n/\log n}(H_{n}-\bar{X}_{n})$ are bounded for each sample size, no matter if the samples are NA or WOD. Moreover, there is no obvious difference for the RWE of the WOD sample mean with different values of $\nu$. This implies that $H_{n}-\bar{X}_{n}$ is convergent with the rate $O(\sqrt{{\log n}/{n}})$ $completely$, which is consistent with what we have proved in Section 2.2.

3.   Some important lemmas

To prove the main results of the paper, we need the following important lemmas. The first one is a basic property for WOD random variables, which was presented by Wang et al. ^[24].

Lemma 3.1. Let $\{X_n, n\geq1\}$ be a sequence of WOD random variables. If $\{f_{n}(\cdot), n\geq1\}$ are all nondecreasing (or nonincreasing), then $\{f_{n}(X_n), n\geq1\}$ are still WOD.

The following important conclusion for WOD random variables can be found in Wu et al. ^[25].

Lemma 3.2. Let $\{X_n, n\geq1\}$ be a nonnegative sequence of WOD random variables with the dominating coefficients $g_{1}(n)$, and let $\{Y_n, n\geq1\}$ also be a nonnegative sequence of WOD random variables with the dominating coefficients $g_{2}(n)$. Assume that $\{X_n, n\geq1\}$ is independent of $\{Y_n, n\geq1\}$, then $\{X_{n}Y_{n}, n\geq1\}$ is still a sequence of WOD random variables with the dominating coefficients $g_{1}(n)g_{2}(n)$.

The next lemma concerning the Bernstein inequality for unbounded WOD random variables was proved in Deng and Wang ^[26].

Lemma 3.3. Let $X_{1}, X_{2}, \cdots, X_{n}$ be WOD random variables with the dominating coefficients $g(n)$ and $EX_{i} = 0$, $E|X_{i}|^{s} < \infty$ for each $1\leq i\leq n$, where $s\geq2$. Set $B_{n}^{2} = \sum_{i = 1}^{n}EX_{i}^{2}$, then for any $\varepsilon > 0$ and $\delta > 0$,

where $C_{\delta, s} > 0$, depending only on $\delta$ and $s$.

Lemma 3.4. Let $r > 0$, $\tau\geq0$, and $\alpha\geq2(r+1+\tau)$. Let $\{X; X_n, n\geq1\}$ be a sequence of identically distributed random variables and $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ be an array of random variables independent of $\{X; X_n, n\geq1\}$. If $\sum_{i = 1}^{n}E|A_{ni}|^{\alpha} = O(n)$, then

Proof. It follows from Jensen's inequality and Hölder's inequality that for any $0 < \alpha' < \alpha$,

It is easy to check that

On one hand, we can obtain by (3.1) and some standard calculation that

On the other hand, we also obtain that

Hence, if $\alpha = 2(r+1+\tau)$, we have

and if $\alpha > 2\left(r+1+\tau\right)$,

A combination of (3.2)–(3.5) derives the desired result immediately. The proof of the lemma is completed. □

Lemma 3.5. Let $r > 0$, $\tau\geq0$, and $\alpha\geq2(r+1+\tau)$. Let $\{X; X_n, n\geq1\}$ be a sequence of identically distributed random variables and let $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ be an array of random variables independent of $\{X; X_n, n\geq1\}$. If $\sum_{i = 1}^{n}E|A_{ni}|^{\alpha} = O(n)$, then for any $s\geq\alpha$,

Proof. Similar to the procedure of Lemma 3.4, we also have

which, together with (3.3)–(3.5), completes the proof of the lemma. □

4.   Proofs of the main results

Proof of Theorem 2.1. By virtue of $EX = 0$ and the independence of $\{A_{ni}, 1\leq i\leq n, n\geq1\}$ and $\{X; X_n, n\geq1\}$, we have that

and, hence,

Therefore, in order to prove (2.4), we only need to show

with $A_{ni}\geq0$ and $X_{i}\geq0$ for each $1\leq i\leq n$, $n\geq1$. For the given $1\leq i\leq n$, $n\geq1$ define

It follows from Lemmas 3.1 and 3.2 successively that $\{Y_{ni}, 1\leq i\leq n, n\geq1\}$ is still an array of row-wise WOD random variables with dominating coefficients $g_{1}(n)g_{2}(n) = O(n^{\tau_{1}+\tau_{2}})$. Note by (3.1) that

Moreover, for any $\varepsilon > \sqrt{2\rho EX^{2}}$, there exist $\varepsilon_{1} > \sqrt{2\rho EX^{2}}$ and $\varepsilon_{2} > 0$ such that $\varepsilon = \varepsilon_{1}+\varepsilon_{2}$. Therefore, by virtue of (4.2), we have that for all $n$ large enough,

which implies

It follows from $\tau_{1}\geq0$, $\tau_{2}\geq0$, and Lemma 3.4 that

It remains to deal with $I_{2} < \infty$. Since $\varepsilon_{1} > \sqrt{2\rho EX^{2}}$, we can take $\delta > 0$ sufficiently small such that $\varrho = :\varepsilon_{1}^{2}/[(2+\delta)EX^{2}] > \rho$. Hence, taking $s\geq\alpha$, we obtain by Lemmas 3.3–3.5 and (2.1) that

The proof is completed. □

Proof of Theorem 2.2. We first estimate $EW_{ni}^{q}$, where $q > 0$. Without loss of generality, we only need to estimate $EW_{n1}^{q}$ for some $n$ large enough. By some standard calculation, we obtain that

By Stirling's approximation and the formula above, we have that for each $1\leq i\leq n$, when $n$ is large enough,

Note that for any $\varepsilon > \sqrt{2\rho EX^{2}}$, where $\rho$ satisfies (2.1) with $r = 1$ and $\tau_{2} = 0$,

The second term in the righthand of the formula above converges by applying Corollary 2.1 with $\alpha > 2(2+\tau_1)$ and $A_{ni} = 1$ for each $1\leq i\leq n$. On the other hand, it follows from Example 4.3 of Hu ^[15] that $(W_{n1}, W_{n2}, \cdots, W_{nn})$ are NSD, and hence, WOD with $\tau_{2} = 0$. Taking $A_{ni} = nW_{ni}$ for each $1\leq i\leq n, n\geq1$ in Corollary 2.1, it is easy to obtain by (4.3) that for all $\alpha > 2(2+\tau_1)$,

Therefore, the first series in (4.4) also converges and, thus, (4.4) has been proved to be finite. This completes the proof of the theorem. □

5.   Conclusions

In this paper, the law of the single logarithm for randomly weighted sums of widely orthant dependent random variables is investigated. The result improves and generalizes some existing ones. A new result on the rate of complete convergence for random weighting estimation with widely orthant dependent samples is further obtained as an application. Some simulation studies are provided to confirm the theoretical results. In future study, we will further investigate more meaningful outcomes and applications on the topic.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Outstanding Youth Research Project of Anhui Colleges (2022AH030156).

Conflict of interest

The authors declare there is no conflict of interest.