Analytical and numerical investigation of beam-spring systems with varying stiffness: a comparison of consistent and lumped mass matrices considerations

Abbreviations

L: Length; E: Young's modulus; I: a moment of inertia of cross section; A: cross section area; $x$: longitudinal axis; $\rho$: density; $s$: Displacement; $K_{1}$, $K_{2}$: linear stiffness of the springs at right and left ends, respectively; $S(x)$: normal function; $\omega$: eigenfequencey; $c$: wave speed; $\eta$: eigenvalues; $C_{i} (i = 1, 2, 3, 4)$: cnstant coefficient; $Q(x)$: weighted functions; $N_{i} (i = 1, 2, 3, 4)$: shape functions; ${s_{j}}$: function of space and time component; $\bar{s_{j}}$: amplitude of vibration varying with time; $k^{\epsilon}$: stiffness matrix; $m^{\epsilon}$: mass matrix; N: number of element

1.   Introduction

The beam, a fundamental structural element, is typically characterized by having one dimension significantly larger than its other dimensions. This elongated geometry allows beams to efficiently carry loads and distribute them along their length. Euler-Bernoulli beam (EBB) theory stands as one of the foundational frameworks used to describe the behavior of beams under certain conditions ^[1]. The development of beam equations has a rich historical context, with contributions from notable figures such as Vinci and Galilei. During the eighteenth century, significant advancements in beam theory were made by eminent mathematicians including Euler, Jacob, and Daniel, culminating in the establishment of comprehensive analytical tools for understanding beam behavior. The application of beam theory extends across a diverse range of engineering disciplines, reflecting its essential role in various practical applications. In transportation engineering, beams are integral components of bridges, roadways, and railway tracks, where they provide structural support and facilitate the safe passage of vehicles and pedestrians. Structural engineering heavily relies on beam theory to design and analyze buildings, bridges, and other infrastructure projects, ensuring their stability and resilience against external forces such as wind and seismic loads. In aerospace engineering, beams play a crucial role in the design and construction of aircraft, spacecraft, and aerospace structures, where they must withstand complex loading conditions and extreme environments. Scholarly research in the field of continuous structural beam systems has yielded valuable insights and methodologies that contribute to advancements in engineering practice. Works by ^[2,3] exemplify the breadth of studies focused on beam theory, covering topics ranging from structural analysis and design optimization to materials research and performance evaluation. These studies underscore the interdisciplinary nature of beam theory and its significance in addressing real-world engineering challenges across multiple sectors.

Numerous researchers have delved into the intricate dynamics of transverse vibrations exhibited by beam-spring systems, conducting both exact and approximate analyses to ascertain the natural frequencies governing their behavior. These investigations have explored the nuanced interplay between beam vibrations and various factors, including the characteristics of the elastic foundation supporting the beam. The effects of springs, rotary inertia, and mass distribution have been subjects of intensive scrutiny across a spectrum of studies, underscoring the multidimensional nature of beam-spring dynamics. The significance of springs in modulating beam vibrations has been a focal point of investigation, with studies such as ^[4,5] shedding light on their role in altering the structural response. Additionally, the influence of rotary inertia, mass distribution, and other dynamic parameters has been rigorously examined in works ^[6], among others. These investigations have contributed valuable insights into the intricate dynamics of beam-spring systems and their implications for diverse engineering applications. $\ddot{O}$z ^[7] and $\ddot{O}$zkaya ^[8] determined beam frequencies, incorporating mass and using both analytic and finite element methods. Grossi and Arenas ^[9] employed Rayleigh-Ritz and optimized Rayleigh-Schmidt methods to investigate frequency variations with changes in height and width. Smith et al. ^[10] introduced the fully Sinc-Galerkin method in space and time to solve beams with cantilever and fixed boundary conditions. Moaaz et al. ^[11] formulated mathematical expressions for transverse resonance in simply supported, axially compressed thermoelastic nanobeams, employing nonlocal elasticity theory and the dual-phase-lag heat transfer model to explore the impact of length scale and axial velocity on system responses. Baccouch ^[12] applied the Galerkin method to solve the Euler-Bernoulli beam equation, while Xie and Zhang ^[13] investigated difference methods for nonlinear equations with damping. Additionally, Shi et al. ^[14] explored the mixed finite element method for solving such equations.

The variational iteration technique was used by Liu and Gurran ^[15] to find the natural frequencies and mode shapes of the beam under different boundary conditions. Galerkin finite element method (FEM), Rayleigh-Ritz, and exact solutions were compared by Hamdan and Latif ^[16], and the exhibited FEM was preferable because of good accuracy. Jafari et al. ^[17] derived the equation of motion of beam by applying Hamilton's principle and obtained the eigenfrequencies and mode shapes for cantilever beam connected with linear spring at the tip by using the FEM.

Unlike boundary element method, finite difference method, and finite volume method, which are widely used in acoustic and fluid mechanics (see for example, ^[18,19]), the study of FEM is considered as the standard approach in presenting solutions to structural problems, see for instance, ^[20,21]. Many industries use FEM software such as ABAQUS (based on Abundant Beads Addition Calculation Utility System tool), NASA structure analysis, and analysis system for the commercial purpose. It has been widely discussed on static problems where numerous codes existed while having less validation and verification for standard problems with respect to dynamics of determining the eigenfrequencies. In the study of beam dynamics using FEM, consistent mass (CM) and lumped mass (LM) matrices are critical in accurately representing the system's behavior. The choice between these two matrices has an impact on the accuracy and computing efficiency of the analysis. The consistent mass matrix accurately preserves the system's mass distribution by taking into account the mass contributions of all finite constituents. This matrix is constructed directly from the discretized governing equations, yielding more accurate results, particularly for bigger models with variable element sizes. However, its bigger size necessitates more computing effort and storage. The lumped mass matrix, on the other hand, combines the mass contributions into nodal points, making the computing process easier. While this matrix decreases computational effort and storage needs, it may produce less accurate results, especially in systems with large mass variations or irregular geometries. Hence, the primary aim of this study is to present a comprehensive analysis of the vibration behavior of beam-spring systems using FEM with a focus on the comparative performance of CM and LM matrices. Our work bridges the gap between mathematical analysis and engineering applications by addressing two primary objectives:

(1) Determining the preferred matrix type (CM or LM) for such analyses from a mathematical perspective;

(2) Examining the deflection behavior while adjusting the stiffness of the supports at each end of the beam from an engineering perspective.

The novelty of our study lies in its detailed comparison of CM and LM matrices and providing insights into their respective accuracies in calculating eigenfrequencies and mode shapes, which has not been extensively covered in existing literature. By varying the stiffness of the beam supports, we analyze the dynamic behavior of the system, offering practical insights valuable for both theoretical and applied contexts. Additionally, we provide a numerical results section to include a deeper analysis of the outcomes prior to yielding a detailed introduction to the FEM procedure, including the assembly of global stiffness and mass matrices and the incorporation of boundary conditions. Therefore, the underlying study is crucial for both mathematical analysis and practical engineering applications, making our study a valuable contribution to the field of applied mathematics.

This article is categorized as follows: the governing problem is formulated in Section 2. The analytical and numerical results are presented in Section 3. Results and discussions are given in Section 4 and the validation has been performed in Section 5 while the study is summarized in Section 6.

2.   Governing problem

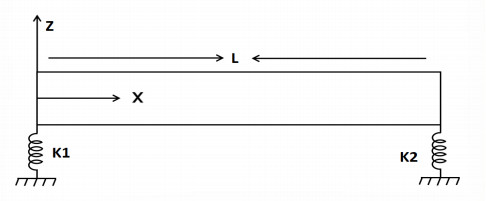
Consider the beam configuration attached to linear springs at both ends having length, as can be viewed through Figure 1. The material of the beam is made of stainless steel. The Young's modulus is 210 GPa and material density is 7850 $Kg/m^{3}$. The length, width, and thickness of the beam are taken as 1 m, 0.02 m, and 0.003 m, respectively.

Figure 1.  Beam-spring configuration.

DownLoad: Full-Size Img PowerPoint

The equation of motion for the transverse deflection function in case of free beam's vibration is given by ^[22]

Equation (2.1) together with the standard linear spring conditions of beam defined in ^[23] will be considered for the correct determination of eigenfrequencies and mode shapes. The objective is to provide a more optimal and accurate solution approach by considering the lumped and consistent mass matrices while providing the finite element solution in proceeding sections. The flexural boundary conditions at $x = 0$ and $x = L$, representing the stiffness of the springs in the positive direction from left to right, are provided below:

Equation (2.1) along with boundary conditions (2.2a–d) is solved by separation of variables to acquire the characteristics and mode shape equations where the roots of the characteristic equation are extracted through Mathematica-based code. These roots are termed as eigenfrequencies and will be useful in determining the eigenmodes in the subsequent section.

3.   Determination of eigenfrequency and mode shape

As we seek to determine the natural frequency and mode shape of the vibrating beam as given by previously defined boundary conditions, we use an analytical and numerical approach to obtain the desired results. It is appropriate to note that a numerical approach is used to consider CM and LM matrices, which provides a justification for solving more complex problems with a similar scheme.

3.1.   Analytical results

We apply separation of variables to the governing problem given in Section 2 by letting

Therefore, Eq (2.1) can be written as ^[24]

where

and Eq (3.2) is further split as

and

where $\eta$ is given by

Equation (3.3) yields the following equation

Using Eq (3.6) in Eq (2.2a–d), we obtain

and

By using Eq (3.7) in Eq (3.6), we obtain

The results obtained by using boundary conditions (2.2a–d) are given by Eqs (3.7)–(3.10) representing a system of four equations with four unknowns $C_{1}$–$C_{4}$. In order to have a nontrivial solution, the determinant of the coefficient matrix must be zero, which leads to a frequency equation given as

After finding the values of $\frac{C_{3}}{C_{1}}$ and $\frac{C_{2}}{C_{1}}$ from Eqs (3.8) and (3.10), respectively, and putting into Eq (3.11), the $n^{th}$ mode shape equation is determined. This equation is used to plot the mode shapes/eigenmodes subject to corresponding eigenfrequencies. The eigenfrequencies are computed by using Eq (3.5), after determining the eigenvalues ($\eta$) from Eq (3.12).

The analytic solution for the beam attached to linear springs is achieved more conveniently. However, in case of more complex and challenging problems with added effects and flexural boundary conditions, and structural and material discontinuities ^[25], it becomes difficult to obtain analytical solutions. Therefore, we propose the finite element scheme with the consideration of LM and CM matrices to obtain numerical solutions for such problems in subsequent section. Albeit the scheme to be adopted herein will provide a reference model for the comparative analysis. In case of substantial problems related to beams, FEM provides a fast and easy method to address these problems.

3.2.   Numerical results

This section aims to provide the workings of FEM by CM and LM matrices to calculate the eigenmodes and eigenfrequencies.

3.2.1.   FEM

The first step in FEM is to discretize the beam into a finite number of elements. There are two end nodes, each with two degrees of freedom, for each beam element. As demonstrated in Figure 2, these degrees of freedom include both translational displacements $(V_{i}$, where $i$ = 1, 2) and rotational displacements $(\theta_{j}$, where $j$ = 1, 2).

Figure 2.  Beam element.

DownLoad: Full-Size Img PowerPoint

The node's movement across the axis of the beam is indicated by the translational degrees of freedom, and its rotation about the corresponding axes is indicated by the rotational degrees of freedom. As the beam under examination is uniform, it is assumed that all elements, utilized to mesh the total beam, are indistinguishable. The subsequent step is to acquire the weak form of the differential equation. For this purpose, the weight functions are multiplied with the residual value of an approximate solution and are then integrated over the domain yielding zero value. While using the process of discretization and weak formation in Eq (2.1), it is found that

It is noted that the highest order of derivative in Eq (3.13) is three; therefore, an approximate function of thrice differentiable is selected. A cubic interpolation polynomial fulfills this requirement ^[26] normally. Applying the Galerkin FEM, a weight function is equated with the approximate function

where these cubic interpolation functions are called cubic spline functions, given as

While putting these shape functions, given by Figure 3, into Eq (3.13) and assuming

Figure 3.  Shape function for EBB.

DownLoad: Full-Size Img PowerPoint

we get

Equation (3.15) can be written as

where ${s_{j}}$ can be written as

Putting Eq (3.17) in Eq (3.16), we obtain

where $[k^{\epsilon}]$ and $[m^{\epsilon}]$ are given as

and the LM matrix ^[21] would be

Here, we clarify the computational procedures using MATLAB codes based on FEM with LM and CM matrices to calculate the eigenfrequencies and mode shapes of the beam subject to linear springs. Below is a detailed description of our approach:

(I) Development of global matrices

(1) The MATLAB code generates the global stiffness, and LM and CM matrices for the highest number of elements.

(2) Boundary conditions are incorporated after forming the global stiffness and mass matrices.

(II) Incorporating boundary conditions

(1) The stiffness of the linear spring attached to the left end is added to the first entry of the first row of the global stiffness matrix.

(2) Similarly, the stiffness of the spring at the right end is added to the second to last entry of the final row of the global stiffness matrix.

(III) Calculation of eigenvalues and eigenfrequencies

(1) Eigenvalues are calculated from the global stiffness and mass matrices according to Eq (3.18).

(2) Eigenfrequencies are then obtained by taking the square root of these eigenvalues.

This procedure follows the methods outlined in several studies, such as references ^{[27,28,29,30,31]}.

4.   Results and discussion

This section aims to discuss the eigenmodes/mode shapes of the structural dynamics of the beam, which actually describes the deformation that the beam component would exhibit if it vibrates at the eigenfrequency. The deformation usually takes place through an excitation, which leads to the overall vibration of a component of the beam that includes the individual shapes of vibration. Therefore, eigenfrequencies and mode shapes indicate how the beam structure behaves under certain boundary conditions. It is noteworthy that the eigenmode characteristic is suitable for the qualitative evaluation of the dynamics of the beam component. The tabular and graphical analysis are presented to discuss beam dynamics at length.

Table 1 lists the comparison of eigenfrequencies determined by analytic method (AM), FEM by CM and LM matrices, receptively, with

Table 1.  Comparison of eigenfrequencies of first four modes for $K_{1} = K_{2} = 10000\ N/m$.

Modes	AM	FEM by CM	FEM by LM	Percentage error
				For CM	For LM
$N=5$
$1^{st}$	$6.90724849$	6.90796199	6.91434953	0.01032973	0.10280563
$2^{nd}$	$26.09674381$	26.13470717	26.42771700	0.14547164	1.26825473
$3^{rd}$	$52.84510702$	53.16067633	54.27922231	0.59715900	2.71380904
$4^{th}$	$81.45836541$	82.55087709	74.63946703	1.34119028	8.37102285
$N=10$
$1^{st}$	$6.90724849$	6.90729342	6.90918512	0.00065048	0.02803765
$2^{nd}$	$26.09674381$	26.09915748	26.18963094	0.00924893	0.35593375
$3^{rd}$	$52.84510702$	52.86511702	53.29345172	0.03786538	0.84841289
$4^{th}$	$81.45836541$	81.53039633	80.56105229	0.08842667	1.10156043
$N=50$
$1^{st}$	$6.90724849$	6.90724856	6.90732785	0.000000101	0.00114894
$2^{nd}$	$26.09674382$	26.09674771	26.10054215	0.00001487	0.01455480
$3^{rd}$	$52.84510702$	52.84513933	52.86350476	0.00006114	0.03481446
$4^{th}$	$81.45836541$	81.45848351	81.43321124	0.00014498	0.03087979
$N=100$
$1^{st}$	$6.90724849$	6.90724851	6.90726831	0.00000029	0.00028694
$2^{nd}$	$26.09674382$	26.09674412	26.09769399	0.00000115	0.00028694
$3^{rd}$	$52.84510702$	52.84510912	52.84970909	0.00000397	0.00870860
$4^{th}$	$81.45836541$	81.45837285	81.45215478	0.00000913	0.00762930

---

 | Show Table

DownLoad: CSV

The accuracy of eigenfrequencies are increased by increasing the number of elements of the beam. The percentage errors (with $N$ = 5) for the CM matrix are 0.01032973, 0.14547164, 0.59715900, and 1.34119028, respectively.

While 0.10280563, 1.26825474, 2.71380904, and 8.37102285 are percentage errors for the LM matrix, this indicates that the CM matrix gives better accuracy for nonclassical boundary conditions as compared to the LM matrix even for the lower number of elements. Table 1 clearly demonstrates that CM gives excellent agreement at

but does not get the same accuracy for LM even by using

It is noteworthy that

yields excellent accuracy; however,

and

are intended merely to demonstrate that increasing the number of elements improves accuracy.

Table 2 is a comparison of natural frequencies calculated by analytical and numerical methods, respectively, by decreasing the spring stiffness of the right end. The table shows that natural frequencies and stiffness of the right end spring are in a direct relationship, where natural frequencies decrease with decreasing spring stiffness. In addition, the numerical results are in close agreement with the analytical results when comparing the numerical solution for the CM matrices instead of the LM matrices. Rather, FEM by the consideration of CM matrices gives excellent accuracy not only for lower modes but also for higher modes.

Table 2.  Comparison of eigenfrequencies of first four modes for $K_{1} = 10000\ N/m, \ K_{2} = 1000\ N/m$.

Modes	AM	FEM by CM	FEM by LM	Percentage error
				For CM	For LM
$N=5$
$1^{st}$	$6.35701924$	6.35757819	6.38367463	0.00879264	0.41930642
$2^{nd}$	$18.88435515$	18.89870611	18.60125288	0.07599391	1.49913654
$3^{rd}$	$37.23312923$	37.33388399	34.14209661	0.27060513	8.30183410
$4^{th}$	$66.98883703$	67.54369195	61.04497484	0.82827967	8.87291440
$N=10$
$1^{st}$	$6.35701924$	6.35705430	6.36418013	0.00055151	0.11264540
$2^{nd}$	$18.88435515$	18.88526930	18.82742317	0.00484077	0.30147696
$3^{rd}$	$37.23312923$	37.23999014	36.48814214	0.01842689	2.00087155
$4^{th}$	$66.98883703$	66.92997846	65.34527890	0.08786325	2.45348061
$N=50$
$1^{st}$	$6.35701924$	6.35701929	6.35730648	0.00000078	0.00451846
$2^{nd}$	$18.88435515$	18.88435660	37.20428112	0.00000767	0.01115087
$3^{rd}$	$37.23312923$	37.23314046	37.20428112	0.00003016	0.07747968
$4^{th}$	$66.98883703$	66.98890259	66.92288123	0.00009786	0.09845789
$N=100$
$1^{st}$	$6.35701924$	6.35701923	6.35709101	0.00000015	0.00112898
$2^{nd}$	$18.88435515$	18.88435528	18.88383000	0.00000068	0.00278087
$3^{rd}$	$37.23312923$	37.23312992	37.22592579	0.00000185	0.01934685
$4^{th}$	$66.98883703$	66.98884110	66.97235365	0.00000607	0.02460615

---

 | Show Table

DownLoad: CSV

Table 3 indicates the comparison of eigenfrequencies by increasing the stiffness of the left end. From tables, it is observed easily by increasing the value of $K_{1}$ that eigenfrequencies are also increased. A study has demonstrated that the CM matrices can give accurate eigenfrequencies for higher modes as well as lower ones, but LM cannot give the best accuracy for lower modes as well as for higher modes.

Table 3.  Comparison of eigenfrequencies of first four modes for $K_{1} = 1000000, \ K_{2} = 10000\ N/m$.

Modes	AM	FEM by CM	FEM by LM	Percentage error
				For CM	For LM
$N=5$
$1^{st}$	$6.96985529$	6.97058784	6.97318699	0.01051026	0.04780157
$2^{nd}$	$27.03932973$	27.08117845	27.20251475	0.15476981	0.60350986
$3^{rd}$	$57.08313134$	57.47001406	57.52811675	0.67775315	0.77953924
$4^{th}$	$92.56612927$	94.07004264	80.41180184	1.62469078	13.13042635
$N=10$
$1^{st}$	$6.96985529$	6.96990142	6.97085023	0.00066185	0.01427757
$2^{nd}$	$27.03932973$	27.04200859	27.09268028	0.00990727	0.19730722
$3^{rd}$	$57.08313134$	57.10818680	57.34259598	0.04389293	0.45453827
$4^{th}$	$92.56612927$	92.67041635	90.82713601	0.11238909	1.87864964
$N=50$
$1^{st}$	$6.96985529$	6.96985536	6.96989697	0.00000100	0.00059800
$2^{nd}$	$27.03932973$	27.03933403	27.04157469	0.00001590	0.00830257
$3^{rd}$	$57.08313134$	57.08317194	57.09446492	0.00007112	0.01985452
$4^{th}$	$92.56612927$	92.56630243	92.51496052	0.00018707	0.05527805
$N=100$
$1^{st}$	$6.96985529$	6.96985538	6.96986568	0.00000129	0.00014907
$2^{nd}$	$27.03932973$	27.03932996	27.03989174	0.00000085	0.00207849
$3^{rd}$	$57.08313134$	57.08313385	57.08597067	0.00000440	0.00497403
$4^{th}$	$92.56612927$	92.56614015	92.55346771	0.00001175	0.01367839

---

 | Show Table

DownLoad: CSV

Table 4 mentions the comparison of numerical and analytical results by increasing the spring stiffness of both ends and shows a similar behavior for natural frequencies and solution accuracy as in case of Tables 1–3.

Table 4.  Comparison of eigenfrequencies of first four modes for $K_{1} = K_{2} = 50000\ N/m$.

Modes	AM	FEM by CM	FEM by LM	Percentage error
				For CM	For LM
$N=5$
$1^{st}$	$7.00984547$	7.01058818	7.01069925	0.01059524	0.01217972
$2^{nd}$	$27.72533453$	27.77009228	27.75837598	0.01614326	0.11917421
$3^{rd}$	$61.16521834$	61.63086692	61.09088070	0.76129635	0.12153580
$4^{th}$	$105.4525306$	107.82633768	101.05828707	2.25106688	4.16703475
$N=10$
$1^{st}$	$7.00984547$	7.00989023	7.01218744	0.00063853	0.03340972
$2^{nd}$	$27.72533453$	27.72813738	27.74771968	0.01010934	0.08273897
$3^{rd}$	$61.16521834$	61.19584117	61.39079599	0.05006575	0.08073897
$4^{th}$	$105.4525306$	105.60832597	106.45143402	0.14773974	0.94725408
$N=50$
$1^{st}$	$7.00984547$	7.00984337	7.00986020	0.00002995	0.00021013
$2^{nd}$	$27.72533453$	27.72529534	27.72631753	0.00014135	0.00354549
$3^{rd}$	$61.16521834$	61.16521665	61.17571474	0.00002763	0.01716073
$4^{th}$	$105.4525306$	105.45258028	105.49998929	0.00004703	0.04500470
$N=100$
$1^{st}$	$7.00984547$	7.00984334	7.00984750	0.00003038	0.00002895
$2^{nd}$	$27.72533453$	27.72529099	27.72554833	0.00015704	0.00077113
$3^{rd}$	$61.16521834$	61.16516979	61.16781319	0.00007937	0.00424236
$4^{th}$	$105.4525306$	105.45234022	105.46427897	0.00018055	0.03111408

---

 | Show Table

DownLoad: CSV

Figures 4–7 represent the first four natural modes for varying the spring stiffness of the underlying beam configuration. It is evident that the number of node points increases with each successive mode. The occurrence of node points indicates negligible deflection at certain locations of the beam. For higher natural modes, deflection becomes zero at multiple locations on the beam. Furthermore, the mode shapes clearly provide alternative symmetric and antisymmetric modes in case of even and odd modes, respectively. It is worth noting that the greatest amount of deflection occurs at the end of the beam because the spring beam system generally shows an initial deflection to obtain the equilibrium position. However, the spring no longer deflects after having static equilibrium.

Figure 4.  Mode shapes of (mode 1): $1^{st}$ eigenmode; (mode 2): $2^{nd}$ eigenmode; (mode 3): $3^{rd}$ eigenmode; (mode 4): $4^{th}$ eigenmode; for $K_{1}$ = $K_{2} = 10000\ N/m$.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Mode shapes of (mode 1): $1^{st}$ eigenmode; (mode 2): $2^{nd}$ eigenmode; (mode 3): $3^{rd}$ eigenmode; (mode 4): $4^{th}$ eigenmode; for $K_{1} = 10000\ N/m, K_{2} = 1000\ N/m$.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Mode shapes of (mode 1): $1^{st}$ eigenmode; (mode 2): $2^{nd}$ eigenmode; (mode 3): $3^{rd}$ eigenmode; (mode 4): $4^{th}$ eigenmode; for $K_{1} = 1000000\ N/m$, $K_{2} = 10000\ N/m$.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Mode shapes of (mode 1): $1^{st}$ eigenmode; (mode 2): $2^{nd}$ eigenmode; (mode 3): $3^{rd}$ eigenmode; (mode 4): $4^{th}$ eigenmode; for $K_{1} = K_{2} = 50000N/m$.

DownLoad: Full-Size Img PowerPoint

5.   Validation of results

The intent of this section is to demonstrate the validity of the results mentioned above. The underlying results for a few specific cases that have already been documented in the literature are rendered for this purpose. The simply supported EBB eigenfrequencies have been determined to be precisely comparable to those reported by Leissa ^[23] when

has been taken into account, as shown in Table 5. Furthermore, letting the stiffness parameters be

Table 5.  Comparison of eigenfrequencies of first four modes for $N$ = 10.

Modes	[23]	FEM by CM	FEM by LM
$K_{1}=K_{2}=10^{12}$
$1^{st}$	$9.8696$	9.8696	9.8695
$2^{nd}$	$39.478$	39.4782	39.4737
$3^{rd}$	$88.876$	88.8769	88.7669
$4^{th}$	$57.914$	157.7529	157.5231
$K_{1}=K_{2}=0$
$1^{st}$	$0.0000$	0, 0000	0.0000
$2^{nd}$	$0.000$	0.0002	0.0041
$3^{rd}$	$22.273$	22.3740	21.7055
$4^{th}$	$61.373$	61.6881	58.6391

---

 | Show Table

DownLoad: CSV

verifies the findings of the free free EBB ^[23].

6.   Conclusions

In this article, the modal analysis of the Euler-Bernoulli beam subject to attached linear springs has been made. Eigenfrequencies and mode shapes were evaluated by comparing the analytic method and FEM using CM and LM matrices by varying the stiffness of the springs. It has been noted that more numbers of beam elements resulted in better accuracy of eigenfrequencies whereas consideration of the CM matrix showed excellent accuracy as compared to the LM matrix for $N$ = 5 or $N$ = 100. This has justified the preference of considering the CM matrix over the LM matrix even for a small number of beam elements for the greater advantage and better accuracy of the solution. Also, it has been observed that a large amount of deflection occurred at the end points of the beam which justified the dynamics of the spring beam system.

While dealing with more complex and practical problems of beam dynamics, obtaining analytical solutions often becomes challenging and sometimes impossible. It has been noticed that the use of FEM with the consideration of the LM matrix is rather convenient in addressing more challenging and practical problems related to beam dynamics. The underlying study concluded with the aim to provide an effective way to treat such problems numerically in a more efficient way. Furthermore, it is important to note that the suggested method can be easily extended to specific two-dimensional structures such as plates and shells with common boundary conditions, albeit with numerical concerns. However, it is critical to recognize that adding plates and shell-like structures may create complexities that are beyond the capability of typical numerical methods. In such circumstances, mode-matching algorithms have emerged as viable options for addressing complex structures; see, for reference, ^[32,33]. While mode-matching methods may neglect some effects, such as break-out, they provide useful insights into vibrating processes and serve as benchmark answers for fully numerical systems. Traditionally, numerical and analytical methods are used to describe finite-length plate or shell-like structures. Numerical methods, such as the finite element method or the boundary element method, allow for the analysis of structures of various shapes and sizes. However, as the excitation frequency and structure dimensions increase, so does the number of degrees of freedom, making these approaches unsuitable even for relatively small structures. As a result, in situations where typical numerical approaches are limited, mode-matching solutions provide a desirable and precisely computed option for handling the complexity inherent in modeling finite-length plate or shell-like structures.

Author contributions

M. Alkinidri: conceptualization, methodology, writing (review and editing), investigation, analysis, visualization, validation, resources; R. Nawaz: conceptualization, methodology, writing (original draft), investigation, analysis, visualization, validation, supervision; H. Alahmadi: methodology, writing (review and editing), investigation, analysis, visualization, validation, resources.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors express their gratitude to Dr. Gulnaz Kanwal for her valuable suggestions, particularly regarding the computational aspects of the study, which significantly improved the quality of the article.

Conflict of interest

The authors declare no conflicts of interest.