Some results on the existence and stability of impulsive delayed stochastic differential equations with Poisson jumps

1.   Introduction

It is well known that there exist instantaneous perturbations and abrupt changes at certain times in different areas of the real world, such as mechanics, electronics, telecommunications, finance markets and so on. We usually call the changes impulsive effects, which are described by impulsive differential equations. In the last decades, the study of corresponding impulsive differential equations has been very extensive. However, noise or stochastic perturbation is unavoidable in the real world, and stochastic differential equations are viewed as powerful tools for describing these stochastic perturbations. Based on the above fact, impulsive stochastic differential equations naturally come into our view, and the topic of impulsive stochastic differential equations has aroused great interest for researchers. Many meaningful results about impulsive stochastic differential equations have been reported (see ^{[1,2,3,4,5,6,7]}).

Also, stability analysis has always been an important problem in the field of impulsive stochastic systems and has been widely studied by numerous works. Meanwhile, the concept of exponential stability plays a crucial role in dynamic systems and its convergence rate is faster than the asymptotic stability. Therefore, the existence and stability of the solutions for stochastic systems have been studied widely, and some interesting results have been presented to us: for instance, Luo ^[8], Chen ^[9], Li and Fan ^[10], Li et al. ^[11], Guo et al. ^[12], Li et al. ^[13], Benhadri et al. ^[14], Cao and Zhu ^[15], Shu et al. ^[16,17], Huang and Li ^[18], Parvizi et al. ^[19,20,21], among others. On the other hand, stochastic differential equations driven by Poisson random measures arise in many different fields. For example, they have been used to develop models for the neuronal activity that for synaptic impulses occur randomly, both in time and at different locations of a spatially extended neuron. Other applications arise in chemical reaction-diffusion systems and stochastic turbulence models. To the best of our knowledge, the existing papers on stability analysis of the mild solutions for stochastic partial differential equations driven by Poisson jump are relatively few. For example, Anguraj et al. ^[22], Hou et al. ^[23], Chen et al. ^[24], Ravikumar et al. ^[25], Chadha and Bora ^[26] all investigated the exponential stability results of mild solutions for impulsive stochastic equations driven by Poisson jumps under some suitable conditions.

However, it should be further emphasized that the existence and exponential stability of solutions for impulsive stochastic systems with Poisson jumps need further study. To the best of authors' knowledge, some authors have established the impulsive-integral inequality to investigate the exponential stability of corresponding impulsive stochastic systems in the above-mentioned ^{[3,9,16,24,26]}, and it should be pointed out that the restrictive conditions of the impulsive-integral inequality in ^{[3,9,16,24,26]} are too strict, which shows that the impulsive-integral inequality has room for improvement. The main contributions of this paper are that the criteria of existence and uniqueness of mild solutions for the considered impulsive stochastic differential equations are discussed by using the successive approximation method, and an improved impulsive-integral inequality is given in later Lemma 4.1 and Lemma 4.2, which are used to obtain the exponential stability in the $p$th moment of mild solutions for impulsive stochastic differential equations.

The remainder of this article is divided into five parts. In Section 2, some preliminaries and results which are applied in this paper are presented. Section 3 is devoted to studying the existence and uniqueness of the mild solution of the system (2.1). The criteria of exponential stability in the $p$th moment of mild solution for impulsive stochastic differential equations are given in Section 4. Finally, an example and numerical simulation are established to illustrate the theoretical results in Section 5.

2.   Preliminaries

Let $X$ and $Y$ be two real, separable Hilbert spaces and $L(Y, X)$ be the space of a bounded linear operator from $Y$ to $X$. For the sake of convenience, we shall use the same notation $\Vert\cdot\Vert$ to denote the norms in $X$, $Y$ and $L(Y, X)$ when no confusion possibly arises. Let $(\Omega, \mathfrak{F}, \{\mathfrak{F}_{t}\}_{t\geq0}, P)$ be a complete filtered probability space with a filtration $\{\mathfrak{F}_{t}\}_{t\geq0}$ satisfying the usual conditions (i.e. right continuous and $\mathfrak{F}_{0}$ containing all $P_{0}$-null sets). Suppose $\{p(t), t\geq 0\}$ is a $\sigma$-finite stationary $\mathfrak{F}_{t}$-adapted Poisson point process taking values in measurable space $(U, \mathcal{B}(U))$. The random measure $N_{p}$ defined by $N_{p}((0, t]\times\Lambda): = \sum_{s\in(0, t]}1_{\Lambda}(p(s))$ for $\Lambda\in\mathcal{B}(U)$ is called the Poisson random measure induced by $p(\cdot),$ and then, we can define the measure $\widetilde{N}$ by $\widetilde{N}(dx, dy) = N_{p}(dt, dy)-v(dy)dt,$ where $v$ is the characteristic measure of $N_{p},$ which is called the compensated Poisson random measure.

For Borel set $z\in\mathcal{B}(U-\{0\}),$ we consider an impulsive stochastic differential equation with Poisson jumps and varying-time delays as follows:

where $\varphi$ is $\mathfrak{F}_{0}$-measure. Let $PC\equiv PC([-\tau, 0];X)$ be the space of all almost surely bounded, $\mathfrak{F}_{0}$-measure and continuous functions everywhere except for an infinite number of point $s$ at which $\xi(s)$ and left limit $\xi(s)$ exists and $\xi(s^{+}) = \xi(s)$ from $[-\tau, 0]$ into $X$ and equipped with the supremum norm $\Vert\varphi\Vert_{0} = \sup_{\theta\in[-\tau, 0]}\Vert\varphi(\theta)\Vert$. $A$ is the infinitesimal generator of an analytic semigroup $(S(t))_{t\geq 0}$ of bounded linear operators in $X$, and for more details about semigroup theory we refer to ^[27]. The functions $\delta_{1}(t), \delta_{2}(t), \delta_{3}(t):[0, T]\rightarrow [0, \tau] (i = 1, 2, 3)$ are continuous. $f_{1}, f_{2}:[0, T]\times X\rightarrow X$ and $f_{3}:[0, T]\times X\times U\rightarrow X$ are all suitable Borel measurable functions, where $L_{2}^{0}(Y, X)$ is defined in a later part. $I_{k}(\cdot):X\rightarrow X$ are continuous functions, and the fixed times $t_{k}$ satisfy $0 = t_{0} < t_{1} < \cdots < t_{k} < ... < T, \Delta x(t_{k}) = x(t_{k}^{+})-x(t_{k}^{-})$ and $x(t_{k}^{-}) = x(t_{k})$, where $x(t_{k}^{+})$ and $x(t_{k}^{-})$ represent the right and left limits of $x(t)$ at $t_{k},$ respectively.

Let $\beta_{n}(t) (n = 1, 2, ...)$ be a sequence of real-valued one-dimensional standard Brownian motions mutually independent over $(\Omega, \mathfrak{F}, P)$. Let $\omega(t) = \sum_{n = 1}^{+\infty}\sqrt{\lambda_{n}}\beta_{n}(t)e_{n}(t\geq 0),$ where $\lambda_{n}\geq 0 (n = 1, 2, ...)$ are nonnegative real numbers, and $\{e_{n}\}(n = 1, 2, ...)$ is a complete orthonormal basis in $Y$. Let $Q\in L(Y, X)$ be an operator defined by $Qe_{n} = \lambda_{n}e_{n}$ with a finite trace $trQ = \sum_{n = 1}^{+\infty}\lambda_{n} < +\infty.$ Then, the above $Y$-valued stochastic process $\omega(t)$ is called a $Q$-Wiener process.

Definition 2.1. Let $\phi\in L(Y, X)$ and define

If $\Vert\phi\Vert_{L_{2}^{0}}^{2} < +\infty,$ then $\phi$ is called a $Q$-Hilbert-Schmidt operator, and define $L_{2}^{0}(Y, X)$, the space of all $Q$-Hilbert-Schmidt operators $\phi:Y\rightarrow X.$

For more details about the $X$-valued stochastic integral of an $L_{2}^{0}(Y, X)$-valued, $\mathfrak{F}_{t}$-adapted predictable process $h(t)$ with respect to the $Q$-Wiener process $\omega(t),$ we can see ^[27].

Lemma 2.1. (^[27]) For any $p\geq 2$ and an arbitrary $L_{2}^{0}(Y, X)$-valued predictable process $\psi(s)$,

where $c_{p} = (\frac{p(p-1)}{2})^{\frac{p}{2}}$ and $t\in[0, +\infty).$

Definition 2.2. (^[24]) An $X$-valued stochastic process $\{x(t), t\in[-\tau, T]\}$ is called a mild solution of (2.1) if

(1) $x(t)$ is an $\mathfrak{F}_{t} (t\geq 0)$ adapted process;

(2) $x(t)\in X$ has a c$\grave{a}$dl$\grave{a}$g path on $t\in [0, T]$ almost surely;

(3) for each $t\in [0, T],$ we have

where $x_{0}(\cdot) = \varphi\in PC,$ a.s.

Definition 2.3. The mild solution of the system (2.1) is said to be exponentially stable in $p$th moment if there exist two positive constants $\lambda > 0$ and $M_{0} > 0,$ for any initial value $\varphi\in PC, a.s.,$ such that

Moreover, to obtain our main results, we give the following assumptions:

(H1) $A$ is the infinitesimal generator of an analytic semigroup of bounded linear operators $(S(t))_{t\geq0}$ in $X$ and satisfies that there exist two positive constants $M > 0$ and $\gamma > 0$ such that $\Vert S(t)\Vert\leq Me^{-\gamma t}, \forall t\in[0, T].$

(H2) There exist three positive constants $C_{1}, C_{2}$ and $C_{3} > 0$ such that

and

where $x, y\in X, z\in Z, t\in[0, T].$

(H3) There exist positive constants $d_{k}, k = 1, 2, ...,$ such that

where $x, y\in X$ and $\sum_{k = 1}^{+\infty}d_{k} < +\infty.$

3.   Existence and uniqueness

In this part, we discuss the existence and uniqueness of the mild solution for the considered system (2.1) via the successive approximation method.

Theorem 3.1. Assume that conditions (H1)–(H3) hold, and then the system (2.1) has a unique mild solution on $[-r, T], \ 0 < T < \infty$ provided that

Proof. To get the existence of the mild solution of the system (2.1), we first need to introduce the sequence of successive approximations to the system (2.1) as follows:

Let $x^{0}(t) = S(t)\varphi(0), \ t\in[0, T]$ and $x_{0}^{n}(t) = \varphi(t), \ t\in[-\tau, 0], \ n = 0, 1, 2, \cdots.$ Then, we define the following iterative scheme:

Next, we prove the criterion of existence and uniqueness of mild solutions for the system (2.1), and the proof is split into the following three steps.

Step 1. The sequence $\{x^{n}(t), \ n\geq0\}$ is bounded.

In fact, by using (3.2) and Lemma 2.1 for $0\leq t\leq T$, we obtain

Then, we will estimate the right-hand side of the above inequality. From (H1), we have

Also, from (H1), (H3) and the Hölder inequality, we have

Similarly, by (H1), (H2), the Hölder inequality and Lemma 2.1, we have

and

Therefore,

Since $\sup_{s\in[-\tau, t]}E\Vert x^{n}(s)\Vert^{p}\leq\sup_{s\in[-\tau, 0]}E\Vert x^{n}(s)\Vert^{p}+\sup_{s\in[0, t]}E\Vert x^{n}(s)\Vert^{p},$ the above inequality implies that

Then, by applying the mathematical induction and known result $E\Vert\varphi\Vert^{p} < \infty$, we obtain that the sequence $\{x^{n}(t)\}$ is bounded.

Step 2. The sequence $\{x^{n}(t), \ n\geq0\}$ is a Cauchy sequence.

A similar estimation to Step 1 and (3.2) for $t\in [0, T]$ yields

Namely,

Note that $\sup_{s\in[0, t]}E\Vert x^{0}(s)\Vert^{p} = \sup_{s\in[0, t]}E\Vert x^{0}(s)\Vert^{p}\leq M^{p}E\Vert \varphi(0)\Vert^{p}$, and from (3.2), we have

Therefore,

which implies that for any $m > n\geq 1$, together with (3.1), we obtain

which implies that the sequence $\{x^{n}(t), \ n\geq0\}$ is a Cauchy sequence.

Step 3. Existence and uniqueness of the mild solution for the system (2.1).

Through the above analysis and combining with the Borel-Cantelli lemma, we know that $x^{n}(t)\rightarrow x(t)$ holds uniformly for $0\leq t\leq T$ as $n\rightarrow \infty.$ Then, taking limits on both sides of (3.2), we obtain that $x(t)$ is a solution of the system (2.1). The uniqueness of the mild solution for the system (2.1) is proved by using a similar estimation as step 2.□

4.   Exponential stability in the $p$th moment

In order to obtain the exponential stability in the $p$th moment of mild solution for the system (2.1), we will first establish an improved impulsive-integral inequality as follows.

Lemma 4.1. Consider a constant $\gamma > 0,$ positive constants: $\xi, \xi^{*}, \xi_{k}(k = 1, 2, ...)$ and a function $y:[-\tau, T]\rightarrow [0, +\infty).$ If the inequality

holds, then we have $y(t)\leq \xi e^{-\lambda t}(t\geq -\tau),$ where $\lambda$ is a positive constant defined by $\lambda = p\gamma-\zeta-\overline{\xi}$, and $\overline{\xi}$ satisfies $\prod_{0 < t_{k} < t}\lambda_{k} < e^{\overline{\xi}t}$, $\overline{\xi} < \gamma-\zeta$, $\lambda_{k} = \max\{1+\xi_{k}, 1\}.$

Proof. In view of the definition of $\lambda$, it is obvious to see $y(t)\leq \xi e^{-\lambda t}$ for $t\in [-\tau, 0]$. Next, multiplying $e^{\gamma pt}$ on both sides of the first inequality of Lemma 4.1 for any $t\in[0, T],$ we obtain

Let $x(t) = y(t)e^{\gamma pt},$ and the above inequality is transformed as

Since $0\leq s\leq t, -\tau\leq\theta\leq0,$ which implies that $t-(s+\theta)\in[0, t+\tau].$ Therefore,

Let $\zeta = \xi^{*}e^{\gamma p(\tau+T)}$ and

Then, we have

and

where $\lambda_{k} = \max\{1+\xi_{k}, 1\}.$

Consider the following equation:

It is easily shown that the solution of (4.4) is $\eta(t) = \Vert \eta_{0}\Vert e^{\zeta t}.$ From the comparison principle, we obtain

and

In view of (4.5) and (4.6), we have

Combining with mathematical induction, we have

Thus,

where $\lambda = p\gamma-\zeta-\overline{\xi}$, $\overline{\xi}$ satisfies $\prod_{t_{k} < t}\lambda_{k} < e^{\overline{\xi}t}$, and $\overline{\xi} < p\gamma-\zeta$. The proof is completed.□

Remark 4.1. It is obviously shown that the value range of $\xi_{k}$ in our results is wider than that in ^[24], which is required to satisfy $\frac{\zeta}{\gamma}+\sum_{k = 1}^{+\infty}\xi_{k} < 1.$ If $\xi_{k}\geq 1,$ the corresponding lemma in ^[24] will be invalid. But in our result, $\xi_{k}$ can be greater than or equal to 1. When $p = 1,$ some known results ^[3,9] can also be broadened.

Lemma 4.2. Consider $\gamma_{1}, \gamma_{2} > 0,$ positive constants: $\xi, \omega, \xi^{*}, \omega^{*}, \xi_{k}, \omega_{k}(k = 1, 2, ...)$ and a function $y:[-\tau, T]\rightarrow [0, +\infty).$ If the inequality

holds, then we have $y(t)\leq (\xi+\omega) e^{-\lambda t}(t\geq -\tau),$ where $\lambda$ is a positive constant defined by $\lambda = p\max\{{\gamma_{1}, \gamma_{2}}\}-\zeta-\overline{\xi}$, and $\overline{\xi}$ satisfies $\prod_{0 < t_{k} < t}\lambda_{k} < e^{\overline{\xi}t}$ and $\overline{\xi} < p\max\{{\gamma_{1}, \gamma_{2}}\}-\zeta$, $\zeta = \xi^{*}e^{\gamma_{1}p(\tau+T)}+\omega^{*}e^{\gamma_{2}p(\tau+T)}$, $\lambda_{k} = \max\{1+\xi_{k}+\omega_{k}, 1\}.$

Proof. The proof is similar to Lemma 4.1, and we omit it here.□

Remark 4.2. When $p = 1$, it is also easy to see that the $\xi_{k}$ and $\omega_{k}$ are more simple in our results than in ^[26], which is required to satisfy $\frac{\xi^{*}e^{\gamma_{1}p(\tau+T)}}{\gamma_{1}}+\frac{\omega^{*}e^{\gamma_{2}p(\tau+T)}}{\gamma_{2}}+\sum_{k = 1}^{+\infty}\xi_{k}+\sum_{k = 1}^{+\infty}\omega_{k} < 1.$ If $\xi_{k}\geq 1$ or $\omega_{k}\geq 1$, the corresponding lemma in ^[26] will not hold, too. But in our result, $\xi_{k}$ or $\omega_{k}$ can be greater than or equal to 1.

Theorem 4.1. Assume that conditions (H1)–(H3) hold, and then the mild solution of the system (2.1) is exponentially stable in the $p$th moment.

Proof. Similar to the estimation of Step 1 in Section 3, that is, from conditions (H1)–(H3) and the Hölder inequality, we have

On the other hand, it is clearly shown that for $t\in[-\tau, 0]$, we have

where $M^{*} = \max\Big\{8^{p-1}M^{p}, 1\Big\}.$ Owing to Lemma 4.1 for all $t\geq -\tau,$ we have

where $\lambda = p\gamma-\zeta-\overline{\lambda}$, $\zeta = 4^{p-1}M^{p}\Big[C_{1}^{p}\gamma^{1-p}+c_{p}C_{2}^{p}\Big(\frac{2\gamma(p-1)}{p-2}\Big)^{1-\frac{p}{2}}+c_{p}C_{3}^{p}\Big(\frac{p-2}{2(p-1)\gamma}\Big)^{\frac{p-2}{2}}\Big],$ $\overline{\lambda}$ satisfies $\prod_{t_{k} < t}\xi_{k} < e^{\overline{\lambda}t}, \xi_{k} = 1+8^{p-1}M^{p}\Big(\sum_{t_{k} < t}d_{k}\Big)^{p-1}\Big(\sum_{t_{k} < t}d_{k}\Big)$ and $\overline{\lambda} < p\gamma-\zeta$. Hence, we prove that the mild solution of the system (2.1) is exponentially stable in the $p$th moment.

Note that if function $f_{3}\equiv 0$, the system (2.1) is changed as

Hence, we have the following corollary:

Corollary 4.1. Assume that conditions (H1)–(H3) hold, and then the mild solution of the system (4.10) is exponentially stable in the $p$th moment.

Proof. Similar to the proof of Theorem 4.1, we also obtain $E\Vert x(t)\Vert^{p}\leq M^{*}E\Vert\varphi(0)\Vert^{p} e^{-\lambda t}$ for all $t\geq -\tau,$ where $\lambda = p\gamma-\zeta-\overline{\lambda}$, $\zeta = 4^{p-1}M^{p}\Big[C_{1}^{p}\gamma^{1-p}+c_{p}C_{2}^{p}\Big(\frac{2\gamma(p-1)}{p-2}\Big)^{1-\frac{p}{2}}\Big],$ $\overline{\lambda}$ satisfies $\prod_{t_{k} < t}\xi_{k} < e^{\overline{\lambda}t}, \xi_{k} = 1+8^{p-1}M^{p}\Big(\sum_{t_{k} < t}d_{k}\Big)^{p-1}\Big(\sum_{t_{k} < t}d_{k}\Big)$ and $\overline{\lambda} < p\gamma-\zeta$. Namely, the mild solution of the system (4.10) is exponentially stable in the $p$th moment.□

Remark 4.3. It is clearly shown that some known results can be broadened by the above Corollary 4.1. In detail, when $p = 2$, Theorem 4.1 in ^[16] is the special case of Corollary 4.1. Comparing Theorem 3.2 in ^[16] with Corollary 4.1, we find the value range of $\xi_{k}$ in our results is more general.

5.   An example

In this part, we support our main obtained results by establishing an effective example as follows.

Example 5.1. Consider the following system:

$\omega(t)$ is a standard cylindrical Wiener process in $X$, $A:D(A)\subset X\rightarrow X$, which is defined by $Ay = y^{''}$ with the domain $D(A) = \{y\in X, \ y, y' \ are \ absolutely \ continuous \ y''\in X, \ y(0) = y(\pi) = 0\}$ and

where $y_{n}(x) = \sqrt{\frac{2}{\pi}}\sin(nx), n\in N$ is the orthonormal set of eigenvectors of $A$, $A$ is the infinitesimal generator of an analytic semigroup $(S(t))_{t\geq 0}$ in $X$, and $\Vert S(t)\Vert\leq e^{-\pi^{2}t}.$

It is easily shown that (5.1) can be transformed in the form of (2.1), where $f_{1} = C_{1}\sin x, f_{2} = C_{2}\cos x, f_{3} = C_{3}y\sin x$. The delay functions are $\delta_{1}(t) = \frac{t}{4}, \delta_{2}(t) = \frac{t}{4}, \delta_{3}(t) = \frac{t}{2}$. The impulsive functions are $I_{k}(x) = d_{k}x, k\in N$. Thus, it is easy to verify the conditions (H1)–(H3) of Theorem 3.1 all hold, and the existence and uniqueness of the mild solution of (5.1) are obtained by Theorem 3.1.

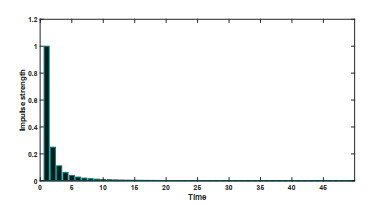
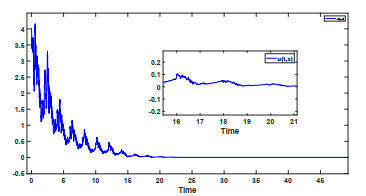
Next, we prove the mild solution of (5.1) is exponentially stable in the 4th moment ($p = 4$). In fact, we know $M = 1, \gamma = \pi^{2}.$ Let $C_{1} = \frac{\pi^{\frac{3}{2}}}{2}, C_{2} = C_{3} = \sqrt{\frac{\pi}{6}}, d_{k} = \frac{1}{k^2}, t_{k} = k$, $k\in\mathbb{Z}_+$, and by simple calculation, we have $\zeta = 4^{p-1}M^{p}\Big[C_{1}^{p}\gamma^{1-p}+c_{p}C_{2}^{p}\Big(\frac{2\gamma(p-1)}{p-2}\Big)^{1-\frac{p}{2}}+c_{p}C_{3}^{p}\Big(\frac{p-2}{2(p-1)\gamma}\Big)^{\frac{p-2}{2}}\Big]\approx9.33,$ $\xi_{1} = 3, \xi_{2}\approx16.42.$ Then we choose $\overline{\lambda} = 6,$ so $\lambda = p\gamma-\zeta-\overline{\lambda} = 4\pi^{2}-9.33-6 > 0.$ On the other hand, the conditions of Theorem 4.1 also hold, that is, the mild solution of the system (5.1) is exponentially stable in the 4th moment. Finally, we give the following numerical simulations for the above impulsive stochastic system with Poisson jumps (see Figures 1 and 2).

6.   Conclusions

In this research article, we consider the existence, uniqueness and exponential stability of mild solution for a class of impulsive stochastic differential equations driven by Poisson jumps and time-varying delays. Utilizing the successive approximation method, we obtain the criteria of existence and uniqueness of mild solution for the considered impulsive stochastic differential equations. Then, the exponential stability in the pth moment of mild solution is also devised for considered equations by establishing an improved impulsive-integral inequality, which improves some known existing ones. In future work, we are intended to study the existence and exponential stability of mild solutions for impulsive neutral stochastic differential equations.

Acknowledgments

This work is supported by the Natural Science Foundation of China (12071105), the Key Projects of Science Research in University of Anhui Province (KJ2021A1049, 2022AH040248), the Natural Science Foundation of Anhui Province of China (2108085MA11), the Philosophy and Social Science Planning Project of Anhui Province (AHSKQ2022D043), and the Talent Foundation of Tongling University (2021tlxyrc24).

Conflict of interest

The authors declare that they have no conflict of interest.