Some new criteria for judging $\mathcal{H}$-tensors and their applications

1.   Introduction and preliminaries

In the past few decades, fixed point theory was developed by a large number of authors, especially in metric spaces, which can be observed in ^{[1,2,3,4,5,6]}. In 1993, Czerwik ^[7] initiated the concept of $b$-metric spaces. Later, many authors proved fixed point theorems in $b$-metric spaces ^[8,9,10]. However, the general metric notion was introduced by Branciari ^[11] in 2000, the so-called Branciari metric. The notion of generalization of Branciari $b$-metric spaces was introduced by George et al. ^[12] in 2015. Johnsonbaugh ^[13] explored certain fundamental mathematical principles, including foundational topics relevant to fixed-point theory and discrete structures, which underpin many concepts in fixed-point applications. Younis et al. ^[14] introduced graphical rectangular b-metric space and proved fixed point theorem. Younis et al. ^[15] presented graphical b-metric space and proved fixed point theorem. Younis et al. ^[16] presented graphical extended b-metric space and proved fixed point theorem. Younis et al. ^[17] proved fixed points results using graphical B c-Kannan-contractions by numerical iterations within the structure of graphical extended $b$-metric spaces. Younis et al. ^[18] presented a fixed point result for Kannan type mappings, in the framework of graphical $b$-metric spaces. Younis et al. ^[19] introduced the notion of controlled graphical metric type spaces and proved the fixed point theorem. Haroon Ahmad et al. ^[20] developed the graphical bipolar b-metric space and proved the fixed point theorem.

The following preliminary is given for better understanding by the readers.

Let $(\varUpsilon, \varrho)$ be a metric space. Let $\Delta$ denote the diagonal of the Cartesian product $\varUpsilon\times\varUpsilon$. Consider a directed graph $\varOmega$ such that the set $\mathcal{V}(\varOmega)$ of its vertices coincides with $\varUpsilon$, and the set $\mathcal{E}(\varOmega)$ of its edges contains all loops, i.e., $\mathcal{E}(\varOmega)\supseteq\Delta$. We assume $\varOmega$ has no parallel edges, so we can identify $\varOmega$ with the pair $(\mathcal{V}(\varOmega), \mathcal{E}(\varOmega))$. Moreover, we may treat $\varOmega$ as a weighted graph (see ^[13], p.$309$) by assigning to each edge the distance between its vertices. By $\varOmega^{-1}$, we denote the conversion of a graph $\varOmega$, i.e., the graph obtained from $\varOmega$ by reversing the direction of edges. Thus, we have

The letter $\tilde{\varOmega}$ denotes the undirected graph obtained from $\varOmega$ by ignoring the direction of edges. Actually, it will be more convenient for us to treat $\tilde{\varOmega}$ as a directed graph for which the set of its edges is symmetric. Under this convention,

We call $(\mathcal{V}^{'}, \mathcal{E}^{'})$ a subgraph of $\varOmega$ if $\mathcal{V}^{'}\subseteq\mathcal{V}(\varOmega), \mathcal{E}^{'}\subseteq\mathcal{E}(\varOmega)$ and, for any edge $(\vartheta, \sigma) \in \mathcal{E}^{'}, \vartheta, \sigma\in\mathcal{V}^{'}$.

If $\vartheta$ and $\sigma$ are vertices in a graph $\varOmega$, then a path in $\varOmega$ from $\vartheta$ to $\sigma$ of length $\mathfrak{r}(\mathfrak{r}\in\mathbb{N})$ is a sequence $(\vartheta_\mathfrak{i})^{\mathfrak{r}}_{\mathfrak{i} = 0}$ of $\mathfrak{r}+1$ vertices such that $\vartheta_0 = \vartheta, \vartheta_\mathfrak{r} = \sigma$ and $(\vartheta_{\zeta-1}, \vartheta_\zeta)\in\mathcal{E}(\varOmega)$ for $\mathfrak{i} = 1, ....., \mathfrak{r}$. A graph $\varOmega$ is connected if there is a path between any two vertices. $\varOmega$ is weakly connected if, treating all of its edges as being undirected, there is a path from every vertex to every other vertex. More precisely, $\varOmega$ is weakly connected if $\tilde{\varOmega}$ is connected.

We define a relation $\mathcal{P}$ on $\varUpsilon$ by: $(\vartheta\mathcal{P} \sigma)_{\varOmega}$ if and only if there is a directed path from $\vartheta$ to $\sigma$ in $\varOmega$. We write $\eta, \kappa\in (\vartheta\mathcal{P} \sigma)_{\varOmega}$ if $\eta, \kappa$ is contained in some directed path from $\vartheta$ to $\sigma$ in $\varOmega$. For $\mathfrak{l}\in \mathbb{N}$, we denote

A sequence $\{\vartheta_{\zeta}\}$ in $\varUpsilon$ is said to be $\varOmega$-term wise connected if $(\vartheta_{\zeta}\mathcal{P}\sigma_{\zeta})$ for all $\zeta\in \mathbb{N}$. Further details one can see ^{[21,22,23,24,25]}.

Definition 1.1. Let $\varUpsilon$ be a nonempty set endowed with a graph $\varOmega$, $\aleph \geq 1$ and $\varrho : \varUpsilon\times\varUpsilon \longrightarrow [0, +\infty)$ satisfy the assumptions below for every $\vartheta, \sigma\in \varUpsilon$:

(T1) $\varrho(\vartheta, \sigma) = 0$ if and only if $\vartheta = \sigma$;

(T2) $\varrho(\vartheta, \sigma) = \varrho(\sigma, \vartheta)$;

(T3) $(\vartheta\mathcal{P} \sigma)_{\varOmega}$, $\eta, \varphi\in(\vartheta\mathcal{P} \sigma)_{\varOmega}$ implies $\varrho(\vartheta, \sigma) \leq \aleph[\varrho(\vartheta, \varphi) + \varrho(\varphi, \omega) +\varrho(\omega, \sigma)]$ for all distinct points $\varphi, \omega \in \varUpsilon/ \{\vartheta, \sigma\}$.

In this case, the pair $(\varUpsilon, \varrho)$ is called a graphical Branciari $\aleph$-metric space with constant $\aleph \geq 1$.

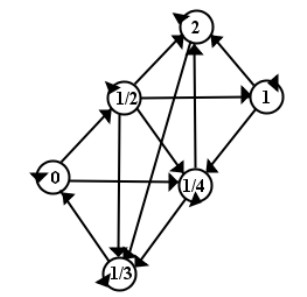
Example 1.1. Let $\varUpsilon = \mathcal{B}\cup \mathcal{U}$, where $\mathcal{B} = \{0, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}\}$ and $\mathcal{U} = [1, 2]$. Define the graphical Branciari $\aleph$-metric space $\varrho : \varUpsilon\times\varUpsilon \longrightarrow [0, +\infty)$ as follows:

and

equipped with the graph $\varOmega = (\mathcal{V}(\varOmega), \mathcal{E}(\varOmega))$ so that $\varUpsilon = \mathcal{V}(\varOmega)$ with $\mathcal{E}(\varOmega))$.

It can be seen that the above Figure 1 depicts the graph given by $\varOmega = (\mathcal{V}(\varOmega), \mathcal{E}(\varOmega))$.

Definition 1.2. Let $\{\vartheta_{\zeta}\}$ be a sequence in a graphical Branciari $\aleph$-metric space $(\varUpsilon, \varrho)$. Then,

(S1) $\{\vartheta_{\zeta}\}$ converges to $\vartheta\in \varUpsilon$ if, given $\epsilon > 0$, there is $\zeta_{0}\in\mathbb{N}$ so that $\varrho(\vartheta_{\zeta}, \vartheta) < \epsilon$ for each $\zeta > \zeta_{0}$. That is, $\lim_{\zeta\rightarrow \infty}\varrho(\vartheta_{\zeta}, \vartheta) = 0$.

(S2) $\{\vartheta_{\zeta}\}$ is a Cauchy sequence if, for $\epsilon > 0$, there is $\zeta_{0}\in\mathbb{N}$ so that $\varrho(\vartheta_{\zeta}, \vartheta_{\mathfrak{m}}) < \epsilon$ for all $\zeta, \mathfrak{m} > \zeta_{0}$. That is, $\lim_{\zeta, \mathfrak{m}\rightarrow \infty}\varrho(\vartheta_{\zeta}, \vartheta_{\mathfrak{m}}) = 0$.

(S3) $(\varUpsilon, \varrho)$ is complete if every Cauchy sequence in $\varUpsilon$ is convergent in $\varUpsilon$.

Definition 1.3. (see ^[8]) A function $\mathcal{Q} : (0, +\infty) \longrightarrow \mathbb{R}$ belongs to $\mathscr{F}$ if it satisfies the following condition:

(F1) $\mathcal{Q}$ is strictly increasing;

(F2) There exists $\mathfrak{k} \in (0, 1)$ such that $\lim_{\vartheta\to{0}^{+}} \vartheta^{\mathfrak{k}}\mathcal{Q}(\vartheta) = 0$.

In ^[8], the authors omitted Wardowski's $({F2})$ condition from the above definition. Explicitly, $(F2)$ is not required, if $\{ \alpha_{\zeta}\}_{\zeta \in \mathbb{N}}$ is a sequence of positive real numbers, then $\lim_{\zeta\to+\infty}\alpha_{\zeta} = 0$ if and only if $\lim_{\zeta\to+\infty}\mathcal{Q}(\alpha_{\zeta}) = -\infty$. The reason for this is the following lemma.

Lemma 1.1. If $\mathcal{Q} :(0, +\infty) \longrightarrow \mathbb{R}$ is an increasing function and $\{\alpha_{\zeta}\}_{\zeta \in \mathbb{N}}\subset(0, +\infty)$ is a decreasing sequence such that $\lim_{\zeta\to+\infty}\mathcal{Q}(\alpha_{\zeta}) = -\infty$, then $\lim_{\zeta\to+\infty}\alpha_{\zeta} = 0$.

We can also see some properties concerning $\mathcal{Q}_{\aleph, \ell}$ and $\mathcal{Q}^{'}_{\aleph, \ell}$.

Definition 1.4. (see ^[9]) Let $\aleph \geq1$ and $\ell > 0$. We say that $\mathcal{Q} \in \mathscr{F}$ belongs to $\mathscr{F}_{\aleph, \ell}$ if it also satisfies $(\mathcal{Q}_{\aleph\ell})$ if $\inf\mathcal{Q} = -\infty$ and $\vartheta, \sigma\in (0, \infty)$ are such that $\ell+\mathcal{Q}(\aleph\vartheta)\leq\mathcal{Q}(\sigma)$ and $\ell+\mathcal{Q}(\aleph\sigma)\leq\mathcal{Q}(\eta)$, then

In ^[10], the authors introduced the following condition $(F4)$.

$(\mathcal{Q}^{'}_{\aleph\ell})$ if $\{\alpha_{\zeta}\}_{\zeta \in \mathbb{N}}\subset(0, +\infty)$ is a sequence such that $\ell +\mathcal{Q}(\aleph\alpha_{\zeta})\leq \mathcal{Q}(\alpha_{\mathfrak{n-1}})$, for all $\zeta \in\mathbb{N}$ and for some $\ell\geq0$, then $\ell +\mathcal{Q}(\aleph^{\zeta}\alpha_{\zeta})\leq \mathcal{Q}(\aleph^{\mathfrak{n-1}}\alpha_{\mathfrak{n-1}})$, for all $\zeta \in\mathbb{N}^{*}$.

Proposition 1.1. (see ^[8]) If $\mathcal{Q}$ is increasing, then $(\mathscr{F}_{\aleph\ell})$ is equivalent to $(\mathscr{F}^{'}_{\aleph\ell})$.

Definition 4.5. Let $(\varUpsilon, \varrho)$ be a graphical Branciari $\aleph$-metric space. We say that a mapping $\varPi : \varUpsilon\to\varUpsilon$ is a $\varOmega$-$\mathcal{Q}$-contraction if

(A1) $\varPi$ preserves edges of $\varOmega$, that is, $(\vartheta, \sigma)\in \mathcal{E}(\varOmega)$ implies $(\varPi\vartheta, \varPi\sigma)\in \mathcal{E}(\varOmega)$;

(A2) There exists $\ell > 0$ and $\mathcal{Q} \in \mathscr{F}_{\aleph, \ell}$, such that

Chen, Huang, Li, and Zhao ^[24], proved fixed point theorems for $\mathcal{Q}$-contractions in complete Branciari $b$-metric spaces. The aim of this paper is to study the existence of fixed point theorems for $\mathcal{Q}$-contractions in complete Branciari $b$-metric spaces endowed with a graph $\varOmega$ by introducing the concept of $\varOmega$-$\mathcal{Q}$-contraction.

2.   Main results

Theorem 2.1. Let $(\varUpsilon, \varrho)$ be a complete graphical Branciari $\aleph$-metric space and $\mathcal{Q}\in\mathscr{F}_{\aleph, \ell}$. Let $\varPi :\varUpsilon\longrightarrow\varUpsilon$ be a self mapping such that

(C1) there exists $\vartheta_{0}\in \varUpsilon$ such that $\varPi\vartheta_{0}\in [\vartheta_{0}]^{\mathfrak{l}}_{\varOmega}$, for some $\mathfrak{l}\in \mathbb{N}$;

(C2) $\varPi$ is a $\varOmega$-$\mathcal{Q}$-contraction.

Then $\varPi$ has a unique fixed point.

Proof. Let $\vartheta_{0}\in\varUpsilon$ be such that $\varPi\vartheta_{0}\in [\vartheta_{0}]^{\mathfrak{l}}_{\varOmega}$, for some $\mathfrak{l}\in \mathbb{N}$, and $\{\vartheta_{\zeta}\}$ be the $\varPi$-Picard sequence with initial value $\vartheta_{0}$. Then, there exists a path $\{\sigma_{\mathfrak{i}}\}^{\mathfrak{l}}_{\mathfrak{i} = 0}$ such that $\vartheta_{0} = \sigma_{0}$, $\varPi\vartheta_{0} = \sigma_{\mathfrak{l}}$ and $(\sigma_{\mathfrak{i}-1}, \sigma_{\mathfrak{i}})\in \mathcal{E}(\varOmega)$ for $\mathfrak{i} = 1, 2, 3....\mathfrak{l}$. Since $\varPi$ is a $\varOmega$-$\mathcal{Q}$-contraction, by (A1), $(\varPi\sigma_{\mathfrak{i}-1}, \varPi\sigma_{\mathfrak{i}})\in \mathcal{E}(\varOmega)$ for $\mathfrak{i} = 1, 2, 3...\mathfrak{l}$. Therefore, $\{\varPi\sigma_{\mathfrak{i}}\}^{\mathfrak{l}}_{\mathfrak{i} = 0}$ is a path from $\varPi\sigma_{0} = \varPi\vartheta_{0} = \vartheta_{1}$ to $\varPi\sigma_{1} = \rho^{2}\vartheta_{0} = \vartheta_{2}$ of length $\mathfrak{l}$, and so $\vartheta_{2}\in [\vartheta_{1}]^{\mathfrak{l}}_{\varOmega}$. Continuing this process, we obtain that $\ \varPi^{\zeta}\sigma_{\mathfrak{i}}\}^{\mathfrak{l}}_{\mathfrak{i} = 0}$, is a path from $\varPi^{\zeta}\sigma_{0} = \varPi^{\zeta}\vartheta_{0} = \vartheta_{\zeta}$ to $\varPi^{\zeta}\sigma_{\mathfrak{l}} = \varPi^{\zeta}\varPi\vartheta_{0} = \vartheta_{\zeta+1}$ of length $\mathfrak{l}$, and so, $\vartheta_{\zeta+1}\in[\vartheta_{\zeta}]^{\mathfrak{l}}_{\varOmega}$, for all $\zeta\in \mathbb{N}$. Thus $\{\vartheta_{\zeta}\}$ is a $\varOmega$-term wise connected sequence. For any $\vartheta_{0}\in\varUpsilon$, set $\vartheta_{\zeta} = \varPi\vartheta_{\zeta-1}, \gamma_{\zeta} = \varrho(\vartheta_{\zeta+1}, \vartheta_{\zeta})$, and $\beta_{\zeta} = \varrho(\vartheta_{\zeta+2}, \vartheta_{\zeta})$ with $\gamma_{0} = \varrho(\vartheta_{1}, \vartheta_{0})$ and $\beta_{0} = \varrho(\vartheta_{2}, \vartheta_{0})$. Now, we consider the following two cases:

(E1) If there exists $\zeta_{0}\in\mathbb{N}\cup\{0\}$ such that $\vartheta_{\zeta_{0}} = \vartheta_{\zeta_{0}+1}$, then we have $\varPi\vartheta_{\zeta_{0}} = \vartheta_{\zeta_{0}}$. It is clear that $\vartheta_{\zeta_{0}}$ is a fixed point of $\varPi$. Therefore, the proof is finished.

(E2) If $\vartheta_{\zeta} \neq\vartheta_{\zeta+1}$, for any $\zeta\in\mathbb{N}\cup\{0\}$, then we have $\gamma_\zeta > 0$, for each $\zeta\in\mathbb{N}$.

By proposition 1.1, we obtain

Furthermore, for any $\zeta\in \mathbb{N}$, we have

Since $\lim_{\zeta\to\infty}(\mathcal{Q}(\gamma_{0})-\zeta\ell) = -\infty$, then

From (2.1) and ((F1)), we derive that the sequence $\{\aleph^{\zeta}\gamma_{\zeta}\}_{\zeta = 1}^{\infty}$ is decreasing. By Lemma1.1, we derive that

By (F2), there exists $\mathfrak{k}\in(0, 1)$ such that

Multiplying (2.2) by $(\aleph^{\zeta}\gamma_{\zeta})^{\mathfrak{k}}$ results

which implies $\lim_{\zeta\to\infty}\zeta(\aleph^{\zeta}\gamma_{\zeta})^{\mathfrak{k}} = 0$. Then, there exists $\zeta_{1}\in\mathbb{N}$ such that $\zeta(\aleph^{\zeta}\gamma_{\zeta})^{\mathfrak{k}}\leq1$, $\forall$ $\zeta\geq\zeta_{1}$. Thus,

Therefore, the series $\sum_{\mathfrak{i} = 1}^{\infty}\aleph^{\mathfrak{i}}\gamma_{\mathfrak{i}}$ is convergent. For all $\zeta, \omega \in\mathbb{N}$, we drive the proof into two cases.

(a) If $\omega > 2$ is odd, we obtain

Consequently,

(b) If $\omega > 2$ is even, we can obtain

Furthermore, we conclude that

Since $\beta_{\zeta}\geq0$, we can assume that $\beta_{\zeta} > 0$, $\forall \zeta\in\mathbb{N}$. By a similar method, replacing $\gamma_{\zeta}$ with $\beta_{\zeta}$ in (2.3), there exists $\zeta_{2}\in\mathbb{N}$ such that

which implies $\lim_{\zeta\to\infty}\aleph^{\zeta}\beta_{\zeta} = 0$ and $\lim_{\zeta\to\infty}\beta_{\zeta} = 0$. Together (a) with (b), for every $\omega\in\mathbb{N}$, letting $\zeta\to \infty$,

Thus, $\{\vartheta_{\zeta}\}_{\zeta\in\mathbb{N}}$ is a Cauchy sequence. Since $(\varUpsilon, \varrho)$ is complete, there exists $\vartheta^{*} \in \varUpsilon$ such that $\lim_{\zeta\to\infty}\vartheta_{\zeta} = \vartheta^{*}$. Now

holds for all $\vartheta, \sigma\in\varUpsilon$ with $\varrho(\varPi\vartheta, \varPi\sigma) > 0$. Since $\mathcal{Q}$ is increasing, then

It follows that

Hence, $\vartheta^{*} = \varPi\vartheta^{*}$. Suppose that $\vartheta^{*}$ and $\sigma^{*}$ are two different fixed points of $\varPi$. Suppose that, $\varPi\vartheta^{*} = \vartheta^{*} \neq \sigma^{*} = \varPi\sigma^{*}$ and $(\vartheta_{*}, \sigma_{*})\in \mathcal{E}(\varOmega)$. Then

As $\zeta\to\infty$, which implies $\ell\leq0$, a contradiction. Therefore $\vartheta^{*} = \sigma^{*}$. Hence, $\varPi$ has a unique fixed point in $\varUpsilon$. □

Next, we prove common fixed point theorems on complete graphical Branciari $\aleph$-metric space.

Theorem 2.2. Let $(\varUpsilon, \varrho)$ be a complete graphical Branciari $\aleph$-metric space with constant $\aleph > 1$. If there exist $\ell > 0$ and $\mathcal{Q}\in\mathscr{F}_{\aleph, \ell}$, such that $\varLambda, \varPi: \varUpsilon\longrightarrow\varUpsilon$ are two self mappings on $\varUpsilon$ and satisfy

(H1) for every $\vartheta\in \varUpsilon$, $(\vartheta, \varLambda\vartheta)\in \mathcal{E}(\mathcal{G})$ and $(\vartheta, \varPi\vartheta)\in \mathcal{E}(\mathcal{G})$;

(H2) $\varPi$ and $\varLambda$ are generalized $\mathcal{G}$-$\mathcal{Q}$ contraction

for any $\xi_{1}, \aleph, \mathfrak{c}\in[0, 1)$ with $\xi_{1}+\aleph +\mathfrak{c} < 1, \aleph\aleph < 1$, and $\min\{\varrho(\varLambda\vartheta, \varPi\sigma), \varrho(\vartheta, \sigma), \varrho(\vartheta, \varLambda\vartheta), \varrho(\sigma, \varPi\sigma)\} > 0$ for any $(\vartheta, \sigma)\in\mathcal{E}(\mathcal{G})$. Then $\varLambda$ and $\varPi$ have a unique common fixed point.

Proof. Let $\vartheta_{0}\in \varUpsilon$. Suppose that $\varLambda\vartheta_{0} = \vartheta_{0}$, then the proof is finished, so we assume that $\varLambda\vartheta_{0}\neq\vartheta_{0}$. As $(\vartheta_{0}, \varLambda\vartheta_{0})\in \mathcal{E}(\mathcal{G})$, so $(\vartheta_{0}, \vartheta_{1})\in \mathcal{E}(\mathcal{G})$. Also, $(\vartheta_{1}, \varPi\vartheta_{1})\in \mathcal{E}(\mathcal{G})$ gives $(\vartheta_{1}, \vartheta_{2})\in \mathcal{E}(\mathcal{G})$. Continuing this way, we define a sequence $\{\vartheta_{\mathfrak{j}}\}$ in $\varUpsilon$ such that $(\vartheta_{\mathfrak{j}}, \vartheta_{\mathfrak{j}+1})\in \mathcal{E}(\mathcal{G})$ with

Combining with (2.5) and (2.6), we have

Let $\lambda = (\xi_{1}+\aleph)/(1-\mathfrak{c})$, $0 < \lambda < 1$ since $\xi_{1}+\aleph +\mathfrak{c} < 1$. Using the strictly monotone increasing property of $\mathcal{Q}$,

Similarly,

Hence,

For any $\zeta\in\mathbb{N}$, we obtain

Notice that

Since $\mathcal{Q}$ is strictly monotone increasing, we have

By induction, we obtain

We consider the following two cases:

(ⅰ) Let $\mathfrak{m} = \zeta+\omega$, if $\omega$ is odd and $\omega > 2$, we have

(ⅱ) Let $\mathfrak{m} = \zeta+\omega$, if $\omega$ is even and $\omega > 2$, we have

As $\mathfrak{m}, \zeta\longrightarrow\infty$, $\varrho(\vartheta_{\zeta}, \vartheta_{\mathfrak{m}})\longrightarrow0$ for all $\omega > 2$. Hence, $\{\vartheta_{\zeta}\}$ is a Cauchy sequence in $\varUpsilon$. Since $(\varUpsilon, \varrho)$ is complete, there exists $\mathfrak{z}^{*}\in\varUpsilon$ such that

Suppose that $\varrho(\varLambda\mathfrak{z}^{*}, \mathfrak{z}^{*}) > 0$, then

Using the strictly monotone increasing property of $\mathcal{Q}$, we get

We can also see that

It follows that

Hence, $\frac{1}{\aleph}\leq\aleph$ which is an absurdity. Therefore, $\varrho(\varLambda\mathfrak{z}^{*}, \mathfrak{z}^{*}) = 0$. Similarly, we can obtain $\varPi\mathfrak{z}^{*} = \mathfrak{z}^{*}$. Therefore, we have

Suppose that $\vartheta^{*}$ and $\sigma^{*}$ are two different common fixed points of $\varLambda$ and $\varPi$. Suppose that, $\varLambda\vartheta^{*} = \vartheta^{*} \neq \sigma^{*} = \varPi\sigma^{*}$ and $(\vartheta^{*}, \sigma^{*})\in \mathcal{E}(\mathcal{G})$. Then,

Using the strictly monotone increasing property of $\mathcal{Q}$, $(1-\xi_{1})\varrho(\vartheta^{*}, \sigma^{*}) < 0$, which is an absurdity. Hence $\vartheta^{*} = \sigma^{*}$. □

Example 2.1. Let $\varUpsilon = \varGamma\cup\varPsi$, where $\varGamma = \{\frac{1}{\zeta}:\zeta\in\{2, 3, 4, 5\}\}$ and $\varPsi = [1, 2]$. For any $\vartheta, \sigma\in\varUpsilon$, we define $\varrho :\varUpsilon\times\varUpsilon\longrightarrow[0, +\infty)$ by

and

Clearly, $(\varUpsilon, \varrho)$ is a complete graphical Branciari $\aleph$-metric space with constant $\aleph = 3 > 1$. Define the graph $\varOmega$ by $\mathcal{E}(\varOmega) = \Delta+\{(\frac{1}{3}, \frac{1}{4}), (\frac{1}{3}, \frac{1}{5}), (\frac{1}{2}, 2), (\frac{1}{2}, \frac{1}{4}), (\frac{1}{5}, \frac{1}{2}), (\frac{1}{5}, 2), (2, 1), (2, \frac{1}{3}), (1, \frac{1}{4}), (1, \frac{1}{2})\}$.

Figure 2 represents the directed graph $\varOmega$. Let $\varPi:\varUpsilon\to\varUpsilon$ be a mapping satisfying

Now, we verify that $\varPi$ is a $\varOmega$-$\mathcal{Q}$-contraction. We take $\vartheta = \frac{1}{4}\in\varGamma, \sigma = 2\in\varPsi$, and $\ell = 0.1$. Then, $\varrho(\varPi\vartheta, \varPi\sigma) = \varrho(\frac{1}{2}, \frac{1}{3}) = \frac{1}{6} > 0$ and

Let $\mathcal{Q}:(0, +\infty)\to\mathbb{R}$ be a mapping defined by $\mathcal{Q}(\vartheta) = \vartheta$, then it is easy to see that $\mathcal{Q}\in\mathscr{F}_{\aleph, \ell}$. Therefore

Hence, $\varPi$ fulfills the conditions of Theorem 2.1 and $\vartheta = \frac{1}{2}$ is the unique fixed point of $\varPi$.

3.   Applications

Consider the integral equation:

Let $\varUpsilon = \mathcal{C}([0, \xi_{1}], \mathbb{R})$ be the set of real continuous functions defined on $[0, \xi_{1}]$ and the mapping $\varPi:\varUpsilon\to\varUpsilon$ defined by

Obviously, $\vartheta(\rho)$ is a solution of integral Eq (3.1) iff $\vartheta(\rho)$ is a fixed point of $\varPi$.

Theorem 3.1. Suppose that

(R1) The mappings $\mathfrak{m}: [0, \xi_{1}]\times\mathbb{R} \to [0, +\infty)$, $\theta: [0, \xi_{1}]\times\mathbb{R} \to \mathbb{R},$ and $\mu: [0, \xi_{1}] \to \mathbb{R}$ are continuous functions.

(R2) $\exists$ $\ell > 0$ and $\aleph > 1$ such that

for each $\varphi\in [0, \xi_{1}]$ and $\vartheta\leq\sigma$ (i.e., $\vartheta(\varphi)\leq\sigma(\varphi)$)

(R3) $\int_{0}^{\xi_{1}}\mathfrak{m}(\rho, \varphi)d\varphi\leq 1$.

(R4) $\exists$ $\vartheta_{0}\in \mathcal{C}([0, \xi_{1}], \mathbb{R})$ such that $\vartheta_{0}(\rho)\leq \mu(\rho) + \int_{0}^{\xi_{1}}\mathfrak{m}(\rho, \varphi) \theta(\varphi, \vartheta_{0}(\varphi))d\varphi$ for all $\rho\in [0, \xi_{1}]$

Then, the integral Eq (3.1) has a unique solution in the set $\{\vartheta\in \mathcal{C}([0, \xi_{1}], \mathbb{R}):\vartheta(\rho)\leq\vartheta_{0}(\rho)\, \, \mathit{\text{or}}\, \, \vartheta(\rho)\geq \vartheta_{0}(\rho), \, \, \mathit{\text{for all}} \, \, \varphi\in [0, \xi_{1}]\}$.

Proof. Define $\varrho :\varUpsilon\times\varUpsilon\to [0, +\infty)$ given by

for all $\vartheta, \sigma\in\varUpsilon$. It is easy to see that, $(\varUpsilon, \varrho)$ is a complete graphical Branciari $\aleph$-metric space with $\aleph\geq 1$. Define $\varPi:\varUpsilon\to\varUpsilon$ by

Consider a graph $\varOmega$ consisting of $\mathcal{V}(\varOmega): = \varUpsilon$ and $\mathcal{E}(\varOmega) = \{(\vartheta, \sigma)\in \varUpsilon\times\varUpsilon: \vartheta(\rho)\leq \sigma(\rho)\}$. For each $\vartheta, \sigma\in \varUpsilon$ with $(\vartheta, \sigma)\in \mathcal{E}(\varOmega)$, we have

Thus,

which implies that

for each $\vartheta, \sigma \in \varUpsilon$. By (R4), we have $(\vartheta_{0}, \varPi\vartheta_{0})\in \mathcal{E}(\varOmega)$, so that $[\vartheta_{0}]^{\mathfrak{l}}_{\varOmega} = \{\vartheta\in \mathcal{C}([0, \xi_{1}], \mathbb{R}):\vartheta(\rho)\leq\vartheta_{0}(\rho)\, \, \text{or}\, \, \vartheta(\rho)\geq \vartheta_{0}(\rho), \, \, \text{for all} \, \, \varphi\in [0, \xi_{1}]\}$. Therefore, all the hypotheses of Theorem 2.1 are fulfilled. Hence, the integral equation has a unique solution. □

4.   Application to fractional differential equations

We recall many important definitions from fractional calculus theory. For a function $\vartheta\in\mathcal{C}[0, 1]$, the Reiman-Liouville fractional derivative of order $\delta > 0$ is given by

provided that the right hand side is pointwise defined on $[0, 1]$, where $[\delta]$ is the integer part of the number $\delta, \Gamma$ is the Euler gamma function. For more details, one can see ^{[26,27,28,29]}.

Consider the following fractional differential equation

where $\mathfrak{f}$ is a continuous function from $[0, 1]\times\mathbb{R}$ to $\mathbb{R}$ and $^\mathfrak{e}\mathcal{D}^\eta$ represents the Caputo fractional derivative of order $\eta$ and it is defined by

Let $\varUpsilon = (\mathcal{C}[0, 1], \mathbb{R})$ be the set of all continuous functions defined on $[0, 1]$. Consider $\varrho:\varUpsilon\times\varUpsilon\to \mathbb{R^+}$ to be defined by

for all $\vartheta, \vartheta^{'}\in \varUpsilon$. Then $(\varUpsilon, \varrho)$ is a complete graphical Branciari $\aleph$-metric space with $\aleph\geq 1$. The given fractional differential equation (4.1) is equivalent to the succeeding integral equation

where

Define $\varPi\colon\varUpsilon\rightarrow \varUpsilon$ defined by

It is easy to note that if $\vartheta^*\in\varPi$ is a fixed point of $\varPi$ then $\vartheta^*$ is a solution of the problem (4.1).

Theorem 4.1. Assume the fractional differential Eq (4.1). Suppose that the following conditions are satisfied:

(S1) there exists $\mathfrak{t}\in[0, 1]$, $\aleph\in(0, 1)$ and $\vartheta, \vartheta^{'}\in\varUpsilon$ such that

for all $\vartheta\leq\vartheta^{'}$ (i.e., $\vartheta(\mathfrak{t})\leq\vartheta^{'}(\mathfrak{t})$).

(S2)

(S3) $\exists$ $\vartheta_{0}\in \mathcal{C}([0, 1], \mathbb{R})$ such that $\vartheta_{0}(\mathfrak{t})\leq \int_{0}^{1}\mathcal{G}(\mathfrak{t}, \mathfrak{e})\mathfrak{f}(\mathfrak{q}, \vartheta(\mathfrak{e}))d\mathfrak{e}$ for all $\mathfrak{t}\in [0, 1]$.

Then the fractional differential Eq (4.1) has a unique solution in the set $\{\vartheta\in \mathcal{C}([0, 1], \mathbb{R}):\vartheta(\mathfrak{t})\leq\vartheta_{0}(\mathfrak{t})\, \, \mathit{\text{or}}\, \, \vartheta(\mathfrak{t})\geq \vartheta_{0}(\mathfrak{t}), \, \, \mathit{\text{for all}} \, \, \mathfrak{t}\in [0, 1]\}$.

Proof. Consider a graph $\varOmega$ consisting of $\mathcal{V}(\varOmega): = \varUpsilon$ and $\mathcal{E}(\varOmega) = \{(\vartheta, \vartheta^{'})\in \varUpsilon\times\varUpsilon: \vartheta(\rho)\leq \sigma(\rho)\}$. For each $\vartheta, \vartheta^{'}\in \varUpsilon$ with $(\vartheta, \vartheta^{'})\in \mathcal{E}(\varOmega)$, we have

Taking the supremum on both sides, we get

for each $\vartheta, \vartheta^{'} \in \varUpsilon$. By (S3), we have $(\vartheta_{0}, \varPi\vartheta_{0})\in \mathcal{E}(\varOmega)$, so that $[\vartheta_{0}]^{\mathfrak{l}}_{\varOmega} = \{\vartheta\in \mathcal{C}([0, 1], \mathbb{R}):\vartheta(\mathfrak{t})\leq\vartheta_{0}(\mathfrak{t})\, \, \mathit{\text{or}}\, \, \vartheta(\mathfrak{t})\geq \vartheta_{0}(\mathfrak{t}), \, \, \mathit{\text{for all}} \, \, \mathfrak{t}\in [0, 1]\}$. Therefore, all the hypotheses of Theorem 2.1 are fulfilled. Hence, the fractional differential Eq (4.1) has a unique solution. □

5.   Conclusions

In this paper, we have established fixed point results for $\varOmega$-$\mathcal{Q}$-contraction in the setting of complete graphical Branciari $\aleph$ -metric spaces. The directed graphs have been supported by Figures 1 and 2. The proven results have been supplemented with a non-trivial example and also applications to solve Fredholm integral equation and fractional differential equation have also been provided.

Author contributions

All authors equally contributed to this work. All authors read and approved the final manuscript.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the Project Number PSAU/2023/01/24098.

The authors convey their sincere appreciation to the Chief/Guest Editor and the anonymous reviewers for their suggestion and valuable comments which helped to bring the manuscript to its present form.

Conflict of interest

The authors declare no conflict of interest.