On stability analysis of a class of three-dimensional system of exponential difference equations

1.   Introduction

Difference equations have a wide range of applications in math, physics and engineering, as well as in business and other professions. See ^[1,2,3,4] and the references given therein for a list of publications and books on difference equations theory and applications. The qualitative features of difference equations of exponential form have recently attracted a lot of attention ^[5,6,7,8]. The authors of ^[9] explored the difference equation's boundedness, asymptotic nature, periodicity of the solutions, and the stability of the non-negative equilibrium:

wherein $\alpha$ and $\beta$ are non-negative constants, and the initial values $u_{-1}, \ u_{0}$ are non-negative numbers. Because it comes from models that investigate the amount of litter in perennial grasslands, this equation can be called a biological model. The authors of ^[10] looked at similar conclusions for a system of difference equations:

wherein $\alpha, \ \beta, \ \gamma$ and $\delta$ are non-negative constants, and the initial values $u_{-1}, \ u_{0}, \ v_{-1}, \ v_{0}$ are non-negative numbers. In addition, the researcher examines the character of boundedness, persistence, and asymptotic nature of the non-negative solutions of the subsequent exponential difference equations in ^[1]:

wherein $\alpha, \ \beta, \ \gamma$ and $\delta$ are non-negative constants, and the initial values $u_{-1}, \ u_{0}, \ v_{-1}, \ v_{0}$ are also non-negative numbers. We explore the character of boundedness, persistence, and the convergence rate of the non-negative outcomes of (1.1) to the unique positive equilibrium point of the subsequent exponential difference equations, motivated by the studies mentioned above:

where $a, \ b, \ c, \ d, \ e$ and $f$ are non-negative real numbers, and the initial values $x_{-1}, \ x_{0}, \ y_{-1}, \ y_{0}, \ z_{-1}, \ z_{0}$ are also non-negative real numbers.

2.   Existence and uniqueness of a positive equilibrium for (1.1)

We look at the existence and uniqueness of the non-negative equilibrium point of the system (1.1) in first theorem.

Theorem 2.1. The foregoing claims are valid.

$\left(i\right)$ Assume that

This leads to a unique equilibrium $(\overline{x}, \ \overline{y}, \ \overline{ z})$ for the system $(1.1)$. However,

$(ii)$ Assume that $a, \ b, \ c, \ d, \ e, \ f\ $ are positive real values such that

The zero equilibrium $(0, \ 0, \ 0)$ is the unique equilibrium solution of system (1.1).

Proof. $\left(i\right)$ Assume the following set of algebraic equations:

or equivalently,

Multiplying Eq (2.4),

then,

Then, from Eq (2.4), if $x\neq 0, \ y\neq 0$ and$\ z\neq 0$, we get

From Eqs (2.4) and (2.5),

Put value of $y = \frac{\left(1-a\right) xe^{x}}{b}$ in Eq (2.5), we get

Now, put value of $\frac{\left(1-c\right) ye^{y}}{d} = z$ in Eq (2.5), we get

Similarly, put $\frac{\left(1-e\right) ze^{z}}{f} = x$ in Eq (2.5), we get

We consider the function:

So, from $\left(2.1\right)$, we get that $F\left(0\right) < 0$ and $\underset{x\rightarrow \infty }{Lim}$ $F\left(x\right) = \infty$. Then, there exist a $\overline{x}\in \left(0, \ \infty \right)$ such that

Similarly, we can prove that there exists a $\overline{y}\in \left(0, \ \infty \right) \ $and$\ \overline{z}\in \left(0, \ \infty \right)$ such that

To find $z$ from $z = ez+fxe^{-z}$ as

So, from (2.5),

Now, we will find $\overline{x}$ at $z = 0$:

Similarly, we will prove that

Therefore, from (2.1), (2.5) and combining with Eqs (2.6) and (2.10), we obtained

In similar way, we obtained

And thus $\left(2.2\right)$ holds. To demonstrate uniqueness, we suppose that another non-negative equilibrium $(\overline{x}_{1}, \ \overline{ y}_{1}, \ \overline{z}_{1})$ of $\left(1.1\right) \ $exists. We can assume that $\overline{x} < \overline{x}_{1}\ $without losing generality. Then we obtain the following from (2.6):

and so $e^{\overline{x}_{1}}\leq e^{\overline{x}}$, which is a contradiction.

So,

similarly,

The proof is now completed.

Proof. $(ii)\ $Since $\left(2.3\right)$ is still valid, then we can deduce from $(2.5)$ that $x+y+z\leq 0$, implying that $\left(0, \ 0, \ 0\right)$ is the only non-negative equilibrium point. The proof is now finished.

3.   Boundedness and persistence of the positive solutions of (1.1)

We explore the boundedness and persistence of the non-negative solutions of (1.1) in the next proposition.

Theorem 3.1. There are valid arguments for the following:

$\left(i\right)$ Assume that

Then, every positive solution of $\left(1.1\right)$ is bounded.

$\left(ii\right)$ Suppose that $\left(3.1\right)$ holds. Suppose also that

Then, every positive solution of $\left(1.1\right)$ is bounded and persists.

Proof. Suppose that$\ \left(x_{n}, \ y_{n}, \ z_{n}\right)$ be an arbitrarily solution to$\ \left(1.1\right)$.

$\left(i\right)$ We will assume $M$ is positive, such that

The following function is considered:

There is also that

In light of this, it follows

Furthermore, we can deduce the following from (3.3):

From $\left(3.4\right)$ and $\left(3.5\right)$, we get that

As a result of relations (1.1), (3.1), (3.3) and (3.6), it follows that

So, $x_{1}\leq M$.

Now, consider the function

Therefore, it holds that

Now, from $\left(3.3\right)$,

From $\left(3.7\right)$ and $\left(3.8\right)$,

Therefore, relations $\left(1.1\right), \ \left(3.1\right), \ \left(3.3\right)$ and $\left(3.8\right)$,

Similarly, if

then, using the same logic as before, we can show that

As a result of our inductive reasoning, we can demonstrate

So, we conclude from above results $\left(x_{n}, \ y_{n}, \ z_{n}\right)$ is bounded.

Proof. $\left(ii\right)$ We can show that $\left(x_{n}, \text{ }y_{n}, \ z_{n}\right)$ persists. We look at the numbers for this.

Let

Then, using $\left(3.2\right)$ and arguing as in the proof of $\left(3.1\right)$ of ^[10], we get the following:

If $x_{0}\leq R$, then,

In addition, if $x_{0} > R, \ y_{-1}\leq R$, we take

Finally, if $x_{0} > R, \ y_{-1} > R$, we get

So, here is what we've got:

In a similar manner, we can demonstrate that

We may prove the following by arguing like we did earlier and using the induction method:

This completes the proof.

4.   Convergence rate

We evaluate the convergence rate of a system (1.1) for all initial values that converge at equilibrium $E(\overline{x}, \ \overline{y}, \ \overline{z})$ in this segment by existing theory ^[11]. For various three-dimensional systems, the convergence rate of solutions that converge to an equilibrium has been determined.

Theorem 4.1. Assume systems $\left(3.1\right)$ and $\left(3.2\right)$ hold and

Then, each non-negative solution of (1.1) tends to the unique non-negative equilibrium of (1.1).

Proof. Consider $\left(x_{n}, \ y_{n}, \ z_{n}\right)$ be an arbitrary solution of $\left(1.1\right)$. From Theorem 3.1 we get that

Then, from $\left(4.2\right)$ and for every $\epsilon > 0, \ $there exist an $n_{0}\left(\epsilon \right)$ such that $n\geq n_{0}(\epsilon)$,

and so from $\left(1.1\right)$ and $\left(4.3\right)$ we have for $n\geq n_{0}$ that

where $g_{L_{2}+\epsilon }\left(x\right) = ax+b\left(L_{2}+\epsilon \right) e^{-x}$.

But we have that

Therefore, for $x\in \lbrack l_{1}-\epsilon, \ L_{1}+\epsilon ]$, we get that

Then, from $\left(4.4\right)$ we take the following:

which implies that

So, for $\epsilon \longrightarrow 0$,

Similarly, from $\left(1.1\right)$ and $\left(4.3\right)$ we have for $n\geq n_{0}$ that

where $h_{L_{3}+\epsilon }\left(y\right) = cy+d\left(L_{3}+\epsilon \right) e^{-y}$.

But we have that

Therefore, for $y\in \lbrack l_{2}-\epsilon, \ L_{2}+\epsilon ]$, we get that

Then, from $\left(4.6\right)$ we take

which implies that

So, for $\epsilon \longrightarrow 0$,

Similarly, from $(1.1)$ and $(4.3)$ we have for $n\geq n_{0}$ that if

we can prove that

We claim that

Suppose on contrary, that either

or

or

Suppose first that $\left(4.10\right)$ valid. Then, since $g_{L_{2}}^{^{\prime }}\left(x\right) = a-bL_{2}e^{-x}$, we have that $g_{L_{2}}$ is a non-increasing for $x\leq \ln \left(\frac{bL_{2}}{a}\right)$ and consequently we obtained from $\left(4.10\right)$ that

Then, from $\left(4.5\right)$ and $\left(4.13\right)$ we have that

Since it hold that $h_{L_{3}}^{^{\prime }}\left(y\right) = c-dL_{3}e^{-y}$, we conclude that $h_{L_{3}}$ is non-increasing function for $y\leq \ln \left(\frac{dL_{3}}{c}\right)$ and non-decreasing for $y\geq \ln \left(\frac{dL_{3}}{c}\right)$. Then, if $l_{2}\geq \ln (\frac{dL_{3}}{c})$, we have that

If $l_{2}\leq \ln \left(\frac{dL_{3}}{c}\right)$, we get that

Relations $\left(4.7\right), \ \left(4.15\right)$ and $\left(4.16\right)$ imply that

Similarly, if $\left(4.12\right)$ holds, then,

Suppose now that $L_{1}\leq L_{2}\leq L_{3}$. Then, from $\left(4.18\right)$, we get that

which implies that

Since $\left(4.10\right)$ holds. We get that

and so $(4.19)$ implies that

We get the following from $(4.1)$:

and so

Then, from $(4.20)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{1}\leq L_{2}\leq L_{3}$.

Suppose now that $L_{1}\leq L_{3}\leq L_{2}$. Then from $\left(4.17\right)$ we take that

which implies that

Since $\left(4.10\right)$ holds. We get that

and so $(4.21)$ implies that

Moreover, from $(4.1)$ we get

so,

Then, from $(4.22)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{1}\leq L_{3}\leq L_{2}$.

Now again suppose that $L_{2}\leq L_{3}\leq L_{1}$. Then, from $\left(4.14\right)$ we take that

and so

Since $\left(4.10\right)$ holds, we get

and so $(4.23)$ implies that

We get from $(4.1)$ that

and so

Then, from $(4.24)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{2}\leq L_{3}\leq L_{1}$.

Now again suppose that $L_{2}\leq L_{1}\leq L_{3}$. Then, from $\left(4.18\right)$ we take that

and so

Since $\left(4.10\right)$ holds. We get

and so $(4.25)$ implies that

We get from $(4.1)$ that

and so

Then, from $(4.26)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{2}\leq L_{1}\leq L_{3}$.

Now again suppose that $L_{3}\leq L_{2}\leq L_{1}$. Then, from $\left(4.14\right)$ we take that

and so

Since $\left(4.10\right)$ holds. We get

Therefore, $(4.27)$ implies that

We get from $(4.1)$ that

and so

Then, from $(4.28)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{3}\leq L_{2}\leq L_{1}$.

Now again suppose that $L_{3}\leq L_{1}\leq L_{2}$. Then, from $\left(4.17\right)$ we take that

Therefore,

Since $\left(4.10\right)$ holds, we get

and so $(4.29)$ implies that

We get from $(4.1)$ that

and so

Then, from $(4.30)$ we have that $l_{1} < 0$, which is a contradiction. So, $\left(4.10\right)$ is not true if $L_{3}\leq L_{1}\leq L_{2}$.

Working in a similar manner and using $(4.1)$, we can prove that $(4.11)$ and $(4.12)$ are not true for each:

So relations $(4.9)$ are satisfied.

Since relations $\left(4.9\right)$ hold, $g_{L_{2}}$ is an increasing function for $x\geq \ln \left(\frac{bL_{2}}{a}\right), \ h_{L_{3}}$ is an increasing function for $y\geq \ln \left(\frac{dL_{3}}{c}\right)$, and $K_{L_{1}}$ is also an increasing function for $z\geq \ln \left(\frac{fL_{1} }{e}\right)$. We then obtain

So, from $\left(4.5\right), \ \left(4.7\right), \ \left(4.8\right)$ and $\left(4.31\right)$ we have that

Then relations $\left(4.32\right)$ imply that

as a result of $(2.4)$, we can simply deduce

As $F$ is a non-decreasing function, we obtain

The following can be proved in a similar way:

where

Due to the fact that $G$ is a non-decreasing function, we obtain

Similarly, $H$ is a non-decreasing function, we get

We can now demonstrate that

We derive the following from $(1.1)$ and $(4.3)$:

We look at the following function:

We have that $g_{l_{2}-\epsilon }$ is non-decreasing for $x\geq \ln \left(\frac{b\left(l_{2}-\epsilon \right) }{a}\right)$. In addition, since $\left(4.9\right)$ valid, then there exists $\epsilon > 0$ such that

Then, from $\left(4.3\right)$ and $\left(4.33\right)$ we get

As a result, relations $(4.37)$ and $(4.39)$ indicate the following:

And so,

For $\epsilon \longrightarrow 0$, we get

Similarly, using $\left(1.1\right)$ and $\left(4.9\right)$ and arguing as above, we get

and

Therefore, from relations (4.33)–(4.35) and (4.40)–(4.42), we have that

This completes the proof.

5.   Numerical examples

In an effort to our theoretical dialogue, we take into account several interesting numerical examples on this segment. These examples constitute distinct varieties of qualitative conduct of solutions to the system (1.1) of nonlinear difference equations. The first example indicates that positive equilibrium of system (1.1) is unstable with suitable parametric choices. Moreover, from the remaining examples it is clear that unique positive equilibrium point of system (1.1) is globally asymptotically stable with different parametric values. All plots on this segment are drawn with the help of MATLAB.

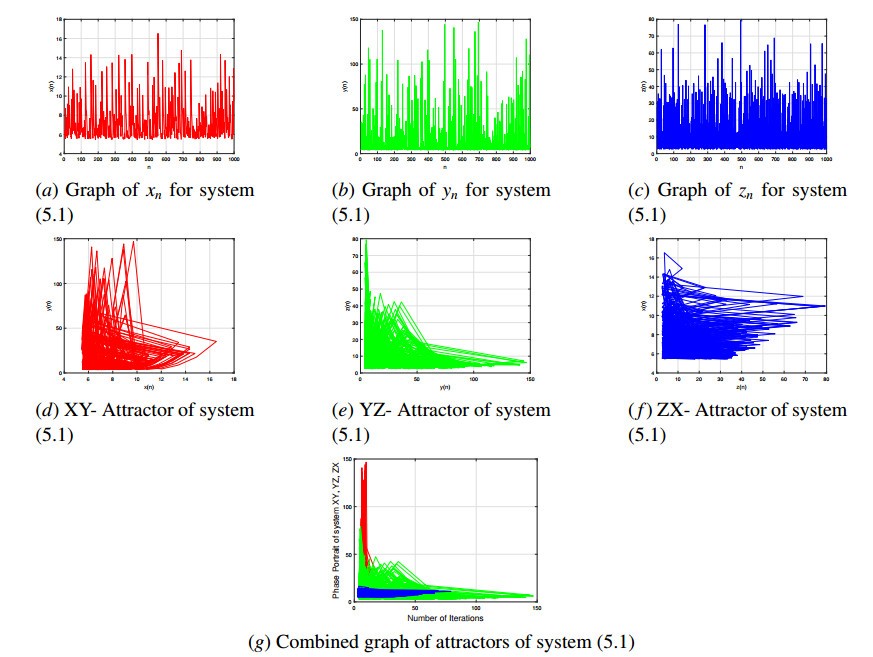
Example 5.1. Let $a = 0.9, \ b = 27, \ c = 0.5, \ d = 94, \ e = 0.3, \ f = 67$. Then the system (1.1) can be written as

with initial conditions $x_{-1} = 8, \ x_{0} = 7, \ y_{-1} = 6, \ y_{0} = 5, \ z_{-1} = 4, \ z_{0} = 3$. In this case, the positive equilibrium point of the system (5.1) is unstable. Moreover, in Figure 1, the graphs of $x_{n}$, $y_{n}$ and $z_{n}$ are shown in Figure (1a), (1b) and (1c) respectively, and XY, YZ and ZX attractors of the system (5.1) are shown in Figure (1d), (1e) and (1f) respectively. Also the combined graph of all respective phase portrait of system (5.1) is shown in Figure (1g).

Example 5.2. Let $a = 0.009, \ b = 0.3, \ c = 0.005, \ d = 0.9, \ e = 0.003, \ f = 0.7$. Then the system (1.1) can be written as

with initial conditions $x_{-1} = 0.008, \ x_{0} = 0.007, \ y_{-1} = 0.006, \ y_{0} = 0.005, \ z_{-1} = 0.004, \ z_{0} = 0.03$. In this case, the positive equilibrium point of the system (5.2) is given by $(\overline{x}, \ \overline{y}, \ \overline{z}) = (9.404\times10^{-11}, \ 4.993\times 10^{-10}, \ 1.276\times10^{-10})$. Moreover, in Figure 2, the graphs of $x_{n}$, $y_{n}$ and $z_{n}$ are shown in Figure (2a), (2b) and (2c) respectively, and XY, YZ and ZX attractors of the system (5.1) are shown in Figure (2d), (2e) and (2f) respectively. Also the combined graph of all respective phase portrait of system (5.2) is shown in Figure (2g).

6.   Conclusions

In this work, we analyze the qualitative behavior of a system of exponential difference equations. Using our model (1.1), we have demonstrated that a positive steady state exists and is unique. We verify the bounds of positive solutions as well as their persistence. We have also established that the positive equilibrium point of system (1.1) under certain parametric conditions is asymptotically stable locally as well as globally. In dynamical structures theory, the goal is to look at a system's global behavior through knowledge of its current state. It is possible to determine what parametric conditions result in these long-term behaviors by determining the possible global behavior of the system. Further, the convergence rate of positive solutions of (1.1) that converge to a unique point of positive equilibrium is determined.

In our future work, we will study some more qualitative properties such as bifurcation analysis, chaos control, and Maximum Lyapunov exponent of the said model. Some interesting numerical simulations with the help of Mathematica presenting bifurcation and chaos control are also part of our future goal.

Conflict of interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.