Approximation of fixed point of generalized non-expansive mapping via new faster iterative scheme in metric domain

1.   Introduction

Images are inevitably deteriorated by noise that is generated during the image acquisition process. Thus, image denoising, which aims to retrieve a clean image by removing noise while conserving important structures and details, is a fundamental issue in image processing. This work focuses on color image denoising in the presence of multiplicative noise. Multiplicative noise usually occurs under coherent image systems such as synthetic aperture radar (SAR) ^[1], ultrasound imaging ^[2], and laser imaging ^[3]. Owing to the coherent nature of these image acquisition procedures, most of the information in an original image may be lost when corrupted by multiplicative noise. Hence, removing multiplicative noise is a more difficult task than removing additive Gaussian noise.

Let $\Omega\subset\mathbb{R}^2$ be an open and bounded domain with a Lipschitz boundary. The observed image $f:\Omega\rightarrow \mathbb{R}$ corrupted by multiplicative noise can be formulated as

where $u:\Omega\rightarrow \mathbb{R}$ is the original clean image, and $\eta$ denotes the multiplicative noise that follows a gamma distribution whose density function ^[4] is given by

where $L > 0$ is an integer representing the noise level, and $\Gamma$ is the gamma function. Thus, the mean of $\eta$ is $1$, and its standard deviation is ${1}/{\sqrt{L}}$. This kind of noise commonly appears in SAR images.

For the removal of multiplicative gamma noise, a variety of filtering-based models ^[5,6,7,8,9] and variational models ^{[10,11,12,13,14,15,16,17,18,19,20,21,22]} have been developed. Among them, SAR-BM3D ^[9] is one of the most widely known filtering-based methods, which integrates nonlocal principles with wavelet representation. Particularly, it uses a similarity measure to collect 3-dimensional (3D) groups of similar image patches and applies wavelet decomposition to compute 3D blocks to achieve denoised images. This algorithm performs well, but is computationally very expensive and produces undesirable artifacts in cases of heavy multiplicative noise. Within a variational framework, Aubert and Aujol (AA) ^[10] proposed a new model combining a data-fidelity term derived from the gamma distribution and the total variation (TV) regularization. TV ^[25] has been widely used due to its edge preserving capacity and convexity. Nevertheless, the data-fidelity term of this model is not convex, thus the resulting computed solution may not be optimal from a global perspective. Moreover, this model highly depends on the initialization. To resolve these problems, previous studies ^[11,16,19] have suggested convex data-fidelity terms, by using a logarithmic transformation or adding a penalty term. In particular, Lu et al. ^[19] developed a convex data-fidelity term that is suitable for removing severe multiplicative noise, which integrates the ideas included in the works of ^[11,16]. All the above-mentioned models are proposed for grayscale image restoration. Recently, several studies ^[23,24] have been proposed to eliminate multiplicative noise in color images by utilizing the data-fidelity terms introduced in ^[10,11]. This work makes use of the data-fidelity term presented in ^[19] to better deal with heavy multiplicative noise in color images.

For color image restoration, TV regularization has been extended and studied in various works ^{[24,26,27,28,29,30,31,32,33,34,35,36,37,38]}. Especially, based on the view of color edge detection, Jia et al. ^[38] introduced a saturation-value-based TV (SVTV) regularization in the HSV color space. They reported in ^[38] that SVTV is superior to the existing RGB-based color TV methods in several image processing problems by considerably reducing artificial color values and producing well-preserved details and edges. Wang et al. ^[23] also adopted SVTV for the removal of multiplicative noise and blur in color images. However, SVTV creates a staircase effect; it produces some staircase shapes in smooth transition regions similar to other TV-based regularizations. To alleviate this shortcoming, higher-order derivatives-based SV regularizers were suggested in ^[24], which were utilized to remove multiplicative noise in color images. These regularizers benefited from both SV-based regularization and higher-order regularization. Despite the excellent performance of SV-based regularization in color image restoration, local derivatives-based regularization is limited due to the smearing of details and repeated patterns.

To overcome this drawback of local regularizers, various methods exploiting the nonlocal properties of images have been developed for Gaussian noise problems. First, based on the nonlocal self-similarity property that expresses the global repetitiveness of textures and structures in images, a nonlocal means filter was proposed in ^[39], which enhanced the local smoothing filters. As an extension, Dabov et al. ^[40] proposed a denoising algorithm, called BM3D, using block matching and 3D transform domain collaborative filtering, through which SAR-BM3D was developed. In addition, a series of nonlocal regularizations have been developed for inverse problems ^{[41,42,43,44,45]}. These nonlocal methods provide superior results in comparison to local methods, but many image details and structures cannot be restored due to inaccurate nonlocal weights. The patch-based sparse representation methods have also attracted much attention. Elad and Aharon ^[46] suggested a denoising algorithm, called K-SVD, by assuming that each patch of an image is accurately represented by a few elements from a dictionary that is learned from natural images. This also led to a variational model in ^[15] for removing multiplicative noise, which combines K-SVD and TV regularization. Regardless of the phenomenal results of K-SVD, it ignores self-similarity as each patch is considered independently in dictionary learning and sparse coding. In addition, the dictionary learning process is computationally expensive. To achieve better performance, sparsity and self-similarity were combined in several works ^[47,48,49], while low-rank-based approaches were also proposed in ^{[22,50,51,52]}. The aforementioned sparse representation methods consider an image patch as the basic unit of sparse representation.

Unlike these sparse representation methods, Zhang et al. ^[53] proposed a group-based sparse representation (GSR) model that uses an image group as its basic processing unit. The GSR model characterizes the local sparsity of patches and nonlocal self-similarity of repeated patterns between patches. This also involves an efficient self-adaptive group dictionary learning method, rather than dictionary learning from images. The model demonstrated excellent performance in image deblurring, inpainting, and compressive sensing. It was also utilized in diverse applications such as image deblocking ^[54], low-light image enhancement ^[55], SAR image despeckling ^[56], and Cauchy noise removal ^[57]. In several works ^[58,59,60], the GSR framework was extended, by integrating it with the low-rank approach or patch-based sparse representation. Despite the outstanding performance of these GSR-based models, for color image processing, they convert the image from the RGB space to the YCbCr space and only extract the Y (luminance) channel. Although the Y channel includes most of the important features of the image, such as edges and textures, the Y channel alone might not be sufficient for image processing when all RGB channels are independently corrupted by noise. Recently, in ^[61], a GSR model utilizing all channel information was proposed and applied to the color image inpainting problem. In this model, an image group corresponding to each RGB channel is constructed, and the final image group is formed from these three image groups. That is, this approach calculates the patch distance between two grayscale patches in each channel, rather than using the patch distance between two color patches. In our work, we exploit a multi-channel-based GSR approach for the removal of multiplicative noise in color images, but unlike the approach in ^[61], we compute the patch distance between two color image patches to form a color image group. Moreover, we also adopt the SVTV regularization to mitigate certain artifacts caused by patches.

The main contribution of our work is to propose a GSR-based model for restoring color images deteriorated by multiplicative gamma noise. The proposed GSR approach is based on multi-color channels, which is different from existing approaches. The model also involves a convex data-fidelity term and SVTV regularization. The proposed model sufficiently denoises color images in smooth regions while maintaining textures, details, and edges, even in the presence of severe multiplicative noise. Moreover, unlike existing methods, it does not generate artificial color values or artifacts. To numerically solve the proposed model, an efficient iterative algorithm is offered based on the alternating direction method of multiplies.

The outline of the paper is as follows. Section 2 reviews several variational models for removing multiplicative gamma noise in grayscale images, as well as SVTV regularization and a GSR approach. In Section 3, we present the proposed model and optimization algorithm. Section 4 presents the experimental results of the proposed model, with comparisons to existing methods. Finally, in Section 5, we summarize and conclude our work with some discussions.

2.   Background

In this section, we review several multiplicative noise removal models for grayscale images, in addition to SVTV regularization and a GSR model.

2.1.   Variational multiplicative noise removal models

First, based on maximum a posterior estimation and Bayes' rule, Aubert and Aujol (AA) ^[10] proposed a TV model for denoising images in the presence of multiplicative gamma noise, with the assumption $f > 0$:

where $\mu > 0$ is a parameter that manages the smoothness of the image $u$, and $\lvert \nabla u\rvert = \sqrt{(\partial_{x_1} u)^2+(\partial_{x_2} u)^2}$ with $x = (x_1, x_2)$. TV regularization ^[25] has been widely utilized owing to its convexity and edge conservation ability. Nevertheless, since the data-fidelity term in model (2.1) is not convex, classical optimization algorithms may not furnish a global optimal solution and are highly reliant on initialization.

To rectify these problems, Shi and Osher (SO) ^[11] proposed the following convex model using the logarithmic transformation, $w = \log u$:

Thus, after solving this minimization problem to obtain $w$, the denoised image $u$ is achieved as $u = e^{w}$. The denoising performance of this model surpasses that of the AA model (2.1) and its denoising results do not depend on initial guesses.

As another approach to build up a convex data-fidelity term, Dong and Zeng ^[16] inserted a penalty term to the data-fidelity term in model (2.1):

where $\alpha > 0$ is a parameter. The objective function in (2.3) is convex if $\alpha \geq \frac{2\sqrt{6}}{9}$. This model is based on the observation that the value of $\mathbb{E}((\sqrt{u/f} -1)^2)$ is close to $0$ with a large $L$, and its value is still rather small even when $L$ is small. However, $\mathbb{E}(\sqrt{u/f})$ is always larger than $1$ and is close to $1$ when $L$ is large enough, i.e., the noise level is relatively small.

To deal with heavy multiplicative noise, Lu et al. ^[19] substituted $1$ in the penalty term with a parameter $\beta\geq 1$. In addition, they adopted the logarithmic transformation, $w = \log(u)$, since exponent-like models provide better denoising performance than logarithm-like models:

where $\beta$ depends on the noise level $L$. The objective function in (2.4) is strictly convex if $\alpha\beta^4\leq \frac{4096}{27}$. The numerical results in ^[19] validated that the data-fitting term in (2.4) is suitable for eliminating heavy multiplicative noise.

2.2.   Saturation-value total variation

The HSV color model is a color system similar to human perception. Hue refers to the color portion, saturation refers to the gray level of the color, and value refers to the brightness of the color and varies depending on saturation. The important contours and textures of an image lie primarily in its saturation and brightness components.

For a color image $\boldsymbol{u} = (\boldsymbol{u}_r, \boldsymbol{u}_g, \boldsymbol{u}_b)$, the saturation (S) and value (V) components can be expressed in $\boldsymbol{u}_r$, $\boldsymbol{u}_g$, and $\boldsymbol{u}_b$ as

where $\|\cdot\|_2$ is the vector Euclidean norm.

Based on the observation that the saturation and value components contain most of the important edges and textures of an image, Jia et al. ^[38] proposed a saturation-value total variation (SVTV) for color images as follows:

where $\mathcal{K}^n = \mathcal{C}^1(\Omega, \mathbb{B}^{2n})$ stands for the set of continuously differentiable and bounded functions from the compact support in $\Omega$ to $\mathbb{B}^{2n}$, with $\mathbb{B}^n$ representing the closed united ball with a positive integer $n$, and the parameter $\gamma > 0$ is the weight of the value component in the SVTV term. The convexity, lower semi-continuity, and compactness properties of SVTV were proven. Assuming $\boldsymbol{u}\in W^{1, 2}(\Omega)$, SVTV can be written as

where $\lvert\partial_{x_j} \boldsymbol{u}(x)\rvert_s$ and $\lvert \partial_{x_j} \boldsymbol{u}(x)\rvert_v$ ($j = 1, 2$) are defined as

with $\partial_{x_j} \boldsymbol{u}(x)^T = (\partial_{x_j} \boldsymbol{u}_r(x), \partial_{x_j} \boldsymbol{u}_g(x), \partial_{x_j} \boldsymbol{u}_b(x))^T$. The experimental results in ^[38] demonstrate the superior restoration performance of SVTV over existing TV-based methods, by reducing the color artifacts induced by noise and better conserving the details.

2.3.   Group-based sparse representation

This subsection discusses the GSR model in ^[53] proposed for grayscale images.

Given a grayscale image $\boldsymbol{x}\in\mathbb{R}^N$, it is divided into $n$ overlapping patches $\boldsymbol{x}_k$ of size $\sqrt{P}\times\sqrt{P}$ ($k = 1, 2, ..., n$), with stride $s$. For each patch $\boldsymbol{x}_k$, $c$ most similar patches are searched in a local window of size $L\times L$, and the selected patches are stacked into a matrix $\boldsymbol{x}_{\boldsymbol{G}_k} = [ \boldsymbol{x}_{ \boldsymbol{G}_{k}, 1}, \boldsymbol{x}_{ \boldsymbol{G}_{k}, 2}, ..., \boldsymbol{x}_{ \boldsymbol{G}_{k}, c}]\in\mathbb{R}^{P\times c}$ as columns. The matrix $\boldsymbol{x}_{\boldsymbol{G}_k}$ is called a group and can be defined by a linear operator $\boldsymbol{R}_{\boldsymbol{G}_k}$ as

The transpose $\boldsymbol{R}_{\boldsymbol{G}_k}^T$ can convert a group into the $k$-th position in the image padded with zeros elsewhere.

The GSR model assumes that each group $\boldsymbol{x}_{\boldsymbol{G}_k}$ can be accurately represented by a few atoms of a self-adaptive learning dictionary $\boldsymbol{D}_{\boldsymbol{G}_k} = [ \boldsymbol{d}_{ \boldsymbol{G}_{k}, 1}, \boldsymbol{d}_{ \boldsymbol{G}_{k}, 2}, ..., \boldsymbol{d}_{ \boldsymbol{G}_{k}, m}]$, where each atom $\boldsymbol{d}_{ \boldsymbol{G}_{k}, i}\in\mathbb{R}^{P\times c}$ is a matrix of the same size as the group $\boldsymbol{x}_{\boldsymbol{G}_k}$ and $m = \min(P, c)$. The sparse coding process of each group $\boldsymbol{x}_{\boldsymbol{G}_k}$ over $\boldsymbol{D}_{\boldsymbol{G}_k}$ is to find a sparse vector $\boldsymbol{\alpha}_{\boldsymbol{G}_k} = [ \boldsymbol{\alpha}_{ \boldsymbol{G}_{k}, 1}, \boldsymbol{\alpha}_{ \boldsymbol{G}_{k}, 2}, ..., \boldsymbol{\alpha}_{ \boldsymbol{G}_{k}, m}]$ such that

Then, the image $\boldsymbol{x}$ is reconstructed from the sparse codes $\{ \boldsymbol{\alpha}_{\boldsymbol{G}_k}\}$ as

where $\boldsymbol{D}_{\boldsymbol{G}}$ and $\boldsymbol{\alpha}_{\boldsymbol{G}}$ denote the concatenation of all $\boldsymbol{D}_{\boldsymbol{G}_k}$ and $\boldsymbol{\alpha}_{\boldsymbol{G}_k}$, respectively, $./$ is the element-wise division of vectors, and $\mathbf{1}_{P\times c}\in \mathbb{R}^{P\times c}$ is a matrix of ones.

Assuming that a degraded image is given by $\boldsymbol{y} = \boldsymbol{H} \boldsymbol{x} + \boldsymbol{n}$, where $\boldsymbol{H}$ is a linear degradation operator and $\boldsymbol{n}$ is noise, the GSR model for image restoration can be formulated as

where $\lambda > 0$ is a regularization parameter, and $\| \boldsymbol{\alpha}_{\boldsymbol{G}}\|_0$ indicates the number of non-zero elements in $\boldsymbol{\alpha}_{\boldsymbol{G}}$. By selecting an appropriate self-adaptive group dictionary, the minimization problem (2.12) can be explicitly solved. Then, the reconstructed image is obtained as $\hat{ \boldsymbol{x}} = \boldsymbol{D}_{\boldsymbol{G}}\circ \hat{ \boldsymbol{\alpha}}_{ \boldsymbol{G}}$.

3.   Proposed model and algorithm

In this section, we present a GSR model to restore color images degraded by multiplicative gamma noise and an optimization algorithm for solving the proposed model.

3.1.   Proposed model

Let us assume that a noisy color image $\boldsymbol{f}\in\mathbb{R}^{3N}$ is given by

where $\boldsymbol{u}\in\mathbb{R}^{3N}$ is the clean image, and ${\eta_{ch}\in\mathbb{R}^{N}}$ represents the gamma noise in the $ch$-channel that follows the distribution in (1.2).

The problem (3.1) is an ill-posed inverse problem, so we formulate a minimization problem to reconstruct $\boldsymbol{u}$ from the given data $\boldsymbol{f}$. First, following the process in (2.1)–(2.4) and by letting $\boldsymbol{w} = \log(\boldsymbol{u})$, we consider the following convex data-fidelity term to handle heavy multiplicative gamma noise:

where $\langle\cdot, \cdot \rangle$ is the inner product, $\mathbf{1}\in\mathbb{R}^{3N}$, and $\alpha$, $\beta > 0$ are parameters satisfying $\alpha\beta^4\leq \frac{4096}{27}$.

Next, we introduce our GSR approach to reconstruct color images corrupted by multiplicative gamma noise. For a color image $\boldsymbol{x}\in\mathbb{R}^{3 N}$, we extract a color image patch $\boldsymbol{x}_k = [ \boldsymbol{x}_k^1, \boldsymbol{x}_k^2, \boldsymbol{x}_k^3]^T \in\mathbb{R}^{3 P}$, where $\boldsymbol{x}_k^{ch}$ is a patch of size $\sqrt{P}\times \sqrt{P}$ in the $ch$-channel ($ch = 1, 2, 3$). Then the group $\boldsymbol{x}_{\boldsymbol{G}_k}$ consisting of $c$ most similar patches is given by

and the self-adaptive learning dictionary $\boldsymbol{D}_{\boldsymbol{G}_k}$ is as follows

where $\boldsymbol{d}_{\boldsymbol{G}_{k, i}} = [ \boldsymbol{d}^1_{\boldsymbol{G}_{k, i}}, \boldsymbol{d}^2_{\boldsymbol{G}_{k, i}}, \boldsymbol{d}^3_{\boldsymbol{G}_{k, i}}]^T \in\mathbb{R}^{3P\times c}$ ($i = 1, \cdots, m$) with $m = \min(3P, c)$.

To search for similar patches in the image $\boldsymbol{w}$, we first take the logarithmic transformation in (3.1), which yields

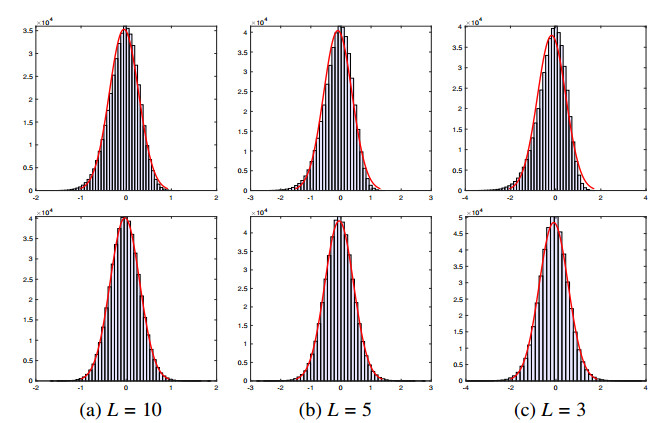
where $\hat{ \boldsymbol{f}} = \log(\boldsymbol{f})$, and $\hat{\eta} = \log(\eta)$. In Figure 1, we plot the histograms of noise $\hat{\eta}$ in the RGB or HSV color spaces when the noise level $L = 10$, $5$, and $3$. The figure shows that the histograms of $\hat{\eta}$ in both color spaces at all noise levels are similar to normal distributions. Especially, the noise distribution in the HSV color space fits better with a normal distribution. Based on this observation, we extract the color patches in the HSV color space and compute the Euclidean distance between them. Specifically, after transforming the RGB-based color image $\boldsymbol{w}$ to the HSV-based image $\tilde{ \boldsymbol{w}}$, we extract two color image patches, $\tilde{ \boldsymbol{w}}_{k_1}$ and $\tilde{ \boldsymbol{w}}_{k_2}\in\mathbb{R}^{3P}$, from the transformed image $\tilde{ \boldsymbol{w}}$ and compute the similarity measure between the two patches using the following distance function:

Thus, the group $\tilde{ \boldsymbol{w}}_{G_k}$ and dictionary $\tilde{ \boldsymbol{D}}_{ \boldsymbol{G}_k}$ will be attained in the HSV color space, which is discussed in the subsequent subsection.

Lastly, despite the outstanding restoration performance of the GSR-based approaches, these patch-based methods also cause some ringing or block artifacts in the restored images. To alleviate these artifacts, we also utilize the local regularizer, SVTV, defined in (2.7). Consequently, by combining the data-fidelity term in (3.2) with GSR and SVTV regularization, we propose the following minimization problem for the elimination of multiplicative gamma noise in color images:

where $\lambda$ and $\mu > 0$ are regularization parameters.

3.2.   Optimization algorithm

Since problem (3.7) is nonconvex and nonsmooth, it is challenging to solve. Therefore, we utilize the alternating direction method of multipliers (ADMM) ^[62,63] that are proposed for solving convex or nonconvex linearly constrained problems.

First, we utilize the variable splitting technique. That is, we introduce an auxiliary variable $\boldsymbol{z}$ to replace $\boldsymbol{w}$ in the SVTV term. Then, problem (3.7) can be transformed into the following constrained problem:

The augmented Lagrangian function (ALF) for problem (3.8) is given by

where ${ \boldsymbol{p}\in\mathbb{R}^{3N}}$ and $\boldsymbol{q}\in\mathbb{R}^{3N}$ are the Lagrangian multipliers, and $\tau > 0$ is a penalty parameter.

The ADMM applied to problem (3.8) results in the following iterative algorithm:

In the subsequent paragraphs, we solve two subproblems in (3.10).

3.2.1.   Solving the $(\boldsymbol{\alpha}_{\boldsymbol{G}}, \boldsymbol{z})$-subproblem in (3.10)

First, we solve the $(\boldsymbol{\alpha}_{\boldsymbol{G}}, \boldsymbol{z})$-subproblem in (3.10), which is formulated as

where $\boldsymbol{r} = \boldsymbol{w}^{\ell}- \boldsymbol{p}^\ell/\tau$, and $\boldsymbol{s} = \boldsymbol{w}^{\ell}+ \boldsymbol{q}^\ell/\tau$.

As perviously mentioned, we measure the Euclidean distance in the HSV color space to find similar patches. Moreover, to handle the SVTV term defined in the RGB color space, we convert the RGB-based model (3.11) to a HSV-based model using the following orthogonal matrix $\bar{\mathbf{P}}$, that is derived the dual-form of SVTV in (2.6) and has a relation with $\mathbf{C}$ in (2.5) as follows:

If we define $\tilde{ \boldsymbol{u}}(x) = \bar{\mathbf{P}} \boldsymbol{u}(x)^T$ for $x\in\Omega$, then the S and V components can also be expressed as $S(x) = \|(\tilde{ \boldsymbol{u}}_1(x), \tilde{ \boldsymbol{u}}_2(x))^T\|_2$ and $V(x) = \lvert \tilde{ \boldsymbol{u}}_3(x)\rvert$ respectively. In addition, $\lvert\partial_{x_j} \boldsymbol{u}(x)\rvert_s$ and $\lvert \partial_{x_j} \boldsymbol{u}(x)\rvert_v$ in (2.8) can be expressed as

where the second equality of the first term is because the transpose of an orthogonal matrix is also orthogonal, $\bar{\mathbf{P}}\bar{\mathbf{P}}^T$ is the identity matrix, and the norm of a vector is invariant under multiplication by an orthogonal matrix.

Now, using the following orthogonal matrix

where $\mathbf{I}\in \mathbb{R}^N$ is the identity matrix, we define $\tilde{ \boldsymbol{D}}_{ \boldsymbol{G}} = \mathbf{P} \boldsymbol{D}_{\boldsymbol{G}}$, $\tilde{ \boldsymbol{r}} = \mathbf{P} \boldsymbol{r}$, $\tilde{ \boldsymbol{s}} = \mathbf{P} \boldsymbol{s}$, and $\boldsymbol{v} = (\boldsymbol{v}_1, \boldsymbol{v}_2, \boldsymbol{v}_3)^T = \mathbf{P} \boldsymbol{z}$. Therefore, problem (3.11) can be converted to

where $\bar{ \boldsymbol{v}} = (\boldsymbol{v}_1, \boldsymbol{v}_2)^T$ and $\nabla \bar{ \boldsymbol{v}} = (\nabla \boldsymbol{v}_1, \nabla \boldsymbol{v}_2)^T$. In this problem, the variables $\boldsymbol{\alpha}_{\boldsymbol{G}}$ and $\boldsymbol{v}$ are independent of each other, so problem (3.15) can be separated into two problems as

Solving the $\boldsymbol{\alpha}_{\boldsymbol{G}}$-subproblem in (3.16). The $\boldsymbol{\alpha}_{\boldsymbol{G}}$-subproblem in (3.16) can be reformulated as

where $\tilde{ \boldsymbol{x}} = \tilde{\boldsymbol{D}}_{\boldsymbol{G}}\circ \boldsymbol{\alpha}_{\boldsymbol{G}}$. The following proposition indicates that the error term in (3.17) can be well approximated by the sum of the error terms of groups under certain assumptions:

Proposition 1. Let $\tilde{ \boldsymbol{x}}$, $\tilde{ \boldsymbol{r}}\in\mathbb{R}^{3N}$, $\tilde{\boldsymbol{x}}_{\boldsymbol{G}_k}$, $\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}\in\mathbb{R}^{3P\times c}$, and assume that each element of $\boldsymbol{e} = \tilde{ \boldsymbol{x}}-\tilde{ \boldsymbol{r}}$ is independent and follows a distribution with zero mean and variance $\sigma^2$. Then, for any $\varepsilon > 0$, a relationship between $\|\tilde{ \boldsymbol{x}}-\tilde{ \boldsymbol{r}}\|_2^2$ and $\sum_{k = 1}^{n} \| \tilde{\boldsymbol{x}}_{\boldsymbol{G}_k}- \tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}\|_2^2$ holds as follows:

where $\textbf{Pr}(\cdot)$ represents the probability, and $K = 3P\times c\times n$.

Proof. It follows from the law of large numbers, see ^[53]. □

According to Proposition 1 and using $\| \boldsymbol{\alpha}_{\boldsymbol{G}}\|_0 = \sum_{k = 1}^n \| \boldsymbol{\alpha}_{\boldsymbol{G}_k}\|_0$, problem (3.17) is equivalent to

where $\tilde{\tau} = \frac{\lambda K}{3\tau N}$. This problem can be efficiently minimized by solving $n \; \boldsymbol{\alpha}_{\boldsymbol{G}_k}$-subproblems, one of which is formulated as

where $\tilde{\boldsymbol{D}}_{\boldsymbol{G}_k}$ is the self-adaptive learned dictionary from $\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}$ as follows.

First, the singular value decomposition is applied to $\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}$:

where $\boldsymbol{\Sigma}_{\boldsymbol{G}_k} = \text{diag}(\boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}})$ is a diagonal matrix with the elements of $\boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}} = [{\boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k, 1}}}, {\boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k, 2}}}, ..., {\boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k, m}}}]$ on its main diagonal, and $\boldsymbol{u}_{\boldsymbol{G}_k, i}$ and $\boldsymbol{v}_{\boldsymbol{G}_k, i}$ are the columns of $\boldsymbol{U}_{\boldsymbol{G}_k}$ and $\boldsymbol{V}_{\boldsymbol{G}_k}$, respectively. Then, the atoms in $\tilde{\boldsymbol{D}}_{\boldsymbol{G}_k}$ is defined as $\tilde{\boldsymbol{d}}_{\boldsymbol{G}_k, i} = \boldsymbol{u}_{\boldsymbol{G}_k, i} \boldsymbol{v}_{\boldsymbol{G}_k, i}^T$, thus the dictionary $\tilde{\boldsymbol{D}}_{\boldsymbol{G}_k}$ for $\tilde{\boldsymbol{x}}_{\boldsymbol{G}_k}$ is given by

Using $\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k} = \tilde{\boldsymbol{D}}_{\boldsymbol{G}_k} \boldsymbol{\gamma}_{\tilde{\boldsymbol{r}}_{\boldsymbol{G}_k}}$ and due to the unitary property of $\tilde{\boldsymbol{D}}_{\boldsymbol{G}_k}$, the $\boldsymbol{\alpha}_{\boldsymbol{G}_k}$-subproblem in (3.19) is equivalent to

This problem has a closed-form solution as

where $hard(\cdot)$ represents the hard thresholding operator, $\odot$ represents the element-wise multiplication, and $\mathbf{1}(y)$ is the indicator function that has a value of $1$ if $y > 0$ and $0$ otherwise.

Solving the $\boldsymbol{v}$-subproblem in (3.16). Next, we solve the $\boldsymbol{v}$-subproblem in (3.16). To solve this convex problem, we again adopt the ADMM in ^[62]. First, to handle the non-differentiable terms, we introduce two auxiliary variables $\boldsymbol{d}_1$ and $\boldsymbol{d}_2$ to substitute $\nabla \bar{ \boldsymbol{v}}$ and $\nabla \boldsymbol{v}_3$, respectively. Then, the unconstrained $\boldsymbol{v}$-problem in (3.16) is converted into the following constrained minimization problem:

The ALF of problem (3.24) is given by

where $\boldsymbol{b}_1\in\mathbb{R}^{3N\times 4}$ and $\boldsymbol{b}_2\in \mathbb{R}^{3N\times 2}$ are the Lagrangian multipliers, and $\xi > 0$ is a penalty parameter.

The ADMM applied to problem (3.24) brings the following iterative algorithm:

The constraint in (3.24) can be written as $(\boldsymbol{d}_{1}, \boldsymbol{d}_2)^T = \mathbf{B}(\bar{ \boldsymbol{v}}, \boldsymbol{v}_3)^T$ with $\mathbf{B} = \begin{bmatrix}\nabla & 0\\ 0 & \nabla \end{bmatrix}$. Since the matrix $\mathbf{B}$ has a full column-rank, we can obtain the following convergence results, according to Theorem 1 in ^[64]: If the sequence $\{(\boldsymbol{v}^{t}, \boldsymbol{d}_1^t, \boldsymbol{d}_2^t, \boldsymbol{b}_1^t, \boldsymbol{b}_2^t)\}$ is generated by ADMM in (3.26), then this sequence has a single limit point $(\boldsymbol{v}^\ast, \boldsymbol{d}_1^\ast, \boldsymbol{d}_2^\ast, \boldsymbol{b}_1^\ast, \boldsymbol{b}_2^\ast)$, and this limit point is a saddle point of the augmented Lagrangian $\mathcal{L}_\xi$. That is, $\{(\boldsymbol{v}^{t}, \boldsymbol{d}_1^t, \boldsymbol{d}_2^t)\}$ has a single limit point $(\boldsymbol{v}^\ast, \boldsymbol{d}_1^\ast, \boldsymbol{d}_2^\ast)$, and this limit point solves problem (3.24).

The $\boldsymbol{v}$-subproblem in (3.26) can be rewritten as

From the first-order optimality condition, $\boldsymbol{v}^{t+1}$ must satisfy the following normal equations:

where $\nabla^T = -\text{div}$ with div being the discrete divergence operator defined as $\text{div}(s_1, s_2) = \partial_{x_1} s_1+\partial_{x_2} {s_2}$. Assuming the periodic boundary condition, the above equations can be explicitly solved using the 2-dimensional discrete Fourier transform (DFT).

The $(\boldsymbol{d}_1, \boldsymbol{d}_2)$-subproblem in (3.26) can be separated into two subproblems for each variable since the variables are independent of each other. Specifically, the $\boldsymbol{d}_i$-subproblems can be written as

Then, the solutions $\boldsymbol{d}_i^{t+1}$ can be obtained as follows

where $shrink(\cdot)$ is the soft-thresholding operator defined as

3.2.2.   Solving the $\boldsymbol{w}$-subproblem in (3.10)

Now, we solve the $\boldsymbol{w}$-subproblem in (3.10), which can be written as

where $\boldsymbol{x}^{\ell+1} = \mathbf{P}^T\tilde{ \boldsymbol{x}}^{\ell+1}$ with ${\tilde{ \boldsymbol{x}}}^{\ell+1} = (\tilde{\boldsymbol{D}}_{\boldsymbol{G}}\circ {\hat{ \boldsymbol{\alpha}}}_{ \boldsymbol{G}})^{\ell+1}$, and $\boldsymbol{z}^{\ell+1} = \mathbf{P}^T \boldsymbol{v}^{\ell+1}$. This minimization problem is convex, but it is difficult to obtain an explicit form of solution due to the complex data-fidelity term. Fortunately, the problem can be efficiently solved by using Newton's method as follows:

where $\hat{F}'(\boldsymbol{w})$ and $\hat{F}''(\boldsymbol{w})$ are given by

In practice, only a few iteration numbers are required for convergence.

Consequently, the algorithm for solving model (3.7) is summarized in Algorithm 1.

4.   Experimental results

This section presents the numerical results of the proposed model, with comparisons to other existing models including L2-SVTV in ^[38] and AA-SVTV in ^[23], that combine SVTV with the $L^2$ data-fidelity term or the data-fidelity term in (2.1), in addition to SO-SVNTVTV2 in ^[24] that integrates the data-fidelity term in (2.2) with a SV-based nonconvex higher-order regularization. We also compare our model with SAR-BM3D which is applied to each RGB channel. For a fair comparison, we adopt the variable splitting approach and ADMM for solving the aforementioned existing variational models. All numerical experiments were implemented using MATLAB R2023a on a 64-bit Windows 10 desktop PC with an Intel CPU at 4.2GHz and 64GB RAM. All numerical results can be found in the material at the following link: https://url.kr/svqunr.

4.1.   Implementation setting

We test each model on 16 natural images and five SAR images, provided in Figure 2. The range of intensity values in the original images is assumed to be $[0, \, 255]$. In the experiments, all test images are corrupted by multiplicative gamma noise with noise levels of $L = 10$, $5$, or $3$.

To evaluate the effectiveness of the models, we calculate the peak-signal-to-noise-ratio (PSNR) value defined as

where $\boldsymbol{u}$ and ${ \boldsymbol{u}}_\ast$ denote the restored and original images, respectively, and $N$ is the image size. We also compute the structural similarity (SSIM) index ^[65], which is a perception-based measure that considers the structure of the objects in the visual scene. Specifically, we compute the average of the SSIM values calculated from each RGB channel. For all models, we adjust the parameters to achieve the optimal restored images, taking into account both the visual quality and the PSNR and SSIM values.

The stopping criterion for the proposed model is as follows:

where $\mathbf{h} = \boldsymbol{w}$ or $\boldsymbol{v}$, and $tol > 0$ and $M > 0$ are the given tolerance and maximum iteration number, respectively. We set $tol = 2\times 10^{-3}$ and $M = 30$ for the outer iteration, and $tol = 10^{-3}$ and $M = 10$ for the $\boldsymbol{v}$-subproblem and Newton's method for $\boldsymbol{w}$.

The parameter settings of the proposed model are as follows. First, in the data-fidelity term, parameter $\alpha$, which controls the effect of the penalty term, is fixed at $0.1$. The value of $\beta$ inside the penalty term is closely related to the noise level $L$ and is chosen as $\frac{1}{0.1113+0.1109 L^2}+1$ as suggested in ^[19]. The parameter $\gamma$ in the SVTV term, which controls the weight of the value component, is set to $0.6$, while parameter $\mu$, which controls the effect of SVTV regularization, is fixed at $0.05$ throughout the experiment. For the GSR representation, the image patch size, $\sqrt{P}\times \sqrt{P}$, is set as $6\times 6$ for natural images and $5\times 5$ for SAR images. The number of similar patches, $c$, is set as $80$, so the size of a group is $108\times 80$ for natural images and $75\times 80$ for SAR images. The size of the search window is $20\times 20$. The overlapping width between adjacent patches is $s = 4$ pixels. The parameters $\tau$ and $\lambda$ also affect the GSR representation; the larger the $\tau$ or $\lambda$, the smoother the restored image becomes. However, the larger the $\tau$, the longer the ADMM algorithm takes, so we fix parameter $\tau$ as $3$. The parameter $\lambda$ mainly affects the quality of restored images, so the optimal values of $\lambda$ are chosen differently depending on the noise levels and images. For instance, $\lambda\in\{0.08, 0.1, 0.11\}$ when $L = 10$, $\lambda\in\{0.13, 0.15, 0.17\}$ when $L = 5$, and $\lambda\in\{0.22, 0.24, 0.26\}$ when $L = 3$. The specific value of $\lambda$ is given in each figure. The ADMM parameter $\xi$ is fixed at $1$. For other variational models, we set $\gamma = 0.4$ for L2-SVTV and $\gamma = 0.6$ for AA-SVTV and SO-SVNTVTV2. Specific values of the regularization parameters for all variational models are provided in each figure in the supplementary file at the above link.

4.2.   Denoising results for natural color images

In Figures 3–6, we present the denoising results of the proposed model tested on natural color images, with comparisons to other models.

First, Figure 3 presents the denoising results tested on the Hill image with different noise levels including $L = 10$, $5$, and $3$. The results show that L2-SVTV does not sufficiently remove the noise in some bright areas, such as the sky and white wall areas. This results in erroneous color values in those areas and makes the entire image dark. It also smooths out dark regions such as the roof and right tree areas, which can be clearly seen in the zoomed-in image in Figure 4. Contrarily, AA-SVTV adequately smooths bright regions while retaining noise in the dark regions. In addition, it induces certain artifacts such as black dots, especially in the dark regions. This becomes worse as the noise level increases, as shown in the zoomed-in image in Figure 4. Moreover, as the noise level increases, the entire color tone of the restored image of AA-SVTV is inclined to be distorted. For instance, the color tone of the red roof is degraded compared to those of SO-SVNTVTV2 and our model. SO-SVNTVTV2 suitably eliminates noise in both bright and dark regions, with fewer faulty color values or artifacts than L2-SVTV and AA-SVTV. These indicate the advantages of the SO data-fidelity term when removing multiplicative gamma noise. Additionally, SO-SVNTVTV2 alleviates the staircase effect caused by TV-based models. However, our model improves SO-SVNTVTV2 by preserving more details and generating more naturally restored images with no staircase artifacts and fewer artificial colors. This also leads to the higher PSNR and SSIM values of our model. In contrast, SAR-BM3D also sufficiently conserves edges and fine features, but it produces artificial color values and undesirable artifacts near edges, which deteriorates the denoising performance of SAR-BM3D on color images. These findings demonstrate the effectiveness of the proposed model for restoring color images polluted by multiplicative gamma noise.

In Figure 5, we present the denoising results of all models when $L = 5$ and $3$. Similar to the previous results, L2-SVTV oversmooths the dark regions, such as the hair and textured background in the Barbara image, the stems of flowers in the Building image and the body of statue in the Statues image. It also yields improper color values in some bright regions. This can be observed in the scarf in the Barbara image, the wall in the Building image and the sky area in the Statues image. AA-SVTV retains some noise or black dots in the aforementioned dark regions. This can also be seen in the sky area in the Building image, as shown in the zoomed-in image in Figure 6. As the noise level increases, the denoising performance of L2-SVTV and AA-SVTV significantly deteriorates. L2-SVTV generates the degraded color tones of restored images, while AA-SVTV supplies the black dots in the entire image region, as observed in the Peppers image. SO-SVNTVTV2 not only properly denoises the image in both the dark and bright regions, but also mitigates the staircase artifacts that appeared in the restored images from L2-SVTV and AA-SVTV. However, SO-SVNTVTV2 fails to preserve fine textures and details, as seen in the scarf in the Barbara image and the window areas in the Building image. In contrast, these textural regions are well conserved in SAR-BM3D and our model. This leads to the higher PSNR values of SAR-BM3D and our model than SO-SVNTVTV2 in the Barbara and Building images. Nevertheless, SAR-BM3D produces faulty color values, especially near edges, while SO-SVNTVTV2 and our model do not. Especially when $L = 3$, SAR-BM3D produces artificial color values in the entire image region and certain artifacts induced by patches. These can be more obviously seen in the entire image of Peppers and the zoomed-in image of Statues in Figure 6. Consequently, our model provides the cleanest and clearest restored images among the models, while retaining textures, details, and sharp edges. This also corresponds to the highest PSNR and SSIM values. These examples also confirm the superior denoising performance of the proposed model over existing models, even in the presence of heavy multiplicative gamma noise.

In Figure 7, we show the effect of our multi-channel-based GSR approach by using the proposed model (3.7) with two different GSR approaches. Specifically, our GSR approach selects similar color image patches by computing the distance between two color patches and constructing an image group using these selected color patches. The other GSR approach chooses similar image patches in each color channel by measuring the patch distance in each channel. For comparable results, we use $P = 8\times 8$ and $c = 80$ for this decoupled GSR approach. In the Barbara image, the decoupled GSR approach slightly better preserves textures such as the scarf parts, which leads to higher SSIM values than our coupled GSR approach. However, the decoupled GSR approach furnishes artificial color values in all the examples, unlike our GSR approach. Thus, our GSR approach provides higher PSNR and SSIM values in most examples. These demonstrate the efficacy of our GSR approach for the removal of multiplicative noise in color images.

Figure 8 displays the effect of the data-fidelity term in the proposed model. In particular, we show the effect of the penalty term, $\left(\sqrt{{e^{ \boldsymbol{w}}}/{ \boldsymbol{f}}}-\beta \right)^2$, included in the data-fidelity term, since the effectiveness of the SO data-fidelity term has already been shown in the previous examples compared to the $L^2$ or AA data-fidelity terms. That is, we compare our model with the model (3.7) without this penalty term. Although the restored images look almost identical, the use of the penalty term produces reconstructed images with higher PSNR and SSIM values. Therefore, these results validate the superiority of our data-fidelity term, compared to the SO data-fidelity term. For more examples, please refer to the supplementary file at the above link.

Figure 9 illustrates the effect of the SVTV term in the proposed model. Specifically, we compare our model with the model (3.7) without the SVTV term. The GSR model (3.7) without the SVTV term generates certain ringing artifacts near edges and block artifacts in homogeneous regions, which are usually induced by patch-based methods. However, the SVTV term alleviates or diminishes these artifacts by sufficiently smoothing these areas, as shown in the images in the bottom row. These show the effectiveness of the SVTV term in the proposed model.

4.3.   Denoising results for color SAR images

Figure 10 presents the denoising results of all models tested on real SAR images, when $L = 3$. The SAR images consist of many dark regions such as trees and shadows, while including some bright regions such as buildings and ships. Similar to the natural color image cases, L2-SVTV smooths out dark areas but does not adequately remove noise in bright areas, leading to inappropriate color values. In addition, the color tone of the restored image of L2-SVTV is significantly degraded compared to other models. In contrast, AA-SVTV sufficiently denoises the bright regions but supplies some black artifacts in the homogeneous regions including the grass or ground, and dark regions such as building shadows and tree areas. On the other hand, the denoising performance of SAR-BM3D on color SAR images is not as good as on natural color images. SAR-BM3D performed somewhat well on natural color images including large repeated textures or various color values, such as the Barbara, Building, and Peppers images, as shown in Figure 5. However, color SAR images do not usually contain large repeated textures or various color values. Instead, they include many small objects and edges. In color SAR images, SAR-BM3D sufficiently eliminates noise in both dark and bright regions and preserves details well, but it produces many erroneous color values in these small objects and edges. Thus, its PSNR and SSIM values are much lower than those of SO-SVNTVTV2 and our model at all noise levels, unlike the case of natural color images. SO-SVNTVTV2 conducts well on color SAR images, by appropriately denoising both dark and bright areas in addition to retaining fine details and edges. Additionally, it does not generate faulty color values or artifacts compared to SAR-BM3D or AA-SVTV. The restored images of SO-SVNTVTV2 and our model are visually very similar, but our model further improves SO-SVNTVTV2 by conserving more details and edges, thereby yielding cleaner and sharper restored images. In all cases, this results in higher PSNR and SSIM values for our model. Therefore, these examples establish the considerable denoising performance of the proposed model, even on real SAR images.

Figure 11 displays plots of the relative errors of $\boldsymbol{w}^{\ell}$ and PSNR values of $\boldsymbol{u}^{\ell} = e^{ \boldsymbol{w}^{\ell}}$ via the outer iteration number $\ell$ for the proposed model, when $L = 10$, $5$, and $3$. The figure shows that as $\ell$ increases, the relative error ultimately decreases, while the PSNR value increases and converges to a certain value. In addition, as the noise level $L$ increases, a higher number of outer iterations is required for convergence. These plots verify the numerical convergence of the proposed algorithm, even though the theoretical convergence of the algorithm is still a remaining issue.

Lastly, in Tables 1–3, we present the PSNR and SSIM values of all models, when $L = 10$, $5$, and $3$, respectively. The results show that the PSNR and SSIM values of AA-SVTV decrease significantly at noise level $L = 3$. Furthermore, SAR-BM3D provides similar PSNR and SSIM values as SO-SVNTVTV2 for natural color images, but its PSNR and SSIM values are considerably diminished for color SAR images. In all cases, the proposed model yields the highest PSNR and SSIM values. These measurements also ensure the outstanding denoising performance of the proposed model compared to other models.

5.   Conclusions

This paper proposes a multi-color channel-based GSR model for the removal of multiplicative gamma noise in color images. The proposed GSR comprises an image group with similar color patches, by measuring the distance between two color patches. This prevented artificial color values produced by separate color channel-based approaches. Furthermore, GSR, which exploits the sparsity and nonlocal similarity of patches, aided in the conservation of fine structures and repeated textures. Additionally, it adequately denoised smooth regions without the staircase artifacts caused by TV-based models, which led to the natural visual quality of restored images. The model also includes a convex data-fidelity term and SVTV regularization. The data-fidelity term facilitated the removal of heavy multiplicative noise, while SVTV helped alleviate some ringing or block artifacts induced by patches, thus enhancing the denoising results. We adopted the ADMM to solve the proposed nonconvex model and its subproblem. These approaches yielded an efficacious iterative algorithm. The experimental results validated the superior denoising performance of the proposed model over other existing models, when it comes to both visual inspection and image quality measurements. However, despite the numerical convergence of the proposed algorithm, the theoretical convergence of the proposed algorithm still remains an issue. Furthermore, the GSR approach requires more computational time than local regularization-based methods due to searching for similar patches and the singular value decomposition of groups. Thus, faster implementation also needs to be investigated in future work.

Use of AI tools declaration

The author declares they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author was supported by the Hankuk University of Foreign Studies Research Fund and the National Research Foundation of Korea (2021R1F1A1048111).

Conflict of interest

The author declares no conflicts of interest in this paper.