Lagrange radial basis function collocation method for boundary value problems in $1$D

1.   Introduction

Partial differential equations (PDEs) arise in various fields of science and engineering as mathematical models to describe complex physical phenomena. In many applications, an accurate and efficient numerical solution to PDEs is crucial. Among the numerous numerical techniques available for solving PDEs, radial basis function (RBF) methods, particularly collocation methods, have received significant attention in recent years ^[1,2,3].

RBF methods were first introduced by Hardy in the 1970s as a tool for spatial interpolation ^[4,5,6]. However, it wasn't until the late 1980s and early 1990s that RBFs began to gain traction as a numerical technique for solving PDEs, see; ^[7,9]. Pioneering work by Kansa, Micchelli, Madych, and Nelson in the early 1990s laid the foundations for the RBF collocation method, which has since become a popular approach to solving PDEs. After that, in the 2000s, many papers had been published to show the effectiveness of the RBF collocation method when applied to a wide range of applications ^[10,11,12]. An interesting modification of the RBF collocation method was introduced in ^[13], in which the authors numerically solve a Poisson equation with Dirichlet conditions through multinode Shepard interpolants by collocation. Furthermore, in ^[14], the Shepard multinode method was used to numerically estimate electric scalar potentials via collocation. RBF-based collocation methods still attract significant interest due to their various advantages, such as high accuracy, flexibility in handling complex geometries as a meshless method, and ease of implementation. One of the well-known element-free Galerkin methods was introduced in ^[15]. However, despite their potential benefits, these methods also come with a set of challenges, one of the main ones being the so-called "trade-off principle", which implies that an increase in the accuracy of the approximation is typically accompanied by a decrease in stability. This trade-off arises due to the ill-conditioning and high condition numbers of the matrix, which can impact the stability and accuracy of the numerical solution. Moreover, stagnation issues in the standard collocation RBF method where ill-conditioning of the problem and the stability issue are managed by adapting the shape parameter to the corresponding level, but where the error stagnates and does not improve-can further limit the effectiveness of these methods.

Several attempts have been made to tackle the trade-off principle in RBF collocation methods, such as using preconditioning techniques ^[16], employing different types of RBFs ^[17], or optimizing the shape parameter ^[18]. Despite these efforts, the trade-off principle remains a fundamental challenge in RBF collocation methods.

This paper introduces a novel numerical method, the Lagrange collocation method with radial basis functions (LRBF), for solving one-dimensional PDEs. Our method is designed to address the primary challenges associated with standard RBF-based collocation methods, especially the trade-off principle, while maintaining the accuracy and convergence properties of the solution. To accomplish this, we focus on specific differential operators such as the Laplacian operator and positive definite RBF functions. Then, we introduce a perturbation to the main matrix, leading to the development of the perturbed LRBF method (PLRBF). This perturbation allows us to apply Cholesky decomposition, significantly reducing the matrix's condition number to its square root. As a result, we can select a large value for the shape parameter without sacrificing either stability or accuracy, as long as the perturbation is chosen carefully. This approach enables us to obtain highly accurate solutions at early levels, thus greatly reducing the computational time and improving the overall efficiency of the method. Furthermore, we establish the existence and uniqueness of the numerical solution to our model.

To tackle the stagnation issues commonly observed in standard RBF collocation methods, we integrate the LRBF and PLRBF approaches with multilevel techniques, culminating in the Multilevel PLRBF method (MuPLRBF). Then, we demonstrate our main findings through numerical experiments in 1D. Although we initially focus on 1D problems, we anticipate that our approach can be extended to higher dimensions, which will be explored in future work.

The remainder of this paper is organized as follows. Section 2 presents the LRBF method, providing an overview of its key concepts and motivation. Section 3 delves deeper into the theoretical foundation and main characteristics of the method, including the existence and uniqueness of the numerical solution for positive definite RBFs. In Section 4, we demonstrate how applying the Cholesky decomposition to the LRBF method significantly improves stability by reducing the condition number of the matrix.

Section 5 introduces the PLRBF method, a novel approach that incorporates a perturbation into the main matrix, thereby further enhancing stability and enabling the use of Cholesky decomposition. Section 6 details the development of the MuLRBF and MuPLRBF methods, which combine the LRBF and PLRBF methods with multilevel techniques to address the stagnation issues commonly encountered in standard RBF collocation methods.

In Section 7, we describe a series of numerical experiments performed to validate our methods and discuss the findings related to accuracy, stability, and convergence. We compare the performance of our proposed methods with that of traditional RBF collocation methods and provide insights into their respective strengths and weaknesses. Finally, in Section 8, we conclude the paper by summarizing our key contributions and offering suggestions for future research directions, including potential extensions to higher-dimensional problems.

2.   Lagrange RBF collocation method in $1$D

Consider the following boundary value problem (BVP) for the target function $U(x)$, in the one-dimensional space $\Omega =]0, 1[$.

where $\mathcal{L}$ is a linear differential operator and $f(x)$ is a given function. To obtain a general domain $[a, b]$ from the considered one, we use the transformation $y = (b-a)x+a$. Therefore, for the rest of this paper, without a loss of generality, we consider $\Omega =]0, 1[$, and we define the nodes $x_{i}\in [0, 1]$ as follows:

where $n$ is the number of nodes distributed on $[0, 1].$ Note that $x_1 = 0$ and $x_n = 1$.

Summarizing the Lagrange RBF collocation method, we define the numerical solution $\widehat{U}$ to the problem (2.1) as follows:

where $\beta _{i}, \, i = 1, 2, \dots, n$ are unknown constant coefficients to be determined, $\mathfrak{\ell }_{i}, \ i = 1, 2, \cdots, n$ are linear combinations of RBFs $\phi (x-x_{j})$, named $\mathcal{L}$-Lagrange, such that $\mathcal{L} \mathfrak{\ell }_{i}$ are Lagrange functions, $\delta _{ik}$ is the usual Kronecker delta symbol, and $\alpha _{i, j}, \ i, j = 1, 2, \dots, n$ are constant coefficients to be determined. In addition, the numerical solution $\widehat{U}$ must satisfy the BVP system (2.1) at the nodes $({x}_{i})_{1\leq i \leq n}$. Hence, we get the following discrete system:

We write $f_{k}: = f(x_{k})$.

2.1.   Determine the $\mathcal{L}$-Lagrange functions

We note that the $\mathcal{L}$-Lagrange functions $(\mathfrak{\ell }_{i})_{1\leq i \leq n}$ depend on the differential operator $\mathcal{L}$ and the chosen grid $({x}_{i})_{1\leq i \leq n}$, but not on the numerical solution, and each Lagrange function $(\mathcal{L} \mathfrak{\ell }_{i})_{1\leq i \leq n}$ satisfies the Lagrange conditions $\mathcal{L}\mathfrak{\ell }_{i}(x_{k}) = \delta _{ik}, i, k = 1, 2, ..., n.$ The term Lagrange is usually applied to polynomials, but is also commonly used in the RBF literature; see ^[12].

Thus, the construction of the $\mathcal{L}$-Lagrange functions can be treated completely independently from the above. In order to determine the unknown constant coefficients $\alpha _{i, j}, \ i, j = 1, 2, \dots, n$, we make use of the second equation in the system (2.2) by applying the linear operator $\mathcal{L}$ on both sides. We then have the following:

Using the Eq (2.4) at the set of nodes $x_{k}$, and the third equation in the system (2.2), we obtain the following:

The relations (2.5) form the main linear systems for the coefficients $\alpha _{i, j}$. These systems can be rewritten as follows:

where the components are given by the following:

As shown in Theorem 3.2, the matrix $\mathbf{A}$ is symmetric and a negative definite for positive definite RBF functions and for a certain differential operator $\mathcal{L} = \gamma D^2_{x}$ with $\gamma > 0$. Thus, we have a unique solution to the main linear system (2.6), and which can be formally written as follows:

The solutions to Eq (2.6) provide the coefficients $\alpha _{i, j},$ as described in (2.8), which determine the $\mathcal{L}$-Lagrange functions $\mathfrak{\ell }_{i}$.

We recall that since the matrix $\mathbf{A}$ is independent of the numerical solution, and the right-hand side is the unit vector, we can solve the above linear system once and for all $\mathfrak{\ell}_{i}$ outside the main program, thus improving the efficiency.

2.2.   The numerical solution

Applying the Kronecker delta condition from (2.2) to the first equation in (2.3), we obtain the following:

This results in the following:

Therefore the numerical solution $\widehat{U}(x)$ in (2.2) can be expressed as follows:

Hence, to determine the approximate solution $\widehat{U}(x),$ we need to determinate the coefficients $\beta _{1}, \beta _{n}$.

Insertion of $\mathcal{L}$-Lagrange functions $\mathfrak{\ell }_{i}$ into the boundary conditions of the system (2.3) leads to the following two equations in $\beta _{1}$ and $\beta _{n}$:

which can be presented in matrix form as follows:

Thus, we have a system with a $2\times2$ matrix, which can be easily solved to determine the coefficients $\beta _{1}, \ \beta _{n}$.

This, combined with (2.9), gives all $\beta$. The fact that the $\mathcal{L}$-Lagrange functions were determined separately in section 2.1 means that the desired numerical solution $\widehat{U}(x)$ in (2.2) has been established.

3.   Well-posedness & main characteristics

So far, we have introduced the LRBF method in 1D for general radial basis functions and general differential operators. In this section, we focus on positive definite RBF functions and the second-order linear differential operator of the form $\mathcal{L} = \gamma D^2_{x}$, with $\gamma > 0$ and $D^2_{x}$ representing the second derivative. For this class, we demonstrate the existence and uniqueness of our solution and show how to improve stability and efficiency without losing accuracy.

To prove the existence and uniqueness of the solution to the system (2.6), it is sufficient to prove that the matrix $\mathbf{A}$ is symmetric and either positive definite or negative definite. In fact, if the matrix is symmetric and either positive or negative definite, then it is invertible, which implies the existence and uniqueness of the solution.

Definition 3.1. (Positive definite matrix) An $N\cdot N$ symmetric real matrix $A$ is said to be positive semi-definite if its associated quadratic form is non-negative, i.e.,

for all vectors $\mathit{\boldsymbol{\lambda}} = \left(\lambda_1, \ldots, \lambda_N\right)^T \in \mathbb{R}^N$. If the only vector $\mathit{\boldsymbol{\lambda}}$ that turns the above quadratic form into an equality is the zero vector, then $A$ is called positive definite.

Definition 3.2 (Positive definite function) A real valued continuous function $\phi: \mathbb{R}^{d} \rightarrow \mathbb{R}$ is said to be {positive semi-definite} on $\mathbb{R}^{d}$ if, and only if, it is even and

for any $N$ pairwise different points $\mathbf{X} = \left\{\mathbf{x}_1, \ldots, \mathbf{x}_N\right\} \subseteq \mathbb{R}^d$, and $\mathit{\boldsymbol{\lambda}} = \left(\lambda_1, \ldots, \lambda_N\right)^T \in \mathbb{R}^N$. The function $\phi$ is strictly positive definite on $\mathbb{R}^d$ if the only vector $\mathit{\boldsymbol{\lambda}}$ that turns the above into an equality is the zero vector.

Note:It is worth noting the two well-known classes of positive definite RBFs, namely the Gaussian RBF $\phi (r) = \exp (-\frac{r^{2}}{c^{2}})$ and the family of Inverse multi-quadric $\phi(r) = (r^2 + c^2)^{-\beta}$, where $\beta \geq 0$, and $c$ is a positive constant. In this paper, we focus on studying the Gaussian RBF and the Inverse multi-quadric, where $\beta = 1/2$, i.e., $\phi(r) = \frac{1}{\sqrt{r^2 + c^2}}$.

To prove our main theorem on the well-posedness of our solution, we introduce the concept of Fourier transformation and make use of the Bochner Theorem 3.1.

Definition 3.3. Let $f \in L^{2}(\mathbb{R}^d)$, where the Fourier transform $\mathcal{F}$ is defined as follows:

and the inverse Fourier transform is defined by the following:

Theorem 3.1. (Bochner, (^[19], p70)) $\phi: \mathbb{R}^{d}\rightarrow \mathbb{R}$ is positive definite if, and only if, $\phi$ is bounded and its Fourier transform $\mathcal{F}(\phi)$, which is nonnegative and nonvanishing.

Now, we are in a position to prove our theorem.

Theorem 3.2. (Existence & uniqueness) For a positive definite radial basis function $\phi: \mathbb{R}^{d}\rightarrow \mathbb{R}$ and a differential operator $\mathcal{L} = \sum_{i, j = 1}^{d} \gamma_{ij} \partial_{x_i} \partial_{x_j}$ with $\Gamma = (\gamma_{ij})_{1\leq i, j \leq d}$ a symmetric and positive definite matrix, we define the matrix $\mathbf{A} \in \mathbb{R}^{n \cdot n}$ as follows:

where $(\mathbf{x}_k)_{k = 1}^{n}$ are distinct points with $\mathbf{x}_k \in \mathbb{R}^d$. The matrix $\mathbf{A}$ is symmetric and negative definite. If $\Gamma$ is a negative definite matrix, then the matrix $\mathbf{A}$ is positive definite.

Proof. First, using the fact that $\phi$ is an RBF and $\mathcal{L}$ is a symmetric differential operator with a direct calculation, we conclude that $\mathcal{L}\phi (\mathbf{x}_{i}-\mathbf{x}_{j}) = \mathcal{L}\phi (\mathbf{x}_{j}-\mathbf{x}_{i})$, proving the symmetry of the matrix $\mathbf{A}$.

Now, we prove that the matrix $A$ is negative definite, i.e.,

for all nonzero vectors $\lambda \in \mathbb{R}^n$.

Using the Fourier transform $\mathcal{F}$ and a straightforward calculation, it can be shown that

Applying the Bochner Theorem 3.1 to the positive definite RBF $\phi$, we have $\mathcal{F}(\phi)(\xi) \geq 0$. Additionally, $\Gamma$ is a positive definite matrix, i.e., $\xi^{T} \Gamma \xi > 0$.

Combining the last two facts, we clearly see that

Now, applying the Bochner theorem from the other side (i.e., using the fact that the Fourier transform of $(\mathcal{L} \phi)$ is nonpositive and nonvanishing), it follows that the function $(\mathcal{L} \phi)$ is negative definite. This gives us the following:

which proves that $\mathbf{A}$ is negative definite. Similarly, if $\Gamma$ is a negative definite matrix, then the matrix $\mathbf{A}$ is positive definite.

In particular, in the one-dimensional case, the differential operator takes the form $\mathcal{L} = \gamma D^2_{x}$ with $\gamma > 0$.

The above theorem proves the existence and uniqueness of the $\mathcal{L}$-Lagrange functions, and thus, the existence and uniqueness of our numerical solution.

3.1.   Main characteristics of the LRBF method

We summarize several noteworthy characteristics of the linear system (2.6) that play a crucial role in enhancing the efficiency and stability of our novel LRBF method. In our numerical experiments in Section 7, we analyse the stability, accuracy, and efficiency of several methods, including RBF, confirming our findings below.

(1) Stability: The matrix $\mathbf{A}$ is symmetric and negative/positive definite (depending on the sign of $\gamma$) which allows for the use of different linear solvers such as $LDL^T$ decomposition, in particular Cholesky decomposition. Using Cholesky decomposition, we show in Section 4 that the condition number of the main problem reduces to its square root (i.e., the condition numbers stay almost all the time under $10^{10}$). However, numerical experiments show that this matrix is numerically unstable and often prevents the use of Cholesky decomposition. Thus, further thoughts and techniques are required to deal with this stability problem. To address this issue, we explore additional techniques and present a solution in Section 5.

(2) Efficiency: The fact that the $\mathcal{L}$-Lagrange functions are independent of the numerical solution allows for a calculation of the coefficients outside of the main program once and for all, saving valuable time during the calculations. In addition, the structure of the matrix $\mathbf{A}$ and the right-hand side $\mathbf{\mathit{\boldsymbol{ \delta _{i}}}}$ significantly improve the calculation speed in the following ways:

a) The matrix $\mathbf{A}$ is symmetric negative/positive definite, thus allowing for the use of a faster linear solver.

b) The right-hand side is the most trivial to calculate as it is the unit vector with $1$ at element $i$ and $0$ elsewhere.

4.   Improved stability of the LRBF method by applying Cholesky decomposition

In this section, the focus is on improving the condition number of the matrix $\mathbf{A}$ given in (2.6), which is negative/positive definite (depending on the sign of $\gamma$), as shown in Theorem 3.2. First, we briefly introduce the well-known Cholesky decomposition ^[20] and highlight its ability to significantly improve our problem's condition number. Next, we show that despite promising theoretical results, our system cannot confirm them numerically, as we encounter a numerically unstable matrix.

4.1.   Recap: Cholesky decomposition

For a given symmetric and positive definite matrix $\mathbf{A}$, the Cholesky decomposition can be represented as follows:

where $L$ is a lower triangular matrix with positive diagonal elements.

Now, recalling the form of our main problem with a symmetric positive definite matrix $\mathbf{A}$,

Applying the Cholesky decomposition of $\mathbf{A} = LL^T$, we obtain the following:

which is equivalent to the linear system

The formal expression for $\alpha$ can be written as follows:

In case $\mathbf{A}$ is negative definitive (i.e., the Cholesky decomposition becomes $\mathbf{A} = -LL^T$), we have the above system (4.3) with a minus on the first equation.

Additionally, we will make use of the following proposition, which can be proven through a direct calculation.

Proposition 4.1. (Improved stability) For a symmetric positive definite matrix $\mathbf{A}$ with a Cholesky decomposition $\mathbf{A} = LL^{T}$, or in case $\mathbf{A}$ is negative definite, ($A = - LL^T$), we have

where $Cond(\mathbf{A}) = \| \mathbf{A} \|_{2} \|\mathbf{A}^{-1} \|_{2}$.

Proof. First, let us remark that, $\| A \|_{2} = \|L\|^{2}_{2}$. Indeed,

Similarly,

Thus,

□ Remark: The benefit of the Cholesky decomposition method lies in its ability to transform the main problem (4.1), which involves a matrix with a large condition number, into two linear systems given by (4.3). The matrices in these systems have much smaller condition numbers (the square root of the original, as shown above), which is expected to yield a more stable solution to our numerical problem. However, as demonstrated in the following section, the original matrix becomes numerically unstable beyond a certain level or for a large shape parameter, and does not even permit the application of Cholesky decomposition.

4.2.   Numerical studies-Part I

In this section, we present our initial numerical studies, focusing on the stability and condition number of the matrix $\mathbf{A}$ for the Laplacian operator ($\mathcal{L} = \Delta$). We define equidistant nodes on the interval $[0, 1]$ and utilize two well-known positive definite RBF functions – the Gaussian function $\phi(r) = e^{(r/c)^2}$ and the inverse multi-quadric $\phi(r) = \frac{1}{\sqrt{r^2 + c^2}}$, where $c > 0$ – is the shape parameter. In our experiments, we systematically explore various levels $i$ and shape parameters $C$ by setting $h_i = 2^{-i}$ and $c_i = C \cdot h_i$, where $C > 0$. We consider a comprehensive range of values, with $i$ ranging from $1$ to $9$ and $C$ given by $2^j$ for $-3\leq j \leq 8$. To maintain the clarity and conciseness of our presentation, we have elected to display a subset of our results, specifically for levels up to $6$ and $C$ values of $1, 8$ and $32$. This allows us to effectively illustrate the key findings of our study without overwhelming the reader with excessive data. Based on Theorem 3.2, we expect that the matrix $\mathbf{A}$ is negative definite, with all eigenvalues being strictly negative, thereby allowing for the Cholesky decomposition of $-\mathbf{A}$ at all costs. However, our experiments reveal that this property only holds for either small shape parameters, $c$, or at the first two levels. The primary observations from our experiments and Tables 1–3 can be summarized as follows:

● In line with expectations, the condition number of the original problem experiences a significant increase up to level $6$.

● Beyond a specific level (e.g., level $4$ and $C = 8$ for Gaussian), our matrix becomes numerically unstable and no longer permits the use of Cholesky decomposition. This instability is dependent on both the level and the shape parameter, $C$.

● A detailed analysis of our data indicates that the main issue lies in the rapid convergence of matrix entries to their diagonal counterparts, resulting in an almost singular matrix. This phenomenon is demonstrated in the Max EV column, where the maximum eigenvalue of the matrix approaches $0$, signifying a numerically singular matrix.

Our numerical results highlight the challenges associated with the original matrix, despite its symmetric and positive definite nature. In certain cases, its numerical instability and near-singularity prevent the effective use of Cholesky decomposition, necessitating the exploration of alternative approaches to address these issues.

5.   Perturbed $\mathcal{L}$-Lagrange functions and Perturbed LRBF method

In the standard LRBF method, we observed stability issues primarily arising due to matrix entries converging to their diagonal when the shape parameter is sufficiently large, and the distance between the points decreases. We introduce a perturbation technique and develop the perturbed LRBF method (PLRBF) to overcome this challenge. Our numerical experiments confirm that the new PLRBF method is more stable and, surprisingly, exhibits superior accuracy, especially when applying the multilevel technique.

First, we introduce a general perturbation to the diagonal entries of the matrix and then demonstrate simple yet very useful properties for the perturbed matrix when the original matrix is either positive or negative definite. We recall the key aspect of our approach is the application of Cholesky decomposition, which, together with the perturbation techniques, significantly improves the numerical stability of the method.

Definition 5.1. (Perturbed matrix) For a small $\varepsilon \ge 0$ and a matrix $\mathbf{A} \in \mathbb{R}^{n\cdot n}$, we define a sequence of matrices of diagonal perturbation as follows:

where $I_n = diag(1, 1, \dots, 1)$ is the identity matrix and $\lambda_{max }$ is the largest eigenvalue of the matrix $\mathbf{A}$.

Proposition 5.1. (Properties of the perturbed matrix) For either a symmetric positive or negative definite matrix $\mathbf{A}$, the perturbed matrix $\mathbf{A}^\varepsilon$ as defined above satisfies the following:

(1) For $\varepsilon \rightarrow 0$ the matrix $\mathbf{A}^\varepsilon$ converges uniformly to $sgn(\lambda) \mathbf{A}$.

(2) $\mathbf{A}^\varepsilon$ is symmetric and positive definite.

(3) When A is positive definite, we have the following:

(4) When A is negative definite, we have the following:

(5) $\mathbf{A}^\varepsilon$ is always as good or better conditioned than $\mathbf{A}$, i.e.,

Proof. A direct calculation. □

5.1.   Perturbed LRBF method

Based on the perturbed matrix $\mathbf{A}^\varepsilon$, we define our perturbed $\mathcal{L}$-Lagrange functions as follows:

where $\alpha^{\varepsilon}_{i, j}$ are the solution of the following perturbed system:

where $\mathbf{\mathit{\boldsymbol{ \alpha_{i}}}}^\varepsilon = \left(\alpha _{i, 1}^\varepsilon, \dots, \alpha _{i, n}^\varepsilon \right)^T$, and $\mathbf{A}^\varepsilon$ is the followingperturbation of the original matrix $\mathbf{A}$ as defined in (2.6).

This allows us to define our Perturbed LRBF (PLRBF) solution as follows:

Remark: By applying the Cholesky decomposition to the system (5.1), we determine the coefficients $\mathbf{\mathit{\boldsymbol{ \alpha_{i}}}^ \varepsilon}$ and, thus, the perturbed $\mathcal{L}$-Lagrange functions $\ell_i^\varepsilon$ and the Cholesky PLRBF (CPLRBF) solution $U^\varepsilon$. A detailed implementation of the (perturbed) $\mathcal{L}$-Lagrange functions and the CPLRBF method is captured in Algorithms 1 and 2. Additionally, we note that $U^\varepsilon$ converges uniformly to $U$ when $\varepsilon \rightarrow 0$.

5.2.   Numerical studies-Part II

In this section, we investigate the condition number of the matrix $\mathbf{A}^\varepsilon$ for the Laplacian operator. To do so, we perform a series of experiments analogous to those in Part I, with $\varepsilon = 10^{-i}$ for $6\leq i \leq 15$. From Theorem 3.2, we expect that the matrix $\mathbf{A}^\varepsilon$ will exhibit positive definiteness, resulting in strictly positive eigenvalues and enabling the Cholesky decomposition of $\mathbf{A}^\varepsilon$ at all $\cdot$. Our experiments validate this hypothesis in most cases, with the choice of $\varepsilon$ proving to be a primary determinant of stability, while the influence of the level and shape parameter, $c$, is less pronounced than with the original matrix $\mathbf{A}$.

As in Part I, to maintain clarity and conciseness in our presentation, we have elected to display a subset of our results, specifically for levels up to $6$, $C$ values of $1$, $8$ and $32$, and $\varepsilon = 10^{-6}, 10^{-15}$. This enables us to effectively convey the key findings of our study without overwhelming the reader with excessive data.

Upon analysing our data, we arrived at the following conclusions, confirmed with Tables 4–9:

● As shown in Proposition 5.1, the condition number of the perturbed matrix $\mathbf{A}^\varepsilon$ is either equal or smaller to the condition number of the original matrix $\mathbf{A}$ (i.e., the problem with $\mathbf{A}^\varepsilon$ is better conditioned).

● Our approach successfully mitigates the instability issues associated with the LRBF matrix, as the matrix $\mathbf{A}^\varepsilon$ demonstrates numerical stability, thereby allowing for Cholesky decomposition in the majority of cases.

● The choice of $\varepsilon$ plays a key role in the system's stability. However, remarkably, in this regard, our experiments encountered only minimal limitations in this regard. For all $\varepsilon = 10^{-12}$ to $10^{-6}$, no stability issues were observed for all levels up to $9$ and all $C$ values as defined in Part I.

Our numerical experiments demonstrate the effectiveness of introducing a perturbed matrix $\mathbf{A}^\varepsilon$ in addressing the stability issues associated with the LRBF matrix. By carefully selecting the value of $\varepsilon$ (e.g., $10^{-13} \leq \varepsilon \leq 10^{-6})$, we could consistently obtain numerically stable solutions and improved condition numbers compared to the original matrix $\mathbf{A}$.

6.   The multilevel full grid PLRBF collocation method in one dimension

This section combines the well-established multilevel approach with our LRBF and PLRBF methods, resulting in the Multilevel LRBF (MuLRBF) and Multilevel PLRBF (MuPLRBF) methods. Our primary objective is to tackle the known stagnation issues in the standard collocation RBF method. By capitalizing on the perturbed matrix's robustness and utilizing the $\mathcal{L}$-Lagrange functions's precalculable nature, we anticipate that our MuPLRBF method will be more stable, efficient, and accurate.

Initially, we will develop the MuLRBF method for the BVP (2.1), followed by a comprehensive presentation of its associated algorithm, which is also valid for MuPLRBF-ensuring a solid foundation for implementing and analysing the MuLRBF/MuPLRBF/MuCPLRBF methods in the following section.

Let $\{\mathbf{X}_{k}\}_{1\leq k \leq m}$ be a strictly increasing sequence of nested full grids in the interval $[0, 1]$, each with $2^{k}+1$ equally spaced nodes.

The approximation $\Delta \widehat{U}_{1}$ on the first grid $\mathbf{X}_{1}$ is constructed in such a way that satisfies the system

We define the approximation $\widehat{U}_{1}(x): =$ $\Delta \widehat{U}_{1}(x)$. Now, for the grids $\mathbf{X}_{{k}},$ $k = 2, \dotsc, m$, the approximations $\Delta \widehat{U}_{k}(x)$ satisfy the residual system, which takes the following form:

where $\widehat{U}_{k}(x) = \widehat{U}_{k-1}(x)+\Delta \widehat{U}_{k}(x).$ The final approximate solution $\widehat{U}_{m}$ is the sum of the numerical solution $\widehat{U}_{1}$ and the defect terms $\Delta \widehat{U}_{k}$$, k = 2, \dotsc, m,$, i.e.,

Since $\widehat{U}_{1}(x) : = \Delta \widehat{U}_{1}(x)$, then

The residual system at level $k$ is written at the nodes $({x}_{i}^{k})_{1\leq i \leq n_k}$ as

The approximation $\Delta \widehat{U}_{k}$ is expressed as follows:

where $n_{k}$ is the number of nodes in the $k^{th}$ grid and $\beta _{i}^{k}$ are unknown coefficients. In the $k^{th}$ level, the Lagrange's functions $\mathfrak{\ell }_{i}^{k}(x)$ are precalculated as described in Section 2, and can be given as follows:

where $\alpha _{i, j}^{k}$ are the constant coefficients calculated in Section 2.

By making use of (6.5) and (6.3), we rewrite the first equation in the system(6.4) as follows:

Using the fact that $\mathcal{L}\ell _{i}^{k}(x_{j}^{k}) = \delta _{ij}$, we obtain the following:

Now, it remains to determine the coefficients $\beta _{1}^{k}$ and $\beta _{n_{k}}^{k}$ to obtain the expression of the approximate solution, as given in (6.5). Using the boundary conditions expressed in the system (6.2), we obtain the following:

Then,

which can be written in the following matrix form

The solution to this system and (6.8) give the coefficients $\beta _{i}^{k}, \ i = 1, 2, \cdots, n_{k}$, which determine the approximation $\Delta \widehat{U}_{k}(x)$ in the $kth$ level. Similarly, we calculate the Multilevel PLRBF (MuPLRBF) solution and the Multilevel CPLRBF (MuCPLRBF) solution, as described in Algorithm 3.

7.   Numerical experiments

In this section, we discuss the numerical experiments conducted to evaluate the performance of our new methods. Our analysis encompasses seven distinct examples to comprehensively assess the methods' accuracy, convergence, and stability. While considering numerous scenarios in our experiments, we have carefully selected a representative subset to include in this paper to maintain clarity and conciseness. First, we will provide a brief overview of the experiments and the parameters under investigation. Following this, we delve into the results of one example in detail, focusing on the aspects of accuracy, convergence, and stability. Finally, we summarize our findings and highlight the key takeaways from these numerical experiments.

7.1.   Overview of the experiments

These are the parameters we considered for our experiments:

● Example: BVP in $1$D with known exact solution, including trigonometric functions.

● Methods: Six methods, namely RBF, MuRBF, LRBF, MuLRBF, CPLRBF, and MuCPLRBF. In the CPLRBF and MuCPLRBF methods, we consider different values for $\varepsilon$; $\varepsilon = 10^{-i}$ for $6\leq i \leq 13$, resulting in a total of 20 methods.

● Levels: Nine levels with $h_i = 2^{-i},$ with $1\leq i\leq 9$.

● Shape parameters: The constant $C$ takes the values $C_j = 2^j$ with $-3\leq j \leq 8$, and the adaptive shape parameter for each level $i$ is $c_{i, j} = C_j \cdot h_i$.

● RBF functions: Gaussian RBF $\phi (r) = \exp (-\frac{r^{2}}{c^{2}}).$

● Norms: Max & RMS Norm defined as $Max\ u = \max_{i} |u(x_i)|$ and $RMS\ u = \sqrt{\sum_i^N u(x_i)^2/N}$, with $x_i$ being the nodes on the interval $[0, 1]$.

● Tools: Matlab and Excel for data analysis (per example, we had 8424 data points).

● Notation: CPLRF & MuCPLRBF will be written as CPL & MuCPL in this section.

● A set of points $(t)$, presenting 64, 000 equally spaced points on $[0, 1]$.

7.2.   Presentation of results for a representative example:

Now, we select the particular example below to illustrate the key performance attributes of our methods, allowing us to discuss the aspects of accuracy, convergence, and stability.

Let the target function $U$ satisfy the following BVP:

The exact solution to this problem as follows:

We solved this BVP using the parameters described in Subsection 7.1.

Our analysis revealed that the results strongly depend on the shape parameter. To make this clear, we present the analysis across three regions, defined by the $C$, and provide key takeaways for each region in terms of convergence, stability and accuracy. Parallel to these observations, we delve into the realm of computational efficiency, which is an oft-neglected, yet crucial aspect of numerical methods. Here, a salient finding is the CPLRBF method's pronounced efficiency from the third level onwards, where it consistently demanded nearly half the computation time of its standard RBF counterpart. This trend, as expected, also finds a reflection in the multilevel variants: the MuCPLRBF, in a race against time, invariably outpaces the MuRBF.

(1) Convergence, Stability and Accuracy

In the following, we show how the shape parameter, $C$, influences convergence, stability, and accuracy. We've categorised our analysis into three regions based on the value of $C$.

(a) Non-convergence region $C \leq c_0$:

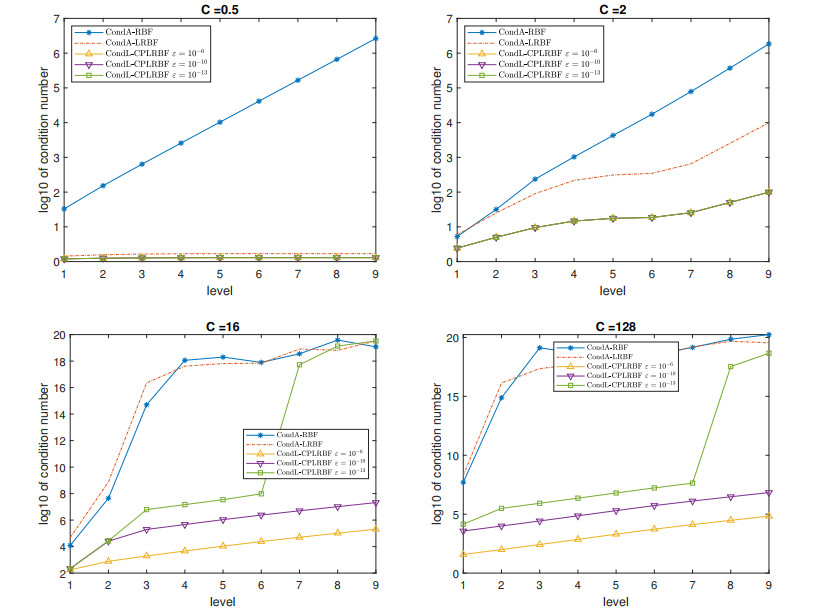
In this region, there is neither convergence nor accuracy, as observed in Figure 1. In our representative example, $c_o$ was equal to 1 (i.e., for $C \leq 1$ the methods were not able to deliver any meaningful solution). Although the condition number appears nearly ideal, as observed in Figure 2, this is primarily because the matrix converges to the identity matrix, which does not yield any meaningful insights into the PDE solution.

^IThe CPLRBF method is treated as the standard PLRBF method as soon as Cholesky is not possible, i.e., when the matrix for the PLRBF system shows numerical instability, the linear system is solved directly and not through a Cholesky decomposition, resulting in showing a higher condition number for the CPLRBF method as observed in Figure 2 in case $\varepsilon = 10^{-13}$ and for $C = 10$ & $C = 128$.

(b) Convergence region $c_0 < C < c_1$:

This region represents the optimal performance for the multilevel methods. As demonstrated in Figure 1, for $C = 2$ and Table 10, the multilevel method effectively overcomes stagnation issues, thereby achieving higher accuracy levels. As we have convergence in this region and the fact that all the multilevel methods achieve the same accuracy level, we observe that the choice of $\varepsilon$ does not significantly impact the accuracy and stability of the CPLRBF and the MuCPLRBF methods, as confirmed in Table 11.

In terms of convergence, our analysis and Tables 12 and 13 strongly suggest that the experimental order of convergence (EOC) for the multilevel methods is equal to the constant $C$ chosen to define the shape parameter at each level for both the maximum and the RMS norm. This finding highlights the relationship between the shape parameter and the convergence behaviour of the multilevel methods, further emphasizing the importance of selecting an appropriate constant $C$ to achieve optimal convergence rates, i.e., we assume that

To show this, we calculated the EOC for our presented multilevel methods as follows:

In terms of stability, the LRBF method displays stability behaviour similar to that of the standard RBF collocation method, with dependencies on both the shape parameter and the level. Perturbing the LRBF method slightly improves the stability, but dependencies still persist. In comparison, the CPLRBF method greatly surpasses the other methods in terms of stability and condition number. Our experiments reveal that the perturbed matrix is numerically stable, and the Cholesky decomposition's condition number supports our theoretical outcome of reducing the original condition number to its square root, as confirmed in Table 14.

(c) Partial convergence region $C > c_1$: Here, standard methods do not demonstrate convergence, accuracy, or stability. As observed in Figure 1 for $C = 16$ and $C = 128$, the errors for the standard methods either dramatically increase after a certain level or achieve a significantly lower accuracy level, as seen with the RBF method. Moreover, for $C = 16$ and $C = 128$, Figure 2 clearly shows that the condition number becomes excessively high after level 3, highlighting the ill-conditioning of the system. In contrast, as observed in Figure 2, our MuCPLRBF method maintains stability and achieves a good level of accuracy, as illustrated in Figure 1, albeit with some stagnation. In Table 15, we list the condition number for CPLRBF, respectively, noting the interesting fact that the condition number increases with the same factor as the $\varepsilon$ decreases. Overall, this suggests that the MuCPLRBF method can deliver stable and accurate solutions at an early level, significantly reducing the computational time when $\varepsilon$ is chosen carefully. Larger $\varepsilon$ values lead to more stable and more accurate solutions, provided that $\varepsilon$ remains sufficiently small (e.g., for $C > 16$, $\varepsilon = 10^{-6}$ delivers the most stable and accurate solution). It appears that the trade-off principle becomes more of a balance between the shape parameter and $\varepsilon$, that is, there is no stability issue for the perturbed methods, and the accuracy, even though not as strong as the standard methods, still depends on the shape parameter, $C$.

(2) Efficiency: Our detailed efficiency analysis shows that the CPLRBF method had a pronounced computational advantage over the standard RBF method, particularly from the third level onward. One of the primary reasons for this efficiency is the pre-calculation of the Lagrange functions outside of the main program once and for all, which greatly conserves computational time. As illustrated in Table 16, the CPLRBF method consistently operates in nearly half the time as the standard RBF. This same efficiency pattern was mirrored in their multilevel variants: MuCPLRBF consistently outperformed MuRBF, as confirmed in Table 17. As expected, this efficiency trend was observed to be consistent, regardless of the shape parameter choice, underscoring our proposed method's robustness. Such consistent time savings, when combined with the ability of the MuCPLRBF method to function optimally even at high $C$ values, underpins a significant advantage of our proposed method. It implies that the MuCPLRBF method can deliver high-level accuracy at a fraction of the computational time, making it a formidable solution for time-intensive problems. Additionally, this can be seen in Table 10, where the MuCPLRBF with $\varepsilon = 10^{-7}$ achieved the best possible accuracy for $C = 8$ and level = 7 at a record time (i.e., 25 times faster than the standard MuRBF for the same accuracy level).

Remark: In our study, we also looked at and analysed four other examples including: polynomial, exponential, log, and trigonometric functions. In all these cases, we established similar results to those detailed in the presented example, thus confirming the summary of our findings in the following section.

7.3.   Summary of our findings

Our investigation has explored various RBF-based methods and their respective properties, focusing on accuracy, stability, and convergence. Here, we summarize our key findings and the main advantages as well as limitations of our CPLRBF method:

(1) Enhanced Stability with Perturbation: The CPLRBF method significantly improves stability over the standard RBF and LRBF collocation methods, largely credited to the use of a perturbed Lagrange matrix and the implementation of Cholesky decomposition.

(2) Optimized Performance in the Convergence Region: Operating within the shape parameter range $c_0 < C < c_1$, the MuCPLRBF method showcases its superiority in terms of stability and condition number. It achieves an EOC that matches $C$, paralleling the accuracy of traditional methods, though with augmented efficiency.

(3) Efficiency from Early Stages: From level 3 onwards, the MuCPLRBF method stands out, not just in terms of matching the accuracy of standard RBF, but also in its computational swiftness, thereby requiring notably shorter durations to deliver an accurate solution.

(4) Reliability in High $C$ Values: With rising values of $C$, while many methods falter, the MuCPLRBF method remains steadfast, delivering solutions with consistent accuracy.

(5) Promising Scalability: While the current focus is on one-dimensional problems, the MuCPLRBF method is not just a solution for the present; it is a promising avenue for tackling higher-dimensional challenges in future research, retaining its advantages in stability and efficiency.

(6) Parameter Interplay Complexity: A deep understanding of the interplay between the shape parameter, $C$, and the perturbation parameter, $\varepsilon$, is still elusive. While our findings suggest a nuanced balance, a comprehensive understanding of their direct relationship might be a limitation of the current method and certainly serves as an exciting avenue for future research.

8.   Conclusions and remarks

In this paper, we have introduced novel numerical methods, the Lagrange collocation method with radial basis functions (LRBF) and the perturbed version (PLRBF) for solving 1D PDEs. We presented an in-depth analysis of various RBF-based methods, with a particular emphasis on the introduction of perturbation and multilevel techniques to address the challenges associated with the standard RBF collocation method. Our findings not only elucidate the properties of these methods, but also provide valuable insights for future research and applications.

We found that incorporating perturbation and developing the CPLRBF method significantly improves stability when applying the Cholesky decomposition compared to standard RBF and LRBF collocation methods. The choice of the perturbation parameter, $\varepsilon$, shape parameter, $C$, and level all play crucial roles in determining stability and convergence. However, a clear relationship between these parameters is still pending and presents one of the main limitations of our method.

Three distinct regions were identified based on the chosen shape parameter, $C$, each with different convergence, accuracy, and stability characteristics. Our numerical experiments in 1D confirmed our main findings and showcased the potential of our proposed methods, particularly the MuCPLRBF method, in delivering accurate solutions at an early level, thereby significantly reducing computational time.

In conclusion, our study highlights the importance of adopting perturbed (thus Cholesky) and multilevel techniques to address challenges in the standard RBF collocation method.

While this paper has focused on one-dimensional problems, we anticipate that our approach can be extended to higher dimensionalities, a topic we plan to explore in future work.

We would expect more challenges around choosing the perturbed parameter $\varepsilon$ and its dependency on the shape parameter $C$. Additionally, while we've emphasised the benefits of pre-calculating the Lagrange functions, the associated computational overhead, particularly for more extensive and complex systems in higher dimensions, is a limitation that warrants further investigation. The results presented in this paper open up new avenues for research and application of RBF-based methods in solving PDEs, offering improved stability and efficiency while maintaining high accuracy and convergence level.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors thank Ruslan Davidchack for proofreading the paper and for the insightful discussions and suggestions on presenting the numerical results.

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. GRANT4010].