Simulating systems of Itô SDEs with split-step $(\alpha, \beta)$-Milstein scheme

1.   Introduction

In this paper, we deal with the following Itô stochastic differential equations (SDEs)

Here $A, B_p:\mathbb{R}^d\times[t_0, T]\rightarrow \mathbb{R}^d$, are drift and diffusion functions, respectively. Also $\varpi_t^p$, $p = 1, \ldots, P$ is an one-dimensional Wiener process. This type of SDE (1.1) are widely applied for describing many real-life phenomena such as economics, epidemiology, chemistry, meteorology and etc, see ^{[1,2,3,4,5,6,7,8]}, for example. For many of them, there is no analytical closed-form solution, so numerical techniques and analysis will become important. For SDE (1.1), Milstein ^[9] proposed an explicit numerical scheme with strong convergence order $1.0$, namely

with

and

such that

where $t_l = t_0+l h$, $l = 0, 1, \ldots, N$, a time step $h = (T-t_0)/N$ with a fixed natural number $N$ and $\xi_p\sim\mathcal{N}(0, 1)$. Furthermore, drifting split-step backward Milstein (DSSBM) scheme is given by ^[10]

The drifting split-step Adams-Moulton Milstein scheme is another modification of the classical Milstein scheme, which was initialized in ^[11]. Recently, Jiang el al. ^[12] propose a new split two-step Milstein scheme as follow

for autonomous stochastic differential systems with one-dimensional Wiener process. Especially, they named method (1.4), Adams-Bashforth Milstein (ABM) scheme when $\beta_2 = 0$, $\beta_0 = -1/2$ and $\sigma = 1$. Furthermore, method (1.4) called Adams-Moulton Milstein (AMM) scheme if $\beta_2 = 5/12$, $\beta_0 = -1/2$ and $\sigma = 1/2$. Also, the family of drift-implicit Milstein schemes has been found in ^[13,14], which is adapted for stiff stochastic problems. Other families of numerical schemes were also studied, for instance ^{[15,16,17,18,19,20,21]}. We just mention some of them here and refer the readers to the references therein, among others.

One way to judge numerical schemes is to use the mean-square (MS-) stability properties. Saito and Mitsui ^[22] studied MS-stability properties of some numerical schemes for linear test equations, as well. Also, in ^[23] the same authors, analyzed the MS-stability of the Euler-Maruyama scheme for linear systems of SDEs. For more study of the MS-stability of various linear systems of SDEs applied to numerical schemes, the reader may refer to ^{[24,25,26,27]} and the references therein.

We emphasize that this paper is motivated by the Higham et al. ^[28], where proposed a new Milstein scheme and they investigated its efficiency in many financial models.

For SDE (1.1), the numerical scheme for the split-step $(\alpha, \beta)$-Milstein (SSABM) approximation is defined by

where $\alpha, \; \beta \in[0, 1]$. By taking $\alpha = \beta = 0$ in (1.5) Milstein method ^[9] is obtained. We gives the split-step theta-Milstein (SSTM) method ^[29], when $\alpha = \theta$, $\beta = 0$. Furthermore if $\alpha = 1$, $\beta = 0$, we obtain DSSBM scheme ^[10]. Obviously, deterministic equations (1.5a) and (1.5b) are implicit in $\overline{\mathscr{W}}_l$ and $\widehat{\mathscr{W}}_l$ when $\alpha, \; \beta \in (0, 1]$ must be solved to obtain the intermediate approximation $\overline{\mathscr{W}}_l$ and $\widehat{\mathscr{W}}_l$, respectively.

In this work the consider the strong convergence properties of the numerical scheme (1.5) in MS sense, we shall follow ^[30,31,32], where assumed that the drift and diffusion coefficients function of SDE (1.1) satisfies the following conditions.

Proposition 1.1. There exist constants $\ell_1 > 0$ and $\ell_2 > 0$ such that

-Lipschitz conditions:

-Linear growth bounds:

for all $s_1, s_2 \in \mathbb{R}^d$.

This paper is constructed as follows. We will devote to our main results about the MS convergence of the numerical scheme (1.5) in Section 2. And then, the MS-stability properties of the SSABM scheme (1.5) are established in Section 3. Section 4 contains examples. The conclusion is stated in Section 5.

2.   Mean-square convergence analysis

To recover the strong convergence order $1.0$ for the scheme (1.5), we need Proposition 1, following Lemma and the local mean error and mean-square error Milstein scheme (1.2):

respectively.

Lemma 2.1. ^[33] Assume for a one-step discrete time approximation $\mathscr{W}$ that the local mean error and mean-square error for all $N = 1, 2, \ldots,$ and $l = 0, 1, \ldots, N-1$ satisfy the estimates

and

when $\varkappa_2\geq \frac{1}{2}$ and $\varkappa_1\geq \varkappa_2+\frac{1}{2}$. Then

holds for each $r = 0, 1, \ldots, N$.

Theorem 2.1. Suppose Proposition 1 holds. Then the numerical scheme SSABM (1.5) strongly converges to SDE (1.1) in the MS sense with order $1.0$.

Proof. First, we compute the local mean error of our scheme in the following

where

Notice that for obtain of inequality (2.5), used global Lipschitz condition (1.6), $\textsf{E}\left[\mathcal{I}_{(p)}\right] = \textsf{E}\left[\mathcal{I}_{(p_1, p_2)}\right] = \; 0$. Also, applying (1.5a), (1.5b), Proposition 1 and

yields

where

and

From the above inequalities, we conclude that

and

Now for $\left(1-h\frac{\beta}{2}\sqrt{\ell_1}\right) \left(1-h\alpha\sqrt{\ell_1}\right) > 0$, we have from (2.4)–(2.8), $\varkappa_1 = h^2$. Similarly by standard arguments, we can prove

By $\textsf{E}\left[\mathcal{I}_{(p)}^2|F_t\right]\leq \mathcal{O}(h)$, $\textsf{E}\left[\mathcal{I}_{(p_1, p_2)}^2|F_t\right] \leq\mathcal{O}(h^2)$ [6,Lemma 5.7.2] and inequality

we can obtain

Using the (1.5a), (1.5b), Proposition 1 and inequality (2.10), we can gets:

where

and

From the above inequalities, we obtain

and

Combining (2.9)–(2.14), implies that for $\left(1-3P\frac{(\beta h)^2}{4}\ell_1\right) \left(1-(\alpha h)^2\ell_1\right) > 0$, $\varkappa_2 = \frac{3}{2}$. Thus, we can choose in Lemma 2.1 $\varkappa_1 = 2$, $\varkappa_2 = \frac{3}{2}$ and can prove that the strong order of SSABM scheme is 1.0.

3.   Linear mean-square stability

In this part of the paper, we consider the scalar linear SDE with a multi-dimensional Wiener process of form

where $\upsilon$, $\nu_p\in \mathbb{R}$, $W(0)\neq0\in \mathbb{R}$. We know that if the coefficient of test Eq (3.1) is satisfied

then the trivial solution is asymptotically MS-stable ^[7,22], i.e. $\lim\limits_{t\rightarrow \infty}\textsf{E}\left[|W(t)|^2\right] = 0$. If applied a SSABM scheme (1.5) to test Eq (3.1), obtained the difference equation

with MS-stability function

Theorem 3.1. For the test Eq (3.1) with a one-dimensional Wiener process ($P = 1$), the SSABM scheme (1.5) is MS-stable, if and only if $3/2\leq\alpha+\beta\leq2$.

Proof. The MS-stability function of SSABM scheme applied to the test Eq (3.1) with $P = 1$ reads

The stochastic difference Eq (3.3) with (3.5) is MS-stable if and only if $\textsf{E}\left[|\mathscr{D}\left(\upsilon, \nu, h\right)|^2\right] < 1$. So, we can write

where

After a little algebra, the condition (3.6) becomes

It is easy to deduce from (3.7) that $3-2\alpha\geq2\beta$. Also, we know $\alpha+\beta\leq 2$. Thus we complete the proof.

Theorem 3.2. For the test Eq (3.1) with commutative noises, SSABM scheme (1.5) is MS-stable, if and only if $3/2\leq\alpha+\beta\leq2$.

Proof. The commutativity condition on the diffusion coefficient of test Eq (3.1) reads as $\nu_{p_1}\nu_{p_2} = \nu_{p_2}\nu_{p_1}$ for all $p_1, p_2 = 1, 2, \ldots, P$ ^[6,25]. Together with the identity $\mathcal{I}_{(p_1, p_2)}+\mathcal{I}_{(p_2, p_1)} = \mathcal{I}_{p_1}\mathcal{I}_{p_2}$ the MS-stability function of SSABM scheme in (3.4) converts to

According Theorem 3.1, our scheme is MS-stable for test Eq (3.1) with with commutative noises if and only if

which, this is equivalent to

It can be easily seen that the above inequality holds if $3-2\alpha\geq2\beta$, which implies the desired assertions.

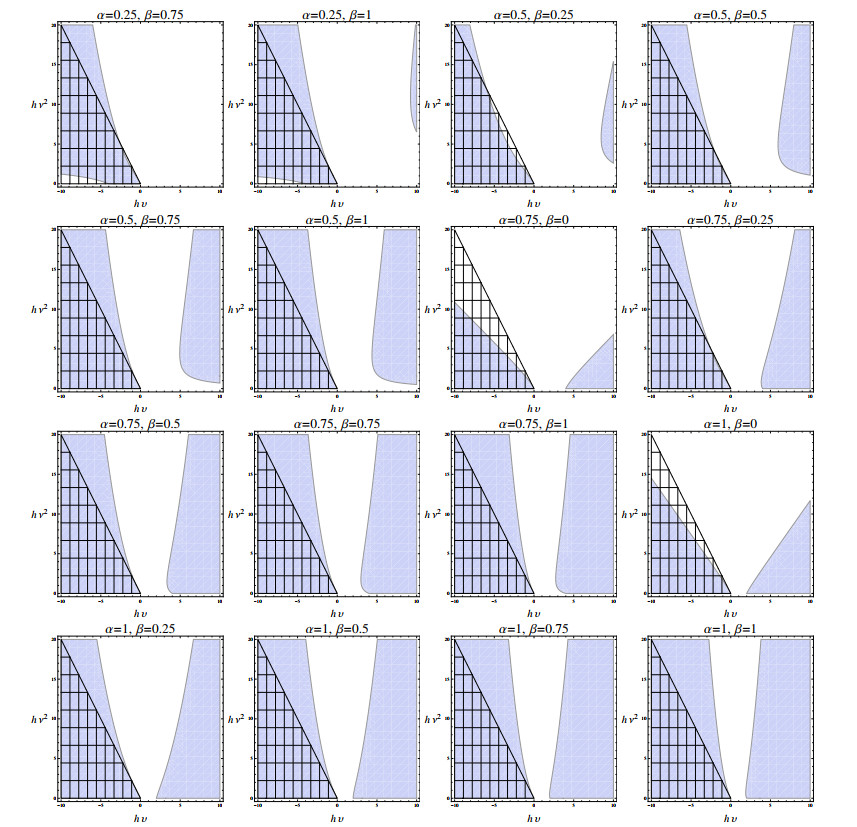
In Figure 1, the behavior of the MS-stability functions of our scheme (3.7) and test Eq (3.2) are compared when $P = 1$. Results of this figure show that the scheme is A-stable if $3/2\leq \alpha+\beta\leq 2$. Similarly, such results can be obtained for the state of commutative noises in Figure 2.

4.   Numerical results

In this section, we compare the convergence rate and the computational performance of our new scheme (1.5) with various $\alpha, \beta$, the Milstein and DSSBM (1.3) schemes. In this work, all the computations are performed by using a MATLAB platform.

Example 4.1. Consider the one-dimensional nonlinear SDE,

The exact solution is given by ^[6]

The means square errors (MSE) of the SSABM (1.5), Milstein, DSSBM (1.3) (SSTM with $\theta = 1$ ^[29]), ABM (1.4) and MMA (1.4) schemes can then be obtained in Figure 3. As shown in Figure 3, the SSABM scheme has better than other schemes for $a = b = 0.5$ and if it is $a = 1.0$ and $b = 0.25$ in (4.1), ABM (1.4) has better than other schemes.

Example 4.2. Consider the following stiff stochastic system ^[34]

By choosing $h = 0.01$, Figure 4 depicts the numerical simulations of the SSABM and Milstein schemes. These figures confirmed that the stability properties of the SSABM scheme are better than the Milstein scheme.

5.   Conclusions

This work has been devoted to the numerically solution to stochastic differential systems (1.1) by the new implicit Milstein scheme. Under given conditions, the strong convergence of the approach has been theoretically investigated and proved that the split-step $(\alpha, \beta)$-Milstein scheme has a convergence order of $1.0$ in MS sense. Furthermore, the MS-stability of the SSABM scheme has been discussed in this paper. For SDE (3.1) with a single noise term, we show that our scheme is mean-square A-stability for any value $3/2\leq \alpha+\beta\leq 2$. Also, this result satisfies for SDE (3.1) with multiplicative commutative noise terms. In the last part of this article, the presented scheme has superior efficiency and accuracy to the Milstein and DSSBM ^[10] schemes.

Conflict of interest

The authors declare no conflicts of interest.