Analysis for the hierarchical architecture of the heterogeneous FitzHugh-Nagumo network inducing synchronization

1.   Introduction

The phenomenon in which different oscillators (objects that show repetitive behavior over time) have rules in repetitive behavior is called synchronization. Similar to groups of fireflies that blink simultaneously or a number of pendulum clocks that sway in the same direction at the same time, the synchronization of various oscillators has been found in nature, in our daily lives ^[6], and in various fields such as neuroscience ^[16], biology ^[13,20], sociology ^[10], physics ^[1,33], chemistry ^[21,24], and computer science ^[36,42].

Because biological neural network synchronization plays an important role in the brain and central nervous system activity, there is extensive and ongoing research among a diverse group of fields, especially in neuroscience and medicine ^{[2,7,8,9,11,17,19,22,26,35,41,42,43]}.

Studies have shown that rapid synchronization can cause functional disturbances in the nervous system and cause pathological patterns such as epilepsy and Parkinson's disease; however, it can also improve the function and performance of the central nervous system. Therefore, research on the mechanisms of synchronization/asynchronization is a key topic in the field of neuroscience. This topic is a core topic not only in the fields of neuroscience and medicine, but also in the field of artificial neural networks. Research on this subject is very interesting, but it is difficult to understand the principle scientifically and mathematically. Therefore, it is important to study synchronization and asynchronous mechanisms in controllable situations through mathematical modeling and analysis.

As previously explained, synchronization is not a phenomenon caused by a single object, but rather a phenomenon caused by interactions between multiple objects. Therefore, the study of the synchronization phenomenon should also consider the interactions between objects. To understand and illustrate the relationship between objects, we formed a network topology using a graph that expresses objects as nodes and the interactions between objects as either links or arrows. The main difficulty in studying network systems is that the more objects and the more complex the relationships, the more complex the network. In particular, it is important to understand the synchronization phenomenon in a network structure because synchronization can occur differently depending on the network structure (i.e, connection relationship).

The brain and central nervous system are among the most complex networks. It is well-known that neurons are embedded in assemblies and networks that influence each other through excitatory and inhibitory synaptic connections. Therefore, they are activated and inhibited rhythmically. We note that this rhythmicity is reflected in oscillations of the extracellular field potential that can be measured through recordings of local field potentials and through electroencephalography (EEG) (for more details, see ^[14] and references therein). There are approximately 86 billion neurons in the human nervous system, which are connected by approximately $10^{14}$ synapses. To study the complex interactions of these large-scale neural networks, the neural network is divided into several neural groups, each of which can be represented as a form of the interactions between the neurons within it.

One of the most simplified models to represent the features of interacting neurons is the FitzHugh–Nagumo (FHN) network ^[15,27], which is described as the following system:

where $u$ and $v$ represent the state variables of a neuron, that is, the membrane potential (activator) and the recovery variable (inhibitor), respectively, and $\epsilon$, $a$, and $b$ are positive constants. The FHN network is a reduced form of the Hodgkin-Huxley equation. Both equations are models that suggest how neural stimuli are transmitted. Each nerve cell stays still and is excited/ignited by external stimuli; thereafter, it quickly returns to its original state, which has some recovery periods and cannot be ignited for some time. The FHN network models only the important characteristics of the neuron properties. After introducing the FHN network, this work was extended in various directions, such as FHN networks coupled with either gap-junctions or spaced clamped ^[19,38,40], mean field models for the FHN network ^[4,7,32], an FHN type coupled reaction-diffusion network on a continuous domain ^[3], a photosensitive memristive FHN network ^[28], and concentration phenomena in FHN network ^[5] (for more topics, see ^[18,29,33] and therein). There is also a lot of research on synchronizing other types of models for heterogeneous neural networks such as the synchronization under Dirichlet boundary conditions ^[23], and the event-triggered synchronization ^[25,44]. In addition, we can find many results for delay-type models such as adaptive control ^[39], pinning control ^[34], and intermittent control ^[37].

Among these studies, those of interest to us are ^[30] and ^[31]. In ^[31], Plotnikov et al. considered heterogeneous FHN networks with diffusive coupling and a greater number of neurons (nodes) as follows:

where $c_{ij}$ is the coupling strength between the $i$th and $j$th neuron for $i, j = 1, \ldots, n$. They presented analytic conditions of synchronization with precision levels (quasi-synchronization) for (1.3)-(1.4). They showed the importance of the coupling strengths for synchronization and presented two precision levels for $u_i$ and $v_i$, which depend on the parameter $a_i$, which is referred to as the natural frequency in this paper.

In ^[30], Plotnikov et al. studied synchronization in heterogeneous FHN networks with hierarchical architecture for the case where $b = 0$. According to ^[30], diffusion tensor magnetic resonance imaging (DT-MRI) studies have revealed the complexity of neuronal interconnections in human and mammalian brains. In particular, from analyzing DT-MRI, it has been shown that the connectivity of the neuron axon network is represented by a hierarchical architecture with fractal dimensions varying between 2.3 and 2.8, which is essential for the fast and optimal handling of information in the brain (for more details, see ^[30] and references therein). To study the synchronization of an FHN network with hierarchical architecture, they considered a leader system, in which all but one node are in complete synchrony (i.e. $u_i\equiv u_j$), and derived a sufficient condition for synchronization.

The purpose of this study is to prove the synchronization phenomenon of a heterogeneous FHN network with a hierarchical architecture through a mathematical analysis of Lyapunov functions and to prove that the Lyapunov function decreases exponentially until synchronization. We also propose conditions for a hierarchical architecture to induce synchronization. In particular, it is noteworthy that the neurons of the first layer (i.e., leaders) are (i.e., not in a synchronized state). Therefore, the results of this study provide a more accurate analysis of how synchronization between neurons spreads. Moreover, we show that the structural connectivity of neurons in the first layer is very important for synchronization, and that in the other layers is not significant.

The rest of this paper is organized as follows. In Section 2, we recall some definitions and properties of graph theory and present our main system, which is a heterogeneous FHN network with a hierarchical architecture that considers multiple leaders. In Section 3, we discuss the synchronization for the first layer. Section 4 presents results concerning the synchronization for the second layer, and Section 5 proves the main result of this paper. In Section 6, we provide a numerical experiment for the main results of this study. Finally, we discuss the conclusions in Section 7.

2.   Preliminaries

2.1.   Preliminaries from the graph theory

We recall some definitions and properties of graph theory used throughout this paper.

An (undirected) graph $\mathbb{G} = \mathbb{G}(V, E)$ consists of a set $V = \{p_i\}_{i = 1}^N$ of vertices and a collection $E$ of unordered pairs $\{p_i, p_j\}$ of vertices, called an edge. For notational convenience, we denote $p_i\in V$ by $i \in V$ (or $i \in \mathbb{G}$) and $\{p_i, p_j\}\in E$ by $\{i, j\} \in E$ or $i\sim j$. A simple graph is a graph without multiple edges and loops. A complete graph is a simple graph $\mathbb{G} = \mathbb{G}(V, E)$ satisfying $p_i \sim p_j$ for all $i, j = 1, \cdots, N$, $(i \not = j)$. A graph $\mathbb{H} = \mathbb{H} (V', E')$ is said to be a subgraph of $\mathbb{G} = \mathbb G (V, E)$ if $V'$ and $E'$ are subsets of $V$ and $E$, respectively. A (vertex) induced subgraph consists of some of the vertices of the original graph and all the edges that connect them in the original graph.

A digraph (or directed graph) is a graph in which the edges have orientations. In this case, we call the oriented edges a directed edge (or arc). For an induced subgraph $\mathbb{H} = \mathbb{H}(V', E')$ of a graph $\mathbb{G} = \mathbb{G}(V, E)$, the boundary $\partial \mathbb{H}$ of $\mathbb{H}$ is the set of all vertices satisfying $q\in V \setminus V'$, and there exists $p\in V'$ such that $p\sim q$; that is,

Hence an induced subgraph $\mathbb{H}$ of a graph $\mathbb{G}$ with a boundary can be expressed as a directed graph whose vertex set is $\mathbb{H} \cup \partial \mathbb{H}$, and the edge set $E$ satisfies $\{p, q\}\not \in E$ for all $p \in \mathbb{H}$; $q \in \partial \mathbb{H}$. $\overline{\mathbb{H}}$, denotes an induced subgraph of $\mathbb{G}$, whose vertices and edges are in $\mathbb{H}$ and vertices in $\partial \mathbb{H}$.

A path $P = \{ p_0, p_1, \cdots, p_n \}$ between two vertices, $p_0$ and $p_n$, is a sequence of distinct vertices satisfying $p_0 \sim p_{1} \sim p_2 \sim \cdots \sim p_{n}$. A cycle is a path between a vertex and itself. A path between two vertices may or may not exist, according to the given graph. Hence, if there exists a path for all pairs of vertices, then we consider the graph $\mathbb{G} = \mathbb{G}(V, E)$ to be connected. In particular, a component of an undirected graph is an induced subgraph in which any two nodes are connected to each other by paths, and it is connected to no additional vertices in the rest of the graph.

A weighted graph $\mathbb{G} = \mathbb{G}(V, E, \omega)$ is a graph associated with a (coupling) weight function $\omega: V \times V \to [0, \infty)$ satisfying

In particular, if a weight function $\omega$ satisfies $\omega_{ij} = 1$ for $i\not = j = 1, \ldots, N$, then we call it the standard weight. We note that if $\omega_{ij} = \omega_{ji}$ for all $i$, $j$, then the weighted graph is an undirected graph with weight; otherwise, the weighted graph is a directed graph with weight.

Throughout this paper, all the subgraphs are assumed to be vertex-induced and connected subgraphs of a weighted graph.

For a weighted subgraph $\mathbb{H}$ of a weighted graph $\mathbb{G}$, the graph Laplacian $\mathcal L$ of functions $u_i : \mathbb{R} \to \mathbb{R}$, $i\in \overline{\mathbb{H}}$ is defined by

It is well-known that there exists a real value $\lambda$ and a non-zero vector $\phi: = (\phi_1, \ldots, \phi_{|\overline{\mathbb{H}}|})$ satisfying the eigenvalue problem for $\mathbb{H}$, that is,

where $|A|$ is the cardinal number of a set $A$. In the case where $\partial \mathbb{H} = \emptyset$, we call $\lambda$ and $\phi$ an eigenvalue and eigenvector corresponding to $\lambda$, respectively. If $\partial \mathbb{H} \not = \emptyset$, we call these the Dirichlet eigenvalues and Dirichlet eigenvector. Because $\omega_{ij}$ is symmetric, if $|\mathbb{H}| = N$, then there are $N$ eigenvalues $\lambda_i\in \mathbb{R}$, $i = 1, \ldots, N$ such that $0\leq \lambda_1 \leq \lambda_2\leq \ldots \lambda_N$. Moreover, for a vertex-induced subgraph $\mathbb{H}$, if $\partial \mathbb{H} = \emptyset$, then $0 = \lambda_1 < \lambda_2\leq \ldots \leq \lambda_N$, and if $\partial \mathbb{H} \not = \emptyset$, then $0 < \lambda_1 \leq \lambda_2\leq \ldots \lambda_N$. In particular, it is well known that the first (Dirichlet) eigenvalue can be represented as the following Rayleigh quotient forms:

and

In general, $\lambda_2$ is called the first eigenvalue, and $\lambda_1$ is called the first Dirichlet eigenvalue. In this paper, for the sake of consistency, we denote the first (Dirichlet) eigenvalue for a subgraph $\mathbb{H}$ as $\lambda_{\omega, 1}^\mathbb{H}$ without boundary (with boundary). For more details, see ^[12].

2.2.   Fitzhugh-Nagumo model with hierarchical architecture

In this subsection, we introduce the concept of an FHN network with a hierarchical architecture.

A hierarchical architecture comprises multiple layers of components that reflect the relationships of neurons within each layer and the relationships between the layers. In this paper, we assume the following:

${\bf{(H1)}}$ two neurons inside each layer either interact with the same intensity (coupling strength) or do not interact at all, and

${\bf{(H2)}}$ the relationship between the layers is unilaterally influenced by the upper layer to the lower layer.

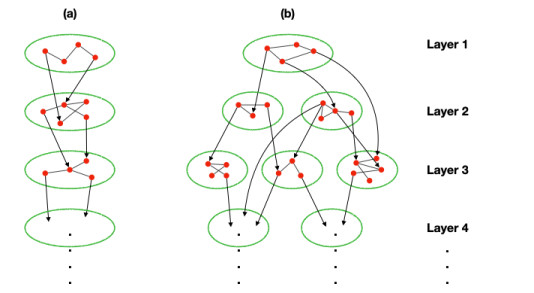
This assumption reflects the hierarchical property of neurons. This hierarchical architecture can be expressed by an undirected graph. First, neurons and their interactions in the $k$-th layer are represented by nodes and edges. In particular, according to hypothesis (H1), each layer is represented by an undirected graph that may or may not be complete. It follows from hypothesis (H2) that the upper layer has no incoming directed edge from the lower layer, whereas the lower layer must have an incoming directed edge from the upper layer. Two examples of this structure are given in Figure 1. Figure 1 (a) is a simple hierarchical architecture in which we assume that the undirected graph for each layer is connected, and the $k$-th layer only affects the $(k+1)$-th layer. Figure 1 (b) shows a typical hierarchical architecture. An important difference between these two examples is the presence or absence of connectivity within each layer, except for the first layer, and the influence from the upper layer to the lower layer is not sequential.

In this paper, the hierarchical architecture that we deal with is a general hierarchical architecture as shown in Figure 1 (b). First, we study a simple type, as shown in Figure 1 (a). Based on the results, we discuss the general type in Figure 1 (b).

For the simple type, we consider a total of $m$ layers for neurons. In this case, because the first layer is not affected by any other layer, the FHN network for the first layer is described as follows:

for $i \in \mathbb{H}_1$, where $\mathbb{H}_1$ is an undirected graph for the first layer, and $f$ is a real-valued function on $\mathbb{R}$ satisfying $f' \geq \alpha$ for some $\alpha\geq0$. We note that $\mathbb{H}_1$ is connected, and thus the first eigenvalue $\lambda_{\omega, 1}^{\mathbb{H}_1} > 0$. In fact, this model is a simple generalization of the term $u_i^3/3$ in a typical FHN network (1.3)-(1.4) to the nonlinear term $f(u_i)$, and we will discuss the synchronization of this model in the next section.

In the case of the second layer— because the second layer is affected by the first layer, while the layers after the 3rd layer do not affect the second layer— the model (2.3)-(2.4) for the first layer becomes the Robin-type boundary condition for the second layer. Hence, the FHN network for the second layer is modeled by the following:

for $i\in \mathbb{H}_2$ subject to (2.3)-(2.4) as the Robin-type boundary condition. Using a similar argument, we model the dynamics of the third layer as follows:

for $i\in \mathbb{H}_3$ subject to (2.5)-(2.6) as the Robin-type boundary condition. In the first equation, the range of the summation is $\mathbb{H}_2 \cup \mathbb{H}_3$ (i.e., $\mathbb{H}_1$ is not included). Moreover, although the third layer appears to be independent of the first layer, it can be seen that the first layer indirectly affects the third layer, as the second layer is actually affected by the first layer.

After the third layer, the dynamics of each layer are expressed by the same type of system as the third layer, as follows:

for $i\in \mathbb{H}_k$, subject to the Robin-type boundary condition:

for $i \in \mathbb{H}_{k-1}$, $k = 4, 5, \ldots, m$.

We now discuss the model for the general type of hierarchical architecture. Let $\mathbb{H}_{k, l}$ be the $l$-th component in the $k$-th layer and $\partial \mathbb{H}_{k, l}$ be the boundary of $\mathbb{H}_{k, l}$. Since the 1st layer is connected and has no boundary, the number of components in the 1st layer is one (simply denoted by $\mathbb{H}_{1, 1} = \mathbb{H}_1$), and $\partial \mathbb{H}_1 = \emptyset$. For $k\geq 2$, the boundary $\partial \mathbb{H}_{k, l}$ can consist of several components $(\partial \mathbb{H}_{k, l})_m$, which are not empty. Since a component $(\partial \mathbb{H}_{k, l})_m$ is the largest induced subgraph in the $i$-th layer for some $i < k$, if the component $(\partial \mathbb{H}_{k, l})_m$ satisfies $\partial((\partial \mathbb{H}_{k, l})_m) = \emptyset$, then $(\partial \mathbb{H}_{k, l})_m = \mathbb{H}_1$; otherwise, $k\geq 3$, and the component $(\partial \mathbb{H}_{k, l})_m$ is a component in the $i$-th layer, $1 < i < k$. Therefore, the heterogeneous FHN network with a general hierarchical architecture is described as follows:

for $i\in \mathbb{H}_{k, l}$, subject to the Robin-type boundary condition:

for $i \in\partial \mathbb{H}_{k, l}$, where $\partial (\partial \mathbb{H}_{k, l})$ is the boundary of $\partial \mathbb{H}_{k, l}$. In particular, for the above system, we additionally assume that $\partial \mathbb{H}_{1} = \emptyset$, $\partial (\partial \mathbb{H}_{1}) = \emptyset$, $\partial \mathbb{H}_{2, l} = \mathbb{H}_{1}$, and $\partial (\partial \mathbb{H}_{2, l}) = \emptyset$ for $l\geq1$, and $\partial \mathbb{H}_{k, l} \not = \emptyset$ for $k\geq 3$, and $l\geq 1$. Then, the above system expresses the dynamics of each component $\mathbb{H}_{k, l}$ for all $k\geq 1$ and $l\geq1$. We note that in the case where $k\geq3$, it is possible that the boundary $\partial \mathbb{H}_{k, l}$ of $\mathbb{H}_{k, l}$ can consist of several components. Thus, $\partial \mathbb{H}_{k, l}$ is generally not connected. Moreover, the boundary between the two different boundaries of $\mathbb{H}_{k, l}$ may include the same component. In particular, because the first layer $\mathbb{H}_1$ is connected, the first eigenvalue $\lambda_{\omega, 1}^{\mathbb{H}_1}$ is strictly positive, and because $\mathbb{H}_{k, l}$ is connected, and $\partial \mathbb{H}_{k, l}\not = \emptyset$ for $k\geq2$, $l\geq 1$, the first Dirichlet eigenvalue $\lambda_{\omega, 1}^{\mathbb{H}_{k, l}}$ is also strictly positive.

Finally, because of the natural frequency $a_i$ (i.e., heterogeneities), the complete synchronization for the system is not possible except when $a_i \equiv 0$. Therefore, in this study, we will discuss the synchronization with precision levels (quasi-synchronization), which is defined as follows.

Definition 2.1 ([31, Definition 2]). Let us consider the following $n$ coupled nonlinear systems :

where ${\bf x}_i = (x_{i1}, \ldots, x_{id}) \in \mathbb{R}^d$ and $F_i$ are vector-valued functions, $i = 1, 2, \cdots, n$. Then, the $n$ coupled nonlinear systems are synchronized with the precision levels $\Delta_1, \Delta_2, \cdots, \Delta_n$ if there exists $t^* > 0$ such that $|{{\bf x}_{ij}(t) - \bar{\bf x}_j(t)} |\leq \Delta_j$, $i = 1, 2, \cdots, n$, $j = 1, 2, \cdots, d$, $t \geq t^*$, where $\bar{{\bf x}}_j : = 1/n \sum_{i = 1}^n x_{ij}(t)$ for $j = 1, 2, \cdots, d$.

3.   Synchronization of Fitzhugh-Nagumo network without boundary

We begin this section with the heterogeneous FHN network without a boundary (i.e., the model for the first layer $\mathbb{H}_1$):

where $c > 0$, and $i \in \mathbb{H}_1$. For the system (3.1)-(3.2), we show the synchronization with precision levels and present the precision levels.

Theorem 3.1. Suppose that there exist $\sigma > 0$ and $\alpha\geq0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j = 1, 2, \cdots, n$ and $f'(s) \geq \alpha$ for all $s\in \mathbb{R}$. If $c$ is sufficiently large to $c\lambda_{\omega, 1}^{\mathbb{H}_1} + \alpha - 1 > 0$, then the FHN network (3.1)-(3.2) synchronizes with precision levels. Moreover, the Lyapunov function $E(t): = \frac{1}{2}\sum_{i\in\mathbb{H}_1} \left( {{\epsilon \hat{u}_i^2 (t) + \hat{v}_i^2 (t)}} \right)$, $t \geq 0$, satisfies

for $t \geq 0$, where $\eta$ is a constant in $(0, 1)$ satisfying $\eta \leq \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1} + \alpha - 1}} \right)$, and $A_\eta : = |\mathbb{H}_1|\sigma^2 /\left( {{4b\left( {1-\eta} \right)}} \right)$.

Proof. First, we consider the fluctuations $\hat{u}_i$, $\hat{v}_i$, and $\hat{a}_i$ defined by $\hat{u}_i = u_i - \bar{u}$, $\hat{v}_i = v_i - \bar{v}$, and $\hat{a}_i = a_i - \bar{a}$, where $\bar{u}$, $\bar{v}$, and $\bar{a}$ are the averages of $u_i$, $v_i$, and $a_i$, respectively. (i.e., $\bar{u} : = \frac{1}{n}\sum_{i = 1}^n u_i$, $\bar{v} : = \frac{1}{n}\sum_{i = 1}^n v_i$, and $\bar{a} : = \frac{1}{n}\sum_{i = 1}^n a_i$). Subsequently, upon differentiating $\hat{u}_i$ and $\hat{v}_i$ with respect to $t$, we find that

for $i = 1, \ldots, n$. The Lyapunov function for the above systems is given by

Differentiating with respect to $t$, we deduce

Since $\sum_{i} \hat{u}_i = 0$, by $\omega_{ij} = \omega_{ji}$ and (2.1), we have

Note that since we assume that $^{\mathbb{H}_1}$ is a connected and undirected graph without a boundary, the first eigenvalue $\lambda_{\omega, 1}^{\mathbb{H}_1}$ is strictly positive. Now, we discuss an estimate of the third term in (3.4). Applying the mean-value theorem, for $i, j = 1, \ldots, n$, there exists $\xi_{ij}$ such that

Since $f^\prime (s) \geq \alpha$ and $\sum_i \hat{u}_i = 0$, we obtain

Hence, the Lyapunov function $E$ satisfies

where $\lambda_\eta = 2 \min \left\{ {{\frac{1}{\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_1} + \alpha - 1}} \right), b\eta}} \right\}$. $A_\eta = |\mathbb{H}_1| \sigma^2 /\left( {{4b\left( {1-\eta} \right)}} \right)$, and we employed Cauchy's inequality with $\eta \in (0, 1)$. Since $\eta$ is arbitrarily chosen in $(0, 1)$, and $c\lambda_{\omega, 1} + \alpha - 1 > 0$, taking $\eta$ satisfying $\eta \leq \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1} + \alpha - 1}} \right)$, we have $\lambda_\eta = b\eta$. Thus, by the Grönwall inequality, we obtain

for $t \geq 0$. Therefore, there exist $t^* > 0$ and $\Delta > 0$ such that $E(t) \leq \Delta$ for $t > t^*$. This implies that $|{u_i - \bar{u}}| \leq \Delta$ and $|{v_i - \bar{v}}| \leq \Delta$ for $i = 1, 2, \cdots, n$. Hence, we have the desired result. □

Remark 3.2. (ⅰ) From (3.6), we can see that the synchronization proceeds exponentially. In particular, in the case where $a_i \equiv 0$, complete synchronization occurs exponentially, (i.e., $u_i - u_j \to 0$ and $v_i - v_j \to 0$ as $t\to \infty$ for all $i$ and $j$).

(ⅱ) Since $\exp{(- 2b \eta t)}\to 0$ as $t \to \infty$, and $| a_i - a_j|\leq \sigma$, the precision level $\Delta$ is asymptotically equal to $\frac{A_\eta}{2b\eta}$ and satisfies

(ⅲ) Since $\eta\in(0, 1)$ is an arbitrary real value satisfying $\eta \leq \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_1} + \alpha - 1}} \right)$, we obtain the minimum of $\frac{A_\eta}{2 b\eta}$ as setting $\eta = \min\{ \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_1} + \alpha - 1}} \right), \frac{1}{2} \} > 0$. Hence, it is clear that the connectivity of the first layer is the crucial condition that induces synchronization. If the first layer is not connected, then it is trivial that no synchronization is induced. Hence, the connectivity is an equivalent condition for synchronization.

(ⅳ) In ^[31], the authors discussed the case where $f(s) = s^3 /3$ and presented two precision levels

as $t\to \infty$. Therefore, from the precision level in (ⅱ), the decay rate of $\Delta$ is better than that of $\Delta_1$.

4.   Synchronization of Fitzhugh-Nagumo network with the Robin-type boundary

In this section, for the simple type of hierarchical architecture introduced in Section 2.2, we consider two kinds of boundary value problems. The first is a case where synchronization has already occurred at the boundary, and the second is a case where synchronization has not occurred. The first case can be represented by a heterogeneous FHN network with Robin-type boundary conditions:

for $i\in \mathbb{H}_2$, which is an index of interior vertices and

for $i\in \mathbb{H}_1$, which is an index of boundary vertices.

We note that this system represents a situation where $u_j$ and $v_j$, $j\in \mathbb{H}_1$, are neurons in the first layer, and $u_i$ and $v_i$, $i\in \mathbb{H}_2$, are neurons in the second layer and are affected by the neurons in the first layer. In particular, we do not consider the Laplacian graph on the boundary because the neurons in the first layer are already synchronized with either a zero precision level or the number of neurons is 1, (i.e., $|\mathbb{H}_1| = 1$). Therefore, we assume that the fluctuations of $u_j$ and $v_j$ on the boundary are bounded, that is, there exists $\sigma_B > 0$ such that $|{u}_j - \bar{u}^B| < \sigma_B$ and $|{v}_j - \bar{v}^B| < \sigma_B$, $j \in \mathbb{H}_1$, where $\bar{u}^{B} : = \frac{1}{|\mathbb{H}_1|}\sum_{i\in \mathbb{H}_1} u_i$ and $\bar{v}^{B} : = \frac{1}{|\mathbb{H}_1|}\sum_{i\in\mathbb{H}_1} v_i$. Henceforth, we consider $m: = |\mathbb{H}_1|$ and $n : = |\mathbb{H}_2|$.

In fact, the case where $b = 0$ and all but one node are in synchrony has already been discussed in ^[30], and Plotnikov et al. proved that the system synchronizes with a precision level $\Delta$ and showed that $\Delta = O(\sigma)$ when $c > 1/d_{\min}$, where $d_{min}$ is the minimal degree of the network.

As the main takeaway from this section, we introduce the Lyapunov function, which is slightly different from ^[30], and present the precision level through mathematical analysis. In particular, we prove the following lemma, which is very useful for dealing with the Lyapunov function:

Lemma 4.1. For a real-valued function $u_i : [0, \infty) \to \mathbb{R}$, $i\in \mathbb{H}_1\cup \mathbb{H}_2$, we have

where $\lambda_{\omega, 1}^B$ is the first Dirichlet eigenvalue.

Proof. First, we have

The first term on the right-hand side of (4.5) satisfies

Hence, (4.5) and (4.6) imply

Since

applying (4.7) to (4.8), we find

Let us swap the indices $i$ and $j$ in the third term on the right-hand side of the inequality above and apply the same method used in deriving the first equality in (4.6). Then,

After some elementary calculations, we obtain

Therefore, if we define a function ${u}_i^0$ as

then

Finally, using the Rayleigh quotient (2.2) of the first Dirichlet eigenvalue $\lambda_{\omega, 1}^B$, we have the desired result that

□

We now show that the system (4.1)–(4.4) synchronizes with precision levels.

Theorem 4.2. Suppose that there exists $\sigma > 0$ and $\alpha\geq0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j \in\mathbb{H}_1\cup \mathbb{H}_2$ and $f'(s) \geq \alpha$ for all $s\in \mathbb{R}$. If $c > 0$ and $\delta > 0$ satisfy $c\lambda^{\mathbb{H}_2}_{\omega, 1} +\alpha - 1 -\delta > 0$, where $\lambda^{\mathbb{H}_2}_{\omega, 1}$ is the first Dirichlet eigenvalue, then the FHN network with Robin-type boundary synchronizes with precision levels. Moreover, there exist $K^B > 0$ and $\sigma_B > 0$ such that the functional $E(t): = \frac{1}{2}\sum_{i\in\mathbb{H}_2} \left( {{\epsilon \hat{u}_i^2 (t) + \hat{v}_i^2 (t) }} \right)$, $t\geq 0$, satisfies

for $t \geq 0$, where $\eta$ is a constant in $(0, 1)$ satisfying $\eta \leq \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_2} + \alpha - 1 - \delta}} \right)$, and $A_\eta^{B} : = \frac{|\mathbb{H}_2| \sigma^2}{4b\left( {1-\eta} \right)} + \frac{nm {K^B}}{4\delta} \sigma_B^2$.

Proof. Let us define fluctuations $\hat{u}_i = u_i - \bar{u}^{B}$, $\hat{v}_i = v_i - \bar{v}^{B}$, and $\hat{a}_i = a_i - \bar{a}^{B}$ for $i\in \mathbb{H}_1\cup \mathbb{H}_2$, where $\bar{u}^{B}$, $\bar{v}^{B}$, and $\bar{a}^{B}$ are the averages of $u_i$, $v_i$, and $a_i$ on the boundary, respectively; that is,

Then, by calculations similar to those used to establish (4.1)-(4.2), we establish that

and

for $i \in\mathbb{H}_2$. The FHN network with a Robin-type boundary admits the following Lyapunov functional $E$, which can be viewed as energy functionals:

Differentiating it with respect to $t$, we deduce that

Since $\hat{u}_j$ is bounded for $j \in\mathbb{H}_1$, there exists $\sigma_B > 0$ such that $|\hat{u}_j|\leq \sigma_B$ for $j \in\mathbb{H}_1$. Then, a direct calculation (the details of which we omit) shows that

where $C_\omega : = \left(m \max_{j \in\mathbb{H}_1} (\sum_{i\in\mathbb{H}_2} \omega_{ij}) + \frac{m^2}{2} \max_{i\in\mathbb{H}_2 \atop j \in\mathbb{H}_1}\omega_{ij} \right)$. Hence, for the second term in (4.10), Lemma 4.1 and (4.11) imply that

For the third term, by the mean-value theorem and the assumption $f'\geq \alpha$, there exists $\xi_{i}^{B}$, $i\in\mathbb{H}_2$, and $\zeta_j^B$, $j\in\mathbb{H}_1$ such that

We note that because $\zeta_j^B$ is between $\bar{u}^B$ and $u_j$ for $j \in\mathbb{H}_1$, it is clear that $|\zeta_j^B| \leq |\bar{u}^B| + |u_{j}| \leq 2\sigma_B$ for $j \in\mathbb{H}_1$. Since $f$ is differentiable, there exists $K^B \geq 0$ such that $f'(\zeta_j^B) \leq K^B$. Therefore, by applying Cauchy's inequality with $\delta$, we obtain

Hence, for $\eta \in (0, 1)$, we obtain

in the same way that we obtained (3.5), where $\lambda_\eta^{B} = 2\min \left\{ {{\frac{1}{\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_2}+\alpha -1-\delta}} \right), \eta b}} \right\}$, and $A_\eta^{B} = \frac{|\mathbb{H}_2| \sigma^2}{4b\left( {1-\eta} \right)} + \frac{nm {K^B}}{4\delta} \sigma_B^2$. Since $\eta$ is arbitrarily chosen in $(0, 1)$ and $c\lambda_{\omega, 1}^{\mathbb{H}_2} + \alpha - 1 - \delta > 0$, we obtain the desired result by the same argument as in the proof of Theorem 3.1. □

Remark 4.3. In ^[30], Plotnikov et al. addressed the case that $b = 0$, $f(s) = s^3/ 3$, and a network in which all but one node are in synchrony for the model (4.1)-(4.4); they obtained the inequality $c > 1/d_i$ as a sufficient condition, where $d_i$ is the degree of the $i$-th neuron whose general definition is $d_i: = \sum_{k \in \mathbb{H}_1\cup \mathbb{H}_2} \omega_{ik}$, $i \in \mathbb{H}_1\cup \mathbb{H}_2$. We note that since they considered a standard weighted graph, in this case, $d_i$ denotes the number of adjacent nodes. Additionally, they showed that the $i$-th neuron synchronizes with the other nodes with a precision level equal to $2\sigma$. More precisely, $t_0 > 0$ such that $|u_i - \bar{u}^B| \leq \Delta_1 = O(\sigma)$, and $|{v_i - \bar{v}^B}| \leq \Delta_2 = O(\sigma)$ holds: for $t > t_0$.

Theorem 4.2 leads to similar results to that obtained in ^[30]. First, it is clear that the precision level presented in Theorem 4.2 is given by

Moreover, since all nodes in the first layer synchronize with the precision level by Theorem 3.1, we also have $\sigma_B = O(\sigma)$. Therefore, in the case where $\sigma = 0$, complete synchronization is achieved. In particular, if all the neurons in $\mathbb{H}_1$ are completely synchronized, that is, $\hat{u}_{i} = 0$, $i \in \mathbb{H}_1$, then $\sigma_B = 0$, which implies $\Delta = O(\sigma)$. Thus, in this case, we can see that Theorem 4.2 and the result in ^[30] present the same decay rate for the precision level. Second, a similar condition to ^[30] has been proposed in Theorem 4.2, which is $c\lambda_{\omega, 1}^{\mathbb{H}_2}+\alpha -1-\delta > 0$. We note that the first Dirichlet eigenvalue $\lambda_{\omega, 1}^{\mathbb{H}_2}$ is also related to the degree. By a proof similar to that provided for Lemma 1.9 in ^[12], it is easy to see that the first (Dirichlet) eigenvalue satisfies

where $D$ is the diameter of $\mathbb{H}_2$. In particular, if we assume that each node in $\mathbb{H}_2$ is connected to at least one boundary node in $\mathbb{H}_1$, as the generalization of the network condition in ^[30], then it follows from the Rayleigh quotient (2.2) that

where $\phi$ is the eigenvector corresponding to $\lambda_{\omega, 1}^{\mathbb{H}_2}$. Hence, we can see that the network structure affects synchronization. Moreover, by increasing the number of boundary nodes, we can derive that the system (4.1)–(4.4) synchronizes with precision levels. It is natural that adding more boundary nodes with the same tendency induces synchronization, even if the attractive force (i.e., the coupling strength $c$) between the interior nodes is weak. Theorem 4.2 explains this phenomenon.

We also note that in ^[30], they did not lead to a mathematical analysis when more than one node was not synchronized with the rest of the network. By contrast, Theorem 4.2 provides a mathematical analysis of the occurrence of synchronization in that case.

Now, we consider the second case where the neurons in the first layer are not synchronized and affect neurons in the second layer. This situation is modeled as a heterogeneous FHN network with the Robin-type boundary:

for $i\in\mathbb{H}_2$, which is an index of interior vertices and

for $i\in\mathbb{H}_1$, which is an index of boundary vertices.

We can show that this system synchronizes with precision levels by the same arguments used in the proof of Theorem 4.2. More specifically, for the same fluctuations $\hat{u}_i$, $\hat{v}_i$, and $\hat{a}_i$ as in Theorem 4.2, we have

and $\dot{\hat{v}}_i = \hat{u}_i - b \hat{v}_i + \hat{a}_i$. In particular, since $\sum_{j\in\mathbb{H}_1} \sum_{k\in\mathbb{H}_1} \omega_{kj} \left( {{u_k - u_j}} \right) = 0$, we obtain

which is the same as (4.11). Hence, by the same arguments with the proof of Theorem 4.2, we obtain the following result.

Theorem 4.4. Suppose $\sigma > 0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j \in \mathbb{H}_1\cup \mathbb{H}_2$ and $f' \geq \alpha \geq 0$ in $\mathbb{R}$. If $c$ and $\delta$ are sufficiently large to $c\lambda^{\mathbb{H}_2}_{\omega, 1} +\alpha- 1 - \delta > 0$, where $\lambda^{\mathbb{H}_2}_{\omega, 1}$ is the first Dirichlet eigenvalue, then the FHN network (4.14)-(4.15) with the Robin-type boundary condition (4.16)-(4.17) synchronizes with the precision levels.

5.   The heterogeneous FHN network with hierarchical architecture

In this section, we discuss the main problem addressed in this study (i.e., the heterogeneous FHN network with hierarchical architecture) when applying Theorem 3.1 and Theorem 4.4. First, we address the simple hierarchical architecture with $n$ layers introduced in Section 2.2. Subsequently, we discuss the general hierarchical architecture.

Since the first layer is not dependent on the other layers, the heterogeneous FHN network is modeled by (3.1)-(3.2) in Section 3. Hence, by Theorem 3.1, the system synchronizes with the precision levels. For the second layer, because the neurons in the second layer are only affected by the neurons in the first layer, we can consider it as the boundary value system (4.14)-(4.17). Therefore, from Theorem 4.4, we can see that the second layer also synchronizes with the precision levels. In particular, in the case where $a_i\equiv 0$, since it follows from Theorem 3.1 that $\hat{u}_i \to 0$ and $\hat{v_i} \to 0$ for $i \in \mathbb{H}_1$, we have $u_i \to (1/n_1)\sum_{i\in \mathbb{H}_1} u_i$ and $v_i \to (1/n_1)\sum_{i \in \mathbb{H}_1} v_i$ for $i \in I_2$ by Theorem 4.4, where $n_k : = |\mathbb{H}_k|$, $k = 1, 2, 3, \ldots$, that is, $u_i$ and $v_i$ in the second layer converge to the average of $u_i$ and $v_i$ in the first layer, respectively.

We now discuss the system for the third layer in the case of the simple hierarchical architecture introduced in Section 2.2:

for $i \in \mathbb{H}_3$, subject to the Robin-type boundary condition

for $i \in \mathbb{H}_2$. Hence, from the results in Section 4, if we assume, without loss of generality, that the solutions $u_i$ and $v_i$ on the first and second layers are bounded, then we have the following result for the third layer.

Theorem 5.1. Suppose that there exists $\sigma > 0$ and $\alpha\geq0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j \in\mathbb{H}_2 \cup \mathbb{H}_3$ and $f'(s) \geq \alpha$ for all $s\in \mathbb{R}$. If $c$ and $\delta$ satisfy $c\lambda^{\mathbb{H}_3}_{\omega, 1} + \alpha - 1 -\delta > 0$, then the FHN network with three-hierarchical architectures synchronizes with the precision level. Moreover, there exist $C > 0$ and $\sigma_B > 0$ such that the functional $E(t): = \frac{1}{2}\sum_{i\in\mathbb{H}_2} \left( {{\epsilon \hat{u}_i^2 (t) + \hat{v}_i^2 (t) }} \right)$, $t\geq 0$, satisfies

for $t \geq 0$, where $\eta$ is a constant in $(0, 1)$ satisfying $\eta \leq \frac{1}{b\epsilon}\left( {{c\lambda_{\omega, 1}^{\mathbb{H}_2} + \alpha - 1 - \delta}} \right)$, and $A_\eta^{B} : = \frac{|\mathbb{H}_3| \sigma^2}{4b\left( {1-\eta} \right)} + C \sigma_B^2$.

Proof. First, we define fluctuations $\hat{u}_i = u_i - \bar{u}^{B}$, $\hat{v}_i = v_i - \bar{v}^{B}$, and $\hat{a}_i = a_i - \bar{a}^{B}$ for $i = \mathbb{H}_2 \cup \mathbb{H}_3$, where

Then, we have

and

for $i\in \mathbb{H}_3$. Now, we consider the following Lyapunov function:

and differentiate it with respect to $t$. Then, it follows from similar arguments used in the proof of Theorem 4.2 that

By applying Cauchy's inequality with $\delta$ to the last term on the right-hand side of the inequality above, the last term satisfies

Therefore, we obtain

for some $C > 0$. Thus, taking a sufficiently small $\eta$, we obtain

Finally, the Grönwall inequality leads to the desired result. □

Now, repeating the above procedure up to the $m$-th layer, we obtain the following result.

Theorem 5.2. Suppose that there exists $\sigma > 0$ and $\alpha\geq0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j \in\mathbb{H}_1 \cup \ldots \cup \mathbb{H}_m$ and $f'(s) \geq \alpha$ for all $s\in \mathbb{R}$. If $c > 0$ and $\delta > 0$ satisfy $c\lambda^{H_k}_{\omega, 1} + \alpha - 1 -\delta > 0$, for $k = 1, 2, \ldots, m$, then the FHN network with $m$-hierarchical architectures synchronizes with the precision level.

We are now in a position to prove the main result of this paper for heterogeneous FHN networks with a general hierarchical architecture:

for $i\in \mathbb{H}_{k, l}$, subject to the Robin-type boundary condition:

for $i \in \partial \mathbb{H}_{k, l}$. The assumptions of $\mathbb{H}_{k, l}$ and $\partial \mathbb{H}_{k, l}$ are described in Section 2.2.

Since the first layer is connected and has no boundary, from Theorem 3.1, it is clear that the system synchronizes with the precision levels. In the case where a component $\mathbb{H}_{2, l}$, since $\partial \mathbb{H}_{2, l} = \mathbb{H}_1 \not = \emptyset$ for all $l\geq 1$, we have $\lambda_{\omega, 1}^{\mathbb{H}_{2, l}} > 0$ for all $l\geq 1$. Thus, by the same proof, as provided for Theorem 4.4, we obtain synchronization with the precision levels. Now, let us consider the $l$-th component $\mathbb{H}_{3, l}$ in the third layer, and $\hat{u}_i = u_i - \bar{u}^{B}$, $\hat{v}_i = v_i - \bar{v}^{B}$, and $\hat{a}_i = a_i - \bar{a}^{B}$ for $i = \mathbb{H}_{3, l} \cup \partial \mathbb{H}_{3, l}$, where

Here, $n_{3, l}: = |\partial \mathbb{H}_{3, l}|$. We note that the boundary $\partial \mathbb{H}_{3, l}$ is not an empty set, but it consists of several disjointed components $(\partial \mathbb{H}_{3, l})_m$ that are either $\mathbb{H}_1$ or a component in the second layer. Hence, we have

and

for $i\in \mathbb{H}_{3, l}$. We note that since $\mathbb{H}_{3, l}$ is a component in the third layer, there exists $m$ such that $(\partial \mathbb{H}_{3, l})_m$ is a component in the second layer, which implies that

Moreover, because of the above argument, the solutions $u_i$ and $v_i$ on the first and second layers are bounded. By applying the same arguments as the proof of Theorem 5.1, we can prove that for each $k\geq3$ and $l\geq1$, the system (5.2)–(5.5) synchronizes with precision levels. Hence, by repeating this process for each component $\mathbb{H}_{m, l}$, we obtain the main result of this paper.

Theorem 5.3. Suppose that there exists $\sigma > 0$ and $\alpha\geq0$ such that $|{a_i - a_j}|\leq \sigma$ for $i, j \in\mathbb{H}_{1, 1} \cup \ldots \cup \mathbb{H}_{m, n}$ and $f'(s) \geq \alpha$ for all $s\in \mathbb{R}$. If $c$ and $\delta$ satisfy $c\lambda^{\mathbb{H}_{k, l}}_{\omega, 1} + \alpha - 1 -\delta > 0$, for $k = 1, 2, \ldots, m$, and $l\geq 1$, then the FHN network with hierarchical architectures synchronizes with the precision level.

Remark 5.4. In proving Theorem 5.3, it can be seen that the connectivity of the first layer plays a very important role in inducing synchronization. However, in the second layer, the connectivity of each layer is not important. We can see that the most important condition for inducing synchronization is the existence of a path from a node in each layer to a node in the first layer.

6.   Simulations

In this section, we present a numerical experience to illustrate the contents of Theorem 5.3. This simulation was run using MATLAB'S ODE solver "ode15s." For the heterogeneous FHN network with hierarchical architecture, we first consider a directed graph with four layers for the hierarchical architecture, as shown in Figure 2. The first layer marked in red is connected, and the second, third, and fourth layers, marked in green, blue, and magenta, have four, two, and three components, respectively. We note that it is a little difficult to distinguish, but the green component in the lower right of Figure 2 is a total of two overlapping components. The index set of nodes of one component is $\{ 6, 7, 12, 19, 22, 24, 27\}$, and the index set of the nodes of the other component is $\{ 8, 11, 14, 18, 20, 25\}$. For $i < j$, the $k$-th component $\mathbb{H}_{i, k}$ in $i$-th layer and the $l$-th component $\mathbb{H}_{j, l}$ in the $j$-th layer are connected by arcs (directed edges) from a node in $\mathbb{H}_{i, k}$ to a node in $\mathbb{H}_{j, l}$. The weights on the edges and arcs are given randomly in the range $[0, 1]$. For the system (5.2)–(5.5), we set $b = 0.5$, $\epsilon = 0.01$, and $f(s) = s^3/3$. The natural frequency $a_i$ has a uniform distribution on $[0.5, 0.7]$, and the initial configurations of $u$ and $v$ are randomly given in $[-20, 20]$ and $[-10, 10]$, respectively. Finally, to determine the coupling strength $c$, we must know the first (Dirichlet) eigenvalue for each layer. Because it is not easy to find the values of the first (Dirichlet) eigenvalues for the components, we propose its lower bound instead of the first (Dirichlet) eigenvalue. By the proof similar to Lemma 1.9 in ^[12], it is easy to see that the first (Dirichlet) eigenvalue satisfies

where $D_{k, l}$ is the diameter of $\mathbb{H}_{k, l}$ and $n_{k, l}$ is the number of nodes in $\mathbb{H}_{k, l}$, $k = 1, 2, 3, 4$. In this simulation, $\max_{k, l} \left(D_{k, l} n_{k, l} \right) = 35$, and the minimum of all the weights given on the edges is 0.0125. Hence, we choose $\delta = 0.5$ and $c = 4000$. Then, all assumptions in Theorem 5.3 are fulfilled. Hence, we can see that the heterogeneous FHN network with hierarchical architecture synchronizes with precision levels. as shown in Figure 3.

From Figure 3 (a) and (b), we can see that $u$ synchronizes very quickly, and the initial behavior of $u_i$ can be confirmed in Figure 3 (c), which are graphs of $u_i$ on a log scale versus time. By contrast, the synchronization of $v_i$ is relatively slow.

Finally, in Figure 4 (a), we provide graphs for $\sum_{i}\hat{u}^2_i$, $\sum_{i}\hat{v}^2_i$, and $E$. The y-axis is logarithmically scaled and $E$ is the sum of all Lyapunov functions of the layers. In this figure, since each function appears to move in an almost straight line in some time interval, each function has an overall exponential decay on the time interval. We can also see that $\sum_{i} \hat{u}_i$ has a large change in a very short time, as shown in Figures 4 (b). In particular, by Figure 3 (a) and (d), we can easily predict that $E$ will oscillate periodically. On the other hand, in Figure 4 (c), this phenomena is not very visible, and it seems as if there is no oscillation. However, as shown in Figure 5, we can see that $E$ is oscillating periodically with a very small amplitude.

In this simulation, although it is not easy to obtain the first (Dirichlet) eigenvalues, the lower bound is proposed. If we directly find the first (Dirichlet) eigenvalues, then we can find a smaller $c$ satisfying the condition $c\lambda^{\mathbb{H}_{k, l}}_{\omega, 1} + \alpha - 1 -\delta > 0$.

7.   Conclusions

We considered a heterogeneous FHN network with a hierarchical architecture—that is, a neuronal model in which the neuronal axon network is not homogeneous and spans various brain regions, and we demonstrated that synchronization occurs in this model through mathematical analyses of the Lyapunov function. It is well known that networks with heterogeneous units are much more difficult to completely synchronize than networks with identical characteristics. Thus, in this paper, synchronization means that all units have similar trajectories within a small deviation.

First, we proposed a generalized model for the first layer based on a traditional heterogeneous FHN network. After the second layer, we constructed a Robin-type boundary value problem by reflecting the characteristics of the hierarchical structure of the neurons. This is because the preceding layer affects the next layer, but not vice versa. Moreover, in these models, we can see that one layer either directly or indirectly affects the next and subsequent layers.

After modeling, we proposed a sufficient condition for synchronization, which is critically dependent on the coupling strength and connectivity of the network topology. In particular, according to the final result of this paper, the importance of the connectivity of the network topology is limited to the first layer and if there exists a path from the first layer to each layer, even if each layer except the first layer is not connected, all layers are synchronized with precision levels. Moreover, we showed that small deviations in synchronization depend on the parameter $\sigma$, which is the deviation of the natural frequencies $a_i$. If $\sigma = 0$, then we have complete synchronization. Finally, we performed simulations to validate the theoretical result of this paper. In fact, there is a limitation in this simulation, that the Dirichlet eigenvalue cannot be directly calculated and its lower bound was used. For this reason, a larger value of the coupling strength $c$ was required. Therefore, computing the Dirichlet eigenvalues is left for future work. In addition, there are different extended models of the present work we are currently addressing: FHN network with delay, a nonlinear dynamical network of Hindmarsh-Rose neurons, and FHN network with nonlinear operators instead of graph Laplacian. Additionally, we expect that the results and mathematical methodology can be applied to study other similar neural models with hierarchical architectures.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by a National Research Foundation of Korea(NRF) grant funded by the Korean government(MSIT) (No. 2021R1A2C1093929) and Heuron company.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.