Pricing equity warrants under the sub-mixed fractional Brownian motion regime with stochastic interest rate

1.   Introduction

An equity warrant allows warrant holders to buy stocks of listed companies at a certain price on a promissory day. It has many similarities with call options; therefore, many researchers ^[1,2] used the same model of option pricing to model the price of equity warrants. The classical option pricing model is the Black-Scholes model, which was proposed by Fischer Black and Myron Scholes in 1973 ^[3]. In the Black-Scholes model, the random driving source of the underlying asset is Brownian motion. However, Brownian motion cannot capture some characteristics of underlying assets, such as long-range correlations and heavy-tailed. Some researchers suggested using fractional Brownian motion to replace Brownian motion as the random driving source and have obtained some research results ^[4,5,6,7,8].

However, as fractional Brownian motion is not a semi-martingale, researchers have found that arbitrage opportunities exist when choosing fractional Brownian motion as the random driving source ^[9,10]. Bojdecki et al. ^[11] proposed a new stochastic process called sub-fractional Brownian motion (sfBm). The sfBm not only captures the long-range correlations of changes in the underlying assets, but also has non-stationary increments that are more weakly correlated in non-overlapping intervals, and the covariance decays faster. Therefore, the sfBm is more reasonable for using in the option pricing model ^[12,13]. To make the market completely free of arbitrage, EI-Nouty and Zili ^[14] presented sub-mixed fractional Brownian motion (smfBm), which is a linear combination of Brownian motion and sub-fractional Brownian motion. Tudor ^[15,16] proposed that when parameter $H \in \left({\frac{3}{4}, 1} \right)$, smfBm is "equivalent in law" to a standard Brownian motion, which means that it is a semi-martingale in that domain. Consequently, the class of regular portfolios is arbitrage-free (i.e., suitable for option pricing). As shown in ^[17], neither is there arbitrage for any value of $H \in (0, 1)$ if a suitable portfolio is adopted. Moreover, there are some studies on pricing models based on the smfBm. For example, Xu and Zhou ^[18] studied the pricing problem of perpetual American put options in sub-mixed fractional Brownian motion. They obtained the pricing formula by using partial differential equations. Araneda and Bertschinger ^[19] established the constant elasticity of variance model driven by sub-mixed fractional Brownian motion. They obtained the relevant Fokker-Planck equations and the prices of the European call options according to the M-Whittaker function and non-central chi square distribution function. Specifically, many scholars have incorporated the stochastic volatility model into the problems of option pricing for research and numerical analysis ^{[20,21,22,23,24,25]}.

However, all the above studies assumed that the short interest rate is constant. This is not consistent with reality. Therefore, many scholars incorporated stochastic interest rates into the option pricing models. Merton ^[26] proposed a stochastic interest rate model based on the BS model. Guo ^[27] established the subdiffusive Merton short rate model and obtained the pricing formula and the call-put parity relationship for European options. Liu and Li ^[28] studied the Merton credit risk pricing model by using sub-fractional as a random driving source, which can describe the characteristic of correlations and modify the classical credit risk structure model. The numerical calculation results show that the stochastic interest rate for the probability of default, values of bonds and equity and credit spreads has a certain influence. Based on these, in this paper, we incorporate sub-mixed fractional Brownian motion and the stochastic short rate into the equity warrants pricing model. We will establish an equity warrant pricing model under the sub-mixed fractional Brownian motion regime with the interest rate following the Merton short rate model.

The rest of the paper proceeds as follows. In Section 2, we briefly introduce the background of sub-mixed fractional Brownian motion. In Section 3, we give the formula for the pricing of a zero-coupon bond. In Section 4, the pricing formula for equity warrants is derived. In Section 5 and Section 6, we provide the numerical results and present an empirical analysis of this model.

2.   Preliminary knowledge

Many models depict changes in the short rate, and the Merton short rate model is one of the most classical stochastic short rate models. An accurate grasp of changes in the short rate can effectively avoid financial risks. An increasing number of people bring long-range correlations into pricing models, and the sub-mixed fractional Brownian motion not only satisfies this property but is also more suitable for the research of financial market modelling. First, we introduce the background of the smfBm, which involves ^[14,19].

Definition 2.1. $\{ M_t^H(\beta, \gamma), t \geqslant 0\} = \beta B(t) + \gamma {\xi _H}(t), \beta \geqslant 0, \gamma \geqslant 0$ is a sub-mixed fractional Brownian motion, where $B(t)$ is a Brownian motion, and ${\xi _H}(t)$ is a sub-fractional Brownian motion. Then we have

while $\beta = 0$ and $\gamma = 1$ , $M_t^H(\beta, \gamma)$ is a sfBm; and while $\beta = 1$ and $\gamma = 0$ or while $\beta = 0$ , $\gamma = 1$ and $H = \frac{1}{2}$ , $M_t^H(\beta, \gamma)$ is a Bm.

Now, we list some properties of the smfBm $M_t^H$ in the following remarks.

Remark 2.1. For $\forall h > 0$ , ${\text{\{ }}M_{ht}^H(\beta, \gamma){\text{\} }} \triangleq {\text{\{ }}M_t^H(\beta {h^{\frac{1}{2}}}, \gamma {h^H}){\text{\}, }}$

where $\triangleq$ means "to have the same law".

Remark 2.2. For $\frac{1}{2} < H < 1$ , $M_t^H(\beta, \gamma)$ has the property of long-range correlations.

Remark 2.3. msfBm has non-stationary increments for any $0 \leqslant s < t$

then

where

Remark 2.4. For $0 \leqslant u < v \leqslant s < t$ , the covariance over non-overlapping increments is given by

where

3.   The valuation of zero-coupon bond

In this section, we incorporate the long-range correlations of the short rate into our pricing model under the condition of $\beta = \gamma = 1$ and calculate the price of a zero-coupon bond when the stochastic interest rate follows the sub-mixed fractional Merton process.

3.1.   The assumptions

The Merton process is a widely used stochastic interest rate model combined with sub-mixed fractional Brownian motion. In the following sections, we will state some basic assumptions that will be used in this paper.

Assumption 3.1. Based on the risk neutral probability measure, we provide some ideal conditions for the market of corporate value and equity warrants:

(i) There are no transaction costs, margins or taxes;

(ii) Dividends are not paid during the time of the outstanding equity warrants;

(iii) The value ${V_t}$ of the firm consists of $N$ shares of stock at price ${S_t}$ and $M$ warrants outstanding at price ${c_t}$ ; thus, we have

(iv) We assume that the short rate ${r_t}$ is given by

and the value of firm ${V_t}$ , in which ${V_t}$ follows

where ${\mu _r}$, ${\sigma _{{r_1}}}$, ${\sigma _{{r_2}}}$, ${\mu _V}$, ${\sigma _{{V_1}}}$ and ${\sigma _{{V_2}}}$ are constants, ${B_{{r_1}}}(t)$, ${\xi _{{H_{{r_2}}}}}(t)$, ${B_{{V_1}}}(t)$ and ${\xi _{{H_{{V_2}}}}}(t)$ are independent Brownian motions.

3.2.   Pricing formula for zero-coupon bond

In this section, $P(r, t; T)$ is the price of a zero-coupon bond with maturity $T$ at time $t \in \left[{0, T} \right]$. Then, we obtain the pricing formula for a zero-coupon bond by the following theorem.

Theorem 3.1. In the sub-mixed fractional Merton model, the price of a zero-coupon bond with maturity $T$ at time $t \in \left[{0, T} \right]$ is given by

where

Proof. Here, $P(r, T; T) = 1$, that is, the zero-coupon bond $P(r, t; T)$ will pay for 1 dollar at expiration date $T$. Using Lemma 2.1 and Theorem 2.1 in ^[19], we can obtain

Denoting $\tau {\text{ = }}T - t$, $P(r, t; T) = {e^{{A_1}(\tau) - r{A_2}(\tau)}}$, it is easy to calculate

Substituting Eq (3.4) into Eq (3.3), we obtain

From Eq (3.5), we can obtain

Then, the pricing formula for the zero-coupon bond can be given by

4.   Corresponding BS equation and pricing formula for equity warrants

In this section, let $K$ be the exercise price, $T$ be the expiration date of the equity warrants and $c = c(V, r, t)$ be the price of equity warrants.

Theorem 4.1. When ${r_t}$ satisfies Eq (3.1) and ${V_t}$ satisfies Eq (3.2), $c(V, r, t)$ satisfies the following BS equation and the boundary condition

where

Proof. Considering a portfolio consisting of $c(V, r, t)$, ${\Delta _{1t}}$ units of stock and ${\Delta _{2t}}$units of zero-coupon bond, we obtain the price of the portfolio at time $t$.

Assuming

as

from Eq (4.2), we have

Denoting

Then

with the boundary condition

Proof is completed.

Solving the partial differential Eq (4.1), we obtain:

Theorem 4.2. When ${r_t}$ satisfies Eq (3.1) and ${V_t}$ satisfies Eq (3.2), we have the pricing formula for equity warrants $c(V, r, t)$ with expiration date $T$ , strike price $X$ , shares of stock $N$ , exercise ratio $k$ and shares of warrants outstanding $M$ , which are

where

and $\Phi (\cdot)$ denotes the cumulative probability function for a standard normal distribution.

Proof. Let us make the following change of variables

By calculating, we can obtain

Substituting Eq (4.6) into Eq (4.1), we have

By the price of zero-coupon bond $P(r, t; T)$ satisfying Eq (3.3), we have $\hat c(y, t)$ that satisfies

Letting $x = \ln y$, Eq (3.5) can be converted to

Letting

then, we obtain

Substituting Eq (4.10) into Eq (4.9), we have

where

By calculating, we obtain

Finally, Eq (4.11) can be written as

with final condition

By Poisson's formula, the solution of the Cauchy problem of the heat equation is expressed as

Thus,

${I_2}$ is relatively easy to compute. We can let ${z_2} = \frac{{\eta - \theta }}{{\sqrt {2\lambda } }}, - \sqrt {2\lambda } {\text{d}}{z_2} = {\text{d}}\theta$; then,

where

We calculate ${I_1}$. Letting ${z_1} = \frac{{\eta - \theta + 2\lambda }}{{\sqrt {2\lambda } }}, {\text{ }} - \sqrt {2\lambda } {\text{d}}{z_1} = {\text{d}}\theta$, in the same way, we have

where

And our model satisfies the following nonlinear equations ^[29]:

Proof is completed.

5.   Numerical simulation

In this section, we present some numerical results of our model.

Corollary 5.1 When $t = 0$ , the price of equity warrants is given by

where

Corollary 5.2 In particular, when the interest rate is constant and $t = 0$ , the price of equity warrants is given by

where

this is consistent with the result in ^[15].

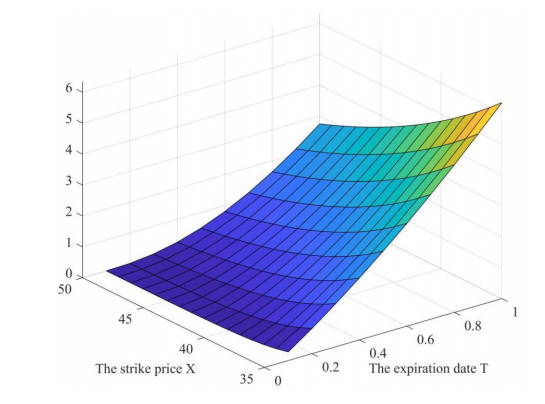
We give relevant numerical calculations by setting different parameter values. From Figure 1 to Figure 5, we can see that the prices of equity warrants decrease when the strike price $X$ is larger. From Figure 2, when the strike price is fixed, the value of equity warrants decreases with the increase in the Hurst index. From Figure 3, we find that when the value of ${S_0}$ is smaller, the declining trend of equity warrant prices is gentler; when the value of ${S_0}$ is larger, the declining speed of the equity warrant prices is faster. From Figure 4, when the expected return rate is smaller, the prices of equity warrant also gradually decrease. From Figure 5, when the risk-free interest rate takes different values, the decline range of equity warrant prices is relatively consistent. They show that the Hurst parameter, initial prices of underlying assets, expected return rate and risk-free interest rate have different effects on the prices of equity warrants.

6.   Empirical analysis

In this section, we verify the equity warrant prices under the sub-mixed fractional Merton short rate model. We derive the prices of equity warrants in the classical Merton stochastic interest rate model, the sub-fractional Merton short rate model, the BS model and the Ukhov model. Then, we compare prices of equity warrants between these models and our model.

The Ukhov model ^[29] is a pricing model for equity warrants based on a new algorithm developed. It is given by

(ⅰ) Solve (numerically) the following system of nonlinear equations for $({V^*}, {\sigma ^*})$,

where

(ⅱ) The warrant price is obtained as

The pricing formula is based on observable variables and is used to calculate the value of equity warrants.

From Table 1, when $T \uparrow 1$, the difference in price between the BS model, the Ukhov model and our model is smaller. We find that the difference in price between the Merton model, the sub-fractional Merton model and our model is relatively small. When the expiration date is smaller, the difference in value between the BS model and our model is larger.

We take three types of equity warrants as research objects for an empirical study. As of May 22, 2008, the selected data are from the GTA Research Service Centre of China.

We set the value of the one-year risk-free rate ${r_1} = 0.02$ and the two-year risk-free rate ${r_2} = 0.04$. To obtain the historical volatility of equity warrants, we calculate it from the closing price of each day. The logarithmic return rate ${\mu _i}$ is computed by using data of the closing price of day ${S_i}$ and yesterday's closing price ${S_{i - 1}}$, $s$ is a standard deviation of the logarithmic return rate, and $\sigma$ is given by

where

Then, we use the R/S method to estimate the value of the Hurst parameter. The logarithmic return series is equally divided into $A$ subsets, with the length $n = N/A$ of each subset. The mean of each subset is equal to ${e_a}(a = 1, 2, \ldots, A)$, and ${X_{k, a}}$ is the cumulative deviation of the first $K$ points relative to the mean value ${e_a}$ of this subset. According to the fluctuation range ${R_a}$ and standard deviation ${S_a}$ of the logarithmic return series in each subset $A$, we have the rescaled range ${\left({\frac{R}{S}} \right)_n}$. Thus, the formula of parameter $H$ is given

where

Finally, we obtain the values of volatility of underlying assets of three equity warrants as 0.44, 0.31 and 0.36, respectively, and the values of the Hurst index as 0.64, 0.66 and 0.61, respectively.

From Table 3, we can see that the MSE (mean square error) of the BS model is the largest, indicating that the simulated value is quite different from the real price. This is because the long-range correlations of underlying assets, the stochastic interest rate and other factors are not considered in the BS model. Although the price of the Merton model is closer to the market price than that of the Ukhov model, it is still not fully considered. The result of the sub-fractional Merton model is the best among the four models compared (i.e., the lowest MSE), and the price of this model is the closest to that of our model. This indicates that the long-range correlations of underlying assets have a certain impact on the option price, which is relatively consistent with the characteristic of the actual financial market. Moreover, it is also found by comparing the sfBm-Merton price and Merton price. Therefore, through comprehensive comparison, we find that the price of our model is closest to the market price.

7.   Conclusions

Option pricing models typically choose geometric Brownian motion or fractional Brownian motion as random driving sources. In this paper, sub-mixed fractional Brownian motion is selected as the random driving source, and the Merton random interest rate is incorporated into the pricing problem of equity warrants. We derive the explicit pricing formula for equity warrants. In the numerical calculation, we discuss the influence of multiple factors on the model results and compare our model with other classical models. The disadvantage is that the Merton model may result in a negative interest rate. In subsequent studies, the CIR model, Hull-White model and other more complex stochastic interest rate models can be considered, or stochastic volatility can be added to expand to a more general process.

Acknowledgments

This work was supported by the Natural Science Foundation of Anhui Province (No.1908085QA29).

Conflict of interest

The authors declare that they have no conflicts of interest to this work.