Pricing green financial options under the mixed fractal Brownian motions with jump diffusion environment

1.   Introduction

Over the past five years, the world economy had a great deal to face some challenges: The COVID-19 epidemic shock has caused economic depression due to the great losses, unexpected inflation, and the more acute influence of global climate change. The potential digitization of the economy and net-zero economy may serve as a pivotal way to increase challenges posed by climate change to the environment and sustainable development [1]. In recent years, the green and digital transformation from integrating green and digital economy is the most critical climate-related issue opened at the prime agenda of sustainable development and net-zero environmental goals. In this study, the integration between the digital currency (Solana, hereafter SOL) and the carbon emission futures, thus, results in new models and produces instruments for digital and green economies (transformation).

Consequently, scholars are looking at several specialized contributors such as green finance (GF) and financial technology (fintech) to seek ways to achieve an environmentally friendly and sustainable economy in the world [1,2,3]. There exist three distinct types of eco-friendly investment funds: carbon emissions trading, green credit, and green bonds. To be specific, carbon emissions trading plays an important role and has been treated as a green finance instrument [4,5]. Carbon emissions trading also is a crucial strategy for international cooperation in struggling with global warming. With the rapid growth of carbon trading and the evolvement of carbon financial derivatives products such as carbon options, green futures have become inescapable [6]. GF also requires financial institutions to consider pollution management and ecological conservation when providing credit to recover loans already granted to such projects [7,8].

Wang et al.'s (2010) [9] study suggested that investors either unwittingly overreact to news or continually overreact to information due to investors' sentiment. The reactional behavior may result in the properties of "leptokurtic" and long-memory processes in the returns of financial assets. Fractional Brownian motion can be a valuable instrument for describing these natural phenomena [7,10]. Although, a variety of models has been employed for pricing European options, using jump fractional Brownian motion to the valuation of green financial options has not been explored. To fill this gap, then we demonstrate how to price European green financial options utilizing the identifying jumps in a GARCH-type model incorporated into a jump-mixed fractional Brownian environment. The numerical and empirical results of our valuation models and other available estimated models suggest that our model is reasonable and easy to perform.

To the best of our knowledge, this is the first study that specifically analyzes the study's implications and could be useful to the pricing of green financial options under the mixed fractal Brownian motions with jump diffusion environment. From the theoretical viewpoint, our study did some pioneering work, we contribute to the recently emerging literature in two ways:

First, to capture the long memory features in time series and the jump of financial asset price behavior, we conduct a mixed fractional Brownian motion model (mfBm, hereafter) with identifying jumps. Afterward, we establish a risk-neutral valuation for pricing European options under the consideration that the underlying carbon price, the volatility, the risk-free interest rate, the jump intensity and the mean value and variance of jump magnitudes are all calculated values from market data. Secondly, empirical results are conducted by applying the underlying carbon returns and European options written on ICE EUA Futures prices.

The aforementioned model is proven to elaborate on how green assets can be captured using the GARCH-type model with the affine jump-diffusion process. We also construct an in-depth theoretical analysis with perfect replication of a contingent claim. The paper empirically analyzes the behavior of green financial prices, thereby contributing to the literature by fitting the suggested model to market data including both the estimated parameters and price jumps. Motivated by the aforementioned insights, the purpose of this study is to focus on the theoretical features of the jump fractional Brownian motion model. The most appropriate model parameters are selected with respect to historical volatility filtered from underlying asset prices, driven by both the mfBm process and Poisson jumps.

The remainder of this paper is organized as follows. In Section 2, we briefly review relevant studies. We describe the theoretical model for the green financial option and explain their properties in Section 3. In Section 4, we derive a European-style derivative for green financial option prices and show empirical results of green financial assets, and outline a numerical application and several fresh empirical results. Finally, Section 5 concludes with some remarks.

2.   Related literature

Fractional Brownian motion (fBm hereafter) has been widely utilized in financial modeling as well as in other fields since an fBm has two prominent properties of long-range dependence and self-similarity to capture these abnormal phenomena [11]. Furthermore, as proposed by some prior research, the return distributions of financial assets are generally influenced by long memory (or long-range dependence) and self-similarity [12]. To deal with this problem, some authors have used to model them by utilizing the fractional Brownian motion (fBm) with Hurst exponent H∈(1/2, 1), see, e.g., [13,14,15,16,17]. However, owing to the nature fact that fBm is neither a Markov process nor a semi-martingale, one should not apply the prevailing stochastic calculus to capture it. To deal with these problems, the long memory property is concerned and analyzed these fluctuations from financial markets. As natural extensions to this strand, several scholars [18,19,20] offered plausible explanations and have introduced to utilization of the so-called mixed fractional Brownian motion (mfBm), i.e., a linear compound of Wiener process and fractional Brownian motion (fBm). While the Hurst exponent of the fBm is larger than 1/2, then mfBm leads to a long-memory Gaussian process appropriate for modeling the financial return time series. Therefore, the mfBm has been commonly used in pricing different kinds of financial derivatives, including stock options [9,21], equity warrants [22], and currency options [15,23], and credit derivatives [24]. The extensive usage of fractional Brownian motion can be synthesized as follows:

The first methodology is to use the mfBm as an alternative approach. Cheridito (2001) [18] has proven that if the Hurst coefficient is located on a specific scale, it is equal to Brownian motion. Several studies also have constructed option pricing models with the mixed fractional Brownian motion [9,24,25,26,27], it also is widely used in developing foreign exchange (FX) option pricing models [10,23,28]. The second methodology is to use approximative fractional Brownian motion developed by Thao (2006) [29] as an alternative approach. Chang et al. (2021) [30] introduced a pricing stock option model by modeling the dynamics of stock and the variance is governed by an approximative fractional process.

Due to surprise macroeconomic news, analyzing ambiguous volatility and jump innovations in asset returns have attracted a great deal of attention. Therefore, several researchers have addressed the pricing contingent claims under jump-diffusion or self-exciting (Hawkes) processes (e.g., [31]). In this regard, there is also a growing literature explaining the sudden shocks or jumps using volatility models as shown by [32,33,34]. The exclusion of sudden shocks (changes) or jumps in the volatility dynamics can generate the persistence of estimated volatility bias (see, e.g., [35]) or jump dynamics in the volatility process [36]. Some studies in the area of option pricing (models) were conducted by [37,38], but an extensive empirical analysis is not undertaken yet. For this, we first apply the nonparametric approach to detect jumps in GARCH models developed by Laurent et al. (2016) [35] on leading green cryptocurrencies such as Solana (SOL) to identify the price jumps. Recognizing surprise news-driven jump phenomena, the difficulty of estimating jump parameters, and the importance of incorporating marketing information into option pricing models, we employ alternately jump models and more advanced option pricing models to obtain an insight into the green financial markets.

Unfortunately, little attention has been dedicated to integrating green financial studies with that of option pricing to establish green financial option pricing models under jump-diffusion process. In the wake of blockchain technology, there is an increasing interest in tokenonomics or 'token finance', and many research papers have begun exploring the price dynamics of cryptocurrencies, see e.g., [32,33]. However, little work has been dedicated to incorporating jump detection into green financial assets to conduct option pricing models with jump fractional Brownian motion.

3.   The representative models of pricing green financial options with jumps

3.1.   Definition

Let a probability space $\left(\Omega , \mathcal{F}, \mathbb{P}\right)$ be a complete probability space with a right-continuous filtration ${\left({\mathcal{F}}_{\mathrm{t}}\right)}_{\mathrm{t} > 0}$. A fractional Brownian motion (fBm) with Hurst exponent $\mathrm{H}$ ∈ (0, 1] follows a centered Gaussian process. A mixed fractional Brownian motion ${M}_{\alpha , \beta }^{H}\left(t\right)$of parameters are α, β and H stands for a linear compound of a Brownian motion or a Wiener process ${W}_{t}$ and fractional Brownian motion ${W}^{H}\left(t\right)$ with a Gaussian zero-mean nonstationary stochastic process indexed by a single scalar of Hurst parameter H ∈ (0, 1), defined on a probability space {$({\mathcal{F}}_{\mathrm{t}}$t≥0, ) $\mathbb{P}$} by:

${M}_{\alpha , \beta }^{H}\left(t\right)$ = α${W}_{t}$ + β${W}_{t}^{H}$,

where ${W}_{t}$ and ${W}_{t}^{H}$ are independent, and α and β denote real constants such that (α, β) ≠ (0, 0). $\mathbb{P}$ is the physical probability measurement and the information filtering {${\mathcal{F}}_{\mathrm{t}}$}t≥0 is produced by (${W}_{\mathrm{\tau }}$, ${W}_{\mathrm{\tau }}^{H}$) for τ ≤ t, which meets the monotonic increasing properties. As shown in previous research, we list some properties of the mfBm.

Proposition 1. The mfBm ${M}_{\alpha , \beta }^{H}\left(t\right)$ satisfies the properties as follow:

(ⅰ) ${M}_{\alpha , \beta }^{H}\left(t\right)$ is a centered Gaussian process with mean zero and the covariation function is regarded as long-range dependence then given by

$Cov({M}^{H}\left(t\right), {M}^{H}\left(s\right)) = {\alpha }^{2}$(t$\bigwedge s$)+$\frac{{\beta }^{2}}{2}$(${t}^{2H}+{s}^{2H}-|$t −s|^2H), s, t > 0;

(ⅱ) ${M}_{\alpha , \beta }^{H}\left(t\right)$ is not a Markovian process for H ∈ (0, 1) \ {$\frac{1}{2}$};

(ⅲ) The increments of ${M}_{\alpha , \beta }^{H}\left(t\right)$ are mixed-self-similar and stationary, in this regard, for any h > 0,

where the symbol $\stackrel{d}{\Rightarrow }$ represents the random variables on both sides of the Eq (3.1) have drawn from the same asymptotic distribution;

(ⅳ) The increments of the process ${M}_{\alpha , \beta }^{H}\left(t\right)$ are positively correlated if H∈($\frac{1}{2}$, 1), uncorrelated if H = $\frac{1}{2}$, and negatively correlated if H ∈ (0, $\frac{1}{2}$);

(ⅴ) The increments of ${M}_{\alpha , \beta }^{H}\left(t\right)$ are long-range dependence if and only if H ∈ ($\frac{1}{2}$, 1);

(ⅵ) The mfBm ${M}_{\alpha , \beta }^{H}\left(t\right)$ is equivalent to BM for H ∈ ($\frac{3}{4}$, 1).

Proof of Proposition 1 and for a comprehensive description of the features of the mfBm, the interested reader is referred to [19,22]. The details of the Hurst exponent algorithms are available from the corresponding author.

Corollary 1. The assets prices at every t of a bounded -measurable claim can be described as

where r is the constant risk-free interest rate.

3.2.   The market model

The price process$S = {\left({S}_{t}\right)}_{t}$ of a green financial asset is defined. Under the physical probability measure $\mathbb{P}$, the green financial prices with return dynamics are given by:

where $\mu$ and $\sigma$ are the instantaneous expected return and the continuous volatility, respectively. The process ${N}_{t}$ is a Poisson process, independent of the jump-sizes J with arrival intensity $\lambda$ per unit time so that its increments satisfy

The corresponding function is in that case, the expected proportional jump size

Recalling a filtered probability measure space$\left[\Omega , \mathcal{F}, \mathbb{P}, {\left({\mathcal{F}}_{\mathrm{t}}\right)}_{\mathrm{t} > 0}\right]$ is supposed where the filtration ${\mathcal{F}}_{\mathrm{t}}$ is the natural filtration yielded by the Wiener process ${W}_{t}$ under the market measure $\mathbb{P}$ and the compound Poisson process $\sum _{j = 1}^{{N}_{t}}{J}_{j}$. Jumps arriving at different times are supposed to be independent of each other. A sample path ${S}_{t}$ for a process described by

The mixed fractional nature and jumps have an impact on the fundamental theorem of asset pricing. This impact involves ensuring martingale properties under the risk-neutral measure¹ $\mathbb{Q}$ and examining conditions that maintain market completeness with these dynamics. Specifically, we define the risk-neutral dynamics for the asset price under mixed fractional Brownian motion with jump diffusion, ensuring that the pricing measure $\mathbb{Q}$ satisfies the no-arbitrage conditions and preserves market completeness.

¹ The authors are thankful to an anonymous referee for suggesting the mixed fractional Brownian motion with jump-diffusion model under risk-neutral measure $\mathbb{Q}$.

Under the risk-neutral measure $\mathbb{Q}$, the asset price ${S}_{t}$ evolves according to

where

- $\widetilde{{W}_{t}}$is a standard Brownian motion under $\mathbb{Q}$.

- $\widetilde{{N}_{t}}$ is a Poisson process with intensity $\lambda$under $\mathbb{Q}$, independent of $\widetilde{{W}_{t}}$.

- $\widetilde{J}$ are the jump sizes with an adjusted distribution under $\mathbb{Q}$ to ensure the martingale property of the discounted asset price.

3.3.   Pricing European green financial option under fractional Brownian motion model with jumps

To solve the prominent issues associated with the construction of our prime model, we model the long memory and jump-type behavior on the underlying asset price under an uncertain environment. Accordingly, pricing the European cryptocurrency option and carbon option in a mixed fractional Brownian motion with detecting jumps is analyzed. More accurately, we first show the dynamics of the underlying asset price driven by a jump fractional Brownian motion and then derive analytical pricing formulae for European options. Recent advances in mathematical models offer a better choice, the mixed fractal Brownian model with jumps (MFBMJ) has extended from mixed fractional Brownian motion (hereafter MFBM) which is a linear component of BM and FBM.

European green financial options

One of our purposes here is exactly to derive the pricing of European-style options for underlying green financial assets. Subsequently, the mfBm with jump model by incorporating the mixed fractional Brownian motion and Poisson jump process is acquired and several prominent features are investigated. To develop the fresh option pricing derivation in a jump mixed fractional market, some assumptions will be given as follows:

(ⅰ) There are no transaction costs or taxes and all green assets are perfectly divisible;

(ⅱ) The risk-free interest rate is constant;

(ⅲ) Assets trading is continuous;

(ⅳ) Asset prices conform to FBM.

Now consider an MFBMJ market that includes two investment possibilities:

(ⅰ) A carbon market account:

where ${r}_{c}$ is the return of carbon emissions prices.

(ⅱ) A green crypto (Solana: SOL) whose price movements are governed by a fractional Wiener process as follows:

where H is Hurst parameter satisfied H > 1/2, where ${S}_{t}$ denote the spot price at time 𝑡 of one unit of the major green cryptocurrency: Solana is measured in low carbon emissions.

Making the change of variable

then under the risk-neutral measure, one can obtain that:

where ${r}_{g}$ is the return of green cryptocurrency (Solana). Hence, we obtain the solution of (3.7) as follows

More importantly, under the risk-neutral measure ${\overline{\mathcal{P}}}_{H}$, the fractional Brownian motion model with jumps can be described as (3.11)

${S}_{0}$ = S, 0≤t≤T,

where ${N}_{t}$ represents a Poisson process with rate λ; $J\left(t\right)$ is the jump size percent at time t which follows a sequence of independent identically distributed (iid) process, and $\left({e}^{J\left(t\right)}-1\right)~N({\mu }_{J\left(t\right)}, {\delta }_{J\left(t\right)}^{2})$.

Besides, the FBM i.e., ${W}_{t}^{{H}_{i}}$, i = $\overline{1, N}$, the Poisson process ${N}_{t}$, and the jump size $\left({e}^{J\left(t\right)}-1\right)$ are supposed to be relatively independent of all sources of randomness.

Let

A risk-neutral measure ${\overline{\mathcal{P}}}_{H}$ is given by

Then ${\overline{W}}_{t}+\sum _{i = 1}^{N}{\overline{W}}_{t}^{{H}_{i}}$ stands for a new MFBM under the risk-neutral measure ${\overline{\mathcal{P}}}_{H}$. Under the risk-neutral measure ${\overline{\mathcal{P}}}_{H}$, Eq (3.11) can be described as (3.15)

Let C(${S}_{t}, t$) be the price of a European contingent claim (option) at time t with a strike price X that expires at time T. Then we present the pricing formula for the green financial call option by the theorem as follows.

Theorem 1. The price at every t ∈ [0, T] of a European call green financial option with strike price $X$ that expires at time 𝑇 is described as

where

${\mathcal{E}}^{n}$, $\tau = T-t$, is the expectation operator over the distribution of ${\prod }_{i = 1}^{n}{e}^{J\left({t}_{i}\right)}$, time to expiration (maturity), respectively. $\mathbb{N}$(⋅) denotes the normal cumulative distribution.

Proof of Theorem 1. In a risk natural world, from Corollary 1, a European call green financial option with maturity 𝑇 and strike price $X$ can be shown. Also, a European call option with maturity 𝑇 and strike price $X$ is theoretically equivalent to

where ${\bf{1}}_{{S}_{T} > X}$ denotes an indicator function.

Then we obtain

let

Using the independence of ${N}_{T-t}$ and 𝐽(t_i) and the theory of Poisson distribution with intensity λ(T−t), we have

By utilizing the fractional Girsanov theorem, we conclude that ${\overline{W}}_{T}^{H}-\overline{{W}_{t}}$ is a new mixed fractional Brownian motion under $\overline{\mathcal{R}}$. Hence, setting

and applying Corollary 1, we infer that

where

Now we consider${\mathbb{E}}_{\mathcal{R}}\left[{{S}_{T}{\bf{1}}}_{{S}_{T} > X}⌊{\mathcal{F}}_{t}^{H}\right]$ and set the following equation

From the Girsanov transformation on the fractional Wiener process, one knows that there exists a probability measure ${\mathbb{E}}_{\mathcal{R}}$ in which ${\sigma W}_{t}^{*}+\sigma {\left({W}_{t}^{H}\right)}^{*}$ is a new MFBM.

Let, then ${S}_{T}={S}_{t}{e}^{({r}_{c}-{r}_{g})(T-)t}{Z}_{t}$ from previous theorem, we can obtain that

where ${d}_{1}$ = $\frac{\mathrm{l}\mathrm{n}\left(\frac{{S}_{t}{\prod }_{i = 1}^{n}\;{e}^{J\left({t}_{i}\right)}}{X}\right)+\left({r}_{c}-{r}_{g}-\lambda {\mu }_{J\left(t\right)}\right)\tau -\frac{1}{2}{\sigma }^{2}\left(T-t\right)+\frac{{\sigma }^{2}}{2}\left({T}^{2H}-{t}^{2H}\right)}{\sigma \sqrt{{T}^{2H}-{t}^{2H}}}$

From the above analysis, it is calculated that the price of the European call green financial option can be expressed as

The proof is achieved.

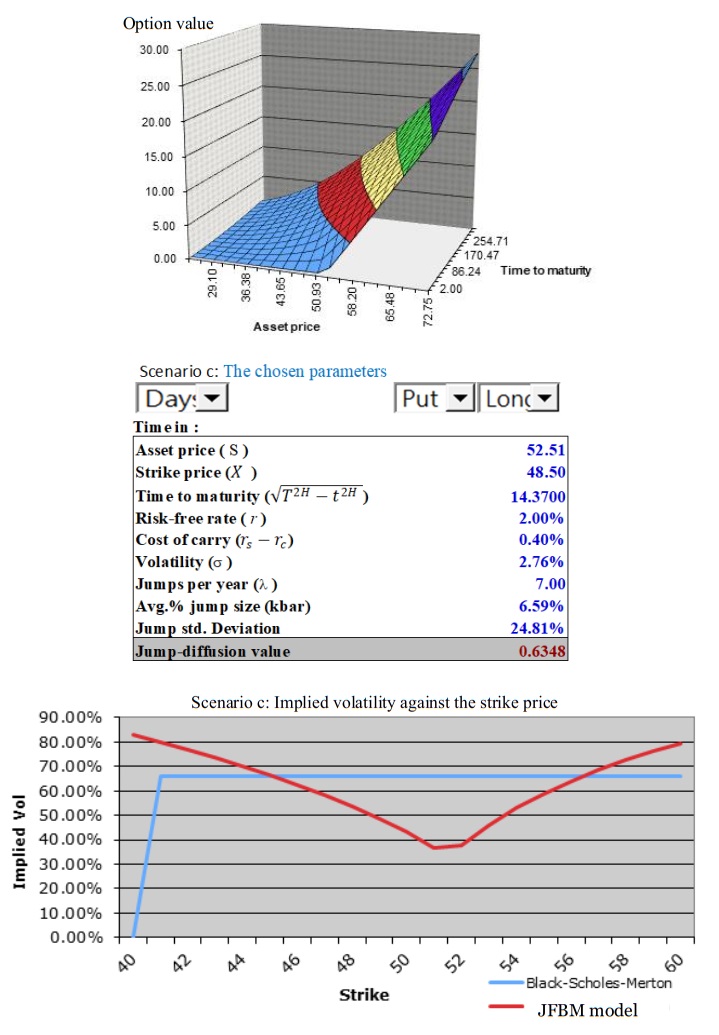
For the sake of simplicity, we consider only the above European call option in the following analysis, while the put option can be handled analogously. Furthermore, we can computer the price of a put green financial option which is produced by the following corollary. Perhaps, utilizing the put–call parity, one can readily acquire the evaluation model for a put green financial option, which the following corollary is given by.

Corollary 2. The price at every 𝑡∈ [0, 𝑇] of a European put green financial option with strike price 𝐾 and maturity 𝑇 is described as follows.

where ${d}_{1i}$ and ${d}_{2i}$ are shown in the preceding equation.

3.4.   Jump detection in the green financial markets

As discussed above, our model assumes that the underlying asset price processes are driven by mfBm and Poisson jumps. Thus, our first procedure is looking to estimate jump instants or excessively volatile, and our second procedure is to calculate the corresponding amplitude of the jump motion. Our approach is based on the argument introduced in [39] Bouri et al.'s (2020) work, in which methodology for estimating jump instants is proposed by Laurent et al. (2016 [35]; hereafter LLP) test. The LLP test is based on the semi-parametric approach which considers additive jumps in AR-asymmetric-GARCH models to take potential asymmetric effects into account. Assume random asset returns (${r}_{t}$) in an AR (1)-GJR-GARCH (1, 1) model are described as follows:

where ${z}_{t}$ denotes the white noise process, and ${\sigma }_{t}^{2}$ represents the conditional variance of ${r}_{t}$. Here is denoted as D_t−1 = 1 if ${\varepsilon }_{t-i}$ < 0 and 0 otherwise.

If a target-independent jump component ${a}_{t}{I}_{t}$ is added to ${r}_{t}$, we can yield

where ${r}_{t}^{\mathrm{*}}$ represents the observed returns, ${I}_{t}$ is a binary variable taking the value of 1 in the case while a jump occurs on day t and 0 otherwise, and ${a}_{t}$ is the jump size. In Eq (3.31), an additive jump ${a}_{t}{I}_{t}$ cannot influence the conditional variance ${\sigma }_{t+1}^{2}$ at the next period$t+1$ (see [35]).

The results are qualitatively the descriptive statistics on significant jumps via LLP test and are shown in Table 2.

Table 1.  Summary statistics of prices and its log-return for the SOL (Solana) and carbon.

	SOL	${r}_{s}$	Carbon	${r}_{c}$
Mean	47.5417	0.0048	63.9873	0.0009
Median	26.4800	0.0019	70.3800	0.0014
Maximum	248.470	0.5805	98.0100	0.1613
Minimum	0.51530	−0.5495	19.3100	−0.1773
Std. Dev.	53.9461	0.0861	23.3654	0.0276
Skewness	1.6470	0.2379	−0.5132	−0.3960
Kurtosis	5.0897	10.2789	1.8545	6.9415
Jarque-Bera	635.359	2221.512	98.768	674.821
Probability	0.0000 ***	0.0000 ***	0.0000 ***	0.0000 ***
Standard error	0.0123		0.0273
t-stat	13.978		2.633
p-value	0.00%***		3.89%**
Observations	2,004
Notes: 1. *, ** and ***, represent statistical significance at the 10%, 5%, and 1% levels, respectively. 2. ${r}_{s}$ and ${r}_{c}$ denote the daily log return computed from closing prices of SOL and carbon. 3. The carbon price is currency in EUR? and ${r}_{s}-{r}_{c}$ = 0.0039.

---

 | Show Table

DownLoad: CSV

Table 2.  Descriptive statistics on significant jumps using LLP statistics.

	SOL	Carbon
Jump Mean	0.1775	0.0658
Jump Std Dev	0.3823	0.2481
Jump probability	0.1766	0.0659
average	0.1214
No. of jumps per year
2020	26	10
2021	38	20
2022	49	26
2023	56	7
2024	9	3
Total jumps	178	66
Notes: 1. Concerning number of jumps and jump intensity are calculated as the total number jumps (# jumps), their proportion (%) over sample observations, i.e., shown as (P(jump) = 100 (#jumps/#obs.)), and their mean and standard deviation of jump components are also reported. Percentage of the year having jumps$= \frac{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{j}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{y}\mathrm{s}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{d}\mathrm{a}\mathrm{y}\mathrm{s}}$∗ 100. 2. Yearly estimates for the Solana (SOL) and Carbon and no. of jumps denote the number of detecting jumps, and P (jump freq.) indicates the proportion of observations with a significant jump occurrence at α = 0.05. 3. LLP statistics is the Laurent et al. (2016) [35] jump test statistic.

---

 | Show Table

DownLoad: CSV

4.   Numerical analysis and results

The study is conducted on green financial options with underlying green asset prices, including quotes according to two leading green assets: SOL (Solana) and Carbon. In this study, we designed a green financial option contract. First, we combined a generalized autoregressive conditional heteroskedasticity model (GARCH) to predict the dynamics jump of green financial assets. Next, we established a fractional Brownian motion option pricing model with temporally variable volatility. Consequently, we apply this approach to the valuation of option pricing by executing the closing price of the underlying assets of SOL (Solana) and Carbon from 14 April 2020 to 29 February 2024 as an empirical analysis. The trend of the prices detected by the GARCH model with jumps was consistent with the actual trend and predictions of actual prices were highly accurate. Our approach is based on ideas proposed in [39] Bouri et al.'s (2020) work, which method for estimating jump instants is introduced by Laurent et al. (2016) [35]. The technique is based on the semi-parametric approach which is extended to consider additive jumps in AR-asymmetric-GARCH models to measure potential asymmetric effects.

4.1.   Data description and statistical analysis

This section aims to present the green financial option value process in the formula (3.20) based on the physical measure of underlying green asset prices. In the physical market, we can get 2,004 historical data on the prices of SOL (Solana) and Carbon at https://coinmarketcap.com/ and https://www.investing.com, respectively. The sample period is April 14, 2020, to February 29, 2024, yielding 1,002 trading days. The selected sample is dictated by the price data availability of SOL, collected from the representative green cryptocurrency by market capitalization to ensure the longest possible period. Solana (briefly denoted as SOL) is regarded as a green cryptocurrency, see the list of sustainable cryptocurrencies (https://dailycoin.com/green-crypto-eco-friendly-cryptocurrencies/#h-top-green-cryptocurrencies).

4.2.   Empirical data analysis on green financial assets

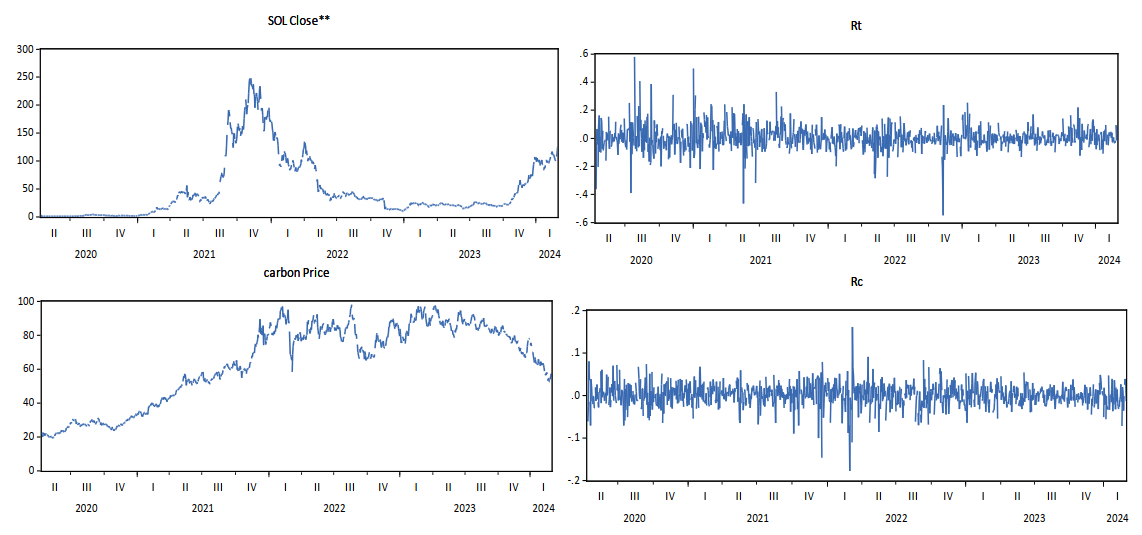
As evidenced in the first-four moments shown in Table 1, the visual impressions are performed by the descriptive statistics for SOL's log-return that the maximum, the minimum, and the mean values are 0.5805, −0.5495, and 0.0048, respectively. Taking into account these historical data, an important SOL (Solana) feature reports that the skewness value is greater than 0, so a large proportion of the data is found in the long right tail, with a relatively fat right tail, however, the opposite result for carbon. Taken together, the measure of log-return distribution is leptokurtic (10.28, 6.94), implying evidence of heavy tails, respectively. It also displays that the kurtosis is greater than the value of 3 for the standard normal distribution. The Jarque-Brea statistic was significant at P < 0.001; as a result, we rejected the hypothesis that the logarithmic return of all series follows a normal distribution. In particular, as depicted in Figure 1, we use daily prices and log-returns of SOL and carbon data to estimate parameter values as far as it is possible to capture the jump and diffuse risk. The bottom panel depicts volatility clustering and asymmetric jump diffusion in the carbon market.

Figure 1.  The evolution of prices and log returns for SOL and carbon.

Notes:
1. As shown in the upper plot, an illustration of price dynamics given the evolution of the SOL (blue line) presents the huge and slight jumps. The most significant jumps are highlighted by red circles when the massive jump occurred. We use Solana (SOL) and carbon data to estimate parameter values as far as it is possible to capture the jump and diffuse risk. The data source is obtained from Coinmarketcap.com.
2. The bottom panel depicts volatility clustering and asymmetric jump diffusion in the SOL and carbon market.

DownLoad: Full-Size Img PowerPoint

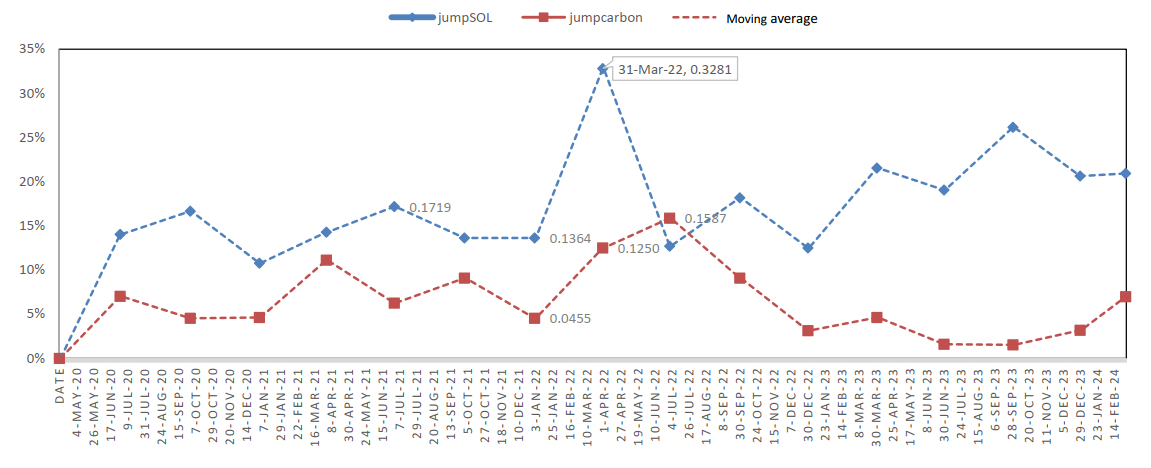
To further analyze the jump dynamics, Table 2 exhibit quarterly statistics of the significant jump components for both SOL and carbon returns. The jump size of carbon observations with mean, standard deviation, and jump probability equal 0.0658, 0.2481 and 0.0659, respectively. As a whole, the jump intensity λ is computed along with an average of 0.1214 for the full sample period. Figure 2 illustrates the jump intensity visualization for the SOL and carbon.

Figure 2.  Jump intensity for SOL and carbon.

Notes:
1. Regarding the definition of jumps and jump intensity, and their mean and standard deviation of jump components, see Note of Table 1.
2. Quarterly estimates for no. of jumps for SOL and carbon denote the number of identifying jumps, and P (jump freq.) indicates the proportion of observations with jumps, and jump frequency accounts for observations with a significant jump occurrence at α = 0.05.

DownLoad: Full-Size Img PowerPoint

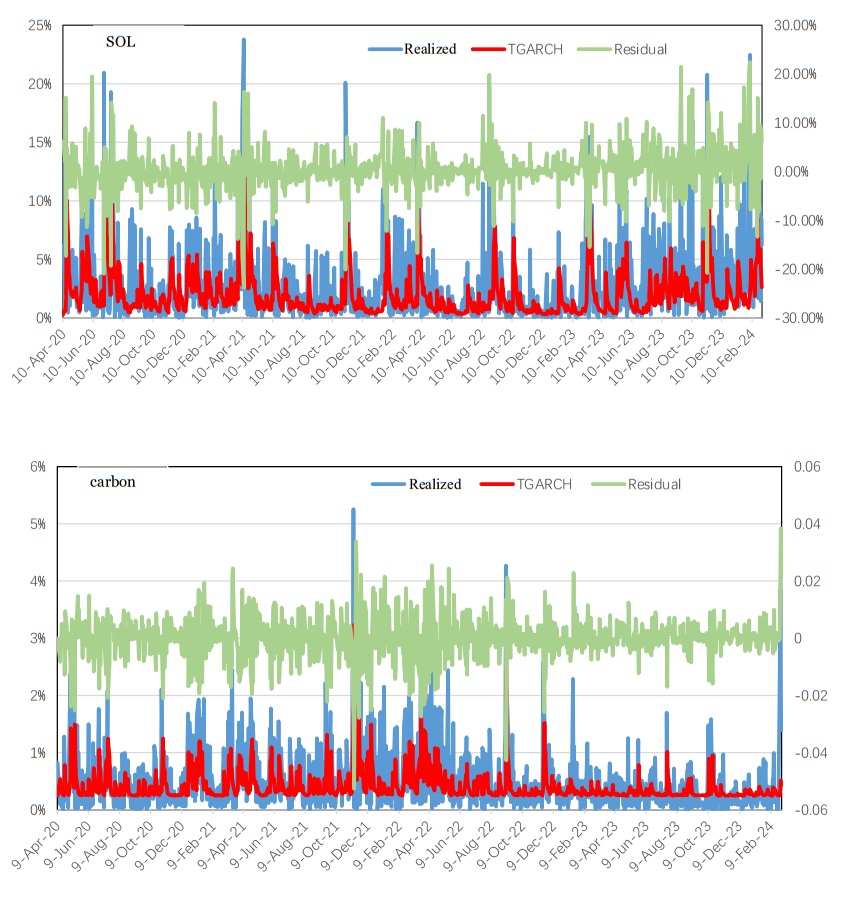
Figure 3 displays the estimated results for respective graphs of the GARCH model's conditional variance as well as standardized residuals. Overall, as depicted in Figure 3, the conditional volatility and residuals of Carbon have smaller amplitude fluctuations than SOL (Solana) via the TGARCH (1, 1) model.

Figure 3.  The conditional variance and standardized residuals of TGARCH model for SOL and carbon.

Notes:
The top panel for respective graphs the TGARCH model’s conditional variance as well as standardized residuals generated from Eq (3.29) for SOL; the second panel plots the conditional variance and standardize residuals of the TGARCH model for carbon. In specific, the mean equation under a TGARCH process can be given in Eq (3.28).

DownLoad: Full-Size Img PowerPoint

Hurst Exponent Calculation

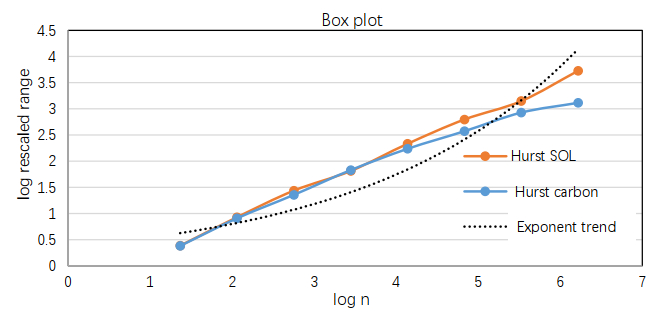
Following the method of Hurst exponent algorithms, a scatter plot of R/S values at window size is drawn with a natural base 𝑒 and the resulting slope of Hurst exponent values is fitted. According to the results in Table 1, the Hurst exponent is computed as 0.6715 and 0.5720 for SOL and carbon, respectively. These coefficients are significant since p-values are greater than the chosen values at a 5% significance level. Table 1 also displays the values of the underlying green assets prices for the intensity of the jump process 0.065 when the power exponent is taken to be ℎ = 0.572 value obtained from Table 1. The R/S statistics cannot reject the null hypothesis of the absence of long-range dependence in the case of return series. The observed results show that the daily log-return series for SOL and carbon display evidence of long memory behaviour since p-values are reported as significantly lower than 5 %. In this sense, this concludes that the returns of the two green assets exhibit the existence of high volatility persistence but follow a non-random walk. The result aligns with [40]. In addition, Figure 4 displays the boxplots of log(n) and log(R/S) and a clear linear pattern in the two markets, with n ranging from 1 to N. Notably, a general property is exhibited in Figure 4, the scatter diagram depicts that while the return series has shown an exponential market trend, and multifractality increased generally after their respective change-points.

Figure 4.  An illustration of Hurst exponent for SOL and carbon.

DownLoad: Full-Size Img PowerPoint

4.3.   Value analysis of the green financial options

Consequently, the above-expected average variance and average jump frequency are substituted into the jump-diffusion approximation, as discussed in [41] Bates (1991), and adequate conditions are determined based on the green financial option pricing. The real-world probabilities computed from historical price data are represented as physical or market probability measures $\mathbb{P}$. Consequently, the estimated model parameters can be employed in the option pricing under the risk-neutral pricing measure $\mathbb{Q}$ for all pricing options formula in Eq (3.16) above. In this context, we will display the values of the green financial options and the basic parameters are primarily listed:

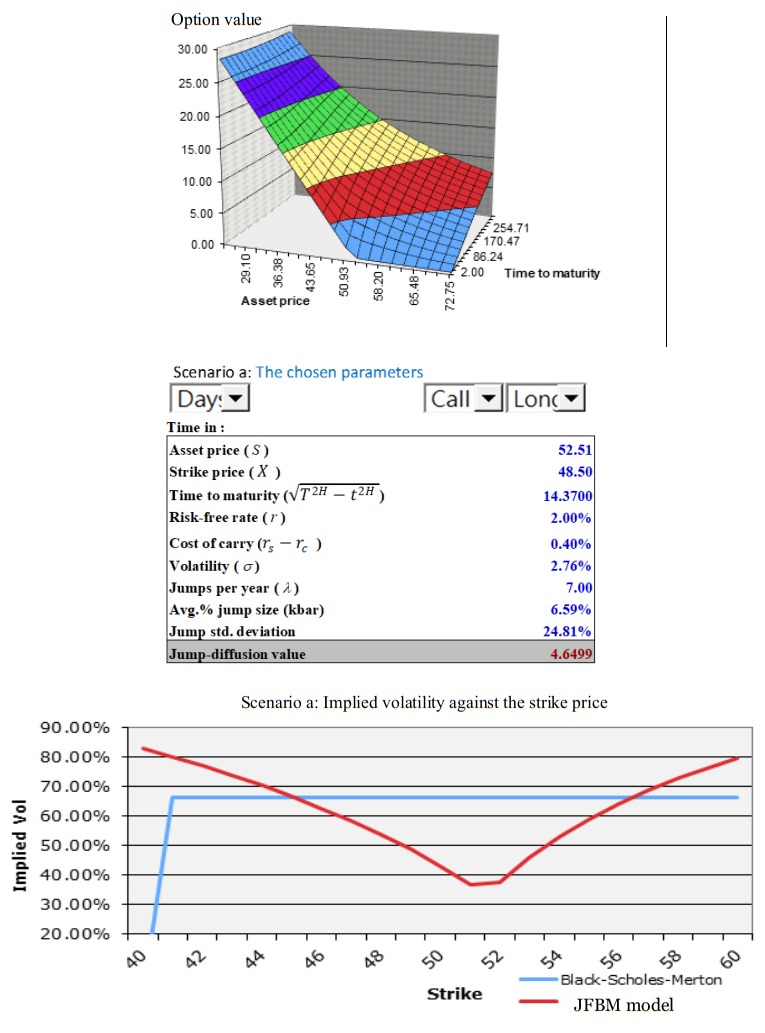
The log return of SOL ${r}_{s}$ is 0.48%, and the carbon ${r}_{c}$ is 0.09%, the ${r}_{s}-{r}_{c}$ (cost of carry or position spread) is about 0.39%, accordingly. Based on the historical datum, we apply the R/S analysis approach to estimate the Hurst exponent (H = 0.572). Next, we can calculate the valuation of the green financial call option using European contingent claims written on the underlying asset of green financial assets with carbon quotations lying in the closed interval of [4.85, 5.30]. The remaining time to maturity T−t is updated according to the underlying asset. The empirical results are reported in Table 3. Now, we consider the values of the computed jump parameters and preceding Hurst parameters 𝐻 = 0.572 and then calculate the values for our green financial options under jump mixed fractional Brownian motion. Table 3 and Figures 5a and 5b display the values of the call green financial option against its parameters, H, λ, and ${\mu }_{J}$. The chosen parameters are acquired from Table 1 as follows: S₀ = 52.51(i.e., carbon price at 23 Feb.2024), K = 48.5, ${r}_{s}$ = 0.0048, ${r}_{c}$ = 0.0009, σ = 0.0276, t = 0, T = 19 (days), H = 0.572, λ = 7, ${\mu }_{J}$ = 0.0065, and δ_J = 0.2418. Not surprisingly Figure 1 depicts that the option value is a decreasing function of ${\mu }_{J}$_, ${\delta }_{J}$_, and the increasing parameter of H and λ is accompanied by an increase of the corresponding option value.

Table 3.  Calculating European call option valuation with jump fractal Brownian motions.

Panel a:
Strike	Market price	Difference	Option value	Delta	Premium	RMSE
48.50C	5.015	0.3651	4.6499	0.4950	1250	0.7325
49.00C	4.65	0.4564	4.1936	0.6070	7600
49.50C	4.295	0.5559	3.7391	0.5951	7300
50.00C	3.955	0.6686	3.2864	0.5831	7010
50.50C	3.63	0.7945	2.8355	0.5710	6725
51.00C	3.32	0.932	2.388	0.5586	6450
51.50C	3.03	1.0304	1.9996	0.5461	6180
52.00C	2.755	0.9314	1.8236	0.5335	5915
52.50C	2.485	0.7321	1.7529	0.5207	5660
53.00C	2.24	0.5499	1.6901	0.5079	5410
Notes: 1. 19 days to expiration on 03/13/24 (Implied Volatility: 58.96%). 2. Price value of option point: EUR 1,000. 3. ICE EUA Futures Mar'24 (CKH24) and options prices for Fri, Feb 23rd, 2024. Also, S0 =52.51 at 23-Feb-24. 4. Downloaded from Barchart.com as of 02-23-2024.
Panel b:
Strike	Market price	Difference	Option value	Delta	Premium	RMSE
49.00C	7.78	(0.0006)	7.7794	0.6071	7600	0.4732
49.50C	7.47	0.0978	7.5678	0.5951	7300
50.00C	7.165	0.1965	7.3615	0.5831	7010
50.50C	6.875	0.2853	7.1603	0.5710	6725
51.00C	6.59	0.3742	6.9642	0.5586	6450
51.50C	6.315	0.4582	6.7732	0.5461	6180
52.00C	6.045	0.5421	6.5871	0.5335	5915
52.50C	5.785	0.6210	6.4060	0.5207	5660
53.00C	5.535	0.6946	6.2296	0.5079	5410
53.50C	5.285	0.7730	6.0580	0.4952	5170
Notes: 1. 117 days to expiration on 06/19/24. 2. ICE EUA Futures Jun '24 (CKM24) and options prices for Fri, Feb 23rd, 2024. 3. Market price downloaded from Barchart.com as of 02-23-2024. Also, a summary of the pricing performance and calibration on 23 February 2024.

---

 | Show Table

DownLoad: CSV

Figure 5a.  Option value against the maturity time and the asset price (Scenario a).

Note: The produced results are performed from the software provided by [43] Haug (2007).

DownLoad: Full-Size Img PowerPoint

Figure 5b.  Option value against the maturity time and the asset price (Scenario b).

DownLoad: Full-Size Img PowerPoint

4.4.   Numerical application

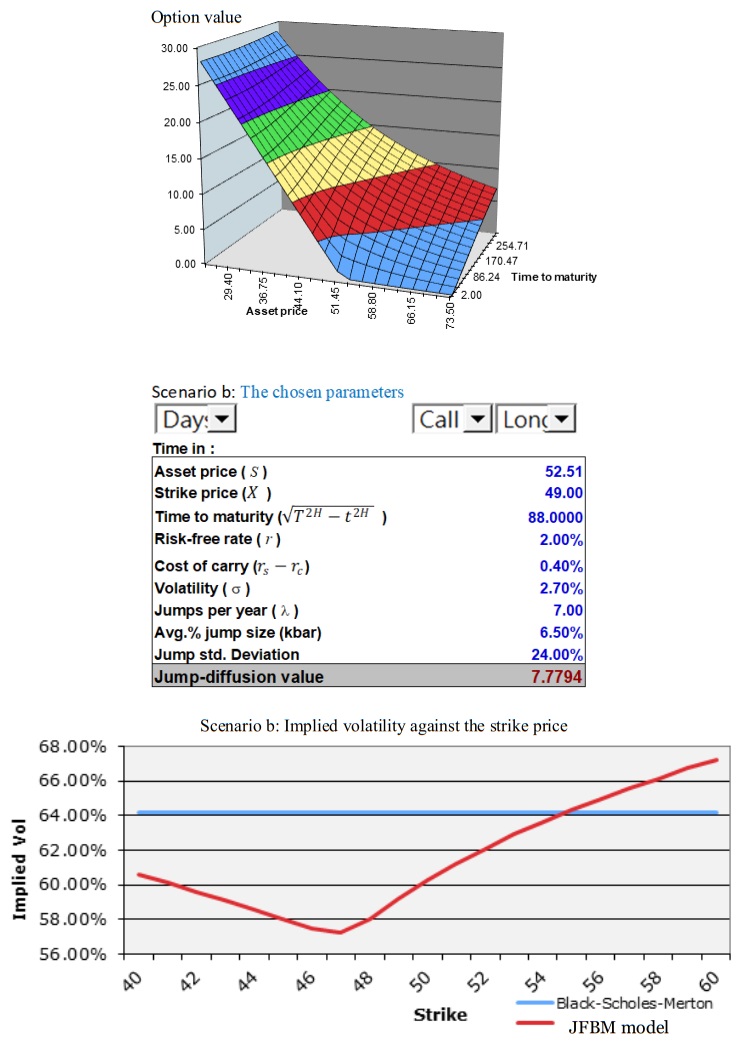
Concerning numerical experiments: Application to green financial derivative valuation, we provide numerical implications by using the asymptotic approximations of the green financial prices under numerical study. We can take a closer look at the values of our jump fractional green financial options for constant Hurst parameters H and then consider the values for computed jump parameters. Panel b of Table 3 exhibits the values of a European green financial call option versus its parameters, H, λ, ${\mu }_{J}$, and δ. The defaulting parameters are S₀ = 52.51, K = 48.5, ${r}_{s}$ = 0.0048, ${r}_{c}$ = 0.0009, σ = 0.0276, t = 0, T = 117 (days), H = 0.572, λ = 7, ${\mu }_{J}$ = 0.0065, and δ_J = 0.2418.

Perhaps unsurprisingly, Figure 5b suggests that the option value is an increasing function of λ, and increasing parameters of ${\mu }_{J}$ and δ_J are accompanied by an increase of the corresponding option value. However, the opposite result was reported in [42].

4.4.1.   Calibration to market data

This study provides a practical example of a green financial options contract written at the strike price on the interval (48.50−53.00) and calls underlying: ICE (Intercontinental Exchange) EUA Futures Mar'24 (CKH24) on 23 February 2024. Our findings displayed in Table 3 should be interpreted with caution.

4.4.2.   Comparison of fits

The fitting results are evaluated in terms of the major measure of the root mean squared error (RMSE) of the calibrated model prices in connection with the market prices. We summarize the pricing performance for the previously calibrated models. Turn to Table 3 displays the RMSE for the calibration on 29 February 2024, while the last column of Table 3 shows each model on the error evaluation indicator of RMSE. The longer maturity pricing options already do a better job than the short maturity pricing options, the call option model results in slightly better fits.

Indeed, the general testing procedure is to compute the implied volatilities of option prices derived by this new model. In what follows, we can account for simultaneously green financial put option prices for various maturities utilizing the JFBM model. In the same way, we present the computed option values generated with our JFBM in Table 4. The calibrated parameters are The strike prices vary from 48.5 to 53.5, S₀ = 52.51, ${r}_{s}$ = 0.0048, ${r}_{c}$ = 0.0009, σ = 0.0276, t = 0, T = 117 (days), H = 0.572, λ = 7, μ_J = 0.0065, and δ_J = 0.2418.

Table 4.  Calculating European put option valuation with jump fractal Brownian motions.

Panel a:
Strike	Market price	Difference	Option value	Delta	Premium	RMSE
48.50P	1.295	0.6602	0.6348	−0.5076	6450	0.9878
49.00P	1.43	0.7519	0.6781	−0.3760	4380
49.50P	1.575	0.8518	0.7232	−0.3899	4580
50.00P	1.735	0.9649	0.7701	−0.4041	4790
50.50P	1.91	1.0912	0.8188	−0.4184	5005
51.00P	2.1	1.2291	0.8709	−0.4329	5230
51.50P	2.31	1.328	0.982	−0.4476	5460
52.00P	2.535	1.2293	1.3057	−0.4624	5695
52.50P	2.765	1.0304	1.7346	−0.4774	5940
53.00P	3.02	0.2486	2.7714	−0.4924	6190
Notes: 1. Time to Maturity=19 days. 2. Downloaded from Barchart.com as of 02-23-2024 06:51pm CST. 3. European put options prices are estimated via Eq (3.27). Calibration of the jump fractal Brownian motions model is simultaneously used to put options, which are the same as Table 3.
Panel b:
Strike	Market price	Difference	Option value	Delta	Premium	RMSE
49.00P	3.98	0.2558	4.2358	-0.3761	4380	0.6920
49.50P	4.17	0.3518	4.5218	-0.3899	4580
50.00P	4.365	0.4481	4.8131	-0.4041	4790
50.50P	4.575	0.5345	5.1095	-0.4184	5005
51.00P	4.79	0.6211	5.4111	-0.4329	5230
51.50P	5.015	0.7026	5.7176	-0.4476	5460
52.00P	5.245	0.7842	6.0292	-0.4624	5695
52.50P	5.485	0.8606	6.3456	-0.4773	5940
53.00P	5.735	0.9318	6.6668	-0.4924	6190
53.50P	5.985	1.0050	6.99	-0.5076	6450
Notes: 1. Time to Maturity=117 days. 2. Numerical results are based on historical parameter estimates and then calibration of the jump fractal Brownian motions model is simultaneously used to put options. 3. Downloaded from Barchart.com as of 02-23-2024 06:51pm CST.

---

 | Show Table

DownLoad: CSV

As can be evidenced in the bottom panel of Figures 5a and 5b, the graphical results are clearly presented as the "smile" effect. That is, the implied volatility is not a constant but varies with moneyness and maturity, exhibiting our model has a good explanation of the "volatility smile" in option pricing.

Regarding inclusive of a comparison between the proposed model and standard models like Black-Scholes or other jump-diffusion models without the fractional component. Now, we compared the implied volatility derived from the mfBm model to that of the conventional Black-Scholes model. More importantly, as depicted in the bottom panel of Figures 5a−5d, the implied volatility in the fitted JFBM model exhibits the "volatility smile" in option pricing for scenario a−d. However, the implied volatility in the fitted Black-Scholes model exhibits a straight line in option pricing. Therefore, we can confirm that our jump fractional Brownian motion (JFBM) model seems a reasonable and efficient one for pricing green financial options.

Figure 5c.  Option value against the maturity time and the asset price (Scenario c).

DownLoad: Full-Size Img PowerPoint

Figure 5d.  Option value against the maturity time and the asset price (Scenario d).

DownLoad: Full-Size Img PowerPoint

4.5.   Valuation implications

This article empirically compounds the jump process and mixed fractional Brownian motion. Besides that, some specific properties of green financial asset pricing formulae are also presented. Moreover, numerical examples acquired in Section 4 suggest that our jump mixed fractional Brownian motion model is commonly used and has particular features to capture the extreme movements of financial markets. In summary, owing to MFBM is a well-developed mathematical model of deeply correlated random processes and jumps can play an important role in financial markets. Meanwhile, JMFBM can be considered a more effective approach for pricing green financial options. In addition, financial asset returns usually have potential jumps, long memory, and volatility clustering. These behaviors cannot be completely captured by geometric Brownian motion. The main objective of this article is to apply a parsimonious parametric model that describes the crucial properties of the data. The major finding from the study is the model specification that allows fractional Brownian motion plus jump processes to quantify these properties of green financial datum.

As usual, a convergent algorithm and a large sample are necessary for relatively precise estimates of the parameters.

To our knowledge, the prior studies on option valuation under an uncertain mixed fractional Brownian motion with a jump model are rare. That is to say, we ought to investigate a more predominate asset-pricing model to capture both the jumps and long-range dependence behaviors of the underlying asset price, and identify key sources of uncertainties, i.e., both uncertain and randomness. Motivated by the aforementioned insights, the major objective of this paper is to expand the tractable analytical tool of the uncertainly mfBm model to alternative models with jumps.

5.   Conclusions and research suggestions

5.1.   Conclusions

At present, In the face of severe climate change, researchers have looked for assistance from financial instruments. They have examined how to hedge the risks of these instruments created by market fluctuations through various green financial derivatives, including green bonds (i.e., fixed-income financial instruments designed to support an environmental goal). In this study, given the historical measure, we use the GARCH-type models with jump innovations to describe the price dynamics of green financial prices as well as the important components in long-memory behavior. As suggested in Figures 2 and 3, we confirm that combining jumps detection of the green financial market with the calibrated parameters in the computational methods for the option pricing model is suitable.

This paper develops a new model and produces instruments for digital currency and green options based on the GARCH model with jumps detection and fractional Brownian motion (FBM). The findings hope to offer a reference for upcoming green financial options trading through the green financial option price predicting technique. The fractal feature of green financial option prices implies that it is reasonable to utilize FBM to predict option prices and the GARCH model incorporating the detected jumps can remedy the lack of constant FBM volatility. The modified fractional Brownian motion option pricing model improved the pricing accuracy. Our results can be treated as a policy reference for the development of a green financial derivatives market and can accelerate the transformation of markets towards a more sustainable economic development model.

To the best of our knowledge, this is the first study to investigate the phenomenon of SOL's jump risk and long-memory gap to explain its valuation as "exceptionally ambiguous". In addition, evidence suggests that SOL price movements have fat-tailed distributions and the returns process of the SOL demonstrates sudden and unexpected price jumps. There is evidence of jumps in the corresponding green financial options. Moreover, these results may be valid for the SOL and carbon of GARCH option pricing models owing to the blockchain progress.

5.2.   Research recommendations

As discussed before, this paper utilizes a jump fractional Brownian motion to describe the behavior of the prices of SOL and carbon and infers the European green financial option pricing model in this jump fractional environment. In addition, some specific features of green assets pricing formulae are also indicated. Our numerical results in Section 4 present that it seems to be necessary to utilize our jump fractional Brownian motion model when the time to maturity is sufficient. At the same time, our JFBM model is essential to use and has the potential to interpret the natural phenomena of volatility smile in option pricing. All in all, jumps play a crucial role in financial markets, and the jump fractional Brownian model can be a more suitable model for pricing green financial options because fractional Brownian motion is a cogent mathematical model for self-similarity with vigorously correlated stochastic processes.

Finally, after analyzing SOL's price under jump-diffusion process, the benefits it may bring, and the potential problems that might arise, we present the specific policy recommendations for the government about green financial assets and derivatives enforcement and regulations that require amendment.

Author contributions

Kuo Shing Chen: Conceptualization, Methodology, Software, Formal analysis, Writing – original draft, review & editing, Validation; Kung-Chi Chen: Writing – original draft, review & editing, Validation. All authors have read and approved the final draft of the paper for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank two anonymous reviewers for their effort and time to offer valuable suggestion on a previous draft of this manuscript.

Conflict of interest

The authors declare there is no conflict of interest.