In this paper, we analyze a modified ratio-dependent predator-prey model with a strong Allee effect and linear prey refugee. The model exhibits rich dynamics with the existence of separatrices in the phase plane in-between basins of attraction associated with oscillation, coexistence, and extinction of the interacting populations. We prove that if the initial values are positive, all solutions are bounded and stay in the interior of the first quadrant. We show that the system undergoes several bifurcations such as transcritical, saddle-node, Hopf, and Bogdanov-Takens bifurcations. Consequently, a homoclinic bifurcation curve exists generating an unstable periodic orbit. Moreover, we find that the Bogdanov-Takens bifurcation acts as an organizing center for the scenario of surviving or extinction of both interacting species. Topologically different phase portraits with all possible trajectories and equilibria are depicted illustrating the behavior of the system.
Citation: Khairul Saleh. Basins of attraction in a modified ratio-dependent predator-prey model with prey refugee[J]. AIMS Mathematics, 2022, 7(8): 14875-14894. doi: 10.3934/math.2022816
| [1] | Na Min, Hongyang Zhang, Xiaobin Gao, Pengyu Zeng . Impacts of hunting cooperation and prey harvesting in a Leslie-Gower prey-predator system with strong Allee effect. AIMS Mathematics, 2024, 9(12): 34618-34646. doi: 10.3934/math.20241649 |
| [2] | Francesca Acotto, Ezio Venturino . How do predator interference, prey herding and their possible retaliation affect prey-predator coexistence?. AIMS Mathematics, 2024, 9(7): 17122-17145. doi: 10.3934/math.2024831 |
| [3] | Qian Xu, Chunfeng Xing . The stability of bifurcating solutions for a prey-predator model with population flux by attractive transition. AIMS Mathematics, 2021, 6(7): 6948-6960. doi: 10.3934/math.2021407 |
| [4] | Yingyan Zhao, Changjin Xu, Yiya Xu, Jinting Lin, Yicheng Pang, Zixin Liu, Jianwei Shen . Mathematical exploration on control of bifurcation for a 3D predator-prey model with delay. AIMS Mathematics, 2024, 9(11): 29883-29915. doi: 10.3934/math.20241445 |
| [5] | Xuyang Cao, Qinglong Wang, Jie Liu . Hopf bifurcation in a predator-prey model under fuzzy parameters involving prey refuge and fear effects. AIMS Mathematics, 2024, 9(9): 23945-23970. doi: 10.3934/math.20241164 |
| [6] | Eric M. Takyi, Charles Ohanian, Margaret Cathcart, Nihal Kumar . Sex-biased predation and predator intraspecific competition effects in a prey mating system. AIMS Mathematics, 2024, 9(1): 2435-2453. doi: 10.3934/math.2024120 |
| [7] | Heping Jiang . Complex dynamics induced by harvesting rate and delay in a diffusive Leslie-Gower predator-prey model. AIMS Mathematics, 2023, 8(9): 20718-20730. doi: 10.3934/math.20231056 |
| [8] | Wei Ou, Changjin Xu, Qingyi Cui, Yicheng Pang, Zixin Liu, Jianwei Shen, Muhammad Zafarullah Baber, Muhammad Farman, Shabir Ahmad . Hopf bifurcation exploration and control technique in a predator-prey system incorporating delay. AIMS Mathematics, 2024, 9(1): 1622-1651. doi: 10.3934/math.2024080 |
| [9] | Weili Kong, Yuanfu Shao . The effects of fear and delay on a predator-prey model with Crowley-Martin functional response and stage structure for predator. AIMS Mathematics, 2023, 8(12): 29260-29289. doi: 10.3934/math.20231498 |
| [10] | Chenxuan Nie, Dan Jin, Ruizhi Yang . Hopf bifurcation analysis in a delayed diffusive predator-prey system with nonlocal competition and generalist predator. AIMS Mathematics, 2022, 7(7): 13344-13360. doi: 10.3934/math.2022737 |
In this paper, we analyze a modified ratio-dependent predator-prey model with a strong Allee effect and linear prey refugee. The model exhibits rich dynamics with the existence of separatrices in the phase plane in-between basins of attraction associated with oscillation, coexistence, and extinction of the interacting populations. We prove that if the initial values are positive, all solutions are bounded and stay in the interior of the first quadrant. We show that the system undergoes several bifurcations such as transcritical, saddle-node, Hopf, and Bogdanov-Takens bifurcations. Consequently, a homoclinic bifurcation curve exists generating an unstable periodic orbit. Moreover, we find that the Bogdanov-Takens bifurcation acts as an organizing center for the scenario of surviving or extinction of both interacting species. Topologically different phase portraits with all possible trajectories and equilibria are depicted illustrating the behavior of the system.
The dynamic of a population depends on its interactions with other species. Several kinds of interactions among species have been observed, for instance, competition, predation, and mutualism. The predator-prey interaction has long been and will remain to be one of the main subjects in both Ecology and Mathematics because of its common existence and significance [11]. The predator-prey model was first introduced by Volterra [44] and Lotka [35] in the 1920s, showing oscillating behaviors in the interacted populations. After this work by Volterra and Lotka, various generalized predator-prey models have been proposed by many researchers. Several aspects have been considered in the predator-prey modeling including infectious diseases and age-structured [7], group defense strategy [42,45,47], delayed, harvesting and prey social behavior [16], etc.
A functional response is the main factor of the predator-prey model. It represents the change of the prey density per unit of time per predator. In the classical model, the prey-dependent consumption rate was considered. Different prey-dependent functional responses were researched extensively [4,28,37,45]. However, several biologists questioned the sole dependence of the functional response on prey density, see for instance [1,13,23,25]. It has been shown that predators might seem to search, share, or compete for food [1,11,23,25,26]. Predators might interfere with each other's foraging and hence, the functional response should depend on both prey and predator densities [1,13]. In some cases, for instance, perfect sharing, the functional response depends on the ratio of prey to predator density [1,11,23,25,26]. The ratio-dependent predator-prey system displays rich, original, and reasonable dynamic properties, which does not generate the so-called paradox of enrichment [29,32,48]. It also allows the predator population or both populations to either become extinct or coexist, depending on the initial values. The use of ratio-dependent functional response is supported by several experiments and observations and is largely employed in the modeling of predator and prey interaction [1,2,8,32,46] and references cited therein.
On the other hand, many species experience a decrease in fitness at a small population density caused by the deficiency of conspecifics. This phenomenon is called the Allee effect [5]. If the Allee effect is sufficiently strong, the species go through negative growth lower than a specific threshold level and then extinct. A strong Allee effect triggers the Allee threshold, which the population needs to overcome to prevent extinction [6,43]. For example, in a predator-prey system, when the prey's density is too small, the prey may have difficulties protecting or hiding from the predator and in displaying an antipredator behavior when its density is too small [45,47]. Naturally, this phenomenon generates an Allee effect on the prey caused by predation [20,21]. The Allee effect has been used in many predator-prey models [9,14,17,18,24,39,42], showing that it produces rich dynamics and eliminates the possibility of prolonged oscillators. Many investigations have been carried out to study the dynamical properties of predator-prey models with the ratio-dependent functional response and Allee effect, see for instance [3,22]. It was shown that including the Allee effect in the ratio-dependent predator-prey model eliminates the chance of lasting oscillations of the populations and produces a richer variety of behavior. It may also expand the basin of attraction of the extinction equilibrium and therefore raises the possibility of extinction of the interacted populations. Prey refuge can lower the predation threat and help in the management of the population caused by the Allee effect. This phenomenon may reduce the risk of extinction of the species by decreasing the predation risk. Several experiments and mathematical models concluded that refuge has a balancing effect on the interactions of both populations. Many researchers have discussed the influence of prey refuge in the dynamical properties of some predator-prey models [12,27,30,31,36,38] and references cited therein. The results showed that the prey refuge can increase the stability of the interior equilibrium. For more biological backgrounds and findings on the effects of refuge of prey, we refer to [12,27,30,31,33,36,38,41] and the references therein.
The purpose of this paper is to investigate a Gause-type predator-prey system with a ratio-dependent functional response, considering prey refuge and a strong Allee effect that affects the prey population. We are interested in the existence and stability of equilibria and periodic orbits of the system, including basins of attractions of stable equilibria and periodic orbits. Especially, the positive equilibria (and periodic orbits) that imply the coexistence of the interacting populations. We are also interested in local and global bifurcations and the organization of trajectories of the system. Under certain conditions, we show that the system possesses a positive equilibrium and undergoes transcritical, saddle-node, Hopf, and Bogdanov–Takens bifurcations. It is known that the existence of Bogdanov-Takens bifurcation induces a global phenomenon, namely homoclinic connection. With the help of the numerical package, MATCONT [15], we illustrate these phenomena using a bifurcation diagram and associated phase portraits, displaying basins of attraction of stable equilibria and periodic orbit. The boundaries of basins of attraction are obtained as invariant manifolds of equilibria also computed with the package MATCONT [15]. We reveal that the Bogdanov-Takens bifurcation acts as an organizing center of the bifurcation diagram in the system. Additionally, to complete the work we prove that the system is well-posed, that is, any solution in the first quadrant stays non-negative and is bounded.
This paper is organized as follows. The model and a preliminary result on the boundedness of positive solutions are given in Section 2. We present results on equilibrium solutions in Section 3. In Section 4, we discuss local and global bifurcations that involve equilibria, periodic orbit, and homoclinic connection. Section 5 gives the changes of basins of attraction of equilibria and periodic orbit. In section 6, we summarize and give concluding remarks on the main results of this paper.
Consider the following family of vector fields describing the interaction of predators and prey populations in an isolated environment:
| $ \begin{equation} {\textbf{U}}: \left\{ \begin{array}{ll} \dfrac{du}{d\tau} = ru(u-a)\left(1-\dfrac{u}{K}\right)-\dfrac{buv}{u+v},\\ \dfrac{dv}{d\tau} = \dfrac{bcuv}{u+v}-ev,\qquad\qquad (a,b,c,e,K,r)\in\mathbb{R}^6. \end{array} \right. \end{equation} $ | (2.1) |
System (2.1) is a modification of the simple Lotka-Volterra model [35,44] and is of a Gauss-type model [19]. The functions $ u(\tau) $ and $ v(\tau) $ represent the sizes of prey and predator populations depending on time $ \tau $, respectively. The constant $ r $ denotes the prey intrinsic growth rate; $ K $ is the prey carrying capacity; $ a $ stands for the Allee threshold of the prey population; $ e $ denotes the predator natural death rate; the coefficient $ b $ represents the predation rate; $ c $ is the rate of conversion representing the size of newly born predators for every eaten prey. The expression $ uv/(u+v) $ denotes the response function depending on the ratio of prey to predator populations.
Introducing the prey refuge in (2.1) yields the following modified system
| $ \begin{equation} {\textbf{V}}: \left\{ \begin{array}{ll} \dfrac{du}{d\tau} = ru(u-a)\left(1-\dfrac{u}{K}\right)-\dfrac{b(1-m)uv}{(1-m)u+v},\\ \dfrac{dv}{d\tau} = \dfrac{bc(1-m)uv}{(1-m)u+v}-ev, \end{array} \right. \end{equation} $ | (2.2) |
where $ m\in[0, 1) $ represents the rate of prey refuge that protects $ mu $ of the prey and leaves $ (1-m)x $ of the prey available to the predator. By means of a rescaling of parameters and time, it can be shown that system (2.2) is topologically equivalent to the system
| $ \begin{equation} {\textbf{X}}:\left\{ \begin{array}{ll} \dot{x} = x(x-A)(1-x)-\dfrac{B(1-\mu)xy}{(1-\mu)x+y},\\ \dot{y} = \dfrac{\alpha(1-\mu)xy}{(1-\mu)x+y}-\delta y, \end{array} \right. \end{equation} $ | (2.3) |
with $ (A, \alpha, B, \delta, \mu)\in(0, 1)\times\mathbb{R}_+^3\times (0, 1), $ and
| $ \dot{x} = \dfrac{dx}{dt}, \; \; \dot{y} = \dfrac{dy}{dt},\; \; A = \frac{a}{K},\; \; \; B = \frac{b}{Kr},\; \; \; \alpha = \frac{bc}{Kr},\; \; \; \mu = \frac{M}{K},\; \; \; \delta = \frac{e}{Kr}. $ |
In the above re-parameterization, we construct a diffeomorphism $ \phi: \mathbb{R}^3\to \mathbb{R}^3 $ defined by
| $ \phi(x,y,t) = (Kx,rKy/b,t/r) = (u,v,\tau). $ |
The diffeomorphism $ \phi $ preserves the time orientation. We set $ \dot{x} = \dot{y} = 0 $ for $ (x, y) = (0, 0). $ Observe that system (2.3) is continuous in the closed first quadrant in the $ xy $-plane. Define the set
| $ \Omega = \{(x,y)\in\mathbb{R}^2, x\geq 0, y\geq 0\}. $ |
As a typical deterministic predator-prey system, all orbits of system (2.3) are trapped in the first quadrant for any positive initial data.
Theorem 2.1. Solutions of system ${\rm(2.3)}$ in $ \Omega $ are uniformly bounded.
Proof. Define $ z(t) = \alpha x(t)+B y(t) $. We obtain
| $ \frac{dz}{dt} = \alpha \frac{dx}{dt}+B \frac{dy}{dt} = \alpha x(x-A)(1-x)-B\delta y. $ |
For every $ \gamma > 0, $
| $ \frac{dz}{dt}+\gamma z = \alpha x[(x-A)(1-x)-\gamma]-(B\delta-\gamma)y. $ |
The function
| $ f(x) = \alpha x[(x-A)(1-x)-\gamma] $ |
has a global maximum at
| $ \tilde{x} = \frac{1}{3}(1+A+\sqrt{1+A^2-A-3\gamma}) $ |
with the maximum value
| $ f(\tilde{x}) = \frac{\alpha}{27} \left(1+A+\sqrt{1+A^2-A-3\gamma}\right)\left(1+A^2-4A-6\gamma+(1+A) \sqrt{1+A^2-A-3\gamma}\right). $ |
Thus,
| $ \frac{dz}{dt}+\gamma z \leq f(\tilde{x})-(B\delta-\gamma)y . $ |
If $ 0 < \gamma\leq B\delta $ and $ 6\gamma\leq 1+A^2-4A+(1+A)\sqrt{1+A^2-A-3\gamma}, $ then there exists $ \psi > 0 $ such that
| $ \frac{dz}{dt}\leq\psi-\gamma z. $ |
Applying the differential inequality [34,40] yields
| $ 0 < z(x,y) < \frac{\psi}{\gamma} (1-e^{-\gamma t} )+z(x(0),y(0)) e^{-\gamma t}. $ |
As $ t\to\infty, $ we obtain $ 0 < z < \psi/\gamma. $ Therefore, there exists a trapping region in $ \Omega $ given by
| $ Q = \{(x,y)\in\Omega|\; z = \psi/\gamma+\psi,\; \psi > 0\} $ |
in which all positive solutions are attracted.
An equilibrium of (2.3) is the point of intersection of the curve
| $ \begin{equation} y = \frac{x(1-\mu)(x-A)(1-x)}{B(1-\mu)-(x-A)(1-x)} \end{equation} $ | (3.1) |
and the line
| $ \begin{equation} y = \frac{x(\alpha-\delta)(1-\mu)}{\delta} \end{equation} $ | (3.2) |
within the first quadrant. System (2.3) has a critical point at the origin $ O(0, 0). $ However, the system cannot be linearized at $ O. $ Hence, we cannot study the local stability of $ O(0, 0). $ Note that our interest is in the dynamics of the system in the interior of the first quadrant. Nevertheless, several authors have discussed this equilibrium for the ratio-dependent predator-prey system, see for instance [3,22,32,48]. By means of a time rescaling, the system changed to an equivalent polynomial dynamical system in the interior of the first quadrant. In the new system, the origin is an isolated critical point of higher order. In [3,22], a ratio-dependent predator-prey system with a strong Allee effect was discussed. The authors showed that the origin was a non-hyperbolic attractor. It is easy to see that the conclusion is the same when the linear prey refuge is added to the system.
If $ y = 0, $ then two equilibria $ E_1(1, 0) $ and $ E_A(A, 0) $ coexist on the positive $ x $-axis. Since $ \mu\in[0, 1) $, the line (3.2) lies in the first quadrant if
| $ (H_1): \alpha \geq \delta. $ |
This means that to have a positive equilibrium, the predation rate should be strictly larger than the natural death rate of the predator. Recall that $ A\in(0, 1). $ Thus, the numerator of (3.1) is positive only for $ A < x < 1. $ Observe that $ f(x) = (x-A)(1-x) $ has a maximum value at $ x = (1+A)/2 $ and
| $ \max\limits_{{A < x < 1}} \{f(x)\}\equiv M = \frac{(1-A)^2}{4}. $ |
We have the following two cases:
Case (i) If
| $ (H_2): B > \frac{M}{1-\mu}, $ |
then $ y > 0 $ for $ A < x < 1. $ The nullcline of prey is a smooth convex curve connecting equilibria $ E_1 $ and $ E_A $ and has a maximum in the interval $ (A, 1). $
Case (ii) If
| $ (H_3):B < \frac{M}{1-\mu}, $ |
then the denominator of (3.1) is positive for $ A < x < x_1 $ and $ x_2 < x < 1, $ where $ x_1 $ and $ x_2 $ satisfy the equation
| $ B(1-\mu) = (x_i-A)(1-x_i ),\; i = 1,2. $ |
The prey zero growth isocline is discontinuous and possesses a couple of vertical asymptotes at $ x = x_1 $ and $ x = x_2. $
System (3.1) has at most two positive equilibria obtained by the intersection between the zero growth isoclines of both populations; $ P_1 (x_1^*, y_1^*) $ and $ P_2(x_2^*, y_2^*), $
| $ x_i^* = \frac{1}{2}\left(1+A+(-1)^i \sqrt{\Delta}\right), \; \; y_i^* = \frac{x_i^*}{\delta} (\alpha-\delta)(1-\mu),\; i = 1,2, $ |
where
| $ \Delta = (A-1)^2-\frac{4B}{\alpha}(1-\mu)(\alpha-\delta). $ |
Note that if we increase the value of $ \mu, $ then both positive equilibria approaches the $ x $-axis. Observe that $ \Delta $ is always positive under conditions $ (H_1) $ and $ (H_3) $. In this case, both $ P_1 $ and $ P_2 $ always coexist. Under restriction $ (H_2), $ an extra condition is needed for the existence of positive equilibrium points, namely
| $ (H_4 ): \delta\geq \alpha-\frac{\alpha(A-1)^2}{4B(1-\mu)} . $ |
Hence, if conditions $ (H_1), (H_2) $ and $ (H_4) $ hold, then two positive equilibria $ P_1 $ and $ P_2 $ appear in the first quadrant. In the case of equality in condition $ (H_4), $ equilibria $ P_1 $ and $ P_2 $ collide and there is only a single positive equilibrium $ P^*(x^*, y^*), $ where
| $ x^* = \frac{1+A}{2}, \; \; y^* = \frac{(\alpha-\delta)(1-\mu)(1+A)}{2\delta}. $ |
Based on the standard linearization technique, we discuss the stability (locally) of equilibrium solutions of system (2.3). The linearized matrix of the system is
| $ \begin{equation*} J(x,y) = \begin{pmatrix} (-3x^2+2(1+A)x-A-\dfrac{B(1-\mu)y^2}{\left[(1-\mu)x+y\right]^2} & -\dfrac{(B(1-\mu)^2 x^2)}{\left[(1-\mu)x+y\right]^2} \\ \dfrac{(\alpha(1-\mu)y^2)}{\left[(1-\mu)x+y\right]^2} & \dfrac{\alpha(1-\mu)^2 x^2}{\left[(1-\mu)x+y\right]^2} -\delta \end{pmatrix}. \end{equation*} $ |
At the equilibrium $ E_1 = (1, 0), $ we obtain
| $ J(E_1 ) = \begin{pmatrix} A-1 & -B \\ 0 & \alpha-\delta \end{pmatrix}, $ |
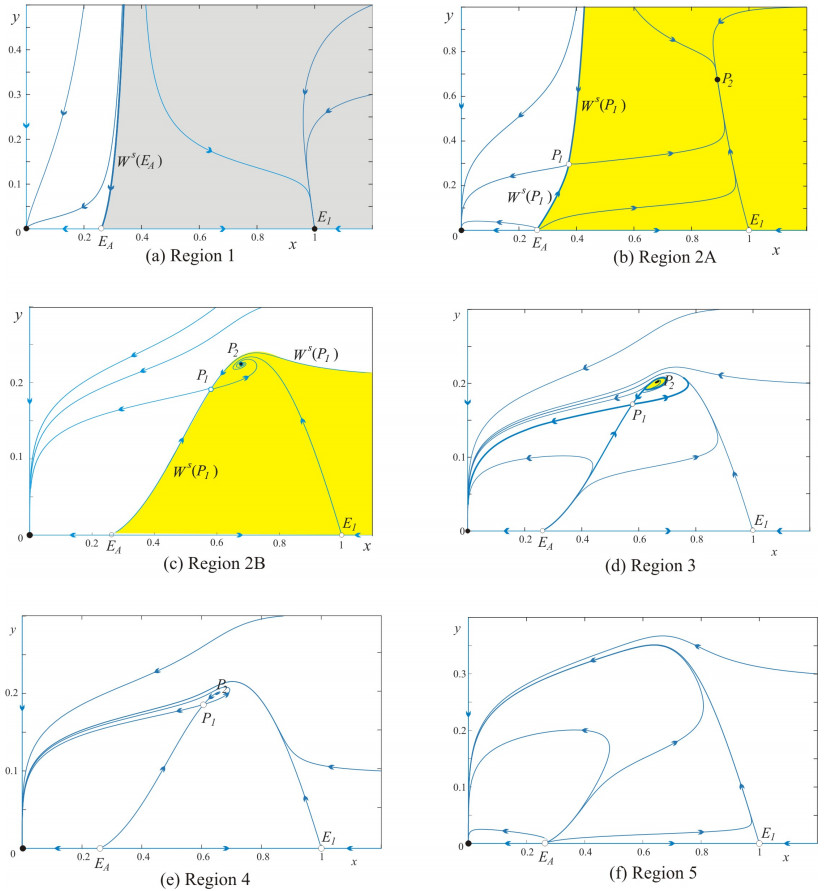
with eigenvalues $ \lambda_1 = A-1 $ (always negative since $ 0 < A < 1 $) and $ \lambda_2 = \alpha-\delta. $ Hence, the equilibrium $ E_1 $ is locally stable for $ \alpha < \delta $ and is a saddle point for $ \alpha > \delta. $ The stable manifold of $ E_1 $ lies on the $ x $-axis, see Figure 1. It can be deduced that the local stability of $ E_1 $ implies the nonexistence of positive equilibria.

The linearized matrix computed at $ E_A = (A, 0) $ is
| $ J(E_A) = \begin{pmatrix} A(1-A) & -B\\ 0 & \alpha-\delta \end{pmatrix}, $ |
with eigenvalues $ \lambda_1 = A(1-A) $ (always positive since $ 0 < A < 1 $) and $ \lambda_2 = \alpha-\delta. $ Thus, $ E_A $ is an unstable equilibrium for $ \alpha > \delta $ and is a saddle point for $ \alpha < \delta $ with unstable manifold on the $ x $-axis, see Figure 1. Therefore, the presence of positive equilibria implies the local instability of $ E_A. $
Let $ J(P_i) $ be the linearized matrix computed at the positive equilibria $ P_i, \; i = 1, 2. $ We obtain
| $ \det(J(P_1) ) = -\frac{\delta(\alpha-\delta)}{2\alpha} \left[(1+A) \sqrt{\Delta}-\Delta\right]. $ |
Under condition $ (H_1), $ if $ \alpha, B, $ and $ \delta $ are all positive, then $ (1+A) > \sqrt{\Delta}. $ This fact and restriction $ (H_3) $ imply that $ \det(J(P_1)) < 0. $ Thus, $ P_1 $ is always a saddle point. At $ P_2, $
| $ \begin{equation} \det(J(P_2)) = \frac{\delta(\alpha-\delta)}{2\alpha} \left[(1+A) \sqrt{\Delta}+\Delta\right] > 0. \end{equation} $ | (3.3) |
Hence, the equilibrium $ P_2 $ is a local attractor if $ \text{Tr}(J(P_2)) < 0 $ and is a source if $ \text{Tr}(J(P_2)) > 0, $ where
| $ \begin{equation} \text{Tr}(J(P_2)) = \frac{B}{\alpha^2} (1-\mu)(\alpha-\delta)(2\alpha+\delta)-\frac{\delta}{\alpha} (\alpha-\delta)-\frac{1}{2} \left[(1-A)^2+(1+A) \sqrt{\Delta}\right]. \end{equation} $ | (3.4) |
In Table 1, we summarize our results on the analysis of stability of the steady states of system (2.3).
| Steady state | Existence | Local stability |
| $ O(0, 0) $ | Always exists | Non-hyperbolic attractor [3,22] |
| $ E_1 (1, 0) $ | Always exists | Saddle point ($ \alpha < \delta $) and unstable ($ \alpha > \delta $) |
| $ E_A (A, 0) $ | Always exists | Stable ($ \alpha < \delta $) and saddle point ($ \alpha > \delta $) |
| $ P_1(x_1^*, y_1^*) $ | $ (H_1), (H_3), \alpha > 0, B > 0, \delta > 0 $ or $ (H_1), (H_2), (H_4) $ | Saddle point |
| $ P_2(x_2^*, y_2^*) $ | $ (H_1) $, $ (H_3) $ or $ (H_1), (H_2), (H_4) $ | Stable ($ \text{Tr}(J(P_2)) < 0 $) Unstable ($ \text{Tr}(J(P_2)) > 0 $) |
| $ P^*(x^*, y^*) $ | $ (H_1), \delta=\alpha\left(1-\dfrac{(A-1)^2}{4B(1-\mu)}\right) > 0 $ | Non-hyperbolic saddle point |
Now we show that system (2.3) exhibits several local and global bifurcations, namely, transcritical, saddle-node, Hopf, heteroclinic and Bogdanov-Takens bifurcations. Sotomayor's theorem [40] and the algorithm introduced in [34] are applied to prove the existence and nondegeneracy of local bifurcations.
Theorem 4.1. (Saddle-node bifurcation) If $ 4B(1-\mu)\neq(A-1)^2, $ then system ${\rm(2.3)}$ undergoes saddle-node bifurcation at $ P^*(x^*, y^*), $
| $ \begin{equation} x^* = \frac{1+A}{2},\; \; y^* = \frac{(\alpha-\delta)(1-\mu)(1+A)}{2\delta}, \end{equation} $ | (4.1) |
whenever the parameters satisfy the condition
| $ \delta = \delta_{SN} = \alpha\left(1-\frac{(A-1)^2}{4B(1-\mu)}\right) > 0. $ |
Proof. The linearized matrix evaluated at $ P^* $ is
| $ \begin{equation} J(P^*) = \begin{pmatrix} -\dfrac{(A-1)^2 \left((A-1)^2-4B(1-\mu)\right)}{16B(1-\mu)} & -\dfrac{\left((A-1)^2-4B(1-\mu)\right)^2}{16B(1-\mu)^2} \\ \dfrac{\alpha(A-1)^4}{16B^2 (1-\mu)}& \dfrac{\alpha(A-1)^2 \left((A-1)^2-4B(1-\mu)\right)}{16B^2 (1-\mu)^2} \end{pmatrix}. \end{equation} $ | (4.2) |
It is easy to check that $ \det(J(P^*)) = 0 $ and hence, $ \lambda = 0 $ is an eigenvalue of $ J(P^*) $ with corresponding eigenvector
| $ \begin{equation*} V = \begin{pmatrix} \dfrac{1}{\mu-1}+\dfrac{4B}{(A-1)^2}\\ 1 \end{pmatrix}. \end{equation*} $ |
The eigenvector corresponding to $ \lambda = 0 $ for $ J(P^*)^T $ is given by
| $ \begin{equation*} W = \begin{pmatrix} \dfrac{(A-1)^2 \alpha}{B(A-1)^2-4B^2 (1-\mu)}\\ 1 \end{pmatrix}. \end{equation*} $ |
Define
| $ \begin{equation} G = \begin{pmatrix} x(x-A)(1-x)-\dfrac{B(1-\mu)xy}{(1-\mu)x+y}\\ \dfrac{\alpha(1-\mu)xy}{(1-\mu)x+y}-\delta y \end{pmatrix}, \end{equation} $ | (4.3) |
which is a vector form of the right hand side of equations in (2.3). Since $ A\in(0, 1) $ and $ \mu\in[0, 1), $ one can compute that
| $ W^T[G_{\delta} (x^*,y^*,\delta_{SN})V] = -\frac{(A-1)^2 (A+1)(1-\mu)}{2((A-1)^2-4B(1-\mu))}\neq 0 $ |
and verify that if $ 4B(1-\mu)\neq(A-1)^2, $ then
| $ W^T [D^2 G(x^*,y^*,\delta_{SN})(V,V)] = \frac{\alpha(A+1)[4B(1-\mu)-(A-1)^2]}{B(A-1)^2 (1-\mu)^2 }\neq 0. $ |
Sotomayor's theorem [40] signifies that system (2.3) undergoes a saddle-node bifurcation when $ \delta = \delta_{SN}. $
Theorem 4.2. (Transcritical bifurcation) System ${\rm(2.3)}$ exhibits transcritical bifurcation at $ E_1(1, 0) $ and $ E_A (A, 0) $ whenever the parameters satisfy the condition $ \delta = \delta_T = \alpha. $
Proof. The linearized matrix at $ E_1(1, 0) $ is
| $ \begin{equation*} J(E_1) = \begin{pmatrix} A-1 & -B \\ 0 & 0 \end{pmatrix}. \end{equation*} $ |
It is easy to check that $ \det(J(E_1)) = 0 $ and hence, $ \lambda = 0 $ is an eigenvalue of $ J(E_1). $ If $ V_1 $ and $ W_1 $ are eigenvectors associated to $ \lambda = 0 $ for $ J(E_1) $ and $ J(E_1)^T, $ respectively, then one can compute
| $ V_1 = \begin{pmatrix} \dfrac{B}{A-1} \\ 1 \end{pmatrix} \; \; \mbox{and} \; \; W_1 = \begin{pmatrix} 0\\ 1 \end{pmatrix} $ |
and obtain
| $ W_1^T G_\delta (1,0,\delta_T ) = \begin{pmatrix}0& 1\end{pmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} = 0, $ |
| $ W_1^T [DG_\delta (1,0,\delta_T )V_1] = \begin{pmatrix} 0 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ -1 \end{pmatrix} = -1, $ |
and
| $ W_1^T \left[D^2 G(1,0,\delta_T )(V_1,V_1)\right] = -\frac{2\alpha}{1-\mu}\neq 0, $ |
where $ G $ is given in (4.3). Sotomayor's theorem implies that system (2.3) exhibits a transcritical bifurcation when $ \delta = \delta_T. $
The Jacobian (linearization) matrix at $ E_A (A, 0) $ is given by
| $ \begin{pmatrix} A(1-A) & -B \\ 0 & 0 \end{pmatrix}. $ |
It is easy to check that $ \det(J(E_A)) = 0 $ and hence, $ \lambda = 0 $ is an eigenvalue of $ J(E_A). $ If $ V_2 $ and $ W_2 $ are eigenvectors associated to $ \lambda = 0 $ for $ J(E_A) $ and $ J(E_A)^T, $ respectively, then one can compute
| $ V_2 = \begin{pmatrix} \dfrac{B}{A(1-A)} \\ 1 \end{pmatrix} \; \; \mbox{and}\; \; W_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $ |
and obtain
| $ W_2^T G_\delta (1,0,\delta_T ) = \begin{pmatrix} 0 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ 0 \end{pmatrix} = 0, $ |
| $ W_2^T [DG_\delta (1,0,\delta_T)V_2] = \begin{pmatrix} 0 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ -1 \end{pmatrix} = -1, $ |
and
| $ W_2^T \left[D^2 G(1,0,\delta_T )(V_2,V_2)\right] = -\frac{2\alpha}{A(1-\mu)}\neq0. $ |
Sotomayor's theorem implies that system (2.3) exhibits a transcritical bifurcation at $ E_A(A, 0) $ when $ \delta = \delta_T = \alpha. $
Remark 4.3. Recall that the parameter $ 0 < A < 1, $ is an Allee threshold for the prey in the absence of predators. However, it is worth mentioning that when $ A = 1, $ equilibria $ P_1, P_2, E_A $ and $ E_1 $ collide at $ E_1. $ It is an interesting phenomenon when transcritical and saddle-node bifurcations occur at the same time. In this case, the Jacobian matrix at $ E_1 $ is given by
| $ \begin{pmatrix} 0 & -B \\ 0 & 0 \end{pmatrix}. $ |
It is a phenomenon called degenerate transcritical bifurcation where the transcritical and saddle-node bifurcations meet tangently [10].
As mentioned in the previous section, the equilibrium $ P_1 $ (if it exists) is a saddle-point for any parameter values. Therefore, a Hopf bifurcation only occurs at $ P_2 $ with the following conditions
| $ \text{Tr}(J(P_2))|_{\delta = \delta_H} = 0 \; \; \; \mbox{and}\; \; \; \det(J(P_2))|_{\delta = \delta_H}\neq 0. $ |
We refer to Eq (3.4) for the trace of $ J(P_2). $ We obtain an implicit expression of $ \delta_H $ as follows.
| $ \begin{equation} 2\alpha^2\left[(1-A)^2+(1+A)K\right]+4(\alpha-\delta_H)\left[\alpha\delta_H-B(1-\mu)(\delta_H+2\alpha)\right] = 0,\quad \delta_H > 0, \end{equation} $ | (4.4) |
where $ K = \sqrt{(1-A)^2-\dfrac{4B}{\alpha}(1-\mu)(\alpha-\delta_H)}. $ From (3.3) we see that if the positive equilibrium $ P_2 $ exists, then $ \det(J(P_2))|_{\delta = \delta_H} > 0. $ Differentiating $ \text{Tr}(J(P_2)) $ with respect to $ \delta, $ we obtain
| $ \dfrac{d}{d\delta} \text{Tr}[J(P_2)]|_{\delta = \delta_H} = \dfrac{1}{\alpha^2}\left[2\alpha\delta-\alpha^2-B(1-\mu)\left(\alpha+2\delta+\dfrac{1+A}{\alpha\sqrt{\Delta}}\right)\right]\neq 0, $ |
| $ 1-\dfrac{(A-1)^2}{4B(1-\mu)} < \dfrac{\delta}{\alpha} < 1. $ |
Therefore, the Hopf bifurcation is transversal [40]. As a result of the Hopf bifurcation, a periodic orbit appears in the interior of the first quadrant with negative first Lyapunov number. This implies that the periodic orbit is unstable. Thus, the following statements are valid.
Theorem 4.4.
(a) For the values of parameters satisfying ${\rm(4.4)}$, the equilibrium $ P_2 $ is a stable weak focus.
(b) System ${\rm(2.3)}$ has a unique unstable limit cycle for certain values of parameters.
System (2.3) exhibits a Bogdanov-Takens (BT) bifurcation of codimension two whenever the parameters satisfy the condition
| $ \alpha_{BT} = \delta+\dfrac{1}{4}(1-A)^2 > 0,\quad B_{BT} = \dfrac{(A-1)^2+4\delta}{4(1-\mu)} > 0. $ |
Using the algorithm introduced in [34], we show that BT bifurcation is nondegenerate. Let $ \lambda = (\lambda_1, \lambda_2) $ be a small parameter. System (2.3) about the BT point $ (\alpha_{BT}, B_{BT}) $ reads
| $ \begin{align*} \dfrac{dx}{dt}& = x(x-A)(1-x)-\dfrac{(B+\lambda_2)(1-\mu)xy}{(1-\mu)x+y}\equiv F_1 (x,y,\lambda_1 )\\ \dfrac{dy}{dt}& = \dfrac{(\alpha+\lambda_1)(1-\mu)xy}{((1-\mu)x+y)}-\delta y\equiv F_2 (x,y,\lambda_2). \end{align*} $ |
Translating the equilibria $ (x^*, y^*) $ to $ (0, 0) $ and expanding $ F_1 $ and $ F_2 $ in power series about $ (x, y) = (0, 0) $ yields the following system:
| $ \begin{align} \dfrac{du_1}{dt} = &\left(c_{11}-\dfrac{(1-\mu)^2 \lambda_1 (y^*)^2}{\left[(1-\mu)x^*+y^*\right]^2}\right) u_1+\left(c_{12}-\dfrac{(1-\mu)^2 \lambda_1(x^*)^2}{\left[(1-\mu) x^*+y^*\right]^2}\right) u_2+a_{11} u_1^2\\ &+a_{12} u_1 u_2+a_{13} u_2^2+R_1(u_1,u_2 )\\ \dfrac{du_2}{dt} = &\left(c_{21}+\dfrac{((1-\mu)^2 \lambda_2 (y^*)^2)}{\left[(1-\mu) x^*+y^*\right]^2}\right) u_1+\left(c_{22}+\dfrac{(1-\mu)^2 \lambda_2 (x^*)^2}{\left[(1-\mu) x^*+y^*\right]^2}\right) u_2+a_{21} u_1^2\\ &+a_{22} u_1 u_2+a_{23} u_2^2+R_2(u_1,u_2 ), \end{align} $ | (4.5) |
where $ u_1 = x-x^*, \; u_2 = y-y^*. $ The constants $ c_{ij} $ are the entries of the Jacobian matrix $ J(P^*) $ given in (4.2). The coefficients $ a_{ij} $ are determined by
| $ \begin{align*} a_{11}& = 1+A-3y^*+\dfrac{(1-\mu)^2 (B+\lambda_1 )(y^*)^2}{[(1-\mu) x^*+y^* ]^3},\qquad a_{12} = -\dfrac{2(1-\mu)^2 (B+\lambda_1 ) x^* y^*}{[(1-\mu) x^*+y^* ]^3},\\ a_{13}& = \dfrac{((1-\mu)^2 (B+\lambda_1 )(x^*)^2)}{[(1-\mu) x^*+y^* ]^3},\qquad\qquad\qquad\quad a_{21} = -\dfrac{(1-\mu)^2 (\alpha+\lambda_2 )(y^*)^2}{[(1-\mu) x^*+y^* ]^3},\\ a_{22}& = \dfrac{2(1-\mu)^2 (\alpha+\lambda_2 ) x^* y^*}{[(1-\mu) x^*+y^* ]^3},\qquad\qquad\qquad\quad a_{23} = -\dfrac{2(1-\mu)^2 (\alpha+\lambda_2 )(x^*)^2}{[(1-\mu)x^*+y^*]^3}. \end{align*} $ |
Put $ v_1 = u_1, \; v_2 = c_{11} u_1+c_{12} u_2. $ System (4.5) becomes
| $ \begin{align} \dfrac{dv_1}{dt}& = \phi_{00} (\lambda)+\phi_{01} (\lambda) v_1+\phi_{02} (\lambda)v_2+\phi_{11} (\lambda) v_1^2+\phi_{12} (\lambda) v_1 v_2+\phi_{13} (\lambda) v_2^2+R_3 (v_1,v_2 ),\\ \dfrac{dv_2}{dt}& = \psi_{00} (\lambda)+\psi_{01} (\lambda) v_1+\psi_{02} (\lambda) v_2+\psi_{11} (\lambda) v_1^2+\psi_{12} (\lambda) v_1 v_2+\psi_{13} (\lambda) v_2^2+R_4 (v_1,v_2). \end{align} $ | (4.6) |
The expressions of $ \phi_{ij} (\lambda) $ and $ \psi_{ij} (\lambda) $ are too long to include in the text. We put values of these functions evaluated at $ \lambda = 0: $
| $ \begin{align*} \phi_{00} (0)& = \phi_{01} (0) = \phi_{12} (0) = 0,\qquad \phi_{02} (0) = 1, \\ \phi_{11} (0)& = -\frac{1}{2}(1+A), \qquad \phi_{13} (0) = \frac{2}{\delta(1+A)}, \\ \psi_{00} (0)& = \psi_{01} (0) = \psi_{02} (0) = \psi_{12} (0) = 0, \\ \psi_{11} (0)& = -\frac{(1-A)^2 (1+A)\delta}{2((1-A)^2+4\delta)}, \qquad \psi_{13} (0) = \frac{2}{1+A}. \end{align*} $ |
We can see that the matrix
| $ \begin{pmatrix} \phi_{01} (0)&\phi_{02} (0) \\ \psi_{01} (0)&\psi_{02} (0) \end{pmatrix} = \begin{pmatrix} 0&1 \\ 0 & 0 \end{pmatrix}, $ |
| $ \phi_{11} (0)+\psi_{12} (0) = -\frac{1}{2}(1+A) \neq 0 $ |
and
| $ \psi_{11} (0) = -\frac{(1-A)^2 (1+A)\delta}{2((1-A)^2+4\delta)}\neq 0. $ |
To determine the structure of the Bogdanov-Takens bifurcation [34], we calculate
| $ \sigma = \mbox{sign}([\phi_{11} (0)+\psi_{12} (0)] \psi_{11} (0)) = (-1)(-1) = 1. $ |
This indicates that the limit cycle appears in the system is unstable, see Figure 1 panel (d). As a result of BT bifurcation [34] we have the following theorem.
Theorem 4.5. System ${\rm(2.3)}$ possesses a unique unstable limit cycle for some parameter values and has a homoclinic connection for other parameter values.
Figure 3 displays the behavior of the system at a Bogdanov-Takes bifurcation point which was detected using MATCONT [15]. There is a non-hyperbolic equilibrium point $ P $ in the interior of the first quadrant. Two orbits meet at this point tangentially in a cusp-like configuration with opposite time direction. All orbits in the interior of the first quadrant converge to the origin except the orbit on the stable manifold of $ P. $ Hence, biologically both species survive if the initial data is on the stable manifold of $ P $ and go extinct otherwise.
Finally, we depict the bifurcation diagram of system (2.3) using MATCONT [15] in Figure 2. The Bogdanov-Takens bifurcation acts as an organizing center of the bifurcations at which saddle-node, Hopf and homoclinic bifurcations emanated.

In this section, we describe the orbits of system (2.3) in different regions of the parametric space separated by the bifurcation curves. We start with Region 1 in which $ \delta > \alpha. $ There is no equilibrium in the interior of the first quadrant, see Figure 1 panel (a). The solution curves tend to either the origin or the equilibrium $ E_1 $. Basins of attraction of the origin and $ E_1 $ are separated by the unstable manifold of $ E_A. $ Biologically, predators go extinct for any initial value. This is because the rate of natural death of predators is larger than the rate of conversion representing the size of newly born predators for every eaten prey. In this case, if the initial densities of the populations fall in the basin of attraction of $ E_1, $ then the prey survive. Similar to trajectories for parameter values in Region 1, the solution curves approach either the origin or the equilibrium $ E_1 $ if the parameter values are on the Transcritical bifurcation line, see Figure 5 panel (d). Hence, we have the same biological conclusion as that in Region 1.
For parameter values in Region 2, two positive equilibria appear in the first quadrat via $ E_1 $ and $ E_A $ as the transcritical bifurcation occurs, see Figure 1 panels (b) and (c). See Figure 4 for the scenario of the transcritical bifurcation. In Region 2, there exists a stable equilibrium $ P_2 $ with a large basin of attraction. The orbits of system (2.3) attracted to either the origin or $ P_2 $. Basins of attraction of both equilibria are separated by the stable manifold of the equilibrium $ P_1 $. Biologically, the survival of both prey and predator populations is guaranteed if the initial densities are in the basin of attraction of $ P_2 $. Otherwise, both populations go extinct as the orbits tend to the origin.

A homoclinic orbit is created if the value of $ (B, \delta) $ is on the homoclinic bifurcation curve surrounding a stable equilibrium, see Figure 5 panel (c). This equilibrium has a narrow basin of attraction which is the interior of the homoclinic orbit. All orbits outside the homoclinic connection tend to the origin. This means that both populations do not survive in a long term. However, there is a small probability for the prey and predators to survive if the initial data is on or in the interior of the homoclinic orbit.
Since the parameter values pass through the homoclinic bifurcation, an unstable periodic orbit is generated if $ (B, \delta) $ is in Region 3. The equilibrium $ P_1 $ remains a saddle point and $ P_2 $ is an attractor with a small basin of attraction, namely, the interior of the periodic orbit. All trajectories outsides the periodic orbit are attracted to the origin. In this case, both populations are most likely to go extinct except when the initial densities fall in the basin of attraction of $ P_2 $ or on the periodic orbit or on the stable manifold of $ P_1 $ for which both populations survive.
The periodic orbit collide with the equilibrium $ P_2 $ when $ (B, \delta) $ is on the Hopf bifurcation curve, see Figure 5 panel (b). The focus $ P_2 $ is not hyperbolic and it is now a repeller. In this case, the extinction of both populations is expected for most of the choices of the initial data. If the parameter $ (B, \delta) $ passes the Hopf curve towards Region 4, the periodic orbit disappears and the focus $ P_2 $ remain a repeller, see Figure 1 panel (e). All orbits tend to the origin if the initial values are not on the stable manifold of $ P_1 $ or that of $ E_1 $. This means that both species are most likely to go extinct.
Equilibria $ P_1 $ and $ P_2 $ collide at the non-hyperbolic saddle $ P^* $ when $ (B, \delta) $ is on the saddle-node bifurcation curve, see Figure 5 panel (a). Equilibrium $ P^* $ has a stable manifold as its basin of attraction. Other points in the interior of the first quadrant belong to the basin of attraction of the origin. Hence, the extinction of both population is observed for this case.
Finally, if $ (B, \delta) $ crosses the segment $ SN, $ both equilibria $ P_1 $ and $ P_2 $ disappear as the system experience saddle-node bifurcation, see Figure 1 panel (f). Since there is no equilibrium and no periodic orbit in the interior of the first quadrant, all orbits that start in the interior of the first quadrant are attracted to the origin. In this case, both species go extinct for any positive initial densities.
We have discussed the dynamical properties of a predator-prey model with a strong Allee effect, a linear prey refuge, and a response function depending on the predator density. We proved that all solutions that started in the first quadrant were trapped in a bounded region in the phase plane, showing that the system is well-posed. Two equilibria always coexist on the positive $ x $-axis, namely $ E_A $ and $ E_1. $ For certain reasonable parameter values, $ E_1 $ is an attractor with a large region of the basin of attraction. This indicates that the prey has a big chance of surviving. The basin of attraction of $ E_1 $ becomes larger when we increase the prey refuge rate parameter. Moreover, the origin is always an attractor and hence, for any choice of parameter values, there is an open region in the first quadrant as a basin of attraction of the origin. Consequently, both populations go extinct with initial densities lying in this region.
However, the existence of positive equilibrium solutions gives the chance of survival of both interacting species. At most two equilibria may coexist in the interior of the first quadrant. We discovered certain conditions on parameters at which the system exhibits transcritical, saddle-node, Hopf, and Bogdanov-Takens bifurcations. We found that the Bogdanov-Takens bifurcation acts as an organizing center of the bifurcation diagram. It is worth mentioning that the rate of prey refuge ($ \mu $) appeared in the expression of these bifurcations except in the condition for the transcritical bifurcation. The saddle-node curve approached the transtrical bifurcation line if we increase the value of $ \mu. $ The value of $ B_{BT} $ in the Bogdanov-Takens bifurcation is very large if $ \mu $ is closed to $ 1. $
As shown in Figure 2, there is a large region in the parameter space (Region 2) where for any choice of parameter values in this region, a stable positive equilibrium exists with a big basin of attraction, see Figure 1 panels (b) and (c). This shows that the survival of both species has a big possibility. The Basin boundary of this attractor is the stable invariant manifold of a positive saddle equilibrium. In this case, both populations may survive when the initial values fall in the basin of attraction of the positive attractor or go extinct if the initial density is in the basin of attraction of the origin. We noted that the Allee effects can narrow the size of the basin of attraction of the stable positive equilibrium. We also observed that if the rate of prey refuge ($ \mu $) is increasing, then the positive attractor is approaching the $ x $-axis with a smaller number of survived predator and a larger number of survived prey. In this case, the basin of attraction of the attractor is also narrowed.
Overall, from our results, we conclude that for a certain set of parameters, the following can occur: (a) The extinction of both species due to the appearance of the zero equilibrium; (b) The survival of both populations associated with the existence of a positive attractor; (c) The survival of prey and extinction of predators related to the detection of a stable equilibrium on the positive $ x $-axis; (d) Both species oscillate for a long-term caused by the existence of a periodic orbit from the Hopf bifurcation. We would like to mention that the mathematical tools used in this paper may also be helpful to analyze any planar dynamical system. For future research, one may consider harvesting and periodic forcing in some parameters. This may lead to the existence of strange attractors (chaotic dynamic) as the autonomous system experience homoclinic bifurcation.
The author would like to thank King Fahd University of Petroleum and Minerals (KFUPM), Saudi Arabia, for supporting this research.
The author declares that there are no conflicts of interest.
| [1] |
H. R. Akcakaya, R. Arditi, L. R. Ginzburg, Ratio-dependent prediction: An abstraction that works, Ecology, 76 (1995), 995–1004. https://doi.org/10.2307/1939362 doi: 10.2307/1939362

|
| [2] |
P. A. Abrams, L. R. Ginzburg, Coupling in predator-prey dynamics: Ratio-dependence, J. Theor. Biol., 139 (1989), 311–326. https://doi.org/10.1016/S0022-5193(89)80211-5 doi: 10.1016/S0022-5193(89)80211-5

|
| [3] |
P. Aguirre, J. D Flores, E. González-Olivares, Bifurcations and global dynamics in a predator-prey model with a strong Allee effect on the prey and ratio-dependent functional response, Nonlinear Anal.: Real Word Appl., 16 (2014), 235–249. https://doi.org/10.1016/j.nonrwa.2013.10.002 doi: 10.1016/j.nonrwa.2013.10.002

|
| [4] |
V. Ajraldi, M. Pittavino, E. Venturino, Modeling herd behavior in population systems, Nonlinear Anal.: Real Word Appl., 12 (2011), 2319–2338. https://doi.org/10.1016/j.nonrwa.2011.02.002 doi: 10.1016/j.nonrwa.2011.02.002

|
| [5] | W. C. Allee, Animal aggregations: A study in general sociology, USA: University of Chicago press, 1931. https://doi.org/10.5962/bhl.title.7313 |
| [6] | J. Bascompte, Extinction thresholds: Insights from simple models, Ann. Zool. Fenn., 40 (2003), 99–114. |
| [7] |
S. Bentout, S. Djilali, A. Atangana, Bifurcation analysis of an age‐structured prey-predator model with infection developed in prey, Math. Methods Appl. Sci., 45 (2022), 1189–1208. https://doi.org/10.1002/mma.7846 doi: 10.1002/mma.7846

|
| [8] |
F. Berezovskaya, G. Karev, R. Arditi, Parametric analysis of the ratio-dependent predator-prey model, J. Math. Biol., 43 (2001), 221–246. https://doi.org/10.1007/s002850000078 doi: 10.1007/s002850000078

|
| [9] |
L. Berec, E. Angulo, F. Courchamp, Multiple Allee effects and population management, Trends Ecol. Evol., 22 (2007), 185–191. https://doi.org/10.1016/j.tree.2006.12.002 doi: 10.1016/j.tree.2006.12.002

|
| [10] |
H. W. Broer, K. Saleh, V. Naudot, R. Roussarie, Dynamics of a predator-prey model with non-monotonic response function, Discrete Cont. Dyn. Syst., 18 (2007), 221–251. https://doi.org/10.3934/dcds.2007.18.221 doi: 10.3934/dcds.2007.18.221

|
| [11] |
A. A. Berryman, The origins and evolutions of predator-prey theory, Ecology, 73 (1992), 1530–1535. https://doi.org/10.2307/1940005 doi: 10.2307/1940005

|
| [12] |
L. Chen, F. Chen, L. Chen, Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge, Nonlinear Anal: Real Word Appl., 11 (2010), 246–252. https://doi.org/10.1016/j.nonrwa.2008.10.056 doi: 10.1016/j.nonrwa.2008.10.056

|
| [13] |
D. L. DeAngelis, R. A. Goldstein, R. V. O'Neill, A model for trophic interactions, Ecology, 56 (1975), 881–892. https://doi.org/10.2307/1936298 doi: 10.2307/1936298

|
| [14] |
B. Dennis, Allee effects: Population growth, critical density, and change of extinction, Nat. Resour. Model., 3 (1989), 481–538. https://doi.org/10.1111/j.1939-7445.1989.tb00119.x doi: 10.1111/j.1939-7445.1989.tb00119.x

|
| [15] |
A. Dhooge, W. Govaerts, Y. Kuznetsov, MATCONT: A MATLAB package for numerical bifurcation analysis of ODEs, ACM Trans. Math. Sofware, 29 (2003), 141–164. https://doi.org/10.1145/779359.779362 doi: 10.1145/779359.779362

|
| [16] |
S. Djilali, S. Bentout, Pattern formations of a delayed diffusive predator-prey model with predator harvesting and prey social behavior, Math. Methods Appl. Sci., 44 (2021), 9128–9142. https://doi.org/10.1002/mma.7340 doi: 10.1002/mma.7340

|
| [17] |
M. Fan, P. Wu, Z. Feng, R. K. Swihar, Dynamics of predator-prey metapopulations with Allee effects, Bull. Math. Biol., 78 (2016), 1727–1748. https://doi.org/10.1007/s11538-016-0197-6 doi: 10.1007/s11538-016-0197-6

|
| [18] |
J. D. Flores, E. González-Olivares, Dynamics of a predator-prey model with Allee effect on prey and ratio-dependent functional response, Ecol. Complex., 18 (2014), 59–66. https://doi.org/10.1016/j.ecocom.2014.02.005 doi: 10.1016/j.ecocom.2014.02.005

|
| [19] | H. I. Freedman, Deterministic mathematical model in population ecology, Marcel Dekker, New York, 1980. |
| [20] |
J. Gascoigne, R. N. Lipcius, Allee effects driven by predation, J. Appl. Ecol., 41 (2004), 801–810. https://doi.org/10.1111/j.0021-8901.2004.00944.x doi: 10.1111/j.0021-8901.2004.00944.x

|
| [21] |
S. Gregory, F. Courchamp, Safety in numbers: Extinction arising from predator-driven Allee effects, J. Anim. Ecol., 79 (2010), 511–514. https://doi.org/10.1111/j.1365-2656.2010.01676.x doi: 10.1111/j.1365-2656.2010.01676.x

|
| [22] |
Y. Gao, B. Li, Dynamics of a ratio-dependent predator-prey system with strong Allee effect, Discrete Cont. Dyn. Syst., 18 (2013), 2283–2313. https://doi.org/10.3934/dcdsb.2013.18.2283 doi: 10.3934/dcdsb.2013.18.2283

|
| [23] |
L. R. Ginzburg, H. R. Akcakaya, Consequences of ratio-dependent predation for steady-state properties of ecosystems, Ecology, 73 (1992), 1536–1543. https://doi.org/10.2307/1940006 doi: 10.2307/1940006

|
| [24] |
E. González-Olivars, R. Ramos-Jiliberto, Dynamics consequences of prey refuges in a simple model system: More prey, few predators and enhanced stability, Ecol. Model., 166 (2003), 135–146. https://doi.org/10.1016/S0304-3800(03)00131-5 doi: 10.1016/S0304-3800(03)00131-5

|
| [25] |
A. P. Gutierrez, Physiological basis of ratio-dependent predator-prey theory: A metabolic pool model of Nicholson's blowflies as an example, Ecology, 73 (1992), 1552–1563. https://doi.org/10.2307/1940008 doi: 10.2307/1940008

|
| [26] |
M. Haque, Ratio-dependent predator-prey models of interacting populations, Bull. Math. Biol., 71 (2009), 430–452. https://doi.org/10.1007/s11538-008-9368-4 doi: 10.1007/s11538-008-9368-4

|
| [27] |
M. Haque, M. S. Rahman, E. Venturino, B. L. Li, Effect of a functional response-dependent prey refuge in a predator-prey model, Ecol. Complex., 20 (2014), 248–256. https://doi.org/10.1016/j.ecocom.2014.04.001 doi: 10.1016/j.ecocom.2014.04.001

|
| [28] |
C. S. Holling, The functional response of predators to prey density and its role in mimicry and population regulation, Mem. Entomol. Soc. Can., 97 (1965), 3–60. https://doi.org/10.4039/entm9745fv doi: 10.4039/entm9745fv

|
| [29] |
S. B. Hsu, T. W. Hwang, Y. Kuang, Global analysis of the Michaelis-Menten type ratio-dependent predator-prey system, J. Math. Biol., 42 (2001), 489–506. https://doi.org/10.1007/s002850100079 doi: 10.1007/s002850100079

|
| [30] |
Y. Huang, F. Chen, L. Zhong, Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge, Appl. Math. Comput., 182 (2006), 672–683. https://doi.org/10.1016/j.amc.2006.04.030 doi: 10.1016/j.amc.2006.04.030

|
| [31] |
T. K. Kar, Stability analysis of a prey-predator model incorporating a prey refuge, Commun. Nonlinear Sci. Numer. Simul., 10 (2005), 681–691. https://doi.org/10.1016/j.cnsns.2003.08.006 doi: 10.1016/j.cnsns.2003.08.006

|
| [32] |
Y. Kuang, E. Beretta, Global qualitative analysis of a ratio-dependent predator-prey system, J. Math. Biol., 36 (1998), 389–406. https://doi.org/10.1007/s002850050105 doi: 10.1007/s002850050105

|
| [33] |
V. Krivan, Effects of optimal antipredator behavior of prey on predator-prey dynamics: The role of refuges, Theor. Popul. Biol., 53 (1998), 131–142. https://doi.org/10.1006/tpbi.1998.1351 doi: 10.1006/tpbi.1998.1351

|
| [34] | Y. A. Kuznetsov, Elements of applied bifurcation theory, Springer, New York, 1998. |
| [35] | A. J. Lotka, Elements of physical biology, Williams and Wilkins, Baltimore MD, 1925. |
| [36] |
Z. Ma, S. Wang, W. Li, Z. Li, The effect of prey refuge in a patchy predator-prey system, Math. Biosci., 243 (2013), 126–130. https://doi.org/10.1016/j.mbs.2013.02.011 doi: 10.1016/j.mbs.2013.02.011

|
| [37] | J. D. Murray, Mathematical biology (Biomathematics, Vol. 19), New York: Springer Verlag, 1993. |
| [38] |
J. N. McNair, The effects of refuges on predator-prey interactions: A reconsideration, Theor. Popul. Biol., 29 (1986), 38–63. https://doi.org/10.1016/0040-5809(86)90004-3 doi: 10.1016/0040-5809(86)90004-3

|
| [39] |
A. Morozov, S. Petrovoskii, B. L. Li, Spatiotemporal complexity of patchy invasion in a predator-prey system with Allee effect, J. Theor. Biol., 238 (2006), 18–35. https://doi.org/10.1016/j.jtbi.2005.05.021 doi: 10.1016/j.jtbi.2005.05.021

|
| [40] | L. Perko, Differential equations and dynamical systems, New York: Springer, 2001. https://doi.org/10.1007/978-1-4613-0003-8 |
| [41] |
G. D. Ruxton, Short term refuge use and stability of predator-prey models, Theor. Popul. Biol., 47 (1995), 1–17. https://doi.org/10.1006/tpbi.1995.1001 doi: 10.1006/tpbi.1995.1001

|
| [42] |
K. Saleh, Dynamics of a predator-prey model with Allee effect and prey group defense, AIP Conf. Proc., 1643 (2015), 655–661. https://doi.org/10.1063/1.4907508 doi: 10.1063/1.4907508

|
| [43] |
P. A. Stephens, W. J. Sutherland, Consequences of the Allee effect for behaviour, ecology and conservation, Trends Ecol. Evol., 14 (1999), 401–405. https://doi.org/10.1016/s0169-5347(99)01684-5 doi: 10.1016/s0169-5347(99)01684-5

|
| [44] | V. Volterra, Variazioni e fluttuaziono del numero di individui in specie animali conviventi, Memoria della Reale Accad. Nazionale dei Lincei, 2 (1926), 31–113. |
| [45] |
G. S. W. Wolkowicz, Bifurcation analysis of a predator-prey system involving group defense, SIAM J. Appl. Math., 48 (1988), 592–606. https://doi.org/10.1137/0148033 doi: 10.1137/0148033

|
| [46] |
D. Xiao, W. Li, M. Han, Dynamics in a ratio-dependent predator-prey model with predator harvesting, J. Math. Anal. Appl., 324 (2006), 14–29. https://doi.org/10.1016/j.jmaa.2005.11.048 doi: 10.1016/j.jmaa.2005.11.048

|
| [47] |
D. Xiao, S. Ruan, Codimension two bifurcations in a predator-prey system with group defense, Int. J. Bifurcat. Chaos, 11 (2001), 2123–2131. https://doi.org/10.1142/S021812740100336X doi: 10.1142/S021812740100336X

|
| [48] |
D. Xiao, S. Ruan, Global dynamics of a ratio-dependent predator-prey system, J. Math. Biol., 43 (2001), 268–290. https://doi.org/10.1007/s002850100097 doi: 10.1007/s002850100097

|
| 1. | Giuseppe Habib, Ádám Horváth, Fold bifurcation identification through scientific machine learning, 2024, 01672789, 134490, 10.1016/j.physd.2024.134490 |
| Steady state | Existence | Local stability |
| $ O(0, 0) $ | Always exists | Non-hyperbolic attractor [3,22] |
| $ E_1 (1, 0) $ | Always exists | Saddle point ($ \alpha < \delta $) and unstable ($ \alpha > \delta $) |
| $ E_A (A, 0) $ | Always exists | Stable ($ \alpha < \delta $) and saddle point ($ \alpha > \delta $) |
| $ P_1(x_1^*, y_1^*) $ | $ (H_1), (H_3), \alpha > 0, B > 0, \delta > 0 $ or $ (H_1), (H_2), (H_4) $ | Saddle point |
| $ P_2(x_2^*, y_2^*) $ | $ (H_1) $, $ (H_3) $ or $ (H_1), (H_2), (H_4) $ | Stable ($ \text{Tr}(J(P_2)) < 0 $) Unstable ($ \text{Tr}(J(P_2)) > 0 $) |
| $ P^*(x^*, y^*) $ | $ (H_1), \delta=\alpha\left(1-\dfrac{(A-1)^2}{4B(1-\mu)}\right) > 0 $ | Non-hyperbolic saddle point |
| Steady state | Existence | Local stability |
| $ O(0, 0) $ | Always exists | Non-hyperbolic attractor [3,22] |
| $ E_1 (1, 0) $ | Always exists | Saddle point ($ \alpha < \delta $) and unstable ($ \alpha > \delta $) |
| $ E_A (A, 0) $ | Always exists | Stable ($ \alpha < \delta $) and saddle point ($ \alpha > \delta $) |
| $ P_1(x_1^*, y_1^*) $ | $ (H_1), (H_3), \alpha > 0, B > 0, \delta > 0 $ or $ (H_1), (H_2), (H_4) $ | Saddle point |
| $ P_2(x_2^*, y_2^*) $ | $ (H_1) $, $ (H_3) $ or $ (H_1), (H_2), (H_4) $ | Stable ($ \text{Tr}(J(P_2)) < 0 $) Unstable ($ \text{Tr}(J(P_2)) > 0 $) |
| $ P^*(x^*, y^*) $ | $ (H_1), \delta=\alpha\left(1-\dfrac{(A-1)^2}{4B(1-\mu)}\right) > 0 $ | Non-hyperbolic saddle point |