R-optimal designs for second-order Scheffé model with qualitative factors

1.   Introduction

In recent years, the mixture models have been widely used in sciences, engineering and business applications. Cornell ^[1] applied models for data from mixture experiments to chick feeding, paper coatings, and many other products. Zijlstra et al. ^[2] embed mixture models in a panel mixed logit framework to describe preferences and preference heterogeneity for the mobility budget. Goos and Hamidouche ^[3] applied the mixture models to a real-life cocktail experiment. In mixture experiments, the factors under study are proportions of the ingredients of a mixture. As the application involves the choice of cocktails, the taste of cocktails only depends on the ingredient proportions, and not on the total amount of cocktail.

To obtain the optimal design under certain optimality criteria has always been a hot topic in the research of the mixture design. Available optimality criteria include $D$-, $A$-, $R$-, and $I$-optimality, etc. (see ^[4,5]). The $D$-optimality and $A$-optimality have been used most frequently. In practice, the efficiency of a specific optimality criterion depends on statistical problem sensitively, and in many cases, the $D$- and $A$-optimal designs are reasonable. However, there are also various situations where the application of the $D$- and $A$-optimality criteria is not appropriate. The efficiency loss may be considerable when the $D$-optimal design is used for the construction of rectangular confidence regions, as stated by Dette ^[6]. For this reason, Dette ^[6] proposed the $R$-optimality criterion, which minimizes the volume of the $p$-dimensional rectangular confidence region for the unknown parameters. Furthermore, the $R$-optimality criterion not only has an excellent statistical interpretation but also satisfies a beneficial invariance property. It allows an easy calculation of optimal designs on many linearly transformed design spaces. Hao et al. ^[7] investigated the $R$-optimal design for the second-order mixture model, while the qualitative factors are not considered.

When an experiment includes qualitative factors, the effects between the quantitative and qualitative factors should be taken into consideration. For example, Lee and Huang ^[8] demonstrated through an example on chemical study how the $D$-optimal design may help to design an experiment with both quantitative and qualitative factors more efficiently. Yue et al. ^[9] investigated the $D$-optimal designs for multiresponse polynomial regression models with both quantitative and qualitative factors. Kao and Hazar ^[10] investigated the optimal designs for mixed continuous and binary responses with quantitative and qualitative factors. Zhang et al. ^[11] proposed a new uniformity criterion for designs with both qualitative and quantitative factors. Although qualitative factors have received increasing attention in the literature, little is known concerning mixture designs with qualitative factors. Following the seminal work of Donev ^[12], the only published results concerning qualitative factors for mixture models are presented in ^[13], which generated the $A$-optimal designs for mixture central polynomial model with qualitative factors. This paper proposes a novel optimal design of mixture model with qualitative factors.

This paper aims at developing a $R$-optimal design for Scheffé models, when the response depends on the joint influence of both mixture and qualitative factors. The remainder of this paper is organized as follows. Section 2 and Section 3 briefly introduce the $R$-optimality, and some basic notations of the two kinds of mixture designs. The main results are presented in Section 4. Finally, the conclusion is drawn in Section 5.

2.   Preliminaries

A mixture experiment design usually assumes that the response variable $y$ is only related to the proportion of each component ${x_1}, \cdots, {x_q}$, but not to the total. The experimental region determined by the component proportions can be expressed as

in which $C's$ are some other constraint conditions. When the model does not contain such constraints, it is called a $(q-1)$-dimensional simplex, denoted as $S^{q-1}$. The response at ${\bf x}$ can be written as

where $\beta = \left({\beta _1, \beta _2, \cdots, \beta _m } \right)^{{T}}$ is the $m$-vector of unknown parameters, $f({\bf{x}}) = ({f_1 ({\bf{x}}), f_2 ({\bf{x}}), \cdots, }$ ${ f_m ({\bf{x}})})^{{T}}$ is a given $m$-vector of regression functions of ${\bf{x}} = (x_1, x_2, \cdots, x_q)^{{T}} \in {\mathcal X} \subseteq S^{q - 1}$. The error $\varepsilon$ is assumed to be independent of ${\bf x}$ and independent identically distributed with a normal distributed with mean 0 and constant variance $\sigma ^2$.

Based on the model (2.1), an approximate design can be expressed as

where ${\bf{x}}_i \in {\mathcal X}$ are support points and their weights $\xi ({\bf{x}}_i) = {r_i}$ satisfy ${r_i} > 0$ and $\sum\limits_{i = 1}^k {r_i} = 1, i = 1, 2, \cdots, k.$ For a design $\xi$, the Fisher information matrix is given by

Moreover, let $\Xi$ denote the set of all designs with non-singular information matrix on $\mathcal{X}$.

Definition 1. A design $\xi ^* \in \Xi$ is called $R$-optimal for the model (2.1) if it minimizes

where $m$ is the number of unknown parameters, $({M^{ - 1} \left(\xi \right)})_{ii}$ is the element on the main diagonal of ${M^{ - 1} (\xi)}$.

For a given design, the equivalence theorem seeks to prove whether the design is the optimal design. Dette ^[6] investigated the equivalence theorem of $R$-optimal design.

Lemma 1. For any ${\bf{x}} \in {\mathcal X}$, the design $\xi^{\ast}$ is $R$-optimal if and only if

where $e_j$ is the unit vector whose $j$-th component is equal to 1 and all others are 0. Moreover, the equality is attained at the support points of the R-optimaldesign $\xi^{\ast}$.

3.   Models and analysis

In the mixture experiments, a simplex-lattice design for $q$ ingredients involves all possible mixture formulations, the set of $q$ components $n$ order lattice points can be expressed as

and there are $\left(\begin{array}{c}q+n-1 \\ n\end{array}\right)$ points in $\mathcal{L}\{q, n\}$.

The matrix $H({\bf x}) = \left\{ {x_{i_j } } \right\}_{i, j = 1}^{N, q}$ generated by all permutations of the coordinates of ${\bf x} = \left({x_1, x_2, \cdots, x_q } \right)^{\bf T} \in {\mathcal X}$ is called permutation matrix, where $i_1, i_2, \cdots, i_q$ is a permutation of the $1, 2, \cdots, q$. Then each row of $H({\bf x})$ is a mixture point and ${\mathcal H}({\bf x}) = \{ {\bf{x, x}}_1, \cdots {\bf{, x}}_{N-1} \}$ is called permutation point set about ${\bf x}$. The set of $q$ components centroid points can be expressed as ${\mathcal C}\left\{ q \right\} = \bigcup\limits_{i = 1}^q {{\mathcal H}({\bf{x}}_i)}$. A simplex-centroid design consists of $2^q - 1$ points: $q$ permutations of $(1, 0, \cdots, 0)$, $\binom{q}{2}$ permutations of $(1/2, 1/2, 0, \cdots, 0)$, $\cdots,$ and one permutation of $(1/q, 1/q, \cdots, 1/q)$. The corresponding model to be fitted to data at the points of the simplex-centroid design is

The Scheffé central polynomial model can reduce the number of trials without reducing the order of the model and maintaining prediction accuracy.

In many practical problems, however, the response is influenced not only by the components' proportion in the mixture, but also by other variables. We can consider the general model which was introduced by Lee and Huang ^[8], this type of model can be expressed as follows:

In the model, $f_1^{T} ({\bf x})\beta _j$ describes the part of the response that is influenced by a qualitative factor, which is generally referred to as the factorial effect, among them, $f_1^{T} ({\bf x}) = ({f_{11} ({\bf x}), f_{12} ({\bf x}), }$ ${ \cdots, f_{1p_1 } ({\bf x})})$, $\beta _j = (\beta _{j1}, \beta _{j2}, \cdots, \beta _{jp_1 })^{T},$ $s$ are the level of qualitative factor, $y(j, {\bf x})$ is the value of the response variable at design point ${\bf x} = (x_1, x_2, \cdots, x_q)^{T} \in {\mathcal{X}} \subseteq S^{q - 1}$ at the $jth$ level. $f_2^{T} ({\bf x})\gamma$ is the part of the response that is not affected by the qualitative factors, generally referred to as fixed effect, where $f_2 ^{T}({\bf x}) = ({f_{21} ({\bf x}), f_{22} ({\bf x}), \cdots, f_{2p_2 } ({\bf x})}),$ $\gamma = (\gamma _1, \gamma _2, \cdots, \gamma _{p_2 })^{T}$.

Taking the second-order general Scheffé central polynomial model as an example, the model (3.1) can be expressed in the following three forms:

Where $f_{L_1 } ({\bf x}) = (x_1, x_2, \cdots, x_q)^{T}$ and $f_{L_2 }({\bf x}) = (x_1 x_2, x_1 x_3, \cdots, x_{q - 1} x_q)^{T}.$ Among them, both the primary and interaction terms in model (3.2) are affected by qualitative factors; while these terms in model (3.3) are factorial effects and fixed effects, respectively, and the case is quite the contrary in model (3.4), with the two terms being fixed and factorial effects, respectively.

For example, a 21-herb formula, referred to as the modified Qing Fei Pai Du Tang (mQFPD) for treating COVID-19, is now being tested in a clinical trial sponsored by the University of California, San Diego. The results obtained by these experiments define the efficacy of the drugs. In this case, the difference between the efficacies of the drugs on the gender of the patient can be considered as the first part of models (3.3) and (3.4), while the fixed efficacy of the drugs can be considered as the second part of the two models. Afterwards, the $R$-optimal design for models (3.3) and (3.4), is presented.

4.   Main results

Denote the index set of the qualitative factor as ${\mathcal D}_s = \{ 1, 2, \cdots, s\}$, and denote $z = (j, {\bf x}) \in \Omega$, $\Omega = {\mathcal D}_s \times {\mathcal X}$ as the product set formed by the mixture experiment region and the qualitative factor. Then the design on the experimental region $\Omega$ can be expressed as a product of two partial designs, i.e., $\zeta (j, {\bf x}) = \eta (j) \times \xi ({\bf x})$, where $\eta$ is the design on ${\mathcal D}_s$ and $\xi ({\bf x})$ is the design on ${\mathcal X}$. Then $\zeta$ has the following form

First note that the information matrix of the design $\xi$ is

which is associated with the quantitative model $E[y({\bf x})] = \left[{f_1 ^{{T}} ({\bf x}), f_2 ^{{T}} ({\bf x})} \right]\left({\beta ^{{T}}, \gamma ^{{T}} } \right)^{{T}}.$ Let the general model (3.1) be rewritten as

By a result in Lee and Huang ^[8], the information matrix of the design $\zeta$ is

where $D = {\rm diag}\left\{ {\eta (1), \eta (2), \cdots, \eta (s)} \right\}, \eta = \left[{\eta (1), \eta (2), \cdots, \eta (s)} \right]^{{T}}.$

According to the $R$-optimality criterion, the minimization of $\prod\limits_{i = 1}^m (M_g^{-1}(\zeta))_{ii}$ amounts to minimization of $tr[log[\prod\limits_{i = 1}^m (M_g^{-1}(\zeta))_{ii}]]$ for all ${\zeta \in \Xi }.$ The following theorem defines the conditions for $R$-optimality of designs and the proof is given in the Appendix.

Theorem 1. For a design $\zeta (j, {\bf x}) = \eta (j) \times \xi ({\bf x})$, where $\eta$ is the design on ${\mathcal D}_s = \{ 1, 2, \cdots, s\}$ and $\xi$ is the design on ${\mathcal X} \subseteq S^{q - 1}$, the following equation holds for model (3.1):

where

Moreover, it also follows that, for $\zeta$ to be optimal, all the elements of $\eta$ must be equal, i.e. $\eta (1) = \eta (2) = \cdots = \eta (s) = 1/s.$

If the optimal marginal design $\eta$ is the uniform design on ${\mathcal D}_s = \{ 1, 2, \cdots, s\},$ then we have

To verify the $R$-optimality of the designs by the equivalence theorem, the decision function presented in Eq (2.3) can be simplified to

where ${B} = {\rm diag}(1/M_{11}, 1/M_{22}, \dots, 1/M_{mm})$, $M_{ii} = ({M^{ - 1} \left(\xi \right)})_{ii}$.

Theorem 2. For a design $\zeta$ on $\Omega$, let $b_{i i},$ $d_{j j}$ and $c_{k k}$ are the element on the main diagonal of $M_{11}^{-1}(\xi),$ $D_{22}(\xi)$ and $K_{(1)}$, respectively, if $\eta$ is a uniform design on ${\mathcal D}_s,$ the decision function of the model (4.1) under the $R$-optimal design is

where$B_{g} = \left[\begin{array}{cc}I_{s} \otimes B(s, 1) & 0 \\0 & H\end{array}\right],$$B(u, v) = \operatorname{diag}\left(1 /\left(u b_{11}+v c_{11}\right), 1 /\left(u b_{22}+v c_{22}\right), \cdots, \right.$ $1 /\left(u b_{p_{1} p_{1}}+v c_{p_{1} p_{1}}\right)),$$H = \operatorname{diag}\left(1 / d_{11}, 1 / d_{22}, \cdots, 1 / d_{p_{2} p_{2}}\right).$

In the following, the approximate $R$-optimal design on the model (3.3) and (3.4) are derived from the results of theorem 2. Suppose $\zeta^{\ast}$ is a $R$-optimal design on the region ${\mathcal D}_s \times {S^{q-1}}$ and denoted by $\eta^{\ast} \times \xi^{\ast},$ where $\eta^{\ast}$ is the uniform design on ${\mathcal D}_s.$ For the model (3.3), the design $\xi$ over the mixture region is arranged by using the set of second-order generalized simplex-centroid points ${\mathcal C}\{ q, 2\}$, denoted as

where ${\bf{x}}_1 = (1, 0, \cdots, 0)^{{T}}$ and ${\bf{x}}_2 = (1/2, 1/2, \cdots, 0)^{{T}}$ are the vertices and mid-points of the edges of the simplex, respectively. ${\mathcal H}({\bf{x}}_i) = \left\{ {{\bf{x}}_{i1}, {\bf{x}}_{i2}, \cdots, {\bf{x}}_{in_i } } \right\}$ is permutation point set about ${\bf{x}}_i, i = 1, 2$, and the weights of corresponding point satisfy $n_1 r_1 + n_2 r_2 = 1$. Then the function $\psi _{R - g} (j, {\bf{x}}; \zeta)$ can be expressed as

where

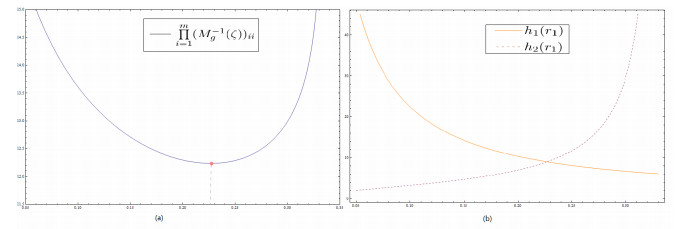
Let $q = 3$, $s = 2$, $\Phi_R(\zeta, r_1) = \prod\limits_{i = 1}^m (M_g^{-1}(\zeta))_{ii},$ $h_i (r_1) = \psi _{R - g} (j, {\bf{x}}; \zeta), {\bf{x}} \in {\mathcal H}({\bf{x}}_i), i = 1, 2$ is adopted to denote the values of the decision function at the two types of design points, respectively. If $\zeta^{\ast}$ is a $R$-optimal design, on the one hand there should be

on the other hand

As $r_1$ transforms, $\Phi_R(\zeta, r_1)$ changes as shown in Figure 1(a), we can find the optimal design

Figure 1(b) shows the changes of $h_1(r_1)$ and $h_2(r_1)$, which can be seen when $r_1 = r_1^{\ast}$, $h_1(r_1)$ and $h_2(r_1)$ intersect at a point, whose coordinates are $\left({r_1^*, sn_1 + n_2 } \right) = \left({0.2269, 9} \right)$. The contour map of the function $\psi _{R - g} (j, {\bf{x}}; \zeta^{\ast})$ on the region $\Omega$ is shown in Figure 2. It is obvious to see that the maximum of the decision function is no greater than the number of model parameters and the maximum is attained at the support points of $\xi^{\ast}$. According to the Eq (2.3), the design $\xi^{\ast}$ is $R$-optimal for model (3.3) and satisfies the equivalence theorem.

Table 1 lists the weights of $R$-optimal designs for model (3.3) and model (3.4) with $3 \le q \le 6$ and $2 \le s \le 6$. The corresponding values of the common logarithm of decision function, $lg[\Phi_R(M(\zeta))]$, are also listed in the fifth and eighth columns of the table. In model (3.3), for any $q$, the weights of vertices increase with the total number of level combinations. On the contrary, in model (3.4), the weights of vertices decrease with the increase of the total number of level combinations.

For any design $\zeta$ of the mixture model with qualitative factors, we measure its quality by efficiency, and the efficiency under $A$-optimality criterion can be expressed as:

The relative $A$-efficiencies of different $R$-optimal designs in model (3.3) are displayed in Table 2. In model (3.3), for any $q$, whereas the efficiencies decrease with the increase of the total number of qualitative levels, the $R$-optimal designs in most cases have relatively high efficiencies. It should be noticed that the $R$-optimal designs for $q = 6$ and $s = 2$ have an $A$-efficiency of 98.89 $\%$ relative to the $A$-optimal designs. In other words, the $R$-optimal designs in model (3.3) perform excellently in terms of the $A$-optimality criterion.

5.   Conclusions

This paper tackles the $R$-optimal design under the interaction of qualitative factors and mixture components. It considers the continuous $R$-optimal designs for the second-order Scheffé model with qualitative factors. The obtained results show that the optimal marginal design $\eta$ is the uniform design under $R$-optimality criterion. For model (3.3), general analytical expressions for the decision function under the $R$-optimal designs are derived, and the $R$-optimality is confirmed by the equivalence theorem. Finally, we remark further that the performance of $R$-optimal designs in terms of the $A$-optimality criterion is excellent.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 12071096, 11901260), Science and Technology Fund for basic research of Guizhou Province ([2020]1Y010).

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix

A.1.   Proof of Theorem 1

The inverse matrices of $M_f (\xi)$ is

we have

where $\zeta = \eta \times \xi$,

and ${\bf{1}}_{s}$ is a $s \times 1$ vector of all ones, ${j}_{s}$ is the $s \times s$ matrix with all elements equal to unity.

As a result, we have

the equality is attained if and only if the elements of $\eta$ is equal, i.e. $\eta (1) = \eta (2) = \cdots = \eta (s) = 1/s.$

A.2.   Proof of Theorem 2

where