Some new numerical schemes for finding the solutions to nonlinear equations

1.   Introduction

Many fundamental problems in combinatorics and related areas can be formulated as decomposition problems-where the aim is to decompose a large discrete structure into suitable smaller ones. Hence, problems of combinatorial design may be efficiently modeled from viewpoint of graph theory. In graph theory, the problems of edge decomposition and graph covering have a great attention as it is of immense importance for numerous applications to a wide range of areas ^[1,2,3]. Here we are concerned with the problem of detecting and correcting the error that may occur through the communication network (system). Despite communication systems may be robust, during the long process of transmitting data, external sources can coincide with the system and manipulate the data. Such manipulation leads to errors in transmitting data. The data received will be different from what was originally transmitted. Consequently, the ability to correct or at least detecting errors is an important issue to the system. The objective of the paper is to construct combinatorial designs which have efficient properties in detecting and correcting errors from viewpoint of coding theory. We call such designs Partially Balanced Network Design (PBNDs). Balanced incomplete block designs (BIBDs) were introduced in (1936). A BIBD is an arrangement of $v$ objects (points) into $b$ blocks each of size $\delta$ such that

1. Every object occurs at most once in each block.

2. Every object occurs in exactly $\alpha$ blocks. ($\alpha$ is the number of replications)

3. Every pair of objects occur together in exactly $\lambda$ blocks.

Any BIBD has to satisfy the following conditions ^[3]:

$v, b, \alpha, \delta, \lambda$ are called the parameters of a BIBD. A restriction on using the BIBD is that it is not available for all parametric combinations. Moreover, even if a BIBD is available for given $v$ objects and block of size $\delta,$ it may require too many replications $\alpha.$ Another restriction that makes BIBD is not desirable for some experiments design is that BIBD is efficiency balanced, i.e., in BIBD every pair of distinct objects should occur together in exactly $\lambda$ blocks. The partially balanced incomplete block designs (PBIBDs) compromise these restrictions up to some extent and help in reducing the number of replications. PBIBDs remain connected like BIBDs but no more balanced. Rather they are partially balanced in the sense that some pairs of objects have the same number of replications whereas some other pairs of objects have the same replications but are different from the replications of earlier pairs of objects. According to such enhancement, PBIBDs are applied for the design of experiments in many areas such as statistics ^[4], game theory ^[5], agriculture ^[6], cryptographic schemes ^[7], and many others. PBIBD was firstly studied by Bose in 1951. Bose et al., ^[8,9,10] introduced a class of binary, equireplicate and proper designs, which called PBIBD with $m$-associate classes. An associate class is a set of objects pairs where each pair from the set occur together with the same number of times, ${\lambda _i}.$

A PBIBD with $m$-associate classes is an arrangement of $v$ objects in $b$ blocks such that:

a) Each object from the set of objects occurs in $\alpha$ blocks.

b) Each block has $\delta$ objects $(\delta < v),$ and no object appears more than once in any block.

c) If two objects are $i$-th associates of each other then, they occur together in ${\lambda _i}(i = 1, 2, \ldots, m)$ blocks.

The number ${\lambda _i}$ is independent of the particular pair of $i$-th associate chosen. ${\lambda _i}$ doesn't need to all be different and some of ${\lambda _i}$'s may be zero. PBIBD is studied and analyzed from viewpoint of graph theory. The relation between PBIBDs and strongly regular graphs is investigated in ^[8]. Bose and Nair ^[9] introduced the concept of association schemes in PBIBDs. Bose and Shimamoto ^[10] studied association schemes of PBIBDs using the graph-theoretic method. Regular graph design (RGD) is an important class of PBIBDs with two association schemes. An RGD $(v, \delta, \alpha)$ is a collection of blocks of size $\delta$ on a $v$-set (with no restriction on repeated blocks) such that every object occurs in $\alpha$blocks and any pair of objects occur together in either ${\lambda _1}$ or ${\lambda _2}$ blocks, where ${\lambda _1}$ is some constant and ${\lambda _2} = {\lambda _1} + 1.$ There are extensive research for RGDs ^{[11,12,13,14,15,16]}.

In this paper, we introduce a significant class of PBIBDs with two association classes with no repeated blocks. We call such a class a partially balanced network design (PBND). The aim of our paper is to show how PBND may be used to construct codes that process a high efficiency in detecting and correcting errors that may occur through the transmission process. The rest of the paper is organized as follows. Section 2 introduces the fundamentals and properties of PBND and the modeling of PBND as a graph design. Section 3 introduces the technique used to construct PBNDs that yield effective error detecting and correcting codes. Some direct constructions of PBNDs and general designs are constructed in Section 4. Section 5 studies the Cartesian product of designs and how that product will lead to codes able to detect and correct more errors. Section 6 shows the advantages of binary codes generated by PBNDs. In Section 7 we summarize the results and the conclusion of the paper.

2.   Partially balanced network design

Network Design (ND) is a pair $(\omega, \tau)$, where $\omega = \{ {\omega _1}, {\omega _2}, \ldots, {\omega _v}\}$ is the whole network (the universal set). The elements of $\omega$ are called points or objectives. $\tau = \{ {\tau _1}, {\tau _2}, \ldots, {\tau _b}\}$ is a collection of nonempty subsets of $\omega.$Each element from $\tau$ is called a subnetwork. ND is described by five parameters $(v, b, \alpha, \delta, \lambda),$ which are nonnegative integers and represent the following:

1) $v$ the size of set $\omega.$

2) $b$ the number of subnetworks in $\tau.$

3) $\alpha$ the number of subnetworks to which every point from $\omega$ belongs.

4) $\delta$ the size of each subnetwork.

5) $\lambda$ the number of subnetworks that contain a pair of distinct points.

A network design (ND) is a complete-ND if $\delta = v,$ whenever $\delta < v$ it refers as incomplete-ND. Let ${\lambda _{{\omega _1}, {\omega _2}}}$ be the number of subnetworks to which two points ${\omega _1}, {\omega _2}$ appear together. If ${\lambda _{{\omega _i}, {\omega _j}}}$ is unique for $i, j$ with $1 \leqslant i < j \leqslant v,$ we call such design as balanced design. If all ${\lambda _{{\omega _i}, {\omega _j}}}$'s are not identical for $i, j$with $1 \leqslant i < j \leqslant v,$ then the design is stated as partially balanced-ND. Here, we are interested in partially balanced incomplete network designs (PBNDs). For our designs we restrict $\lambda \leqslant 1$. If ${\lambda _{{\omega _i}, {\omega _j}}}$ is a constant for $i, j$ with $1 \leqslant i < j \leqslant v,$ then the network design coincides with balanced incomplete block design (BIBD) and each subnetwork is viewed as a block of size $\delta.$ Through the paper we use $(v, b, \alpha, \delta, \lambda)$-ND for a network design (ND) with parameters $(v, b, \alpha, \delta, \lambda).$

Another form to express and determine a PBND is the incidence matrix. Let $(\omega, \tau)$ be a PBND with parameters $(v, b, \alpha, \delta, \lambda).$ The incidence matrix $M = ({m_{i, j}})$ of a $(v, b, \alpha, \delta, \lambda)$-ND is a $b \times v$ binary matrix, where every row corresponds to a subnetwork, and every column corresponds to a point in the set $\omega.$

Theorem 1. Any PBND with parameters $(v,b,\alpha ,\delta ,\lambda )$ should satisfy the following condition $v\alpha = b\delta .$

Proof. Consider the number of 1’s in the incidence matrix $M$ of the given PBND. As matrix $M$ inherited from its PBND then it has the following certain properties:

1) Every row has $\delta$ number of 1's.

2) Every column has $\alpha$ number of 1's.

3) Two distinct columns both have 1's in at most $\lambda$ rows.

Since $M$ has $b$ rows and following property 1, then the number of 1's in the matrix is $b\delta.$ Now we are analyzing the columns of $M.$ Property 2 and the number of columns of $M$ imply that $M$ has $v\alpha$ of 1's. Hence, $v\alpha = b\delta.$

We now review the connection between graph codes and PBND. When a PBND is transformed into an incidence matrix, the rows and the columns can be both viewed as binary codes. The binary code formed from the rows will be denoted as ${C_{row}},$ and the binary code formed from the columns will be referred as ${C_{column}}.$ The minimum distance in binary codes is a significant concept. The role of such a concept is to check whether the binary code can detect or correct errors ^{[17,18,19,20]}.

Let $C$ be a binary code where every element (coding word) belongs to $C$ has length $n.$ Let $P = ({p_1}, {p_2}, ..., {p_n})$ and $Q = ({q_1}, {q_2}, ..., {q_n})$ be two coding words from $C.$ The minimum distance $d(P, Q)$ between $P$ and $Q$ is calculated from the following relation:

According to relation (1), the minimum distance between two coding words $P$ and $Q$ defines the number of positions where $P$ and $Q$ differ i.e. ${p_i} \ne {q_i}$ for $1 \leqslant i \leqslant n.$ The minimum distance $\theta$ of a code $C$ is defined as:

In the following sections, we show how to use the minimum distance in detecting and correcting errors of constructed codes. All graphs described here are finite, undirected, without loops and multiple edges. Let $V(H)$ and $E(H)$ be the vertex set and edge set of the graph $H,$ respectively. The degree of a vertex $u \in V(H)$ is the number of vertices from $V(H)$ that are adjacent to $u.$ The graph is regular if and only if all vertices have a unique degree.

Hereafter, we illustrate the modeling of PBND in terms of graphs.

Definition 1. Let $H$ be a $s$-regular graph of order$n.$ An $(H, F, k, X)$-graph design is a collection $\varphi = \{ {F_0}, {F_1}, \ldots, {F_{b - 1}}\}$ of $b$ subgraphs of $H$ such that:

1) For every $0 \leqslant i \leqslant b - 1;{F_i} \cong F.$

2) For every $0 \leqslant i \leqslant b - 1;{F_i}$ is a spanning subgraph of $H.$

3) Every ${F_i}$ contains at most $s$ edges.

4) Every edge of $H$ exists in exactly $k$ subgraphs from $\varphi.$

5) For any $i, j$ such that $i \ne j, {F_i} \cap {F_j} \cong X.$

From Definition 1 an $(H, F, k, X)$-graph design is a PBDN. There is a correspondence between the parameters $(H, F, k, X)$ of a graph design and the parameters for the corresponding PBDN. Namely, $v = \left| {E(H)} \right|, b = \left| \varphi \right|, \, \, \alpha = k, \, \, \delta = \left| {E(F)} \right|$ and $\lambda = \left| {E(X)} \right|.$ According to that correspondence, in the following we use $(H, F, k, X)$-ND for an $(H, F, k, X)$-graph design. Moreover, if the graph $H$ is a complete bipartite graph ${K_{n, n}}, X \cong {K_{1, 1}}$ and $\left| {E(F)} \right| < n$ then $({K_{n, n}}, F, k, {K_2})$-ND is a sub-orthogonal double cover (SODC) of ${K_{n, n}}$by $F.$ The construction of SODCs of ${K_{n, n}}$ and ${K_n}$ by $F$for different classes of $F$ has been studied in ^{[21,22,23,24,25]}. The design $({K_{n, n}}, F, k, {K_2})$-ND is equivalent to an orthogonal double cover (ODC) of ${K_{n, n}}$ by $F$ if and only if $\left| {E(F)} \right| = n,$ see ^{[26,27,28,29,30,31,32,33,34,35]}. If $H$ is a Cayley graph and $\left| {E(F)} \right| = s < n,$then the constructed design $({K_{n, n}}, F, k, {K_2})$-ND is considered as an ODC of Cayley graphs which have been studied in ^[36]. For the $(H, F, k, X)$-ND, if the graph $H$ is a complete bipartite graph ${K_{n, n}}, k \geqslant 3, X \cong {K_2},$and $\left| {E(F)} \right| = n,$ then $({K_{n, n}}, F, k, {K_2})$-ND is a mutually orthogonal $k$ cover (MOkC) of ${K_{n, n}}$ by $F,$ see ^{[37,38,39,40,41,42,43,44]}. In ^[45], the authors have constructed the circular intensely ODC design of balanced complete multipartite graphs. Additional background material for this field may be found in ^{[46,47,48,49,50]}. For many communication systems (networks), bipartite graphs are good tools in modeling such systems. In the next section, we are concerned with $(H, F, k, X)$-ND for a network $H$ modeled as a bipartite graph and refer to it as a bipartite network.

3.   Design of bipartite graph-codes and partially balanced bipartite network

The complete bipartite network ${K_{n, n}}$ consists of two independent sets of nodes. The first set of the nodes is labeled by $\{ 0, 1, ..., n - 1\} \times \{ 0\},$ and the second set of the nodes is labeled by $\{ 0, 1, ..., n - 1\} \times \{ 1\}.$ Each link ${u_0}{v_1}$ in the network has a weight equals to $v - u$ (sums and differences are calculated modulo$n).$

The network design $(H, F, k, X)$-ND is a collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_{n - 1}^{ij}\}; i \in \{ 0, 1, ..., n - 1\}, j \in \{ 0, 1, ..., k - 1\}$ of $kn$ isomorphic subnetworks (each of them is isomorphic to the network$F)$of the complete bipartite network ${K_{n, n}}$ such that:

a) For a certain $j = \eta, j \in \{ 0, 1, ..., k - 1\}$, every link of the complete bipartite network ${K_{n, n}}$ is found in exactly one subnetwork of $\{ G_0^{i\eta }, G_1^{i\eta }, ..., G_{n - 1}^{i\eta }\}.$

b) For any two subnetworks $G_c^{aw}, G_z^{xy}$ from the collection $\mathcal{G},$ if $a \ne x, w = y, c \ne z,$ then there are no common links between these two subnetworks.

c) For any two subnetworks $G_c^{aw}, G_z^{xy}$ from the collection $\mathcal{G},$ if $w \ne y,$ then these two subnetworks intersect in a common network which is isomorphic to the subnetwork $X.$

In the $(H, F, k, X)$-ND, we have $v = \left| {E({K_{n, n}})} \right| = {n^2}, \;b = k\left| {E\left(F \right)} \right| = kn, \;\alpha = k, \;\delta = \left| {E\left(F \right)} \right| = n, X \cong {K_{1, 1}}.$ Then, $v\alpha = k{n^2}, b\delta = k{n^2} \Rightarrow v\alpha = b\delta.$

The incidence matrix $I = ({I_{ij}})$ for the $({K_{n, n}}, F, k; {K_{1, 1}})$-ND is a $kn \times {n^2}$ binary matrix showing the relation between the links and the subnetworks of the complete bipartite network ${K_{n, n}},$where every row in $I$ corresponds to a subnetwork ${F_i}$ in $({K_{n, n}}, F, k; {K_{1, 1}})$-ND and every column in $I$ corresponds to a link ${l_j}$ in the complete bipartite network ${K_{n, n}},$

Any code word from ${C_{row}}$ represents a bipartite graph that is isomorphic to the graph $F.$ In this case, the ${C_{row}}$ is called a $F$-graph code. The rules of building the incidence matrix $I = ({I_{ij}})$ of $(H, F, k, X)$-ND lead to the following lemma.

Lemma 1. An $F$-graph code exists if and only if the $(H, F, k, X)$-ND is available.

Moreover, since $I$ is a binary matrix, then its rows or columns can be used as binary codes. For instance, the encoding function of the code ${C_{column}}$ is defined as; with $W = \mathbb{Z}_n^2,$ let encoding function $E:W \to \mathbb{Z}_2^{kn},$ be given by $E(ij) = {C_{ni + j}}(I)$ (the $(ni + j)$th column of the matrix $I).$ Section 4 contains examples explain the methodology of the coding and decoding processes with the help of the minimum distance of the considered code.

Definition 2. (^[18]) For $m, \lambda \in {\boldsymbol{Z}^ + }$ and $\varepsilon \in \mathbb{Z}_{2}^{m}$, the sphere of radius $\lambda$ centered at $\varepsilon$ is defined as $S(\varepsilon, \lambda) = \{ \gamma \in _2^m:d(\varepsilon, \gamma) \le \lambda \}.$

Theorem 2. (^[18]) Supposeis $E: W \rightarrow C$ is an encoding function where $W \subseteq \mathbb{Z}_{2}^{n}$ is the set of messages and $E(W) = C \subseteq \mathbb{Z}_{2}^{m}$ is the set of code words with $n < m$. If the minimum distance between code words is at least $\lambda+1, \lambda \in \boldsymbol{Z}^{+}$, then we can detect all transmission errors of weight $\leq \lambda$.

Theorem 3. (^[18]) Suppose $E: W \rightarrow C$ is an encoding function where $W \subseteq \mathbb{Z}_{2}^{n}$ is the set of messages and $E(W) = C \subseteq \mathbb{Z}_{2}^{m}$ is the set of code words with $n < m$. If the minimum distance between code words is at least $2 \lambda+1, \lambda \in \boldsymbol{Z}^{+}$, then we can construct a decoding function $D: \mathbb{Z}_{2}^{m} \rightarrow W$ that corrects all transmission errors of weight $\leq \lambda$.

The following theorem gives the range of errors that can be detected or corrected when either ${C_{row}}$or ${C_{column}}$ is used.

Theorem 4. Let ${C_{row}}$, ${C_{column}}$ be the binary codes constructed from the rows and columns of the incidence matrix of $({K_{n, n}}, F, k; {K_{1, 1}})$-ND, respectively. We have the following:

1) For the binary code ${C_{row}}$, we can detect up to $2n{\rm{ - }}3$ errors or correct up to $\left\lfloor {\frac{{2n - 3}}{2}} \right\rfloor$ errors.

2) For the binary code ${C_{column}}$, we can detect up to $2k{\rm{ - }}3$ errors or correct up to $\left\lfloor {\frac{{2k - 3}}{2}} \right\rfloor$ errors.

Proof. From the definition of the $\left(K_{n, n}, F, k; K_{1, 1}\right)$-ND, in the incidence matrix of $\left(K_{n, n}, F, k; K_{1, 1}\right)$-ND, there exists n number of 1's in every row. Any two rows have at most 1 position of 1's in common. Then the minimum distance of $C_{ {row }}$ is $\theta\left(C_{ {row }}\right) = 2(n-1) = 2 n-2$. Therefore, for $C_{ {row }}$, we can detect up to $\theta\left(C_{r o w}\right)-1 = 2 n-3$ errors and correct up to $\left\lfloor {\frac{{\theta ({C_{row}}) - 1}}{2}} \right\rfloor = \left\lfloor {\frac{{2n - 3}}{2}} \right\rfloor.$ Considering ${C_{column}}$ there exists k number of 1's in every column. Any two columns have at most 1 position of 1's in common, then the minimum distance of ${C_{column}}$ is $\theta ({C_{column}}) = 2(k - 1) = 2k - 2.$ Therefore, for ${C_{column}}$ we can detect up to $({C_{column}}) - 1 = 2k - 3$ and correct up to $\left\lfloor {\frac{{\theta ({C_{column}}) - 1}}{2}} \right\rfloor = \left\lfloor {\frac{{2k - 3}}{2}} \right\rfloor.$

Method for constructing $({K_{n, n}}, F, k; {K_{1, 1}})$-ND

In what follows, we are concerned with the links of the network $G.$ Consequently, we will use $G$ for the links set of $G.$

Definition 3. If we have a subnetwork $G = \left\{ {\left({u_0^1, v_1^1} \right), \left({u_0^2, v_1^2} \right), \left({u_0^3, v_1^3} \right), ..., \left({u_0^n, v_1^n} \right)} \right\}$ (the weights of these links are mutually distinct and equal to $\{ 0, 1, \ldots, n - 1\}$) of the complete bipartite network ${K_{n, n}},$ then the translated subnetwork $G + \sigma = \left\{ {\left({u_0^1 + \sigma, v_1^1 + \sigma } \right), \left({u_0^2 + \sigma, v_1^2 + \sigma } \right), \left({u_0^3 + \sigma, v_1^3 + \sigma } \right), ..., \left({u_0^n + \sigma, v_1^n + \sigma } \right)} \right\}$ is called the G-translate of the subnetwork G where $\sigma \in \{ 0, 1, ..., n - 1\}$. The union of the subnetworks $G + \sigma$ gives the complete bipartite network ${K_{n, n}}.$ The subnetwork G will be called the basis of the complete bipartite network ${K_{n, n}}.$

In what follows, the basis $G$ will be represented by a vector $\phi (G) = ({\varphi _0}, {\varphi _1}, \ldots, {\varphi _{n - 1}})$ where ${\phi _x} \in \{ 0, 1, ..., n - 1\}$ and ${({\phi _x})_0}$ is the unique node $({\phi _x}, 0) \in \left\{ {0, 1, ..., n - 1} \right\} \times \left\{ 0 \right\}$ that belongs to the unique link of weight $x$ in the basis $G$ Note that the links of the basis $G$are $\left\{ {{{({\phi _x})}_0}, {{({\phi _x} + x)}_1}} \right\},$ which will be represented by $({({\phi _x})_0}, {({\phi _x} + x)_1}).$

Definition 4. The two bases G and H represented by the vectors $\phi (G)$ and $\psi (H)$ are said to be intersected if $\left\{ {{\phi _i}(G) - {\psi _i}(H):i \in \{ 0, 1, \ldots, n - 1\} } \right\} = \{ 0, 1, ..., n - 1\}.$

Definition 5. If the two bases vectors $\phi (G)$ and $\psi (H)$ are intersected and $G \cong H,$ then the translated subnetworks $G + \sigma$ and $H + \sigma, \;\sigma \in \{ 0, 1, ..., n - 1\}$ gives a $({K_{n, n}}, G, 2;{K_{1, 1}})$-ND.

Definition 6. The subnetwork ${H_s}$ of the complete bipartite network ${K_{n, n}}$ is the symmetric subnetwork of the subnetwork $H$ if $H = \left\{ {\left({u_0^1, v_1^1} \right), \left({u_0^2, v_1^2} \right), \left({u_0^3, v_1^3} \right), ..., \left({u_0^n, v_1^n} \right)} \right\}, {H_s} = \left\{ {\left({v_0^1, u_1^1} \right), \left({v_0^2, u_1^2} \right), \left({v_0^3, u_1^3} \right), ..., \left({v_0^n, u_1^n} \right)} \right\}.$ It is clear that if the subnetwork $H$ is a basis, then the subnetwork ${H_s}$ is also a basis. If the two bases $H$ and ${H_s}$ are intersected, then the basis $H$ is called a symmetric basis.

Definition 7. The basis H represented by the vector $\psi (H)$ is a symmetric basis if $\left\{ {{\psi _\tau }(H) - {\psi _{n - \tau }}(H) + \tau :\tau \in \{ 0, 1, ..., n - 1\} } \right\} = \{ 0, 1, \ldots, n - 1\}.$

4.   Constructions of some small and generalized PBNDs

In this section, we introduce some small PBNDs based on the direct construction method. Also, we introduce some generalized PBNDs.

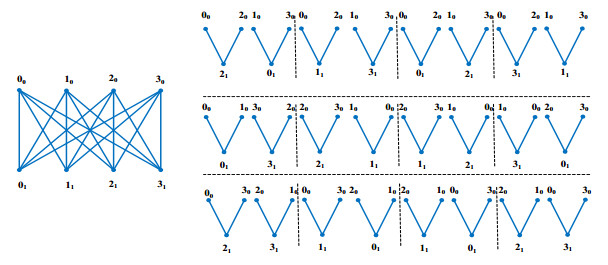
Lemma 2. There exists a $({K_{4, 4}}, 2{K_{1, 2}}, 3;{K_{1, 1}})$-ND. Hence, there is a $2{K_{1, 2}}$-code.

Proof. Let $\mathcal{G} = \{ G_0^{00}, G_1^{10}, G_2^{20}, G_3^{30}, G_0^{01}, G_1^{11}, G_2^{21}, G_3^{31}, G_0^{02}, G_1^{12}, G_2^{22}, G_3^{32}\}$with $G_0^{00} = \{ {0_0}{2_1}, {2_0}{2_1}, {1_0}{0_1}, {3_0}{0_1}\}, G_1^{10} = \{ {0_0}{1_1}, {2_0}{1_1}, {1_0}{3_1}, {3_0}{3_1}\}, G_2^{20} = \{ {0_0}{0_1}, {2_0}{0_1}, {1_0}{2_1}, {3_0}{2_1}\}$, $G_3^{30} = \{ {0_0}{3_1}, {2_0}{3_1}, {1_0}{1_1}, {3_0}{1_1}\}, G_0^{01} = \{ {0_0}{0_1}, {1_0}{0_1}, {3_0}{3_1}, {2_0}{3_1}\}, G_1^{11} = \{ {2_0}{2_1}, {3_0}{2_1}, {1_0}{1_1}, {0_0}{1_1}\}$, $G_2^{21} = \{ {2_0}{1_1}, {3_0}{1_1}, {1_0}{2_1}, {0_0}{2_1}\}, G_3^{31} = \{ {1_0}{3_1}, {0_0}{3_1}, {2_0}{0_1}, {3_0}{0_1}\}, G_0^{02} = \{ {0_0}{2_1}, {3_0}{2_1}, {2_0}{3_1}, {1_0}{3_1}\}$,$G_1^{12} = \{ {0_0}{1_1}, {3_0}{1_1}, {2_0}{0_1}, {1_0}{0_1}\}, G_2^{22} = \{ {2_0}{1_1}, {1_0}{1_1}, {0_0}{0_1}, {3_0}{0_1}\}, G_2^{32} = \{ {2_0}{2_1}, {1_0}{2_1}, {0_0}{3_1}, {3_0}{3_1}\},$ see Figure 1. All the subnetworks are isomorphic to $2{K_{1, 2}}.$ Let ${i_0}{j_1}$ be a link from the complete bipartite network ${K_{4, 4}}$. The constructed design forces every link ${i_0}{j_1}$ to occur in exactly 3 subnetworks from $\mathcal{G}.$ Moreover, such design fulfills the following total function $\cap :A \to \{ 0, 1\}$, where $A = \{ G_c^{aw}, G_z^{xy}\}$ be a set of 2-elements subsets of $\mathcal{G}$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = \left\{ {\begin{array}{*{20}{c}} {1;} & {w \ne y, } \\ {0;} & {a \ne x, w = y, c \ne z.} \end{array}} \right.$ Here, $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 1$ means that the intersection of two subnetworks $G_c^{aw}, G_z^{xy}$ is isomorphic to subnetwork ${K_{1, 1}},$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 0$ refers that they have no subnetworks in common.

The incidence matrix $I$for $({K_{4, 4}}, 2{K_{1, 2}}, 3;{K_{1, 1}})$-ND is

Example 1. From Lemma 2,

$W = \mathbb{Z}_4^2 = \{ 0, 1, 2, 3\} \times \{ 0, 1, 2, 3\} = \{ 00, 01, 02, 03, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33\},$

Example 1. From Lemma 2, $W = \mathbb{Z}_4^2 = \{ 0, 1, 2, 3\} \times \{ 0, 1, 2, 3\} = \{ 00, 01, 02, 03, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33\}, E:W \to \mathbb{Z}_2^{12}, E(ij) = {C_{4i + j}}(I),$ hence,

$E(00) = {C_0}(I) = 001010000010, E(01) = {C_1}(I) = 010001000100, E(02) = {C_2}(I) = 100000101000, E(03) = {C_3}(I) = 000100010001, \\ E(10) = {C_4}(I) = 100010000100, E(11) = {C_5}(I) = 000101000010, E(12) = {C_6}(I) = 001000100001, E(13) = {C_7}(I) = 010000011000, \\ E(20) = {C_8}(I) = 001000010100, E(21) = {C_9}(I) = 010000100010, E(22) = {C_{10}}(I) = 100001000001, E(23) = {C_{11}}(I) = 000110001000, \\ E(30) = {C_{12}}(I) = 100000010010, E(31) = {C_{13}}(I) = 000100100100, E(32) = {C_{14}}(I) = 001001001000, E(33) = {C_{15}}(I) = 010010000001.$

The minimum distance between code words is 4, so we can correct all single and double errors. For instance,

$\begin{gathered} S({C_0}(I), 2) = \{ 001010000010\} \, \cup \, \{ 101010000010, 011010000010, 001110000010, 001011000010, 001010100010, 001010010010, \hfill \\ 001010001010, 001010000110, 001010000011\} \, \cup \, \{ 111010000010, 101110000010, 101011000010, 101010100010, 101010010010, \hfill \\ 101010001010, 101010000110, 101010000011, 011110000010, 011011000010, 011010100010, 011010010010, 011010001010, \hfill \\ 011010000110, 001110010010, 001110001010, 001110000110, 011010000011, 001111000010, 001110100010, 001110000011, \hfill \\ 001011100010, 001011010010, 001011001010, 001011000110, 001011000011, 001010110010, 001010101010, 001010100110, \hfill \\ 001010100011, 001010011010, 001010010110, 001010010011, 001010001110, 001010001011, 001010001110, 001010001011, \hfill \\ 001010000111\}. \hfill \\ \end{gathered}$

The decoding function $D:\mathbb{Z}_2^{12} \to W$ gives $D(\varepsilon) = {C_0}(I) = 001010000010$ for all$\varepsilon \in S({C_0}(I), 2).$

Lemma 3. There exists a $({K_{4, 4}}, {K_{2, 2}}, 3;{K_{1, 1}})$-ND. Hence, there is a ${K_{2, 2}}$-code.

Proof. Let $\mathcal{G} = \{ G_0^{00}, G_1^{10}, G_2^{20}, G_3^{30}, G_0^{01}, G_1^{11}, G_2^{21}, G_3^{31}, G_0^{02}, G_1^{12}, G_2^{22}, G_3^{32}\}$ with $G_0^{00} = \{ {2_0}{0_1}, {2_0}{3_1}, {1_0}{0_1}, {1_0}{3_1}\}, G_1^{10} = \{ {3_0}{1_1}, {3_0}{2_1}, {0_0}{1_1}, {0_0}{2_1}\}, G_2^{20} = \{ {3_0}{3_1}, {3_0}{0_1}, {0_0}{3_1}, {0_0}{0_1}\}$, $G_3^{30} = \{ {1_0}{1_1}, {1_0}{2_1}, {2_0}{1_1}, {2_0}{2_1}\}, G_0^{01} = \{ {1_0}{2_1}, {1_0}{0_1}, {3_0}{2_1}, {3_0}{0_1}\}, G_1^{11} = \{ {2_0}{1_1}, {2_0}{3_1}, {0_0}{1_1}, {0_0}{3_1}\}$, $G_2^{21} = \{ {2_0}{2_1}, {2_0}{0_1}, {0_0}{2_1}, {0_0}{0_1}\}, G_3^{31} = \{ {1_0}{1_1}, {1_0}{3_1}, {3_0}{1_1}, {3_0}{3_1}\}, G_0^{02} = \{ {2_0}{2_1}, {2_0}{3_1}, {3_0}{2_1}, {3_0}{3_1}\}$, $G_1^{12} = \{ {1_0}{2_1}, {1_0}{3_1}, {0_0}{2_1}, {0_0}{3_1}\}, G_2^{22} = \{ {2_0}{1_1}, {2_0}{0_1}, {3_0}{1_1}, {3_0}{0_1}\}, G_2^{32} = \{ {1_0}{1_1}, {1_0}{0_1}, {0_0}{1_1}, {0_0}{0_1}\}.$ All the subnetworks are isomorphic to ${K_{2, 2}}.$ Let ${i_0}{j_1}$ be a link from the complete bipartite network ${K_{4, 4}}.$The constructed design forces every link ${i_0}{j_1}$ to occur in exactly 3 subnetworks from $\mathcal{G}.$ Moreover, such design fulfills the following total function $\cap :A \to \{ 0, 1\}$, where $A = \{ G_c^{aw}, G_z^{xy}\}$ be a set of 2-elements subsets of $\mathcal{G}$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = \left\{ {\begin{array}{*{20}{c}} {1;} & {w \ne y, } \\ {0;} & {a \ne x, w = y, c \ne z.} \end{array}} \right.$

Here, $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 1$ means that the intersection of two subnetworks $G_c^{aw}, G_z^{xy}$ is isomorphic to subnetwork ${K_{1, 1}}$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 0$ refers that they have no subnetworks in common.

Theorem 5. There exists a $({K_{n, n}}, {P_{n + 1}}, n; {K_{1, 1}})$-ND where $n$ is a prime number.

Proof. We define ${\psi _\tau }({H_x}) = \tau (x - \tau)$ where $\tau, x \in \{ 0, 1, \ldots, n - 1\}.$Assume that $p \ne q \in \{ 0, 1, \ldots, n - 1\},$then ${\psi _\tau }({H_p}) - {\psi _\tau }({H_q}) = \tau (p - q); \, \tau \in \{ 0, 1, \ldots, n - 1\}.$ It is easy to check that the differences ${\psi _\tau }({H_p}) - {\psi _\tau }({H_q})$ give the group $\{ 0, 1, \ldots, n - 1\}$ since $n$ is a prime and $p - q$ is not equal to zero. Hence, ${H_p}$ and ${H_q}$ are intersected. Now, we will prove that all the bases ${H_p}, p \in \{ 0, 1, \ldots, n - 1\}$ are paths. The basis ${H_p} = \{ {(\tau (p - \tau))_0}, {(\tau (p - \tau) + \tau)_1}:\tau, p \in \{ 0, 1, \ldots, n - 1\} \},$ it is trivial to show that ${H_p}$ is a path at $n = 2,$for$n > 2,$assume that $r = s/2,$ then for each $\lambda \in \{ 0, 1, \ldots, n - 1\}, \, \, {l_\lambda } = {((\lambda + r)(s - r - \lambda))_0}, {((\lambda + r)(s - r - \lambda) + \lambda + r)_1}),$ where ${l_\lambda }$ is the link of weight $\lambda + r.$ Consider the two links $\, {l_\lambda }$ and $\, {l_\mu }$ with $\lambda \ne \mu,$ these two links are adjacent and incident in the node with zero subscript if $(\lambda + r)(s - r - \lambda) = (\mu + r)(s - r - \mu).$ Putting $s = 2r$gives $(\lambda + \mu)(\lambda - \mu) = 0.$ This means that $\lambda + \mu = 0$ since $\lambda \ne \mu.$ Now, we can conclude that $\, {l_\lambda } = \, {l_{ - \mu }} = {l_{n - \mu }}.$ Hence, there is only value of $\mu$ verifies the previous claim provided that $\lambda \ne 0.$ Similarly, the two links $\, {l_\lambda }$ and $\, {l_\mu }$ with $\lambda \ne \mu$ are adjacent and incident in the node with one subscript if $(\lambda + r)(s - r - \lambda) + (\lambda + r) = (\mu + r)(s - r - \mu) + (\mu + r).$ This gives $(\lambda + \mu - 1)(\lambda - \mu) = 0.$ Hence, $\, \, {l_\mu } = {l_{1 - \lambda }}$ and there is only value of $\mu$ verifies the previous claim provided that $\lambda \ne 1/2.$ Finally, the sequence ${l_0}, {l_1}, {l_{n - 1}}, {l_2}, {l_{n - 2}}, \ldots, {l_{(n - 1)/2}}, {l_{n - (n - 1)/2}}$represents a path.

Lemma 4. There exists a$({K_{3, 3}}, {P_4}, 3;{K_{1, 1}})$-ND. Hence, there is a ${P_4}$-code, where ${P_4}$ is a path graph with four vertices and three edges.

Proof. Let $\mathcal{G} = \{ G_0^{00}, G_1^{10}, G_2^{20}, G_0^{01}, G_1^{11}, G_2^{21}, G_0^{02}, G_1^{12}, G_2^{22}\}$ with $G_0^{00} = \{ {0_0}{0_1}, {0_0}{1_1}, {1_0}{0_1}\}$, $G_1^{10} = \{ {2_0}{0_1}, {2_0}{2_1}, {0_0}{2_1}\}, G_2^{20} = \{ {1_0}{2_1}, {1_0}{1_1}, {2_0}{1_1}\}, G_0^{01} = \{ {0_0}{0_1}, {0_0}{2_1}, {1_0}{2_1}\}, G_1^{11} = \{ {0_0}{1_1}, {2_0}{1_1}, {2_0}{2_1}\}$, $G_2^{21} = \{ {1_0}{0_1}, {2_0}{0_1}, {1_0}{1_1}\}, G_0^{02} = \{ {0_0}{0_1}, {2_0}{0_1}, {2_0}{1_1}\}, G_1^{12} = \{ {0_0}{1_1}, {0_0}{2_1}, {1_0}{1_1}\}, G_2^{22} = \{ {1_0}{0_1}, {1_0}{2_1}, {2_0}{2_1}\}.$ All the subnetworks are isomorphic to ${P_4}.$ Let ${i_0}{j_1}$ be a link from the complete bipartite network ${K_{3, 3}}.$The constructed design forces every link ${i_0}{j_1}$ to occur in exactly 3 subnetworks from $\mathcal{G}.$ Moreover, such design fulfills the following total function $\cap :A \to \{ 0, 1\}$, where $A = \{ G_c^{aw}, G_z^{xy}\}$ be a set of 2-elements subsets of $\mathcal{G}$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = \left\{ {\begin{array}{*{20}{c}} {1;} & {w \ne y, } \\ {0;} & {a \ne x, w = y, c \ne z.} \end{array}} \right.$

Here, $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 1$ means that the intersection of two subnetworks $G_c^{aw}, G_z^{xy}$ is isomorphic to subnetwork ${K_{1, 1}},$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 0$ refers that they have no subnetworks in common.

In what follows, the link $({a_0}, {b_1})$ will be written as $(a, b)$ for simplification.

Theorem 6. There exists a $({K_{n, n}}, \frac{{n - 1}}{2}{P_3} \cup {K_{1, 1}}, n; {K_{1, 1}})$-ND where $n > 2$ is a prime number. Hence, there is a $(\frac{{n - 1}}{2}{P_3} \cup {K_{1, 1}})$-code.

Proof. Define all subnetworks of a $({K_{n, n}}, \frac{{n - 1}}{2}{P_3} \cup {K_{1, 1}}, n; {K_{1, 1}})$-ND by the following table where $x \in \{ 0, 1, \ldots, n - 1\}.$

From Table 1, we have a collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_{n - 1}^{ij}\}; i, j \in \{ 0, 1, ..., n - 1\}$ of ${n^2}$ subnetworks. Now, we want to prove the isomorphism of all subnetworks in Table 1. Suppose $\varepsilon \in \{ 0, 1, ..., n - 1\}$is a fixed number and $\xi \in \{ 0, 1, ..., n - 1\}$is an arbitrary number. By taking the subnetworks in the first column of Table 1, we have to prove that ${x^2} + \varepsilon x = \xi$ has a unique solution for exactly one $\xi,$ two solutions for $\frac{{n - 1}}{2}\;\xi$'s, and no solution for the remaining $\frac{{n - 1}}{2}\;\xi$'s. There is a number$h \in \{ 0, 1, ..., n - 1\}$ with $h = 2\varepsilon$ since $n > 2$ is a prime. Hence, ${(x + h)^2} = {h^2} + \xi$ from the equation ${x^2} + \varepsilon x = \xi.$ Now, we have a unique solution $x = - h$ if ${h^2} + \xi = 0.$For any other ${h^2} + \xi,$ the desired property is verified. Similarly, the isomorphism for the remaining subnetworks in Table 1 can be proved. Hence, all subnetworks in Table 1 are isomorphic to $\frac{{n - 1}}{2}{P_3} \cup {K_{1, 1}}$. It is clear that the subnetworks in the same row in Table 1 have no common links and any two subnetworks from two different rows have only one common link.

Lemma 5. There exists a $({K_{3, 3}}, {P_3} \cup {K_{1, 1}}, 3;{K_{1, 1}})$-ND. Hence, there is a ${P_3} \cup {K_{1, 1}}$-code.

Proof. Let$\mathcal{G} = \{ G_0^{00}, G_1^{10}, G_2^{20}, G_0^{01}, G_1^{11}, G_2^{21}, G_0^{02}, G_1^{12}, G_2^{22}\}$ with $G_0^{00} = \{ {0_0}{0_1}, {0_0}{1_1}, {2_0}{2_1}\}$, $G_1^{10} = \{ {1_0}{0_1}, {1_0}{1_1}, {0_0}{2_1}\}, G_2^{20} = \{ {2_0}{0_1}, {2_0}{1_1}, {1_0}{2_1}\}, G_0^{01} = \{ {0_0}{0_1}, {0_0}{2_1}, {2_0}{1_1}\}, G_1^{11} = \{ {1_0}{0_1}, {1_0}{2_1}, {0_0}{1_1}\}$, $G_2^{21} = \{ {2_0}{0_1}, {2_0}{2_1}, {1_0}{1_1}\}, G_0^{02} = \{ {1_0}{1_1}, {1_0}{2_1}, {0_0}{0_1}\}, G_1^{12} = \{ {2_0}{1_1}, {2_0}{2_1}, {1_0}{0_1}\}, G_2^{22} = \{ {0_0}{1_1}, {0_0}{2_1}, {2_0}{0_1}\}.$ All the subnetworks are isomorphic to ${P_3} \cup {K_{1, 1}}.$ Let ${i_0}{j_1}$ be a link from the complete bipartite network ${K_{3, 3}}.$The constructed design forces every link ${i_0}{j_1}$ to occur in exactly 3 subnetworks from $\mathcal{G}.$ Moreover, such design fulfills the following total function $\cap :A \to \{ 0, 1\},$ where $A = \{ G_c^{aw}, G_z^{xy}\}$ be a set of 2-elements subsets of $\mathcal{G}$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = \left\{ {\begin{array}{*{20}{c}} {1;} & {w \ne y, } \\ {0;} & {a \ne x, w = y, c \ne z.} \end{array}} \right.$

Here, $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 1$ means that the intersection of two subnetworks $G_c^{aw}, G_z^{xy}$ is isomorphic to subnetwork ${K_{1, 1}},$ and $\cap \left({\left\{ {G_c^{aw}, G_z^{xy}} \right\}} \right) = 0$ refers that they have no subnetworks in common.

Theorem 7. There exists a $({K_{n, n}}, n{K_{1, 1}}, n - 1;{K_{1, 1}})$-ND where $n$ is a prime number. Hence, there is a $(n{K_{1, 1}})$-code.

Proof. Define all subnetworks of a $({K_{n, n}}, n{K_{1, 1}}, n - 1;{K_{1, 1}})$-ND by the following table where$x \in \{ 0, 1, \ldots, n - 1\}.$

From Table 2, the collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_{n - 1}^{ij}\}; i \in \{ 0, 1, ..., n - 1\}, j \in \{ 0, 1, ..., n - 2\}$ of $n(n - 1)$ subnetworks. Now, we want to prove the isomorphism of all subnetworks in Table 2. By taking the subnetworks in the first column of Table 2, for all $\varepsilon \in \{ 0, 1, ..., n - 1\},$ we have $gcd(\varepsilon, n) = 1.$ Hence, the nodes $\varepsilon x$ are mutually distinct in $\{ 1, 2, ..., n - 1\}$ and all the subnetworks in the first column of Table 2 are isomorphic to $n{K_{1, 1}}.$ Similarly, the isomorphism for the remaining subnetworks in Table 2 can be proved. Hence, all subnetworks in Table 2 are isomorphic to $(n{K_{1, 1}}).$ It is clear that the subnetworks in the same row in Table 2 have no common links and any two subnetworks from two different rows have only one common link.

Theorem 8. There exists a $({K_{n, n}}, (n - 2){K_{1, 1}} \cup {K_{1, 2}}, n - 1;{K_{1, 1}})$-ND where $n$ is a prime number. Hence, there is a $(n - 2){K_{1, 1}} \cup {K_{1, 2}}$-code.

Proof. Define all subnetworks of a $({K_{n, n}}, (n - 2){K_{1, 1}} \cup {K_{1, 2}}, n - 1;{K_{1, 1}})$-ND by the following table where$x \in \{ 0, 1, \ldots, n - 1\}.$

From Table 3, the collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_{n - 1}^{ij}\}; i \in \{ 0, 1, ..., n - 1\}, j \in \{ 0, 1, ..., n - 2\}$ of $n(n - 1)$subnetworks. Now, we want to prove the isomorphism of all subnetworks in Table 3. By taking the subnetworks in the first column of Table 3, for all $\varepsilon \in \{ 0, 1, ..., n - 1\},$ we have $gcd(\varepsilon, n) = 1.$ Hence, the nodes $\varepsilon x$ are mutually distinct in $\{ 1, 2, ..., n - 1\}$ and the nodes $\varepsilon x + 1$ are mutually distinct in $\{ 1, 2, ..., n - 1\}.$ Together with the link $(0, 0)$ we conclude that every subnetwork in the first column of Table 3 is isomorphic to $((n - 2){K_{1, 1}} \cup {K_{1, 2}}).$Similarly, the isomorphism for the remaining subnetworks in Table 3 can be proved. Hence, all subnetworks in Table 3 are isomorphic to $((n - 2){K_{1, 1}} \cup {K_{1, 2}}).$ It is clear that the subnetworks in the same row in Table 3 have no common links and any two subnetworks from two different rows have only one common link.

Theorem 9. There exists a $({K_{9, 9}}, 3{K_{1, 2}} \cup {K_{1, 3}}, 3;{K_{1, 1}})$-ND. Hence, there is a $3{K_{1, 2}} \cup {K_{1, 3}}$-code.

Proof. Define all subnetworks of a $({K_{9, 9}}, 3{K_{1, 2}} \cup {K_{1, 3}}, 3;{K_{1, 1}})$-ND by the following table where$x \in \{ 0, 1, \ldots, 8\}.$

From Table 4, the collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_8^{ij}\}; i \in \{ 0, 1, ..., 8\}, j \in \{ 0, 1, 2\}$ of $24$ subnetworks. It is clear that all the subnetworks in the first column of Table 4 are isomorphic to the network $(3{K_{1, 2}} \cup {K_{1, 3}}).$ Similarly, the isomorphism for the remaining subnetworks in Table 4 can be proved. Hence, all subnetworks in Table 4 are isomorphic to $(3{K_{1, 2}} \cup {K_{1, 3}}).$ It is clear that the subnetworks in the same row in Table 4 have no common links and any two subnetworks from two different rows have only one common link.

Theorem 10. There exists a $({K_{12, 12}}, 2{K_{1, 2}} \cup 2{K_{1, 4}}, 2;{K_{1, 1}})$-ND. Hence, there is a $2{K_{1, 2}} \cup 2{K_{1, 4}}$-code.

Proof. Define all subnetworks of a $({K_{12, 12}}, 2{K_{1, 2}} \cup 2{K_{1, 4}}, 2;{K_{1, 1}})$-ND by the following table where$x \in \{ 0, 1, \ldots, 11\}.$

From Table 5, the collection $\mathcal{G} = \{ G_0^{ij}, G_1^{ij}, ..., G_{11}^{ij}\}; i \in \{ 0, 1, ..., 11\}, j \in \{ 0, 1\}$ of $24$ subnetworks. It is clear that all the subnetworks in the first column of Table 5 are isomorphic to the network $(2{K_{1, 2}} \cup 2{K_{1, 4}}).$ Similarly, the isomorphism for the remaining subnetworks in Table 4 can be proved. Hence, all subnetworks in Table 5 are isomorphic to $(2{K_{1, 2}} \cup 2{K_{1, 4}}).$ It is clear that the subnetworks in the same row in Table 5 have no common links and any two subnetworks from two different rows have only one common link.

5.   Constructions of generalized PBNDs based on Cartesian products

Theorem 11. Let $\phi (G) = ({\varphi _0}, {\varphi _1}, \ldots, {\varphi _{n - 1}})$ be a symmetric basis of $({K_{n, n}}, G, 2;{K_{1, 1}})$-ND and $\psi (H) = ({\psi _0}, {\psi _1}, \ldots, {\psi _{m - 1}})$ be a symmetric basis of $({K_{m, m}}, H, 2;{K_{1, 1}})$-ND, then the Cartesian product$\phi (G) \times \psi (H) = ({\varphi _0}, {\varphi _1}, \ldots, {\varphi _{n - 1}}) \times ({\psi _0}, {\psi _1}, \ldots, {\psi _{m - 1}}) = ({\varphi _0}{\psi _0}, {\varphi _0}{\psi _1}, \ldots, {\varphi _\rho }{\psi _\upsilon }, \ldots, {\varphi _{n - 1}}{\psi _{m - 1}})$ where $\rho \in \{ 0, 1, ..., n - 1\}, v \in \{ 0, 1, ..., m - 1\}$ is a symmetric basis of $({K_{mn, mn}}, G \times H, 2;{K_{1, 1}})$-ND.

Proof. Since $\phi (G) = ({\varphi _0}, {\varphi _1}, \ldots, {\varphi _{n - 1}})$ is a symmetric basis of $({K_{n, n}}, G, 2;{K_{1, 1}})$-ND, then

Since $\psi (H) = ({\psi _0}, {\psi _1}, \ldots, {\psi _{m - 1}})$is a symmetric basis of $({K_{m, m}}, H, 2;{K_{1, 1}})$-ND, then

Then, $\phi (G) \times \psi (H) = ({\varphi _0}, {\varphi _1}, \ldots, {\varphi _{n - 1}}) \times ({\psi _0}, {\psi _1}, \ldots, {\psi _{m - 1}}) = ({\varphi _0}{\psi _0}, {\varphi _0}{\psi _1}, \ldots, {\varphi _\rho }{\psi _\upsilon }, \ldots, {\varphi _{n - 1}}{\psi _{m - 1}})$ where $\rho \in \{ 0, 1, ..., n - 1\}, v \in \{ 0, 1, ..., m - 1\}.$From (3) and (4), we can conclude $\{ {\phi _\rho }{\psi _v} - {\phi _{n - \rho }}{\psi _{m - v}} + \rho v:\rho v \in \{ 0, 1, ..., n - 1\} \times \{ 0, 1, ..., m - 1\} \} = \{ ({\phi _\rho }(G) - {\phi _{n - \rho }}(G) + \rho)({\psi _v}(H) - {\psi _{m - v}}(H) + v) :\rho \in \{ 0, 1, ..., n - 1\}, v \in \{ 0, 1, ..., m - 1\} \} = \{ 0, 1, ..., n - 1\} \times \{ 0, 1, ..., m - 1\}.$Then, $\phi (G) \times \psi (H)$ is a symmetric basis of $({K_{mn, mn}}, G \times H, 2;{K_{1, 1}})$-ND. The incidence matrix of $({K_{n, n}}, G, 2;{K_{1, 1}})$-ND has $2n$ rows and ${n^2}$ columns and the incidence matrix of $({K_{m, m}}, H, 2;{K_{1, 1}})$-ND has $2m$ rows and ${m^2}$ columns. The incidence matrix of $({K_{mn, mn}}, G \times H, 2;{K_{1, 1}})$-ND has $2mn$ rows and ${n^2} \times {m^2}$columns. Hence, $\left| {{C_{column}}} \right| = {n^2} \times {m^2}$ and $\left| {{C_{row}}} \right| = 2mn.$ When ${C_{row}}$ is used for coding, we can detect up to $\, \theta ({C_{row}}) - 1 = 2mn - 3$ errors and correct up to $\left\lfloor {\frac{{\theta ({C_{row}}) - 1}}{2}} \right\rfloor = \left\lfloor {\frac{{2mn - 3}}{2}} \right\rfloor.$

Example 2. Let $\phi ({P_3}) = (0, 0)$ be a symmetric basis of $({K_{2, 2}}, {P_3}, 2;{K_{1, 1}})$-ND and $\psi ({P_4}) = (0, 1, 1)$ be a symmetric basis of $({K_{3, 3}}, {P_4}, 2;{K_{1, 1}})$-ND, then the Cartesian product $\phi ({P_3}) \times \psi ({P_4}) = (0, 0) \times (0, 1, 1) = (00, 01, 01, 00, 01, 01)$ is a symmetric basis of $({K_{6, 6}}, {P_3} \times {P_4}, 2;{K_{1, 1}})$-ND. Note that if $ij \in \phi ({P_3}) \times \psi ({P_4}),$then $f(ij) = 3i + j$ gives a compact representation for the vector $\phi ({P_3}) \times \psi ({P_4})$ which is $(0, 1, 1, 0, 1, 1).$

6.   Characteristics of binary codes based on PBNDs

Combinatorial designs and several related structures can be used to generate codes based on the incidence matrix. Many interesting and useful results have been provided as a result of the interplay between designs and codes. For an excellent survey on the topic, see ^[51]. Recently there is more attention of codes generating from graphs. The connection of codes and graphs has been explored from different aspects in the literature. The main objective in these works is to take a special class of graphs and construct codes from the adjacency matrix of the graph. Nice codes can be generated by some strongly regular graphs ^[52,53]. Binary codes can be generated by different graphs such as Paley graphs, the block graphs of Steiner 2-designs, and the Latin square graphs ^[54]. Non-isomorphic codes have been produced by non-isomorphic graphs, see ^[54]. The structure of the graph may lead to different types of codes as a result, such as self-dual codes, self-orthogonal codes, etc. We refer the reader to ^{[55,56,57,58,59,60,61]} for some of these works. Higazy et al. ^[62] studied the group-generated graph designs for certain circulant graphs and the generation of codes from such designs. Here, we examine binary codes obtained from the row or column span of the incidence matrices of some graphs that occur as induced subgraphs of the complete bipartite graphs. In this paper, we introduce a method from which we can generate a special type of orthogonal codes. These codes are depending on the orthogonality of graphs found in the design $({K_{n, n}}, F, k; {K_{1, 1}}).$ Two graphs are orthogonal if they intersect in at most one edge. Our method constructs binary codes satisfying that the inner product of any two codewords $\le 1$. We introduce PBNDs that lead to efficient error detection and correction codes. In order to increase the dimension of code and keeping efficient properties for error detection and correction, we introduce a technique that generates codes based on the Cartesian product of earlier designs. We should notify the reader that our method for such a product differs from those studied in ^[63].

In this paper, we studied binary codes based on PBNDs, $({K_{n, n}}, F, k; {K_{1, 1}}).$ For instances, the advantages of binary codes generated by $({K_{n, n}}, F, 2;{K_{1, 1}})$ are as follows: From the binary codeword generator of length ${n^2},$ we can get $2n - 1$ new binary codewords of length ${n^2},$ this can be shown as follows, where these codewords represent the rows of the incidence matrix of $({K_{n, n}}, F, 2;{K_{1, 1}}).$

Definition 8. For the binary codeword with length ${n^2}, {v_{ij}}$ is called a binary codeword generator, if $(j - i)$ gives $\{ 0, 1, ..., n - 1\}$ for $\, ij$ with which ${v_{ij}} = 1.$

Definition 9. If $v_{ij}^0 = 1,$ then $v_{(i + x)(j + x)}^x = 1, x \in \{ 0, 1, ..., n - 1\}$ is called $x -$translate of ${v^0}.$

Example 3. Let $x \in {\mathbb{Z}_n}, \; v_{ij}^x = \left\{ \begin{gathered} 1;\, ij \in A = \{ x\} \times {\mathbb{Z}_n}, \hfill \\ 0;\, ij \in \mathbb{Z}_n^2\backslash A. \hfill \\ \end{gathered} \right.$ and $u_{ij}^x = \left\{ \begin{gathered} 1;\, ij \in B = {\mathbb{Z}_n} \times \{ x\}, \hfill \\ 0;\, ij \in \mathbb{Z}_n^2\backslash B, \hfill \\ \end{gathered} \right.$ the rows of the following matrix $M$ represent $2n$ binary codewords of length ${n^2}, \; M = \left[\begin{gathered} v_{ij}^0 \hfill \\ v_{ij}^1 \hfill \\ \vdots \hfill \\ v_{ij}^{n - 1} \hfill \\ u_{ij}^0 \hfill \\ u_{ij}^1 \hfill \\ \vdots \hfill \\ u_{ij}^{n - 1} \hfill \\ \end{gathered} \right].$

Put $n = 4,$ then $x \in {\mathbb{Z}_4}, \; v_{ij}^x = \left\{ \begin{gathered} 1;\, ij \in A = \{ x\} \times {\mathbb{Z}_4}, \hfill \\ 0;\, ij \in \mathbb{Z}_4^2\backslash A. \hfill \\ \end{gathered} \right.$ and $u_{ij}^x = \left\{ \begin{gathered} 1;\, ij \in B = {\mathbb{Z}_4} \times \{ x\}, \hfill \\ 0;\, ij \in \mathbb{Z}_4^2\backslash B, \hfill \\ \end{gathered} \right.$ the rows of the following matrix $M$ represent $8$ binary codewords of length $16.$ Also, if $v_{ij}^x = 1,$ then there is a graph corresponding to this vector with the edge set $E({G^x}) = \{ ({i_0}, {j_1}):i, j \in {\mathbb{Z}_4}\},$ see Figure $2$.

Also we can add the following to the advantages of PBNDs: For the generalized binary codes generated by the Cartesian products of PBNDs. The Cartesian products of PBNDs is an easier method than the previously defined methods for constructing new binary codes from the old ones ^[64].

7.   Conclusions

In the paper, we propose a novel technique for constructing a partially balanced network design (PBND). These networks are used to model the information transmission represented by strings of the signals zero and one. Certain problems appear in the transmission of information in digital communications when this information is transmitted in the form of strings of zeros and ones. The noise in the transmission channel changes the original transmitted signal to a different signal. Therefore, the receiver takes a wrong decision. The PBND is a helping tool that manages us to detect and correct the errors in the coded messages. A graphical model is introduced for the PBND. Also, the PBNDs are represented by their corresponding incidence matrices. These matrices compromise new and several codes. The nodes of these networks are labeled by the Cartesian product of additive abelian groups. Some direct constructions of small and generalized PBND are introduced. Finally, we prove that the Cartesian product of two small symmetric bases gives a larger symmetric basis that generates new codes with larger lengths. The Cartesian products of PBNDs is an easier method than the previously defined methods for constructing new binary codes from the old ones. The following table presents the summary of the results in the paper. It should be noted that$p$is a prime number in Table 6.

Acknowledgments

This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/155), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.