Globally projective synchronization for Caputo fractional quaternion-valued neural networks with discrete and distributed delays

1.   Introduction

In recent decades, the integer-order real-valued neural networks (RVNNs) and integer-order complex-valued neural networks (CVNNs) have been extensively studied and applied in pattern recognition, signal processing, associative memory ^[1,2,3] and so on. Nonetheless, the multidimensional data processing cannot be solved through RVNNs or CVNNs such as body images and color images ^[4]. As the quaternion-valued neurons processing is more efficiently and compactly, more and more scholars have combined the quaternion valued with the conventional neural network to study the QVNNs. It is widely known that three feasible methods are generally used to discuss the dynamic behaviors of integer-order QVNNs: the decomposition of integer-order QVNNs into four RVNNs ^[5]; the decomposition of integer-order QVNNs into two CVNNs ^[6]; the discussion of integer-order QVNNs as a whole ^[7].

Time delay is a common phenomenon in neural networks (NNs), which will produce oscillation, chaos and instability. The limited transmission speed and traffic congestion of neural networks make discrete delays inevitable ^[8]. Furthermore, the large number of parallel paths of varying axon size and length make a certain spatial extent frequently present in the NNs, which is the distribution delay ^[9]. Recently, a flurry of research has been done on the stabilization and synchronization of integer-order NNs with mixed delays. In ^[10], Yang et al. studied the finite-time stability of NNs with mixed delays. In ^[11], Song and Wen investigated the exponential synchronization of memristor-based NNs with random mixed delays. The study of synchronization with mixed delays still attracts a large number of scholars' attention.

Synchronization of NNs is an interesting and crucial dynamic behaviors that is extensive applied in information science, signal processing, secure communication. Researchers have proposed several synchronization patterns including phase synchronization ^[12], projective synchronization ^[13], exponential synchronization ^[14], Mittag-Leffler synchronization ^[15], as well as plentiful results have been obtained. The projective synchronization means that the slave system synchronizes with the master system by a specific scale factor under the appropriate controller.

Note that the fractional order model can provide more accurate description of the memory and genetic characteristics than the integer order model. To our knowledge, many results have been achieved in analysing the dynamics of FOQVNNs ^{[16,17,18,19,20]}. In ^[17], Yang et al. investigated the global Mittag-Leffler synchronization of FOQVNNs by applying a linear feedback controller with transforming the system into four equivalent real-valued systems. In ^[19], Li et al. studied the global asymptotic synchronization of FOQVNNs by choosing an appropriate controller and Lyapunov function. However, the results of FOQVNNs with discrete delay and distributed delay are very rare. Based on these considerations, the aim of this paper focuses on the projective synchronization of FOQVNNs with discrete and distributed delays. The highlights of this paper are shown as below.

$\bullet$ The paper is concerned with the FOQVNNs including the discrete delay and distributed delay, and the considered models are more general and less conservative.

$\bullet$ The method of this paper is the direct quaternion approach rather than decomposing FOQVNNs into subsystems, which significantly reduces the complexity of the calculation.

$\bullet$ The synchronisation conditions are described by the algebraic inequality forms, which are easy to check in practical applications.

2.   Preliminaries and model representation

In this section, we will describe the related notations and basic concepts with regard to fractional calculation. Moreover, the FOQVNNs model and several lemmas are introduced.

Notations: The quaternion valued function $h_p (\cdot)$ is defined as $h_p = h_p^R+ih_p^I+jh_p^J+kh_p^K$, where $h_p^R, h_p^I, h_p^J, h_p^K \in \mathbb{R}$, $i, j, k$ satisfy the Hamilton rules: $ij = -ji = k, jk = -kj = i, ki = -ik = j, i^2 = j^2 = k^2 = -1; \overline{h_p} = h_p^R-ih_p^I-jh_p^J-kh_p^K$ is the conjugate of $h_p$, $\left | h_{p} \right | = \sqrt{\overline{h_{p}}h_{p} } = \sqrt{h_{p}\overline{h_{p}}}$ denotes the module of $h_p$. For $h = \left (h_{1}, h_{1}, ..., h_{n} \right) ^{T} \in \mathbb{Q}^{n}, ||h|| = (\sum\limits_{p = 1}^{n} |h_{p}|^2) ^\frac{1}{2}$ represents the norm of $h$.

Definition 1. (^[21]) The fractional integral of function $\varphi \left (t \right)$ with order $q > 0$ is defined as:

Definition 2. (^[21]) The Caputo derivative of fractional $0 < q < 1$ of function $\varphi(t)$ is defined as:

Remark 1. Compared with the Riemann-Liouville derivative in ^[21], the Caputo type fractional-order derivative of a constant is identically equal to zero, that is not the case for the Riemann-Liouville type fractional-order derivative. Moreover, the Caputo type fractional-order derivative is a formal generalization of the integer-order derivative in the sense of the Laplace transformation. Based on the above considerations, the Caputo derivative has been adopted in this paper.

Lemma 1. (^[22,23]) If the function $\varphi(\cdot) \in \mathbb{Q}$ is differentiable, then

Lemma 2. (^[24]) For any $\eta, \mu \in \mathbb{Q}$, the following inequality holds:

Lemma 3. (^[25]) Assuming that $V\left (\cdot \right) \in \mathbb{R}$ be bounded and continuous. If there exist $\chi > \varphi > 0$ such that

then $\lim\limits_{t \to +\infty} V\left (t \right) = 0.$

Next, consider the FOQVNNs model including discrete and distributed delays as follows:

where $0 < q < 1, h_{p} \left (\cdot \right) \in \mathbb{Q}$ denotes the state vector of $p$th; $a_{p} \in \mathbb{R}$ stand for the self-regulating coefficient; respectively, $b_{pq}, c_{pq}, d_{pq} \in \mathbb{Q}$ are the connection weights; $\tau_{1}, \tau_{2}$ represent the delay; $I_{p} \in \mathbb{Q}$ is the external input; $f\left (\cdot \right) \in \mathbb{Q}$ denotes the activation function. For any $h_{q}, {h}' _{q}\in \mathbb{Q}$, the activation function $f_q \left (\cdot \right)$ satisfies the following Lipschitz condition:

where $l_q$ is a positive constant.

3.   Main results

Consider system (2.6) as master system, and the controlled slave model is depicted below

where $U_p(\cdot) \in \mathbb{Q}$ is the controller.

The error is $e_{p} \left (t \right) = {h}'_{p}\left (t \right) -\zeta h_p\left (t \right)$, and the hybrid quaternion-valued controller $U_p(\cdot)$ is defined as follows:

Combining (2.6), (3.1) and (3.2), the error system is

Theorem 1. Suppose that the activation function $f_q \left (\cdot \right)$ satisfies the Lipschitz condition (2.7), for the controller $U_p(\cdot)$ in (3.2), if there exist $\mu _{1} > 0, \ \mu _{2} > 0, \ \mu _{3} > 0$, such that for some $\alpha > 0$, the following LMI holds:

then system (2.6) and (3.1) can realize globally projective synchronization.

{Proof.} Choosing a Lyapunov function

From Lemma 1, we can get that

According to the Lipschitz condition (2.7) and Lemma 2, we have

Similarly,

Combining (3.7)–(3.9) with (3.6), one can get

It follows from fractional-order Razumikhin theorem ^[26] that

From Lemma 3, we have $\lim\limits_{t \to +\infty} V(t) = 0$. Therefore, systems (2.6) and (3.1) can realize the globally projective synchronization.

Remark 2. If $d_{pq} = 0$, then system (2.6) was considered without the distributed delay in ^[27]. If $d_{pq} = 0, \ \tau_1 = \tau_2 = 0$, then system (2.6) without delays was discussed in ^[5]. Note that the distributed delay can affect the dynamics of NNs, comparing with the models ^{[5,6,9,23,27]}, the considered model including discrete and distributed delays in this paper is more general.

Remark 3. Compared with the real decomposition method ^[5] and plural decomposition method ^[6], without decomposing the FOQVNNs into several subsystems in this paper, the globally projective synchronization criterion (3.4) of FOQVNN is obtained by the algebraic inequality forms, which is easy to check in practical applications and reduces the complexity of the calculation.

4.   Numerical simulation

Example 1. Consider the FOQVNNs with discrete and distributed delays described by:

where $a_1 = a_2 = 1, I_1 = I_2 = 0,$ $l_1 = l_2 = l_3 = 1,$ $b_{11} = 2+2i+2j+2k, b_{12} = -0.1-0.1i-0.1j-0.1k,$ $b_{21} = 2-3i+2j-3k,$ $b_{22} = 1+i+j+k,$ $c_{11} = -2-1.5i-2j-1.5k,$ $c_{12} = -0.2+0.5i-0.2j+0.5k,$ $c_{21} = 6.5-i+6.5j-k,$ $c_{22} = -3.5+2.5i-3.5j+2.5k,$ $d_{11} = 2.5-4.5i+2.5j-4.5k,$ $d_{12} = -0.3+0.2i-0.3j+0.2k,$ $d_{21} = -3-2i-3j-2k,$ $d_{22} = -1+i-j+k, \tau_1 = \tau_2 = 1.$

The corresponding slave system is described by:

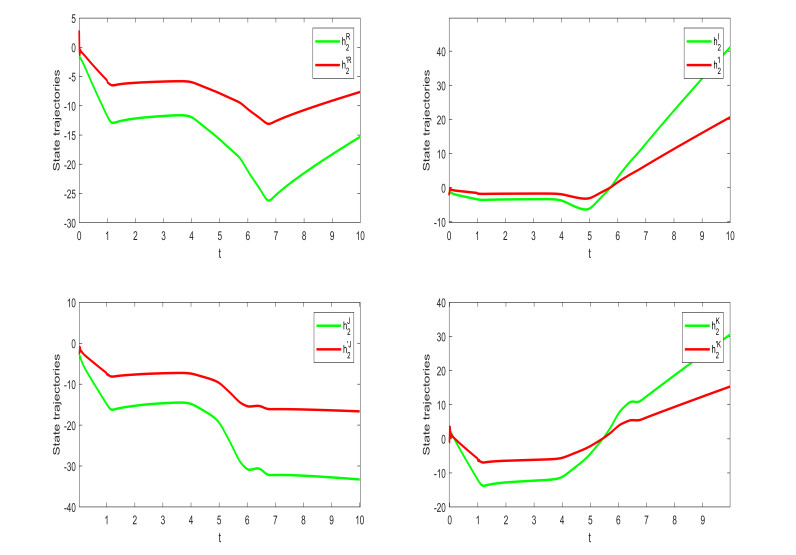
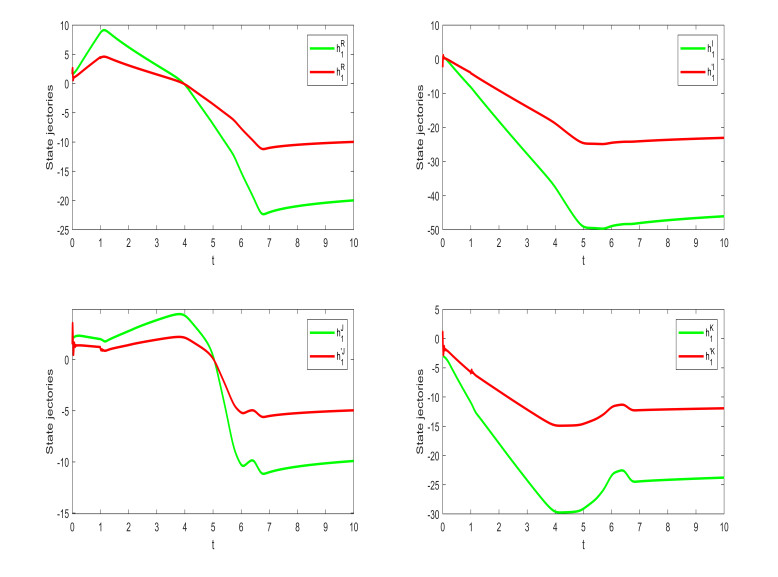
By using the MATLAB toolbox, Figures 1 and 2 shows the state trajectories in the absence of a controller with the order $q = 0.93$.

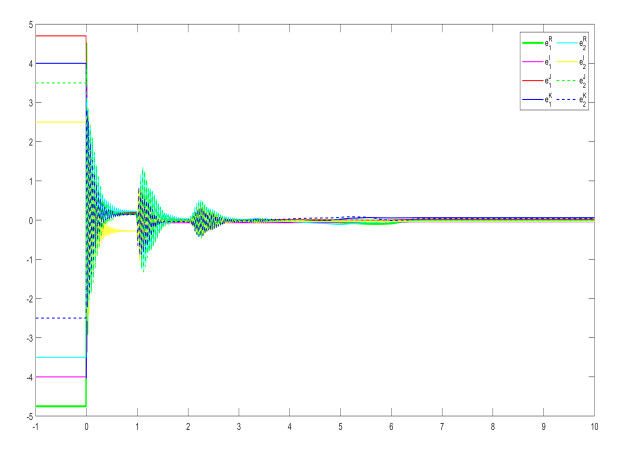
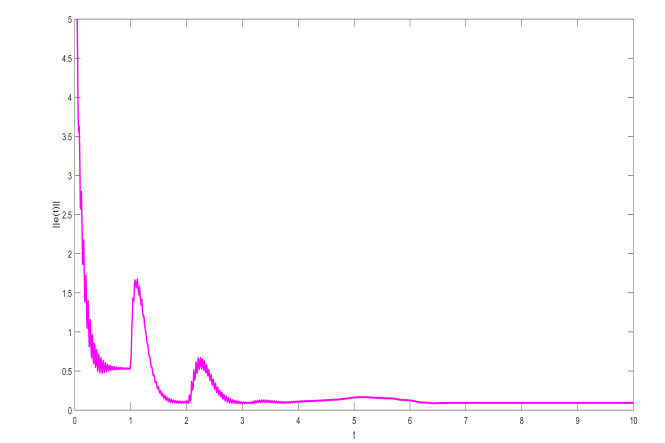
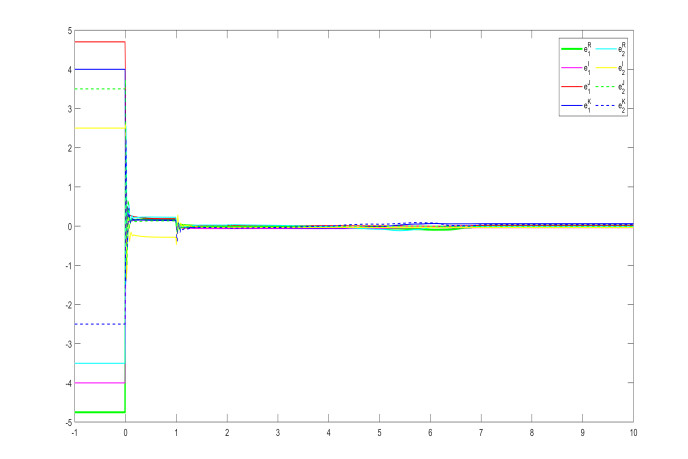
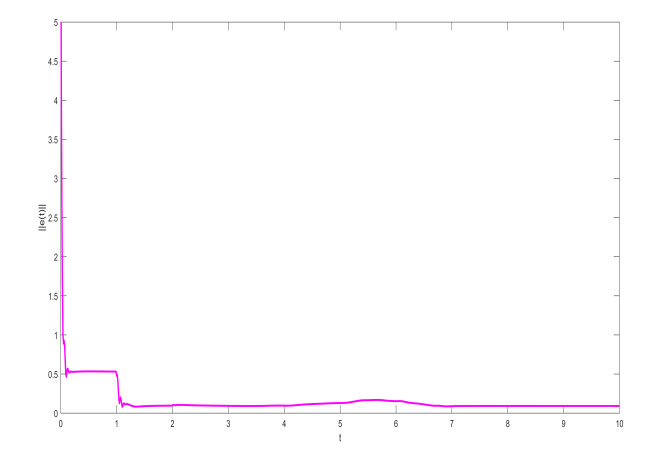
In controller (3.2), if we choose the coefficients $\mu_1 = 190, \ \mu_2 = 125, \ \mu_3 = 55, \alpha = 1$, then the conditions of Theorem 1 hold. The initial values are selected as $h_{10} = 1.5+i+2j-3k, \ h_{20} = -1.4-i-2j+3k, \ {h}'_{10} = -4-3.5i-2.5j+k, \ {h}'_{20} = 4+3.5i+2.5j-k$. The projective parameters is chosen as $\zeta = 0.5$. Thus, Figures 3 and 5 shows the state trajectories with the different orders $q = 0.83$ and $q = 0.93$ respectively. The synchronization error norms are depicted with the different orders $q = 0.83$ and $q = 0.93$ in Figures 4 and 6. The numerical simulation shows that the figures are consistent with the theoretical results.

Remark 4. In order to further characterize the influence of the system order $q$ on the performance of projective synchronization, we have chosen the different orders $q = 0.83$ and $q = 0.93$ in Example 1 to present the state trajectories and error norms by Figures 3–6. It can be seen that the speed of projective synchronization becomes faster and faster along with the increase of the order $q$.

5.   Conclusions

The globally projective synchronization for a class of FOQVNNs with discrete and distributed delays is investigated through the direct quaternion approach rather than decomposing the QVNNs into several subsystems. By constructing an appropriate controller, the synchronization conditions were obtained by using fractional differential inequality techniques and fraction-order Razumikhin theorem. Finally, an example are performed to show the effectiveness of the method. The proposed results are easy to check in practical applications and reduces the complexity of the calculation.

Acknowledgments

This work was jointly supported the Natural Science Foundation of Anhui Province of China (No. 1908085MA01), the Natural Science Foundation of the Higher Education Institutions of Anhui Province (No. KJ2019A0557) and the Excellent Young Talents Fund Program of Higher Education Institutions of Anhui Province (No. gxyq2019048).

Conflict of interest

The authors declare that they have no competing interests.