Linear Bayesian equilibrium in insider trading with a random time under partial observations

1.   Introduction

In Kyle's ^[11] seminal contribution, a continuous auction model of insider trading on a risky asset is proposed, in which an insider is assumed to possess complete information about the asset value with normal distribution, noise traders without any information on the asset randomly submit orders and market makers excavate the insider's private information based on the total market order flow to make the market efficient. It shows that there is a unique linear Bayesian equilibrium consisting of insider's trading intensity and market liquidity parameter such that the intensity is increasing to infinity and the market liquidity keeps constant as time goes to the final trading time.

Later, Kyle's model ^[11] is extended from different perspectives. For a class of continuous-time insider trading on a risky asset with general distributions, Back ^[2] obtained a closed form of Bayesian equilibrium. In Cho's ^[8] view, he believed that there is risk behavior for the insider, and found that in the Bayesian equilibrium, the price pressure with risk aversion converges to the risk-neutral price pressure as the insider becomes less and less risk-averse. Furthermore, Caldentey and Stacchetti ^[5] considered a setting of insider trading when an insider may trade at a random deadline and also established its Bayesian equilibrium. Note that all of the above results are deduced by the principle of dynamic programming. Recently, Aase, Bjuland and Øksendal^[1] applied the maximum principle to solve continuous-time insider trading problem to establish a closed form of none Bayesian equilibrium. And Zhou ^[18] also obtained a unique none Bayesian equilibrium when market makers observe some information about the risky asset. There is much literature on this topic, see ^{[3,4,6,7,9,10,14,15]} and so on.

In fact, there may be multifactorial to influence a financial market. Based on ^[5,18], Xiao and Zhou ^[16] studied an insider trading model, in which partial information on a risky asset with value $v$ as

is observed by market makers and the trading will be ended at a random time $\tau$. And they obtained a closed form of none Bayesian equilibrium of the model by the maximum principle method. However, the model ^[16] can be simplified: for the market makers, only the initial information

in the formula (1.1) is useful to make market efficient, since the standard Brownian motion ${B}_{ut}$ is independent of $v$ and $\epsilon$ for $t > 0$. That is to say, only the information $v+\epsilon$ at the beginning of trading is useful while ${B}_{ut}$ is not for market makers to set the asset's price, therefore, we think that ${B}_{ut}$ is redundant and can be omitted. In this paper, applying dynamic programming principle, we further establish Bayesian equilibrium of this simplified model, and clearly deduce the none Bayesian equilibrium in ^[16]. To illustrate some characteristics of the Bayesian equilibrium, simulations are given.

The rest of the paper is organized as follows. In Section 2, our model of insider trading with the definition of linear Bayesian equilibrium will be introduced. In Section 3, a necessary condition of market efficiency is given. Section 4 includes the important HJB equation. In Section 5, the existence and uniqueness of linear equilibrium is established. In Section 6, we give some simulations to describe properties about the equilibrium. Conclusions are drawn in the last section. The model with linear Baysian equilibrium

2.   The model with linear Baysian equilibrium

The model of insider trading here is a new version of the model in ^[16]. Basically, There is a risky asset whose value $v$ is a normal distribution with mean $0$ and variance $\sigma_{v}^{2}$ trading until a random time $\tau$ when the value $v$ becomes public knowledge, which has a geometric distribution with probability of failure $e^{-\mu t}$ for some $\mu > 0$ and is independent of the history of transactions and prices ^[5]. And there are three types of traders: (1) An insider, who knows the risky asset value $v$ with its current market price and submits her/his order $x_{t}$ at time $t$; (2) Noise traders, who have no information about the underlying asset and submit total order $z_t = \sigma_zB_{zt}$ ^[8], where the number $\sigma_z > 0$ and $B_{zt}$ is a standard Brownian motion; (3) Market makers, who observe not only the total traded volume $y_t = x_{t}+z_{t}$ (can not discriminate $x_{t}$ and $z_{t}$ respectively) but also another signal of the asset value as (1.2): $v+\epsilon$, where $\epsilon$ is normally distributed with mean $0$ and variance $\sigma_{\epsilon}^{2}$ and is independent of $v$ and $B_{zt}$, and then set the market price of the underlying asset in a semi-strong way as in ^[11]:

where ${\cal F}^M_{t} = \sigma\{y_s, 0\leq s\leq t, \}\vee\sigma\{v+\epsilon\}$.

As in ^[1,2,11,18], the dynamic of the insider's strategy $x_t$ and the dynamic of the market pricing $p_t$ are assumed local linear respectively as follows:

where $x_0 = 0$ and $p_{0} = E[v|v+\epsilon] = \frac{\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}(v+\epsilon)$.

Roughly speak, the insider's expected profit ^[5] is written as

where both $\beta_{t} > 0$ and $\lambda_{t} > 0$ are two deterministic, smooth function on $[0, \infty)$; technically, $E[\int_{0}^{\infty}e^{-\mu t}\beta_{t}(v-p_{t})^{2}dt] < \infty$ should be satisfied. Note that $\beta_{t}$ and $\lambda_t$ (or ${\frac{1}{\lambda_t}}$) are called trading intensity of the insider and market liquidity parameter (or market depth) respectively, and $\Sigma_t = E[v-p_t]^2$ is called residual information ^[11].

The collection of all these functions $\beta$ and the collection of all these functions $\lambda$ are denoted by $\Theta$ and $\Lambda$ respectively. Clearly, given a pair $(\beta, \lambda)\in (\Theta, \Lambda)$, there is a unique insider trading market; and sometimes we also call it market $(\beta, \lambda)$.

Definition 2.1 A linear Bayesian equilibrium is a pair $(\beta, \lambda)\in (\Theta, \Lambda)$ such that

(i) (maximization of profit) given $\lambda$, $\beta$ maximizes

where ${\cal F}_{t}^{I} = \sigma\{p_s, 0\leq s\leq t\}\vee \sigma\{v\}$;

(ii) (market efficiency) given $\beta$, $\lambda$ satisfies

3.   Necessary condition for market efficiency

Before establishing the existence of linear equilibria in our insider trading model, we first give some necessary conditions for market efficiency.

Lemma 1. Let $(\beta, \lambda)\in (\Theta, \Lambda)$ be a market with $\lambda$ satisfying the market efficiency condition (2.4). Then

where $\Sigma_0 = \frac{\sigma_{\epsilon}^{2}\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}$.

Proof. At first, the total traded volume

and (1.2) observed by market makers can be written as a vector dynamic equation

where

$\xi_{t} = \begin{pmatrix} y_{t} \\ u_{t} \end{pmatrix}$, $\xi_{0} = \begin{pmatrix} 0 \\ v+\epsilon \end{pmatrix}$, $A_{0} = \begin{pmatrix} -p_t\beta_{t} \\ 0 \end{pmatrix}$, $A_{1} = \begin{pmatrix} \beta_{t} \\ 0 \end{pmatrix}$, $A_{2} = \begin{pmatrix} \sigma_{z} & 0 \\ 0 & 0 \end{pmatrix}$, $B_t = \begin{pmatrix} B_{zt} \\ 0 \end{pmatrix}$.

Therefore at time $t$, the market makers' information

Note that the matrix $A_{2}$ is irreversible, we need to construct a new dynamic equation which must be equivalent to $\xi_t$ for market makers setting price such that a new version of $A_{2}$ is reversible.

For convenience, we consider the following signal-observation dynamic system

where $\eta_{t} = \begin{pmatrix} y_{t} \\ u_{t} \end{pmatrix}$, $\eta_{0} = \begin{pmatrix} 0 \\ v+\epsilon \end{pmatrix}$, $A^*_{2} = \begin{pmatrix} \sigma_{z} & 0 \\ 0 & \sigma \end{pmatrix}$, $B^*_t = \begin{pmatrix} B_{zt} \\ W_{t} \end{pmatrix}$, $u_t = v+\epsilon+\sigma W_t$, and $\sigma$ is a positive real number and $W$ is a standard Brownian motion independent of $v$, $\epsilon$ and $B_z$. Clearly, for any time $t$,

Denote $p^*_{t} = E[v|{\cal F}^\eta_{t}]$ and $\Sigma^*_{t} = E[(v-p^*_{t})^{2}]$. Then by Theorems 12.7 and 12.9 of optimal filtering equations in ^[12,13] or Lemma 3.3 in ^[18], we have

with

Then, by the expression of $p_t^*$ above, we have that $p^*_t$ is ${\cal F}_t^\xi$ measurable. And by tower law of conditional expectation,

Note that $\lambda$ satisfies the market efficiency condition (2.4):

then we have

Therefore, by the equations in (3.3), we have

with $\Sigma_0 = \frac{\sigma_{\epsilon}^{2}\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}$, and the proof is complete.

Remark 1. In our model, for the risky value $v$, the observation of market makers is $v+\epsilon$ at any time $t\geq 0$. However, to obtain our desired result, we take $u_t = v+\epsilon+\sigma W_t$ as the observation of market makers at time $t > 0$ where $\sigma > 0$, since the standard Brownian motion $W$ is independent of $v$, $B_{z}$ and $\epsilon$ and then only the initial information $v+\epsilon$ is useful for market makers to make market efficient. In fact, the information $v+\epsilon$ in the signal $u_{t}$ for any $t > 0$ has been integrated into $\Sigma_{0}$, which is verified by the expression of $\lambda_t$, $\beta_t$ and $\Sigma_t$ independent of $\sigma$ and $W_{ut}$ in Lemma 1.

4.   HJB equation

Given a market liquidity parameter $\lambda\in \Lambda$, the object of the insider is to take her/his information advantage and find an optimal strategy $\beta\in \Theta$ to maximize the profit ^[5]:

under the following stochastic control system, the second dynamic in (2.1):

This is a classical stochastic control problem, which can be solved by the dynamic programming principle ^[17].

Since the random continuing time $\tau$ obeys a life distribution which has no memory, the insider's value function at time $t$ can be written as

Lemma 2. The value function $\pi(t, p_{t})$ satisfies the HJB equation below:

Proof. According to the equality (4.2), we can denote

Note that $p_t$ evolves the dynamic (4.1). Then by Proposition 3.5 in ^[17], the value function $\widetilde{\pi}(t, p_t)$ satisfies

which can be easily simplified as the HJB (4.3), and the proof is complete.

5.   Existence and uniqueness of linear equilibrium

Now the existence and uniqueness of linear equilibrium in our model can be given below.

Theorem 1. There is a unique linear equilibrium $(\beta, \lambda)\in (\Theta, \Lambda)$ satisfying

and at the equilibrium, the remained information

where $\Sigma_0 = \frac{\sigma_{\epsilon}^{2}\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}$; the insider's profit from $t$ onwards

with the whole expect profit

Proof. Let $(\beta, \lambda)\in (\Theta, \Lambda)$ be a linear equilibrium in the insider trading market. Then by Theorem 3.4 in ^[17], the value function at any time $t$ is equal to the optimal profit from $t$ onward, that is,

Note that the value function $\pi(t, p_{t})$ satisfies the HJB (4.3), which is equivalent to the following system

with boundary condition: $\lim_{t\rightarrow \infty}\pi(t, p_{t}) = 0$.

By Lemma 1, we have $\frac{d\Sigma_t}{dt} = -\frac{\beta_{t}^{2}{\Sigma}_{t}^{2}}{\sigma_{z}^{2}} < 0$. Since $\Sigma_t = E(v-p_t)^2$, then

Then by the second equation of (5.1), we obtain that

where $g_t$ is some smooth, deterministic function respect to $t$.

Then taking (5.2) into the first equation of (5.1), we obtain the equation

Since $p_t$ can be taken any real number, then

which can be easily solved as follows:

where both $\lambda_0$ and $g_0$ are some positive real numbers.

In the following, let us determine the values of $\lambda_0$ and $g_0$. By Lemma 1, we also have

Then bring the value of $\lambda_t$ in (5.4) into (5.5),

By the lemma 1, we can assume that $\lim_{t\rightarrow \infty}\Sigma_t = a$, where $a$ is a real number, and so

So we have

And according to (5.2), (5.4), (5.6) and the above two equations, we have

So by the boundary condition $\lim_{t\rightarrow \infty}\pi(t, p_{t}) = 0$, by Fatou Lemma, there must be

So we have

and so

or

Finally, by Lemma 1,

where $\Sigma_0 = \frac{\sigma_{\epsilon}^{2}\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}$.

Since the random time $\tau$ is life distributed with parameter $\mu$, $E(\tau) = \frac{1}{\mu}$. And the optimal profit from time $t$ onward of the insider is

Then

Since the insider's expected profit is maximal, there must be $a = 0$. That is to say

Then

and other conclusions hold.

Remark 2. Clearly, the linear Bayesian equilibrium in Theorem 5.1 here obtained by dynamic programming principle is the same as the linear equilibrium in Theorem 4.1 obtained by maximal principle in ^[16]. However, the former equilibrium can tell us the insider's profit from any trading time $t$ onwards under her/his current information, but the latter can not do that; that is our motivation of this paper. Of course, the former equilibrium has the same properties of the latter in Corollary 4.1 in ^[16]. For readers' convenience, we restate them bellow (and give simulations in Section 6 as supplement):

(i) As time goes by, both trading intensity $\beta_{t}$ and market depth $\frac{1}{\lambda_{t}}$ increase exponentially, while residual information $\Sigma_{t}$ decreases exponentially even approaching zero as trading time going to $\infty$;

(ii)

(iii)

6.   Simulations

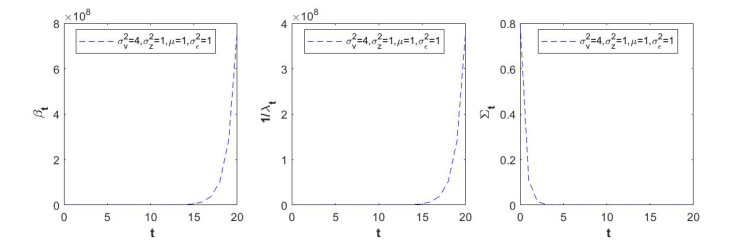
To see more clearly those properties of linear Bayesian equilibrium about Theorem 1 and Remark 2, some simulations are illustrated, where we always assume that $\sigma_{z}^{2} = 1$ and $\Sigma_{v}^{2} = 4$.

According to those expressions in Theorem 1, as trading time $t$ increasing, both trading intensity $\beta$ and market depth $\frac{1}{\lambda}$ increase exponentially, but residual information $\Sigma$ decreases exponentially, see Figure 1.

Figure 2 tells us that (1) with the average trading time $E(\tau)$ increasing, trading intensity $\beta$ decrease but residual information $\Sigma$ increase, while market depth $\frac{1}{\lambda}$ is a unimodal function of average trading time with a unique minimum value; and (2) if the average trading time $E(\tau)$ is longer, the insider will make more expect profit $E(\pi)$.

Figure 3 shows that if partial information on the risky value observed by market makers is less and less ($\sigma_{\epsilon}^{2}\rightarrow \infty$), both trading intensity $\beta$ and market depth $1/\lambda$ is decreasing while both residual information $\Sigma$ and the whole expect profit $E(\pi)$ earned by the insider is more and more.

7.   Conclusions

In this paper, the insider trading model in ^[16] is revisited, in which market makers observe partial information about a risky asset and an insider stops trading at a random time. By dynamic programming principle, we obtain a unique linear Bayesian equilibrium consisting of insider's trading intensity and market liquidity parameter which is the same as that deduced by maximal principle in ^[16], including the insider's profit from any trading time onwards.

It shows that trading time, average trading time and partial information on the risky asset value observed by market makers have some impacts on the linear Bayesian equilibrium: (1) As trading time goes by, both trading intensity and market depth increase, while residual information decreases even closing to zero; (2) With average trading time increasing, trading intensity decrease but residual information increase, while market depth is a unimodal function with respect to average trading time with a unique minimum, and if average trading time is longer, the insider will make more expect profit; (3) As partial information on the risky value observed by market makers is less and less, both trading intensity and market depth is decreasing while both residual information and the whole expect profit earned by the insider is more and more. All of these results are in accord with our economic intuition.

Acknowledgments

The work is supported by NSF China (11861025), Guizhou QKHPTRC[2018]5769-07, Guizhou EDKY[2016]027, Guizhou QKZYD[2016]4006 and Guizhou ZDXK[2016]8.

Conflict of interest

The authors declare no conflict of interest in this paper.