Spatial decay estimates for the Fochheimer equations interfacing with a Darcy equations

1.   Introduction

The model equations (Brinkman, Forchheimer and Darcy equations) have been widely studied by many authors. If the net flow into the infinite end of the cylinder is zero, then the velocity can decay to zero as the distance tends to infinity. The result can be explained by Saint-Venant's Principle. Early results on Saint-Venant's principle mainly focused on the elliptic equations. Boley ^[1] in 1856 firstly proved that Saint-Venant's principle was valid for the heat equations. Then, many efforts were to the parabolic equations. References ^[2,3,4] gave a review of recent development on Saint-Venant's principle.

There has been substantial interest in spatial decay estimates for the model equations in porous medium. In fact, the Brinkman-Forchheimer type equations have been studied by many papers in the literature. Following the paper ^[5] which studied the model equations (Brinkman, Darcy, Forchheimer and Brinkman-Forchheimer equations) describing flow in a porous medium, several papers have appeared (see ^{[6,7,8,9,10,11,12]}). Ames and Payne ^[13], and Franchi and Straughan ^[14] analyzed certain structural stability questions and Payne and Straughan ^[9] studied the question of continuous dependence of solutions of both systems on the initial-time geometry for bounded spatial domains both forward and backward in time. Other questions for these systems have been treated by Ames and Payne ^[15], Franchi ^[16], Morro and Straughan ^[17], Qin and Kaloni ^[18], and Richardson and Straughan ^[19]. For more recent work, one may refer to ^[20]. In that paper, Payne and Song examined the time-dependent double diffusive convection in Brinkman flow in a semi-infinite cylinder. Under appropriate initial and boundary conditions the authors established the exponential decay of solutions in energy norm with distance from the finite end of the cylinder. Other results for models of Brinkman, Forchheimer and Darcy equations were found in ^{[21,22,23,24,25,26,27,28]}. Some new results about properties of solutions for fluids in porous medium may be found in ^{[29,30,31,32,33,34,35,36]}.

In ^[37], the authors studied the spatial decay for the stokes flow interfacing with a Darcy flow in a cylinder. Under homogeneous initial lateral surface boundary conditions and some other interface conditions, they established the exponential decay estimates for the energy expression. For a review of other porous interface problems, one could see ^[38,39,40]. Some new results about the structural stability of the interfacing problems may be found in ^{[41,42,43,44,45]}. In ^[46], Payne and Song obtained the spatial decay result for flows in a porous medium. For other Saint-Venant's principal results on penetrative convention, one could see ^[5]. Most of these papers studied only one fluid in a domain. In reality, there usually exist two or more fluids interfacing with each other in a domain. People want to know the behavior of their solutions. Inspired by paper ^[37], we continue to study these interfacing problems. We replace the Brinkman term $\Delta u_i$ by a nonlinear item $b|u|u_i$. The nonlinear term is difficult to tackle. We cannot follow the method used in ^[37]. A new method should be developed to deal with this nonlinear term. We want to establish exponential decay results for the interfacing problems. We have never seen such results for the interfacing fluids in literature except ^[37].

We assume that one part is filled with the Forchheimer flow, while the other part is filled with the Darcy fluid. Some new results for the Forchheimer-Darcy equations may be found in ^{[47,48,49,50,51,52,53]}.

Let

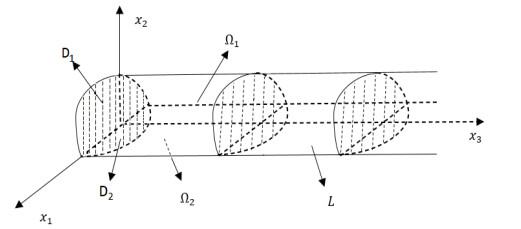
be the interior of a semi-infinite cylinder. The generators of the cylinder are paralleled to the $x_3$-axis. $\Omega_1$ is a portion lying above the $x_1x_3$-plane. While $\Omega_2$ is a portion lying below the $x_1x_3$-plane. $L$ denotes the common plane boundary of $\Omega_1$ and $\Omega_2$. The plane $x_3 = 0$, $L$, and a lateral surface $\Gamma_1$ can bound $\Omega_1$. The plane $x_3 = 0$, $L$, and a lateral surface $\Gamma_2$ can bound $\Omega_2$. We further define (see Figure 1)

$D_1$ is the cross-section of $\Omega_1$, and $D_2$ is the cross-section of $\Omega_2$. We can easily get the results $x_2 > 0$ ($x\in\Omega_1$) and $x_2 < 0$ ($x\in\Omega_2$). We assume that the fluid satisfies the Forchheimer equations in $\Omega_1$ and the Darcy equations in $\Omega_2$.

The Forchheimer model is believed accurate when the flow velocity is too large for Darcy's law to be valid and additionally the porosity is not too small. They usually use the Boussinesq approximation to get the equation.

The Forchheimer equations are the governing equations in $\Omega_1$ (see ^[54]).

Here $u_i$ denotes the velocity, $T$ denotes the temperature and $p$ denotes the pressure. $b$ and $\gamma$ are positive constants. The gravity field is represented by the vector $g_i$. We assume

$\kappa$ is the thermal diffusivity. In $\Omega_2$, the governing equations are the Darcy equations

where $v_i$ denotes the velocity, $S$ denotes the temperature and $q$ denotes the pressure. $k$ denotes the permeability and $\kappa_s$ denotes the thermal diffusivity of the porous medium. We impose the following boundary and initial conditions:

We assume when $x_3\rightarrow \infty$, the following conditions are satisfied

uniformly in $x_1, x_2$.

At last, we impose the same conditions at the interface as ^[37]:

on $L\times\{t > 0\}$.

We will use the following notations for convenience (see Figure 2).

We want to formulate a first-order differential inequality for a weighted energy expression. An inequality which will imply exponential decay.

In the present paper, the partial differentiation with respect to the direction $x_k$ is defined by $, k$. Thus, $u_{, i}$ denotes $\frac{\partial u}{\partial x_i}$. The usual summation convection is used in this paper. The repeated Latin subscripts is used to sum from 1 to 3. While repeated Greek subscripts is used to sum from 1 to 2. Hence we have $u_{i, i} = \sum\limits_{i = 1}^3\frac{\partial u_i}{\partial x_i}$, $u_{\alpha, \alpha} = \sum\limits_{\alpha = 1}^2\frac{\partial u_i}{\partial x_i}$.

2.   Weighted energy $\psi(z, t)$

In this section, we want to derive a weighted energy $\psi(z, t)$. If we define a function

using the Eq (1.4) and integrating by parts, we have

Using the interface condition (1.9), we have

Using the Eq (1.6) and integrating by parts, we obtain

If we define

Combining (2.2)–(2.4), we have

We now begin to deal with items involving $T$ and $S$. We know

Following the same procedure, we obtain the following results for items contain $S$

We define

We now define

where $A$ is a positive constant to be determined later.

Combining (2.6)–(2.10), we can also get

In this paper, we want to obtain a first-order differential inequality for $\psi(z, t)$.

3.   Decay estimates

In the proof of our main result, we will use the following Lemmas:

Lemma 1. (see ^[37]) We suppose $\bar{\Omega}$ is a bounded region in $R^3$ which has Lipschitz boundary. $\chi$ is a bounded function in $\bar{\Omega}$ satisfies $\int_{\bar{\Omega}}\chi dx = 0$. There exists a vector function $\omega_i$ satifies

and

with $C$ is a constant which is dependent on the shape of $\bar{\Omega}$.

Lemma 2. (See ^[37]) The temperatures $T$ and $S$ satisfy the following maximum estimates:

with $T_M = \max\{\sup\limits_{D_1(0)\times[0, \infty]}|g|, \sup\limits_{D_2(0)\times[0, \infty]}|\tau|\}$. For $g\geq0$, using the maximum principle, we can easily get $T\geq0$ in $\Omega_1\times\{t\geq 0\}$.

Lemma 3. For $K_n$ defined in (2.11), we have the following estimates:

with $n_1$ is a positive constant to be defined later.

Proof. We give a bound for $K_1+K_2$.

where $\lambda$ is the lowest eigenvalue of

and $\upsilon$ is the lowest eigenvalue of

For $K_5+K_6$, we have

Similarly, we can get

Combining (3.5), (3.8), (3.9) and (2.10), and choosing $A > \max\left\{\frac{\zeta^2}{\kappa\lambda}, \frac{\zeta^2}{\kappa_s\upsilon}\right\}$, we have

with $n_1 = \max\left\{\frac{AT_M}{4\lambda\kappa}+\frac{1}{2\lambda}+\frac{1}{2}, \frac{AT_M}{4}, \frac{\kappa AT_M}{4b}, \frac{1}{2\upsilon}+\frac{1}{2}+\frac{T_M}{4\upsilon \kappa_s}\right\}$.

Lemma 4. For $K_n$ defined in (2.11), we have the following estimates:

where $\tilde{k}_5$ is a computable constant.

Proof. We define

We then rewritten $J$ as

with

and

Therefore, we find

with $a$ is an arbitrary positive constant. We note that

Using integration by parts, we have

We have

Thus, we can obtain

Using the result of Lemma 1, we have

We have

with $\hat{\wedge}$ is the first eigenvalue of the following problem.

and $\tilde{k}$ is the constant satisfies the following poincar$\acute{e}$ inequality

Using (3.20), we have

Using the Schwarz and poincar$\acute{e}$ inequalities, we can get

Following the same procedure as (3.24), we have

We can also get

Inserting (3.23)–(3.26) into (3.19), we obtain

where $\tilde{k}_1$, $\tilde{k}_2$, $\tilde{k}_3$ and $\tilde{k}_4$ are computable positive constance.

Thus

We can easily get

where $\tilde{k}_5$ is a computable constant.

Lemma 5. The velocity $u_i$ satisfies

with $\delta$ is a positive constant.

Proof. From the definition of $\Omega_1(z)$, we have

We now define a function

The following method was used in ^[23] in deriving (3.8). Since $F(s)$ is continuous on [0, t], there exists a $\tilde{t}\in [0, t]$ such that

The following discussions will be divided into three cases. If $\tilde{t} = 0$, there exists a $0 < \delta_1 < t$, when $s\in (0, \delta_1)$, we have

We can get

We can easily get

If $\tilde{t} = t$, there exists a $0 < \delta_2 < t$, when $s\in (t-\delta_2, t)$, we also get

If $\tilde{t}\in (0, t)$, there exists a $0 < \delta_3 < t-\tilde{t}$, when $s\in (\tilde{t}, \tilde{t}+\delta_3)$, we can get

A combination of $(3.33)$–$(3.35)$ gives

with $\delta = \min\{\delta_1, \delta_2, \delta_3\}.$

Inserting (3.36) and (3.32) into (3.31), we obtain

Lemma 6. From the definition of $\psi(z, t)$ in (2.11), we can get

where $\tilde{k}_6$ and $\tilde{k}_7$ are computable positive constants.

Proof. We know

Inserting (3.30) and (3.39) into (3.11), we have

From the definition of $\psi(z, t)$ in (2.10), we have

A combination of (3.4) and (3.41) gives

where $\tilde{k}_6$ and $\tilde{k}_7$ are computable positive constants.

In this part, we will get the following main result.

Theorem 1. The energy $\psi(z, t)$ defined in (2.10) satisfies the following decay estimates:

Proof. We rewrite (3.38) as

We can easily get

An integration of (3.44) from 0 to $z$, we get

Inequality (3.45) shows the desired decay estimates.

4.   Conclusions

In this paper, we study the spatial decay estimates for the Forchheimer-Darcy interfacing problems in a semi-infinite pipe. We get the Saint-Venant type result for the interfacing fluids. We can extend the result to the equations which the velocity eqaution contains a nonlinear term. We have never seen similar results in literature. Our method is useful to study other interfacing problems in porous medium. If the velocity equation contains the derivative of time, the problem will become very complex. We can not get similar result by using the method proposed in this paper. For the pressure term is difficult to tackle. We must seek new method to overcome this difficulty. We will discuss this problem in the following paper. We can further study the structural stability for these equations based on the result obtained in this paper. We think it would be interesting.

Acknowledgments

The work was supported national natural Science Foundation of China (Grant #61907010), natural Science foundation in Higher Education of Guangdong, China (Grant #2018KZDXM048; #2019KZDXM036; #2019KZDXM042; #2020ZDZX3051), the General Project of Science Research of Guangzhou (Grant #201707010126), and the science foundation of Huashang College Guangdong University of Finance & Economics (Grant #2019HSDS28).

Conflict of interest

The authors declare that they have no competing interests.