Inference of fuzzy reliability model for inverse Rayleigh distribution

1.   Introduction

The stress-strength reliability model is significant in reliability literature, medical, economic, and engineering applications where systems or specialized units may be exposed to randomly occurring environmental stresses such as pressure, temperature, and humidity. In this case, the survival of the system depends on its resistance. During World War Ⅱ, it was found that some of the equipment such as radar and communication systems failed to work efficiently when they were used in an environment different from the environment for which they were designed. For that, experts started to consider the effects of environmental conditions while evaluating the reliability of equipment.

The computations of fuzzy reliability have been addressed by ^[1], where if $X$ and $Y$ are independent but not identical random variables in distribution. The idea behind fuzzy reliability is that including fuzziness in the stress-strength interference enables researchers to make more sensitive and precise analyses about the underlying systems of life reliability and the system becomes more stable and reliable when the difference $(x-y)$ gets larger. The advantages of the fuzzy stress-strength reliability model over the traditional stress-strength reliability model are in considering the randomness in reliability engineering and the fuzziness of operating time. For more information see ^[1,2,3,4,5].

The fuzzy reliability ${R}_{F} = P(Y < X)$ is defined as

where $A\left(y\right) = \left\{x:y < x\right\}$ is a fuzzy set and ${\mu }_{A\left(y\right)}\left(x\right)$ is an appropriate membership function on $A\left(y\right)$; that is assumed increasing on the difference $(x-y)$ (readers are encouraged to read ^[5,6] who used the definition of the fuzzy stress-strength model to estimate ${R}_{F} = (Y < X)$, when $X$ and $Y$ were independent inverse exponential random variables).

The probability that the system is strong enough to overcome the stress imposed on it is defined as system reliability. Traditional reliability $R = P(Y < X)$ may be equally explained as the region under the receiver operating characteristic (ROC) for diagnostic test or biomarkers, see reference ^[7]. The ROC curve is exceedingly used in medical, biological, economic, and health service research, to evaluate the reliability and distinguish between two groups of subjects, generally non-satisfied and satisfied subjects. The research conducted on the traditional stress-strength reliability model focuses on computing, calculating, and estimating the reliability of different stress and strength distributions. For example, reference ^[8] estimated the traditional reliability of the stress-strength model for a generalized exponential distribution with three parameters. Confidence intervals estimation of traditional reliability of stress-strength model for generalized Pareto distribution has been discussed by ^[9]. The stress-strength model of a generalized logistic distribution has been studied by ^[10]. Reference ^[11] estimated the $R$ when $X$ and $Y$ independent Lindley populations. In 2020, ^[12] and others discussed the estimation of $R$ when $X$ and $Y$ are independent exponentiated Pareto random variables when samples are selected using some ranked set sampling designs. Reference ^[13] presented a comprehensive review of the traditional reliability of the stress-strength model. In 2021, ^[14] estimated the traditional stress strength reliability by the use of the MPS estimation method.

In our study, we used failure times in insulating fluid between two electrodes subjected to a voltage of 34 kV and 36 kV as an application and for illustrative purposes. These failure times were randomly observed and there was no reliable information available. Moreover, the failure times model may be difficult to measure due to the complexity of the action of electrodes. So, we used stress-strength reliability model in the presence of fuzziness.

In this article, estimation of fuzzy stress-strength reliability model ${R}_{F} = P(Y < X)$, when $X$ and $Y$ are independent but not symmetrically distributed inverse Rayleigh random variables, is discussed. The product of the spacing method was presented to infer the reliability of fuzzy stress strength by using different methods. The proposed estimators are obtained using the maximum likelihood estimation method (MLE) and the maximum product of the spacing estimation method (MPS) as well as Bayesian estimation when prior distributions are assumed exponential. Besides, a Monte Carlo simulation study is made to analyze and compare the performance of the different estimators. A real data application is conducted for illustration purposes and to test the estimated functions of the reliability parameter ${R}_{F}$. Finally, the paper is concluded.

2.   The stress strength model

An increase in the values of $x-y$ can be thought of equivalently as the increase in the difference of $\frac{1}{{y}^{2}}-\frac{1}{{x}^{2}}$. With such consideration, the membership function can be redefined as

where $k>0.$

Let $X$ and $Y$ be two independent inverse Rayleigh random variables with scale parameters ${\lambda }_{1}$ and ${\lambda }_{2}$, respectively. The inverted Rayleigh [$IR\left(\lambda \right)]$ distribution has the following cumulative distribution function (CDF) and probability density function (PDF) for $x>0$:

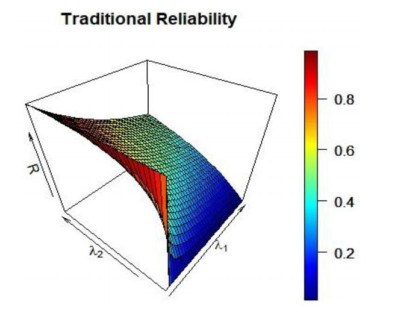
respectively, where $\lambda >0$ is a scale parameter. The traditional reliability of the stress-strength model for inverse Rayleigh distribution was studied and calculated to be $R = {\lambda }_{2}/({\lambda }_{1}+{\lambda }_{2})$ (see Kotz et al. ^[9]). Therefore, the fuzzy reliability of stress-strength ${R}_{F} = P(Y\prec X)$ is given by

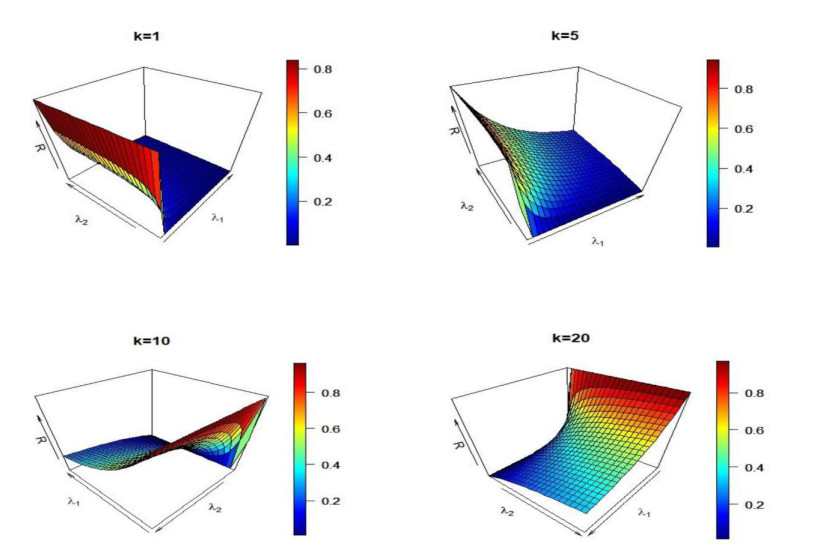
The traditional reliability $R$ is always greater than the fuzzy reliability ${R}_{F}$, and as $k\to \mathrm{\infty }, {R}_{F}\to R$. Figure 1 shows different values for $R$ when ${\lambda }_{1}$ and ${\lambda }_{2}$ changes simultaneously, Figure 2 shows fuzzy reliably values for different values of the constant $k$ and when also ${\lambda }_{1}$ and ${\lambda }_{2}$ changes simultaneously.

3.   Inference of stress-strength model

In this section, the two methods (MLE and MPS) of estimation are used to estimate the fuzzy reliability parameter ${R}_{F}$. Let $\left({X}_{1}, { X}_{2}, \dots, \mathrm{ \;}{X}_{n}\right)$ and $\left({Y}_{1}, { Y}_{2}, \dots, \mathrm{ \;}{Y}_{m}\right)$ be two independent random samples from IR (${\lambda }_{1}$) and IR (${\lambda }_{2}$), respectively.

3.1.   Likelihood estimation

The joint likelihood function of the IR distribution for the stress-strength model can be written as

and the log-likelihood function is given as

The normal equations for unknown parameters ${\lambda }_{1}, {\lambda }_{2}$, are obtained by differentiating (6) partially concerning the parameters ${\lambda }_{1}, {\lambda }_{2}$, and equate them to zero. The estimators ${\widehat{\lambda }}_{1}, {\widehat{\lambda }}_{2}$ can be obtained as a solution to the following equation:

where ${\mathcal{g}}_{ji} = ({x}_{i}, {y}_{i})$, ${\mathrm{\aleph }}_{j} = (n, m)$. The estimate by using MLE is ${\widehat{\lambda }}_{j} = \frac{{\mathrm{\aleph }}_{j}}{\sum _{i = 1}^{{\mathrm{\aleph }}_{j}}{\mathcal{g}}_{ji}^{2}}$. By using the invariance property of MLE, traditional reliability $R$ and the fuzzy reliability ${R}_{F}$ of IR distribution for the stress-strength model are obtained by using MLE's as following

3.2.   Maximum product of spacing estimation

The maximum product spacing for stress-strength model is denoted as following.

such that $\sum _{i}{\mathrm{D}}_{i}({\mathcal{g}}_{ji}; {\lambda }_{j}) = 1$, where

The natural logarithm of the product spacing function of the exponential distribution for stress-strength model is denoted as following

To obtain the normal equations for the unknown parameters, we partially differentiate Eq (8) concerning the parameters ${\lambda }_{1}, {\lambda }_{2}$, and equate them with zero. The estimators ${\widehat{\lambda }}_{1}, {\widehat{\lambda }}_{2}$ can be obtained as a solution of the following equations.

The above nonlinear equations can't be solved analytically to find ${\widehat{\lambda }}_{1}, {\widehat{\lambda }}_{2}$ of ${\lambda }_{1}, {\lambda }_{2}$. So, by using optimization algorism as conjugate-gradient or Newton-Raphson optimization methods, the estimators of ${\lambda }_{1}, {\lambda }_{2}$ are obtained. Using the invariance property of MPS estimators of the MPS's which have been discussed by ^{[13,14,15,16,17,18]} and have concluded that it is the same as that of MLE, traditional reliability $R$ and fuzzy reliability ${R}_{F}$ for IR distribution for the stress-strength model can be computed.

4.   Bayesian estimation

Assume that the parameters ${\mathrm{\lambda }}_{1}$ and ${\mathrm{\lambda }}_{2}$ are random variables with exponential prior distributions ^[11] with density function given by

where ${b}_{1}>0$ and ${b}_{2}>0$ are hyperparameters of the prior distributions of ${\mathrm{\lambda }}_{1}$ and ${\mathrm{\lambda }}_{2}$. The posterior distributions of ${\mathrm{\lambda }}_{1}$ and ${\mathrm{\lambda }}_{2}$ are obtained by combining the likelihood function with the prior distributions of both ${\mathrm{\lambda }}_{1}$ and ${\mathrm{\lambda }}_{2}$ and are found to be

and

Also,

and

Now, let ${T}_{1} = {b}_{1}+\sum _{i = 1}^{n}{x}_{i}^{-2}$ and ${T}_{2} = {b}_{2}+\sum _{i = 1}^{m}{y}_{i}^{-2}$. After some manipulations and simplifications, we have that ${\pi }_{1}\left({\lambda }_{1}\backslash \boldsymbol{u}\right) \sim Gamma(n+1, {T}_{1})$ and ${\pi }_{2}\left({\lambda }_{2}\backslash \boldsymbol{v}\right) \sim Gamma(m+1, {T}_{2})$ respectively. The joint posterior distribution of ${\mathrm{\lambda }}_{1}$ and ${\mathrm{ }\mathrm{\lambda }}_{2}$ is then given by

Let ${S = \mathrm{\lambda }}_{1}{+\mathrm{\lambda }}_{2}$ and since $R = \frac{{\mathrm{\lambda }}_{2}}{{\mathrm{\lambda }}_{1}{+\mathrm{\lambda }}_{2}}$, then using standard transformation techniques, the joint posterior pdf of $R$ and $S$ will be

Under squared error loss function, the Bayes estimate ${\widetilde{R}}_{F}$ is the expected value of ${R}_{F}$ and is given by,

where $A = \frac{{T_1^{n + 1}T_2^{m + 1}}}{{\Gamma (n + 1)\Gamma (m + 1)}}$.

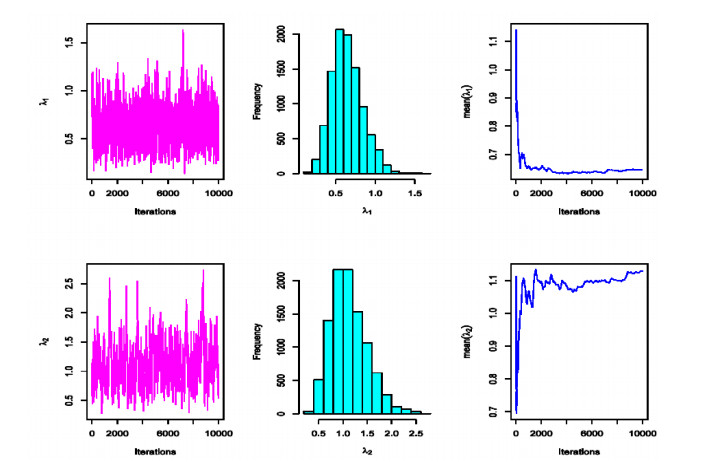
The above integrals are hard to obtain, so numerical technique is used to evaluate the Bayes estimate. Markov Chain Monte Carlo (MCMC) approach is used to obtain Bayesian estimators. An important sub-class of the MCMC techniques is Gibbs's sampling and more general Metropolis within Gibbs samplers see ^[24,25]. The Metropolis-Hastings algorithm, together with the Gibbs sampling, are the two most popular examples of an MCMC method. It's similar to acceptance-rejection sampling, and the Metropolis-Hastings algorithm considers that to each iteration of the algorithm, a candidate value can be generated from the IR distributions. We use the Metropolis-Hastings within Gibbs sampling steps to generate random samples from conditional posterior densities of ${\mathrm{\lambda }}_{1},$ ${\mathrm{\lambda }}_{2}$, and${R}_{F}$. For more information, see ^{[19,20,21,22,23]}.

5.   Simulation study

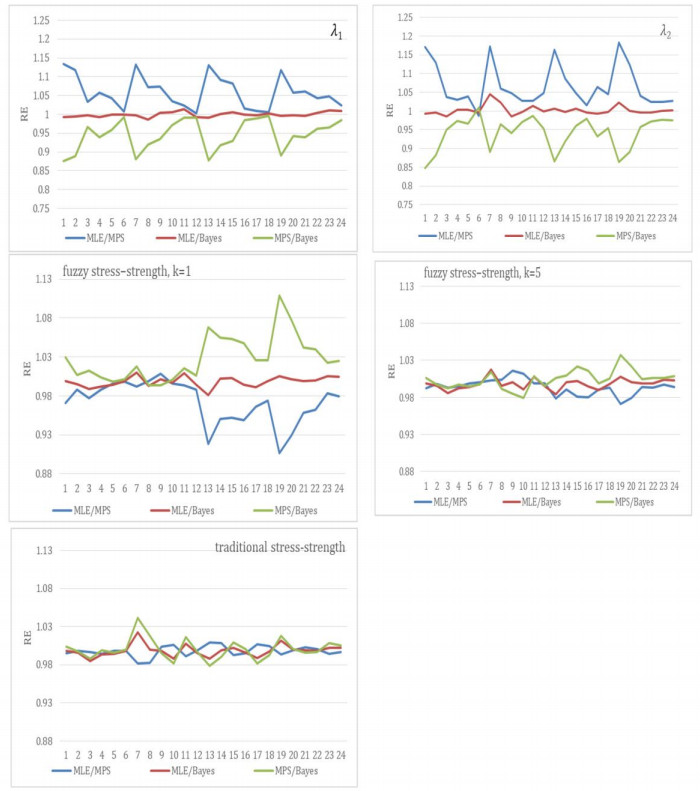
In this section, we provide a numerical comparison using the Monte Carlo simulation algorithm. We explain our algorithm through an application of fuzzy and traditional stress-strength models by different estimation methods. In this current simulation, we will compare MLE, MPS, and Bayesian estimation methods based on traditional and fuzzy stress-strength measures for estimating the parameter of IR distribution. The comparison is made through bias and mean squared errors (MSE) of the different measures. The simulations are made using the $R$ program for several combinations of the parameters and $m, n$, and $k$.

Simulation Algorithm:

We build our model by creating all simulation controls. At this point, we must follow the following steps in order:

Step 1: Suppose different values of the parameters vector of IR distribution.

Step 2: Choose the different sample size of strength

$n = 30, \mathrm{ \;}50, \mathrm{ \;}80, \mathrm{ \;}100, \mathrm{ \;}150\mathrm{ \;}200$ and different sample size of stress

$m = 20, \mathrm{ \;}40, \mathrm{ \;}90, \mathrm{ \;}110, \mathrm{ \;}120\mathrm{\; }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{\; }150$ respectively.

Step 3: Generate the sample random values of IR distribution by using quantile function in equation

Step 4: Solve differential equations for each estimation method. To obtain the estimators of the parameters for IR distribution, we calculate ${\widehat{\mathrm{\lambda }}}_{1}, {\widehat{\mathrm{\lambda }}}_{2}$, ${R}_{F1}$ when k = 1; and ${R}_{F2}$ when k = 5.

Step 5: Repeat this experiment (L-1) iterations. In each experiment, the parameter values are the same. The generated random values are certainly varying from experiment to experiment even though the sample size is not changed. In the end, we have L-values of mean and MSE, and we restricted the number of repeats in this experiment to 10,000. Take the averages of these values and call them Monte Carlo estimates.

After completing the treatment stage, simulated outcomes are listed in Tables 1–4, Figure 3, and the following observations were observed:

● The Bias and MSE decrease as sample sizes increase for all estimates.

● For fixed values of ${\lambda }_{1}$, the biases and MSE's of estimates of parameters are increasing with ${\lambda }_{2}$ increasing.

● For fixed values of ${\lambda }_{1}$, the biases and MSE's of estimates of parameters are increasing with ${\lambda }_{2}$ increasing, but the estimate of R for fuzzy stress strength and tradition are decreasing in approximately most situations.

● For fixed values of ${\lambda }_{2}$, the bias and MSE of estimates of ${\lambda }_{1}$, R for fuzzy stress strength and tradition are decreasing with ${\lambda }_{1}$ increasing, but the estimates of ${\lambda }_{2}$ are increasing, in approximately most situations.

● The MPS method is found to be superior to the MLE and Bayesian methods in most cases.

● From the observed results of reliability, we note the efficiency of the fuzzy stress strength is over traditional stress strength in most situations according to Bias and MSE.

● In fuzzy stress strength, the efficiency is better with decreased values of k according to Bias and MSE.

6.   Application of real data

The numerical results of tradition and fuzzy stress-strength reliability estimation of the IR distribution for real data are presented in this section.

Two real stress and strength data sets contained times to breakdown down an insulating fluid between electrodes recorded at different voltages; these data have been discussed by ^[26]. Data Ⅰ and data Ⅱ as presented in Table 4, are the failure times (in minutes) are presented, which are for an insulating fluid between two electrodes subject to a voltage of 34 kV (data set Ⅰ) and 36 kV (data set Ⅱ). Table 6 provides information about the estimated parameters of the IR model and the corresponding traditional and fuzzy reliability measures

The graph of MCMC estimates for ${\lambda }_{1}$ and ${\lambda }_{2}$ using the MH algorithm are the plotting of estimates, histogram of estimates, and convergence of estimates are shown in Figure 3. In Figure 4, we note the convergence of MCMC estimates for ${\lambda }_{1}$ and ${\lambda }_{2}$ in the first quartile iteration.

7.   Conclusions

The new approach of estimating fuzzy stress-strength reliability ${R}_{F} = P(Y < X)$ is getting much attention because of the properties of ${R}_{F}$, which makes the analysis more sensitive and more reliable. Also, when the study results are not known completely, the use of traditional methods may be misleading, and the need for new approaches that can handle such situations is very important. In this paper, the stress and strength variables were distributed as inverted Rayleigh distribution. It can be noted that different membership functions will provide different measures of ${R}_{F}$. It is also noted that the MPS method is superior to the MLE and Bayesian methods in most cases.

Acknowledgments

Thanks a lot for everyone's help.

Conflict of interest

The authors declare that they have no conflict of interest to report regarding the present study.