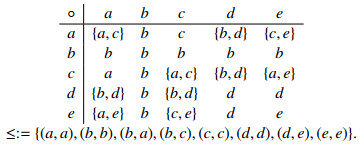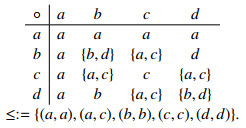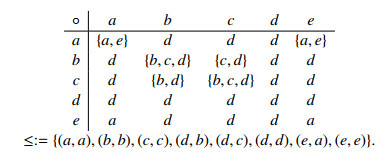1.
Introduction
In algebraic structure, the composition of two elements is an element, while in algebraic hyperstructure, the composition of two elements is a set, and the French mathematician Marty [1] was the first who introduced some results on hypergroups and applied them in different branches of algebras. Moreover, algebraic hyperstructure theory can be applied in different disciplines as geometry, graphs, fuzzy sets, rough sets, automata, cryptography, codes, artificial intelligence, probabilities and so on. Some essential books on these topics are "Applications of Hyperstructure Theory", by P. Corsini and V. Leoreanu [2], "Hyperstructures and their Representations" written by Vougiouklis [3] and "Fuzzy algebraic hyperstructures" written by Davvaz and Cristea [4]. Left almost semihypergroups were introduced by Hila et al. [5] and Yaqoob et al. [6] which comes from the generalization of left almost semigroup by Kazim and Naseeruddin [7]. Partially ordered left almost semihypergroups were studied by Yaqoob and Gulistan [8]. The concept of LA-hypergroup was first introduced in [9], where the authors provided the definition and examples on LA-hypergroup and then they further defined the concept of LA-hyperrings. Weak LA-hypergroups were studied in the paper [10]. Hu et al. [11] applied the neutrosophic sets to LA-hypergroups and strong pure LA-semihypergroups. Yaqoob et al. [12] introduced the concept of left almost polygroups. Yaqoob [13] applied the rough set theory to left almost polygroups.
The theory of filters play a significant role in computer science and non-classical logic. Various filters correspond to various sets of provable formulas. The properties of filters on the different algebraic structures have already been considered by several mathematicians. New type of filter called "quasi-filter" was given by Jirojkul and Chinram [14] in ordered semigroups. Motivated by the work of Jirojkul and Chinram, we generalized quasi-filter for ordered hyperstructures in particular for ordered LA-semihypergroups. For the general development of ordered LA-semihypergroups, the hyperfilter theory and hyperideal theory plays an important role. Filters of ordered semigroups was studied by Jakubík [15] and in ordered Γ-semigroups was studied by Hila [16]. Filters generated in poe-semigroups was first introduced by Kehayopulu [17]. Principal filters of po-semigroups were studied by Ren et al. [18]. And then the concept of hyperfilters of ordered semihypergroups were studied by Tang et al. [19].
Rough set theory is a significant mathematical tool to address imprecise data and it has been introduced by Pawlak [20] in 1982. Biswas and Nanda [21] delivered the concept of roughness of both groups and subgroups. Abd-Allah et al. [22] studied rough intuitionistic fuzzy subgroup. Jun [23] discussed the roughness of Γ
-subsemigroups and ideals in Γ-semigroups. Also roughness in ordered semigroups was investigated by Shabir and Irshad [24]. Roughness has been studied in many hyperstructures as well, for example Ameri [25] studied roughness in semihypergroups using fundamental relation β∗ on semihypergroups. The roughness of Γ-subsemihypergroups and Γ-hyperideals was studied in [26]. Yaqoob and Aslam [27] studied generalized rough approximations in Γ
-semihypergroups, see also [28]. The roughness of hyperrings and Γ-semihyperrings were considered in [29,30]. Also, the rough set has been investigated in hyperlattices [31], hypergroup [32], quantales [33], quantale modules [34], and non-associative po-semihypergroups [35]. Roughness has also considered in fuzzy filters [36,37,38], in filters of residuated lattices [39], in filters of BL-algebras [40] and hyperfilters in po-LA-semihypergroups [41].
In section 2, we added some basic definitions related to ordered LA-semihypergroups. In section 3, we provided the definitions of different types of hyperfilters and also proved some results related to these newly defined hyperfilters. In section 4, we applied the theory of rough sets to these hyperfilters.
2.
Preliminaries and basic definitions
In this section, we provide some basic definitions on ordered LA-semihypergroups.
Definition 2.1. [5,6] A hypergroupoid (H,∘) is said to be an LA-semihypergroup if for all a,b,c∈H,
Definition 2.2. [8] Let H be a non-empty set and "≤" be an ordered relation on H. Then (H,∘,≤) is called an ordered LA-semihypergroup if
(i) (H,∘) is an LA-semihypergroup;
(ii) (H,≤) is a partially ordered set;
(iii) for every a,b,c∈H, a≤b implies a∘c≤b∘c and c∘a≤ c∘b,
where a∘c ≤b∘c means that for every x∈a∘c there exists y∈b∘c such that x≤y.
Definition 2.3. [8] If A is a non-empty subset of (H,∘,≤), then (A] is the subset of H defined as follows:
Definition 2.4. [8] A non-empty subset A of an ordered LA-semihypergroup (H,∘,≤) is called an LA-subsemihypergroup of H if (A∘A]⊆(A].
Definition 2.5. [35] A relation ρ on an ordered LA-semihypergroup H is called a pseudohyperorder if
(1) ≤ ⊆ρ
(2) ρ is transitive, that is (a,b),(b,c)∈ρ implies (a,c)∈ρ for all a,b,c∈H.
(3) ρ is compatible, that is if (a,b)∈ρ then (a∘x,b∘x)∈ρ and (x∘a,x∘b)∈ρ for all a,b,x∈H.
Definition 2.6. A pseudohyperorder ρ on an ordered LA-semihypergroup H is said to be complete if ρN(x∘y)=ρN(x)∘ρN(y).
3.
Quasi and interior hyperfilters in ordered LA-semihypergroups
In this section, we provide some results on quasi-hyperfilters and interior hyperfilters in ordered LA-semihypergroups.
Definition 3.1. Let (H,∘,≤) be an ordered LA-semihypergroup and Q a non-empty subset of H. Then Q is called a type-1 quasi-hyperfilter of H if
(i) Q∘Q⊆Q;
(ii) for all a,b,c∈H, a∘b=c∘a⊆Q ⟹a∈Q;
(iii) for all a,b∈H, a∘b=b∘a⊆Q ⟹a∈Q or b∈Q;
(iv) for all b∈H and a∈Q, a≤b⟹b∈Q.
Definition 3.2. Let (H,∘,≤) be an ordered LA-semihypergroup and Q a non-empty subset of H. Then Q is called a type-1 strong quasi-hyperfilter of H if
(i) Q∘Q⊆Q;
(ii) for all a,b,c∈H, (a∘b=c∘a)∩Q≠∅ ⟹a∈Q;
(iii) for all a,b∈H, (a∘b=b∘a)∩Q≠∅ ⟹a∈Q or b∈Q;
(iv) for all b∈H and a∈Q, a≤b⟹b∈Q.
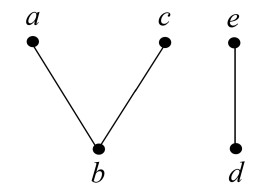
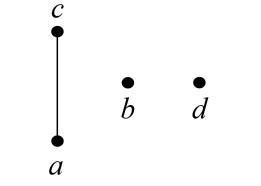
Example 3.3. Consider an ordered LA-semihypergroup H={a,b,c,d,e} with the following hyperoperation "∘" and order "≤" :
We give the covering relation ≺={(b,a),(c,a),(d,a)}, and the figure of H in Figure 1.
All the LA-subsemihypergroups of H are {a}, {e}, {a,d}, {a,e}, {a,b,c}, {a,d,e}, {a,b,c,d}, {a,b,c,e} and H. The type-1 quasi-hyperfilters of H are {a}, {e}, {a,d}, {a,e}, {a,d,e}, {a,b,c,e} and H. The LA-subsemihypergroups {a,b,c} and {a,b,c,d} of H are not type-1 quasi-hyperfilters of H, because
Also the type-1 strong quasi-hyperfilters of H are {e}, {a,d}, {a,d,e} and H. The type-1 quasi-hyperfilters {a}, {a,e}, {a,b,c,e} are not strong because
Definition 3.4. Let (H,∘,≤) be an ordered LA-semihypergroup and Q a non-empty subset of H. Then Q is called a type-2 quasi-hyperfilter of H if
(i) Q∘Q⊆Q;
(ii) for all a,b,c∈H, (a∘b∩c∘a)⊆Q ⟹a∈Q;
(iii) for all a,b∈H, (a∘b∩b∘a)⊆Q ⟹a∈Q or b∈Q;
(iv) for all b∈H and a∈Q, a≤b⟹b∈Q.
Definition 3.5. Let (H,∘,≤) be an ordered LA-semihypergroup and Q a non-empty subset of H. Then Q is called a type-2 strong quasi-hyperfilter of H if
(i) Q∘Q⊆Q;
(ii) for all a,b,c∈H, (a∘b)∩(c∘a)∩Q≠∅
⟹a∈Q;
(iii) for all a,b∈H, (a∘b)∩(b∘a)∩Q≠∅
⟹a∈Q or b∈Q;
(iv) for all b∈H and a∈Q, a≤b⟹b∈Q.
Example 3.6. Consider Example 3.3, the only type-2 quasi-hyperfilters of H are {e} and H. The type-1 quasi-hyperfilters {a}, {a,d}, {a,e}, {a,d,e}, {a,b,c,e} are not type-2 quasi-hyperfilters of H because
Let H be an ordered LA-semihypergroup. Then
(1) Q1 denote the set of all type-1 quasi-hyperfilters of H.
(2) QS1 denote the set of all type-1 strong quasi-hyperfilters of H.
(3) Q2 denote the set of all type-2 quasi-hyperfilters of H.
(4) QS2 denote the set of all type-2 strong quasi-hyperfilters of H.
From Example 3.3 and Example 3.6, we conclude that Q1⊇QS1⊇Q2⊇QS2. This relation of all quasi-hyperfilters of H can be seen in Figure 2.
Definition 3.7. Let (H,∘,≤) be an ordered LA-semihypergroup and I a non-empty subset of H. Then I is called an interior hyperfilter of H if
(i) I∘I⊆I;
(ii) for all a,b,c∈H, (a∘b)∘c⊆I ⟹b∈I;
(iii) for all b∈H and a∈I, a≤b⟹b∈I.
Definition 3.8. Let (H,∘,≤) be an ordered LA-semihypergroup and I a non-empty subset of H. Then I is called a strong interior hyperfilter of H if
(i) I∘I⊆I;
(ii) for all a,b,c∈H, ((a∘b)∘c)∩I≠∅ ⟹b∈I;
(iii) for all b∈H and a∈I, a≤b⟹b∈I.
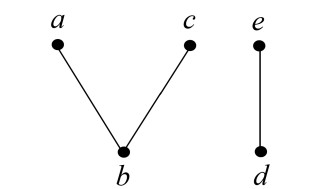
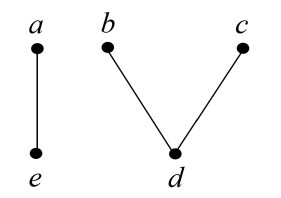
Example 3.9. Consider an ordered LA-semihypergroup H={a,b,c,d,e} with the following hyperoperation "∘" and order "≤" :
We give the covering relation ≺={(b,a),(b,c),(d,e)}, and the figure of H in Figure 3.
All the LA-subsemihypergroups of H are {e}, {a,c}, {d,e}, {a,b,c}, {a,c,e}, {a,b,c,e} and H. The interior hyperfilters of H are {e}, {a,c}, {d,e}, {a,c,e} and H. The LA-subsemihypergroups {a,b,c} and {a,b,c,e} of H are not interior hyperfilters, because
Also the strong interior hyperfilters of H are {a,c,e} and H. The interior hyperfilters {e}, {a,c}, {d,e} are not strong because
Definition 3.10. Let (H,∘,≤) be an ordered LA-semihypergroup and I a non-empty subset of H. Then I is called an interior semihyperfilter of H if
(i) I∘I⊆I;
(ii) for all a,b∈H, (a∘b)∘a⊆I ⟹b∈I;
(iii) for all b∈H and a∈I, a≤b⟹b∈I.
Definition 3.11. Let (H,∘,≤) be an ordered LA-semihypergroup and I a non-empty subset of H. Then I is called a strong interior semihyperfilter of H if
(i) I∘I⊆I;
(ii) for all a,b,c∈H, ((a∘b)∘a)∩I≠∅ ⟹b∈I;
(iii) for all b∈H and a∈I, a≤b⟹b∈I.
Lemma 3.12. Let (H,∘,≤) be an ordered LA-semihypergroup and S be an LA-subsemihypergroup of H. Then for a type-1 quasi-hyperfilter (resp., type-2 quasi-hyperfilter, interior hyperfilter, interior semihyperfilter) Q of H, either Q∩S=∅ or Q∩S is a type-1 quasi-hyperfilter (resp., type-2 quasi-hyperfilter, interior hyperfilter, interior semihyperfilter) of S.
Proof. Consider S is an LA-subsemihypergroup of H and Q is a type-1 quasi-hyperfilter of H. Suppose that Q∩S≠∅.
(i) Now (Q∩S)2⊆Q2⊆Q and (Q∩S)2⊆S2⊆S. Therefore (Q∩S)2⊆Q∩S. So Q∩S is an LA-subsemihypergroup of S.
(ii) Suppose that, for any a,b,c∈S, a∘b=c∘a⊆Q∩S. Therefore a∘b=c∘a⊆Q. As a∈S and Q is a type-1 quasi-hyperfilter of H, then a∈Q. Thus a∈Q∩S.
(iii) Suppose that, for any a,b∈S, a∘b=b∘a⊆Q∩S. Therefore a∘b=b∘a⊆Q. As a,b∈S and Q is a type-1 quasi-hyperfilter of H, then a∈Q or b∈Q. Thus a∈Q∩S or b∈Q∩S.
(iv) Now take any a∈Q∩S and b∈S such that a≤b. As Q is a type-1 quasi-hyperfilter of H with a∈Q and a≤b∈S, b∈Q. Therefore b∈Q∩S.
Hence Q∩S is a type-1 quasi-hyperfilter of S. The other cases can be seen in similar way.
Lemma 3.13. Let (H,∘,≤) be an ordered LA-semihypergroup and S be an LA-subsemihypergroup of H. Then for a type-1 strong quasi-hyperfilter (resp., type-2 strong quasi-hyperfilter, strong interior hyperfilter, strong interior semihyperfilter) Q of H, either Q∩S=∅ or Q∩S is a type-1 strong quasi-hyperfilter (resp., type-2 strong quasi-hyperfilter, strong interior hyperfilter, strong interior semihyperfilter) of S.
Proof. Proof is straightforward.
Theorem 3.14. Let (H,∘,≤) be an ordered LA-semihypergroup and {Qi|i∈I} a family of type-1 quasi-hyperfilters (resp., type-2 quasi-hyperfilters, interior hyperfilters, interior semihyperfilters) of H. Then ∩i∈IQi is a type-1 quasi-hyperfilter (resp., type-2 quasi-hyperfilter, interior hyperfilter, interior semihyperfilter) of H if ∩i∈IQi≠∅, where |I|≥2.
Proof. Consider {Qi|i∈I} is a family of type-1 quasi-hyperfilters of H. Assume that ∩i∈I Qi≠∅.
(i) Let a,b∈∩i∈IQi. Then a,b∈Qi for all i∈I. As, for all i∈I, Qi is a type-1 quasi-hyperfilter of H, so a∘b⊆Qi. Hence a∘b⊆ ∩i∈IQi, i.e., ∩i∈IQi is an LA-subsemihypergroup of H.
(ii) Suppose that, for any a,b,c∈H, a∘b=c∘a⊆∩i∈IQi. Therefore a∘b=c∘a⊆Qi for all i∈I. As Qi is a type-1 quasi-hyperfilter of H, then a∈Qi for all i∈I. Thus a∈∩i∈IQi.
(iii) Suppose that, for any a,b∈H, a∘b=b∘a⊆∩i∈IQi. Therefore a∘b=b∘a⊆Qi for all i∈I. As Qi is a type-1 quasi-hyperfilter of H, then a∈Qi or b∈Qi, for all i∈I. Thus a∈∩i∈IQi or b∈∩i∈IQi.
(iv) Now, take any a∈∩i∈IQi and b∈H such that a≤b. Therefore a∈Qi for all i∈I. As Qi is a type-1 quasi-hyperfilter of H with a∈Qi and a≤b∈S, this implies b∈Qi for all i∈I. Therefore b∈∩i∈IQi.
Hence ∩i∈IQi is a type-1 quasi-hyperfilter of H. The other cases can be seen in similar way.
Theorem 3.15. Let (H,∘,≤) be an ordered LA-semihypergroup and {Qi|i∈I} a family of type-1 strong quasi-hyperfilters (resp., type-2 strong quasi-hyperfilters, strong interior hyperfilters, strong interior semihyperfilters) of H. Then ∩i∈IQi is a type-1 strong quasi-hyperfilter (resp., type-2 strong quasi-hyperfilter, strong interior hyperfilter, strong interior semihyperfilter) of H if ∩i∈IQi≠∅, where |I|≥2.
Proof. Consider {Qi|i∈I} is a family of type-2 strong quasi-hyperfilters of H. Assume that ∩i∈I Qi≠∅.
(i) Let a,b∈∩i∈IQi. Then a,b∈Qi for all i∈I. As, for all i∈I, Qi is a type-2 strong quasi-hyperfilter of H, so a∘b⊆Qi. Hence a∘b⊆ ∩i∈IQi, i.e., ∩i∈IQi is an LA-subsemihypergroup of H.
(ii) Suppose that, for any a,b,c∈H, (a∘b)∩(c∘a)∩∩i∈IQi≠∅. Then there exists t∈∩i∈IQi for some t∈a∘b and t∈c∘a. Indeed, since t∈∩i∈IQi, we have t∈Qi for all i∈I. So t∈(a∘b)∩(c∘a)∩Qi. Therefore (a∘b)∩(c∘a)∩Qi≠∅. As Qi is a type-2 strong quasi-hyperfilters of H, thus a∈Qi. Therefore a∈∩i∈IQi.
(iii) Suppose that, for any a,b∈H, (a∘b)∩(b∘a)∩∩i∈IQi≠∅. Then there exists t∈∩i∈IQi for some t∈a∘b and t∈b∘a. Indeed, since t∈∩i∈IQi, we have t∈Qi for all i∈I. So t∈(a∘b)∩(b∘a)∩Qi. Therefore (a∘b)∩(b∘a)∩Qi≠∅. As Qi is a type-2 strong quasi-hyperfilters of H, thus a∈Qi or b∈Qi. Therefore a∈∩i∈IQi or b∈∩i∈IQi.
(iv) Now, take any a∈∩i∈IQi and b∈H such that a≤b. Therefore a∈Qi for all i∈I. As Qi is a type-2 strong quasi-hyperfilter of H with a∈Qi and a≤b∈S, this implies b∈Qi for all i∈I. Therefore b∈∩i∈IQi.
Hence ∩i∈IQi is a type-2 strong quasi-hyperfilter of H. The other cases can be seen in similar way.
4.
Rough quasi-(interior) hyperfilters of ordered LA-semihypergroups
In this section, we applied rough set theory to quasi- (interior) hyperfilters of ordered LA-semihypergroups.
Definition 4.1. [35] Let X be a non-empty set and ρ be a binary relation on X. By ℘(X) we mean the power set of X. For all A⊆X, we define ρ− and ρ+:℘(X)⟶℘(X) by
and
Where ρN(x)={y∈X:xρy}. ρ−(A) and ρ+(A) are called the lower approximation and the upper approximation operations, respectively.
Definition 4.2. [35,Definition 4.1] Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset A of H is called a ρ-upper (resp., ρ-lower) rough LA-subsemihypergroup of H if ρ+(A) (resp., ρ−(A)) is an LA-subsemihypergroup of H.
Theorem 4.3. [35,Theorem 4.3] Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H and A an LA-subsemihypergroup of H. Then
(1) ρ+(A) is an LA-subsemihypergroup of H.
(2) If ρ is complete, then ρ−(A) is, if it is non-empty, an LA-subsemihypergroup of H.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset Q of H is called a ρ-lower rough type-1 quasi-hyperfilter of H if ρ−(Q) is a type-1 quasi-hyperfilter of H.
Theorem 4.4. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and Q a type-1 quasi-hyperfilter of H. Then ρ−(Q) is, if it is non-empty, a type-1 quasi-hyperfilter of H.
Proof. Let Q be a type-1 quasi-hyperfilter H.
(i) Since Q is an LA-subsemihypergroup of H, then by Theorem 4.3(2), ρ−(Q) is an LA-subsemihypergroup of H. Thus ρ−(Q)∘ρ−(Q)⊆ρ−(Q).
(ii) Let x∘y=z∘x⊆ρ−(Q) for some x,y,z∈H. Then ρN(x∘y)=ρN(z∘x)⊆Q. So, ρN(x)∘ρN(y)=ρN(z)∘ρN(x)⊆Q. We suppose that ρ−(Q) is not a type-1 quasi-hyperfilter of H. Then there exist x,y,z∈H such that x∘y=z∘x⊆ρ−(Q) but x∉ρ−(Q). Thus ρN(x)⊈Q. Then there exist a∈ρN(x) such that a∉Q, b∈ρN(y) and c∈ρN(z). Thus
Since Q is a type-1 quasi-hyperfilter of H, so we have a∈Q, which is a contradiction.
(iii) Let x∘y=y∘x⊆ρ−(Q) for some x,y∈H. Then ρN(x∘y)=ρN(y∘x)⊆Q. So, ρN(x)∘ρN(y)=ρN(y)∘ρN(x)⊆Q. We suppose that ρ−(Q) is not a type-1 quasi-hyperfilter of H. Then there exist x,y∈H such that x∘y=y∘x⊆ρ−(Q) but x∉ρ−(Q) and y∉ρ−(Q). Thus ρN(x)⊈Q and ρN(y)⊈Q. Then there exist a∈ρN(x) and b∈ρN(y) such that a∉Q and b∉Q. Thus
Since Q is a type-1 quasi-hyperfilter of H, so we have a∈Q or b∈Q, which is a contradiction.
(iv) Now, let x∈ρ−(Q) and y∈H such that x≤y. Then ρN(x)⊆Q and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)⊆Q, so ρN(y)⊆Q. Thus y∈ρ−(Q). Thus ρ−(Q) is a type-1 quasi-hyperfilter of H.
This completes the proof.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset Q of H is called a ρ-upper rough type-1 quasi-hyperfilter of H if ρ+(Q) is a type-1 quasi-hyperfilter of H.
Theorem 4.5. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and Q a type-1 quasi-hyperfilter of H. Then ρ+(Q) is a type-1 quasi-hyperfilter of H.
Proof. Let Q be a type-1 quasi-hyperfilter of H.
(i) Since Q is an LA-subsemihypergroup of H, then by Theorem 4.3(1), ρ+(Q) is an LA-subsemihypergroup of H. Thus ρ+(Q)∘ρ+(Q)⊆ρ+(Q).
(ii) Let x∘y=z∘x⊆ρ+(Q) for some x,y,z∈H. Then
So, there exist a∈ρN(x), b∈ρN(y) and c∈ρN(z) such that a∘b=c∘a⊆Q. Since Q is type-1 quasi-hyperfilter of H, so we have a∈Q. Thus ρN(x)∩Q≠∅ which implies that x∈ρ+(Q).
(iii) Let x∘y=y∘x⊆ρ+(Q) for some x,y∈H. Then
So, there exist a∈ρN(x) and b∈ρN(y) such that a∘b=b∘a⊆Q. Since Q is type-1 quasi-hyperfilter of H, so we have a∈Q or b∈Q. Thus ρN(x)∩Q≠∅ or ρN(y)∩Q≠∅ which implies that x∈ρ+(Q) or y∈ρ+(Q).
(iv) Now, let x∈ρ+(Q) and y∈H such that x≤y. Then ρN(x)∩Q≠∅ and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)∩Q≠∅, so ρN(y)∩Q≠∅. Thus y∈ρ+(Q). Thus ρ+(Q) is a type-1 quasi-hyperfilter of H.
This completes the proof.
The converse of Theorem 4.4 and Theorem 4.5 is not true in general.
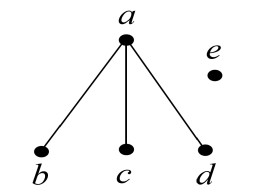
Example 4.6. Consider an ordered LA-semihypergroup H={a,b,c,d} with the following hyperoperation "∘" and order "≤" :
We give the covering relation ≺={(a,c)}, and the figure of H in Figure 4.
Now let ρ={(a,a),(a,c),(b,b),(b,d),(c,a),(c,c),(d,b),(d,d)} be a complete pseudohyperorder on H, such that
Now for {b,c,d}⊆H,
It is clear that ρ−({b,c,d}) and ρ+({b,c,d}) are both type-1 quasi-hyperfilters of H, but {b,c,d} is not a type-1 quasi-hyperfilter of H.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset Q of H is called a ρ-lower rough type-2 strong quasi-hyperfilter of H if ρ−(Q) is a type-2 strong quasi-hyperfilter of H.
Theorem 4.7. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and Q a type-2 strong quasi-hyperfilter of H. Then ρ−(Q) is, if it is non-empty, a type-2 strong quasi-hyperfilter of H.
Proof. Let Q be a type-2 strong quasi-hyperfilter of H.
(i) Since Q is an LA-subsemihypergroup of H, then by Theorem 4.3(2), ρ−(Q) is an LA-subsemihypergroup of H. Thus ρ−(Q)∘ρ−(Q)⊆ρ−(Q).
(ii) Let (x∘y)∩(z∘x)∩ρ−(Q)≠∅ for some x,y,z∈H. There exists t∈ρ−(Q) for some t∈x∘y and t∈z∘x. We get ρN(t)⊆Q. Now for t∈x∘y, we have ρN(t)⊆ρN(x∘y)=ρN(x)∘ρN(y). Similarly for t∈z∘x, we have ρN(t)⊆ρN(z)∘ρN(x). So, we get
We suppose that ρ−(Q) is not a type-2 strong quasi-hyperfilter of H. Then there exist x,y,z∈H such that (x∘y)∩(z∘x)∩ρ−(Q)≠∅ but x∉ρ−(Q). Thus ρN(x)⊈Q. Then there exist a∈ρN(x) such that a∉Q. Thus, for b∈ρN(y) and c∈ρN(z), we take
Since Q is a type-2 strong quasi-hyperfilter of H, so we have a∈Q, which is a contradiction.
(iii) Let (x∘y)∩(y∘x)∩ρ−(Q)≠∅ for some x,y∈H. There exists t∈ρ−(Q) for some t∈x∘y and t∈y∘x. We get ρN(t)⊆Q. Now for t∈x∘y, we have ρN(t)⊆ρN(x∘y)=ρN(x)∘ρN(y). Similarly for t∈y∘x, we have ρN(t)⊆ρN(y)∘ρN(x). So, we get
We suppose that ρ−(Q) is not a type-2 strong quasi-hyperfilter of H. Then there exist x,y∈H such that (x∘y)∩(y∘x)∩ρ−(Q)≠∅ but x∉ρ−(Q) and y∉ρ−(Q). Thus ρN(x)⊈Q and ρN(y)⊈Q. Then there exist a∈ρN(x) and b∈ρN(y) such that a,b∉Q. Thus, for a∈ρN(x) and b∈ρN(y), we take
Since Q is a type-2 strong quasi-hyperfilter of H, so we have a∈Q or b∈Q, which is a contradiction.
(iv) Now, let x∈ρ−(Q) and y∈H such that x≤y. Then ρN(x)⊆Q and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)⊆Q, so ρN(y)⊆Q. Thus y∈ρ−(Q). Hence ρ−(Q) is a type-2 strong quasi-hyperfilter of H.
This completes the proof.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset Q of H is called a ρ-upper rough type-2 strong quasi-hyperfilter of H if ρ+(Q) is a type-2 strong quasi-hyperfilter of H.
Theorem 4.8. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and Q a type-2 strong quasi-hyperfilter of H. Then ρ+(Q) is a type-2 strong quasi-hyperfilter of H.
Proof. Let Q be a type-2 strong quasi-hyperfilter of H.
(i) Since Q is an LA-subsemihypergroup of H, then by Theorem 4.3(1), ρ+(Q) is an LA-subsemihypergroup of H. Thus ρ+(Q)∘ρ+(Q)⊆ρ+(Q).
(ii) Let (x∘y)∩(z∘x)∩ρ+(Q)≠∅ for some x,y,z∈H. There exists t∈ρ+(Q) for some t∈x∘y and t∈z∘x. We get ρN(t)∩Q≠∅. Now for t∈x∘y, we have ρN(t)⊆ρN(x∘y)=ρN(x)∘ρN(y). Similarly for t∈z∘x, we have ρN(t)⊆ρN(z)∘ρN(x). So, we get
There exist a∈ρN(x), b∈ρN(y) and c∈ρN(z), such that
Since Q is type-2 strong quasi-hyperfilter of H, so we have a∈Q. Thus ρN(x)∩Q≠∅, which implies that x∈ρ+(Q).
(iii) Let (x∘y)∩(y∘x)∩ρ+(Q)≠∅ for some x,y∈H. There exists t∈ρ+(Q) for some t∈x∘y and t∈y∘x. We get ρN(t)∩Q≠∅. Now for t∈x∘y, we have ρN(t)⊆ρN(x∘y)=ρN(x)∘ρN(y). Similarly for t∈y∘x, we have ρN(t)⊆ρN(y)∘ρN(x). So, we get
There exist a∈ρN(x) and b∈ρN(y), such that
Since Q is type-2 strong quasi-hyperfilter of H, so we have a∈Q or b∈Q. Thus ρN(x)∩Q≠∅ or ρN(y)∩Q≠∅, which implies that x∈ρ+(Q) or y∈ρ+(Q).
(iv) Now, let x∈ρ+(Q) and y∈H such that x≤y. Then ρN(x)∩Q≠∅ and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)∩Q≠∅, so ρN(y)∩Q≠∅. Thus y∈ρ+(Q). Thus ρ+(Q) is a type-2 strong quasi-hyperfilter of H.
This completes the proof.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset I of H is called a ρ-lower rough interior hyperfilter of H if ρ−(I) is an interior hyperfilter of H.
Theorem 4.9. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and I an interior hyperfilter of H. Then ρ−(I) is, if it is non-empty, an interior hyperfilter of H.
Proof. Let I be an interior hyperfilter of H.
(i) Since I is an LA-subsemihypergroup of H, then by Theorem 4.3(2), ρ−(I) is an LA-subsemihypergroup of H. Thus ρ−(I)∘ρ−(I)⊆ρ−(I).
(ii) Let (x∘y)∘z⊆ρ−(I) for some x,y,z∈H. Then (ρN(x)∘ρN(y))∘ρN(z)=ρN((x∘y)∘z)⊆I. We suppose that ρ−(I) is not an interior hyperfilter of H. Then there exist x,y,z∈H such that (x∘y)∘z⊆ρ−(I), but y∉ρ−(I). Thus ρN(y)⊈I. Then there exist b∈ρN(y) such that b∉I. Now, for a∈ρN(x) and c∈ρN(z), we have (a∘b)∘c⊆(ρN(x)∘ρN(y))∘ρN(z)⊆I. Since I is an interior hyperfilter of H, so we have b∈I, which is a contradiction.
(iii) Now, let x∈ρ−(I) and y∈H such that x≤y. Then ρN(x)⊆I and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)⊆I, so ρN(y)⊆I. Thus y∈ρ−(I). Hence ρ−(I) is an interior hyperfilter of H.
This completes the proof.
Let ρ be a pseudohyperorder on an ordered LA-semihypergroup H. Then a non-empty subset I of H is called a ρ-upper rough interior hyperfilter of H if ρ+(I) is an interior hyperfilter of H.
Theorem 4.10. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and I an interior hyperfilter of H. Then ρ+(I) is an interior hyperfilter of H.
Proof. Let I be an interior hyperfilter of H.
(i) Since I is an LA-subsemihypergroup of H, then by Theorem 4.3(1), ρ+(I) is an LA-subsemihypergroup of H. Thus ρ+(I)∘ρ+(I)⊆ρ+(I).
(ii) Let (x∘y)∘z⊆ρ+(I) for some x,y,z∈H. Then ((ρN(x)∘ρN(y))∘ρN(z))∩I=ρN((x∘y)∘z)∩I≠∅, so there exist a∈ρN(x), b∈ρN(y) and c∈ρN(z) such that (a∘b)∘c⊆I. Since I is interior hyperfilter of H, so we have b∈I. Thus ρN(y)∩I≠∅, which implies that y∈ρ+(I).
(iii) Now, let x∈ρ+(I) and y∈H such that x≤y. Then ρN(x)∩I≠∅ and xρy. This implies that ρN(x)=ρN(y). Since ρN(x)∩I≠∅, so ρN(y)∩I≠∅. Thus y∈ρ+(I). Thus ρ+(I) is an interior hyperfilter of H.
This completes the proof.
The converse of Theorem 4.9 and Theorem 4.10 is not true in general.
Example 4.11. Consider an ordered LA-semihypergroup H={a,b,c,d,e} with the following hyperoperation "∘" and order "≤" :
We give the covering relation ≺={(d,b),(d,c),(e,a)}, and the figure of H in Figure 5.
Now let ρ be a complete pseudohyperorder on H, such that
Now for {a,b,e}⊆H,
It is clear that ρ−({a,b,e}) and ρ+({a,b,e}) are both interior hyperfilters of H but {a,b,e} is not an interior hyperfilter of H.
Theorem 4.12. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and I an interior semihyperfilter (resp., strong interior hyperfilter, strong interior semihyperfilter) of H. Then ρ−(I) is, if it is non-empty, an interior semihyperfilter (resp., strong interior hyperfilter, strong interior semihyperfilter) of H.
Proof. The proof is similar to the proof of Theorem 4.9.
Theorem 4.13. Let ρ be a complete pseudohyperorder on an ordered LA-semihypergroup H and I an interior semihyperfilter (resp., strong interior hyperfilter, strong interior semihyperfilter) of H. Then ρ+(I) is an interior semihyperfilter (resp., strong interior hyperfilter, strong interior semihyperfilter) of H.
Proof. The proof is similar to the proof of Theorem 4.10.
5.
Conclusions
In this paper, we have defined the quasi-hyperfilters and interior-hyperfilters of partially ordered LA-semihypergroups and present some properties related to them. After investigating some results concerning the quasi and interior hyperfilters, our study has focussed on the roughness of these hyperfilters. We have studied the relation between the rough set theory and the quasi-(interior) hyperfilters of partially ordered LA-semihypergroups. Our future work may be on the following topics:
(i) Fuzzy quasi-hyperfilters in partially ordered LA-semihypergroups.
(ii) Fuzzy interior-hyperfilters in partially ordered LA-semihypergroups.
(iii) Soft quasi-(interior) hyperfilters in partially ordered LA-semihypergroups.
(iv) Rough fuzzy quasi-(interior) hyperfilters in partially ordered LA-semihypergroups.
(v) Fuzzy soft quasi-(interior) hyperfilters in partially ordered LA-semihypergroups.
Acknowledgments
This work was supported by the National Natural Science Foundation (No. 11801081) and the Anhui Provincial Excellent Youth Talent Foundation (No. gxyqZD2019043).
Conflict of interest
The authors declare no conflict of interest.









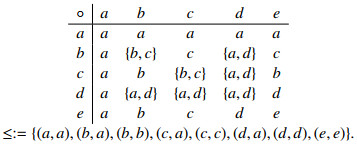
 DownLoad:
DownLoad: