Positive solutions to a semipositone superlinear elastic beam equation

1.   Introduction

The generalized linear model (GLM), a generalization of the linear model with wide applications in many research areas, was proposed by Nelder and Wedderburn ^[1] in 1972 for discrete dependent variables, which cannot be dealt with by the ordinary linear regression model. The GLM allows the response variable to be nonnormal distributions, including binomial, Poisson, gamma, and inverse Gaussian distributions, whose means are linked with the predictors by a link function.

Nowadays, with the rapid development of science and technology, massive data is ubiquitous in many fields, including medicine, industry, and economics. Extracting effective information from massive data is the core challenge of big data analysis. However, the limited arithmetic power of computers tends to consume a lot of computing time. In order to deal with this challenge, parallel computing and distributed computing are commonly used, and subsampling techniques have emerged as a result, i.e., a small number of representative samples are extracted from massive data. Imberg et al. ^[2] proposed a theory on optimal design in the context of general data subsampling issues. It includes and extends most existing methods, works out optimality conditions, and offers algorithms for finding optimal subsampling scheme designs, which introduces a new class of invariant linear optimality criteria. Chao et al. ^[3] presented an optimal subsampling approach for modal regression with big data. The estimators are obtained by means of a two-step algorithm based on the modal expectation maximization when the bandwidth is not related to the subsample size.

There has been a great deal of research on subsampling algorithms of specific models. Wang et al. ^[4] devised a rapid subsampling algorithm to approximate the maximum likelihood estimators in the context of logistic regression. Based on the previous study, Wang ^[5] presented an enhanced estimation method for logistic regression, which has a higher estimation efficiency. In the case that data are usually distributed in multiple distributed sites for storage, Zuo et al. ^[6] developed a distributed subsampling procedure to effectively approximate the maximum likelihood estimators of logistic regression. Ai et al. ^[7] focused on the optimal subsampling method under the A-optimality criteria based on the method developed by Wang ^[4] for generalized linear models to quickly approximate maximum likelihood estimators from massive data. Yao and Wang ^[8] examined optimal subsampling methods for various models, including logistic regression models, softmax regression models, generalized linear models, quantile regression models, and quasi-likelihood estimators. Yu et al. ^[9] proposed an efficient subsampling procedure for online data streams with a multinomial logistic model. Yu et al. ^[10] studied the subsampling technique for the Akaike information criterion (AIC) and the smoothed AIC model-averaging framework for generalized linear models. Yu et al. ^[11] reviewed several subsampling methods for massive datasets from the viewpoint of statistical design.

To the best of our knowledge, all the existing methods above assume that the covariates are fully observable. However, in practice, this assumption is not realistic, and covariates may be inaccurately observed owing to measurement errors, which will lead to biases in the estimators of the regression coefficients. This means that we may incorrectly determine some unimportant variables as significant, which in turn affects the model selection and interpretation. Therefore, it is necessary to consider measurement errors. Liang et al. ^[12], Li and Xue ^[13], and Liang and Li ^[14] investigated the partial linear measurement error models. Stefanski ^[15] and Nakamura ^[16] obtained the corrected score functions of the GLM, such as linear regression, gamma regression, inverse gamma regression, and Poisson regression. Yang et al. ^[17] proposed an empirical likelihood method based on the moment identity of the corrected score function to perform statistical inference for a class of generalized linear measurement error models. Fuller ^[18] estimated the variable error model using the maximum likelihood method and studied statistical inference. Hu and Cui ^[19] proposed a corrected error variance method to accurately estimate the error variance, which can effectively reduce the influence of measurement error and false correlation at the same time. Carroll et al. ^[20] summarized the measurement errors in linear regression and described some simple and universally applicable measurement error analysis methods. Yi et al. ^[21] presented a regression calibration method, which is one of the first statistical methods introduced to address measurement errors in the covariates. In addition, they presented an overview of the conditional score and corrected score approaches for measurement error correction. Regarding the measurement errors in different situations existing in actual data, extensive research has been carried out, and a variety of methods have been proposed, see ^{[22,23,24,25]}. Recently, a class of variable selection procedures has been developed for measurement error models, see ^[26,27]. More recently, Ju et al. ^[28] studied the optimal subsampling algorithm and the random perturbation subsampling algorithm for big data linear models with measurement errors. The aim of this paper is to estimate the parameters using a subsampling algorithm for a class of generalized linear measurement error models in the massive data analysis.

In this paper, we study a class of the GLM with measurement errors, such as logistic regression models and Poisson regression models. We combine the corrected score function method with subsampling techniques to investigate subsampling algorithms. The consistency and asymptotic normality of the estimators obtained in the general subsampling algorithm are derived. We optimize the subsampling probabilities based on the design of A-optimality and L-optimality criteria and incorporate a truncation method in the optimal subsampling probabilities to obtain the optimal estimators. In addition, we develop an adaptive two-step algorithm and obtain the consistency and asymptotic normality of the final subsampling estimators. Finally, the effectiveness of the proposed method is demonstrated through numerical simulations and real data analysis.

The remainder of this paper is organized as follows: Section 2 introduces the corrected score function under different distributions and derives the general subsampling algorithm and the adaptive two-step algorithm. Sections 3 and 4 verify the effectiveness of the proposed method by generating simulated experimental data and two real data sets, respectively. Section 5 provides conclusions.

2.   Model and methodology

In the GLM, it is assumed that the conditional distribution of the response variable belongs to the exponential family

where $a(\cdot), b(\cdot), c(\cdot, \cdot)$ are known functions, $\theta$ is called the natural parameter, and $\phi$ is called the dispersion parameter.

Let $\left\{ {\left({{{\mathit{\boldsymbol{X}}}_i}, {{{Y}}_i}} \right)} \right\}_{i = 1}^N$ be independent and identically distributed random samples, ${\mu_i } = E\left({{Y}_i} \mid {\mathit{\boldsymbol{X}}_i}\right), \; V\left({\mu}_i \right) = \text{Var}\left({{Y}_i}\mid {\mathit{\boldsymbol{X}}_i}\right)$, where the covariate ${\mathit{\boldsymbol{X}}}_i \in{\mathbb{R}{^p}}$ and the response variable ${{Y}}_i \in{\mathbb{R}}$, $V(\cdot)$ is a known variance function. The conditional expectation of ${Y_i}$ given ${{\mathit{\boldsymbol{X}}}_i}$ is

where $g(\cdot)$ is the canonical link function, and $\mathit{\boldsymbol{\beta}} = {\left({{\beta _1}, \ldots, {\beta _p}} \right)^{\rm T}}$is a $p$-dimensional unknown regression parameter.

In practice, covariates are not always accurately observed, and there are measurement errors that cannot be ignored. Let ${{\mathit{\boldsymbol{W}}}_i}$ be an accurate observation of the covariate ${{\mathit{\boldsymbol{X}}}_i}$. Assuming that the additive measurement error model is

where ${\mathit{\boldsymbol{U}}_i} \sim N_p({{\mathbf{0}}}, {{\mathit{\boldsymbol{\Sigma}}}_u})$, and it is independent of $({{\mathit{\boldsymbol{X}}}_i}, {Y_i})$. Combining (2.1) and (2.2) yields a generalized linear model with measurement errors.

Define the log-likelihood function as $\ell (\mathit{\boldsymbol{\beta}}; Y_i) = \sum\limits_{i = 1}^N \log f(Y_i; \mathit{\boldsymbol{\beta}})$. If ${{\mathit{\boldsymbol{X}}}_i}$ is observable, the score function for $\mathit{\boldsymbol{\beta}}$ in (2.1) is

and satisfies $E[{\mathit{\boldsymbol{\eta}}}_i \left(\mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{X}}}_i}, {Y_i} \right) \mid {{\mathit{\boldsymbol{X}}}_i}] = {\mathbf{0}}$. However, when there is an error in ${{\mathit{\boldsymbol{X}}}_i}$, directly replacing ${{\mathit{\boldsymbol{X}}}_i}$ with ${{\mathit{\boldsymbol{W}}}_i}$ to calculate ${\mathit{\boldsymbol{\eta}}}_i \left(\mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{X}}}_i}, {Y_i} \right)$ causes a bias, i.e., $E[{\mathit{\boldsymbol{\eta}}}_i \left(\mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{X}}}_i}, {Y_i} \right)] = {{\mathbf{0}}}$ will not always hold, hence a correction is needed. We define an unbiased score function ${{\mathit{\boldsymbol{\eta}}}_i^*}({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{W}}}_i}, {Y_i})$ for $\mathit{\boldsymbol{\beta}}$ satisfying $E[{{\mathit{\boldsymbol{\eta}}}_i^*} ({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{W}}}_i}, {Y_i}) \mid {{\mathit{\boldsymbol{X}}}_i}] = {\mathbf{0}}$ by the idea of ^[16]. The maximum likelihood estimator ${\hat {\mathit{\boldsymbol{\beta}}} _{\text{MLE}}}$ of $\mathit{\boldsymbol{\beta}}$ is the solution of the estimating equation

Based on the following moment identities associated with the error model (2.2),

then we can construct the unbiased score function for binary logistic measurement error regression models and Poisson measurement error regression models, which are widely used in practice.

(1) Binary logistic measurement error regression models.

We consider the logistic measurement error regression model

with mean ${\mu_i } = {\left[ {1 + \exp \left({ - {{\mathit{\boldsymbol{X}}}_i^{\rm T}}\mathit{\boldsymbol{\beta}}} \right)} \right]^{ - 1}}$ and variance $\text{Var}\left({Y_i \mid {{\mathit{\boldsymbol{X}}}_i}} \right) = {\mu_i }\left({1 - {\mu_i }} \right)$. Followed by Huang and Wang ^[29], the corrected score function is

and its first-order derivative is

(2) Poisson measurement error regression models.

Let $Y_i$ follow the Poisson distribution with mean ${\mu }_i$, $\text{Var}\left({Y_i \mid {\mathit{\boldsymbol{X}}}_i} \right) = {\mu }_i$. Consider the log linear measurement error model

then we have the corrected score function

and its first-order derivative is

2.1.   General subsampling algorithm

It is assumed that ${\pi_i}$ is the probability of sampling the $i$-th sample $\left({{{\mathit{\boldsymbol{W}}}_i}, {{Y}_i}} \right)$, $i = 1, \ldots, N$. Let $S$ be the set of the subsamples $\left({{{\widetilde {\mathit{\boldsymbol{W}}}_i}}, {\widetilde {{Y}_i}}} \right)$ with corresponding sampling probabilities $\widetilde {\pi_{i}}$, i.e., $S = \left\{ { {\left({{\widetilde {{\mathit{\boldsymbol{W}}}_i}}, {\widetilde {{Y}_i}}, {\widetilde {\pi_i}}} \right)} } \right\}$ with the subsample size $r$. The general subsampling algorithm is shown in Algorithm 1.

To obtain the consistency and asymptotic normality of $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$, the following assumptions should be made. For simplicity, denote $\mathit{\boldsymbol{\eta}} _i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{W}}}_i}, {Y_i})$ and ${\mathit{\boldsymbol{\Omega}}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}; {{\mathit{\boldsymbol{W}}}_i}, {Y_i})$ as $\mathit{\boldsymbol{\eta}} _i^*\left({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}\right)$ and ${\mathit{\boldsymbol{\Omega}}}_i^*\left({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}\right)$.

A1: It is assumed that ${{\mathit{\boldsymbol{W}}}_i^{\rm T}} \mathit{\boldsymbol{\beta}}$ is almost necessarily in the interior of a closed set $K \in \Theta$, $\Theta$ is a natural parameter space.

A2: The regression parameters are located in the ball $\Lambda = \left\{ {\mathit{\boldsymbol{\beta}} \in {\mathbb{R}{^p}}:{{\left\| \mathit{\boldsymbol{\beta}} \right\|}_1} \le B} \right\}, {{\mathit{\boldsymbol{\beta}}} _t}$ and ${\hat {\mathit{\boldsymbol{\beta}}}_{\text{MLE}}}$ are true parameters and maximum likelihood estimators, which are interior points of $\Lambda$, and $B$ is a constant, where $\| \cdot \|_1$ denotes $\ell_1$-norm.

A3: As $n \to \infty$, the observed information matrix ${{\bf{M}}_X} : = \frac{1}{N} \sum\limits_{i = 1}^N {{\bf{\Omega}}_{i}^*} \left(\mathit{\boldsymbol{\Sigma}}_u, {\hat {\mathit{\boldsymbol{\beta}}}_{\text{MLE}}}\right)$ is a positive definite matrix in probability.

A4: Assume that for all $\mathit{\boldsymbol{\beta}} \in \Lambda$, $\frac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {\mathit{\boldsymbol{\eta}}_{_i}^*\left({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}}\right)} \right\|}^4}} = {O_P}(1)$, where $\| \cdot \|$ denotes the Euclidean norm.

A5: Suppose that the full sample covariates have finite 6th-order moments, i.e., $E{\left\| {{\mathit{\boldsymbol{W}}_1}} \right\|^6} \le \infty$.

A6: For any $\delta \ge 0$, we assume that

where ${\bf{\Omega}}_{_i}^{*(j_1j_2)}$ represents the elements of the $j_1$-th row and $j_2$-th column of the matrix ${\bf{\Omega}}_{i}^*$.

A7: Assume that $\mathit{\boldsymbol{\eta}} _i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}})$ and ${\mathit{\boldsymbol{\Omega}}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}})$ are $m({{\mathit{\boldsymbol{W}}}_i})$-Lipschitz continuous. For any ${\mathit{\boldsymbol{\beta}} _1}, \; {\mathit{\boldsymbol{\beta}} _2} \in \Lambda$, there exist functions ${m_1}({{\mathit{\boldsymbol{W}}}_i})$ and ${m_2}({{\mathit{\boldsymbol{W}}}_i})$ such that $\left\| {\mathit{\boldsymbol{\eta}} _i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {\mathit{\boldsymbol{\beta}} _1}) - \mathit{\boldsymbol{\eta}} _i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {\mathit{\boldsymbol{\beta}} _2})} \right\| \le {m_1}({{\mathit{\boldsymbol{W}}}_i})\left\| {{\mathit{\boldsymbol{\beta}} _1} - {\mathit{\boldsymbol{\beta}} _2}} \right \|$, ${{\left\| {{\bf{\Omega}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {\mathit{\boldsymbol{\beta}} _1}) - {\bf{\Omega}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {\mathit{\boldsymbol{\beta}} _2})} \right\|}_S \le {m_2}({{\mathit{\boldsymbol{W}}}_i})\left\| {{\mathit{\boldsymbol{\beta}} _1} - {\mathit{\boldsymbol{\beta}} _2}} \right\|}$, where ${\| \bf{A} \|}_S$ denotes the spectral norm of matrix $\bf A$. Further assume that $E\left\{ {{m_1}({{\mathit{\boldsymbol{W}}}_i})} \right\} \le \infty$ and $E\left\{ {{m_2}({{\mathit{\boldsymbol{W}}}_i})} \right\} \le \infty$.

Assumptions A1 and A2 are also used in Clémencon et al. ^[30]. The set $\Lambda$ in Assumption A2 is also known as the admissible set and is a prerequisite for consistency estimation for the GLM with full data ^[31]. Assumption A3 imposes a condition on the covariates to ensure that the MLE based on the full dataset is consistent. In order to obtain the Bahadur representation of the subsampling estimators, Assumptions A4 and A5 are required. Assumption A6 is a moment condition for the subsampling probability and is also required for the Lindberg-Feller central limit theorem. Assumption A7 adds a restriction on smoothing, which can be found in ^[32].

The following theorems show the consistency and asymptotic normality of the subsampling estimators.

Theorem 2.1. If Assumptions A1–A7 hold, as $r \to \infty$ and $N \to \infty$, $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$ converges to $\hat{\mathit{\boldsymbol{\beta}}}_{\mathit{\text{MLE}}}$ in conditional probability given $\mathcal{F}_N$, and the convergence rate is ${r^{\frac{1}{2}}}$. That is, for all $\varepsilon > 0$, there exist constants ${\Delta _\varepsilon }$ and ${r_\varepsilon }$ such that

for all $r > {r_\varepsilon }$.

Theorem 2.2. If Assumptions A1–A7 hold, as $r \to \infty$ and $N \to \infty$, conditional on $\mathcal{F}_N$, the estimator $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$ obtained from Algorithm 1 satisfies

where ${\bf{V}} = {\bf{M}}_X^{ - 1}{{\bf{V}}_{\mathit{\text{C}}}}{\bf{M}}_X^{ - 1} = {O_P}({r^{ - 1}})$, and

Remark 1. In order to get the standard error of the corresponding estimator, we estimate the variance-covariance matrix of $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$ by

where

Based on the A-optimality criteria in the optimal design language, the optimal subsampling probabilities are obtained by minimizing the asymptotic mean square error of $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$ in Theorem 2.2.

However, ${\mathit{\boldsymbol{\Sigma}}}_u$ is usually unknown in practice. Therefore, we need to estimate the covariance matrix ${\mathit{\boldsymbol{\Sigma}}}_u$ as suggested by ^[12]. We observe that the consistent, unbiased moment estimator of ${\mathit{\boldsymbol{\Sigma}}}_u$ is

where ${\overline{\mathit{\boldsymbol{W}}}}_i$ is the sample mean of the replicates, and $m_i$ is the number of repeated measurements of the $i$-th individual.

Theorem 2.3. Define $g_i^{\mathit{\text{mV}}} = \left\| {{\bf{M}}_X^{-1}}\mathit{\boldsymbol{\eta}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, \hat{\mathit{\boldsymbol{\beta}}}_{\mathit{\text{MLE}}}) \right\|, \; i = 1, \ldots, N$. The subsampling strategy is mV-optimal if the subsampling probability is chosen such that

which is obtained by minimizing $tr({\bf{V}})$.

Theorem 2.4. Define $g_i^{\mathit{\text{mVc}} } = \left\| {\mathit{\boldsymbol{\eta}}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, \hat{\mathit{\boldsymbol{\beta}}}_{\mathit{\text{MLE}}}) \right\|, \; i = 1, \ldots, N$. The subsampling strategy is mVc-optimal if the subsampling probability is chosen such that

which is obtained by minimizing $tr({{\bf{V}}_{\mathit{\text{C}}}})$.

Remark 2. ${{\bf{M}}_X}$ and ${{\bf{V}}_{\text{C}}}$ are non-negative definite matrices, and ${\bf{V}} = {\bf{M}}_X^{ - 1}{{\bf{V}}_{\text{C}}}{\bf{M}}_X^{ - 1}$, then $tr({\bf{V}}) = tr\left({{\bf{M}}_X^{ - 1}{{\bf{V}}_{\text{C}}}{\bf{M}}_X^{ - 1}} \right) \le {\sigma _{\max }}\left({{\bf{M}}_X^{ - 2}} \right)tr\left({{{\bf{V}}_{\text{C}}}} \right)$, where ${\sigma_{\max}}\left({\bf{A}} \right)$ represents the maximum eigenvalue of square matrix ${\bf{A}}$. As ${\sigma _{\max }}\left({{\bf{M}}_X^{ - 2}} \right)$ does not depend on $\mathit{\boldsymbol{\pi}}$, minimizing $tr({{\bf{V}}_C})$ means minimizing the upper bound of $tr({\bf{V}})$. In fact, for two given subsampling probabilities ${\mathit{\boldsymbol{\pi}}_1}$ and ${\mathit{\boldsymbol{\pi}}_2}$, ${\bf{V}}\left({{\mathit{\boldsymbol{\pi}}_1}} \right) \le {\bf{V}}\left({{\mathit{\boldsymbol{\pi}}_2}} \right)$ if and only if ${{\bf{V}}_{\text{C}}}\left({{\mathit{\boldsymbol{\pi}}_1}} \right) \le {{\bf{V}}_{\text{C}}}\left({{\mathit{\boldsymbol{\pi}}_2}} \right)$. Therefore, minimizing $tr({{\bf{V}}_{\text{C}}})$ reduces considerable computational time compared to minimizing $tr({\bf{V}})$, and $tr({{\bf{V}}_{\text{C}}})$ does not take into account the structural information of the data.

2.2.   Optimal subsampling algorithm

The optimal subsampling probabilities are defined as $\left\{ \pi_i^{\text{op}} \right\}_{i = 1}^N = \left\{ \pi_i^{\text{mV}} \right\}_{i = 1}^N$ or $\left\{ \pi_i^{\text{mVc}} \right\}_{i = 1}^N$. However, because $\pi _i^{\text{op}}$ depends on ${{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}$, it cannot be used directly in applications. To calculate $\pi _i^{\text{op}}$, it is necessary to use a prior estimator ${{\tilde{\mathit{\boldsymbol{\beta}}}}_0}$, which is obtained by the prior subsample of size ${r_0}$.

We know $\pi _i^{\text{op}}$ is proportional to $\left\| {{\mathit{\boldsymbol{\eta}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}})}} \right\|$, however, in actual situations, there may be some data points that make $\mathit{\boldsymbol{\eta}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) = {\mathbf{0}}$, which will never be included in a subsample, and some data points with $\mathit{\boldsymbol{\eta}}_i^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) \approx {\mathbf{0}}$ also have small probabilities of being sampled. If these special data points are excluded, some sample information will be missed, but if these data points are included, the variance of the subsampling estimator may increase.

To avoid Eq (2.4) from being inflated by these special data points, this paper adopts a truncation method, setting a threshold $\omega$ for $\left\| \mathit{\boldsymbol{\eta}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, {\hat{\mathit{\boldsymbol{{\beta}}}}}_{\text{MLE}}) \right\|$, that is, replacing $\left\| \mathit{\boldsymbol{\eta}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) \right\|$ with $max \left\{ \left\| \mathit{\boldsymbol{\eta}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) \right\|, \omega \right\}$, where $\omega$ is a very small positive number, for example, $10^{-4}$. In applications, the choice and design of the truncation weight function, which is a commonly used technique, are crucial to improving the robustness of the model and optimizing the performance.

We replace $\hat{\mathit{\boldsymbol{{\beta}}}}_{\text {MLE}}$ in the matrix $\bf{V}$ with $\tilde{\mathit{\boldsymbol{{\beta}}}}_0$, denoted as $\widetilde{\bf{{V}}}$, then $tr\left(\widetilde{\bf{{V}}} \right) \le tr\left(\widetilde{\bf{{V}}}^\omega \right) \le tr\left(\widetilde{\bf{{V}}} \right) + \frac{\omega^2}{N^2 r} \sum\limits_{i = 1}^N \frac{{\left\| {\bf{M}}_X^{-1} \right\|}^2}{\pi_i^{\text {op}}}$. Therefore, when $\omega$ is sufficiently small, $tr\left(\widetilde{\bf{{V}}}^\omega \right)$ approaches $tr\left(\widetilde{\bf{{V}}} \right)$. The threshold $\omega$ is set to make the subsample estimators more robust without sacrificing excessively estimation efficiency. ${\widetilde{\bf{{M}}}}_X = \frac{1}{Nr_0} \sum\limits_{i = 1}^{r_0} {\bf{\Omega}}_i^*(\mathit{\boldsymbol{\Sigma}}_u, {\tilde{\mathit{\boldsymbol{\beta}}}}_0)$ based on the prior subsample can be used to approximate ${\bf{M}}_X$. The two-step algorithm is presented in Algorithm 2.

Remark 3. In Algorithm 2, ${\tilde{\mathit{\boldsymbol{\beta}}}}_0$ in Step 1 satisfies

with the prior subsample set $S_{r_0}$, and

In Step 2, the subsampling probabilities are $\left\{{\pi}_i^{\text{opt}}\right\}_{i = 1}^N = \left\{ \pi_i^{\text{mVt}} \right\}_{i = 1}^N$ or $\left\{ \pi_i^{\text{mVct}} \right\}_{i = 1}^N$, let

then

The subsample set is $S_{r_0} \cup \left\{ \left(\widetilde{\mathit{\boldsymbol{W}}}_i, \widetilde{Y}_i, \widetilde{\pi}_i^{\text{opt}} \right) \mid i = 1, \ldots, r \right\}$ with a subsample size of $r + r_0$, and $\check{\mathit{\boldsymbol{\beta}}}$ is the solution to the corresponding estimating equation

where

Theorem 2.5. If Assumptions A1–A7 hold, as ${r_0}{{r}^{-1}} \to 0$, ${r_0} \to \infty, r \to \infty$ and $N \to \infty$, if ${\tilde {\mathit{\boldsymbol{\beta}}}}_0$ exists, then the estimator $\check{\mathit{\boldsymbol{\beta}}}$ obtained from Algorithm 2 converges to $\hat{\mathit{\boldsymbol{\beta}}}_{\mathit{\text{MLE}}}$ in conditional probability given $\mathcal{F}_N$, and its convergence rate is ${r^{\frac{1}{2}}}$. For all $\varepsilon > 0$, there exist finite $\Delta_\varepsilon$ and $r_\varepsilon$ such that

for all $r > r_\varepsilon$.

Theorem 2.6. If Assumptions A1–A7 hold, as ${r_0}{{{r}^{-1}}} \to 0$, ${r_0} \to \infty, r \to \infty$ and $N \to \infty$, conditional on $\mathcal{F}_N$, the estimator $\check{\mathit{\boldsymbol{\beta}}}$ obtained from Algorithm 2 satisfies

where ${{\bf{V}}_{\mathit{\text{opt}}}} = {\bf{M}}_X^{ - 1}{\bf{V}}_{\mathit{\text{C}}}^{\mathit{\text{opt}}}{\bf{M}}_X^{ - 1} = {O_P}({r^{ - 1}})$, and

Remark 4. We estimate the variance-covariance matrix of $\check{\mathit{\boldsymbol{\beta}}}$ by

where

3.   Simulation studies

In this section, we perform numerical simulations using synthetic data to evaluate the finite sample performance of the proposed method in Algorithm 2 (denoted as mV and mVc). For a fair comparison, we also give the results of the uniform subsampling method and set the size to be the same as that of Algorithm 2. The estimators of the above three subsampling methods, uniform—the uniform subsampling, mV—the mV probability subsampling, and mVc—the mVc probability subsampling, are compared with MLE—the maximum likelihood estimators for full data. In addition, we conduct simulation experiments using two models: the logistic regression model and the Poisson regression model.

3.1.   Binary logistic measurement error regression model

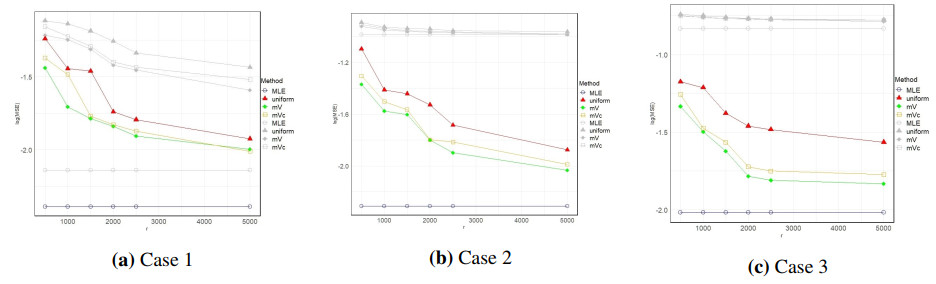
Set the sample size $N = 100000$, the true value ${\mathit{\boldsymbol{\beta}}}_{t} = (0.5, -0.6, 0.5)^{\rm T}$, the covariate ${\mathit{\boldsymbol{X}}}_i \sim N_3({{\mathbf{0}}}, {\boldsymbol \Sigma})$, where ${\mathit{\boldsymbol{\Sigma}}} = 0.5{\bf I} +0.5 {{\mathbf{1}}}{{\mathbf{1}}}^{\rm T}$, ${\bf I}$ is an identity matrix. The response $Y_i$ follows a binomial distribution with $P \left(Y_i = 1 \mid {\mathit{\boldsymbol{X}}_i} \right) = \left(1+\exp(-{\mathit{\boldsymbol{X}}_i^{\rm T}}{\boldsymbol \beta_t}) \right)^{-1}$. We consider the following three cases to generate the measurement error term ${\boldsymbol{U}} _i$.

● Case 1: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.4^2{\bf I})$;

● Case 2: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.5^2{\bf I})$;

● Case 3: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.6^2{\bf I})$.

The subsample size in Step 1 of Algorithm 2 is selected as $r_0 = 400$. The subsample size $r$ is set to be 500, 1000, 1500, 2000, 2500, and 5000. In order to verify that $\check{\mathit{\boldsymbol{\beta}}}$ can asymptotically approach ${\mathit{\boldsymbol{\beta_{t}}}}$, we repeat $K = 1000$ and calculate $MSE = \frac{1}{K}{\sum\limits_{k = 1}^K {\left\| {{{\check{\mathit{\boldsymbol{\beta}}}}^{\left(k \right)}} - {\mathit{\boldsymbol{\beta}}_t}} \right\|} ^2}$, where ${\check{\mathit{\boldsymbol{\beta}}}}^{\left(k \right)}$ is the parameter estimator of the subsample generated by the $k$-th repetition.

The simulation results are shown in Figure 1, which can be seen that both mV and mVc always have smaller MSEs than uniform subsampling. The MSEs of all the subsampling methods decrease as an increase of $r$, which confirms the theoretical results of the consistency of the subsampling methods. As the variance of the error term increases, the MSEs of uniform, mV, and mVc also increase. The mV is better than the mVc because the subsampling probabilities of mV take the structural information of the data into account. A comparison between the corrected and uncorrected methods shows that the MSEs of the corrected methods are much smaller than those of the uncorrected methods, and the difference between the corrected and uncorrected methods increases as the error variance increases.

Now, we evaluate the statistical inference performance of the optimal subsampling method for different $r$ and variances of ${{\boldsymbol{U}}}_i$. The parameter ${\beta}_1$ is taken as an example, and a $95\%$ confidence interval is constructed. Table 1 reports the empirical coverage probabilities and average lengths of three subsampling methods. It is evident that both mV and mVc have similar performance and consistently outperform the uniform subsampling method. As $r$ increases, the length of the confidence interval uniformly decreases.

3.2.   Poisson measurement error regression model

Let ${\mathit{\boldsymbol{\beta}}}_{t} = (0.5, -0.6, 0.5)^{\rm T}$, the covariate ${{\boldsymbol{X}}}_i \sim N_3({{\mathbf{0}}}, {\boldsymbol \Sigma})$, where ${\mathit{\boldsymbol{\Sigma}}} = 0.3{\bf I} +0.5 {{\mathbf{1}}}{{\mathbf{1}}}^{\rm T}$, ${\bf I}$ is an identity matrix. We consider the following three cases to generate the measurement error term ${\boldsymbol{U}} _i$.

● Case 1: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.3^2{\bf I})$;

● Case 2: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.4^2{\bf I})$;

● Case 3: ${\mathit{\boldsymbol{U}}}_i \sim N_3({{\mathbf{0}}}, 0.5^2{\bf I})$.

We also generate a sample of $N = 100000$ following $Poisson \left({{\mu _i}} \right)$, where ${\mu _i} = \exp \left({\mathit{\boldsymbol{X}}_i^{\rm T}{\mathit{\boldsymbol{\beta}}_t}} \right)$. distribution, and summarize the MSEs with the number of simulations $K = 1000$ in Figure 2. The other settings are the same as those in the logistic regression example.

In Figure 2, it can be seen that the MSEs of both the mV and mVc methods are smaller than those of the uniform subsampling, with the mV method being the optimal. In addition, the corrected method is obviously effective, which is consistent with Figure 1. Table 2 reports the empirical coverage probabilities and average lengths of $95\%$ confidence interval of the parameter ${\beta}_3$ for three subsampling methods. The conclusions of Table 2 are consistent with those of Table 1, but the average lengths of the intervals for Poisson regression are significantly longer than those for logistic regression.

In order to explore the influence of different subsample size allocated in the two-step algorithm, we calculate the MSEs for $r_0$ at different proportions under the condition that the total subsample size remains constant. Set the total subsample size $r_0 + r = 3000$, and the result is shown in Figure 3. It can be seen that the accuracy of the two-step algorithm will initially improve with the increase of $r_0$. However, when $r_0$ increases to a certain extent, the accuracy of the algorithm begins to decrease. There are two reasons: (1) if $r_0$ is too small, the estimators in the first step will be biased, and it is difficult to ensure the accuracy; (2) if $r_0$ are too large, then the performances of mV and mVc are similar to that of the uniform subsampling. When $r_0/(r_0 + r)$ is around 0.25, the two-step algorithm performs the best.

We use the Sys.time() function in R to calculate the running time of three subsampling methods and full data. We conduct 1000 repetitions, set $r_0 = 200$, and consider different $r$ values in Case 1. The results are shown in Tables 3 and 4. It is easy to find that the uniform subsampling algorithm requires the least computation time. Because there is no need to calculate the subsampling probabilities. In addition, the mV method takes longer than the mVc method, and this result is consistent with the theoretical analysis in Section 2.

4.   Real data

4.1.   Global census dataset

In this section, we apply the proposed method to analyze the 1994 global census data, which contains 42 countries, from the Machine Learning Database ^[33]. There are 5 covariates in the data: $x_1$ represents age; $x_2$ represents the population weight value, which is assigned by the Population Division of the Census Bureau and is related to socioeconomic characteristics; $x_3$ represents the highest level of education, that is, the highest level of education since primary school; $x_4$ represents capital loss, which refers to the loss of income from bad investment, which is the difference between the lower selling price and the higher purchase price of an individual's investment; $x_5$ represents weekly working hours. If an individual's annual income exceeds 50,000 dollars, it is expressed as $y_i = 1$ and $y_i = 0$ otherwise.

To verify the effectiveness of the proposed method, we add the measurement errors to the covariates $x_2$, $x_4$ and $x_5$ in this dataset, and the covariance matrix of the measurement error is

We split the full dataset into a training set of 32561 observations and a test set of 16281 observations in a 2:1 ratio. We apply the proposed method to the training set and evaluate the classification performance with the test set. We calculate $LEMSE = \log \left(\frac{1}{K}{\sum\limits_{k = 1}^K {\left\| {{{\check{\mathit{\boldsymbol{\beta}}}}^{\left(k \right)}} - {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}} \right\|} ^2}\right)$ based on 1000 bootstrap subsample estimators with $r = 500, 1000, 1500, 2200, 2500,$ and $r_0 = 500$. The corrected MLE estimators for the training set are ${{\hat \beta }_{\text{MLE, 0}}^{\text{err}}} = -1.6121$, ${{\hat \beta }_{\text{MLE, 1}}^{\text{err}}} = 1.1992$, ${{\hat \beta }_{\text{MLE, 2}}^{\text{err}}} = 0.0103$, ${{\hat \beta }_{\text{MLE, 3}}^{\text{err}}} = 0.9142$, ${{\hat \beta }_{\text{MLE, 4}}^{\text{err}}} = 0.2617$, ${{\hat \beta }_{\text{MLE, 5}}^{\text{err}}} = 0.8694$.

Table 5 shows the average estimators and the corresponding standard errors based on the proposed method ($r_0 = 500$, $r = 2000$). It can be seen that the estimators from three subsampling methods are close to the estimators from the full data. In general, the mV and mVc subsampling methods produce small standard errors.

All subsampling methods show that each variable has a positive impact on income, with age, highest education level, and weekly working hours having significant impacts on income. Interestingly, capital losses have a significant positive impact on income because low-income people rarely invest. However, the population weight value has the smallest impact on income, the reason should be more inclined to reflect the overall distribution characteristics among groups rather than the specific economic performance of individuals. Income is a highly volatile variable, and the income gap between different groups may be large. Even under the same socioeconomic characteristics, the income distribution may have a large variance. This high variability weakens the overall impact of the population weight on income.

Fix $r_0 = 500$, Figure 4(a) shows the LEMSEs calculated for the subsample with measurement errors. We can see that the LEMSEs of the corrected methods are much smaller than those of the uncorrected methods. As $r$ increases, the LEMSEs become increasingly small. The estimators of the subsampling methods are consistent and the mV method is the best. Figure 4(b) shows the proportion of responses in the test set being correctly classified for different subsample sizes. The mV performs slightly better than the mVc. It can also be seen that the prediction accuracy of the corrected subsampling methods is slightly greater compared with the correspondingly uncorrected methods.

4.2.   Creditcard fraud dataset

This subsection applies the corrected subsampling method to creditcard fraud detection dataset from Kaggle ^*, and the dependent variable is whether an individual has committed creditcard fraud. There are 284,807 pieces of data in the dataset, with a total of 492 fraud cases. Since the data involves sensitive information, the covariates have all been processed by principal component analysis with a total of 28 principal components. Amount represents the consumption amount, class is the dependent variable, 1 represents fraud, and 0 means normal. The first four principal components and the consumption amount are selected as independent variables.

^*https://www.kaggle.com/datasets/creepycrap/creditcard-fraud-dataset

To verify the effectiveness of the proposed method, we add the measurement errors to the covariates, and the covariance matrix of the measurement error is ${\mathit{\boldsymbol{\Sigma}}}_{u} = 0.16{\bf I}$. We split the dataset into the training set and the test set in a 3:1 ratio and summarize the LEMSEs based on the number of simulations $K = 1000$ with $r = 500, 1000, 1500, 2200, 2500, 5000,$ and $r_0 = 500$.

The MLE estimators for the training set are ${{\hat \beta }_{\text{MLE, 0}}^{\text{err}}} = -8.8016$, ${{\hat \beta }_{\text{MLE, 1}}^{\text{err}}} = -0.6070$, ${{\hat \beta }_{\text{MLE, 2}}^{\text{err}}} = 0.0737$, ${{\hat \beta }_{\text{MLE, 3}}^{\text{err}}} = -0.9056$, ${{\hat \beta }_{\text{MLE, 4}}^{\text{err}}} = 1.4553$, ${{\hat \beta }_{\text{MLE, 5}}^{\text{err}}} = -0.1329$. Table 6 shows the average estimators and the corresponding standard errors ($r_0 = 500$, $r = 2000$). It can be seen that the estimators from three subsampling methods are close to the estimators from the full data. In general, the mV and mVc subsampling methods produce small standard errors. From Figure 5, we can obtain similar results as in Figure 4.

5.   Conclusions

In this paper, we not only combine the corrected score method with the subsampling technique, but also theoretically derive the consistency and asymptotic normality of the subsampling estimators. In addition, an adaptive two-step algorithm is developed based on optimal subsampling probabilities using A-optimality and L-optimality criteria and the truncation method. The theoretical results of the proposed method are tested with simulated and two real datasets, and the experimental results demonstrate the effectiveness and good performance of the proposed method.

This paper merely assumes that the covariates are affected by the measurement error. However, in practical applications, the response variables can be influenced by measurement errors. The optimal subsampling probabilities are obtained by minimizing $tr(\bf V)$ or $tr({\bf V}_{\text{C}})$ using the design ideas of the A-optimality and L-optimality criteria. In the future, the other optimality criteria for subsampling can be considered to develop more efficient algorithms.

Author contributions

Ruiyuan Chang: Furnished the algorithms and numerical results presented in the manuscript and composed the original draft of the manuscript; Xiuli Wang: Rendered explicit guidance regarding the proof of the theorem and refined the language of the entire manuscript; Mingqiu Wang: Rendered explicit guidance regarding the proof of theorems and the writing of codes and refined the language of the entire manuscript. All authors have read and consented to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (12271294) and the Natural Science Foundation of Shandong Province (ZR2024MA089).

Conflict of interest

The authors declare no conflict of interest.

Appendix

The proofs of the following lemmas and theorems are primarily based on Wang et al. ^[5], Ai et al. ^[7] and Yu et al. ^[34].

Lemma 1. If Assumptions A1–A4 and A6 hold, as $r \to \infty$ and $N \to \infty$, conditional on $\mathcal{F}_N$, we have

where

and

Proof.

By Assumption A6, we have

It follows from Chebyshev's inequality that (A.1) holds.

By Assumption A4, we have

Now (A.2) follows from Markov's Inequality.

Let $\mathit{\boldsymbol{\gamma}} _i^{*} = {\left(N{\pi _i}\right)}^{-1} {{\tilde {\mathit{\boldsymbol{\eta}}} }_{_i}^*({{\mathit{\boldsymbol{\Sigma}}}_u}, {{\hat{\mathit{\boldsymbol{\beta}}}}_{\text {MLE}}})}$, then $N^{-1}{\mathit{\boldsymbol{Q}}^{*}}({\hat{\mathit{\boldsymbol{\beta}}}_{\text {MLE}}}) = {r}^{-1}\sum\limits_{i = 1}^r {\mathit{\boldsymbol{\gamma}} _i^{*}}$ holds. Based on Assumption A6, for all $\varepsilon > 0$, we have

This shows that the Lindeberg-Feller conditions are satisfied in probability. Therefore (A.3) is true. □

Lemma 2. Assumptions A1–A7 hold, as $r \to \infty$ and $N \to \infty$, conditional on $\mathcal{F}_N$, for all ${{{\boldsymbol{s}}}_r} \to {\mathbf{0}}$, we have

Proof. The Eq (A.4) can be written as

Let

then by Assumption A7, we have

It follows from Markov's inequality that ${{\mathit{\boldsymbol{\tau}}} _1} = {o_{P\mid\mathcal{F}_N}}(1)$.

Let

then

From the proof of Lemma 1, it follows that

Therefore ${{\mathit{\boldsymbol{\tau}}} _2} = {o_{P\mid\mathcal{F}_N}}(1)$, and (A.4) holds

□

Next, we will prove Theorems 2.1 and 2.2.

Proof of Theorem 2.1. $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$ is the solution of ${\mathit{\boldsymbol{Q}}^{*}}(\mathit{\boldsymbol{\beta}}) = \frac{1}{r}\sum\limits_{i = 1}^r {\frac{1}{{{{\widetilde \pi }_i}}}}{{\tilde{\mathit{\boldsymbol{\eta}}}}_{_i}^*({{\mathit{\boldsymbol{\Sigma}}}_u}, \mathit{\boldsymbol{\beta}})} = {\mathbf{0}}$, then

By Assumption A6, we have

Therefore, as $r \to \infty$, ${N}^{-1} \mathit{\boldsymbol{Q}}^{*}(\mathit{\boldsymbol{\beta}}) - {N}^{-1} \mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\beta}}) \xrightarrow{} 0$ for all ${\boldsymbol \beta} \in \Lambda$ in conditional probability given $\mathcal{F}_N$. Thus, from Theorem 5.9 in ^[32], we have $\left\| \overset{\smile}{\mathit{\boldsymbol{\beta}}} - \hat{\mathit{\boldsymbol{\beta}}}_{\text{MLE}} \right\| = o_{P\mid\mathcal{F}_N}(1)$. By Taylor expansion,

By Lemma 2, it follows that

then

Here is

we have

By Lemma 1 and Assumption A3, ${\bf{M}}_X^{ - 1} = {O_{P\mid\mathcal{F}_N}}\left(1 \right)$, we have $\overset{\smile}{\mathit{\boldsymbol{\beta}}} - \hat{\mathit{\boldsymbol{\beta}}}_{\text{MLE}} = {O_{P\mid\mathcal{F}_N}}\left({{r^{ - \frac{1}{2}}}} \right)$. □

Proof of Theorem 2.2. By Lemma 1 and (A.5), as $r \to \infty$, conditional on $\mathcal{F}_N$, it holds that

By Lemma 1 and Slutsky's theorem, it follows that

□

Proof of Theorem 2.3. To minimize the asymptotic variance $tr({\bf{V}})$ of $\overset{\smile}{\mathit{\boldsymbol{\beta}}}$, the optimization problem is

Define $g_i^{\text{mV}} = \left\|{{\bf{M}}_X^{-1}} {\mathit{\boldsymbol{\eta}}}_i^*\left(\mathit{\boldsymbol{\Sigma}}_u, \hat{\mathit{\boldsymbol{\beta}}}_{\text {MLE}}\right)\right\|, \; i = 1, \ldots, N$, it follows from Cauchy's inequality that

The equality sign holds if and only if ${\pi _i} \propto g_i^{\text{mV}}$, therefore

is the optimal solution. □

The proof of Theorem 2.4 is similar to Theorem 2.3.

Lemma 3. If Assumptions A1–A4 and A6 hold, as $r_0 \to \infty$, $r \to \infty$ and $N \to \infty$, conditional on $\mathcal{F}_N$, we have

where

Proof.

By Assumption A6, we have

It follows from Chebyshev's inequality that (A.7) holds. Similarly, (A.8) also holds.

By Assumption A6, we have

Therefore, the (A.9) and (A.10) follow from Markov's Inequality.

Let

for all $\varepsilon > 0$, it follows that ${N}^{-1}\mathit{\boldsymbol{Q}}_{{{\tilde{\mathit{\boldsymbol{\beta}}}}_0}}^{*}({{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) = {r}^{-1}\sum\limits_{i = 1}^r {\mathit{\boldsymbol{\gamma}} _{i, {{\tilde{\mathit{\boldsymbol{\beta}}}}_0}}^{*}}$,

This shows that the Lindeberg-Feller conditions are satisfied in probability. Therefore (A.11) is true. □

Lemma 4. If Assumptions A1–A7 hold, as $r_0 \to \infty$, $r \to \infty$ and $N \to \infty$, for all ${{{\boldsymbol{s}}}_{r_0}} \to \boldsymbol0$ and ${{{\boldsymbol{s}}}_r} \to {\mathbf{0}}$, conditional on $\mathcal{F}_N$, we have

Proof. The Eq (A.12) can be written as

Let

then by Assumption A7, we have

It follows from Markov's inequality that $\mathit{\boldsymbol{\tau}}_1^0 = {o_{P\mid\mathcal{F}_N}}(1)$.

Let

then

By the proof of Lemma 3, it follows that

we have $\mathit{\boldsymbol{\tau}}_2^0 = {o_{P\mid\mathcal{F}_N}}(1)$. Therefore (A.12) holds. Similarly, (A.13) is also true. □

Next, we will prove Theorems 2.5 and 2.6.

Proof of Theorem 2.5.

By Assumption A6, we have

Hence, as $r \to \infty$, ${N}^{-1} \mathit{\boldsymbol{Q}}_{{\tilde{\mathit{\boldsymbol{\beta}}}}_0}^{*}(\mathit{\boldsymbol{\beta}}) - {N}^{-1} \mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\beta}})\mathop \to \limits^{} {{\mathbf{0}}}$ for all ${\boldsymbol \beta} \in \Lambda$ in conditional probability given $\mathcal{F}_N$.

$\check {\mathit{\boldsymbol{\beta}}}$ is the solution of $\mathit{\boldsymbol{Q}}_{{{{\tilde{\boldsymbol \beta}}}_0}}^{two - step}(\mathit{\boldsymbol{\beta}}) = {\mathbf{0}}$, we have

By Lemma 4, we have

and

By Taylor expansion, we have

Similarly,

As ${{{r_0}}}{{r}^{-1}} \to 0, {N}^{-1} \mathit{\boldsymbol{Q}}_{{{\tilde{\mathit{\boldsymbol{\beta}}}}_0}}^{*0}({{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}}) = {O_{P|\mathcal{F}_N}}\left(r_0^{ - \frac{1}{2}}\right)$, then

Combining this with (A.14)–(A.16), we have

which implies that ${\check {\boldsymbol \beta}} - {\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}} = {O_{P|\mathcal{F}_N}} \left(r^{ - \frac{1}{2}} \right)$. □

Proof of Theorem 2.6. By Lemma 3, $\frac{1}{N}{\bf{V}}_{\text {C}}^{ - \frac{1}{2}}\mathit{\boldsymbol{Q}}_{{{\tilde{\mathit{\boldsymbol{\beta}}}}_0}}^{*}({{\hat{\mathit{\boldsymbol{\beta}}}}_{\text{MLE}}})\mathop \to \limits^d N({{\mathbf{0}}}, {\bf I})$, we have

Taking $\pi _i^{\text{mVc}}$ as an example, by Assumpion A4, the above equation can be summarized as

Therefore ${\left\| {{{\bf{V}}_{\text {C}}} - {\bf{V}}_{\text {C}}^{opt}} \right\|_S} = {o_{P\mid\mathcal{F}_N}}\left({{r^{ - 1}}} \right)$, and

which implies that

$\\ $ Therefore

□