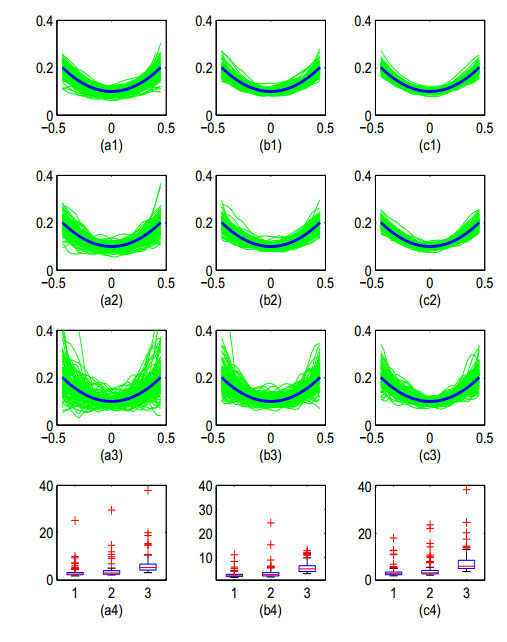
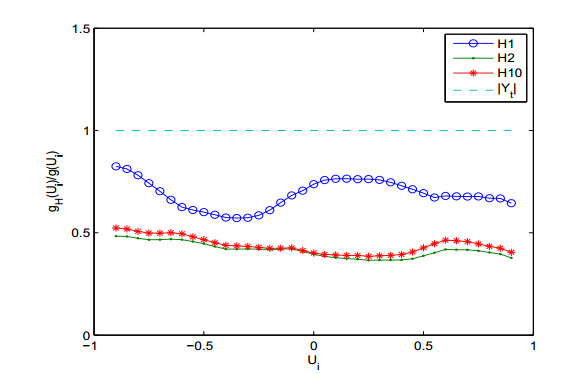
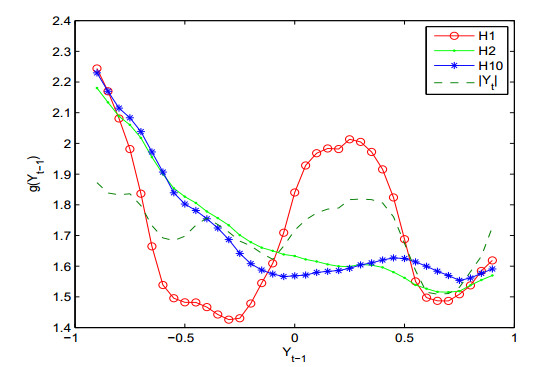
In this paper, the intraday high-frequency data are used to estimate the volatility function of daily nonparametric ARCH(1) model. A nonparametric volatility proxy model is proposed to achieve this objective. Under regular assumptions, the asymptotic distribution of the proposed estimator is established. The impact of different proxies on the estimation precision is also discussed. Simulation and empirical studies show that using the intraday high frequency data can significantly improve the estimation accuracy of the considered model. The idea of this article can be easily extended to other nonparametric or semiparametric ARCH/GARCH models.
1.
Introduction
Statistical distributions play a crucial role in modeling and analyzing real data with complex behavior in many fields, such as biology, engineering, and medicine. Traditional distributions sometimes fail to adequately represent the patterns seen in real world data. Thus, researchers have introduced sophisticated alternatives to existing distributions. These new flexible distributions have high performance in modeling complex patterns, and they are in high demand as users seek to achieve accurate modeling and robust analysis.
In recent years, several approaches have been suggested to achieve highly accurate distributions when fitting different types of data. One popular method for generating more flexible distributions involves raising the cumulative distribution function (cdf) of the base distribution using a shape parameter. This approach was proposed by [1] and is called the exponentiated method. The researchers in [2] extended this approach to more a general class of distributions, calling it the exponentiated generalized (EG) method, by adding another shape parameter to the cdf of the base distribution as follows:
with the probability density function (pdf)
where the shape parameters a,b>1, and ζ is a vector of parameters for the base distribution with the cdf G(x,ζ).
Since its publication, this approach has been adopted by many researchers working to introduce new flexible distributions. Examples include the exponentiated generalized inverted Gompertz [3], exponentiated generalized exponential geometric [4], exponentiated generalized inverse flexible Weibull [5], exponentiated generalized gull alpha power Rayleigh [6], generalized exponentiated Fréchet–Weibull [7], Burr Ⅲ extended exponentiated Weibull [8], exponentiated generalized Marshall Olkin exponential [9], generalized exponentiated unit Gompertz [10], and type-Ⅰ heavy-tailed exponentiated generalised-log-logistic [11] distributions.
Another well-known method for attaining more versatile distributions is the transformed-transformer (T-X) method, in which any continuous distribution can be used as a generator. The researchers in [12] proposed the widely known Weibull-G class of distributions with the following cdf and pdf:
where c,β>0 are the shape and scale parameters of the Weibull distribution, and W(G(x,ζ)) is the weight function. This family with different forms of W(G(x,ζ)) has been used extensively by researchers to generate more adaptable distributions capable for the fitting of lifetime data. Some of these distributions include Weibull–Gompertz Makeham [13], generalized Weibull–Lindley [14], extended Weibull Fréchet [15], Weibull Marshall–Olkin power Lomax [16], four-parameter Weibull extended Weibull [17], odd Weibull inverse Gompertz [18], Weibull-inverse Nadarajah Haghighi [19], and type-2 Gumbel Weibull exponential [20].
In this research, the EG method and Weibull-G approach are combined to introduce a new extension of the Rayleigh distribution with five parameters: the exponentiated generalized Weibull–Rayleigh (EGWR) distribution. The introduction of the EGWR model was motivated by the following objectives:
● Deliver a new extension of the Rayleigh distribution with improved efficiency and flexibility.
● Enhance the elasticity of the Rayleigh distribution by combining two attractive techniques: the EG approach and the Weibull-G class, both of which have shown great flexibility in a wide range of applications.
● Provide an adaptable distribution with great versatility as an alternative to existing distributions in modeling data with different forms as observed from the different shapes of the density function.
● Compared to competing distributions, offer a better representation of the variability of real-world data in the field of medicine.
The remaining sections of this paper are arranged as follows: In Section 2, the EGWR distribution is introduced. In Section 3, important properties of the proposed distribution are presented. In Section 4, we provide the estimators of the distribution parameters using four different methods. To test the efficiency of these methods, related simulation studies were performed, and their results are described in Section 5. In Section 6, different medical datasets are analyzed to compare various estimation methods and illustrate the flexibility of the proposed distribution. Finally, in Section 7, we conclude the paper.
2.
The exponentiated generalized Weibull Rayleigh distribution
If X is a random variable from the Rayleigh distribution with scale parameter σ>0, then the cdf and pdf are given by the following:
By considering weight function W(G(x,ζ))=−log(1−(G(x,ζ))), using (2.1) in (1.3), the Weibull Rayleigh distribution is obtained with the following cdf:
Substituting (2.3) in (1.1), the EGWR distribution is defined by the following cdf:
The corresponding pdf is as follows:
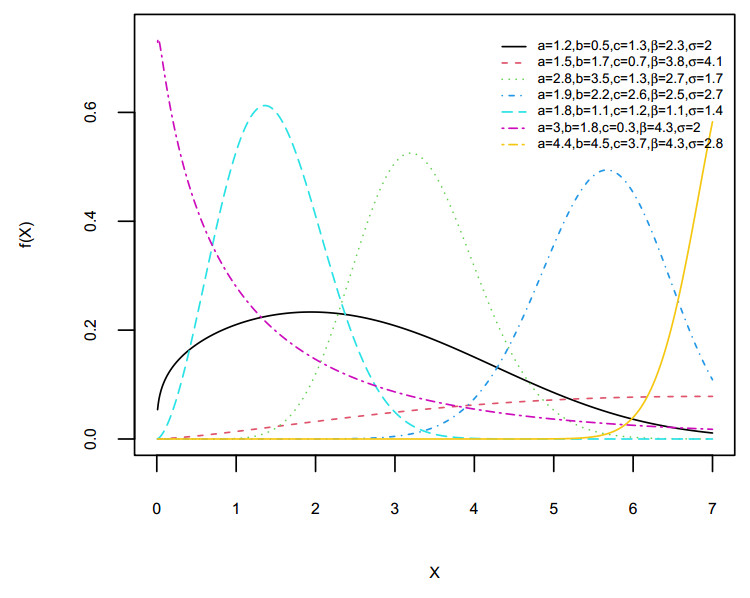
Figures 1 and 2 display different shapes for the pdf and the hazard function (hf) of the EGWR distribution achieved using various parameter values. The pdf takes various forms, such as symmetric, asymmetric, increasing, J-shaped, and reverse J-shaped. In addition, the hf can model data with bathtub and upside-down bathtub shapes. This demonstrates the distribution's capacity to accommodate diverse forms of data, making it a valuable tool for modeling complex phenomena.
2.1. Expansion of the density function
The binomial expansion theorem is defined as follows:
where |x|<1 and n>0. Therefore,
Thus, the pdf can be re-written as
from the following power series:
Hence, the pdf of the EGWR distribution takes the following form:
3.
Statistical properties
Some important statistical properties of the EGWR distribution—moments, incomplete moments, moment generating function, order statistics, and Rényi entropy—are presented in this section.
3.1. Quantile and median
For a random variable X from the EGWR distribution, the quantile function can be obtained by inverting (2.4) and presenting the expression in an explicit form as follows:
Therefore, the median is given by
3.2. Moments
The rth moment [21] of the EGWR distribution is given by
Using (2.6) for (1−e−a(x22σ2β)c)b−1, we have
The mean and variance of the EGWR distribution can be found from (3.3) as follows:
Thus, the coefficient of variation (COV), the dispersion index (DI), skewness (SK), and kurtosis (K) can be obtained as follows:
These measures can be calculated using any reputable statistical software, such as R.
Table 1 displays the measures' values for the following cases of parameters:
As shown in Table 1, the EGWR distribution can be negatively (left) skewed or positively (right) skewed; this illustrates the flexibility of the distribution in fitting various types of asymmetrical data. Moreover, the kurtosis values indicate that the distribution can be leptokurtic or platykurtic. Hence, the distribution is capable for modeling data with sharp peaks and lighter tails or flat peaks with heavier tails. Additionally, the values of the dispersion index shows the flexibility in modeling data with various spreads.
3.3. Incomplete moments
The sth incomplete moment [22] of the EGWR distribution is defined as
where from binomial expansion (2.6), we have
where uz=a(i+1)(z22σ2β)c.
3.4. Moment generating function
The moment generating function [23] for the EGWR distribution is obtained as follows:
By applying the binomial expansion (2.6), we obtain
where by using the power series expansion for etx, we have
3.5. Rényi entropy
The Rényi entropy [24] for the EGW-R distribution is defined as
where
Using the binomial expansion (2.6),
Thus,
and therefore,
The Rényi entropy is then given by the following:
3.6. Distribution of order statistics
Let x1,x2,…,xn be a sample selected from the EGW-R distribution with order statistics x1:n,x2:n,…,xn:n. The ith order statistics then have the following distribution[25]:
By using the binomial expansion (2.6),
where
By the applying binomial expansion (2.6),
Thus,
By applying the power series expansion for e−a(j+1)(x22σ2β)c, we obtain
Therefore, the distribution takes the following form:
4.
Methods of estimation
4.1. Maximum likelihood method
The maximum likelihood (ML) method is one of the most widely applied methods of estimation in the literature [26,27]. In this method, the values of the parameters are obtained by maximizing the log-likelihood function. Thus, if x1,x2, …, xn follows the EGWR distribution with the vector of parameters θ=(a,b,c,β,σ), then the log-likelihood function (ℓ) is defined by
The aforementioned log-likelihood function is too complicated and difficult to solve analytically. Thus, the derivative of (4.1), with respect to each parameter, is calculated as follows:
and
Therefore, the MLEs of the parameter vector θ can be achieved by equating the Eqs (4.2)–(4.6) to zero and solving them in an iterative manner using any numerical method, such as the Newton–Raphson method. Alternatively, the optimization function optim in the statistical software R can be employed to maximize (4.1) directly and obtain the MLEs.
4.2. Ordinary least squares method
The ordinary least squares (LS) method [28] estimates the distribution parameters by minimizing the square difference between the theoretical cdf and the empirical cdf. Let x(1),x(2), …, x(n) follow the EGWR distribution. The LS method minimizes the following sum of squares:
Differentiating (4.7) with respect to the vector of parameters θ results in the following equations:
Therefore, minimizing Eq (4.7) or equivalently solving Eqs (4.8)–(4.12) analytically or numerically using R provides the estimates of the vector of parameters θ=(a,b,c,β,σ).
4.3. Maximum product of spacing method
The maximum product of spacing (MPS) method was produced by [29] as an improvement of the ML method. Let x1,x2, …, xn be a sample from an EGWR distribution with a vector of parameters θ=(a,b,c,β,σ) and order statistics x(1),x(2),…,x(n). The idea of the MPS is to maximize the following equation:
where Di(θ)=F[x(i)∣θ]−F[x(i−1)∣θ],i=1,2,…,n+1 are the uniform spacings between the consecutive ordered values, F[x(0)∣θ]=0, and F[x(n+1)∣θ]=1. The estimates of the vector of parameters θ can be obtained by maximizing (4.13) or equivalently solving the system of Eqs (4.15)–(4.19) using any optimization function in R.
where Ai=[(1−e−a(x2(i)2βσ2)c)b−(1−e−a(x2(i−1)2βσ2)c)b].
4.4. Cramér–von Mises method
The Cramér–von Mises method, also called the minimum distance estimator, was proposed by the researchers in [30] to estimate the values of the parameters by minimizing the following objective function:
Minimizing (4.20) or solving the following system of nonlinear equations (4.21)–(4.25) numerically yields the estimate of the vector of parameters θ:
5.
Simulation study
To assess and evaluate the performance of the four methods of estimation in determining the parameters of the EGWR distribution, three cases of simulation studies are presented. A number of iterations equal to nsim=10,000 were applied with different sample sizes (n=50,100,300,and500) for the following three cases of true values of the vector of parameters θtr:
The root mean square error (RMSE) measure was used to assess the efficiency of estimation methods selected for each estimator ˆθ. The RMSE can be obtained as follows:
The estimates obtained by the four methods of estimation together with the RMSE are shown in Tables 2–4 and Figures 3–5.
As can be seen from the above tables and figures, all of the examined estimation methods achieved consistency. When the sample size n increased, the RMSE decreased, and the estimate approached its true value. Moreover, For sample size n=50, except for parameter c, the LS method provided the closest estimate to the true value for all parameters. Thus, it was considered the most precise method of estimation, followed by the CVM method, while MPS was considered the worst out of all examined methods. Furthermore, when the sample size increased and reached n=500, the MPS and ML methods outperformed the others. These methods produced the lowest RMSE values, with the MPS method having a slight advantage in most cases.
6.
Real application
In this section, three medical datasets were used to provide insights into which method had the best performance in estimating the parameters of the EGWR distribution.
Dataset 1
Provided by a Saudi Ministry of Health hospital, this dataset was reported in [31] and represents the lifetimes (in years) of 40 individuals who were diagnosed with leukemia. The data are listed below: 0.315, 0.496, 0.616, 1.145, 1.208, 1.263, 1.414, 2.025, 2.036, 2.162, 2.211, 2.370, 2.532, 2.693, 2.805, 2.910, 2.912, 3.192, 3.263, 3.348, 3.348, 3.427, 3.499, 3.534, 3.767, 3.751, 3.858, 3.986, 4.049, 4.244, 4.323, 4.381, 4.392, 4.397, 4.647, 4.753, 4.929, 4.973, 5.074, 5.381.
Dataset 2
The second dataset was reported by [32] and lists the periods of symptom relief for 36 bladder cancer patients. The durations (in days) were as follows: 0.08, 0.2, 0.4, 0.5, 0.51, 0.81, 0.87, 0.9, 1.05, 1.19, 1.26, 1.35, 1.4, 1.46, 1.76, 2.02, 2.02, 2.07, 2.09, 2.23, 2.26, 2.46, 2.54, 2.62, 2.64, 2.69, 2.69, 2.75, 2.83, 2.87, 3.02, 3.02, 3.25, 3.31, 3.36, 3.36.
Dataset 3
The last dataset was reported in [33] and consists of the relief times (in minutes) of 20 patients who received a pain reliever as follows: 1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3, 1.7, 2.3, 1.6, 2.
6.1. Comparison between methods of estimation
The accuracy of the ML, LS, MPS, and CVM methods in estimating the distribution parameters and fitting the data were compared. Tables 5–7 offer the estimate and standard error for each parameter along with the Kolmogorov–Smirnov (KS) test statistic and P-value for all the methods of estimation.
As displayed in Tables 5–7, from a precision perspective, the ML method provided the smallest values of standard error and would be the most suitable method of estimation for the leukemia dataset. The CVM method would be considered the worst of those examined as it had the highest standard error values. A similar pattern can be seen with the pain relief dataset, except for parameter β. However, for the bladder cancer dataset, MPS slightly outperformed ML although both methods had the lowest standard error, while the worst method for estimation of those examined was the LS method. From a goodness-of-fit perspective, the CVM method produced good fit for the leukemia and the bladder cancer datasets as it provided higher P-values and lower KS statistics among all the examined methods, while LS offered a more suitable fit for the pain relief dataset.
6.2. Comparison between the EGWR and other distributions
In this section, the ML method was used to assess the performance of the EGWR distribution in fitting the aforementioned datasets. A comparison was made between the EGWR distribution and some competitors: the exponentiated Weibull Rayleigh (EWR), based on the idea of the researchers in [34]; the Marshall–Olkin Weibull Rayleigh (MOWR), a sub-model from the general class proposed by the researchers in [35]; the Weibull Rayleigh (WR) by [34]; the Kumaraswamy Rayleigh (KumR) presented by the researchers in [36]; the Marshall–Olkin alpha power Rayleigh (MOAPR) by the researchers in [37]; and the generalized Rayleigh (GR) explored by the researchers in [38]. To pick the most suitable of these models, the Akaike information criterion (AIC), Bayesian information criterion (BIC), Hannan–Quinn information criterion (HQIC), and KS statistic with P-value were computed. Tables 8–10 display the values of the MLEs and goodness-of-fit measures for the EGWR and competing distributions, while the theoretical and empirical cdf and pdf are displayed in Figures 6–8.
The above tables and figures show the potential flexibility of the EGWR distribution in modeling medical data compared to other competing distributions.
7.
Conclusions
We extended the Rayleigh distribution to obtain a more flexible distribution capable of modeling complex patterns in medical data. The hazard function of the proposed distribution can take on different patterns, which shows great flexibility as required by many lifetime datasets. The statistical characteristics of the new distribution, such as quantile, median, moment-generating function, Rényi entropy, and order statistics, were studied in this research. The distribution's parameters were estimated using ML, LS, MPS, and CVM, and the efficiency of the estimators obtained by the different methods was assessed in the reported Monte Carlo simulation studies. The results revealed that for the three simulated cases, the LS method had better estimation for smaller samples, while the ML and MPS methods performed better for larger samples. The efficiency of the estimation methods was also evaluated using three medical datasets. The results demonstrated the ability of ML and MPS in estimating the model parameters, as they provided lower standard error values compared to other examined methods in most cases. Finally, the EGWR distribution was compared with a selection of competitive distributions to investigate its ability in modeling the provided medical data, and the results clearly demonstrated that the EGWR outperformed other distributions in analyzing the data. Thus, it can provide insights for scientists to better understand and address complex patterns in healthcare data. As future work, more advanced methods of estimation, such as the Bayesian method, could be employed to enhance the estimation of the parameters. Moreover, the development of a discretised version of the EGWR distribution would offer crucial tools for describing, evaluating, and modeling different phenomena with countable and distinct outcomes, which would lead to precise decision-making and offer better understanding of data across a variety of fields.
Use of Generative-AI tools declaration
The author declares she has not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
For the editor-in-chief and anonymous reviewers, the author extends great gratitude for their insightful comments, which refined the quality of this work.
Conflict of interest
The author declares that she has no conflicts of interest.









 DownLoad:
DownLoad: