The investigation of univalent functions is one of the fundamental ideas of Geometric function theory (GFT). However, the class of these functions cannot be investigated as a whole for some particular kind of problems. As a result, the study of its subclasses has been receiving numerous attentions. In this direction, subfamilies of the class of univalent functions that map the open unit disc onto the domain bounded by limaçon of Pascal were recently introduced in the literature. Due to the several applications of this domain in Mathematics, Statistics (hypothesis testing problem) and Engineering (rotary fluid processing machines such as pumps, compressors, motors and engines.), continuous investigation of these classes are of interest in this article. To this end, the family of functions for which ςf′(ς)f(ς) and (ςf′(ς))′f′(ς) map open unit disc onto region bounded by limaçon are studied. Coefficients bounds, Fekete Szeg ¨o inequalities and the bounds of the third Hankel determinants are derived. Furthermore, the sharp radius for which the classes are linked to each other and to the notable subclasses of univalent functions are found. Finally, the idea of subordination is utilized to obtain some results for functions belonging to these classes.
1.
Introduction
One of the most fascinating areas of Complex analysis is the study of geometric characterization of univalent functions in the open unit disc U. Because of the challenging problem in studying the class S(1−1) of univalent functions in U as a whole, several subclasses of it emerged. The most studied of these are the classes CCV, SST, CCV(β) and SST(β)(0≤β<1) of convex functions, starlike functions and, convex and starlike functions of order β, respectively. Since the image domains of U plays a significant role in their geometric characterization, various subclasses of S(1−1) have been receiving attention in different directions and perspectives (see [4,6,20,23,28,32,33,36,37,38]). For this reason, Ma and Minda [17] gave a unified treatment of both SST and CCV. They considered the class Ψ of analytic univalent functions ψ(ς) with Reψ(ς)>0 and for which ψ(U) is symmetric with respect to the real axis and starlike with respect to ψ(0) such that ψ′(0)>0. They initiated the following classes of functions that generalized and unified many renowned subclasses of S(1−1):
and
where A is the class of analytic functions f(ς) of the form
If
then CCV(ψ)=UCV is the Goodman class of uniformly convex functions [8,30], which was later modified and examined by Kanas and Wisniowska [13,14]. Similarly, SThpl(s)=S∗(1(1−ς)s), CVhpl(s)=C(1(1−ς)s)(0<s≤1), are made-known by Kanas and Ebadian [15,16], respectively. These consist of functions f∈A such that ςf′(ς)/f(ς) and (ςf′(ς))′/f′(ς) lie in the domain bounded by the right branch of a hyperbola
More special families of Ma and Minda classes can be found in [3,9,10,24,25,26,31,34,39].
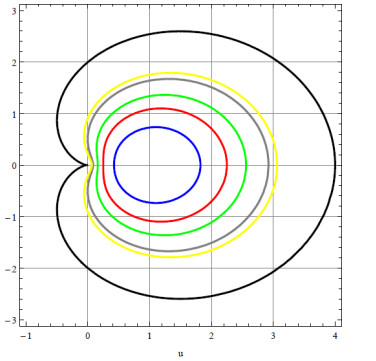
Recently, Kanas et al [18] introduced novel subclasses STL(s) and CVL(s) of SST and CCV, respectively. Geometrically, they consist of functions f(ς)∈A such that ςf′(ς)/f(ς) and (ςf′(ς))′/f′(ς) lie in the region bounded by the limaçon defined as
as shown in Figure 1 for different values of s. s=0.35,0.5,0.6,0.71,0.75 and 1 corresponds to blue, red, green, gray, yellow and black. Some novel properties of these classes were derived in [18].
Motivated by this present work and other aforementioned articles, the goal in this paper is to continue with the investigation of some interesting properties of the classes STL(s) and CVL(s). To this end, the sharp bounds of the Hankel determinant, subordination conditions as well as some radius results for these novel classes are investigated.
2.
Materials and method
To put our investigations in a clear perspective, some preliminaries and definitions are presented as follows:
Denoted by W is the class of analytic functions
such that w(0)=0 and |w(ς)|<1. These functions are known as Schwarz functions. If f(ς) and g(ς) are analytic functions in U, then f(ς) is subordinate to g(ς) (written as f(ς)≺g(ς)) if there exists a Schwarz function w(ς)∈W such that f(ς)=g(w(ς)),ς∈U.
Janowski [12] introduced the class P(A⅁,B⅁),−1≤B⅁<A⅁≤1 of functions p(ς) satisfying the subordination condition
or equivalently, satisfying the inequality
As a special cases, P(1,−1)≡P and P(1−2β,−1)≡P(β)(0≤β<1) are the classes of functions of positive real part and that whose real part is greater than β, respectively (see [7]).
Definition 2.1. Noonan and Thomas [22] defined for q≥1,n≥1, the qth Hankel determinant of f(ς)∈S1−1 of the form (1.1) as follows:
This determinant has been studied by many researchers. In particular Babalola [2] obtained the sharp bounds of H3(1) for the classes SST and CCV. By this definition, H3(1) is given as:
and the by triangle inequality,
Clearly, one can see that H2(1)=|δ3−δ22| is a particular instance of the well-known Fekete Szeg¨o functional |δ3−μδ22|, where μ is a real number.
Definition 2.2. [18] Let p(ς)=1+∞∑n=1cnςn. Then p∈P(Ls) if and only if
or equivalently, if p(ς) satisfies the inequality
Demonstrated in [18], was the inclusion relation
It is worthy of note that the function Ls(ς)=(1+sς)2 is the analytic characterization of Ls(U) given by (1.2). Also, Ls(ς) is starlike and convex univalent in U for 0<s≤12. Furthermore, Ls(ς)∈P(β), where β=(1−s)2,0<s≤12.
Definition 2.3. Let f∈A. Then f∈STL(s) if and only if
Also, f∈CVL(s) if and only if
Moreover, the integral representation of functions f∈STL(s) is given as
while that of g∈CVL(s) is given as
Furthermore, the extremal functions for each of the classes are given by
and for Ks,n(ς)∈CVL(s),
3.
A set of lemmas
Lemma 3.1. [1] If w∈W is of the form (2.1), then for a real number σ,
When σ<−1 or σ>1, equality holds if and only if w(ς)=ς or one of its rotations. If −1<σ<1, then equality holds if and only if w(ς)=ς2 or one of its rotations. Equality holds for σ=−1 if and only if w(ς)=ς(x+ς)1+xς(0≤x≤1) or one of its rotations while for σ=1, equality holds if and only if w(ς)=−ς(x+ς)1+xς(0≤x≤1) or one of its rotations.
Also, the sharp upper bound above can be improved as follows when −1≤σ≤1 :
and
Lemma 3.2. [16] If w∈W is of the form (2.1), then for some complex numbers ξ and η such that |ξ|≤1 and |η|≤1,
and
Lemma 3.3. [19,Theorem 3.4h,p. 132] Let q(ς) be univalent in U and let θ and φ be analytic in a domain D containing q(U) with φ(ω)≠0, when ω∈q(U). Set Q(ς)=ςq′(ς)⋅φ(q(ς)),h(ς)=θ(q(ς))+Q(ς), and suppose that either
(i) h(ς) is convex, or Q(ς) is starlike,
(ii)
If p(ς) is analytic in U with p(0)=q(0),p(U)⊂D and
then p(ς)≺q(ς), and q(ς) is the best dominant in the sense that p≺t⇒q≺t for all t.
Lemma 3.4. [29] Let h(ς)=1+∞∑n=1cnςn,G(ς)=1+∞∑n=1dnςn and h(ς)≺G(ς). If G(ς) is univalent in U and G(U) is convex, then |cn|≤|d1|, for all n≥1.
Lemma 3.5. [11] Let w∈W. If |w(ς)| attains its maximum value on the circle |ς|=r at a point ς0∈U, then we have ς0w′(ς0)=kw(ς0), where k≥1.
Throughout this work f(ς) is taken to be of the form (1.1) while w(ς) is of the form (2.1). In the next sections, the main results are presented.
4.
Coefficient results
In this section, we assume 0<s≤12. First, we establish a few auxiliary results whose applications will be needed hereafter.
Lemma 4.1. Let f∈STL(s). Then
Proof. From the definition of f∈STL(s), we have
where
Comparing the coefficients of ςn in (4.2), it follows that
It is obvious from Lemma 3.4 and the fact that Ls(ς) is convex for 0<s≤12 that
Using this result in (4.4), we obtain
We need to show (4.1) by Mathematical induction. For this reason, assume (4.1) is true and proceed to prove
From (4.6),
and finally,
Therefore,
Hence, by Mathematical induction, we have the desired result.
In view of Theorem 4.1 and the definition of functions in CVL(s), we are led to the following result.
Lemma 4.2. Let f∈CVL(s). Then
Lemma 4.3. Let f∈STL(s). Then
The bound 19s412 is sharp for the function
Proof. For f∈STL(s),
where w∈W. Comparing coefficients of ς,ς2 and ς3 in (4.8), we arrive at
By Lemma 3.1, we obtain
Let x=w1,ξ=y with 0≤x≤1 and |y|≤1. Then the triangle inequality gives
where
and
This means that F(x,|y|) is increasing on the interval [0,1]. So,
where
which implies that F(x) is an increasing function of x on [0,1]. Consequently,
Lemma 4.4. Let f∈CVL(s). Then
The bound s29 is sharp for the function
Proof. From the definition of f∈CVL(s) and (4.9), it is easy to see that
The rest of the proof follows as in Theorem 4.3.
Lemma 4.5. Let f∈STL(s). Then
The bound 2s3 is best possible for the function
Proof. From (4.9), a computation gives
Employing Lemma 3.2, we write the expression for w3, and applying the triangle inequality together with Lemma 3.1, we obtain
where we have taken w1=x,ξ=y with 0≤x≤1 and |y|≤1. Let H(x,|y|) represents the right side of (4.12). Then
Thus,
where
It is clear that H(x) attains its maximum value at x=7s2. Thus, H(x)≤H(7s2)=2s3. Consequently,
Lemma 4.6. Let f∈CVL(s). Then
This bound cannot be improved since the function
attains the equality.
Proof. Using the definition of f∈CVL(s) and (4.9), we find
Let w1=x(0≤x<1) and ξ=y with |y|≤1. Then applying Lemma 3.2 and following the procedure of proof as in Theorem 4.5, we arrive at the desired result.
5.
Fekete Szeg¨o inequality for the classes STL(s) and CVL(s)
Lemma 5.1. Let f∈STL(s). Then for a real number μ,
It is asserted also that
and
These inequalities are sharp for the functions
where |λ|=1 and
Proof. From (4.9), we have
Then using Lemma 3.1 with σ=s(8μ−5)2, we obtain the required result. For μ=1 in Theorem 5.1, we deduce the following sharp result.
Corollary 5.1. Let f∈STL(s). Then
Lemma 5.2. Let f∈CVL(s). Then for a real number μ,
It is asserted also that
and
These inequalities are sharp for the functions
where |λ|=1 and
Proof. Using the definition of CVL(s) and (4.9), we get
Then using Lemma 3.1 with σ=s(6μ−5)2, we obtain the desired result. For μ=1 in Theorem 5.2, we deduce the following sharp result.
Corollary 5.2. Let f∈CVL(s). Then
Theorem 5.3. Let f∈STL(s). Then
Proof. The proof is immediate from (2.4), Lemma 4.1, Lemma 4.3, Lemma 4.5 and Corollary 5.1.
Theorem 5.4. Let f∈CVL(s). Then
Proof. The proof is straightforward from (2.4), Lemma 4.2, Lemma 4.4, Lemma 4.6 and Corollary 5.2.
6.
STL(s) and CVL(s) radii
Theorem 6.1. The CVL(s)-radius for the class SST(β) (where β=(1−s)2) is given by
This radius is sharp for the functions given by
Proof. Let f∈SST(β). Then
This means that there exists w∈W such that
Let
Then by Schwarz lemma,
It follows from logarithmic differentiation of (6.3) that
It is known from [27] that for p∈P(β),
Using this result together with (6.4), we write
We need to show that
However, it holds if
Let T(r)=3(1−2β)r2+2(2+β)r−1. Then T(0)=−1<0 and T(1)=6−4β>0 such that T(0)T(1)<0. Thus, there exists R1∈[0,1] such that
Therefore, 3(1−2β)r2+2(2+β)r−1≤0 for all r<R1 and R1 is the smallest roots of (6.5) given by (6.1).
For sharpness, we consider the functions f0(ς) defined by (6.2). At the point z=R1, we have
Theorem 6.2. Let f∈STL(s). Then f∈CCV for all z in the disc |ς|<R2, where R2 is the positive roots of the equation
Proof. For f∈STL(s),
where w∈W. Therefore
where we have used the extension of Schwarz lemma (see [21]). Thus,
if (1−sr)3(1−r2)−2r>0. Let T(r)=(1−sr)3(1−r2)−2r. Then T(0)=1>0 and T(1)=−2<0 with T(0)T(1)<0. Therefore, there exists R2∈[0,1] such that (1−sR2)3(1−R22)−2R2=0. Hence, (1−sr)3(1−r2)−2r>0 holds for all r<R2, where R2 is the smallest positive roots of (6.6).
Theorem 6.3. Let p∈P. Then p∈P(Ls) for all z in the disc
Proof. Let p∈P. Then
We want to prove that
Now,
if (6.7) is satisfied. To show that the radius cannot be improved, we consider the function
Then for ς=2s−s22+2s−s2,
which shows that equality is attained for (6.7).
Corollary 6.1. The STL(s)-radius and CVL(s)-radius for the classes of starlike and convex functions are given by (6.7).
7.
Some properties of the function Ls(ς)
Theorem 7.1. If p(ς) is analytic in U with p(0)=1 and satisfies the condition
or
then p(ς)≺(1+sς)2 for −1<s<0.
Proof. Let p(ς) be defined by
Clearly, w(ς) is analytic in U with w(0)=0. To prove our result, it is required to show that |w(ς)|<1 for all ς∈U. From (7.3), a simple calculation gives
Suppose there exists a point ς0∈U such that
Then by Lemma 3.5, w(ς0)=eiθ and ς0w′(ς0)=kw(ς0). Thus,
This contradicts (7.1). Therefore, there exists no ς0∈U such that |w(ς0)|=1. Thus |w(ς)|<1 in U, so that p(ς)≺(1+sς)2 for −1<s<0.
Similarly,
which contradicts the assumption (7.2). Hence, the proof is completed.
Following the discussion demonstrated by Sharma et al in [35] for Theorem 3, we present the following results.
Theorem 7.2. Let −1<B⅁<A⅁≤1, 0<s≤1√2 and p(ς)=1+A⅁ς1+B⅁ς. Then p∈P(Ls) if and only if
or, equivalently, if and only if
Proof. The proof follows the techniques presented in [35,Theorem 3] For B⅁=0,A⅁=0 and B⅁=−A⅁, we give the following consequences of Theorem 7.2.
Corollary 7.1.
(i) p(ς)=1+A⅁ς∈P(Ls)⟺0<A⅁≤2s−s2.
(ii) p(ς)=1/(1+B⅁ς)∈P(Ls)⟺(s2−2s)/(1+2s−s2)≤B⅁<0.
(iii) p(ς)=(1+A⅁ς)/(1−A⅁ς)∈P(Ls)⟺0<A⅁≤(2s−s2)/(2+2s−s2).
Corollary 7.2. Let −1<B⅁<A⅁≤1 and consider
Then f∈STL(s) and f∈CVL(s), respectively if and only if conditions (7.4) or (7.5) is satisfied
Applying Corollary 7.1 along with the integral representation for the classes STL(s) and CVL(s), respectively, we present the following examples.
Example 7.3.
(i) For 0<A⅁≤2s−s2,
(ii) For s2−2s1+2s−s2≤B⅁<0,
(iii) For 0<A⅁≤2s−s22+2s−s2,
8.
Sufficient conditions and related results
Theorem 8.1. Let −1≤B⅁<A⅁≤1,0<s≤12 and p(ς) be analytic in U with p(0)=1 such that
If
then p∈P(Ls).
Proof. Let q(ς)=(1+sς)2,0<s≤12. Then q(ς) is convex univalent in U. Consider the functions ϕ(ω)=ρ and θ(ω)=1. These functions are both analytic in a domain containing q(U) with ϕ(ω)≠0. A computation shows that
Further,
and
Using Lemma 3.3, the subordination condition
implies p(ς)≺q(ς). To complete the proof, it suffices to prove that the circular disc 2.2 is contained in the region bounded by the curve h(eiθ)(θ∈[0,2π)). To this end, we must show that
Now,
Thus,
if (8.2) is satisfied.
Theorem 8.2. Let 0<s≤12 and p(ς) be analytic in U with p(0)=1 such that
If
then p∈P(Ls).
Proof. Following the same arguments as in the proof of Theorem 8.1, we arrive at where to show that
To achieve this, it is enough to show that the domain bounded by the limaçon is inside the region bounded by the curve h(eiθ)(θ∈[0,2π)). As a result, we need to find ρ for which
Now,
if
Theorem 8.3. Let −1≤B⅁<A⅁≤1,0<s≤1√2 and p(ς) be analytic in U with p(0)=1 such that
If
then
Proof. Let q(ς)=1+A⅁ς1+B⅁ς. We have that q(ς) is convex univalent in U. Therefore, following the method of proof in Theorem 8.1, we arrive at where to show that
For this, we need to establish that the region bounded by the limaçon lies inside the domain bounded by the curve h(eiθ)(θ∈[0,2π). A simple observation of (2.5) suggests it suffices to show
Now,
But
provided (8.6) holds. This completes the proof.
Theorem 8.4. Let 0<s≤1√2 and p(ς) be analytic in U with p(0)=1 such that
If
then
Proof. Let q(ς)=(1+sς)2. Then q(ς) is convex univalent in U. The function ϕ(ω)=ρ/ω and θ(ω)=1 are analytic in the domain containing q(U). Set
and
Then
From Lemma 3.3, the differential subordination
implies p(ς)≺q(ς). To finalize the proof, we need to prove
which is equivalent to showing
It is easy to see that the transformation h(ς)=1+ρςq′(ς)q(ς) maps U onto the disc D(a,r), where
Therefore (8.9) holds if and only if
which implies
We choose to omit the proof of the next theorem since it follows the same argument as in Theorem 8.3.
Theorem 8.5. Let −1≤B⅁<A⅁≤1, 0<s≤1√2 and p(ς) be analytic in U with p(0)=1 such that
If
then
Remark 8.1.
(ⅰ) If we put p(ς)=ςf′(ς)/f(ς) and p(ς)=(ςf′(ς))′/f′(ς) in Theorem 8.1-8.5, we obtain the conditions on ρ for which the respective subordination conditions (8.1), (8.3) and (8.7) imply f∈STL(s) and f∈CVL(s).
(ⅱ) We note that our condition 0<s≤12 cannot be relaxed in Theorem 8.1 and Theorem 8.2. Otherwise, starlikeness of Q will not be achieved. As such, the proof of the theorems will be extremely difficult to obtain via Lemma 3.3.
9.
Conclusion
The Ma and Minda classes of functions are the comprehensive generalization of the classes SST and CCV. These classes are vital in (GFT) because of their importance in science and technology. To this end, continuous studies of their subfamily, which are related to Limaçon domain were investigated. Coefficients bounds, Fekete Szeg¨o inequality as well as the upper bounds of the third Hankel determinants for these subclasses were derived. Finally, the techniques of differential subordination were also used to obtain some restrictions for which analytic functions belonged to these families. In addition, to have more new theorems under present examinations, new generalization and applications can be explored with some positive and novel outcomes in various fields of science, especially, in applied mathematics. These new surveys will be presented in future research work being processed by authors of the present paper.
Acknowledgments
The authors would like to thank the Rector of COMSATS University Islamabad, Islamabad, Pakistan, for providing excellent research and academic environment. The fourth author is supported by UKM grant: GUP-2019-032.
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad:



