Investigation of novel turbulator with and without twisted configuration under turbulent forced convection of a CuO/water nanofluid flow inside a parabolic trough solar collector

1.   Introduction

Infectious diseases (such as influenza, malaria, cholera, tuberculosis, hepatitis, AIDS, etc) have always seriously threatened humans' life and health. With in-depth understanding of infectious diseases, scientists have been continuing to explore effective methods to prevent and control the outbreaks of various infectious diseases. It is well known that mathematical models have played very important roles in analysis of control strategies for disease transmission ^{[1,2,3,4,5,6,7,8,9,10]}.

When studying the long-term evolutionary behavior of an ecological system, as pointed in ^[11], the equilibrium of biological system may not be the desirable one, and smaller value is required. This can be achieved by introducing suitable feedback control variable. The feedback control mechanism might be implemented through harvesting or culling procedures or certain biological control schemes ^[12]. In addition, in a control system, the time delay factor generally exists in the signal transmission process. Thus, feedback control with coupled time delay may have better biological significance ^[12] and has been extensively introduced into some important population ecological systems (see, for example, ^{[13,14,15,16]} and the references cited therein).

In recent years, feedback control has also been successfully applied to some infectious disease dynamical systems. For example, in ^[17], the authors considered the following SI epidemic model with two feedback control variables:

In model (1.1), the state variables $S(t)$ and $I(t)$ represent the numbers of susceptibles and infectives at time $t$, respectively; $u_{1}(t)$ and $u_{2}(t)$ are feedback control variables. The number of susceptibles grows according to the regulation of a logistic curve with the capacity $r/a$ ($r > 0$, $a > 0$) and a constant recruitment rate $r$; the constant $b > 0$ is the transmission rate when susceptibles contact with infectives; the constants $\mu > 0$ and $f > 0$ are the death rates of the infectives with respect to single and mutiple of infectives, respectively; the constants $c_1 > 0$, $c_2 > 0$, $d_1 > 0$, $d_2 > 0$, $e_1 > 0$ and $e_2 > 0$ are the feedback control parameters. By constructing suitable Lyapunov functions, the authors established threshold dynamics of model (1.1) completely determined by the threshold parameter $\gamma_{0} = (br-a\mu)e_1/(c_1d_1\mu)$. The results in ^[17] indicate that, by appropriately choosing feedback control parameters, it can make the disease infection endemic or extinct. In ^[18], the author considered a two-group SI epidemic model with feedback control only in the susceptible individuals, and showed that the disease outbreaks can be controlled by adjusting feedback control parameters. In addition, in ^[19], the authors further extend model (1.1) to the case of patchy environment.

Since the authors of ^[20] have introduced a nonlinear incidence rate $g(I)S$ into classic Kermack-McKendrick SIR model, nonlinear incidence rate has been further introduced into more general SIR/SIRS epidemic models with time delays or infection age etc (see, for example, ^{[21,22,23,24,25,26,27]} and the references cited therein). Usually, the function $g(I)$ takes the following two types: (ⅰ) saturated, such as $g(I) = bI/(1+kI)$, or $g(I) = bI^2/(1+kI^2)$; (ⅱ) unimodal, such as $g(I) = bI/(1+kI^2)$, here $k > 0$ is constant. In biology, $bI$ or $bI^2$ measures the infection force of the disease, $1/(1+kI)$ or $1/(1+kI^2)$ measures the inhibition effect from the behavioral change of the susceptible individuals when their number increases or from the crowding effect of the infective individuals ^[21,22].

Recently, in ^[28], the authors further extended model (1.1) to the following more general case with the saturated incidence rate $bSI/(1+kI)$ and feedback controls:

and some sufficient conditions for global asymptotic stability of the disease-free equilibrium and the endemic equilibrium of model (1.2) are established by the method of Lyapunov functions. In addition, the authors also considered permanence and existence of almost periodic solutions for a class of non-autonomous system based on model (1.2).

Motivated by the above works and model (1.2), we further consider the following SI epidemic model with saturated incidence rate, two feedback control variables and four time delays:

The biological significance of all the parameters of model (1.3) are the same as in model (1.2) except time delays $\tau_{i}\geq0$ ($i = 1, 2, 3, 4$). In model (1.3), $u_1(t)$ and $u_2(t)$ are introduced as control variables. Usually, there always exist time delays in the transmission of information. Therefore, $\tau_1$ and $\tau_2$ can be understood as the result of transmission of information, and while $\tau_3$ and $\tau_4$ represent usual feedback control delays.

The purpose in this paper focuses on global dynamics of the equilibria of model (1.3) by constructing appropriate Lyapunov functionals, and our results further extend and improve works in ^[17,28].

The rest of the paper is organized as follows. In Section 2, we provide some preliminary results, including the well-posedness and dissipativeness of the solutions of model (1.3), the expression of the basic reproduction number and the classification of the equilibria of model (1.3). In Sections 3 and 4, we establish some sufficient conditions for global asymptotic stability and global attractivity of the disease-free equilibrium and the endemic equilibrium of model (1.3), which are the main results of this paper. In the last section, the conclusions and some numerical simulations are given.

2.   Preliminary results

2.1.   The well-posedness and dissipativeness

Let $C^{+} = C([-\tau, 0], \mathbb{R}_{+}^{4})$ be the Banach space of continuous functions mapping the interval $[-\tau, 0]$ into $\mathbb{R}_{+}^{4}$ equipped with the supremum norm, where $\tau = \max\{\tau_1, \tau_2, \tau_3, \tau_4\}$. The initial condition of model (1.3) is given as follows,

where $\phi = (\phi_{1}(\theta), \phi_{2}(\theta), \phi_{3}(\theta), \phi_{4}(\theta))\in C^{+}$.

By using the standard theory of delay differential equations (DDEs) (see, for example, ^[29,30,31]), we can easily establish the following result.

Theorem 2.1. The solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3) with the initial condition (2.1) is existent, unique and nonnegative on $[0, \infty)$, and satisfies

Moreover, the following bounded set

is positively invariant with respect to model (1.3).

Proof. It is not difficult to show that the solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3) with the initial condition (2.1) is existent, unique and nonnegative on $[0, \infty)$. Let us consider ultimate boundedness of model (1.3). According to the first equation of model (1.3), we have that for $t\geq 0$,

which implies $\limsup_{t\rightarrow+\infty}S(t)\leq \frac{r}{a}$. For any sufficiently small $\varepsilon > 0$, there exists a $\widehat{t} > 0$ such that $S(t) < \frac{r}{a}+\varepsilon$ for $t\geq \widehat{t}$. Further, according to the second equation of model (1.3), we have for $t\geq \widehat{t}$,

which implies

Since inequality (2.4) holds for arbitrary $\varepsilon > 0$, we obtain $\limsup_{t\rightarrow+\infty}I(t)\leq \frac{rb}{af}$. Similarly, according to the last two equations of model (1.3), we can obtain $\limsup_{t\rightarrow+\infty}u_{1}(t)\leq\frac{rd_{1}}{ae_{1}}$, $\limsup_{t\rightarrow+\infty}u_{2}(t)\leq\frac{rbd_{2}}{afe_{2}}$.

Let $(S(t), I(t), u_{1}(t), u_{2}(t))$ be the solution of model (1.3) with the initial function $\phi = (\phi_{1}, \phi_{2}, \phi_{3}, \phi_{4})\in \Omega$. { For $t\geq0$, we have $\dot{S}(t)\leq S(t)\left(r-aS(t)\right)$, which implies that for $t\geq0$,

where $\phi_{1}(0)\leq \frac{r}{a}$ is used. Further combining the second equation of model (1.3), for $t\geq0$, we have $\dot{I}(t)\leq I(t)(\frac{rb}{a}-fI(t))$, which implies that for $t\geq0$,

where $\phi_{2}(0)\leq \frac{rb}{af}$ is used. Thus, for $t\geq0$, we have $\dot{u}_{1}(t)\leq \frac{rd_{1}}{a}-e_{1}u_{1}(t), \; \; \dot{u}_{2}(t) \leq \frac{rbd_{2}}{af}-e_{2}u_{2}(t)$. This implies that for $t\geq0$,

where $\phi_{3}(0)\leq \frac{rd_{1}}{ae_{1}}$ and $\phi_{4}(0)\leq \frac{rbd_{2}}{afe_{2}}$ are used. Hence, it has that $\Omega$ is positively invariant with respect to model (1.3).

The proof is completed.

2.2.   The basic reproduction number and the equilibria

Obviously, model (1.3) always has a trivial equilibrium $\widetilde{E} = (0, 0, 0, 0)$ and a disease-free equilibrium $E_{0} = (S^{0}, 0, u_{1}^{0}, 0)$, where

Then, by the methods in ^[32,33], we can derive the expression of the basic reproduction number of model (1.3) as follows. First we define matrices $\mathbb{F}$ and $\mathbb{V}$ as

Then the basic reproduction number $R_0$ is defined as the spectral radius of $\mathbb{F}\mathbb{V}^{-1}$. Therefore,

Suppose $(S, I, u_{1}, u_{2})$ is an endemic equilibrium (positive equilibrium) of model (1.3), where $S > 0$, $I > 0$, $u_{1} > 0$, $u_{2} > 0$ satisfy the following equations

From Eq (2.5), it is not difficult to obtain the following relationships

Through Eq (2.6) and combining the second equation of Eq (2.5), we can obtain that $I$ satisfies the following equation,

According to Eq (2.6), in order to ensure that $S > 0$, we need to consider the following two cases:

(ⅰ) $rk < b$, $0 < I < \frac{r}{b-rk}\equiv \widetilde{I}$;

(ⅱ) $rk\geq b$, $I > 0$.

Clearly, for both case (ⅰ) and case (ⅱ), we have that

Hence, $F(I)$ is monotonically decreasing with respect to $I$ and

If $R_{0}\leq1$, then $\lim_{I\rightarrow 0^{+}}F(I)\leq0$ and $F(I) = 0$ has no positive roots. If $R_{0} > 1$, then $\lim_{I\rightarrow 0^{+}}F(I) > 0$.

For case (ⅰ), we have that

For case (ⅱ), we have that

Therefore, for cases (ⅰ) and (ⅱ), $F(I) = 0$ has a unique positive root $I = I^{*}$ if $R_{0} > 1$.

From the above discussions, we have the following result.

Theorem 2.2. The following statements are true.

(i) Model (1.3) always has a trivial equilibrium $\widetilde{E} = (0, 0, 0, 0)$.

(ii) Model (1.3) always has a disease-free equilibrium $E_{0} = (S^{0}, 0, u_{1}^{0}, 0)$.

(iii) Only for $R_{0} > 1$, model (1.3) has a unique endemic equilibrium $E^{*} = (S^{*}, I^{*}, u_{1}^{*}, u_{2}^{*})$, where

and $I^{*}$ is the unique positive root of the equation $F(I) = 0$.

Remak 2.1. In fact, the classifications of the equilibria of models (1.2) and (1.3) are exactly the same for any $\tau_{i}\geq0$. Clearly, comparing with the reference ^[28], our Theorem 2.2 gives more complete classification of the equilibria of model (1.2) and clearer expression of the basic reproduction number $R_0$.

3.   Global stability of the disease-free equilibrium

Let $\overline{E} = (\overline{S}, \overline{I}, \overline{u}_{1}, \overline{u}_{2})$ be any equilibrium of model (1.3). In order to investigate local stability of the equilibrium $\overline{E}$, we easily have that the characteristic equation of the corresponding linearized system of model (1.3) at $\overline{E}$ is given by

At the trivial equilibrium $\widetilde{E} = (0, 0, 0, 0)$, the characteristic Eq (3.1) becomes

which has a positive real root $\lambda = r$. Hence, $\widetilde{E}$ is unstable for any $\tau_{i}\geq0$ ($i = 1, 2, 3, 4$).

At the disease-free equilibrium $E_{0} = (S^{0}, 0, u^{0}_{1}, 0)$, the characteristic Eq (3.1) becomes

It is clear that Eq (3.2) has two real roots $\lambda_{1} = -e_{2} < 0$ and $\lambda_{2} = -\mu+bS^{0} = \mu(R_{0}-1)$. Obviously, when $R_0 > 1$, Eq (3.2) has a positive real root $\lambda_{2} > 0$, and hence, $E_{0}$ is unstable for any $\tau_{i}\geq0$ ($i = 1, 2, 3, 4$). When $R_0 < 1$, then $\lambda_{2} < 0$. When $R_0 = 1$, then $\lambda_{2} = 0$ is a simple root of Eq (3.2).

Let

The distribution of the roots of Eq (3.3) in the complex plane has been discussed in detail in ^[30,31,34]. Therefore, we have the following conclusions.

Lemma 3.1. The following statements are true.

(i) If $d_{1}c_{1}\leq ae_{1}$, then all the roots of Eq (3.3) have negative real parts.

(ii) If $d_{1}c_{1} > ae_{1}$, then all the roots of Eq (3.3) have negative real parts for $\tau_{1}+\tau_{3} < \tau_{13}^{0}$, and Eq (3.3) has at least one root which has positive real part for $\tau_{1}+\tau_{3} > \tau_{13}^{0}$, where

According to the discussions above and Lemma 3.1, it follows from stability theory and Hopf bifurcation theorem for DDEs (see, for example, ^[29,30,31]) that the following results hold.

Theorem 3.1. The trivial equilibrium $\widetilde{E}$ of model (1.3) is unstable for any $\tau_{i}\geq0 \; ($$i = 1, 2, 3, 4$$)$.

Theorem 3.2. For any $\tau_{2}\geq0$ and $\tau_{4}\geq0$, the following statements are true.

(i) If $R_{0} > 1$, then the disease-free equilibrium $E_{0}$ is unstable for any $\tau_{1}\geq0$ and $\tau_{3}\geq0$.

(ii) Assume that $d_{1}c_{1}\leq ae_{1}$. If $R_{0} < 1$, then the disease-free equilibrium $E_{0}$ is locally asymptotically stable for any $\tau_{1}\geq0$ and $\tau_{3}\geq0$; If $R_{0} = 1$, then the disease-free equilibrium $E_{0}$ is linearly stable for any $\tau_{1}\geq0$ and $\tau_{3}\geq0$.

(iii) Assume that $d_{1}c_{1} > ae_{1}$. If $R_{0} < 1$, then the disease-free equilibrium $E_{0}$ is locally asymptotically stable for $\tau_{1}+\tau_{3} < \tau_{13}^{0}$, and is unstable for $\tau_{1}+\tau_{3} > \tau_{13}^{0}$. Moreover, model (1.3) undergoes a Hopf bifurcation at the disease-free equilibrium $E_{0}$ when $\tau_{1}+\tau_{3} = \tau_{13}^{0}$.

Remak 3.1. Theorem 3.2 indicates that time delays $\tau_2$ and $\tau_4$ do not affect local asymptotic stability of the disease-free equilibrium $E_{0}$, and under the condition of $d_{1}c_{1}\leq ae_{1}$, time delays $\tau_1$ and $\tau_3$ also do not affect local asymptotic stability of $E_{0}$. But under the condition $d_{1}c_{1} > ae_{1}$, for larger time delay $\tau_1$ or $\tau_3$, stability of $E_0$ will be lost.

In the following discussions, we establish some sufficient conditions for global asymptotic stability of the disease-free equilibrium $E_{0}$.

Theorem 3.3. Assume that $d_{1}c_{1}\leq ae_{1}$. For any $\tau_{i}\geq0$ $(i = 1, 2, 3, 4)$, the following statements are true.

(i) If $R_{0} < 1$, then the disease-free equilibrium $E_{0}$ is globally asymptotically stable in $\Omega_{1}: = \{\phi\in \Omega:\phi_{1}(0) > 0\}$.

(ii) If $R_{0} = 1$, then the disease-free equilibrium $E_{0}$ is globally attractive in $\Omega_{1}$.

Proof. First, it is easy to show that the set $\Omega_{1}$ is positively invariant for model (1.3). If $R_0 < 1$, by Theorem 3.2, we only need to show that the disease-free equilibrium $E_{0}$ is globally attractive.

Define a Lyapunov functional $L_{1}$ on $\Omega_{1}$ as follows,

where

It is clear that $L_{1}$ is continuous on $\Omega_{1}$ and satisfies the condition (ii) of Lemma 3.1 in ^[35] on $\partial \Omega_{1} = \overline{\Omega}_{1}\setminus \Omega_{1}$.

Calculating the derivative of $L_{1}$ along any solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3), it follows that, for $t\geq0$,

where

here $r = aS^{0}+c_{1}u_{1}^{0}$ and $e_{1}u_{1}^{0} = d_{1}S^{0}$ are used. Using the following inequality of arithmetic and geometric means,

we further have that

Note that, if $R_{0}\leq1$, we have that

Assume that $d_{1}c_{1} < ae_{1}$ and $R_{0}\leq1$. By inequalities (3.6) and (3.7), we can obtain that $\frac{dL_{1}}{dt}\leq0$ for $t\geq0$. Let $M$ be the largest invariant set in the following set $G$:

Then, it follows from inequalities (3.6) and (3.7) that

We can easily have from model (1.3) and the invariance of $M$ that $M = \{E_{0}\}$. Therefore, it follows from Lemma 3.1 in ^[35] that the disease-free equilibrium $E_{0}$ is globally attractive.

Assume that $d_{1}c_{1} = ae_{1}$ and $R_{0}\leq1$. In this case, it is not easy to conclude that the largest invariant set $M$ is the singleton $\{E_{0}\}$. Hence, it is necessary to analyze Eq (3.4).

Note that

Hence, Eq (3.4) can be rewritten as

By inequality (3.7) and Eq (3.8), we can obtain that $\frac{dL_{1}}{dt}\leq0$ for $t\geq0$. Let $M_{1}$ be the largest invariant set in the following set $G_1$:

Then, it follows from Eq (3.8) that

For any $\varphi = (\varphi_{1}, \varphi_{2}, \varphi_{3}, \varphi_{4})\in M_{1}$, let $(S(t), I(t), u_{1}(t), u_{2}(t))$ be the solution of model (1.3) with the initial function $\varphi$. From the invariance of $M_{1}$, we have that $(S_{t}, I_{t}, u_{1t}, u_{2t})\in M_{1}\subset G_{1}$ for any $t\in R$. Obviously, $I(t)\equiv0$ for any $t\in R$, and then from the fourth equation of model (1.3) and the invariance of $M_{1}$, it is not difficult to obtain $u_{2}(t)\equiv0$ for any $t\in R$. In addition, according to the first and third equations of model (1.3), we can obtain, for any $t\in R$,

Thus, there exist constants $\delta_1$ and $\delta_2$ such that $S(t)\equiv \delta_{1}$ and $u_{1}(t)\equiv \delta_{2}$ for any $t\in R$. It is not difficult to find that $\delta_1$ and $\delta_2$ satisfy

which imply that $\delta_1 = S^{0}$ and $\delta_2 = u_{1}^{0}$. Hence, $S(t)\equiv S^{0}$ and $u_{1}(t)\equiv u_{1}^{0}$ for any $t\in R$. This shows that $M_{1} = \{E_{0}\}$. Then, it follows from Lemma 3.1 in ^[35] that the disease-free equilibrium $E_{0}$ is globally attractive.

The proof is completed.

Remak 3.2. Note the conclusion (ii) of Theorem 3.2, where we see that Theorem 3.3 gives complete conclusion of the global dynamics of the disease-free equilibrium $E_{0}$ in the case of $d_{1}c_{1}\leq ae_{1}$.

Now, we continue to discuss global dynamics of the disease-free equilibrium $E_{0}$ in the absence of condition $d_{1}c_{1}\leq ae_{1}$. The following lemmas will be used.

Lemma 3.2. $($Barbalat's lemma ^[37,36]$)$ Let $x(t)$ be a real valued differentiable function defined on some half line $[a, +\infty)$, $a\in(-\infty, +\infty)$. If

(i) $\lim_{t\rightarrow+\infty}x(t) = \alpha$; $|\alpha| < \infty$.

(ii) $\dot{x}(t)$ is uniformly continuous for $t > a$.

Then $\lim_{t\rightarrow+\infty}\dot{x}(t) = 0$.

Lemma 3.3. Let $(S(t), I(t), u_{1}(t), u_{2}(t))$ be any solution of model (1.3) with the initial condition (2.1), then the following statements are true.

(i) If $rb\leq a\mu$ (which implies $R_{0} < 1$), then $\lim_{t\rightarrow+\infty}I(t) = 0$, $\lim_{t\rightarrow+\infty}u_{2}(t) = 0$.

(ii) If $rb > a\mu$, then $\limsup_{t\rightarrow+\infty}I(t)\leq I_{M}$, where

Proof. By inequality (2.2), for arbitrary $\varepsilon > 0$, there exists a $T > 0$ such that $S(t) < \frac{r}{a}+\varepsilon$ for $t > T$. Then, it follows from the second equation of model (1.3) that, for $t > T$,

If $rb\leq a\mu$, by inequality (3.9), it follows that, for $t > T$,

which implies

Since $I(t)\geq0$ and inequality (3.10) holds for arbitrary $\varepsilon > 0$, we obtain that $\lim_{t\rightarrow+\infty}I(t) = 0$. Further, according to the last equation of model (1.3), $\lim_{t\rightarrow+\infty}u_{2}(t) = 0$ can be easily obtained.

If $rb > a\mu$, it follows from inequality (3.9) that, for $t > T$,

where

Similarly, it follows that

The proof is completed.

For convenience, let us give the following conditions $(H_1)$, $(H_2)$ and $(H_3)$:

We can obtain the following result.

Theorem 3.4. Assume that $R_{0}\leq1$. For any $\tau_{2}\geq0$ and $\tau_{4}\geq0$, the following statements are true.

(i) If $rb\leq a\mu$ and conditions $(H_{1})$–$(H_{2})$ hold, then the disease-free equilibrium $E_{0}$ is globally attractive in $X_{1}: = \{\phi\in C^{+}:\; \phi_{1}(0) > 0\}$.

(ii) If $rb > a\mu$ and conditions $(H_{1})$–$(H_{3})$ hold, then the disease-free equilibrium $E_{0}$ is globally attractive in $X_{1}$.

Proof. It is easy to show that $X_{1}$ is positively invariant for model (1.3). Let $(S(t), I(t), u_{1}(t), u_{2}(t))$ be the solution of model (1.3) with any initial function $\phi\in X_{1}$. By inequality (2.2), for any sufficiently small $\varepsilon_{0} > 0$, there exists a $t_{1} > 0$ such that $S(t) < \frac{r}{a}+\varepsilon_{0}\equiv S_{1}(\varepsilon_{0})$ for $t > t_{1}$.

We continue to analyze $\frac{dV_{1}}{dt}$ given by Eq (3.5). From Eq (3.5) and inequality (3.7), we have that, for $t\geq 0$,

Note that, for $t > \tau_1+\tau_3$, $\Lambda_{1}$ can be rewritten as

where

In addition, for $t > \tau_1+\tau_3$, we have

Similarly, for $t > t_{1}+\tau_1+\tau_3$, we have

here $S(t) < S_{1}(\varepsilon_{0})$ for $t > t_{1}$ is used. For $t > t_{1}+\tau_1+\tau_3$, let us define the following function $L_2$,

where $V_1$ is defined as in the proof of Theorem 3.3,

For $t > t_{1}+\tau_1+\tau_3$, we calculate the derivatives of $V_{i} \; (i = 2, \cdots, 6)$ as follows,

Combining (3.12)–(3.19), for $t > t_{1}+\tau_1+\tau_3$, we finally have

Let us show global attractivity of the disease-free equilibrium $E_{0}$ in the following two cases.

Case (ⅰ) $rb\leq a\mu$ (which implies $R_{0} < 1$) and $(H_1)$–$(H_2)$ hold.

From conditions $(H_{1})$–$(H_{2})$, it has that, for sufficiently small $\varepsilon_{0} > 0$, the inequalities

hold. Furthermore, from Lemma 3.3, we have that $\lim_{t\rightarrow\infty}I(t) = 0$ and $\lim_{t\rightarrow\infty}u_{2}(t) = 0$. Thus, there exists a $t_{2} > 0$ such that, for $t > t_{2}$,

In addition, note that

from which we have that, for $t > t_{2}$,

Hence, it follows from inequalities (3.20)–(3.22) that $\frac{dL_{2}}{dt}\leq0$ for $t > \widetilde{T}: = \max\{t_{1}+\tau_{1}+\tau_3, t_{2}\}$. This indicates that, for $t > \widetilde{T}$, the function $L_{2}(t)$ is monotonically decreasing and bounded. Thus, the limitation $\lim_{t\rightarrow+\infty}L_{2}(t)$ exists.

In addition, by Theorem 2.1, it is not difficult to show that, for $t > \widetilde{T}$, the second derivative $L''_2(t)$ is also bounded. This implies that $L'_{2}(t)$ is uniformly continuous for $t > \widetilde{T}$. Therefore, it follows from Lemma 3.1 that $\lim_{t\rightarrow\infty}L'_{2}(t) = 0$. Again from inequalities (3.20)–(3.22), it follows that

This shows that the disease-free equilibrium $E_{0}$ is globally attractive.

Case (ⅱ) $rb > a\mu$ and $(H_1)$–$(H_3)$ hold.

Similarly, from condition $(H_{3})$, we have that the inequality

holds for sufficiently small $\varepsilon_{0} > 0$. From Lemma 3.3, there exists a $t_{3} > 0$ such that $I(t) < I_M+\varepsilon_{0}$ for $t > t_{3}$. Then, we have that, for $t > t_3$,

Hence, by inequalities (3.20), (3.21) and (3.24), we can also obtain $\frac{dL_{2}}{dt}\leq0$ for $t > \hat{T}: = \max\{t_{1}+\tau_{1}+\tau_3, t_{3}\}$. By the same arguments as in Case (i), we can obtain

Furthermore, from the last equation of model (1.3), we can easily have $\lim_{t\rightarrow\infty}u_{2}(t) = 0$. This shows that the disease-free equilibrium $E_{0}$ is globally attractive.

The proof is completed.

From Theorems 3.2 and 3.4, we have the following two corollaries.

Corollary 3.1. Assume that $R_{0} < 1$, $d_{1}c_{1} > ae_{1}$ and $\tau_{1}+\tau_{3} < \tau_{13}^{0}$. For any $\tau_{2}\geq0$ and $\tau_{4}\geq0$, the following statements are true.

(i) If $rb\leq a\mu$ and conditions $(H_{1})-(H_{2})$ hold, then the disease-free equilibrium $E_{0}$ is globally asymptotically stable in $X_{1}$.

(ii) If $rb > a\mu$ and conditions $(H_{1})-(H_{3})$ hold, then the disease-free equilibrium $E_{0}$ is globally asymptotically stable in $X_{1}$.

Corollary 3.2. Assume that $R_{0} < 1$ and $\tau_{1} = \tau_{3} = 0$. For any $\tau_{2}\geq0$ and $\tau_{4}\geq0$, then the disease-free equilibrium $E_{0}$ is globally asymptotically stable in $X_{1}$.

Remak 3.3. If $\tau_{i} = 0 \; ($$i = 1, 2, 3, 4$$)$, then model (1.3) reduces into model (1.2). Clearly, Theorems 3.2, 3.3 and 3.4 extend and improve Theorem 1 in ^[28]. Further, if $k = 0$, model (1.2) becomes the model discussed in ^[17]. Hence, Theorems 3.2, 3.3 and 3.4 also include Theorem 2.1 in ^[17] as a special case.

4.   Global stability of the endemic equilibrium

Theoretical analysis of the distribution of the characteristic roots of characteristic equation (3.1) at the endemic equilibrium $E^{*} = (S^{*}, I^{*}, u_{1}^{*}, u_{2}^{*})$ usually involves some complicated computations, since there are four time delays $\tau_{i}\geq0 \; ($$i = 1, 2, 3, 4$$)$ in model (1.3). However, the numerical simulations in Section 5 show that, each of time delays $\tau_{i}$ ($i = 1, 2, 3, 4$) can destroy stability of the endemic equilibrium $E^{*}$ of model (1.3) by properly choosing parameters. Hence, it is natural to consider the following two problems.

(ⅰ) Under what conditions, the time delays $\tau_{i}\geq0 \; ($$i = 1, 2, 3, 4$$)$ are harmless for global asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3).

(ⅱ) Under what conditions, the time delays $\tau_{i}\geq0 \; ($$i = 1, 2, 3, 4$$)$ may be harmful for global asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3).

In this section, we study the above problems (i)–(ii) by constructing suitable Lyapunov functionals.

For convenience, let us denote the following conditions,

For problem (ⅰ) above, we have the following result.

Theorem 4.1. Assume that $R_{0} > 1$. If one of conditions $(H_4)$–$(H_7)$ holds, then the endemic equilibrium $E^{*}$ is globally asymptotically stable in $X_{2}: = \{\phi\in C^{+}: \phi_{i}(0) > 0, \; i = 1, 2\}$.

Proof. It is easy to show that the set $X_{2}$ is positively invariant for model (1.3). Since $E^{*}$ is the equilibrium of model (1.3), the following equalities hold,

Define a Lyapunov functional $W_{1}$ on $X_{2}$ as follows,

It is clear that $W_{1}$ is continuous on $X_{2}$ and positive definite with respect to $E^{*}$.

Calculating the derivative of $W_{1}$ along any solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3), it follows that, for $t\geq0$,

here Eq (4.1) is used. Note that

from which we have that, for $t\geq0$,

where

We consider global asymptotic stability of the endemic equilibrium $E^{*}$ in the following four cases.

If condition $(H_4)$ holds, it has that $\Upsilon_{1} = \Pi_{1} = 0$ and $\frac{dW_{1}}{dt}$ is negative definite with respect to $E^{*}$. Hence, the endemic equilibrium $E^{*}$ is globally asymptotically stable (see, for example, ^[29,30]).

If condition $(H_5)$ holds, we have that $\Pi_{1} = 0$. Let us consider another functional as follows,

$W_{2}$ is continuous on $X_{2}$, positive definite with respect to $E^{*}$, and satisfies condition (ii) of Lemma 3.1 in ^[35] on $\partial X_{2} = \overline{X_{2}}\setminus X_{2}$.

Calculating the derivative of $W_{2}$ along any solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3), it follows that, for $t\geq0$,

By Eqs (4.2) and (4.3), and the following inequality of arithmetic and geometric means:

we have that, for $t\geq0$,

It follows from condition $(H_{5})$ that $\frac{dW_{2}}{dt}\leq0$ for $t\geq0$. Hence, the endemic equilibrium $E^{*}$ is stable. Furthermore, $\frac{dW_{3}}{dt} = 0$ implies $I(t) = I^{*}$ and $u_{2}(t) = u_{2}^{*}$.

Let $M_{2}$ be the largest invariant set in the set

Then, it follows that

From model (1.3) and the invariance of $M_{2}$, we can easily get that $M_{2} = \{E^{*}\}$. Thus, it follows from Lemma 3.1 in ^[35] that the endemic equilibrium $E^{*}$ is globally asymptotically stable.

If condition $(H_6)$ holds, it follows that $\Upsilon_{1} = 0$. Let us consider a functional as follows,

$W_{3}$ is continuous on $X_{2}$, positive definite with respect to $E^{*}$, and satisfies condition (ii) of Lemma 3.1 in ^[35] on $\partial X_{2} = \overline{X_{2}}\setminus X_{2}$.

Calculating the derivative of $W_{3}$ along any solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3), it follows that, for $t\geq0$,

By Eqs (4.2) and (4.5), and the following inequality of arithmetic and geometric means:

we have that, for $t\geq0$,

It follows from condition $(H_{6})$ that $\frac{dW_{3}}{dt}\leq0$ for $t\geq0$. Furthermore, $\frac{dW_{3}}{dt} = 0$ implies $S(t) = S^{*}$ and $u_{1}(t) = u_{1}^{*}$. By the same arguments as in the situation of condition $(H_5)$, we can also show that the endemic equilibrium $E^{*}$ is globally asymptotically stable.

If condition $(H_7)$ holds, let us consider the following Lyapunov functional,

$W_{4}$ is continuous on $X_{2}$, positive definite with respect to $E^{*}$, and satisfies condition (ii) of Lemma 3.1 in ^[35] on $\partial X_{2} = \overline{X_{2}}\setminus X_{2}$.

Calculating the derivative of $W_{4}$ along any solution $(S(t), I(t), u_{1}(t), u_{2}(t))$ of model (1.3), it follows that, for $t\geq0$,

Further, by Eq (4.2) and inequalities (4.4) and (4.6), we have that, for $t\geq0$,

It follows from condition $(H_{7})$ that $\frac{dW_{4}}{dt}\leq0$ for $t\geq0$. Furthermore, if $d_{1}c_{1} < ae_{1}$, then $\frac{dW_{4}}{dt} = 0$ implies that $S(t) = S^{*}$ and $u_{1}(t) = u_{1}^{*}$. By the same arguments as in the situation of condition $(H_5)$, we can show that the endemic equilibrium $E^{*}$ is globally asymptotically stable. If $d_{1}c_{1} = ae_{1}$, also by the same arguments as in the situation of $d_{1}c_{1} = ae_{1}$ in Theorem 3.3, we can show that $E^{*}$ is globally asymptotically stable.

The proof is completed.

Remak 4.1. In the situation of condition $(H_7)$, Theorem 4.1 indicates that the time delays $\tau_{i}\geq0 \; (i = 1, 2, 3, 4)$ are harmless for global asymptotic stability of the endemic equilibrium $E^{*}$.

Now, let us consider problem (ⅱ). Note that $R_{0} = \frac{bre_{1}}{\mu(ae_{1}+d_{1}c_{1})} > 1$ implies $rb > a\mu$. Let us denote the following conditions,

In conditions $(H_8)$–$(H_{11})$ above, the definition of $I_{M}$ is given in Lemma 3.3 (ⅱ). We have the following result.

Theorem 4.2. Assume that $R_{0} > 1$. If conditions $(H_{8})$–$(H_{11})$ hold, then the endemic equilibrium $E^{*}$ is globally attractive in $X_{2}$.

Proof. Let $(S(t), I(t), u_{1}(t), u_{2}(t))$ be the solution of model (1.3) with any initial function $\phi\in X_{2}$. From Theorem 2.1 and Lemma 3.3, for sufficient small $\varepsilon_1 > 0$, there exists a $T_{1} > 0$ such that, for $t > T_{1}$,

Hence, from Eq (4.2), it has that, for $t > T_{1}$,

For simplicity, denote

Note that $\Upsilon_{1}$ and $\Pi_{1}$ can be rewritten as

Let us give appropriate estimations on $|\Upsilon_{2}|$, $|\Upsilon_{3}|$, $|\Pi_{2}|$ and $|\Pi_{3}|$.

It follows that, $t > \tau_1+\tau_2+\tau_3+\tau_4+T_1$,

For $t > \tau_1+\tau_2+\tau_3+\tau_4+T_{1}$, let us define the following function,

where

Computing the derivatives of $U_1$ and $U_2$, we easily get that, for $t > \tau_1+\tau_2+\tau_3+\tau_4+T_{1}$,

In summary, by (4.7)–(4.13), we have that, for $t > \tau_1+\tau_2+\tau_3+\tau_4+T_{1}$,

Furthermore, from conditions $(H_8)$–$(H_{11})$, we see that, for sufficiently small $\varepsilon_{1} > 0$, we have that $Q_i(\varepsilon_{1}) > 0 \; (i = 1, 2, 3, 4)$. This shows that $\frac{dU}{dt}\leq0$ for $t > \tau_1+\tau_2+\tau_3+\tau_4+T_{1}$. By similar arguments as in the proof of Theorem 3.4, we can have

This proves that the endemic equilibrium $E^{*}$ is globally attractive.

The proof is completed.

Remak 4.2. If $\tau_{i} = 0 \; ($$i = 1, 2, 3, 4$$)$, then model (1.3) reduces into model (1.2). Clearly, Theorem 4.1 extends and improves Theorem 2 in ^[28]. Further, if $k = 0$, Theorem 4.1 also include Theorem 2.2 in ^[17] as a special case.

5.   Conclusions and numerical simulations

In this paper, we consider the SI epidemic model (1.3) with two feedback control variables and four time delays. In biology, model (1.3) has more general biological significance. Then, by skillfully constructing appropriate Lyapunov functionals, and combining Lyapunov–LaSalle invariance principle and Barbalat's lemma, some sufficient conditions for global dynamics of the equilibria of model (1.3) are established. In the case of $d_{1}c_{1}\leq ae_{1}$, Theorem 3.3 gives complete conclusion on global asymptotic stability of the disease-free equilibrium $E_{0}$. In the case of $d_{1}c_{1} > ae_{1}$, in Theorem 3.4, global attractivity of the disease-free equilibrium $E_{0}$ is considered under conditions $(H_1)$–$(H_3)$. Note that, in the case, it has from Theorem 3.2 that local asymptotic stability of the disease-free equilibrium $E_{0}$ also depends on the time delays $\tau_1$ and $\tau_3$. Hence, The set of conditions $(H_1)$–$(H_3)$ has certain rationality. Furthermore, as a special case, Theorems 3.2, 3.3 and 3.4 improve and generalize Theorem 1 in ^[28] and Theorem 2.1 in ^[17].

We also establish some sufficient conditions for global dynamics of the endemic equilibrium $E^{*}$ of model (1.3). Theorem 4.1 shows that, if condition $(H_5)$, or $(H_6)$, or $(H_7)$ holds, the time delays $\tau_1$ and $\tau_3$, or $\tau_2$ and $\tau_4$, or $\tau_i \; (i = 1, 2, 3, 4)$ are harmless for global asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3). If condition $(H_4)$ holds, i.e., $\tau_i = 0 \; (i = 1, 2, 3, 4)$, we see that Theorem 4.1 includes Theorem 2 in ^[28] and Theorem 2.2 in ^[17] as a special case. Furthermore, in Theorem 4.2, under condition $R_0 > 1$, a set of sufficient conditions $(H_8)$–$(H_{11})$ is obtained to ensure global attractivity of the endemic equilibrium $E^{*}$ of model (1.3). Note that the subsequent numerical simulations imply that any one of time delays $\tau_i \; (i = 1, 2, 3, 4)$ may destroy local asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3) and result in the occurrence of periodic oscillations etc.. Hence, in the set of conditions $(H_8)$–$(H_{11})$, it should be feasible to have some certain limits on the lengths of time delays $\tau_i \; (i = 1, 2, 3, 4)$.

In the following, let us give some numerical simulations to summarize the applications of Theorem 3.4, Corollary 3.1 and Theorem 4.2.

Firstly, let us choose the values of a set of parameters as follows,

By computations, we have that $0.96 = d_1c_1 > ae_1 = 0.6$, $0.48 = rb > a\mu = 0.25$, $R_{0}\approx0.738 < 1$, $E_{0} = (0.462, 0, 0.923, 0)$ and $\tau_{13}^{0}\approx4.542$. Furthermore, conditions $(H_1)$–$(H_3)$ become the following inequalities,

It has from Theorem 3.2 that the disease-free equilibrium $E_{0}$ is locally asymptotically stable for $\tau_{1}+\tau_{3} < \tau_{13}^{0}\approx4.542$ and unstable for $\tau_{1}+\tau_{3} > \tau_{13}^{0}\approx4.542$. If time delays $\tau_{1}$ and $\tau_{3}$ satisfy more restrictive condition $(\hat{H})$, it has from Theorem 3.4 or Corollary 3.1 that the disease-free equilibrium $E_{0}$ is also globally asymptotically stable.

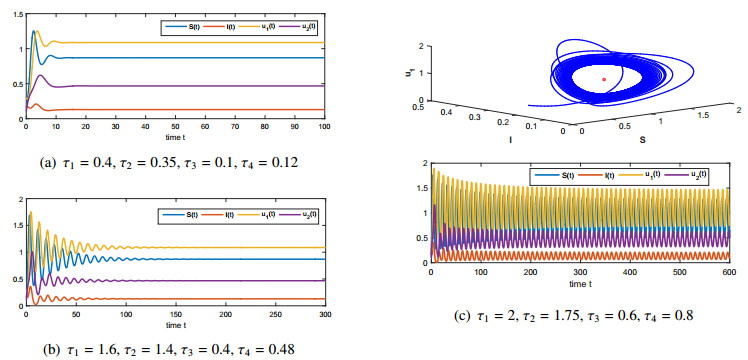
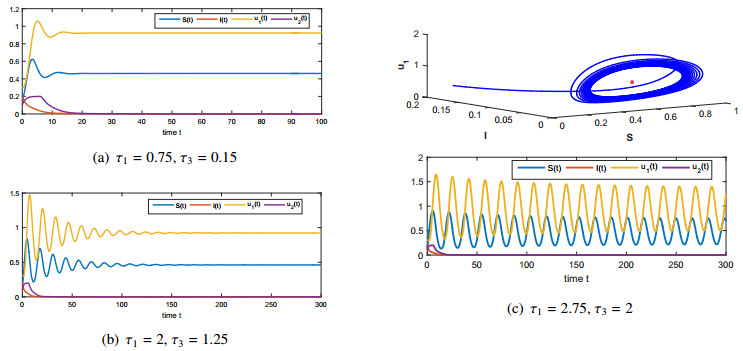
Let us choose $\tau_1 = 0.75$ and $\tau_{3} = 0.15$. We see that conditions $\tau_{1}+\tau_{3} < \tau_{13}^{0}\approx4.542$ and $(\hat{H})$ are satisfied. Figure 1(a) shows that the disease-free equilibrium $E_{0}$ is globally asymptotically stable.

Let us choose $\tau_1 = 2$ and $\tau_{3} = 1.25$. We see that condition $(\hat{H})$ does not hold, but condition $\tau_{1}+\tau_{3} < \tau_{13}^{0}\approx4.542$ is still satisfied. Figure 1(b) shows that the disease-free equilibrium $E_{0}$ is locally asymptotically stable.

Let us further choose $\tau_1 = 2.75$ and $\tau_{3} = 2$. We see that condition $\tau_{1}+\tau_{3} > \tau_{13}^{0}\approx4.542$ holds. Figure 1(c) shows that the disease-free equilibrium $E_{0}$ becomes unstable and periodic oscillations occur. In Figure 1(a)–(c), for simplicity, $\tau_2$ and $\tau_4$ are fixed as $\tau_2 = 3$ and $\tau_4 = 6$, respectively.

Secondly, let us give numerical simulations in the situation of the basic reproduction number $R_{0} > 1$.

Let us choose the values of set of parameters as follows,

By computations, we have that $R_{0}\approx3.678 > 1$, $E^{*}\approx(0.870, 0.130, \; 1.087, 0.467)$. Furthermore, conditions $(H_8)$–$(H_{11})$ approximately become the following inequalities,

If time delays $\tau_i \; (i = 1, 2, 3, 4)$ satisfy condition $(\tilde{H})$, it has from Theorem 4.2 that the endemic equilibrium $E^{*}$ is globally attractive.

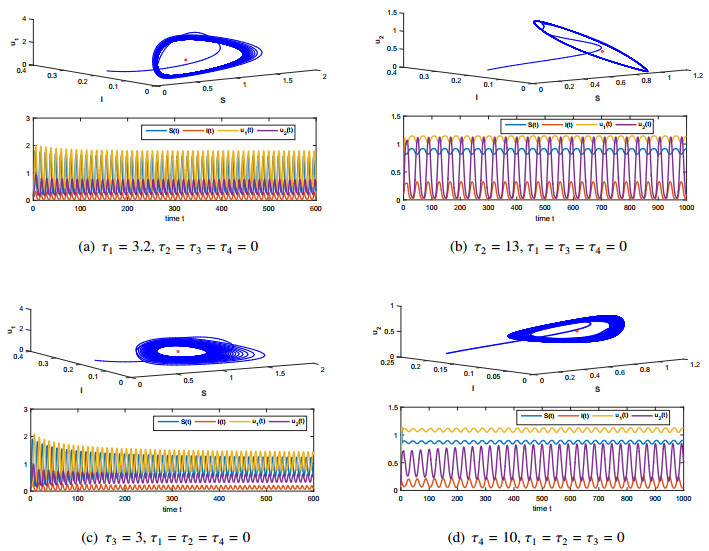
Let us choose $\tau_1 = 0.4$, $\tau_{2} = 0.35$, $\tau_3 = 0.1$ and $\tau_{4} = 0.12$. We see that condition $(\tilde{H})$ is satisfied. Figure 2(a) shows that the endemic equilibrium $E^{*}$ is globally attractive.

Let us choose larger values here, $\tau_1 = 1.6$, $\tau_{2} = 1.4$, $\tau_3 = 0.4$ and $\tau_{4} = 0.48$. We see that condition $(\tilde{H})$ does not hold. Figure 2(b) show that the endemic equilibrium $E^{*}$ may be still attractive.

Let us further choose $\tau_1 = 2$, $\tau_{2} = 1.75$, $\tau_3 = 0.6$ and $\tau_{4} = 0.8$. We see that condition $(\tilde{H})$ does not hold. Figure 2(c) shows that the endemic equilibrium $E^{*}$ becomes unstable and periodic oscillations occur.

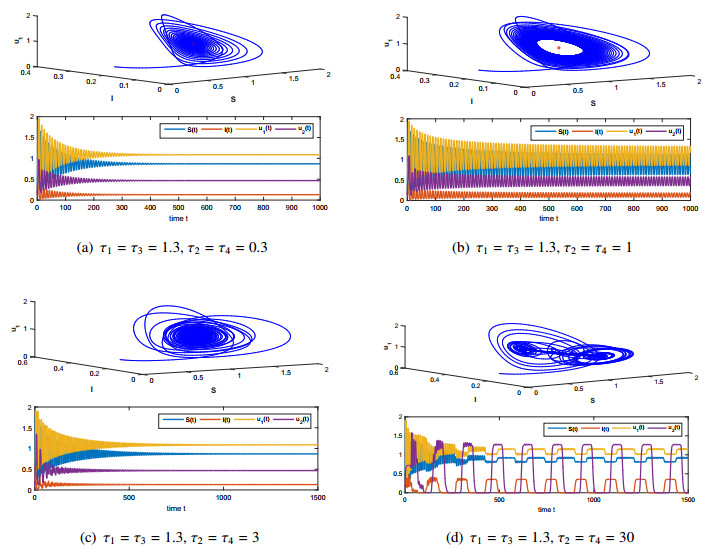
Moreover, Figure 3(a)–(d) show that any one of time delays $\tau_{i}$ ($i = 1, 2, 3, 4$) can destroy local asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3). Here, the values of the parameters of model (1.3) are the same as Eq (5.2).

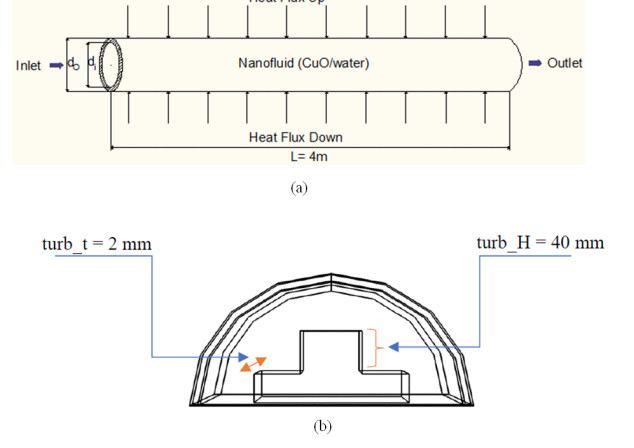
At the end of the paper, in view of Figure 1(b) and Figure 2(b) above, we would like to point out that conditions $(H_1)$–$(H_3)$ in Theorem 3.3 and conditions $(H_8)$–$(H_{11})$ in Theorem 4.2 are actually conservative and worth of further improving. In addition, for global asymptotic stability of the endemic equilibrium $E^{*}$ of model (1.3), in the case of $d_{1}c_{1} > a_{1}e_{1}$ or $d_{2}c_{2} > f e_{2}$, to give some sufficient conditions which are different from conditions $(H_{8})$–$(H_{11})$ may be also interesting, since Figure 4(a)–(d) show that model (1.3) may have richer dynamic behaviors. Here, the values of the parameters of model (1.3) are also the same as Eq (5.2). Further, it would be interesting to extend model (1.3) to the case of non-autonomous model and to consider the uniform persistence and existence of almost periodic solutions etc. ^[38,39].

Acknowledgments

This paper is supported by Beijing Natural Science Foundation (No.1202019) and National Natural Science Foundation of China (No.11971055). The authors would like to thank the reviewers and the editor for their careful reading, helpful comments and suggestions that greatly improved the paper.

Conflict of interest

All authors declare no conflicts of interest in this paper.