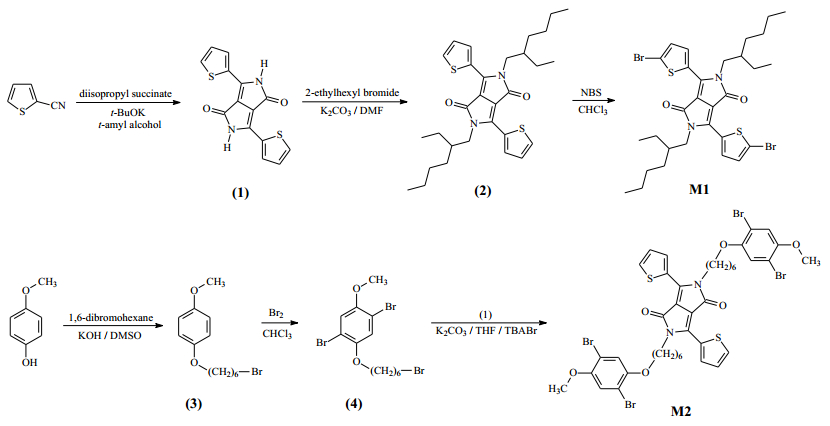
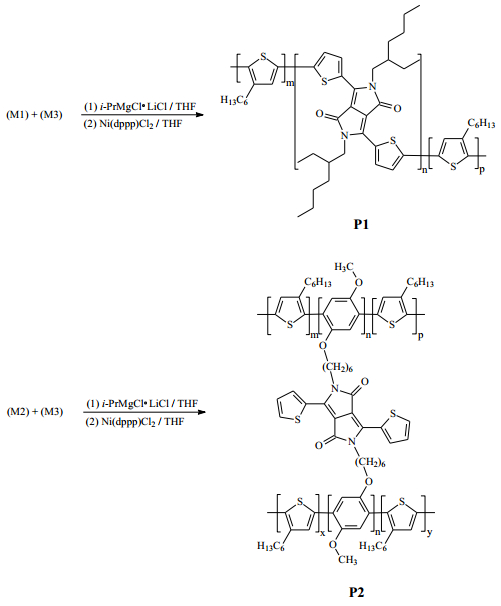
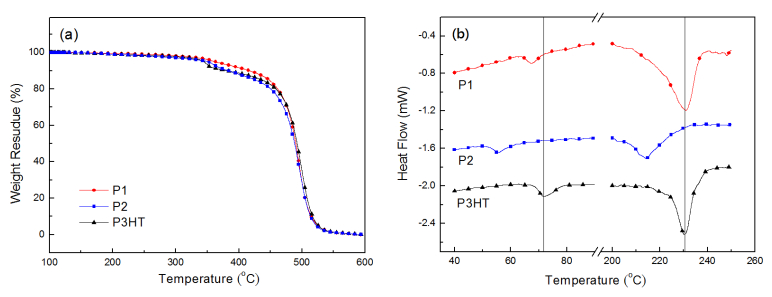
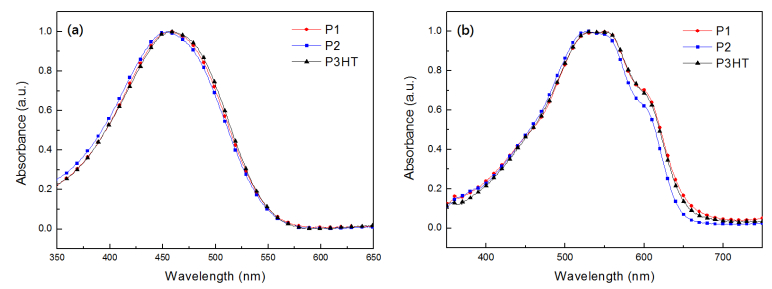
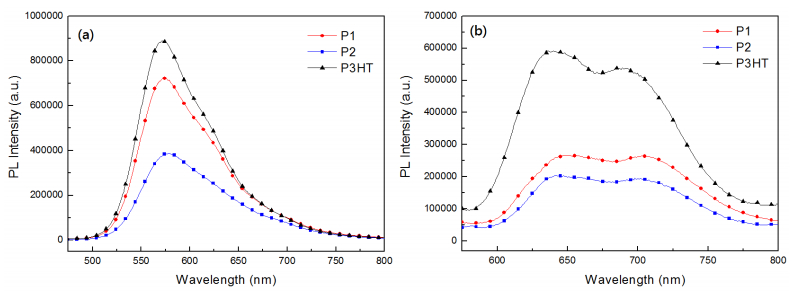
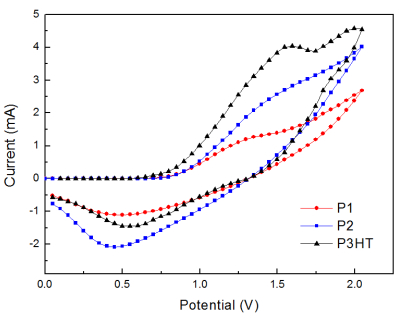
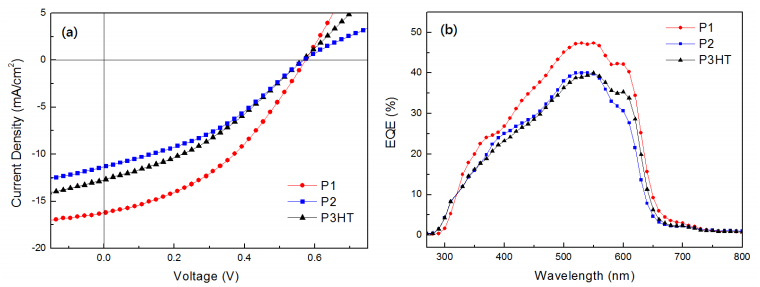
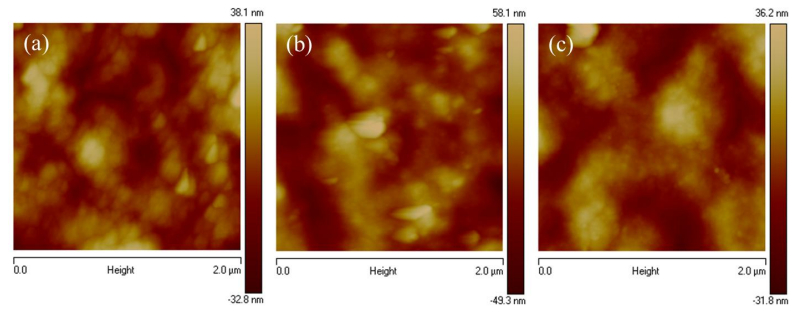
Two novel polythiophene derivatives with linear or hyperbranched architectures using diketopyrrolopyrrole (DPP) as linking groups as well as normal poly(3-hexylthiophene) (P3HT) were synthesized via the Universal Grignard metathesis polymerization. The molecular weights of the linear polythiophene containing DPP linking moieties are higher than those of P3HT, while molecular weights of the hyperbranched one are smaller. The main decomposition temperatures of polymers were measured at 470 °C from TGA experiments. The UV-vis absorption behaviors of the DPP-containing polymers are similar to that of P3HT; moreover, these DPP-containing polythiophenes show distinct PL decay both in solution and thin film states. The electrochemical experiments reveal that the incorporation of DPP groups resulted in lowering HOMO levels of polymers. All polymers were blended with PC61BM and used as active layers for the fabrication of inverted polymer solar cells. The power conversion efficiency of devices based on linear and hyperbranched polythiophenes reached 3.74% and 2.38%, respectively, revealing comparable or even higher efficiency than the one based on normal P3HT.
1.
Introduction
We consider the system of Dirac equations
where B=(01−10), Q(x)=(p(x)q(x)q(x)−p(x)), y(x)=(y1(x)y2(x)), p(x), q(x) are real valued functions in L2(a,b) and λ is a spectral parameter, with boundary conditions
and with transmission conditions
where fi(λ), hi(λ)(i=1,2) are rational functions of Herglotz-Nevanlinna type such that
ai, bi, fik, gik,mi,ni,uik and tik are real numbers, a1<0, f1k<0, a2>0, f2k>0,mi>0, uik>0 and gi1<gi2<...<giNi, ti1<ti2<...<tiPi, αi>0 and a<w1<w2<b. In special case, when fi(λ)=∞, conditions (2) and (3) turn to Dirichlet conditions y1(a)=y1(b)=0 respectively. Moreover, when hi(λ)=∞, conditions (4) turn to y1(w2+0)=α2y1(w2−0), y2(w2+0)=α−12y2(w2−0)+h2(λ)y1(w2−0) and y1(w1+0)=α1y1(w1−0), y2(w1+0)=α−11y2(w1−0)+h1(λ)y1(w1−0) according to order i=1,2.
Inverse problems of spectral analysis compose of recovering operators from their spectral data. Such problems arise in mathematics, physics, geophysics, mechanics, electronics, meteorology and other branches of natural sciences. Inverse problems also play important role in solving many equations in mathematical physics.
R1(λ)y1(a)+R2(λ)y2(a)=0 is a boundary condition depending spectral parameter where R1(λ) and R2(λ) are polynomials. When degR1(λ)=degR2(λ)=1, this equality depends on spectral parameter as linearly. On the other hand, it is more difficult to search for higher orders of polynomials R1(λ) and R2(λ). When R1(λ)R2(λ) is rational function of Herglotz-Nevanlinna type such that f(λ)=aλ+b−N∑k=1fkλ−gk in boundary conditions, direct and inverse problems for Sturm-Liouville operator have been studied [1,2,3,4,5,6,7,8,9,10,11]. In this paper, direct and inverse spectral problem is studied for the system of Dirac equations with rational function of Herglotz-Nevanlinna in boundary and transmission conditions.
On the other hand, inverse problem firstly was studied by Ambarzumian in 1929 [12]. After that, G. Borg was proved the most important uniqueness theorem in 1946 [13]. In the light of these studies, we note that for the classical Sturm-Liouville operator and Dirac operator, the inverse problem has been studied fairly (see [14,15,16,17,18,19,20], where further references and links to applications can be found). Then, results in these studies have been extended to other inverse problems with boundary conditions depending spectral parameter and with transmission conditions. Therefore, spectral problems for differential operator with transmission conditions inside an interval and with eigenvalue dependent boundary and transmission conditions as linearly and non-linearly have been studied in so many problems of mathematics as well as in applications (see [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] and other works, and see [44,45,46,47,48,49,50,51,52,53,54] and other works cited therein respectively).
The aim of this article is to get some uniqueness theorems for mentioned above Dirac problem with eigenvalue dependent as rational function of Herglotz-Nevanlinna type in both of the boundary conditions and also transmission conditions at two different points. We take into account inverse problem for reconstruction of considered boundary value problem by Weyl function and by spectral data {λn,ρn}n∈Z and {λn,μn}n∈Z. Although the boundary and transmission conditions of the problem are not linearly dependent on the spectral parameter, this allows the eigenvalues to be real and to define normalizing numbers.
2.
Preliminaries
Consider the space H:=L2(a,b)⊕L2(a,b)⊕CN1+1⊕CN2+1⊕CP1+1⊕ CP2+1 and element Y in H is in the form of Y=(y1(x),y2(x),τ,η,β,γ), such that τ=(Y1,Y2,…,YN1,YN1+1), η=(L1,L2,…,LN2,LN2+1), β=(R1,R2,…,RP1,RP1+1), γ=(V1,V2,…,VP2,VP2+1). H is a Hilbert space with the inner product defined by
for Y=(y1(x),y2(x),τ,η,β,γ) ve Z=(z1(x),z2(x),τ′,η′,β′,γ′) in H. Define the operator T on the domain
D(T)={Y∈H:y1(x),y2(x)∈AC(a,b),
ly∈L2(a,b), y1(w+i)=αiy1(w−i),i=1,2
YN1+1:=−a1y1(a), LN2+1:=−a2y1(b),
RP1+1:=−m1y1(w−1),VP2+1:=−m2y1(w−2)}
such that
where
Accordingly, equality TY=λY corresponds to problem (1)-(4) under the domain D(T)⊂H.
Theorem 1. The eigenvalues of the operator T and the problem (1)-(4) coincide.
Proof. Assume that λ is an eigenvalue of T and Y(x)=(y1(x),y2(x),τ,η,β,γ)∈H is the eigenvector corresponding to λ. Since Y∈D(T), it is obvious that the condition y1(wi+0)−αiy1(wi−0)=0 and Eq (1) hold. On the other hand, boundary conditions (2)-(3) and the second condition of (4) are satisfied by the following equalities;
Tτ=TYi=g1i−Yi−f1iy1(a)=λYi, i=¯1,N1
TYN1+1=y2(a)+b1y1(a)+N1∑k=1Yk=−a1y1(a)λ
Tη=TLi=g2iLi−f2iy1(b)=λLi, i=¯1,N2
TLN2+1=y2(b)+b2y1(b)+N2∑k=1Lk=−a2y1(b)λ
Tβ=TRi=t1iRi−u1iy1(w−1), i=¯1,P1
TRP1+1=−y2(w+1)+α−11y2(w−1)+n1y1(w−1)+P1∑k=1Rk=−m1y1(w−1)λ
Tγ=TVi=t2iVi−u2iy1(w−2), i=¯1,P2
TVP2+1=−y2(w+2)+α−12y2(w−2)+n2y1(w−2)+∑k=1P2Vk=−m2y1(w−2)λ.
If λ=gik(i=1,2 and k={1,2,…Ni}) are eigenvalues of operator T, then, from above equalities and the domain of T, equalities (1), y1(a,g1k)=0, y1(b,g2k)=0 and (4) are satisfied.
Moreover, If λ=tik(i=1,2 and k={1,2,…Pi}) are eigenvalues of operator T, from above equalities and the domain of T, Eqs (1)-(3) and y1(w−i,tik)=0=y1(w+i,tik) are valid. In that case, λ is also an eigenvalue of L.
Conversely, let λ be an eigenvalue of L and (y1(x)y2(x)) be an eigenfunction corresponding to λ. If λ≠gik(i=1,2, k={1,2,…Ni}) and λ≠tik(i=1,2, k={1,2,…Pi}) then, it is clear that λ is an eigenvalue of T and the vector
Y=(y1(x),y2(x),f11g11−λy1(a),f12g12−λy1(a),…,f1N1g1N1−λy1(a),−a1y1(a),
f21g21−λy1(b),f22g22−λy1(b),…,f2N2g2N2−λy1(b),−a2y1(b),
u11t11−λy1(w−1),u12t12−λy1(w−1),…,u1P1t1P1−λy1(w−1),−m1y1(w−1),
u21t21−λy1(w−2),u22t22−λy1(w−2),…,u2P2t2P2−λy1(w−2),−m2y1(w−2)) is the eigenvector corresponding to λ.
If λ=g1k(k={1,2,…N1}), then,
Y=(y1(x),y2(x),Y1,Y2,…,YN1,0,L1,L2,…,LN2,LN2+1,R1,R2,…,RP1,RP1+1,
V1,V2,…,VP2,VP2+1),
Yi={0, i≠k−y2(a),i=k,i=1,2,…,N1 is the eigenvector of T corresponding to g1k.
If λ=g2k(k={1,2,…N2}), then,
Y=(y1(x),y2(x),Y1,Y2,…,YN1,YN1+1,L1,L2,…,LN2,0,R1,R2,…,RP1,RP1+1,V1,V2,…,VP2,VP2+1), Li={0, i≠k−y2(b),i=k,i=1,2,…,N2 is the eigenvector of T corresponding to g2k.
Furthermore, if λ=t1k(k={1,2,…P1}), then,
Y=(y1(x),y2(x),Y1,Y2,…,YN1,YN1,L1,L2,…,LN2,LN2+1,R1,R2,…,RP1,0,V1,V2,…,VP2,VP2+1), Ri={0, i≠ky2(w+1)−α−11y2(w−1),i=k,i=1,2,…,P1 is the eigenvector corresponding to t1k.
If λ=t2k(k={1,2,…P2}), then, Y=(y1(x),y2(x),Y1,Y2,…,YN1,YN1,L1,L2,…,LN2,LN2+1,R1,R2,…,RP1,RP1+1,
V1,V2,…,VP2,0), Vi={0, i≠ky2(w+2)−α−12y2(w−2),i=k,i=1,2,…,P2 is the eigenvector corresponding to t2k.
It is possible to write fi(λ) as follows:
fi(λ)=ai(λ)bi(λ), i=1,2 where
ai(λ)=(aiλ+bi)Ni∏k=1(λ−gik)−Ni∑k=1Ni∏j=1(j≠k)fik(λ−gij)
bi(λ)=Ni∏k=1(λ−gik).
Assume that a2(λ) and b2(λ) do not have common zeros.
Let functions φ(x,λ) and ψ(x,λ) be the solutions of (1) under the initial conditions
as well as the transmission conditions (4) respectively such that
φ(x,λ)={φ1(x,λ), x<w1φ2(x,λ), w1<x<w2φ3(x,λ), w2<x<b and ψ(x,λ)={ψ3(x,λ), x<w1ψ2(x,λ), w1<x<w2ψ1(x,λ), w2<x<b.
Then it can be easily proven that φi(x,λ) and ψi(x,λ), i=¯1,3 are the solutions of the following integral equations;
φi+1,1(x,λ)=αiφi1(wi,λ)cosλ(x−wi)
−[α−1iφi2(wi,λ)+hi(λ)φi1(wi,λ)]sinλ(x−wi)
+x∫wi[p(t)sinλ(x−t)+q(t)cosλ(x−t)]φi+1,1(t,λ)dt
+x∫wi[q(t)sinλ(x−t)−p(t)cosλ(x−t)]φi+1,2(t,λ)dt,
and
Lemma 1. For the solutions φi(x,λ) and ψi(x,λ), i=¯1,3 as |λ|→∞, the following asymptotic estimates hold;
φ11(x,λ)={a1λN1+1sinλ(x−a)+o(|λ|N1+1exp|Imλ|[(x−a)]),
φ12(x,λ)={a1λN1+1cosλ(x−a)+o(|λ|N1+1exp|Imλ|[(x−a)]),
φ21(x,λ)={a1m1λL1+N1+2sinλ(w1−a)sinλ(x−w1)+o(|λ|L1+N1+2exp|Imλ|[(w1−a)+(x−w1)])
φ22(x,λ)={a1m1λL1+N1+2sinλ(w1−a)cosλ(x−w1)+o(|λ|L1+N1+2exp|Imλ|[(w1−a)+(x−w1)])
φ31(x,λ)={−m2m1a1λL1+L2+N1+3sinλ(w1−a)sinλ(w2−w1)sinλ(x−w2)+o(|λ|L1+L2+N1+3exp|Imλ|[(w1−a)+(w2−w1)+(x−w2)])
φ32(x,λ)={m2m1a1λL1+L2+N1+3sinλ(w1−a)sinλ(w2−w1)cosλ(x−w2)+o(|λ|L1+L2+N1+3exp|Imλ|[(w1−a)+(w2−w1)+(x−w2)])
ψ11(x,λ)={−a2λN2+1sinλ(x−b)+o(|λ|N2+1exp|Imλ|[(x−b)])
ψ12(x,λ)={a2λN2+1cosλ(x−b)+o(|λ|N2+1exp|Imλ|[(x−b)])
ψ21(x,λ)={−m2a2λN2+L2+2sinλ(w2−b)sinλ(x−w2)+o(|λ|N2+L2+2exp|Imλ|[(w2−b)+(x−w2)])
ψ22(x,λ)={m2a2λN2+L2+2sinλ(w2−b)cosλ(x−w2)+o(|λ|N2+L2+2exp|Imλ|[(w2−b)+(x−w2)])
ψ31(x,λ)={−m1m2a2λN2+L1+L2+3sinλ(w2−b)sinλ(w1−w2)sinλ(x−w1)+o(|λ|N2+L1+L2+3exp|Imλ|[(w2−b)+(w1−w2)+(x−w2)])
ψ32(x,λ)={m1m2a2λN2+L1+L2+3sinλ(w2−b)sinλ(w1−w2)cosλ(x−w1)+o(|λ|N2+L1+L2+3exp|Imλ|[(w2−b)+(w1−w2)+(x−w1)])
Theorem 2. The eigenvalues {λn}n∈Z of problem L are real numbers.
Proof. It is enough to prove that eigenvalues of operator T are real. By using inner product (7), for Y in D(T), we compute that
If necessary arrangements are made, we get
Accordingly, since ⟨TY,Y⟩ is real for each Y in D(T), λ∈R is obtained.
Lemma 2. The equality ‖Yn‖2=ρn is valid such that Yn is eigenvector corresponding to eigenvalue λn of T.
Proof. Let λn≠gik. When λn=gik, following proof is done with minor changes. By using the structure of D(T) and the Eqs (8)-(12), we get
On the other hand, the expression
is called characteristic function of problem (1)-(4). Moreover, since solutions φ(x,λ) and ψ(x,λ) satisfy the problem L,
for ∀x∈[a,b]
is obtained. Furthermore, since solutions φ(x,λ) and ψ(x,λ) also satisfy transmission conditions (4), we get
Therefore, since characteristic function W(φ,ψ) is independent from x,
can be written.
It is clear that Δ(λ) is an entire function and its zeros namely {λn}n∈Zcoincide with the eigenvalues of the problem L.
Accordingly, for each eigenvalue λn equality ψ(x,λn)=snφ(x,λn) is valid where sn=ψ1(a,λn)−b1(λn)=ψ2(a,λn)a1(λn).
On the other hand, since ai(gik)≠0 ve bi(gik)=0 for ∀i∈{1,2} and k={1,2,…,Ni}, gik is an eigenvalue if and only if φ1(b,g2k)=0, φ1(a,g1k)=0 i.e., Δ(gik)=0.
At the same time, tik is an eigenvalue if and only if φ1(w−i,tik)=0=φ1(w+i,tik) i.e., Δ(tik)=0 such that i=1,2 and k={1,2,…Pi}.
Theorem 3. Eigenvalues of problem L are simple.
Proof. Let λn≠gik and φ(x,λn) be eigenfunction corresponds to the eigenvalue λn. In that case, the Eq (1) can be written for ψ(x,λ) and φ(x,λn) as follows;
If we multiply these equations by φ(x,λn) and ψ(x,λ) respectively and add side by side, we get the following equality;
Then if last equality is integrated over the interval [a,b] and the initial conditions (13) and transmission conditions (4) are used to get
Then, considering that ψ(x,λn)=snφ(x,λn)
if the limit is passed when λ→λn, snρn=−˙Δ(λn) is obtained.
If g1k and g2k are non-simple eigenvalues then φ1(a,g1k)=0, φ1(b,g2k)=0 and so b∫a(φ21(x,λn)+φ22(x,λn))dx=−[α1φ21(w−1,λn)h′1(λn)+α2φ21(w−2,λn)h′2(λn)] is obtained. Since α1, α2 and for all λn, h′1(λn), h′2(λn) are positive, we have a contradiction. Therefore, eigenvalues gik are also simple.
3.
Inverse problem
Using expressions a2(λ), b2(λ) and asymptotic behaviour of solution φ(x,λ), we obtain the following asymptotic of characteristic function Δ(λ) as |λ|→∞; Δ(λ)=−a1a2m1m2λN1+N2+L1+L2+4sinλ(w1−a)sinλ(w2−w1)sinλ(b−w2)+o(|λ|N1+N2+L1+L2+4e|Imλ|(b−a)).
Let Φ(x,λ):=(Φ1(x,λ)Φ2(x,λ)) be the solution of Eq (1) under the conditions U(Φ)=1, V(Φ)=0 as well as the transmission conditions (4).
Since V(Φ)=0=V(ψ), it can be supposed that Φ(x,λ)=kψ(x,λ) (k≠0) where k is a constant.
By the relation U(Φ)=1, we get k[b1(λ)ψ2(a,λ)+a1(λ)ψ1(a,λ)]=1. Since U(ψ)=−Δ(λ), we obtain Φ(x,λ)=kψ(x,λ)=−ψ(x,λ)Δ(λ) for λ≠λn.
Let S(x,λ)=(S1(x,λ)S2(x,λ)) and C(x,λ)=(C1(x,λ)C2(x,λ)) be solutions of (1) satify the conditions S(a,λ)=(01), C(a,λ)=(10) and transmission conditions (4).
Accordingly, the following equalities are obtained:
The function Φ(x,λ) is called Weyl solution and the function M(λ)=−Φ1(a,λ) is called Weyl function of problem L. Therefore, since Φ(x,λ)=−ψ(x,λ)Δ(λ), we set M(λ):=ψ1(a,λ)Δ(λ).
Consider the boundary value problem ˜L in the same form with L but different coefficients. Here, the expressions related to the L problem are shown with s and the ones related to ˜L are shown with ˜s. According to this statement, we set the problem ˜L as follows:
where ˜Q(x)=(˜p(x)q(x)q(x)−˜p(x)).
Theorem 4. If M(λ)=˜M(λ), f1(λ)=˜f1(λ), then Q(x)=˜Q(x) almost everywhere in (a,b), f2(λ)=˜f2(λ), hi(λ)=˜hi(λ),and αi(λ)=˜αi(λ) (i=1,2).
Proof. Introduce a matrix P(x,λ)=[Pij(x,λ)]i,j=1,2 by the equality as follows;
(P11P12P21P22)(˜φ1˜Φ1˜φ2˜Φ2)=(φ1Φ1φ2Φ2).
According to this, we get
or by using the relation Φ(x,λ)=−ψ(x,λ)Δ(λ),
we obtain
Taking into account the Eqs (15) and (16) and M(λ)=˜M(λ), we can easily get
Hence, the functions Pij(x,λ) are entire in λ. Denote
Gδ:={λ:|λ−λn|≥δ, n=0,±1,±2,…},δ>0 and
˜Gδ:={λ:|λ−˜λn|≥δ, n=0,±1,±2,…} where δ>0 is sufficiently small and fixed.
Clearly, for λ∈Gδ∩˜Gδ, |sinλx|≥Cδe|Imλ|x, |λ|→∞.
Therefore, |Δ(λ)|≥CδλN1+N2+L1+L2+4e|Imλ|(b−a), \ λ∈Gδ∩˜Gδ, |λ|≥λ∗ for sufficiently large λ∗=λ∗(δ) and from (18) we see that Pij(x,λ) are bounded with respect to λ where λ∈Gδ∩˜Gδ and |λ| sufficiently large. From Liouville's theorem, it is obtained that these functions do not depend on λ.
On the other hand, from (18)
P11(x,λ)−1=φ1(x,λ)(˜ψ2(x,λ)˜Δ(λ)−ψ2(x,λ)Δ(λ))−ψ1(x,λ)Δ(λ)(˜φ2(x,λ)−φ2(x,λ))
P12(x,λ)=˜φ1(x,λ)(ψ1(x,λ)Δ(λ)−˜ψ1(x,λ)˜Δ(λ))−˜ψ1(x,λ)˜Δ(λ)(φ1(x,λ)−˜φ1(x,λ))
P21(x,λ)=φ2(x,λ)(˜ψ2(x,λ)˜Δ(λ)−ψ2(x,λ)Δ(λ))−ψ2(x,λ)Δ(λ)(˜φ2(x,λ)−φ2(x,λ))
P22(x,λ)−1=ψ2(x,λ)Δ(λ)(˜φ1(x,λ)−φ1(x,λ))−φ2(x,λ)(˜ψ1(x,λ)˜Δ(λ)−ψ1(x,λ)Δ(λ)).
If it is considered that Pij(x,λ) do not depend on λ and asymptotic formulas of solutions φ(x,λ) and ψ(x,λ), we obtain
limλ→−∞φ1(x,λ)(˜ψ2(x,λ)˜Δ(λ)−ψ2(x,λ)Δ(λ))=0,
limλ→−∞ψ1(x,λ)Δ(λ)(˜φ2(x,λ)−φ2(x,λ))=0
for all x in [a,b]. Hence, limλ→−∞[P11(x,λ)−1]=0.
Thus, P11(x,λ)=1 and similarly, P22(x,λ)=1 and P12(x,λ)=P21(x,λ)=0.
Substitute these relations in (17), to obtain
φ1(x,λ)=˜φ1(x,λ), ψ1(x,λ)Δ(λ)=˜ψ1(x,λ)˜Δ(λ)
φ2(x,λ)=˜φ2(x,λ), ψ2(x,λ)Δ(λ)=˜ψ2(x,λ)˜Δ(λ) for all x and λ.
Taking into account these results and Eq (1), we have
Therefore, Q(x)=˜Q(x) i.e., p(x)=˜p(x). Moreover, it is considered that
ψ1(x,λ)Δ(λ)=˜ψ1(x,λ)˜Δ(λ), ψ2(x,λ)Δ(λ)=˜ψ2(x,λ)˜Δ(λ)
and
b2(λ)ψ2(x,λ)+a2(λ)ψ1(x,λ)=0
˜b2(λ)˜ψ2(x,λ)+˜a2(λ)˜ψ1(x,λ)=0
we get a2(λ)˜b2(λ)−b2(λ)˜a2(λ)=0. As we have said above, a2(λ), b2(λ) as well as ˜a2(λ), ˜b2(λ) do not have common zeros. Hence, a2(λ)=˜a2(λ), b2(λ)=˜b2(λ), i.e., f2(λ)=˜f2(λ).
On the other hand, substituting φ1 and φ2 into transmission conditions (4), we get
φ1(w+i,λ)=αiφ1(w−i,λ), ˜φ1(w+i,λ)=˜ai˜φ1(w−i,λ)
φ2(w+i,λ)=α−1iφ2(w−1,λ)+hi(λ)φ1(w−i,λ),
˜φ2(w+i,λ)=˜α−1i˜φ2(w−i,λ)+˜hi(λ)˜φ1(w−i,λ), i=1,2.
Therefore, since φ1(x,λ)=˜φ1(x,λ), φ2(x,λ)=˜φ2(x,λ), these yield that α1=˜α1, α2=˜α2
and h1(λ)=˜h1(λ), h2(λ)=˜h2(λ).
Theorem 5. If {λn,ρn}n∈Z={˜λn,˜ρn}n∈Z, f1(λ)=˜f1(λ) then Q(x)=˜Q(x) almost everywhere in (a,b), f2(λ)=˜f2(λ), hi(λ)=˜hi(λ),and αi(λ)=˜αi(λ) (i=1,2).
Proof. Since λn=˜λn, Δ(λ)=c˜Δ(λ). On the other hand, also since snρn=−˙Δ(λn) and ρn=˜ρn, we get that sn=c˜sn. Therefore, ψ1(a,λn)=c˜ψ1(a,λn) is obtained.
Denote H(λ):=ψ1(a,λ)−c˜ψ1(a,λ)Δ(λ) which is an entire function in λ. Since lim|λ|→∞H(λ)=0, H(λ)≡0 and so ψ1(a,λ)=c˜ψ1(a,λ). Hence, M(λ)=˜M(λ). As a result, the proof of theorem is finished by Theorem 4.
We examine the boundary value problem L1 with the condition y1(a)=0 instead of (2) in problem L. Let {μn}n∈Z be eigenvalues of the problem L1. It is clear that {μn}n∈Z are zeros of Δ1(μ):=−ψ1(a,μ).
Theorem 6. If {λn,μn}n∈Z={˜λn,˜μn}n∈Z, f1(λ)=˜f1(λ) and K=˜K such that K=a2m1m2, ˜K=˜a2˜m1˜m2 then Q(x)=˜Q(x) almost everywhere in (a,b), f2(λ)=˜f2(λ), hi(λ)=˜hi(λ),and αi(λ)=˜αi(λ) (i=1,2).
Proof. Since for all n∈Z, λn=˜λn and μn=˜μn, Δ(λ)˜Δ(λ) and Δ1(μ)˜Δ1(μ) are entire functions in λ and in μ respectively. On the other hand, taking into account the asymptotic behaviours of Δ(λ), Δ1(μ) and K=˜K, we obtain limλ→−∞Δ(λ)˜Δ(λ)=1 and limμ→−∞Δ1(μ)˜Δ1(μ)=1. Therefore, since λn=˜λn and μn=˜μn, we get Δ(λ)=˜Δ(λ) and Δ1(μ)=˜Δ1(μ). If we consider the case Δ1(μ)=˜Δ1(μ), then ψ1(a,μ)=˜ψ1(a,μ) is obtained. Furthermore, since M(λ)=ψ1(a,λ)Δ(λ), M(λ)=˜M(λ). Hence, the proof is completed by Theorem 4.
4.
Conclusions
The purpose of this paper is to state and prove some uniqueness theorems for Dirac equations with boundary and transmission conditions depending rational function of Herglotz-Nevanlinna. Accordingly, it has been proved that while f1(λ) in condition (2) is known, the coefficients of the boundary value problem (1)-(4) can be determined uniquely by each of the following;
i) The Weyl function M(λ)
ii) Spectral data {λn,ρn} forming eigenvalues and normalizing constants respectively
iii) Two given spectra {λn,μn}
These results are the application of the classical uniqueness theorems of Marchenko, Gelfand, Levitan and Borg to such Dirac equations. Considering this study, similar studies can be made for classical Sturm-Liouville operators, the system of Dirac equations and diffusion operators with finite number of transmission conditions depending spectral parameter as Herglotz-Nevanlinna function.
Conflict of interest
There is no conflict of interest.













 DownLoad:
DownLoad: