Tsunami damage estimation in Esmeraldas, Ecuador using fragility functions

1.   Introduction

Earthquakes remain as the leading cause of triggering tsunamis worldwide ^[1,2]. According to their area of impact, tsunamis can be classified as local, regional, or teletsunami ^[3]. Despite their varying levels of risk, local tsunamis have caused 90% of human losses in history ^[3,4]. Also, nearly 90% of earthquakes occur in shallow subduction zones ^[5]; thus, generating the most destructive tsunamis in history ^[6]. In the last two thousand years, 83% of the tsunamis recorded in the Pacific Ocean had seismic genesis ^[5]. The South American west coast is an area of high seismic and volcanic activity due to the presence of the Ring of Fire in the Pacific Ocean ^[7]. This feature comprises long borders of tectonic plates in the Pacific basin, which are also subduction zones ^[8]. Approximately 17,000 earthquakes of Mw > 4.5 (i.e., located at 100 °W Longitude and extending from Panamá to Patagonia) have been recorded as reviewed-status in the USGS database in this area ^[9]. The majority of these events showed aligned with the border of the tectonic plates.

Ecuador is located on the northwest coast of South America, where the Nazca plate subducts under the overriding South American plate. In this zone, earthquakes of Mw > 7.0 have been recorded ^[10,11]. Six other major events associated with near-field tsunamis have occurred near the Ecuadorian coast (i.e., Jan. and Feb. of 1906, 1933, 1958, 1979, and 2016) ^[12,13]. Twelve earthquakes of Mw > 6.9 and less than 70 km in-depth have been registered in the coastal zone of Ecuador from 1900 to 2018 ^[9]. The northern Ecuadorian coast has been particularly acknowledged as a scenario prone for most of the megathrust events in the region, as evidenced by the Muisne earthquake in 2016 (Esmeraldas Province) ^{[14,15,16,17,18,19]}. Previous investigations have comprehensively assessed tsunami hazards in Ecuador, including that of the earthquake in Muisne 2016 ^{[19,20,21,22,23,24]}. Results from those studies indicated that there is a low risk of earthquakes higher than Mw = 8.0 from faults in the northern zone of the Ecuadorian coast, where the subduction margin remains the main source. The more destructive tsunamis recorded in the Ecuadorian coasts in the last 426 years were near field events and their impacts in past centuries were low due to the scarce development of the region. Additionally, Esmeraldas province has been protected from tsunamis due to distinct geomorphological features (e.g., promontory towards South Atacames, or a submarine channel in their river mouth).

Briefly, a tsunami damage estimation (i.e., often related to building vulnerability) is performed through a tsunami hazard assessment where the negative impacts on population and buildings in a particular zone of interest are analyzed. This tsunami hazard assessment can be conducted following three directives: a) through a probabilistic tsunami hazard analysis (PTHA), b) using a worst-case scenario approach (deterministic approach), and c) by sensitivity analysis ^[25]. Also, damage estimation can be calculated using Fragility Functions (FFs). FFs are statistical models extensively used for quantitative risk assessment that correlate an intensity tsunami parameter to the probabilities of damage in buildings and population for several damage levels ^{[26,27,28,29]}. The statistical model used in FFs has been evolving from ordinary linear regression, normal/lognormal probability density functions, Generalized linear models, to General Additive Models ^[30,31]. Remarkably, empirical FFs remains the most commonly used model in the literature ^[27]. However, an alternative family of analytical FFs, derived from synthetic tsunami data of damaged structural analysis of buildings, as described by Macabuag ^[27], have been generated in several previous research ^{[32,33,34,35,36,37,38,39]}. These analytical FFs have the tsunami intensity measure (h) in common, but also explicit differences in terms of explanatory and response variable characteristics and the statistical model adopted. Medina (2019) ^[40] developed a numerical method (i.e., also termed as theoretical or analytical) for obtaining fragility curves for typical buildings in the study area (two-Storey RC), showing the role of selected damage models over FFs and the validity of h as an intensity measure. In other cases, researchers have recently developed analytical FFs for residential masonry buildings following Japanese guidelines for modeling tsunami forces, large-scale approach, building classification by age, design criteria and Storey number, and using the MonteCarlo technique ^[41]. Another study at the Mediterranean coast proposed a specific procedure to generate analytical FFs, which was applied for three characteristic masonry buildings. The resulting FFs were compared with empirical FFs, validated through similar results, and ultimately compared to other studies ^[42].

Approximately 30% of the total population in Ecuador (i.e., grouped in 99 population centers) are settled in the coastal region. Nearly 4.2 million people live within 10 km from the coast ^[43]; whereby a significant fraction is concentrated in few cities, e.g., Esmeraldas city, Bahía de Caráquez, Manta, La Libertad, Salinas, and Playas (i.e., combined projected population of 675,670 inhabitants at 2020) ^[43]. Among these, Esmeraldas city (northern coast) is of particular interest considering its population (i.e., among the ten most densely populated cities and highly touristic), strategic industrial activities (port, fishery, and oil refinery), and geographic location of high seismicity ^{[10,19,20,44,45]}.

The current study conducted a tsunami damage estimation on buildings and population in Esmeraldas city-Ecuador using Fragility Functions. Numerical simulations of near-field tsunami propagation and inundation were performed for several extreme scenarios based on historical events, where the worst-case was selected. The potential impacts of a tsunami on population and infrastructure were estimated. A numerical simulation was performed for tsunami hazard assessment. Empirical Fragility Functions (FFs) were used for the first time at this important coastal location in order to quantify damages. Results from this study would be highly useful for designing or improving tsunami risk reduction strategies and planning for better policies and use of coastal zones, including risk and disaster management.

2.   Materials and methods

2.1.   Area of study: demographics, infrastructure, and economics

2.1.1.   Area of Study and demographics

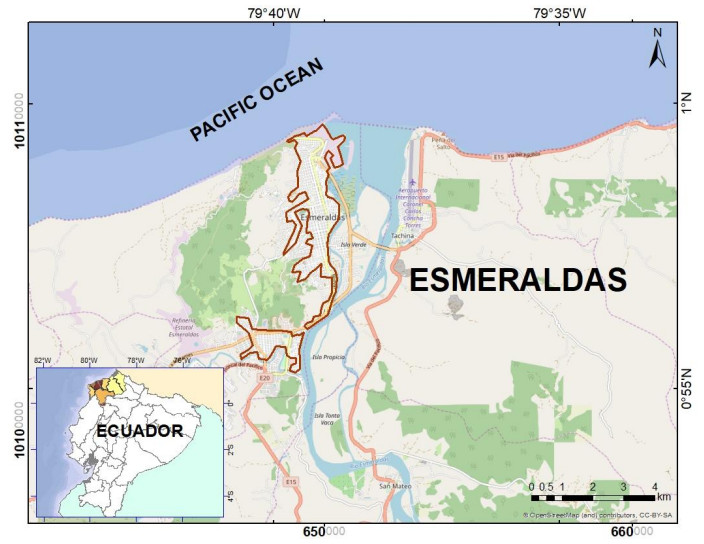
Esmeraldas city (68 km²) is located along the northern Pacific Ecuadorian coastline, next to the Esmeraldas river, and comprises five urban parishes (Figure 1). The population in Esmeraldas city projected to 2020 is 180,550 (48% male and 52% female; 38% are under 15 and over 64 years; 670 female and 763 males are disabled) ^[43], making it the third most populated city on the Ecuadorian coastline. According to the Ecuadorian Social Indicators System (SIISE) ^[46], the extreme poverty at Esmeraldas encompasses 25.3% of the total population, in comparison to the 10.1% for the whole country as in 2017.

2.1.2.   Infrastructure

While 12% of households (e.g., houses, departments, and rooms) in Esmeraldas city are low in quality (e.g., huts), approximately 50% of households have walls, roofs, or floors in regular or bad condition ^[47]. These statistics indirectly reflect the social and physical vulnerability of the inhabitants and buildings ^[48]. The accessibility to Esmeraldas City is good due to its roads in excellent condition. Esmeraldas is a highly touristic destination, encompassing 9% of the total national hotel capacity (i.e., 358 establishments, 6,561 rooms, and 20,385 beds), and highly visited beaches (i.e., Las Palmas, Camarones, and Las Peñas Beaches) ^[49].

2.1.3.   Economics

The main productive activities at Esmeraldas are services (i.e., restaurants, food trucks, car workshops), trade (e.g., small commerce), and labor ^[50]. Remarkably, a key strategic national industry is the Esmeraldas Refinery Plant (RE), which operates together with the two main oil pipes (SOTE and OCP) connecting to the Balao oil port for maritime oil export. According to Valdivia ^[51], the national exports summed up to US ＄ 1.5 billion in 2013, with a daily processing capacity of 110,000 oil barrels for the RE. However, official statistics in 2017 reported incomes from oil exports reaching US ＄ 6.19 billion, with RE processing approximately 67% of this total ^[52,53]; thus, indicating the existence of crucial infrastructures in Esmeraldas city.

In 2017, the international arrival of tourists to Ecuador grew by 13.4%, which was approximately 10% more than the average in Latin America. After banana and shrimp industries, the tourism industry ranked third in foreign exchange earnings between non-oil goods and services with 1,633 million dollars ^[54].

2.2.   Data on population and buildings

The sources of data used in this investigation for demographic and building spatial databases and administrative-geographic databases were the National Institute for Statistics and Census (INEC) and the National Information System (SNI), respectively. Both institutions offer web pages and geoweb services to access and download data freely. REDATAM, a software for interaction and queries provided by INEC, was used for accessing the Census databases, while ArcGIS software was used for spatial and attribute queries and analysis of the geographic INEC database. REDATAM queries return tabulated data aggregated at the sector census level, where spatial databases for population and buildings are disaggregated at block and lot levels, respectively. A census sector is a spatial territory with defined limits that includes up to 70 houses for the case of dispersed sectors and approximately 150 houses for the case of blocked sectors ^[55].

Data regarding buildings (i.e., amount, type, material of walls, etc.) in each sector was also obtained from REDATAM (Census INEC, 2010). There were 46,848 households at Esmeraldas city, from which 2,825 are rural. The distribution (%) by walls material and type of those households are shown in Figure 2.

Approximately 81% of the buildings at Esmeraldas are made of concrete, brick, or block walls, where 53% of the structures have shown structurally compromised walls or walls in regular conditions. Also, there were 1,109 households in Tachina (a rural parish of Esmeraldas county), 71% have walls made of concrete, bricks, or blocks, while the others are made of adobe, wood, coated and uncoated cane, and other materials. Regarding types, 15% of them are precarious (Mediagua, ranch, covacha, hut). The other 85% are mainly houses/detached bungalows. Regarding the status of walls, 60% were compromised or in regular shape. The population growth rate projections do not apply to buildings data.

Because of the different data aggregation levels of REDATAM and INEC spatial databases, the latter was preferred. However, REDATAM data were also reviewed to validate the results. The quantity of attribute data is larger in REDATAM. Briefly, Esmeraldas city data is distributed in 328 units of study or census sectors (polygons in GIS) in REDATAM, while the spatial database layers have 2,145 and 44,768 polygon-type objects for population representing the blocks and individual properties (lots), respectively. The difference in the aggregation of population data between REDATAM and INEC was an essential factor to consider during the analysis of the results (Figure 3).

Other components in the population (e.g., tourists or local visitors to the city and Las Palmas beach) besides permanent residents were also considered. Tourism, as an influencing parameter on vulnerability, has been previously identified ^[56]. Tourism at Esmeraldas county is local and from neighboring provinces and shows peaks during holydays and dry season (summer). Esmeraldas has an international airport and one of the four most important seaports in the country, where 5,418 foreigners entered the airport in the city of Esmeraldas in 2016, and 11,330 by the sea in 2015 ^[57]. Likewise, 7,117 Ecuadorian citizens were mobilized by air for 2015, while 1,100 by sea.

Therefore, the selected demographic scenario included an estimation of the population of tourists in Esmeraldas during one of the highest peaks. According to the Ecuadorian Ministry of Tourism, high season occurs during the following nine national holydays: Carnival (February), Good Friday (April), Labor Day (May), Independence Day (May), Declaration of Independence (August), Independence Day of Guayaquil (October), Day of the Dead (November), Christmas and New Year (December). Also, these national holidays are planned by the Ecuadorian Congress as long weekends, i.e., each holiday period includes the Saturday and Sunday preceding or following the holiday. Consequently, there were officially 29 and 31 days of national holidays during 2017 and 2018, respectively. Both permanent residents and tourists during high season (i.e., national holidays) were considered for the selected worst-case scenario in terms of people exposed to Tsunami risk.

2.3.   Tectonic aspects

Mainland Ecuador is located on the South American plate, which is surrounded by the Nazca, Caribbean, North American, African, Scotia, and Antarctic plates. This group, like all the plates on earth, has relative movements between them and they are mutually influencing each other. The Nazca plate's movement at Equador (Latitude 0°) is in east-northeast direction (79.5°–87.1°) with a horizontal velocity 50–67 mm/y ^[58]. The South American plate (SAm), located on its east limit, is moving in the opposite direction. At the same time, a section called the North Andean Block (NAB) is constrained and pushed in the Northeast direction parallel to the margin among both plates ^[59]. Nazca and SAm plates converge and collide in a geologic feature called the Ecuador-Colombian trench, which extends around 7,000 km from Colombia to Chile. The global model NUVEL-1 estimates the velocity of the convergence in 78 mm/y in the N87E direction ^[60]. Other characteristics like subduction angles are expected to be not so significant compared to divergent zones. The depths of subduction zones are between 150–200 km ^[61] and considered shallow. In general, the subduction angle of the plates has been estimated in less than 30°. Kendrick, Bevis ^[58] presented a range of estimates values for velocity and direction of Nazca relative to SAm plate for various locations along the boundary.

One of the significant features on the Nazca Plate in the study zone is the Carnegie Ridge (CR), which is according to Ioualalen ^[12], a 200 km-wide buoyant ridge carried by the down-going oceanic Nazca Plate. This feature stands over the Nazca plate for approximately 3,000 km and subducts in front of the Ecuadorian coast in the west-east direction. This feature and the Grijalva fracture (GF) zone ^[62] to the south of the equator are important factors on the tectonics of the whole area ^[59,63,64]. The Nazca plate is consumed under the South American plate, where intense crustal deformation occurs, and represents the most important seismogenic source of the country ^[44,65,66].

2.4.   Seismicity

Ecuador is a country with high seismicity strongly associated with the trench near and parallel to the coastline. Strong earthquakes (EQ) have historically occurred ^[12,67] there. The USGS database for EQ using criteria Mw > 2.5, period 1900–01–01 to 2019–01–31, at the region in 1.5 to -5 latitude and -83.3 and -77.6 longitude, and any depth, reported 1,468 events. However, constraining those results to those occurring 100 km offshore and 5 km inland, resulted in 498 events. The Ecuadorian north coast section (i.e., the current study zone) between 0°–0.5° N, has been identified as one with the highest probability of occurrence of big EQ ^[12,68]. Bethoux, Segovia ^[14] mentioned two coastal regions having contrasting seismicity and tectonism at north and south of 0.5° S parallel. Otero, Restrepo ^[10] indicated northern Ecuador and southern Colombia as regions of intense seismic activity.

Among the significant EQ recorded in the study area are: the 1906 strongest event of Mw 8.8, which has been recently proposed as Mw 8.4 ^[45] with a rupture area of approx. 500 Km as found by Kelleher (1972) at ^[18,67], the 1942 EQ Mw 7.8 which had a probable rupture extension of 80 km Beck and Ruff, 1989 ^[12], the 1958 EQ Mw 7.7 which ruptured a length of 110 km ^[12,18], the 1979 EQ Mw 8.2 ruptured approx. 230 km ^[18], the 1998 EQ Mw 7.2 in front of Bahia de Caraquez ^[12,69], and the 2016 EQ Mw 7.8 which rupture length was 100–120 km ^[13,70] and according to several authors, overlaps the 1942 EQ segment ^{[13,45,70,71]}. Toward the south, strong activities have been also recorded with events of magnitudes between 6.9–7.5 around the Gulf of Guayaquil ^[12] and further along Perú coast ^[67].

2.5.   Historical tsunamis in Ecuador

Espinoza ^[22] indicated five tsunamis recorded since 1906; Ioualalen ^[12] and others mentioned that four of them had taken place in the north region of the subduction zone in front of Ecuador. Contreras ^[72] in his chronology of tsunamis for the 1586–2012 period on the Ecuadorian coast, identified a total of 58 tsunamis arriving at Ecuadorian coasts. In the 20^th century, 10 of them were near-field tsunamis. The last recorded tsunami was associated with the 2016 Muisne EQ, which due to its shallow and small slip on fault plane and little vertical displacement offshore, caused a small wave event ^[15,70]. Pararas ^[24], based on measured crustal deformations and statistical estimations, appointed the current study zone as showing a rising risk of tsunamigenic earthquakes. Nocques et al. ^[70], based on slip and moment balances of big EQ recorded in the area, mentioned a seismic cycle in the zone lasting more than a century, in which a cluster sequence of EQs could still occur; thus, implying a high tsunami risk.

2.6.   Selection of tsunami extreme impact scenario

In the approach by deterministic scenario-based models, hazards causing the worst-case scenarios are found from historical events. This task is accomplished by numerical tsunami simulations. For the selection of the characteristic of the source earthquake and the geometry of fault plane (i.e., where displacement would be the tsunami generator, bibliography covering tsunamis, seismicity, tectonics, scaling laws), previous studies in the area, and statistical analysis of the records existing in world catalogs, such as CMT and USGS, were reviewed. Then, a group of parameters for some scenarios was tested and checked using the scaling laws of Papazachos, Scordilis ^[73]. The location of the hypocenter was moved around the location of the 1906 EQ. The locations suggested by Otero, Restrepo ^[10] and Arreaga, Ortiz ^[19] were also tested. The methodology for the distribution of slips and fractioning fault posed by Jimenez, Moggiano ^[74] was partially tested. Finally, the worst ever expected scenario was selected because it met the criteria of being one with the highest values of inundation depth (Id) and also the largest total inundated area. In the selected scenario corresponding to a near field seismic source, the possible consequences caused by ground shaking on buildings and people were not considered.

2.7.   Tsunami numerical simulation

Tsunami numerical simulation was conducted using the TUNAMI N2 code ^[75], which is based on shallow water theory applied to tsunamis (long waves). The basic equations governing tsunami phenomena propagation are the continuity and momentum conservation equations. To discretize the differential equations, the model used the staggered leap-frog scheme. The set of equations of long-wave theory, written in a Cartesian or spherical reference system (the latter is used in the current study), was usually resolved with initial conditions (initial elevation) representing a free surface displacement, equivalent to vertical residual deformations of the ocean bottom resulting from an earthquake. The starting point for the numerical calculation of tsunami propagation at the initial time (t = 0) is the deformation caused for a submarine EQ, transmitted without change to the sea surface (η) at the place and time the event occurs. The set of causing fault parameters and its geometry were determined as follows. Okada ^[76] deformation equations were used to determine the distribution of seafloor deformations. However, only vertical compounds were considered because, according to Tanioka and Satake ^[77], the horizontal displacement effect can be neglected when they are small in relation to the vertical ones and the involved slab is not steep, this is the case in the current study zone ^[17]. TUNAMI N2 operated with nested grids for applying more detailed data and, therefore, obtaining more detailed results in the region of interest.

Bathymetry data for simulations were obtained from the GEBCO database (i.e., 30 arc-second grid size resolution) and INOCAR (i.e., detailed bathymetric data for coastal study area). Topography data was obtained from ASTER GDEM (i.e., 30 m grid size). The area was analyzed by four computational domains arranged as a nesting grid of 810 m, 270 m, 90 m, and 30 m. The tidal level used for conducting simulations was mean sea level. Simulations results could not be validated due to the little or no available information related to those historical seismic events in Ecuador ^[78]. The values calculated for maximum inundations were used in the FFs, as they become the explanatory variable (Tsunami Intensity Measure-TIM) found in the x-axis of Fragility Functions ^[79].

2.8.   Fragility functions

Simplifying Macabuag (2017), Fragility Functions (FFs) are statistical models that explain the relationship between the probability of tsunami damage and a tsunami intensity parameter. In the current study, FFs developed in a previous study with the empirical approach are used. In the approach proposed by Koshimura et al. ^[26], the damage probability of structures or person fatality ratio related to a hydrodynamic feature of tsunami, is expressed as the cumulative probability P of occurrence of damage, as seen in the next equation (1):

In this study, and as previously used by Suppasri, Mas ^[80], ϕ is an exponential function of the standardized normal distribution. At a seismic field, x and ln x represent the maximum ground acceleration, velocity, or seismic intensity, which stands now at tsunamis field for the hydrodynamic feature of the tsunami used, i.e., inundation depth, current velocity or hydrodynamic force, and μ and σ are the mean and the standard deviation of x (or ln x) ^[80].

There is no consensus about the best method to generate empirical FFs ^[27]. The main changing factor among different alternatives is the statistical model used, i.e., Linear models, Generalized Linear Model, and Generalized Additive Model ^[79]. Linear Regression Model has its constraints; however, in the absence of available analytical options, those generated under this approach in a previous study considering similar building environments to the current study area were selected (section 2.9).

2.9.   Methods for damage estimations

Fragility functions were used to estimate the probability of damage caused by a tsunami using the depth of flood as an Intensity Measure (IM). In the absence of FF for the area of study (analytical or empirical), the curves generated for Banda Aceh (Indonesia) by ^[81] for the estimation of the probability of damage in buildings and impact on population were used because of the similar characteristics of the building environment. (Table 1).

The next protocol was followed to calculate probable damages using these FFs: a) to obtain the maximum and average flood depth in each spatial unit of analysis, i.e., census sectors, blocks, lots (minimum unit of disaggregated information); b) to generate the corresponding damage probability value from Fragility functions Y-axis using maximum flood depth value (X-axis) as input; c) to multiply the value of damage probability obtained in b by the number of people or houses/buildings in each block and census sector (i.e., for instance, for a census sector in Esmeraldas of 10 houses and 34 people, the maximum inundation depth was modeled as 3.9 m, while the damage probability was calculated as 0.79 and 0.55 for building and people, respectively. Then, the affected buildings and people would be estimated as 8 and 19, respectively); and d) the results in step c (i.e., affected houses and people) were summed up to obtain a total estimate of damage in buildings and affected population in the study area. Steps c and d were applied only for aggregated data (block and census sector data).

The results were plotted on maps. The damage estimation was performed in a Geographic Information System (GIS) environment, by intersecting the layers corresponding to buildings and population data with the flood layer from the simulation. With the maximum flood depth data for each block or census sector, the probability of damage was estimated using FF.

For the current investigation, the concepts of affected people and buildings were used for the assessment of impacts. UNDRR ^[82] defines directly affected people as the population suffering injury or any health effects, evacuation, displacement, or direct damage to their livelihoods (e.g., economic, physical, social, cultural, or environmental standards). Similarly, affected buildings are all the structures that have undergone any level of damage because of a tsunami or any collateral effect. Exposure, where or when people, infrastructure, housing, production capacities, and other human assets are located in hazard-prone areas, during a disaster interacts with Hazards and Environmental Systems to produce losses and damages, which generally include social and economic elements ^[83]. In the current investigation, an exposed element is referred to as those that are inside the layer representing hazard (i.e., inundation depth layer), without previously considering a measure of damage or loss.

3.   Results and discussion

3.1.   Tsunami numerical simulation

3.1.1.   Co-seismic deformations

Four domains in each run were tested (D1 to D4 in Figure 4), uplift and subsidence (bottom vertical displacements) values for each one were obtained, which were the inputs for the tsunami simulation. Domains (D) follow the nested setting, with D1 being the largest and D4 the smallest.

Figure 5 shows the outputs for the deformations calculated using Okada equations at each domain of the scenarios tested (16), only the maximum value in each result is plotted, uplifts above zero, down subsidence values, also the data table is attached. The maximum value for total uplift (12.21 m) appeared in the Domain 3 of Case 8, probably due to a shallow focal depth. The top-depth of that source is 0 km, and it is located inside this domain, approximately on the trench. Remarkably, the maximum uplift at each case occurred at this domain, except for Case 4, which hypocenter is out of D2. The uplifts on Domain 4 for almost all cases (except for C8, C14, C15) were the smallest compared to the other domains. That domain, nested in the others, showed the best resolution and hosted the study area. Subsidence resulted in values smaller in magnitude than uplifts and with a maximum on Domain 4 for Cases 1 and 8. The subsidence phenomenon is undesirable on the coastal side due to enhanced tsunami flooding effects. The absolute values of uplift ranged from 0–12.21 m, while the subsidence ranged from 0–6.85 m, occurring in the adjacent area to the trench related to the location of the hypocenter tested in the simulation. Analysis of results in Esmeraldas city study zone (D4) show uplifts ranging from 1–3 m and small spots of subsidence near to submarine canyon adjacent to the Esmeraldas river discharge in some models.

The deformation effects of sea bottom and land extended by several hundreds of kilometers offshore and inland, this was represented for Case 8 and Case 11 in Figures 6 and 7, respectively. Blue lines are subsided areas and red lines are uplifted areas. A cross-section (green line) is plotted on each graph. All cases showed deformations occurring mostly to the east side of the trench. Remarkably, the net vertical movement of the bottom on Domain 4 at Case11 is 5.63 m, the second biggest among its similar.

3.1.2.   Tsunami inundation

For each scenario, information about the levels of inundation depths in Domain 4 was obtained and plotted on maps overlaying Esmeraldas city. Then, the extent of the inundated areas was calculated; thus, allowing to select the case with the highest values of inundation depths. The map for the case with the highest inundation depth values is shown in Figure 9.

From this analysis, Case 11 (Mw 8.7) was identified as the worst scenario due to one of the highest values of inundation depth and also the largest total inundated areas; therefore, this result (layer) was used to develop the tsunami damage estimation. Case 11 is hypothetic, corresponding to a shallow earthquake source occurring around 100 km offshore Esmeraldas city nearby the Ecuador-Colombia trench, where the fault plane was fragmented in 3 parts conserving the estimated seismic Moment (Mo), and with the highest dislocation values among the tested scenarios. The focal and fault parameters for the selected tsunamigenic earthquake are shown in Table 2, the fragmented fault plane in Figure 8.

In this scenario, 2.7 km² of Esmeraldas city territory would be inundated at some level, where the maximum value for Id was 7.65 m (Figure 9). The classification of these data confirmed that 10% of the inundated area has an Id lower than 30 cm, and 48% has an Id higher than 2 meters. Approximately 4.8 km of the Esmeraldas northern coastal line was among the zones affected in this scenario. Also, the Esmeraldas Port, the Las Palmas urban beach and neighborhood, a portion of rural beaches, and Balao oil Port facilities were affected. At the river basin, some zones on the Esmeraldas river borders were also affected. The inundation depth ranges were also analyzed (Figure 9b). Most of the affected areas were located on the beaches and riverine shorelines. The Esmeraldas river is well known for this kind of geographical features, allowing tsunami waves through them to reach inner lands to an inshore distance of approximately 8 km from the estuary mouth, a tsunami behavior appointed in previous studies ^[8]. Although an inundated zone according to the output of the model was located on the east side of the Esmeraldas river mouth, the data resolution of the used DEM in that area was not precise enough to reflect topography and confident results.

Following this analysis and in order to work overlaying layers in the GIS environment among the Inundation layer and other layers as blocks and lot data layers, the hazard layer was resampled. While inundation values itself did not suffer any change, there is a difference in the extent of inundated surface. Specifically, the total flooded area was 8% larger, changing from 30 m to 5 m in pixel size. Briefly, resizing did not improve the accuracy or quality of raster data; also, this is a well know issue known as a modifiable areal unit problem related to the effects of zoning or scaling changes in spatial data.

4.   Tsunami damage estimation

The damage estimation considered those inland areas reached by the inundation layer. People exposed to inundation depths higher than 0.3 m (i.e., a level higher than 30 cm from the ground) are likewise exposed to danger. For buildings, previous studies have suggested 2–3 meters inundation depth as a critical level compromising their structures ^[81,84,85]. The results were separated and tabulated considering the source of data of the elements exposed (people and buildings), specifically, the level of aggregation and the critical levels of inundation depth above mentioned. The estimated damage using FFs is presented in Table 3 (Household or HH is a living place, and Pop is population).

In the damage estimation results using Sector data (Table 3), the total population that would be exposed to the inundation caused by tsunami was 11,938 people; where 44% (5,265) of the total would be affected according to estimations using fragility functions. The majority of the affected people was the young segment of the population (<20 years) and 51% women. In the case of households, from the total exposed 3,050 households, 50% (1,532 households) would be damaged at any level by tsunami forces. This population and buildings are located at zones near to the beach and riverside and correspond to areas with a high population density that has been identified under risk in previous tsunami risk studies ^[68,86,87].

Results using more disaggregated data, i.e., block census data (Table 3), showed smaller figures compared to those above analyzed. Exposed and affected values decreased the relationship among quantities. For this case (analysis by block data layer), exposed households would be affected, and therefore, 41% of exposed people would also be affected. Considering the population projection for 2018, 1827 persons would be affected, assuming no changes in density or spatial distribution of the population. There are no more attributes related to population or building structure that allowed any additional analysis; however, it can be assumed that demographic characteristics are also not variables, and the segments and quantities by gender and age would be similar for sector analysis.

The statistics between sector and block census data in Table 3 were different; however, the proportions or percentages are similar, as shown in Table 4 (Damage/Exposed people and Damage/Exposed buildings ratios). There were differences in the order of 3 centesimal in the damaged/exposed elements ratio for both buildings and people, while Blocks data results were always below 50% of the results obtained from the Sector data (Table 4). This can be explained by the fact that a Census Sector is defined as a territorial spatial extension with defined limits and comprising up to 70 houses for the disperse case. If it is geographically continuum, comprising one or more blocks, and around 150 houses, is known as a blocked case ^[88]. By examining block data for Esmeraldas city, the distribution of data inside a block (the unit of analysis) showed dispersion. Then, for households, the mean value was 22, standard deviation 22.39, and range 243, while the same statistical analysis for people was 75, 80.34, and 868, respectively. Therefore, that variability is masked on the aggregated data, but appear when working with resampled hazard layer and more disaggregated data.

A comparison of the range of values for areas at sector and block datasets was 41.99 and 1.26 km², respectively, which is significantly different and also helps to explain the differences in results obtained from each source. In a detailed analysis of buildings considering its use or type in the affected zone, the data downloaded from Open Street Map was incorporated to complement Google earth and available official sources. Consequently, more information about the affected zones was obtained (Figure 10). Clearly, households, commerce infrastructure, services, and important industrial facilities were majorly affected. The following key infrastructure affected in the selected scenario was observed: offices of Government (2), Ministry (2), Township bureaus (2), Provincial justice Court, Police stations (2), Consulate (1), Provincial Sport Associations (3), Port and Navy (8) and others (5).

Regarding the temporal population (Tourists), the most severe scenario results in 2,460 people exposed and correspond to a Carnival holiday. Similar to 2017, even after considering an average day, there would be approximately 1,731 people exposed. The analysis of tsunami inundation on land parcels showed a total of 966 buildings exposed to inundation, Id data distribution is skewed toward lower ranges of depth (right-skewed), and 62% of buildings underwent an inundation layer lower or equal to 2 meters. In contrast, 82% of exposed buildings were households type.

The values on the table of Figure 11 correspond to households (living places), and other 7 classes of function/use for buildings, as shown in lot database, Inundation depth ranges, and the number of elements (buildings) located in that range. The largest quantity of affected buildings has Inundation depths (Id) between 0.3–1 m, a big portion of total affected (78%) is concentrated in the lower levels of Id, i.e., between 0–3 m. Residential households were the dominant type found in use in the affected area and in each class of Id.

Compared to other similar investigations in Esmeraldas city, these results are significantly different if the inundation map published by SGR in 2012 is considered ^[86]. The affected buildings in Esmeraldas city would be 15,187, with 13,657 and 869 of them showing a high and low probability of inundation, respectively. Other 661 buildings would be located in the limits of probability levels. It was not possible to estimate these same figures for Arreaga et al. ^[78] (the whole map was not available in bibliographic sources), where the inundated area is smaller than the SGR source and larger than the current results. Such differences observed among this current study and others would be attributed to differences in the inundation layer, which was obtained following different parameters of source earthquake ^[19] and applied methodology for mapping (as seen at SGR, 2012).

Even when using empirical fragility curves from a foreign event based on similarities in building structures, materials, and techniques, this kind of relationships (FFs) also reflect other particularities belonging the site of tsunami occurrence as building types and design, applied construction codes, and coastal landforms. Nevertheless, all these variables involved are necessary to develop analytical FFs for at least those buildings similar in Esmeraldas city and those considered strategic in hazard management.

5.   Conclusions and recommendations

This study covered numerical tsunami simulations from 16 case scenarios and the damage estimation from the worst-case using fragility functions (FFs) and different levels of aggregated data of exposed elements. The worst scenario obtained was a case of Mw = 8.7, which could cause inundation depths as high as 7.6 m, where the inundation can be spread over a surface of 2.7 km² at Esmeraldas city. The damage estimation revealed that a fraction of the total population would be exposed to the inundation caused by a tsunami. Results in the same scenario change depending on the aggregation level of the data. The more aggregated, the more affected elements. Briefly, 11,938 people would be affected (44% of the total), at which the majority would the young segment of the population (<20 years). In the case of buildings, the total exposed reaches 3,050, 50% would be damaged by tsunami forces. These populations and buildings would be located at zones near to the beach and river side, which correspond to areas of high population density. The result from more disaggregated data was less than 50%. While the strategic productive structures (oil industry) would not be directly damaged in this scenario, populated and touristic zones would be highly impacted. Indeed, an event of this nature can disrupt the operations of strategic and no strategic labors. Vera et al. ^[89] presented various limitations that should be considered when using FFs; those were appointed at previous study ^[29] and also considered in this. Besides, there is a different result depending on the aggregation of data because working with different zoning o scaling of data produces very different results. The results obtained for damage evaluation were satisfactory in pragmatic terms and provided preliminary estimates of damages caused by a potential tsunami. The results of this study should be used only as a reference because of the use of FFs from Banda Aceh, Indonesia. Also, the differences in the aggregation level of data can significantly change these results. An additional investigation should be conducted to overcome all the limitations identified in the current study. Effective management plans can be designed only from accurate estimates of the impacts of a tsunami. The following additional recommendations are proposed.

a) To develop analytical tsunamis fragility functions for the most important buildings in terms of their functionality or utility for vertical evacuation.

b) To generate detailed databases with information on buildings and their environment, including variables according to the reality of the site of study. Spatially disaggregated to the building and building-level are required to evaluate the vulnerability to the tsunamigenic threat as well as other (multi) threats.

c) To incorporate the impact on tangible and intangible tourism assets in the tsunami damage estimation, which would have a significant effect on the local economy.

d) To develop a detailed database on the tourist population that includes temporal, spatial, and attributes characteristics, and to perform analysis to better temporal, spatial, and social scale.

Acknowledgments

Dr. Fujii Y. and Dr. Shibazaki B., the whole staff of Building Research Institute, the Japanese International Cooperation Agency, and Dr. María del Pilar Cornejo are acknowledged for their advice and contribution to the current investigation.

Conflict of interest

The authors declare no conflict of interest.