Trivariate distribution modelling of flood characteristics using copula function—A case study for Kelantan River basin in Malaysia

1.   Introduction

Water-related operational planning, managements or either flood defence infrastructure designs often demands accurate estimations of the flood exceedance probability for assessing the hydrologic risk ^[1,2,3]. The probabilistic assessment often provides a flexible way to inference and extrapolates long term historical streamflow characteristics by fitting the most justifiable probability distribution functions and estimating their specified flood exceedance probability or return periods. The flood frequency analysis or FFA is an approach to relate flood design quantiles and their frequency of occurrence or non-exceedance probability by fitting the probability distribution functions ^[4,5]. The unreliability of univariate FFA are already highlighted through numerous studies (e.g. ^[4,6]), which cannot sufficiently characterize the full structure of flood hydrograph and might reveals the underestimation or overestimation of associated risk of correlated flood characteristics. In actuality, the flood is a multidimensional random consequence usually characterized completely through its trivariate mutual correlated vector such as flood peak discharge flow, volume and duration of flood hydrograph ^[7,8]. The multivariate distribution modelling often facilitates an effective approach in the prediction of hydrologic risk through visualizing the mutual dependencies among its multiple intercorrelated characteristics based on the joint probability density functions or JPDFs and joint cumulative distribution functions or JCDFs ^[5,9] also, to demonstrate the uncertainties interlinked with these hydrologic events. More especially, from the hydraulic designing perspective where, the accountability of multivariate design variables is often an insightful strategies ^[10,11]. The necessity of estimating flood design hydrograph instead of the single variable flood modelling or FFA i.e., either flood peak /or volume /or duration as a function with non-exceedance probabilities motivated numerous demonstrations (e.g. ^[6,12,13]), towards the incorporation of distinguished varieties of traditional bivariate or trivariate distribution functions for establishing the joint relationship among flood characteristics.

All the above distribution-based flood modelling approaches often surrounded with several statistical limitations such as (a) each flood characteristics must assume to have gaussian (or normal) distributions (b) statistical parameter of univariate marginal structure is often employed to model their joint dependence structure (c) limited space are available for the justification of their joint dependence structure under the traditional probability functions (d) complexity in the mathematical formulation as the number of random variable got increases ^[2,7,15]. Therefore, De Michele and Salvadori (e.g., ^[16]) firstly introduced copulas function for establishing the joint dependence structure between storm intensity and duration series. After that, extended literatures incorporated bivariate or few trivariate copulas distribution as a model risk for tackling different hydrological extremes (i.e., ^[15,17,18]). In actual, the copula function perform the modelling of individual univariate distribution and their joint dependence structure separately into two different stages, which allow higher degree of flexibility in the selection best fitted marginal distributions and their joint structure to capture a wider extent of linear and non-linear dependencies alongwith their preservation in their mutual dependence structure ^[19,20,21].

Existing copula distribution modelling frequently focused towards the establishment of bivariate joint analysis of the flood attribute pairs such as between peak flow and volume series and/or volume and duration series, and/or peak flow and -duration series(i.e., ^[9,22]). But the more comprehensive flood risk analysis can be achieved through accounting all the trivariate random vector simultaneously by introducing the trivariate copula distribution modelling. Multiple relevant vectors of the specified hydrological episodes could likely depends upon the potential damage also, the ignorance of spatial dependency among these uncertain flood characteristics may responsible for the underestimation of uncertainty ^[11,23]. Therefore, the consideration of multiple flood relevant random vectors could provide better demonstration of their correlation or mutual dependence structure. Few existing incorporations such as Grimaldi and Serinaldi (i.e., ^[17]), performed flood distribution modelling by adapting different trivariate functions such as the mono-parametric and fully nested structure of Frank functions, Gumbel logistic distributions and pointed the significance of Frank function under FNA structure. Similarly, Serinaldi and Grimaldi, (i.e., ^[24]), derived trivariate flood dependence structure using the same fully nested structure. Genest et al., (i.e., ^[25]), modelled the annual spring flood analysis over Romaine River in Canada using the meta-elliptical copulas and their results revealed that such incorporation facilities an effective modelling environment for the analysis of multi-dimensional observations alongwith the preservation of the pair-wise dependencies among multiple random vectors through the correlation matrix but exhibited some modelling limitation such as might be ineffective under the low probabilities unless the asymptotic properties of data will be justified through the strong arguments. Similarly, Reddy and Ganguli (i.e., ^[3]), applied the fully nested Archimedean or FNA class copula and Student’s t copula (Elliptical class copula) for the annual flood characteristics and examined the significance of multidimensional designs events by comparing univariate, bivariate and trivariate return periods and thus revealed that it could be an essential effort to demonstrate the joint and conditional flood occurrence in the light of trivariate return periods. Similarly, Fan and Zheng (i.e., ^[26]), adopted the entropy copula based on the Gibbs sampling procedure along with the Gaussian and the Archimedean copula for simulation of trivariate flood characteristics and revealed that using the entropy copula one can easily projected into higher dimensional frame directly just like as the Gaussian copula.

The Kelantan River basin is often affected by the most intensive monsoonal flooding in Malaysia and perceiving for increasing in term of their frequency and magnitude ^[27,28,29]. Few historical extremes happening such as intense and prolonged precipitation in the year 2002 caused flooding of a total area of 1640 km² and affected the population of 714,287 or either in the early month of December 2014, much heavy precipitation occurred for many of days triggered the flood event in most of the part of eastern coast of Kelantan river basin and it was the worst flood ever recorded in history and affected more than 200,000 people ^[29]. The cause of frequent failure of flood defence infrastructure in Malaysia due to the impact of moderately severe of flood episodes might be responsible due to the lack of complete flood hydrograph or in other words, where only flood peak discharge samples often targeted in deriving flood frequency curve during the structural development. Therefore, multivariate probabilistic assessments of flood characteristics and their associated return periods could be a comprehensive way for making a defensive risk-based decision making in the various basin perspective water-related issues. In this study, the copulas distribution modelling is incorporated for establishing trivariate joint dependence structure of flood peak, volume and duration series. The probabilistic model is implemented on the block (annual) maxima based flood sampling procedure, also called at-site event-based methodology, in which the daily basis streamflow discharge records from period 1961–2016 are collected for the Kelantan River Basin at the Gulliemard Bridge gauge station in Malaysia. Both the Archimedean class and Elliptical class copula function are introduced and their adequacy are tested in the establishment of trivariate joint dependency simulations of flood characteristics. For the trivariate cases, joint primary return period in both “OR” and “AND” cases (for annual flood analysis) are estimated and also compared with the bivariate and univariate return periods. Also, trivariate conditional distribution and their associated return periods are investigated and compared with the bivariate cases.

2.   Theoretical framework

2.1.   Trivariate distribution using the copula function

Let us consider, if the flood peak flow, P, volume, V and duration, D series be the three intercorrelated flood characteristics then the joint probability distribution, F, can join the probabilities of these random variables and can be expressed as ^[8,30];

where ${\rm{p}}, {\rm{v}}, {\rm{q}}$ = values of flood characteristics P, V and D; and P’ = Non-exceedance probability.

According to Salvadori and De Michele (i.e., ^[31]), the multivariate joint return period can be derived from the Eq 1, as given below;

where F(.) = joint CDF or JCDF; T = return period; μ = average inter-arrival time of sequential hydrologic or flood event = 1.

The ideas of the copula method have been developed by Saklar (i.e., ^[19]). According to Nelsen (i.e., ^[20]), the copula are function that connects multivariate probability distributions to their univariate marginal functions. One of the major advantages of copula function is to modelling the dependence structure of the multiple intercorrelated univariate marginal distribution independently. Mathematically, let us consider the situation of bivariate random series, according to Sklar’s theorem ^[20], if (X, Y) be the bivariate random variables with continuous marginal distributions ${{\rm{u}}_1} = {{\rm{F}}_{\rm{X}}}\left({\rm{x}} \right) = {\rm{P}}\left({{\rm{X}} \le {\rm{x}}} \right), {\rm{and}}\; {{\rm{u}}_2} = {\rm{}}{{\rm{F}}_{\rm{Y}}}\left({\rm{y}} \right) = {\rm{P}}\left({{\rm{Y}} \le {\rm{y}}} \right)$, then it can be characterized uniquely by its associated dependence function called Copula or C which can be defined on the unit square, can be expressed as;

where, C = any type of bivariate copulas under consideration; F_X(x) = F_Y(y) = CDF of univariate random variables “X” and “Y”; H_{X, Y}(x, y) = bivariate joint probability distribution functions which can be expressed in terms of its univariate marginal functions and the associated dependence function C, as revealed from Eq 3. According to Shiau (i.e., ^[32]) and Zhang and Singh (i.e., ^[7]), the copula C must be unique if are continuous and thus can easily capture the wider extent of dependencies among the random variables. Conversely, if F_X(x), F_Y(y) and the copula functions is given, then the above Eq 1 must define the bivariate joint distribution functions with its marginal distributions and Similarly, if f_X(x) and f_Y(y) are the PDF of variable X and Y, then the joint probability density of the two random variables can be expressed as;

where, c is the density function of bivariate copula C, can be defined as;

in which, u₁ = F_X(x) and u₂ = F_Y(y).

Similarly, we consider the situation of trivariate distribution series where the joint distribution of random variables can be expresses as;

where H_{X, Y, Z}(x, y, z) = trivariate joint distribution of random variables; F(.) = marginal distribution; and C = trivariate copula function.

In this study, we introduced the Archimedean copula called Frank copula and elliptical copula called the Gaussian copula for establishing trivariate joint dependency of the annual basis (i.e., block (annual) maxima) flood characteristics i.e., flood peak flow, volume and duration series. The Archimedean copulas are widely accepted in numerous demonstration which exhibited a different varieties of families and also much effective and flexible to capture wider extent of joint dependencies ^[17,20]. On the other side, the elliptical family-based Gaussian copula is also introduced as a candidate model for testing their adequacy in the establishment of trivariate joint dependency simulations of flood characteristics. The Gaussian copula is an implicit copula which can be expressed as an integral over the density of X, and that can expressed mathematically for bivariate case as given below ^[33];

The Gaussian copula shows almost no dependence in the tails and is mostly distributed around centre of the distribution but because of simple intuition as it is based on normal distribution, it is quite popular among the hydrologist and water practioner in extreme event modelling (i.e., ^[33,34,35]).

Mathematically, the two and three-dimensional Frank and Gaussian (or Normal) copula can be expressed as:

For the 3-dimension Frank copula;

where, $\phi \left({\rm{t}} \right) = - \ln \left({\frac{{{{\rm{e}}^{ - {\rm{ \mathsf{ θ} t}}}} - 1}}{{{{\rm{e}}^{ - {\rm{ \mathsf{ θ} }}}} - 1}}} \right) =$ generating function.

Similarly, the expression for 2-dimension Frank copula;

where, $\phi \left({\rm{t}} \right) = - \ln \left({\frac{{{{\rm{e}}^{ - {\rm{ \mathsf{ θ} t}}}} - 1}}{{{{\rm{e}}^{ - {\rm{ \mathsf{ θ} }}}} - 1}}} \right)$ = generating function; C_θ² & C_θ³ = two-dimensional and three-dimensional copula with parameter θ; u₁ = F_P(p), u₂ = F_V(v), u₃ = F_D(d) = marginal distribution of trivariate random characteristics.

For the 2-dimensional Gaussian copula;

And, for 3-dimensional Gaussian copula;

where Φ = cumulative distribution function of standard normal or gaussian distribution.

2.2.   Estimation of copula dependence parameters

In this literature, the parameter of the 3-dimensional copula, also the 2-dimensional bivariate copulas are estimated using the ranked-based Maximum pseudo-likelihood estimations (MPL) estimation procedure ^[9,36,37]. The MPL estimators is the modified version of traditional maximum likelihood method where the rank based empirical distributions are used for estimating copula parameters and can be applied for both one or multi-parameter copula functions also, copula parameters are usually estimated independently from their univariate marginal distribution functions ^[9,38,39]. MPL estimation procedure required firstly, to transform the univariate flood marginal variables into uniformly distributed vectors using its empirical distribution function. After that, through the maximization of pseudo-loglikelihood function one can easily estimate copula dependence parameters.

Mathematically,

where, θ = copula parameter; l(θ) = pseudo log-likelihood function; F₁(X_{i, 1}) = F₁(X_{i, 2}) = ……. = F_k(X_{i, k}) = empirical CDFs. Eq 12 is estimated by putting the value of empirical cumulative density or CDFs into copula density function and taking the logarithm to the likelihood function of the copula. Also, the empirical CDF is used as a substitute for the unknown univariate marginals distribution. Finally, the copula parameter can be derived through maximizing Eq 12, as given below;

After the estimation of copula dependence parameter “θ”, it can be used for the representation of multivariate structure of flood characteristics and estimation of joint and conditional return periods that are needed for the hydrologic design.

2.3.   Goodness-of-fit Statistics

In the estimation of multivariate copula joint distribution, the Cramer-von Mises test statistics is employed to evaluate the adequacy of hypothesized copulas fitted to trivariate (or bivariate) flood characteristics ^[40,41]. According to Genest et al., (i.e., ^[41]) and Reddy and Ganguli (i.e., ^[9]), this test makes the use of the Cramer-von Mises statistic “Sn” through a comparative assessment between empirical, and theoretical probability distribution, using the following mathematical algorithm as given below;

For testing the fitness level of 2-dimensional or bivariate copula function

For testing the fitness consistency during 3-dimensional or trivariate copula construction

where, c_n(u₁, u₂, u₃) & c_n(u₁, u₂) = trivariate and bivariate empirical copulas estimated using the “n” observational flood attribute pairs; C_θ = parametric copula derived under the null hypothesis; u₁, u₂, u₃ = univariate marginal distribution of flood characteristics say P, V and D; U_{1i, n}, U_{2i, n} or U_{1i, n}, U_{2i, n}, U_{3i, n} = pseudo-observations of C transformed from (X₁, Y₁), (X₂, Y₂), …….(X_n, Y_n) or (X₁, Y₁, Z₁), (X₂, Y₂, Z₂), …….(X_n, Y_n, Z_n). Numerically, the value of U_{1i, n}, U_{2i, n} and U_{3i, n} can be estimated by using following mathematical approach;

In this demonstration, the p-values for each fitted copulas are estimated using the parametric bootstrapping technique (i.e., ^[40]), during the simulation of bivariate copulas structure and using the faster multiplier approach (i.e., ^[42,43]) during the simulation of trivariate copulas function. Although the empirical processes involved in the multiplier and the parametric bootstrap-based test are asymptotically equivalent under the null, the finite-sample behaviour of the two tests might differ significantly. Mathematically, the parametric bootstrapping procedure can be formulated as given below;

where N = number of simulations.

This fitness statistics actually involve testing of null hypothesis H₀ against the against hypothesis H_a as given below;

Null hypothesis (H₀ ) = C∈ C₀ {where, C₀ = C_θ; θ∈O).

Alternate hypothesis (H_a) = C∉ C₀.

where, O is the open subset of ${\Re ^{\rm{q}}}$ for some integer value q. On the other side, the test statistics “Rn” (i.e., ^[44]) is also incorporated for testing the adequacy of best-fitted trivariate copulas to flood characteristics. The “Rn” test is an information ratio statistic which is approximately equivalent to the “Tn” test, which is the PIOS (or Pseudo in-and-out-of-sample test). The acceptance or rejection of the considered copulas is based on estimated p-values. The null hypothesis must be accepted if the estimated p-value is larger than a significance level and which in result that copula must be considered as satisfactory performance otherwise will be liable for rejections. Overall, from the Eq 15, it must be conclude that minimum the value of “Sn” and “Rn” test value must indicates for minimum gap or distance between an empirical and derived parametric copulas word thus, most justifiable copula for establishing multivariate (trivariate and bivariate) joint relationship between flood variables.

2.4.   Flood risks estimation

The study of the joint and conditional probability distribution for estimating the different notation of return periods (i.e., joint return periods, conditional joint return periods) is often considered as an essential concern for hydrologic design, that can be easily facilitated using the copulas function (i.e., ^[10,11,45]). Hydrologist and water practioner are mostly interested in the evaluation of the average inter-arrival duration between two design events and which usually defined in a year called the return period ^[10]. According to Yue and Rassumesen (i.e., ^[5]), the concurrence probability defines the chance that any hydrologic happening, which either characterizing through univariate or either multivariate exceeding certain a threshold level. Mathematically, the univariate return period that occurs once in a year can be defined from univariate cumulative distribution function or CDF of the variable (say “X”) as given below;

where, T_Univariate is return period in years; F(x) is univariate CDF of random variable, X; μ = 1, for annually basis or annual maxima-based flood analysis ^[5].

2.4.1.   Derivation of joint return periods

According to Salvadori (i.e., ^[10]) and Zhang and Singh (i.e., ^[8]), the joint return periods of triplet flood characteristics can be estimated using the inclusive probability, also called “OR” and “AND” cases. The joint probability distributions for annual flood analysis can describe the following two situation such that in the first condition when all the flood variables (say, P≥p, V≥v, and D≥d) simultaneously exceed certain threshold during a flood events and their associated return period called AND joint period and it can be written as;

A.For the trivariate joint distribution case;

B.For the bivariate distribution case (any flood combinations i.e., between P and V);

where H(p, v, d) = trivariate joint CDF of random variable P, V and D; H(p, v) = bivariate joint CDF of flood random variables; C(F(p), F(v), F(d)) = trivariate copulas CDFs for flood characteristics; F(p) = F(v) = F(d) = univariate marginal distribution of flood variables.

In the second situation, probability either the first or second or third flood variable (say, P≥p, V≥v, and D≥d) exceed given threshold and thus their associated return period called OR joint return period can be expressed as;

C.For trivariate case;

D.For bivariate case (for any combination i.e., between P and V);

2.4.2.   Derivation of return periods from conditional distribution

Besides the necessity of joint return periods, it could be an essential concern to investigate flood events in such a manner that one could highlights the priority of one design variables over another design variables therefore, from this prospects numerous demonstration focused towards defining the concept of the conditional distributional framework in order to derive the conditional return periods (i.e., ^{[3,7,8,31,32]}). For example, the conditional return period of flood peak series given various percentile value of flood volume or vice-versa or in another words, where the flood peak “P” exceeds a threshold “p” given that the volume “V” series exceeds a threshold “v”. The conditional distributions based on the different conditions are firstly estimated thereafter the associated conditional return periods are derived.

A.For trivariate case,

The conditional distribution of peak (P), volume (V) given duration (D≤d) in “OR” case is given by

where, F(d) = univariate marginal CDF of flood variable, D. therefore under this condition, their corresponding return period can be estimated as,

Similarly, the conditional return period of peak (P), duration (D) given volume (V≤v) in “OR” case is given by;

Similarly, the conditional return period of Volume (V), duration (D) given peak (P≤p) in “OR” case is given by;

Again, the conditional distribution of peak (P) given (volume(V≤v), duration(D≤d)) is given by,

The corresponding return period can be estimated as;

where, C(d, v) = bivariate copula CDF of flood characteristics duration(D) and volume (V). Therefore, using Eq 27, it can be possible to estimate trivariate conditional return period for various possible combinations of flood characteristics.

B.For bivariate distribution case;

The conditional return periods between flood peak (P) given volume (V≤v) (or vice-versa) can be obtained from the conditional probability distribution function is given by;

Overall, using Eq 29 we can easily estimate return periods of one variable conditioning to another variable for any possible combination of flood characteristics.

3.   Case study

3.1.   Trivariate flood characteristics of Kelantan River basin

To illustrate the trivariate distribution analysis of flood episodes, the 50 years (1961–2016) of daily streamflow discharge records of the Kelantan River basin at Gulliemard Bridge gauge station in Malaysia (which are collected from the Drainage and Irrigation Department, Malaysia) are employed. The Gulliemard bridge station is located at the downstream of Kelantan river near the Kuala Kari region. The geographical location of this river basin is Lat 4°30′ N to 6°15′ N and Long 101°E to 101°E to 102°45′ E. It is the longest river of Kelantan state, which originating from the Tahan mountain range to the South China Sea in the north-eastern part of Peninsular Malaysia. The river is about 248 km long with a drain area of 13100 km² and which occupying more than 85% of the state of Kelantan. The estimated runoff is about 500 m³sec⁻¹ and the variations of annual precipitations for this region in between 0 mm (dry period)–1750mm (wet or north-eastern monsoonal period) ^[27]. The major land use of this area is agriculture (i.e., paddy, rubber and oil palm) for midstream and downstream and forest for the upstream (i.e. near to Gua Musang).

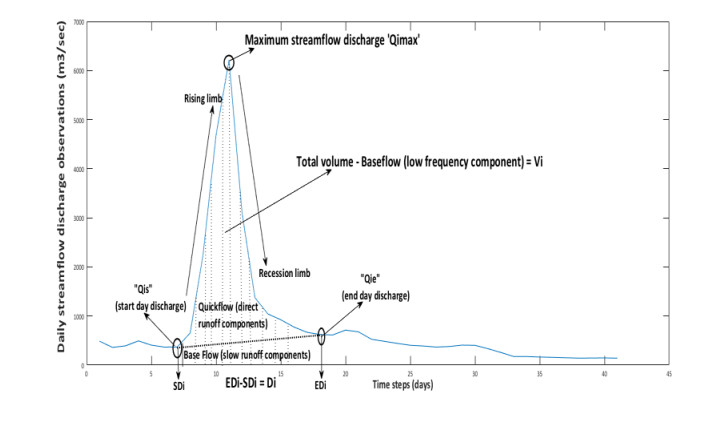
In this study, we adopted the Annual (Maximum) series or AM approach, also called block (annual) maxima to delineate the triplet flood vectors i.e., flood peak discharge flow (P), volume (V) and duration (D) from the daily basis stream flow discharge records ^[9,37]. The characterizations of flood peak flow values are based on their maximum streamflow discharge records at an annual scale using Eq 31, such that at the targeted site there is only one flood episodes at each year (refer to Figure 1) ^[4,5,37]. Figure 1, illustrating the single-peaked flood hydrograph where both the flood duration (D), which are estimated by recognizing the time of rise and fall of the flood hydrograph (i.e., points at Qis and Qie in the Figure 1) and volume (V) series are obtained using algorithm which is reported in the literature (i.e., ^[4,5]) (see Eqs 32 and 33). Flood peak discharge often attains their maximum value but not mandatory for hydrograph volume and duration series ^[37].

Mathematically,

where, Q_ij = j^th days streamflow magnitude for the i^th year; and Q_is & Q_ie = streamflow magnitude for the start date “SD_i” and end date “ED_i”of the flood runoff.

3.2.   Descriptive behaviour and relationship between hydrological characteristics

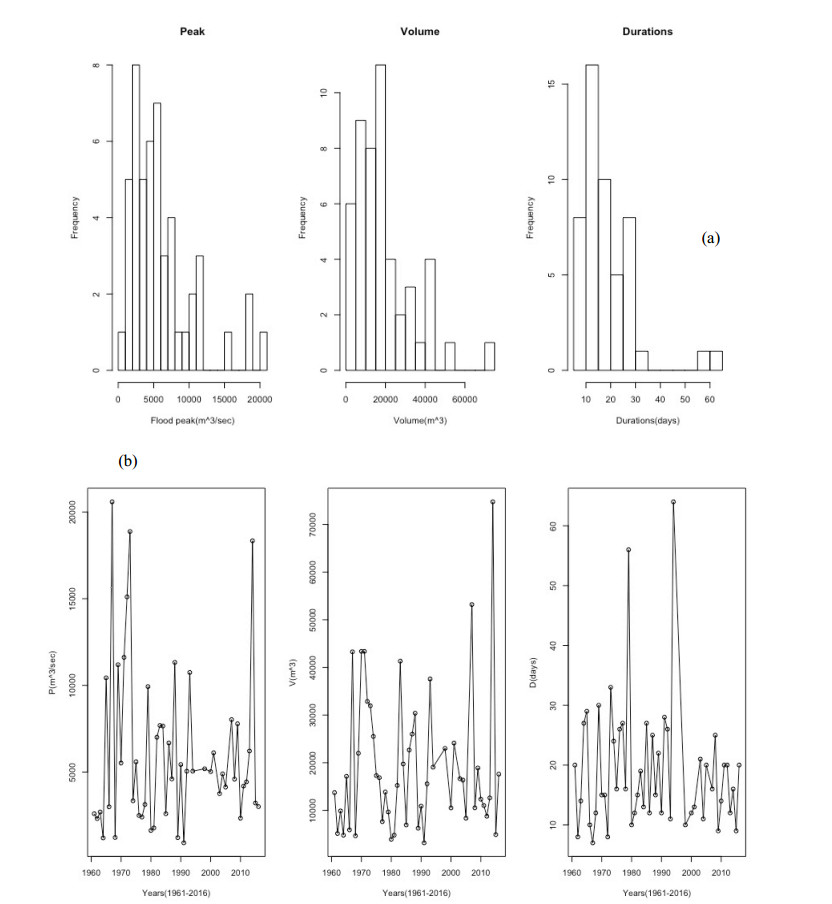
In this research methodology, the flood events are characterized based on annual maximum discharge series method which is also called partial data series based distribution modelling. Table 1 representing the descriptive behaviour of individual flood characteristics which indicating that each flood characteristics exhibiting positively skewed distribution. Figure 2a, b representing the histogram distributions plot and time-series visualization of the annual flood characteristics.

3.2.1.   Dependency measures via analytical approach

The strength of dependency between the targeted flood vectors i.e., flood peak, volume and duration series are estimated using the Pearson’s linear correlation (r), and the two non-parametric dependence measures, also called the rank based correlations statistics such as Kendall’s tau (t) and Spearman’s rho (ρ) and their estimated values are listed in Table 2. The Pearson coefficient only capture the linear dependencies therefore might be incompatible for heavy-tailed distribution series. On other side, Kendall’s tau (t) and Spearman’s rho (ρ) are invariant under monotonic non-linear transformations without any assumption of underlying distribution structure which frequently used as effective dependence measures for the nonlinear modeling in multivariate statistics also, it possess high resistance to outliers ^[39].

3.2.2.   Via graphical investigation

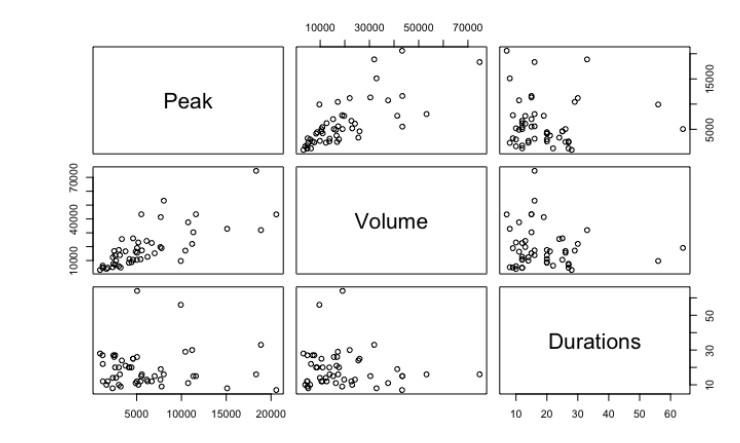
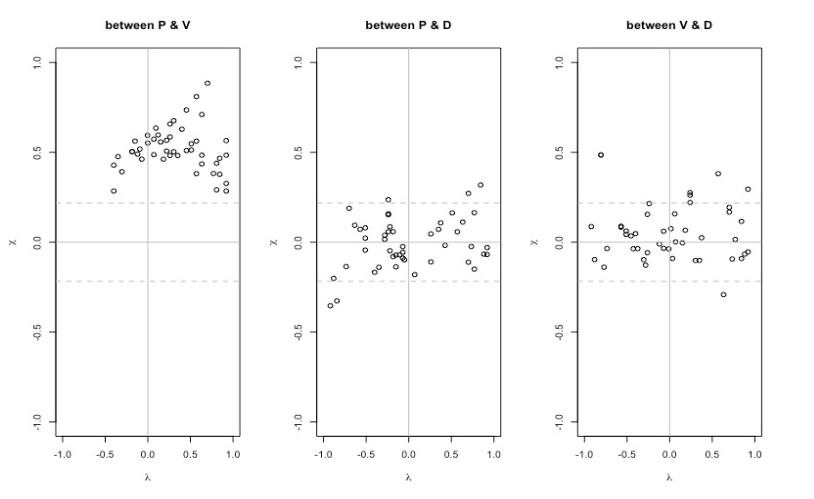
Graphical based dependency investigation among the flood characteristics are also undertaken using the scatter plots, chi plots (i.e., ^[46]) and Kendall’s plots (i.e., ^[47]), as illustrated in the Figures 3–5. Chi-plot is actually a scatter pot of the pairs (λ_iχ_i), where it uses the data ranks and λ_i values is a measure of the distance of bivariate random observations (say p_iv_i) from the center of the data sets within the range of [−1(negatively correlated), 1(positively correlated)]. Also, the control limits χ_i are the another measuring factor in chi-plot that are placed at ${\rm{ \mathsf{ χ} }} = \pm {{\rm{c}}_{\rm{p}}}/\sqrt {\rm{n}}$ ^[46]. Thus, in case of stronger dependency the random pairs must be outside the control limit of chi-plot otherwise, inside the control limit region can be indicated for independence between random pairs. On other side, when the point data are largely on the upper side of control limits, which could indicate for positively correlated variables and for negatively correlated random variables, the data points are distributed in the lower side of the control limits. Similarly, the Kendall’s plot are analogous to quantile-quantile (Q-Q) plot such that, deviation of random pairs from the main diagonal of K-plot is the indication of inter-dependence otherwise could be revealing for independence when the pot tends to be linear ^[21,47].

3.3.   Estimating marginal distribution of flood characteristics

3.3.1.   Empirical probabilities

The empirical nonexceedance probabilities are estimated for the each individual flood characteristics by using commonly used the Gringorten based position-plotting formula ^[7,48], which usually compared with CDF of the fitted distributions for pointing the gaps and deviations between empirical and fitted samples, as given below,

where N = length of the sample (i.e., the total number of flood observations); and k = k^th smallest observations where the dataset is arranged in an ascending order.

3.3.2.   Univariate flood marginal distributions

Selecting the most justifiable univariate probability distribution functions for defining flood marginal distribution is often a mandatory pre-requisite demands before the establishment of flood dependence structure. Several models often would fit the data equally well but, each would give different estimates of a given quantile especially, in the tails of the distribution and which is solely based on the goodness-of-fit procedure to visualize the compatibility of the fitted distributions ^[49]. A distinguish varieties of univariate parametric family-based probability distribution are selected and introduced as a possible marginal distribution. The parameter of each distributions is first estimated using maximum likelihood estimation (MLE) (i.e., ^[50]), method of moments (MOM) (i.e., ^[1]), least square method (LS), and L statistics-based method of L-moments (i.e., ^[51]) and then the best fitted distributions are selected for each individual flood characteristics using different goodness-of-fit test statistics. All the univariate distribution fitting procedures are carried out using the Easyfit-distribution fitting software.

4.   Results and discussions

4.1.   Modeling of univariate marginal distribution

A distinct variety of univariate parametric families-based probability distributions (i.e., 1-parameter, 2-parameters, 3-parameters & 4-parameters) are introduced as a candidate models as listed in the Table 3 and their estimated parameters values are listed in the Table 4. Fitness level of each fitted distributions are examined through different analytical based goodness-of-fit measures such as based on distance criteria statistics Kolmogorov-Smirnov (or K-S) test and Anderson-Darling (or A-D) test (i.e., ^[37,52]), based on information criteria statistics such as Akaike Information criteria (or AIC) (i.e., ^[53]), Schwartz’s Bayesian Information criteria (or BIC) (i.e., ^[54]) and Hannan-Quinn Information criteria (HQIC) (i.e., ^[55]), and also based on error indices statistics such as Mean square error (or MSE) and Root mean square error (or RMSE) (i.e., ^[56]). Table 5a–c listed the performance level of different univariate distributions for fitting the marginal distribution for the flood characteristics. Investigation results reveals that the Lognormal-2P distribution are much satisfactory for flood peak flow series, the Johnson SB (4P) for volume and the Gamma(3P) distribution for duration series because these distribution possess the minimum values of K-S, A-D, AIC, BIC HQC, MSE and RMSE test statistics in compare with their peer candidates function for each individual flood characteristics.

4.2.   Bivariate modeling using the 2-dimensional copulas

Before initiating the fitting procedure of two-dimensional copulas function for establishing bivariate joint relationship among the flood characteristics, we investigated the level of dependency through both analytical and graphical procedure. The Pearson’s linear correlation (r), Kendall’s tau (t) and Spearman’s rho (ρ) are used to measure the strength of dependency (see Table 2). Analytical investigation reveals that flood peak and volume pair exhibited strong positive correlation but the correlation structure between flood peak-duration, and flood volume-duration pair are very weak and negatively correlated. On the otherside, the graphical illustrations i.e., based on scatter plot (see, Figure 3), chi-plots (see, Figure 4) and Kendall’s plots (see, Figure 5) are also in support of the analytical approach. Based on scatter plot, it clearly indicating the existence of positive and strong dependency between peak-volume pairs because the increased density of points are located near the diagonal region (i.e., close to 45° angle) but weak and negative dependencies are exhibited between flood volume-duration and flood peak-duration pairs. Similarly, based on chi-plot, strong deviation from the control limit is observed for flood peak-volume pairs (indicates for high and positive correlation) but most of the data samples are within the region of control limit for peak-duration and volume-duration pairs. Similarly based on the Kendall’s plot, peak-volume data pairs are much deviated from the main diagonal (high and positive correlation) but much closer to main diagonal for peak-duration and volume-duration pairs (low and negative correlation).

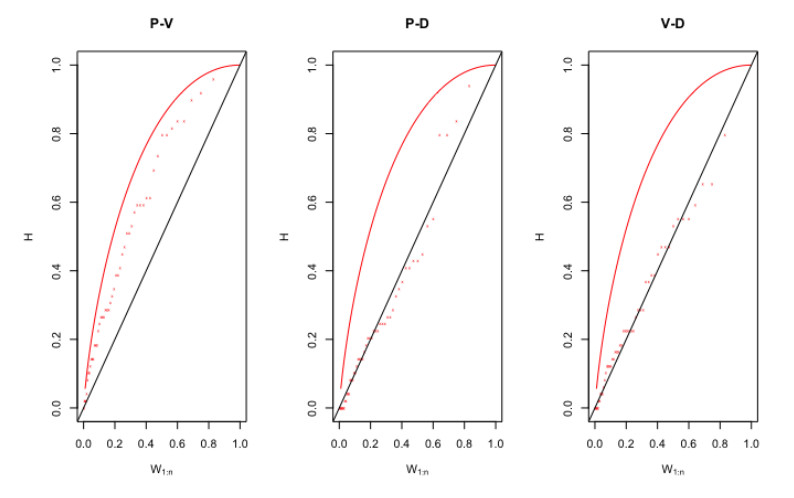
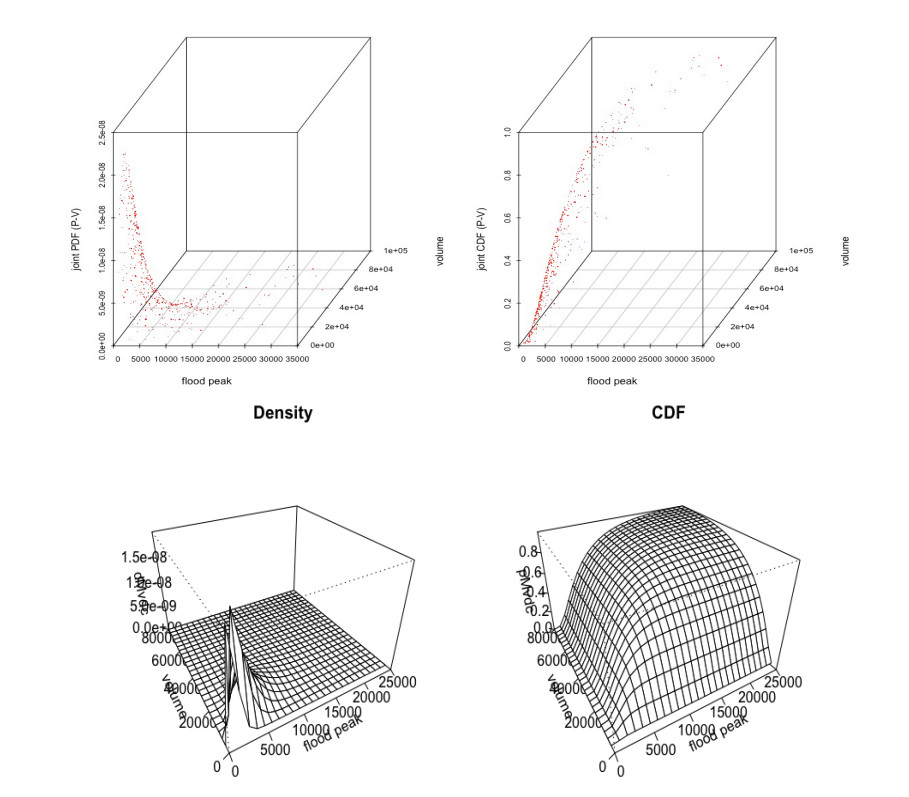
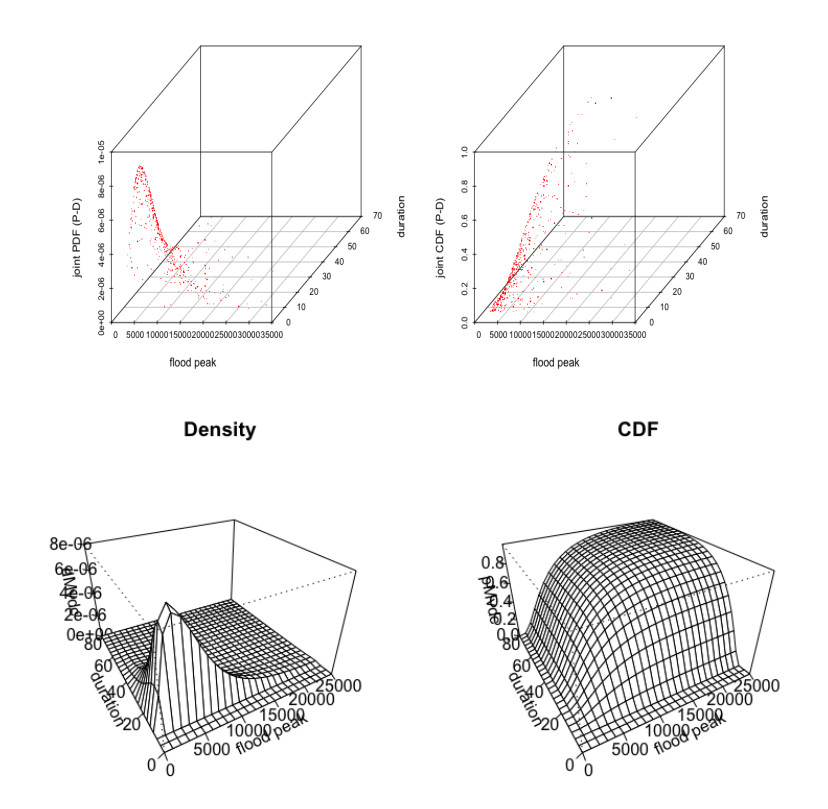
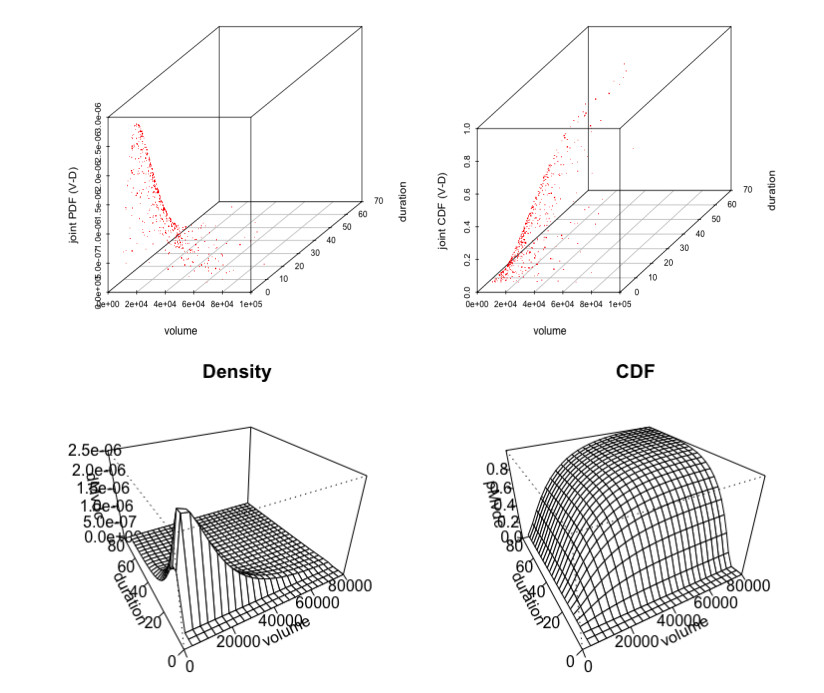
Referred to Table 6, the mono-parametric Archimedean copulas such as the Clayton copula, Gumbel copula, Frank copula, and Joe copula and also, one Elliptical copula such as the Gaussian or normal copula are introduced and tested for establishing bivariate joint distribution of flood characteristics. Actually, the Gumbel-Hougaard, Clayton and Joe copula cannot be used for negatively dependent flood characteristics (i.e., only applicable to model positively correlated random variables). The copulas dependence parameter are estimated using maximum pseudo log-likelihood (or MPL) estimation procedure, using Eqs 12 and 13 and their estimated values are listed in Table 7. Identification and selection of most parsimonious copulas for each flood attribute pairs are performed using the Cramer-von Mises distance statistics with parametric bootstrap procedure, using Eq 14. The test statistics “S_n” and its associated p-value have been computed from 1000 and 500 simulated random samples by the mean of parametric bootstrap procedure and their values are listed in the Table 6. Investigation reveals that the Gaussian copula exhibited minimum “S_n” statistics and highest p-value for flood peak-volume pair and thus identified as most appropriate for this pair. On other side, the Frank copula is identified as the most justifiable bivariate model for capturing the joint structure of both flood peak-duration and volume-duration pairs, referred to the same Table 7. Figures 6–8 represents the joint probability density function (JPDF) and joint cumulative distribution function (JCDF) (i.e., scatterplot and surface plot) derived from the best-fitted bivariate copulas for flood peak-volume, volume-duration and peak-duration pairs.

4.3.   Trivariate modeling using the 3-dimensional copulas

The Archimedean class copula called the Frank copula and the elliptical copula called the Gaussian copula are incorporated (see Eqs 8 and 11) and their adequacy for establishing the trivariate joint distribution among flood characteristics flood peak flow, volume and duration series are investigated. The dependence parameter of trivariate copulas are estimated using the maximum pseudo log-likelihood (or MPL) estimation procedure of Eqs 12 and 13 and their estimated values are listed in the Table 8. To analytically validate and identify the best-fitted copula for describing trivariate joint distribution of flood characteristics, the Cramer-von Mises distance statistics are employed where the approximation of p-values for the test statistics are obtained by means of a faster multiplier bootstrapping approach (i.e., ^[42,43]) followed by Eq 15. For this purpose both the test statistics “Sn” and its associated p-values and also, the test statistics “Rn” (i.e., ^[57]) and its associated p-value has been computed from 1000 and 500 simulated random samples by the mean of faster multiplier approach and their estimated values are listed in Table 8. Result reveals that the Gaussian copula is recognized as most consistence copula for establishing the trivariate joint distribution of flood characteristics, which exhibited minimum “Sn” test statistics (i.e., “Sn” = 0.082819) their p-value (i.e., p-value = 0.01748, for N = 1000 bootstrap samples and p-value = 0.01098, for N = 500 random bootstrap samples) than the Frank copula test statistics. Also, for the Gaussian copula the “Rn” test statistics is less than the Frank copula statistics (i.e., “Rn” = 1.2742) and their p-value (i.e., p-value = 0.1294, for N = 1000 bootstrap samples and p-value = 0.1307, for N = 500 random bootstrap samples) such that based on both test statistics it is concluded that the estimated p-values are exceeding the specified significance level (i.e., α = 0.05), and which is higher than the Frank copulas, referred to same Table 8.

4.4.   Probabilistic analysis of flood characteristics

4.4.1.   Via joint return periods

In order to analyse the critical hydrologic behaviour of flood episodes for tackling the several basin perspective water-related issues the multivariate frequency analysis is much comprehensive approach. The univariate return periods are derived from the best-fitted CDFs for each flood characteristics i.e., Lognormal-2P distribution for flood peak, Johnson SB-4P distribution for volume and Gamma-3P distribution for duration series using Eq 18 and their estimated values are listed in Table 9. It is already pointed in the section 1 that estimation of univariate return period as a design criterion would be problematic and might attributes for underestimations or overestimations of hydrologic risk. Therefore, the bivariate joint CDFs which are derived from the best-fitted copulas for each flood attribute pairs are employed to derived primary return period for both the “OR” and “AND” case using Eqs 20, 21 and their estimated values are listed in Table 10. It is revealed that the AND-joint cases produce higher return period than the OR-joint cases for different possible combination of flood characteristics i.e., T_PV^AND > T_PV^OR or T_VD^AND > T_VD^OR or T_PD^AND > T_PD^OR. In other words, the occurrence of bivariate flood characteristics simultaneously is less frequent in “AND” case in compare with “OR” case of joint return periods (i.e., more frequent). For example, a flood event with peak flow, P = 10463.8 m³s⁻¹, volume, V = 17148 m³, and duration, D = 29 days, then OR-joint return period between P-V is, T_PV^OR = 2.2037 years, between P-D, T_PD^OR = 3.7524779 years and between V-D pair is, T_VD^OR = 1.94310711 years. On otherside, joint return for “AND” case for same flood combination is, between P-V, T_PV^AND = 7.5013958 years, between P-D, T_PD^AND 66.4233248 years and between V-D pair, T_VD^AND = 17.1879396 years, (see Table 10). Also, the univariate return periods derived from flood peak, T(P) and volume, T(V) is higher than that derived from their joint distribution for “OR” cases but produces low return periods than “AND” joint cases i.e., T(P) > T(V) > T_PV^OR and T(P) < T(V) < T_PV^AND . Similarly, univariate return periods derived from peak, T(P) and duration, T(D) as well as volume, T(V) and duration T(V) is higher than the joint return periods for “OR” cases for the same flood attributes but lower return periods for “AND” joint cases i.e., T(V) > T(D) > T_VD^OR and T(P) > T(D) > T_PD^OR also, T(V) < T(D) < T_VD^AND and T(P) < T(D) < T_PD.^AND

Actually, the estimation of trivariate joint and conditional distribution and their associated return periods often required at first to determine bivariate joint copula distribution i.e., C(p, v), C(v, d)or C(p, d) of flood characteristics for various possible combinations (see Eqs 19, 27 & 28). At first, the trivariate return periods for the conditions (1) when all the flood characteristics (say, P≥p, V≥v, and D≥d) simultaneously exceed certain threshold (also called “AND” primary joint return period) and (2) probability either any of the flood variable (say, P≥p, V≥v, and D≥d) exceed given threshold (also called “OR” primary joint return period)) during a flood events are examined using Eqs 19 and 21 and their estimated values are listed in Table 11. For example, the flood event having peak, P = 10463.8 m³s⁻¹, volume, V = 17148 m³ and duration, D = 29 (days), in joint return period for “OR” and “AND” cases are T_PVD^AND = 34.8401 years and T_PVD^OR = 1.87605 years. Similarly, for P = 18875.4 m³s⁻¹, V = 31945.6 m³and D = 33 (days), T_PVD^AND = 547.92 years and T_PVD^OR = 4.12544 years. It is also clearly revealed from Table 10 that for all the cases considering trivariate flood characteristics (i.e., P, V, D) the joint return periods in “AND” case is greater than “OR” case i.e., T_PVD^AND > T_PVD^OR. In other words, we can say that the occurrence of trivariate flood characteristics simultaneously is less frequent in “AND” case in compare with “OR” case of joint return periods (i.e., more frequent).

4.4.2.   Via conditional joint return periods

The joint return period of two flood characteristics conditional on third flood characteristic, i.e., conditional distribution of peak (P), volume (V) given duration (D≤d), T(p, v\D≤d), T(p, d\V≤v) and T(v, d\P≤p) are estimated using Eqs 24–26 and their estimated values are listed in Table 11. For example, a flood episode characterized with peak flow, P = 10463.8 m³s⁻¹, volume, V = 17148 m³ and duration, D = 29 (days), using Eq 24–26, then joint return period of, “P” and “V” conditional to “D” is T(p, v\D≤d) = 2.19874 years, T(p, d\V≤v) = 5.50286 years and T(p, d\V≤v) = 2.1822555 years. Similarly, for P = 20586.4 m³s⁻¹, V = 43273.2 m³, D = 7 (days) the conditional return periods are T(p, v\D≤d) = 83.650777 years, T(p, d\V≤v) = 1.0034823 years and T(v, d\P≤p) = 1.0032946 years. On the other side, the joint return periods of one flood characteristics conditional on other two flood characteristics i.e., T_P\DV(p\V≤v, D≤d), T_V\PD(v\D≤d, P≤p), T_D\PV(d\V≤v, P≤p) and are estimated using Eq 27. For example, a flood event with P = 10463.8 m³s⁻¹, V = 17148 m³ and D = 29 (days), then the conditional return period of peak (P) given (volume(V≤v), duration(D≤d)) is T_P\DV(p\V≤v, D≤d) = 26.386055 years, T_V\PD(v\D≤d, P≤p) = 2.7519296 years and T_D\PV(d\V≤v, P≤p) = 5.718863 years. Similarly, for the flood events (P = 18875.4 m³s⁻¹, V = 31945.6 m³ and D = 33 (days)), T_P\DV(p\V≤v, D≤d) = 404.30955, years, T_V\PD(v\D≤d, P≤p) = 7.25924 years and T_D\PV(d\V≤v, P≤p) = 10.4372045 years. Similarly, for the flood episode (P = 4603 m³s⁻¹, V = 25999 m³ and D = 25 (days)), T_P\DV(p\V≤v, D≤d) = 2.44463, years, T_V\PD(v\D≤d, P≤p) = 19.3565 years and T_D\PV(d\V≤v, P≤p) = 3.7111744 years.

The bivariate conditional return periods for different possible combination of flood characteristics are also estimated using Eq 30 and their values are listed in the same Table 12. For example, a flood episode characterized with flood peak, P = 10436.8 m³s⁻¹ and volume, V = 17148 m³ then, the conditional return periods T(P/V≤v) = 120.216827 years and T(V/P≤p) = 2.9117633 years. Similarly, for the flood events (P = 20586.4 m³s⁻¹ and D = 7 (days), then the conditional return periods T(P/D≤d) = 33.5532361 years and T(D/P≤p) = 1.0032349 years. Similarly, the flood episode which has volume of V = 31945.6 m³ and duration D = 33 days, the return period of volume given duration or vice versa is T(V/D≤d) = 6.19127366 years and T(D/V≤v) = 10.4428152 years. Again, the flood episodes characterized based on peak, P = 18875.4 m³s⁻¹ and duration, D = 33days then conditional return periods, T(P/D≤d) = 33.3736912 years and T(D/P≤p) = 10.525197 years.

5.   Research conclusions

This literature incorporated the copula-based methodology to establishing the trivariate distribution modelling of the flood episodes for the Kelantan River basin in Malaysia. Firstly, a distinguish varieties of parametric families-based probability functions are tested for defining the univariate marginal structure of each flood characteristics. Results reveals that the Lognormal (2P), Johnson SB (4P) and Gamma (3P) distribution are recognized as most justifiable for describing marginal distribution of flood peak, volume and duration series. Based on the correlation measuring statistics, via the analytical approach such as the Pearson, Kendall’s tau and Spearman rho correlation coefficient as well as the graphical visual inspection (i.e., based on ranked based scatter plot, K-plot and Chi-plot). It is found that flood peak flow and volume pair exhibited higher and positive dependence structure but both flood volume and duration pairs as well as peak flow and duration pairs are found to be negatively correlated random pairs with very weak correlation and thus considered for flood frequency analysis. The adequacy of one elliptical copula, the Gaussian copula and one Archimedean copula, the Frank copula are introduced to model the trivariate joint distribution of flood characteristics. The copula dependence parameter of fitted trivariate copulas are estimated using maximum pseudo log-likelihood (or MPL) estimation procedure. The best fitted trivariate copulas are selected using the Cramer-von Mises distance statistics where the approximation of p-values for the test statistics are obtained using the faster multiplier bootstrapping approach. The test statistics “Sn” and “Rn” and their associated p-values are computed from 1000 and 500 simulated random samples by the mean of the faster multiplier approach. Result reveals that the Gaussian copula is recognized as most justifiable copula function for establishing the trivariate flood dependence structure as it exhibited the minimum values for “Sn” and “Rn” test statistics. The estimation of trivariate joint probability distribution often required at first to determine bivariate joint copula distribution. Therefore, the mono-parametric Archimedean copulas such as the Clayton copula, Gumbel copula, Frank copula, Joe copula and one Elliptical copula such as the Gaussian or normal copula are tested for establishing the bivariate joint distribution of the flood characteristics. Investigation reveals that the Gaussian copula is identified as most appropriate for flood peak flow and volume pair and the Frank copula is for volume and duration and peak flow and duration pairs. Finally, the cumulative distribution function or CDF of the best fitted trivariate copula is further employed to derive trivariate joint and conditional return periods. The bivariate and univariate return periods are also estimated and compared with trivariate return periods. It reveals that the trivariate joint return period for “OR” case is less than return periods for “AND” case for triplet flood characteristics. In other words, the occurrence of trivariate flood characteristics simultaneously is less frequent in “AND” case in compare with “OR” case of joint return periods (i.e., more frequent). Overall, it is concluded that copula function effectively preserving the flood dependence structure and thus found as very flexible and dynamic tools for the assessments of multidimensional extreme episodes i.e., flood. From the estimated trivariate return periods it could be revealed that for an effective flood risk assessments, it could be an essential concern to take the accountability of trivariate return periods, by considering all the inter-associated random vector simultaneously, instead of just pair-wise joint association or bivariate return periods.

Acknowledgements

Special thanks is extended to the Drainage and Irrigation Department, Malaysia for supplying streamflow data of the Kelantan river basin.

Conflict of interest

All authors declare no conflicts of interest in this manuscript.