Local porosity of the free boundary in a minimum problem

1.   Introduction

The concept of the hyperchaos was first put forward by Rössler ^[1] in 1979. Any system with at least two positive Lyapunov exponents is defined as hyperchaotic. Compared to chaotic attractors, hyperchaotic attractors have more complicated dynamical phenomena and stronger randomness and unpredictability. Hyperchaotic systems have aroused wide interest from more and more researchers in the last decades. A number of papers have investigated various aspects of hyperchaos and many valuable results have been obtained. For instance, in applications, in order to improve the security of the cellular neural network system, the chaotic degree of the system can be enhanced by designing 5D memristive hyperchaotic system ^[2]. For higher computational security, a new 4D hyperchaotic cryptosystem was constructed by adding a new state to the Lorenz system and well used in the AMr-WB G.722.2 codec to fully and partially encrypt the speech codec ^[3]. In fact, hyperchaos has a wide range applications such as image encryption ^[4], Hopfield neural network ^[5] and secure communication ^[6] and other fields ^[7,8]. Meanwhile, there are many hyperchaotic systems have been presented so far. Aimin Chen and his cooperators constructed a 4D hyperchaotic system by adding a state feedback controller to Lü system ^[9]. Based on Chen system, Z. Yan presented a new 4D hyperchaotic system by introducing a state feedback controller ^[10]. By adding a controlled variable, Gao et al. introduced a new 4D hyperchaotic Lorenz system ^[11]. Likewise, researchers also formulated 5D Shimizu-Morioka-type hyperchaotic system ^[12], 5D hyperjerk hypercaotic system ^[13] and 4D T hyperchaotic system ^[14] and so on.

In ^[15], a chaotic Rabinovich system was introduced

where $(x, y, z)^{T}\in { \mathbb R^3}$ is the state vector. When $(h, a, b, c) = (0.04, 1.5, -0.3, 1.67)$, (1.1) has chaotic attractor^[15,16]. System (1.1) has similar properties to Lorenz system, the two systems can be considered as special cases of generalized Lorenz system in ^[17]. Liu and his cooperators formulated a new 4D hyperchaotic Rabinovich system by adding a linear controller to the 3D Rabinovich system ^[18]. The circuit implementation and the finite-time synchronization for the 4D hyperchaotic Rabinovich system was also studied in ^[19]. Reference ^[20] formulated a 4D hyperchaotic Rabinovich system and the dynamical behaviors were studied such as the hidden attractors, multiple limit cycles and boundedness. Based on the 3D chaotic Rabinovich system, Tong et al. presented a new 4D hyperchaotic system by introducing new state variable ^[21]. The hyperchaos can be generated by adding variables to a chaotic system, which has been verificated by scholars ^{[3,9,10,11,14]}. In ^{[18,19,20,21]}, the hyperchaotic systems were presented by adding a variable to the second equation of system (1.1). In fact, hyperchaos can also be generated by adding a linear controller to the first equation and second equation of system (1.1). Based on it, the following hyperchaotic system is obtained

where $k_{0}, \, h, \, a, \, b, \, d, \, k, \, k_{0}, \, m\,$ are positive parameters. Like most hyperchaotic studies (see ^{[14,22,23,24]} and so on), the abundant dynamical properties of system (1.2) are investigated by divergence, phase diagrams, equilibrium points, Lyapunov exponents, bifurcation diagram and Poincaré maps. The results show that the new 4D Rabinovich system not only exhibit hyperchaotic and Hopf bifurcation behaviors, but also has the rich dynamical phenomena including periodic, chaotic and static bifurcation. In addition, the 4D projection figures are also given for providing more dynamical information.

The rest of this paper is organized as follows: In the next section, boundedness, dissipativity and invariance, equilibria and their stability of (1.2) are discussed. In the third section, the complex dynamical behaviors such as chaos and hyperchaos are numerically verified by Lyapunov exponents, bifurcation and Poincaré section. In the fourth section, the Hopf bifurcation at the zero equilibrium point of the 4D Rabinovich system is investigated. In addition, an example is given to test and verify the theoretical results. Finally, the conclusions are summarized in the last section.

2.   Dynamical analysis of (1.2)

2.1.   Boundedness

Theorem 2.1. If $k_{0} > m$, system (1.2) has an ellipsoidal ultimate bound and positively invariant set

where

Proof. $V(x, y, z, u) = m{x}^{2}+k_{{0}}{y}^{2}+ (k_{{0}}-m)[z-{\frac {h (k_{{0}}+m) }{k_{{0}}-m}}] ^{2}+{\frac {k_{{0}}m{ u}^{2}}{k}}$. Differentiating $V$ with respect to time along a trajectory of (1.2), we obtain

When $\frac{\dot V(x, y, z, u)}{2} = 0$, we have the following ellipsoidal surface:

Outside $\Sigma$ that is,

$\dot V < 0$, while inside $\Sigma$, that is,

$\dot V > 0$. Thus, the ultimate bound for system (1.2) can only be reached on $\Sigma$. According to calculation, the maximum value of $V$ on $\Sigma$ is $V_{max} = \frac{1}{4}\, {\frac {{h}^{2}{d}^{2} \left(m+k_{{0}} \right) ^{2}}{ \left(k_{ {0}}-m \right) a \left(d-a \right) }}, \, (k_{0} > m, \, d > a)$ and

In addition, $\Sigma \subset \Omega$, when a trajectory $X(t) = (x(t), y(t), z(t), u(t))$ of (1.2) is outside $\Omega$, we get $\dot V(X(t)) < 0$. Then, $\mathop{lim}\limits_{t\to+\infty}\rho(X(t, t_{0}, X_{0}), \Omega) = 0$. When $X(t)\in \Omega$, we also get $\dot V(X(t)) < 0$. Thus, any trajectory $X(t)$ ($X(t)\neq X_{0}$) will go into $\Omega$. Therefore, the conclusions of theorem is obtained.

2.2.   Dissipativity and invariance

We can see that system (1.2) is invariant for the coordinate transformation

Then, the nonzero equilibria of (1.2) is symmetric with respect to $z$ axis. The divergence of (1.2) is

system (1.2) is dissipative if and only if $a+b+d > 0$. It shows that each volume containing the system trajectories shrinks to zero as $t\to \infty$ at an exponential rate $-(a+b+d)$.

2.3.   Equilibria

For $m\leq k_{0}$, system (1.2) only has one equilibrium point $O(0, 0, 0, 0)$ and the Jacobian matrix at $O$ is

Then, the characteristic equation is

where

According to Routh-Hurwitz criterion ^[25], the real parts of eigenvalues are negative if and only if

When $m > k_{0}$, system (1.2) has other two nonzero equilibrium points $E_{1}(x_{1}^{*}, y_{1}^{*}, z_{1}^{*}, u_{1}^{*})$ and $E_{2}(-x_{1}^{*}, -y_{1}^{*}, z_{1}^{*}, -u_{1}^{*})$, where

The characteristic equation of Jacobi matrix at $E_{1}$ and $E_{2}$ is

where

Based on Routh-Hurwitz criterion ^[25], the real parts of eigenvalues are negative if and only if

Therefore, we have:

Theorem 2.2. (I) When $m\leq k_{0}$, system (1.2) only has one equilibrium point $O(0, 0, 0, 0)$ and $O$ is asymptotically stable if and only if (2.3) is satisfied.

(II) when $m > k_{0}$, system (1.2) has two nonzero equilibria $E_{1}$, $E_{2}$, (2.4) is the necessary and sufficient condition for the asymptotically stable of $E_{1}$ and $E_{2}$.

3.   Hyperchaos

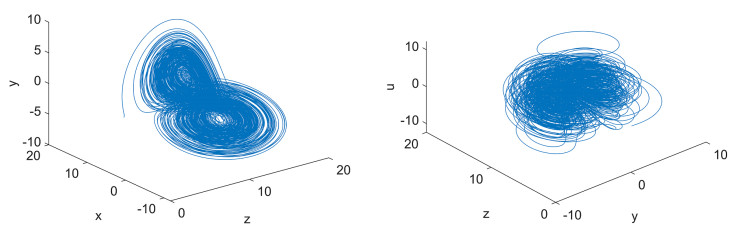
When $(b, d, h, a, k_{0}, k, m) = (1, 1, 10, 10, 0.8, 0.8, 0.8)$, system (1.2) only has zero-equilibrium point $E_{0}(0, 0, 0, 0, 0)$, its corresponding characteristic roots are: $-1, \, 0.230, \, 5.232, \, -16.462$, $E_{0}$ is unstable. The Lyapunov exponents are: $LE_{1} = 0.199$, $LE_{2} = 0.083$, $LE_{3} = 0.000$, $LE_{4} = -12.283$, system (1.2) is hyperchaotic. Figure 1 shows the hyperchaotic attractors on $z-x-y$ space and $y-z-u$ space. The Poincaré mapping on the $x-z$ plane and power spectrum of time series $x(t)$ are depicted in Figure 2.

In the following, we fix $b = 1, \, d = 1, \, h = 10, \, a = 10, \, k_{0} = 0.8, \, m = 0.8$, Figure 3 indicates the Lyapunov exponent spectrum of system (1.2) with respect to $k\in [0.005, 1.8]$ and the corresponding bifurcation diagram is given in Figure 4. These simulation results illustrate the complex dynamical phenomena of system (1.2). When $k$ varies in $[0.005, 1.8]$, there are two positive Lyapunov exponents, system (1.2) is hyperchaoic as $k$ varies.

Assume $b = 1, \, d = 1, \, h = 10, \, k = 0.8, \, k_{0} = 0.8, \, m = 0.8$, the different Lyapunov exponents and dynamical properties with different values of parameter $a$ are given in Table 1. It shows that system (1.2) has rich dynamical behaviors including periodic, chaos and hyperchaos with different parameters. The bifurcation diagram of system (1.2) with $a\in [0.5, 5]$ is given in Figure 5. Therefore, we can see that periodic orbits, chaotic orbits and hyperchaotic orbits can occur with increasing of parameter $a$. When $a = 1.08$, Figure 6 indicates the $(z, x, y, u)$ 4D surface of section and the location of the consequents is given in the $(z, x, y)$ subspace and are colored according to their $u$ value. The chaotic attractor and hyperchaotic attractor on $y-x-z$ space and hyperchaotic attractor on $y-z-u$ space are given in Figures 7 and 8, respectively. The Poincaré maps on $x-z$ plane with $a = 2$ and $a = 4$ are depicted in Figure 9.

4.   Hopf bifurcation

Theorem 4.1. Suppose that $ab > h^{2}$ and $k_{0}(a-h)+m(b-h) < 0$ are satisfied. Then, as $m$ varies and passes through the critical value $k = {\frac {a{h}^{2}+b{h}^{2}-{a}^{2}b-a{b}^{2}}{ak_{{0}}+bm-hm-hk_{{0}}}}$, system (1.2) undergoes a Hopf bifurcation at $O(0, 0, 0, 0)$.

Proof. Assume that system (1.2) has a pure imaginary root $\lambda = {\rm i}\omega, \, (\omega \in {\mathbb {R}}^{+})$. From (2.2), we get

then

Substituting $k = k_{*}$ into (2.2), we have

Therefore, when $ab > h^{2}$, $k_{0}(a-h)+m(b-h) < 0$ and $k = k_{*}$, the first condition for Hopf bifurcation ^[26] is satisfied. From (2.2), we have

Thus, the second condition for a Hopf bifurcation ^[26] is also met. Hence, Hopf bifurcation exists.

Remark 4.1. When $ab-h^{2}+k(k_{0}+m)\leq 0$, system (1.2) has no Hopf bifurcation at the zero equilibrium point.

Theorem 4.2. When $ab > h^{2}$ and $k_{0}(a-h)+m(b-h) < 0$, the periodic solutions of (1.2) from Hopf bifurcation at $O(0, 0, 0, 0)$ exist for sufficiently small

And the periodic solutions have the following properties:

(I) if $\delta_{g}^{1} > 0$ (resp., $\delta_{g}^{1} < 0$), the hopf bifurcation of system (1.2) at $(0, 0, 0, 0)$ is non-degenerate and subcritical (resp. supercritical), and the bifurcating periodic solution exists for $m > m_{*}$ (resp., $m < m_{*}$) and is unstable (resp., stable), where

(II) The period and characteristic exponent of the bifurcating periodic solution are:

where $\epsilon = \frac{k-k_{*}}{\mu_{2}}+O[(k-k_{*})^2]$ and

(III) The expression of the bifurcating periodic solution is

Proof. Let $k = k_{*}$, by straightforward computations, we can obtain

which satisfy

Now, we use transformation $X = QX_{1}$, where $X = (x, y, z, u)^{T}$, $X_{1} = (x_{1}, y_{1}, z_{1}, u_{1})^{T}$, and

then, system (1.2) is transformed into

where

$\delta = \omega_{{0}}$ $[(-ab+{h}^{2}) (akk_{{0}}+hkk_ {{0}}-hs_{{1}}) +k (bm-hk_{{0}}) (ha+{h}^{2 }+kk_{{0}})-k(ak-hm)$ $({a}^{2}+ha-kk_{{0}} +s_{{1}})]$,

$F_{1}(x_{1}, y_{1}, z_{1}, u_{1})$ $= \frac{1}{\delta}z_{1}(f_{11}x_{1}+f_{12}y_{1}+f_{13}u_{1})$,

$f_{11} = -kk_{{0}}\omega_{{0}}(abh-a{k}^{2}-{h}^{3}+hkm)+$ $(kk_{{0}}-s_{{1}}) \omega_{{0}} ({a}^{2}b-a{h}^{2} -bkm+hkk_{{0}})$,

$f_{12} = -kk_{{0}}\omega_{{0}}(abh-a{k}^{2}-{h}^{3}+hkm)+$ $(kk_{{0}}-s_{{1}}) \omega_{{0}} ({a}^{2}b-a{h}^{2} -bkm+hkk_{{0}})$,

$f_{13} = -kk_{{0}}\omega_{{0}}(abh-a{k}^{2}-{h}^{3}+hkm)+$ $(kk_{{0}}-s_{{1}}) \omega_{{0}} ({a}^{2}b-a{h}^{2} -bkm+hkk_{{0}})$,

$F_{2}(x_{1}, y_{1}, z_{1}, u_{1}) =$ $-\frac{1}{\delta}z_{1}(f_{21}x_{1}+f_{22}y_{1}+f_{23}u_{1})$,

$f_{21} = (-ab+{h}^{2}) (2\, {k}^{2}{k_{{0}}}^{2}-2\, kk_{{0} }s_{{1}}+{s_{{1}}}^{2})$ $-k (a+h) (a{k}^{2}k_{{0}}-bkmk_{{0}}-hkmk_{{0}}+$ $hk {k_{{0}}}^{2}+bms_{{1}}-hk_{{0}}s_{{1}})$,

$f_{22} = -a\omega_{{0}}[abk(m-k_{0})-hk(ak_{0}-bm)]$ $+abs_{{1}}-{h}^{2 }s_{{1}}] -h\omega_{{0}} [ak(ak+bk_{0}+hk-hm)-h^2k(m+k_{0})]$,

$f_{23} = (h^2-ab)[hkk_{{0}}(m-k_{{0}})-kk_{{0}} (ak-bm)-s_{{1}}(bm-hk_{{0}})]+k(a+h)[ak(ak-2\, hm)$ $+bm (bm-2\, hk_{{0}}) +{h}^{2}({m}^{2}+{k_{{0}}}^{2})]$,

$F_{3}(x_{1}, y_{1}, z_{1}, u_{1}) =$ $[-kk_{{0}}x_{{1}}-h\omega_{{0}}y_{{1}}+ (ak-hm) u_ {{1}}] [(kk_{{0}}-s_{{1}}) x_{{1}}-a\omega _{{0}}y_{{1}}+ (bm-hk_{{0}}) u_{{1}}]$,

$F_{4}(x_{1}, y_{1}, z_{1}, u_{1}) =$ $\frac{1}{\delta}z_{1}(f_{41}x_{1}+f_{42}y_{1}+f_{43}u_{1})$,

$f_{41} = kk_{{0}}$ $(h\omega_{{0}}ka+{h}^{2}\omega_{{0}}k+{k}^{2}k_{{0}} \omega_{{0}}) -$ $(kk_{{0}}-s_{{1}}) k\omega_{{0}} ({a}^{2}+ah-kk_{ {0}}+s_{{1}})$,

$f_{42} =$ ${a}^{3}{\omega_{{0}}}^{2}k+{a}^{2}{\omega_{{0}}}^{2}kh+{h}^{2}{\omega_ {{0}}}^{2}ka-a{k}^{2}k_{{0}}{\omega_{{0}}}^{2}+{h}^{3}$ ${\omega_{{0}}}^{ 2}k+{k}^{2}k_{{0}}h{\omega_{{0}}}^{2}+$ $ak{\omega_{{0}}}^{2}s_{{1}}$,

$f_{43} = -{a}^{2}bkm\omega_{{0}}-{a}^{2}h{k}^{2}\omega_{{0}}+$ ${a}^{2}hkk_{{0}} \omega_{{0}}-abhkm\omega_{{0}}-a{h}^{2}{k}^{2}$ $\omega_{{0}}+a{h}^{2}km \omega_{{0}}+a{h}^{2}kk_{{0}}\omega_{{0}}-a{k}^{3}$ $k_{{0}}\omega_{{0}}$ $+b{k}^{2}mk_{{0}}\omega_{{0}}+$ ${h}^{3}km\omega_{{0}}+h{k}^{2}mk_{{0}} \omega_{{0}}-h{k}^{2}{k_{{0}}}^{2}\omega_{{0}}-bkm$ $\omega_{{0}}s_{{1}}+$ $hkk_{{0}}\omega_{{0}}s_{{1}}$.

Furthermore,

By solving the following equations

where

one obtains

where

where

where

Based on above calculation and analysis, we get

where

Note $\alpha'(0) < 0$. From $ab > h^{2}$ and $k_{0}(a-h)+m(b-h) < 0$, we obtain that if $\delta_{g}^{1} > 0$ (resp., $\delta_{g}^{1} < 0$), then $\mu_{2} > 0$ (resp., $\mu_{2} < 0$) and $\beta_{2} > 0$ (resp., $\beta_{2} < 0$), the hopf bifurcation of system (1.2) at $(0, 0, 0, 0)$ is non-degenerate and subcritical (resp. supercritical), and the bifurcating periodic solution exists for $k > k_{*}$ (resp., $k < k_{*}$) and is unstable (resp., stable).

Furthermore, the period and characteristic exponent are

where $\epsilon = \frac{k-k_{*}}{\mu_{2}}+O[(k-k_{*})^2]$. And the expression of the bifurcating periodic solution is (except for an arbitrary phase angle)

where

and

By computations, we can obtain

Based on the above discussion, the conclusions of Theorem 4.2 are proved.

In order to verify the above theoretical analysis, we assume

According to Theorem 4.1, we get $k_{*} = 1$. Then from Theorem 4.2, $\mu_{2} = -4.375$ and $\beta_{2} = -0.074$, which imply that the Hopf bifurcation of system (1.2) at $(0, 0, 0, 0)$ is nondegenerate and supercritical, a bifurcation periodic solution exists for $k < k_{*} = 1$ and the bifurcating periodic solution is stable. Figure 10 shows the Hopf periodic solution occurs when $k = 0.999 < k_{*} = 1$.

5.   Conclusions

In this paper, we present a new 4D hyperchaotic system by introducing a linear controller to the first equation and second equation of the 3D Rabinovich system, respectively. If $k_{0} = 0$, $m = 1$ and the fourth equation is changed to $-ky$, system (1.2) will be transformed to 4D hyperchaotic Rabinovich system in ^[18,19]. Compared with the system in ^[18], the new 4D system (1.1) has two nonzero equilibrium points which are symmetric about $z$ axis when $m > k_{0}$ and the dynamical characteristics are more abundant. The complex dynamical behaviors, including boundedness, dissipativity and invariance, equilibria and their stability, chaos and hyperchaos of (1.2) are investigated and analyzed. Furthermore, the existence of Hopf bifurcation, the stability and expression of the Hopf bifurcation at zero-equilibrium point are studied by using the normal form theory and symbolic computations. In order to analyze and verify the complex phenomena of the system, some numerical simulations are carried out including Lyapunov exponents, bifurcations and Poincaré maps, et al. The results show that the new 4D Rabinovich system can exhibit complex dynamical behaviors, such as periodic, chaotic and hyperchaotic. In the real practice, the hyperchaotic Rabinovich system can be applied to generate key stream for the entire encryption process in image encryption scheme ^[27]. In some cases, hyperchaos and chaos are usually harmful and need to be suppressed such as in biochemical oscillations ^[8] and flexible shaft rotating-lifting system ^[28]. Therefore, we will investigate hyperchaos control and chaos control in further research.

Acknowledgments

Project supported by the Doctoral Scientific Research Foundation of Hanshan Normal University (No. QD202130).

Conflict of interest

The authors declare that they have no conflicts of interest.