Estimation of the time cost with pinning control for stochastic complex networks

1.   Introduction

Networks are ubiquitous in nature and human society, such as the World Wide Web, electricity networks, protein interaction networks, ecological networks, and so on. Complex networks are networks with high complexity, and studying the collective behavior of complex networks has important practical significance for our work and life. As one of the basic nonlinear phenomena of complex networks, synchronization has received extensive attention ^[1,2]. Synchronization means that as the network evolves, all individuals eventually reach the same state through coupling. Complex network synchronization has great application prospects in the fields of wireless sensor networks and robot control.

Synchronization of complex networks has had many interesting results over the past few decades. At the end of the 20th century, Reference ^[3] and ^[4] revealed the small-world characteristics and scale-free nature of complex networks, setting off a research boom in complex networks. Pecora and Carroll proposed that the main stability function of a coupled system can be used to describe the synchronization capability of the network, and pointed out that the synchronization is determined by the network topology ^[5]. In Reference ^[6], random matrix theory was shown to be able to predict the synchronization of networks, and it is pointed out that the speed of synchronization depends on network connectivity. After that, many scholars have studied the synchronization problem of complex networks ^[7,8,9,10]. It is pointed out in Reference ^[11] that the convergence speed without time delay is proportional to the second smallest Laplace eigenvalue of the network, and the time delay can improve the convergence speed of synchronization. However, in the above studies, most of them refer to asymptotic synchronization, which means the time required to achieve synchronization is infinite.

Existing studies have shown that convergence rate is an important criterion for network synchronization research. To speed up the convergence of the system, finite-time synchronization was proposed. Compared with asymptotic synchronization, finite-time synchronization not only has a faster convergence rate, enabling the system to achieve synchronization within a finite time but also has stronger disturbance rejection properties ^[12]. But the settling time of finite-time synchronization depends on the initial state of the network, that is, the initial state of the network is necessary to estimate the settling time. To overcome this disadvantage, fixed-time synchronization was proposed ^[13]. The convergence time of fixed-time synchronization is independent of the initial state of the network, which expands the application scope of finite-time synchronization and has been widely studied in recent years ^{[14,15,16,17,18,19,20,21]}. For example, in Reference ^[14], the finite-time and fixed-time synchronization of complex networks with discontinuous dynamics was discussed. Kinds of control protocols were proposed to achieve synchronization under different conditions. In Reference ^[20], the fixed-time synchronization problem of nonlinear coupled neural networks was studied and an estimate of the settling time was given.

Besides the time cost, the energy cost is another important criterion to consider in network synchronization. Most of the existing research controls each agent of the network, which will increase the control cost of the system. Therefore, to reduce the energy cost, pinning control was proposed, which refers to selecting part of the agents in the network for control. The pinning control technique has been successfully applied to the research of multi-agent system consensus and network synchronization ^{[22,23,24,25,26,27]}. In Reference ^[22], the pinning problem of complex networks controlled by a single controller was studied. They found that a single controller can pin a coupled complex network to a homogenous solution without assuming symmetry, irreducibility, or linearity of the couplings. The finite-time and fixed-time cluster synchronization problem for complex networks with or without pinning control was studied in Reference ^[25]. Furthermore, the cluster synchronization problem for a class of the nonlinearly coupled delayed neural networks was investigated in Reference ^[24] by using the pinning control technique.

However, most of the above studies do not consider the impact of noise on network synchronization. In the real world, as a result of random uncertainties such as stochastic forces on the physical systems and noisy measurements caused by environmental uncertainties, a system should be produced with random perturbations rather than deterministic forms. The finite-time stochastic synchronization problem for complex networks with stochastic noise perturbations was studied in Reference ^[28]. The finite-time stochastic outer synchronization between two complex dynamical networks with different topologies was studied in Reference ^[29]. In recent years, there have been many novel results in the study of stochastic synchronization of complex networks ^{[16,24,30,31,32,33]}.

From the above discussions, finite-time and fixed-time stochastic synchronization with pinning control are investigated in this paper. It is proved by theoretical analysis and numerical simulation that the network can achieve stochastic synchronization in a finite time only by controlling a small fraction of agents. The main contributions of this paper can be summarized as follows: 1) The finite/fixed-time pinning controller is proposed to ensure the convergence rate and effectively reduce the control cost. 2) The influence of noise on synchronization is considered, and sufficient conditions for the network to achieve stochastic synchronization are given. 3) The effects of control parameters, noise intensity, and the number of control agents on the network synchronization rate are investigated.

The remainder of this paper is organized as follows. In Section 2, the problem statement and some useful preliminaries are introduced. In Sections 3 and 4, based on the stability theory of stochastic differential equations, the finite-time and fixed-time stochastic synchronization problems are considered. In Section 5, numerical simulations are given to demonstrate the effectiveness of the proposed control protocols. Finally, the conclusion is given in Section 6.

Notation. Throughout this paper unless specified we have the following definitions. Let $\parallel \cdot \parallel$ be Euclidean norm. $A^{T}$ denotes the transpose of $A$, if $A$ is a vector or matrix. Moreover, a symmetric matrix $A$ is called a negative definite matrix if all eigenvalues of the matrix $A$ are less than zero. $I_n$ is the n-dimension unit matrix. Symbol $\otimes$ is the Kronecker product and $\mathbb E(\cdot)$ represents the expectation operator.

2.   Preliminaries and problem formulation

In this section, preliminaries about graph theory and problem formulation are briefly introduced. Let $\mathcal{G}(A) = (\mathcal{V}, \mathcal{E}, A)$ be a weighted digraph of order $N$. $\mathcal{V} = \{v_1, v_2, \cdots, v_N\}$ is the set of nodes, $\mathcal{E}\subseteq \mathcal{V}\times\mathcal{V}$ is the set of edges and matrix $A = [a_{ij}]_{N\times N}$ is a weighted adjacency with nonnegative adjacency elements $a_{ij}$. An edge $(v_i, v_j)$ in $\mathcal{G}(A)$ denotes that node $v_i$ can obtain information from node $v_j$ and $(v_i, v_j)\in \mathcal{E}$ if and only if $a_{ij} > 0$. Moreover, assume that $a_{ii} = 0$ for all $i\in \{1, 2, \cdots, N\}$. The set of neighbors of node $v_i$ is $N_i = \{v_j\in \mathcal{V}:(v_i, v_j)\in \mathcal{E}\}$. Let a diagonal matrix $D =$diag$(d_1, \cdots, d_N)$ be the degree matrix of $\mathcal{G}(A)$, where $d_i = \sum_{j = 1}^{N}a_{ij}$. Then, the Laplacian matrix of $\mathcal{G}(A)$ can be denoted by $L = D-A$.

Consider a complex network consisting of $N$ agents :

where ${x_i = (x_{i1}, x_{i2}, \cdots, x_{in})^T}\in{R^n}$ is the state vector of the $i$th agent, $f:R^n \rightarrow R^n$ is a continuous and differentiable nonlinear vector function, $u_i(t)$ is the controller to be designed. In real environments, complex networks are inevitably affected by random perturbations, that is, each agent cannot accurately measure the states of its neighbors. In order to solve this problem, this paper considers the influence of noise and nonlinear dynamics. The network (1) can be written as

Here, parameters $\gamma > 0$, $\sigma_{ij}$ is an element of noise intensity matrix and $\xi_i(t)$ is independent white noise. The noise terms in system (2) are often used to describe the coupling process of coupling factors, such as inaccurate design of coupling strength and environmental fluctuation. Notice that the aim of synchronization is all agents reach a synchronise state $s(t)$, and assume that $\dot{s}(t) = f(s(t))$. Moreover, let $e_i(t) = x_i(t)-s(t)$ be the synchronization error, ${\bf{e}} = (e_1^T, e_2^T, \cdots, e_N^T)^T$.

Before moving on, the definition of complex network stochastic synchronization and several useful lemmas are given.

Definition 2.1. System (2) is said to achieve stochastic synchronization, if there exists a time function $T_0$ depending on (or independent of) the initial values, such that

Assumption 1. Assume the function $f(\cdot)$ satisfies the Lipchitz condition, i.e., $\forall x, y\in \mathbb{R}^N$, there exists a positive constant $l$ such that

Lemma 2.1. ^[23] Assume that there's a function $\psi$, which satisfies $\psi(x_i, x_j) = -\psi(x_j, x_i), \forall i, j\in \{1, 2, \cdots, N\}, i\ne j$. Thus, for any undirected graph and set of numbers $y_1, y_2, \cdots, y_N$,

Lemma 2.2. ^[34] If the graph $\mathcal{G}(A)$ is strongly connected, then the eigenvalue 0 of the graph Laplacian $L_{A}$ is algebraically simple and all other eigenvalues are with positive real parts. If $\mathcal{G}(A)$ is also undirected, then

where $x = (x_{1}, \cdots, x_{N})^{T}\in \mathbb{R}^{N}$.

Lemma 2.3. ^[35] Let $z\in \mathbb{R}^{n}$ and $0 < a < b$. Then the following norm equivalence property holds

and

Consider a stochastic differential equation $\mathrm{d}x = {f}(x)\mathrm{d}t+{g}(x)\mathrm{d}W(t)$. Here, $f:\mathbb{R}^n\rightarrow \mathbb{R}^n, g:\mathbb{R}^n\rightarrow \mathbb{R}^{n\times m}$ are continuous functions, satisfying initial conditions${f}(0) = 0, {g}(0) = 0$. The variable $x\in \mathbb{R}^n$ represents the state of system and $x(0)$ is the initial state. $W$ represents a standard Brownian motion. Assume that formula has a unique and global solution, which is represented by $x(t, x(0)), 0\leq t < +\infty$. Then, the following conclusion can be obtained:

where $\frac{\partial V}{\partial x} = \bigg(\frac{\partial V}{\partial x_1}, \ldots, \frac{\partial V}{\partial x_n}\bigg), \frac{\partial^2 V}{\partial x^2} = \bigg[\frac{\partial^2 V}{\partial x_i\partial x_j}\bigg]_{n\times n}$.

Definition 2.2. ^[36] A function $v: \mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$ is said to be a class $\mathcal{K}$ function if it is continuous, strictly increasing, and $v(0) = 0$. A class $\mathcal{K}$ function is said to belong to class $\mathcal{K}_{\infty}$ if $v(r)\rightarrow \infty$ as $r\rightarrow \infty$.

Lemma 2.4. ^[36] Assume the above $n$-dimensional equation has a unique solution. If the function $V: \mathbb{R}^{n}\to \mathbb{R}^{+}$ is quadratic continuously differentiable, and there are $\mathcal{K}_{\infty}$ class functions $v_1$ and $v_2$, positive constants $\eta > 0$ and $0 < \rho < 1$, for all $x\in \mathbb{R}^{n}$ and $t\ge 0$ such that

Then the system is finite-time stable in probability one. The stochastic convergence time is estimated as

where $x_0$ is the initial state of system.

Lemma 2.5. ^[37] Consider the above $n$-dimensional equation and assume that function $V: \mathbb{R}^{n}\to \mathbb{R}^{+}$ is a regular, positive definite and radially unbounded function. There are positive constants $0 < p < 1 < q, \varphi > 0, \varrho > 0$, such that

Then the system is fixed-time stable in probability one. The stochastic convergence time is estimated as

3.   Finite-time stochastic synchronization with pinning control

Most of the existing research controls all agents of the network, which will increase the energy cost. Therefore, the pinning control technique is considered, that is, only controlling a small number of agents to make the network achieve stochastic synchronization. Combining finite-time control technology and pinning control technology, the stochastic synchronization problem of complex networks under noise disturbance is studied in this section.

Generally, suppose the first $m$ nodes $\{ i_1, i_2, \cdots, i_m \}$ in the system are selected. Define the proportion of controlled agents as $n_D, n_D = m/N \in [0, 1]$. Notice that $\sigma_{ij}$ is an element of the noise intensity matrix, let $\sigma_i = \sum_{j\in N_i} \sigma_{ij}$ and matrix $\Pi = [\sigma_{ij}]\in \mathbb{R}^{N \times N}$, then matrix $L_{\sigma} = \text{diag}(\sigma_1, \cdots, \sigma_N)-\Pi$ is the Laplacian matrix of matrix $\Pi$. Let matrix $D_\alpha = \text{diag}(\alpha, \cdots, \alpha)$, $D_{l} = \text{diag}(l, \cdots, l)$, $D_{\epsilon_1} = \text{diag}(\underbrace{(2\epsilon_1)^\frac{2}{1+p}, \cdots, (2\epsilon_1)^\frac{2}{1+p}}_{m}, \underbrace{0, \cdots, 0}_{N-m})$. Matrix $L_B$ denotes the Laplacian matrix of the graph $\mathcal{G}(B)$. For the purpose of achieving synchronization in a finite time, the following pinning controller is proposed:

where $(L_A{\bf{x}})_i = \sum_{j\in N_i}a_{ij}(x_i-x_j), 0 < p < 1, (\triangle_{p+1}{\bf{x}})_i = \sum_{j\in N_i}a_{ij}\phi_{p+1}(x_i-x_j)$. Define $\phi_{p+1}(z) = \text{sign}(z)|z|^p$, $\text{sign}(\cdot)$ is a sign function. Parameters $\alpha > 0, \epsilon_1 > 0$ are control intensity. $a_{ij}$ is an element of the adjacency matrix, representing the agent $j$ has an impact on the agent $i$. $A = [a_{ij}]$ is the adjacency matrix of the graph $\mathcal{G}(A)$. $\mathcal{I}_c = \{1, 2, \cdots, m\}$ is the set of controlled nodes, and the set of remaining nodes is $\bar{\mathcal{I}}_c = \{m+1, m+2, \cdots, N\}$.

Theorem 3.1. Consider a complex network (2) with topology $\mathcal{G}(A)$. Assume $\mathcal{G}(A)$ is undirected and connected. Using the proposed pinning controller (3) and supposing that $[D_l \otimes I_n+\frac{\gamma^2}{2}(L_\sigma\otimes I_n)^T(L_\sigma\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, system (2) can achieve the finite-time stochastic synchronization. Furthermore, the settling time can be estimated as

where $\lambda = \lambda_{\min}(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$.

Proof. From the definition of error, the error system corresponding to the complex network (2) under the proposed pinning controller (3) is

Take the Lyapunov function

Let $(L_{\sigma})_i$ denote the $i$th row of matrix $L_{\sigma}$. Thus, $\sum_{j\in N_i} \sigma_{ij}(e_j-e_i) = -((L_{\sigma})_i\otimes I_n){\bf{e}}.$ Then,

From the Itô's formula, one has

By Assumption 1 and the definition of matrix $D_l$, one can obtain

According to Lemmas 2.1 and 2.2, we have

Here, matrix $L$ is the Laplacian matrix of $\mathcal{G}(A)$ and the smallest eigenvalue of matrix $(L\otimes I_n)$ is $0$, which means $V_2\le 0$.

Let parameter ${\epsilon_1}^i = \epsilon_1$ when $i\in \mathcal{I}_c$, otherwise let ${\epsilon_1}^i = 0$. Thus, using Lemmas 2.1 and 2.3, one has

Here, matrix $B = [b_{ij}]$, where $b_{ij} = a_{ij}^{\frac{2}{p+1}}$. $L_B$ denotes the Laplacian matrix of the graph $\mathcal{G}(B)$. Notice that the undirected graph $\mathcal{G}(A)$ is connected, then $\mathcal{G}(B)$ is also undirected and connected. Matrix $D_{\epsilon_1} = \text{diag}(\underbrace{(2\epsilon_1)^\frac{2}{1+p}, \cdots, (2\epsilon_1)^\frac{2}{1+p}}_{m}, \underbrace{0, \cdots, 0}_{N-m})$. Notice that $D_\alpha = \text{diag}(\alpha, \cdots, \alpha)$, we have

Combing (6)–(10), we get that

Since $\mathcal{G}(B)$ is connected and undirected, matrix $(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$ is irreducibly diagonally dominant if $m\ge 1$. And matrix $(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$ is symmetric and all its diagonal elements are strictly positive. That is, matrix $(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$ only has positive eigenvalues.

If matrix $[D_l\otimes I_n+\frac{\gamma^2}{2}(L_{\sigma}\otimes I_n)^T(L_{\sigma}\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, we can reach the conclusion

where $\lambda = \lambda_{ \text{min}}(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$. Now, from Lemma 2.4, we know $V(t)\to 0$ in a finite time with probability one and the setting time can be estimated by

where $V(0) = \frac{1}{2}\sum_{i = 1}^{N}{e_i}^2(0)$, $e_i(0) = x_i(0)-s(0)$.

Remark 1. Based on the pinning control technique, the proposed protocol (3) can make the system achieve the stochastic synchronization by controlling a small fraction of agents, even with the influence of nonlinear dynamics and the perturbation of noise. Note that $\alpha$ is the strength of linear feedback term, $\gamma$ represents the strength of noise and $l$ is the Lipchitz constant of the node dynamics. Moreover, the upper bound of the settling time depends on $\lambda$ and control parameter $p$. Large values of $\lambda$ and $p$ yield fast convergence rate.

Remark 2. Different from the protocols in ^[16] and ^[18], the proposed pinning protocol makes the system reach the stochastic synchronization in finite time by controlling a small fraction of agents, and the effect of noise is considered. Compared with the protocol in ^[17], the pinning protocol (3) contains both finite-time control terms and linear control terms, and uses the graph Laplacian operator. By comparison, it can be found that the proposed pinning protocol can realize stochastic synchronization of the system only by controlling part of agents, which ensures the convergence speed and reduces the energy cost.

In the following, we present several special cases of Theorem 3.1.

Corollary 3.1. Suppose all agents in Theorem 3.1 are controlled, i.e. $n_D = 1$. Using the designed protocol (3), if $[D_l \otimes I_n+\frac{\gamma^2}{2}(L_\sigma\otimes I_n)^T(L_\sigma\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, system (2) can achieve the finite-time stochastic synchronization.

Corollary 3.2. Without taking into account the effect of noise in Theorem 3.1, i.e., $\gamma = 0$. Using the designed protocol (3), if matrix $[D_l \otimes I_n-(D_\alpha \otimes I_n)]$ is negatively definite, then system (2) can achieve the finite-time synchronization.

Remark 3. Corollaries 3.1 and 3.2 are special cases of Theorem 3.1. Compared to ^[25], Corollary 3.1 differs in that it takes into account the effect of noise. Corollary 3.2 shows that, regardless of the influence of noise, even if the states of some agents are unknown, the network can also achieve finite-time synchronization by the pinning protocol.

4.   Fixed-time stochastic synchronization with pinning control

Although the finite-time controller can synchronize the network in a finite time, the settling time depends on the initial state of the network. This means that the initial state of the network is essential to estimate the settling time. To solve this problem, the fixed-time pinning technology is considered. The stochastic synchronization problem of networks with fixed-time pinning control is investigated in this section and estimate of the upper bound on the settling time independent of the initial state of the network is given.

In this section, definitions of matrix $D_l$, $L_{\sigma}$, $D_\alpha$, $D_{\epsilon_1}$ and $L_B$ are the same as those in Section 3. Let $C = [c_{ij}]_{N\times N}$ and $c_{ij} = a_{ij}^\frac{2}{q+1}$. Matrix $L_C$ denotes the Laplacian matrix of $\mathcal{G}(C)$. Take $D_{\epsilon_2} = \text{diag}(\underbrace{(2{\epsilon_2})^\frac{2}{q+1}, \cdots, (2{\epsilon_2})^\frac{2}{q+1}}_{m}, \underbrace{0, \cdots, 0}_{N-m})$. Then, the following pinning controller is proposed

where $0 < p < 1$, $q > 1$, $\alpha > 0$, $\epsilon_1 > 0$, $\epsilon_2 > 0$.

Theorem 4.1. Consider a complex network (2) with undirected topology $\mathcal{G}(A)$. Assume $\mathcal{G}(A)$ is connected. Using the protocol (14), if $[D_l\otimes I_n+\frac{\gamma^2}{2}(L_{\sigma}\otimes I_n)^T(L_{\sigma}\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, system (2) can reach the fixed-time stochastic synchronization and the settling time can be estimated as

where $\lambda = \lambda_{\min}(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n), \mu = \lambda_{\min}(2L_C\otimes I_n+D_{\epsilon_2} \otimes I_n)$.

Proof. From the definition of error, the error system corresponding to the complex network (2) under the proposed pinning controller (14) is

Taking the Lyapunov function (5), from the Itô's formula and the definition of operator $\mathcal{L}$, one has

From (6) and (11), we have

When $i\in \mathcal{I}_c$, let ${\epsilon_2}^i = \epsilon_2$, otherwise ${\epsilon_2}^i = 0$. According to Lemmas 2.1 and 2.3, one has

Here, matrix $C = [c_{ij}]$, where $c_{ij} = a_{ij}^\frac{2}{q+1}$, $L_C$ denotes the Laplacian matrix of the graph $\mathcal{G}(C)$. If the undirected graph $\mathcal{G}(A)$ is connected, then $\mathcal{G}(C)$ is also undirected and connected. Matrix $D_{\epsilon_2} = \text{diag}(\underbrace{(2{\epsilon_2})^\frac{2}{q+1}, \cdots, (2{\epsilon_2})^\frac{2}{q+1}}_{m}, \underbrace{0, \ldots, 0}_{N-m})$. Combining (16)–(18), we have

Since $\mathcal{G}(C)$ is connected and undirected, matrix $(2L_C\otimes I_n+D_{\epsilon_2} \otimes I_n)$ is irreducibly diagonally dominant if $m\ge 1$. And matrix $(2L_C\otimes I_n+D_{\epsilon_2} \otimes I_n)$ is symmetric and all its diagonal elements are strictly positive. That is, matrix $(2L_C\otimes I_n+D_{\epsilon_2} \otimes I_n)$ only has positive eigenvalues.

If matrix $[D_l\otimes I_n+\frac{\gamma^2}{2}(L_{\sigma}\otimes I_n)^T(L_{\sigma}\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, we can reach the conclusion

where $\lambda = \lambda_{ \text{min}}(2L_B\otimes I_n+D_{\epsilon_1} \otimes I_n)$, $\mu = \lambda_{ \text{min}}(2L_C\otimes I_n+D_{\epsilon_2}\otimes I_n)$. Now, from Lemma 2.5, we know $V(t)\to 0$ in a finite time with probability one and the setting time can be estimated by

Remark 4. Theorem 4.1 shows that system (2) with protocol (14) can achieve the fixed-time stochastic synchronization only by controlling a small fraction of agents. Compared with Theorem 3.1, the estimation of convergence time in (21) is independent of the initial states of agents and only depends on $N, \lambda, \mu$ and $p$. Here, the eigenvalue $\mu$ depends on the proportion of controlled agents and the value of parameter $\epsilon_2$.

In the following, we present several special cases of Theorem 4.1.

Corollary 4.1. Suppose all agents are controlled, i.e., $n_D = 1$. Using the protocol (14), if $[D_l\otimes I_n+\frac{\gamma^2}{2}(L_{\sigma}\otimes I_n)^T(L_{\sigma}\otimes I_n)-(D_\alpha \otimes I_n)]$ is negatively definite, system (2) achieves the fixed-time stochastic synchronization.

Corollary 4.2. Without taking into account the effect of noise in Theorem 4.1, i.e., $\gamma = 0$. Using the designed protocol (14), if matrix $[D_l \otimes I_n-(D_\alpha \otimes I_n)]$ is negatively definite, then system (2) can achieve the fixed-time synchronization.

Remark 5. Corollaries 4.1 and 4.2 are special cases of Theorem 4.1. Corollary 4.1 shows that, considering the effect of noise, the protocol (14) is able to achieve fixed-time stochastic synchronization of the network. Corollary 4.2 shows that, regardless of the influence of noise, even if the states of some agents are unknown, the network can also achieve fixed-time synchronization by the pinning protocol.

5.   Simulation results

In order to verify the theoretical results obtained in previous sections, numerical simulations will be given in this section. The effects of noise intensity, control parameters and the number of control agents on the synchronization rate of the system are studied. In the simulations, use the scale-free networks with $\gamma_d = 2.5$ as the networks structure and all stochastic differential equations are numerically solved with the Euler-Maruyama scheme ^[38]. Considering the influence of inherent dynamics on system synchronization, the R$\ddot{o}$ssler-like system is taken to characterize the nonlinear dynamics of complex networks, which can be described as

where $x = (x_1, x_2, x_3)^T\in R^3$ is the state vector,

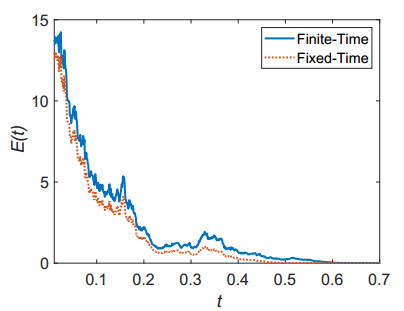
Taking $a = 0.03, b = 1.5, c = 0.2, \rho = 21.43, \mu = 1.5, \Gamma = 0.075, \lambda = 0.75$, we obtain the chaotic inherent dynamics of complex network. From the definition of synchronization error $e_i$, let $E(t) = \sum_{i = 1}^{N}e_i^Te_i$. The complex system (2) is said to achieve stochastic synchronization after time $T$ if, for $t\ge T$, $E(t) < 10^{-3}$. Taking parameters $N = 50, n_D = 0.4, \epsilon_1 = 2, \alpha = 2, \sigma = 1.5, p = 0.2$, the finite-time pinning protocol (3) is used to control the complex network (2). Furthermore, let $\epsilon_2 = 10, q = 1.8$, using the fixed-time protocol (14), the evolution process of error $E(t)$ is given in Figure 1. Figure 1 shows that when $t > 0.598$ and $t > 0.475$, the finite-time protocol and the fixed-time protocol can drive the system to achieve stochastic synchronization, respectively. That means the pinning controllers proposed in this paper are effective and correct.

To investigate the influence of control parameters on the system convergence rate, taking $N = 100, n_D = 0.4, \sigma = 1.5$, Figures 2–5 give the evolutions of error $E(t)$ under different control parameters of the fixed-time pinning protocol (14). Let $\epsilon_2 = 1, \alpha = 2, p = 0.2, q = 1.8$, taking $\epsilon_1 = 0.5, 1, 2$, the evolutions of $E(t)$ are given in Figure 2. It can be seen from the Figure 2 that the value of the parameter $\epsilon_1$ is proportional to the speed of system convergence. That means the pinning control $\epsilon_1\phi_{p+1}(x_i-s)$ has an important influence on synchronization. Let $\epsilon_1 = 2, \epsilon_2 = 1, p = 0.2, q = 1.8$, Figure 3 displays the evolutions of $E(t)$ with $\alpha = 0.5, 1, 2$. Figure 3 shows that the larger the parameter $\alpha$, the faster the system achieves stochastic synchronization, which is consistent with the theoretical results.

Taking $\epsilon_1 = 2, \epsilon_2 = 1, \alpha = 2, q = 1.8$, Figure 4 displays the trajectories of $E(t)$ with $p = 0.2, 0.5, 0.8$. It is shown that the proposed controller with smaller parameter $p$ can make the system reach stochastic synchronization faster. Let $\epsilon_1 = 1, \epsilon_2 = 10, \alpha = 1, p = 0.2$, Figure 5 displays the synchronization error $E(t)$ with $q = 1.5, 2, 3$. The simulation results in Figure 5 imply that, for given parameter $p$, the settling times with different parameter $q$ are similar. Therefore, it can be obtained that parameter $p$ plays an important role in the protocol, in contrast parameter $q$ has less effect.

To verify the influence of noise intensity $\sigma$ on the synchronization speed of the system, we simulate the systems with fixed-time pinning protocol (14) by taking different values of $\sigma$ in Figure 6. Taking $N = 50, n_D = 0.4, \epsilon_1 = 1, \epsilon_2 = 2, \alpha = 2, p = 0.2, q = 1.8$, Figure 6 gives the evolutions of $E(t)$ with $\sigma = 1, 2, 4$. The results show that the greater the noise intensity, the faster the system achieves stochastic synchronization. This means that noise can promote network synchronization, contrary to the common perception that noise has a negative effect on synchronization.

From theoretical results (13) and (21), we find the upper bound of settling time for the finite-time and fixed-time synchronization is affected by the parameter $n_D$. In Figure 7, taking $N = 20, \epsilon_1 = 2, \epsilon_2 = 5, \alpha = 1, \sigma = 1, p = 0.8, q = 1.2$, the settling times for different parameters $n_D$ are given. It can be seen from Figure 7 that the settling time decreases by increasing $n_D$, which means the more agents are controlled, the faster synchronization is reached. What's more, for any given density of controlled agents, the fixed-time pinning controller has a lower time cost to achieve stochastic synchronization than the finite-time pinning controller. Figure 7 shows that the fixed-time pinning controller proposed in this paper can effectively reduce the energy cost while ensuring the convergence rate.

To further study the effect of pinning control on the synchronization of complex networks, we select different types of agents for control. A network consisting of $100$ agents is selected, and the agents are sorted according to their degree. The agents with large degrees and the agents with small degrees are respectively selected for pinning control. The results show that when the proportion of control agents is lower than 0.4, the agents with a large degree of control are better than agents with a small degree of control, and the network convergence speed is faster. When the proportion of control agents is higher than 0.5, the agents with small control degree can make the network reach stochastic synchronization faster. It can be seen from Figure 8 that no matter which control strategy is used, the more agents are controlled, the faster the convergence speed of the network is.

6.   Conclusions

In this paper, we have investigated the finite-time and fixed-time stochastic synchronization of complex networks with pinning control and noise perturbation. Most of the existing research controls all individuals in the network to achieve asymptotic synchronization and does not consider the influence of noise on synchronization. Using the finite/fixed-time control technology and the pinning control technology, we propose new effective controllers, which can make the network achieve stochastic synchronization by only controlling part of individuals. Different from the previous controllers, the finite/fixed-time pinning controller can realize stochastic synchronization of complex networks in a finite time, which ensures the convergence rate and reduces the energy cost of control. The effects of controller parameters, noise intensity, and the number of control agents on the network synchronization rate are investigated. Numerical simulations verify the effectiveness and correctness of the proposed controllers. The work in this paper is the first step toward the time cost for stochastic synchronization of complex networks. In this paper, the stochastic synchronization problem of a single network is studied. It would be interesting to study the stochastic synchronization problem of multiple networks. This problem is our future research direction.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant 22120102001, and the Fundamental Research Funds for Central Universities under Grant 2019XKQYMS92.

Conflict of interest

The authors declare there is no conflicts of interest.