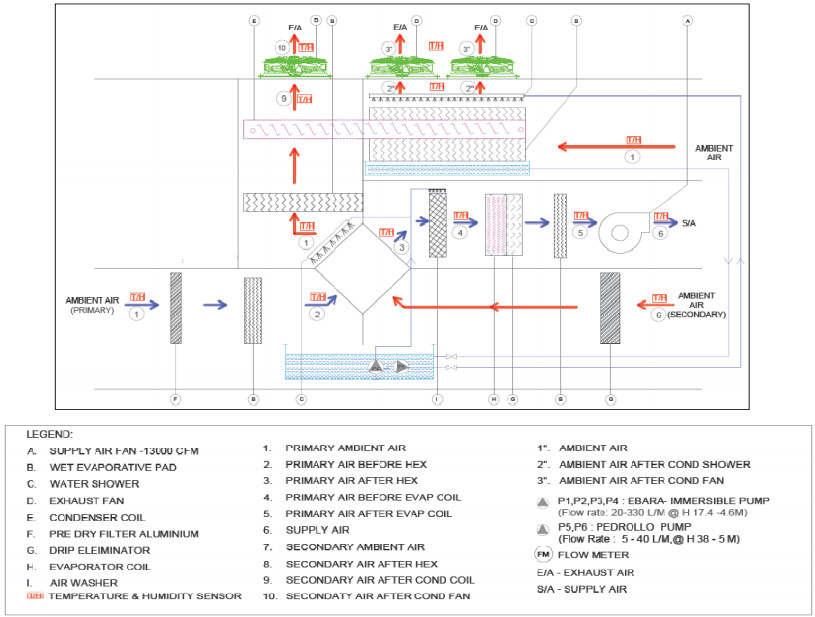
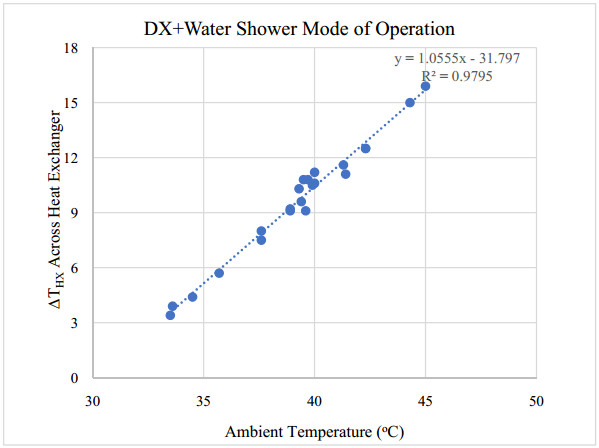
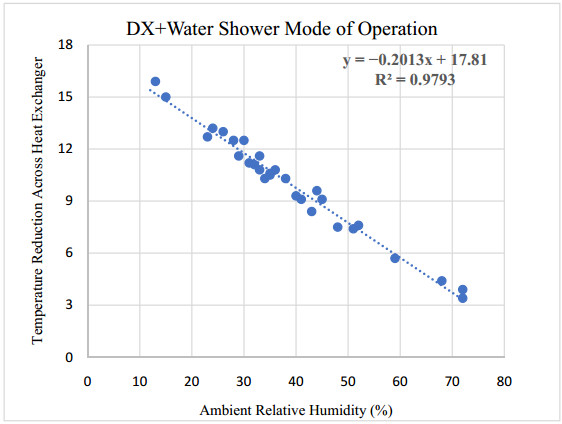
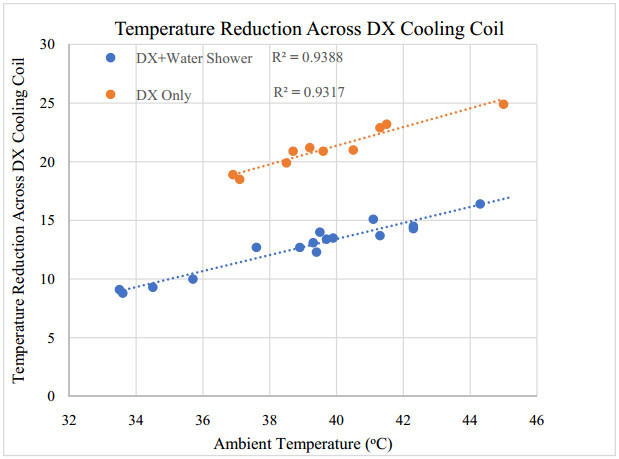
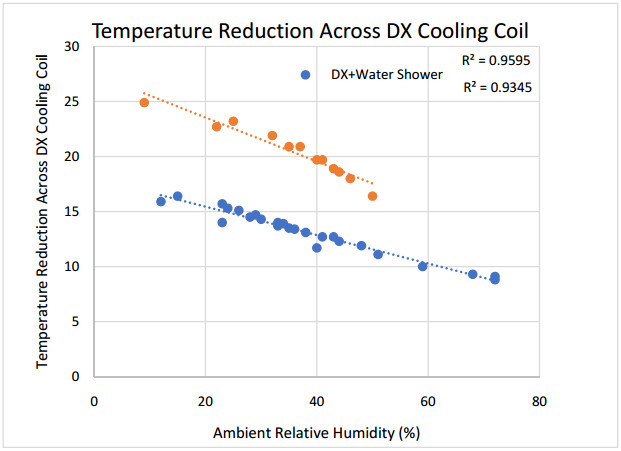
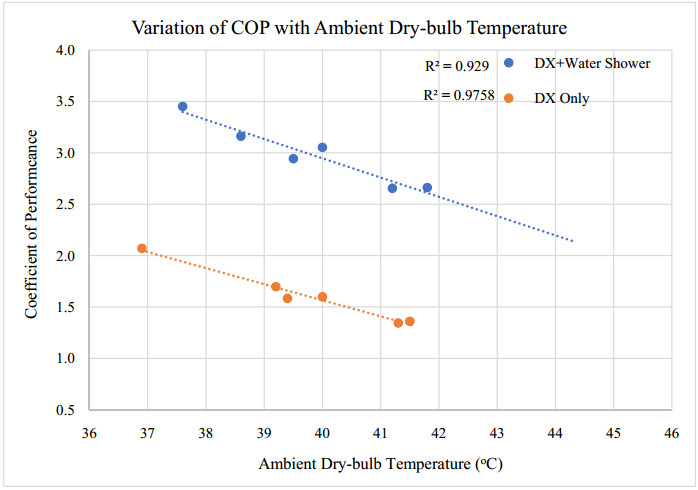
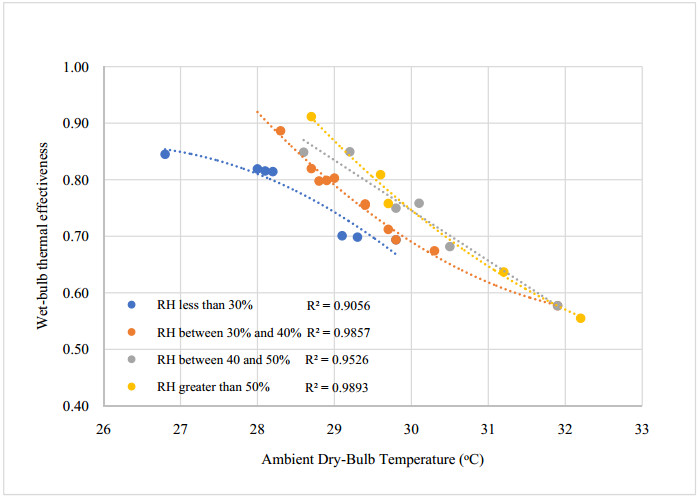
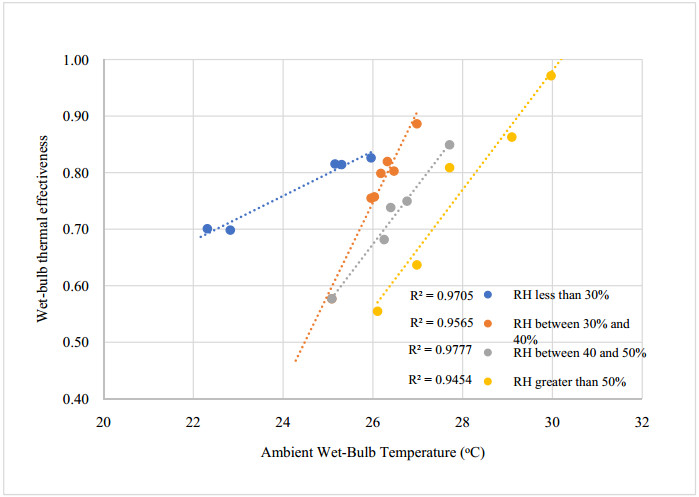
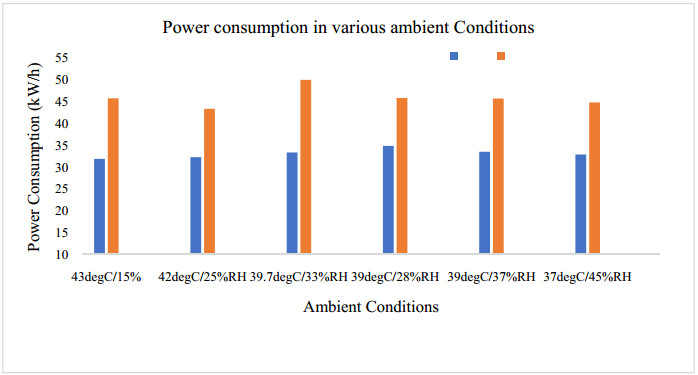
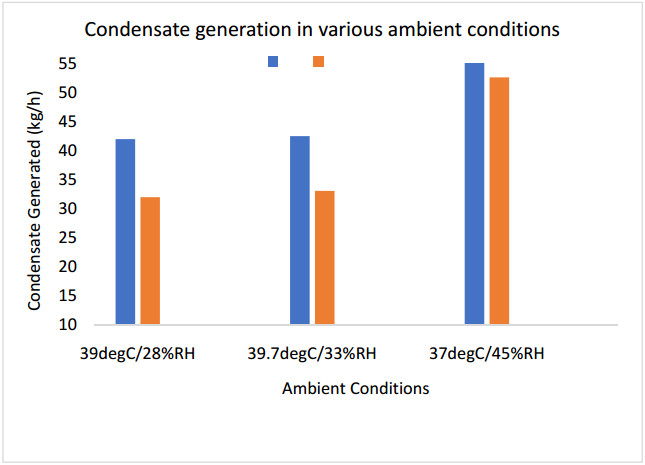
An experimental investigation of the performance of a fresh air handling unit integrating indirect evaporative and vapor compression cooling is conducted. Temperature and relative humidity measurements at main points within the cooling unit were logged using a wireless data acquisition system. Experimental data downloaded from the acquisition system is used for linear regression analysis, and to calculate the wet-bulb thermal effectiveness, cooling capacity and coefficient of performance of the unit. The air conditioning unit is a patented system designed and assembled at the Gulf Organisation for Research and Development (GORD) in Qatar. The peak wet-bulb thermal effectiveness of the system was found to be 1.3, and the COP was 3.4. The results showed that the unit could save as nearly 60% of the sensible cooling load required by a conventional vapor compression cooling unit. In addition, the unit could reduce power consumption by 36% when utilizing the indirect evaporative cooling cycle. Depending on ambient conditions, the investigated unit generated enough condensate to meet the water requirements of the indirect evaporative cooling cycle, which made the air conditioning system sustainable.
1.
Introduction
We consider a viscous fluid obeying the Stokes system in a thin porous medium Ωε of thickness ε which is perforated by periodically distributed cylinders (obstacles) of size ε. On the boundary of the obstacles, we prescribe a Robin-type condition depending on a parameter γ∈R. The aim of this work is to prove the convergence of the homogenization process when ε goes to zero, depending on the different values of γ.
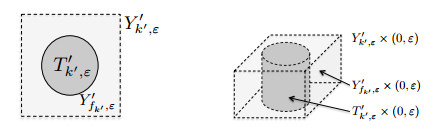
The domain: the periodic porous medium is defined by a domain ω and an associated microstructure, or periodic cell Y′=[−1/2,1/2]2, which is made of two complementary parts: the fluid part Y′f, and the obstacle part T′ (Y′f⋃T′=Y′ and Y′f⋂T′=∅). More precisely, we assume that ω is a smooth, bounded, connected set in R2, and that T′ is an open connected subset of Y′ with a smooth boundary ∂T′, such that ¯T′ is strictly included in Y′.
The microscale of a porous medium is a small positive number ε. The domain ω is covered by a regular mesh of square of size ε: for k′∈Z2, each cell Y′k′,ε=εk′+εY′ is divided in a fluid part Y′fk′,ε and an obstacle part T′k′,ε, i.e. is similar to the unit cell Y′ rescaled to size ε. We define Y=Y′×(0,1)⊂R3, which is divided in a fluid part Yf=Y′f×(0,1) and an obstacle part T=T′×(0,1), and consequently Yk′,ε=Y′k′,ε×(0,1)⊂R3, which is also divided in a fluid part Yfk′,ε and an obstacle part Tk′,ε.
We denote by τ(¯T′k′,ε) the set of all translated images of ¯T′k′,ε. The set τ(¯T′k′,ε) represents the obstacles in R2.
The fluid part of the bottom ωε⊂R2 of the porous medium is defined by ωε=ω∖⋃k′∈Kε¯T′k′,ε, where Kε={k′∈Z2:Y′k′,ε∩ω≠∅}. The whole fluid part Ωε⊂R3 in the thin porous medium is defined by (see Figures 2 and 3)
We make the following assumption:
We define Tεk′,ε=T′k′,ε×(0,ε). Denote by Sε the set of the obstacles contained in Ωε. Then, Sε is a finite union of obstacles, i.e.
We define
We observe that ˜Ωε=Ω∖⋃k′∈Kε¯Tk′,ε, and we define Tε=⋃k′∈Kε¯Tk′,ε as the set of the obstacles contained in ˜Ωε.
The problem: let us consider the following Stokes system in Ωε, with a Dirichlet boundary condition on the exterior boundary ∂Λε and a non-homogeneous slip boundary condition on the cylinders ∂Sε:
where we denote by uε=(uε,1,uε,2,uε,3) the velocity field, pε is the (scalar) pressure, fε=(fε,1(x1,x2),fε,2(x1,x2),0) is the field of exterior body force and gε=(gε,1(x1,x2),gε,2(x1,x2),0) is the field of exterior surface force. The constants α and γ are given, with α>0, μ is the viscosity and n is the outward normal to Sε.
This choice of f and g is usual when we deal with thin domains. Since the thickness of the domain, ε, is small then vertical component of the forces can be neglected and, moreover the force can be considered independent of the vertical variable.
Problem (3) models in particular the flow of an incompressible viscous fluid through a porous medium under the action of an exterior electric field. This system is derived from a physical model well detailed in the literature. As pointed out in Cioranescu et al. [12] and Sanchez-Palencia [32], it was observed experimentally in Reuss [31] the following phenomenon: when a electrical field is applied on the boundary of a porous medium in equilibrium, a motion of the fluid appears. This motion is a consequence of the electrical field only. To describe such a motion, it is usual to consider a modified Darcy's law considering of including an additional term, the gradient of the electrical field, or consider that the presence of this term is possible only if the electrical charges have a volume distribution. However, this law contains implicitly a mistake, because if the solid and fluid parts are both dielectric, such a distribution does not occur, the electrical charges act only on the boundary between the solid and the fluid parts and so they have necessarily a surface distribution. If such hypothesis is done, we can describe the boundary conditions in terms of the stress tensor σε as follows
which is precisely the non-homogeneous slip boundary condition (3)4 and means that the stress-vector σε⋅n induces a slowing effect on the motion of the fluid, expressed by the term αεγ. Moreover, if there are exterior forces like for instance, an electrical field, then the non-homogeneity of the boundary condition on the ∂Sε is expressed in terms of surface charges contained in gε.
On the other hand, the behavior of the flow of Newtonian fluids through periodic arrays of cylinders has been studied extensively, mainly because of its importance in many applications in heat and mass transfer equipment. However, the literature on Newtonian thin film fluid flows through periodic arrays of cylinders is far less complete, although these problems have now become of great practical relevance because take place in a number of natural and industrial processes. This includes flow during manufacturing of fibre reinforced polymer composites with liquid moulding processes (see Frishfelds et al. [22], Nordlund and Lundstrom [29], Tan and Pillai [34]), passive mixing in microfluidic systems (see Jeon [23]), paper making (see Lundström et al. [25], Singh et al. [33]), and block copolymers self-assemble on nanometer length scales (see Park et al. [30], Albert and Epps [1], Farrell et al. [21]).
The Stokes problem in a periodically perforated domain with holes of the same size as the periodic has been treated in the literature. More precisely, the case with Dirichlet conditions on the boundary of the holes was studied by Ene and Sanchez-Palencia [20], where the model that describes the homogenized medium is a Darcy's law. The case with non-homogeneous slip boundary conditions, depending on a parameter γ∈R, was studied by Cioranescu et al. [12], where using the variational method introduced by Tartar [35], a Darcy-type law, a Brinkmann-type equation or a Stokes-type equation are obtained depending of the values of γ. The Stokes and Navier-Stokes equations in a perforated domain with holes of size rε, with rε≪ε is considered by Allaire [2]. On the boundary of the holes, the normal component of the velocity is equal to zero and the tangential velocity is proportional to the tangential component of the normal stress. The type of the homogenized model is determined by the size rε, i.e. by the geometry of the domain.
The earlier results relate to a fixed height domain. For a thin domain, in [4] Anguiano and Suárez-Grau consider an incompressible non-Newtonian Stokes system, in a thin porous medium of thickness ε that is perforated by periodically distributed solid cylinders of size aε, with Dirichlet conditions on the boundary of the cylinders.
Using a combination of the unfolding method (see Cioranescu et al. [13] and Cioranescu et al. [16] for perforated domains) applied to the horizontal variables, with a rescaling on the height variable, and using monotonicity arguments to pass to the limit, three different Darcy's laws are obtained rigorously depending on the relation between aε and ε. We remark that an extension of the unfolding method to evolution problems in which the unfolding method is applied to the spatial variables and not on the time variable was introduced in Donato and Yang [18] (see also [19]).
The behavior observed when aε≈ε in [4] has motivated the fact of considering non-homogeneous slip conditions on the boundary of the cylinders. In this sense, our aim in the present paper is to consider a Newtonian Stokes system with the non-homogeneous slip boundary condition (3)4 in the thin porous medium described in (1) and we prove the convergence of the homogenization process depending on the different values of γ. To do that, we have to take into account that the normal component of the velocity on the cylinders is different to zero and the extension of the velocity is no longer obvious. If we consider the Stokes system with Dirichlet boundary condition on the obstacles as in [4], the velocity can be easily extended by zero in the obstacles, however in this case we need another kind of extension and adapt it to the case of a thin domain.
One of the main difficulties in the present paper is to treat the surface integrals. The papers mentioned above about problems with non-homogeneous boundary conditions use a generalization (see Cioranescu and Donato [9]) of the technique introduced by Vanninathan [36] for the Steklov problem, which transforms the surface integrals into volume integrals. In our opinion, an excellent alternative to this technique was made possible with the development of the unfolding method (see Cioranescu et al. [13]), which allows to treat easily the surface integrals. In the present paper, we extend some abstract results for thin domains, using an adaptation of the unfolding method, in order to treat all the surface integrals and we obtain directly the corresponding homogenized surface terms. A similar approach is made by Cioranescu et al. [14] and Zaki [37] with non-homogeneous slip boundary conditions, and Capatina and Ene [7] with non-homogeneous pure slip boundary conditions for a fixed height domain.
In summary, we show that the asymptotic behavior of the system (3) depends on the values of γ:
− for γ<−1, we obtain a 2D Darcy type law as an homogenized model. The flow is only driven by the pressure.
− for −1≤γ<1, we obtain a 2D Darcy type law but in this case the flow depends on the pressure, the external body force and the mean value of the external surface force.
− for γ≥1, we obtain a 2D Darcy type law where the flow is only driven by the pressure with a permeability tensor obtained by means of two local 2D Stokes problems posed in the reference cell with homogeneous Neumann boundary condition on the reference cylinder.
We observe that we have obtained the same three regimes as in Cioranescu et al. [14] (see Theorems 2.1 and 2.2), and Zaki [37] (see Theorems 14 and 16). Thus, we conclude that the fact of considering the thin domain does not change the critical size of the parameter γ, but the thickness of the domain introduces a reduction of dimension of the homogenized models and other consequences. More precisely, in the cases γ<−1 and −1≤γ<1, we obtain the same Darcy type law as in [14,37] with the vertical component of the velocity zero as consequence of the thickness of the domain. The main difference appears in the case γ≥1, in which a 3D Brinkmann or Stokes type law were derived in [14,37] while a 2D Darcy type law is obtained in the present paper.
We also remark the differences with the result obtained in [4] where Dirichlet boundary conditions are prescribed on the cylinders in the case aε≈ε. In that case, a 2D Darcy law as an homogenized model with a permeability tensor was obtained through two Stokes local problems in the reference cell with Dirichlet boundary conditions on the reference cylinder. Here, we obtain three different homogenized model depending on γ. The case γ≥1 gives a similar 2D Darcy type law, but the permeability tensor is obtained through two Stokes local problems with homogeneous Neumann boundary conditions. In the cases γ<−1 and −1≤γ<1, we obtain a 2D Darcy type law without microstructure.
The paper is organized as follows. We introduce some notations in Section 2. In Section 3, we formulate the problem and state our main result, which is proved in Section 4. The article closes with a few remarks in Section 5.
2.
Some notations
Along this paper, the points x∈R3 will be decomposed as x=(x′,x3) with x′∈R2, x3∈R. We also use the notation x′ to denote a generic vector of R2.
In order to apply the unfolding method, we need the following notation: for k′∈Z2, we define κ:R2→Z2 by
Remark that κ is well defined up to a set of zero measure in R2, which is given by ∪k′∈Z2∂Y′k′,1. Moreover, for every ε>0, we have
For a vectorial function v=(v′,v3) and a scalar function w, we introduce the operators: Dε, ∇ε and divε, by
We denote by |O| the Lebesgue measure of |O| (3-dimensional if O is a 3-dimensional open set, 2-dimensional of O is a curve).
For every bounded set O and if φ∈L1(O), we define the average of φ on O by
Similarly, for every compact set K of Y, if φ∈L1(∂K) then
is the average of φ over ∂K.
We denote by L2♯(Y), H1♯(Y), the functional spaces
and
We denote by : the full contraction of two matrices, i.e. for A=(ai,j)1≤i,j≤2 and B=(bi,j)1≤i,j≤2, we have A:B=∑2i,j=1aijbij.
Finally, we denote by Oε a generic real sequence, which tends to zero with ε and can change from line to line, and by C a generic positive constant which also can change from line to line.
3.
Main result
In this section we describe the asymptotic behavior of a viscous fluid obeying (3) in the geometry Ωε described in (1). The proof of the corresponding results will be given in the next section.
The variational formulation: let us introduce the spaces
and
Then, the variational formulation of system (3) is the following one:
Assume that fε(x)=(f′ε(x′),0)∈L2(ω)3 and gε(x)=g(x′/ε), where g is a Y′-periodic function in L2(∂T)2. Under these assumptions, it is well known that (6) has a unique solution (uε,pε)∈H3ε×L2(Ωε) (see Theorem 4.1 and Remark 4.1 in [17] for more details).
Our aim is to study the asymptotic behavior of uε and pε when ε tends to zero. For this purpose, we use the dilatation in the variable x3, i.e.
in order to have the functions defined in the open set with fixed height ˜Ωε defined by (2).
Namely, we define ˜uε∈˜H3ε, ˜pε∈L2(˜Ωε) by
Using the transformation (7), the system (3) can be rewritten as
with the non-homogeneous slip boundary condition,
where e3=(0,0,1)t.
Taking in (6) as test function ˜φ(x′,x3/ε) with ˜φ∈˜H3ε and ˜ψ(x′,x3/ε) with ˜ψ∈˜Hε, applying the change of variables (7) and taking into account that dσ(x)=εdσ(x′)dy3, the variational formulation of system (8)-(9) is then the following one:
In the sequel, we assume that the data f′ε satisfies that there exists f′∈L2(ω)2 such that
Observe that, due to the periodicity of the obstacles, if f′ε=f′ε where f′∈L2(ω)2, then
assuming εf′ε extended by zero outside of ωε, where θ denotes the proportion of the material in the cell Y′ given by
We also define the constant μ1:=|∂T′||Y′|.
Main result: our goal then is to describe the asymptotic behavior of this new sequence (˜uε, ˜pε) when ε tends to zero. The sequence of solutions (˜uε, ˜pε)∈˜Hε×L2(˜Ωε) is not defined in a fixed domain independent of ε but rather in a varying set ˜Ωε. In order to pass the limit if ε tends to zero, convergences in fixed Sobolev spaces (defined in Ω) are used which requires first that (˜uε, ˜pε) be extended to the whole domain Ω. For the velocity, we will denote by ˜Uε the zero extension of ˜uε to the whole Ω, and for the pressure we will denote by ˜Pε the zero extension of ˜pε to the whole Ω.
Our main result referred to the asymptotic behavior of the solution of (8)-(9) is given by the following theorem.
Theorem 3.1. Let (˜uε,˜pε) be the solution of (8)-(9). Then there exists an extension operator ˜Πε∈L(˜H3ε;H10(Ω)3) such that
i) if γ<−1, then
Moreover, (ε−1˜Uε,ε−γ˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(ω) and any weak-limit point (˜u(x′,y3),˜p(x′)) of this sequence satisfies ˜u′=0 on y3={0,1}, ˜u3=0 and the following Darcy type law:
where ˜v(x′)=∫10˜u(x′,y3)dy3,
ii) if −1≤γ<1, then
Moreover, (εγ˜Uε,ε˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(ω) and any weak-limit point (˜u(x′,y3),˜p(x′)) of this sequence satisfies ˜u′=0 on y3={0,1}, ˜u3=0 and the following Darcy type law:
where ˜v(x′)=∫10˜u(x′,y3)dy3,
iii) if γ≥1, then
Moreover, (˜Uε,ε2˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(ω) and any weak-limit point (˜u(x′,y3),˜p(x′)) of this sequence satisfies ˜u=0 on y3={0,1} and the following Darcy type law:
where ˜v(x′)=∫10˜u(x′,y3)dy3, and the symmetric and positive permeability tensor A∈R2×2 is defined by its entries
For i=1,2, wi(y′), denote the unique solutions in H1♯(Y′f)2 of the local Stokes problems with homogeneous Neumann boundary conditions in 2D:
Remark 1. We observe that in the homogenized problems related to system (8)-(9), the limit functions do not satisfy any incompressibility condition, so (12), (13) and (14) do not identify in a unique way (˜v,˜p). This is a consequence of the fact that the normal component of ˜uε does not vanish on the boundary of the cylinders, so the average fluid flow, given by ˜v, is (eventually) represented by the motion of a compressible fluid. As pointed out in Conca [17] (see Remark 2.1) and Cioranescu et al. [12] (see Remarks 2.3 and 2.6), this result, which at first glance seems unexpected, can be justified as follows: the boundary condition (9) implies that the normal component ˜uε⋅n of ˜uε is not necessarily zero on ∂Tε so we can not expect that the extension ˜Uε will be a zero-divergence function. In fact, from the second variational formulation in (10), we have
and the term on the right-hand side is not necessarily zero. Therefore, by weak continuity, it is not possible to obtain an incompressibility condition of the form divx′˜v′(x′)=0 in ω as it is obtained in the case with Dirichlet condition considered in [4]. Roughly speaking, ˜uε⋅n≠0 on ∂Tε means that some fluid ``disappear" through the cylinders, and this fact implies that the incompressibility condition is not necessary verified at the limit in ω.
4.
Proof of the main result
In the context of homogenization of flow through porous media Arbogast et al. [5] use a L2 dilation operator to resolve oscillations on a prescribed scale of weakly converging sequences. It was observed in Bourgeat et al. [6] that this operator yields a characterization of two-scale convergence (see Allaire [3] and Nguetseng [28]). Later, Cioranescu et al. [13,14] introduced the periodic unfolding method as a systematic approach to homogenization which can be used for H1 functions and take into account the boundary of the holes by using the so-called boundary unfolding operator. In this section we prove our main result. In particular, Theorem 3.1, is proved in Subsection 4.3 by means of a combination of the unfolding method applied to the horizontal variables, with a rescaling on the vertical variable. One of the main difficulties is to treat the surface integrals using an adaptation of the boundary unfolding operator. To apply this method, a priori estimates are established in Subsection 4.1 and some compactness results are proved in Subsection 4.2.
4.1. Some abstract results for thin domains and a priori estimates
The a priori estimates independent of ε for ˜uε and ˜pε will be obtained by using an adaptation of the unfolding method.
Some abstract results for thin domains: let us introduce the adaption of the unfolding method in which we divide the domain ˜Ωε in cubes of lateral lengths ε and vertical length 1. For this purpose, given ˜φ∈Lp(˜Ωε)3, 1≤p<+∞, (assuming ˜φ extended by zero outside of ωε), we define ˆφε∈Lp(R2×Yf)3 by
where the function κ is defined in (4).
Remark 2. The restriction of ˆφε, to Y′f′k,ε×Yf does not depend on x′, whereas as a function of y it is obtained from ˜vε, by using the change of variables
which transforms Yfk′,ε into Yf.
Proposition 1. We have the following estimates:
i) for every ˜φ∈Lp(˜Ωε), 1≤p+∞, we have
where ˆφε is given by (16),
ii) for every ˜φ∈W1,p(˜Ωε)3, 1≤p<+∞, we have that ˆφε, given by (16), belongs to Lp(R2;W1,p(Yf)3), and
Proof. Let us prove i). Using Remark 2 and definition (16), we have
We observe that ˜φ does not depend on x′, then we can deduce
For every k′∈Z2, by the change of variable (17), we have
and we obtain
which gives (18).
Let us prove ii). Taking into account the definition (16) of ˆφε and observing that ˜φ does not depend on x′, then we can deduce
By (20), we obtain
For the partial of the vertical variable, proceeding similarly to (18), we obtain
which together with (21) gives (19).
In a similar way, let us introduce the adaption of the unfolding method on the boundary of the obstacles ∂Tε (see Cioranescu et al. [14] for more details). For this purpose, given ˜φ∈Lp(∂Tε)3, 1≤p<+∞, we define ˆφbε∈Lp(R2×∂T)3 by
where the function κ is defined in (4).
Remark 3. Observe that from this definition, if we consider ˜φ∈Lp(∂T), 1≤p<+∞, a Y′-periodic function, and we define ˜φε(x′,y3)=˜φ(x′/ε,y3), it follows that ˆφbε(x′,y)=˜φ(y).
Observe that for ˜φ∈W1,p(˜Ωε)3, ˆφbε is the trace on ∂T of ˆφε. Therefore ˆφbε has a similar properties as ˆφε.
We have the following property.
Proposition 2. If ˜φ∈Lp(∂Tε)3, 1≤p<+∞, then
where ˆφbε is given by (22).
Proof. We take (x′,y3)∈∂Tk′,ε. Taking into account (22), we obtain
For every k′∈Z2, by taking x′=ε(k′+y′), we have dσ(x′)=εdσ(y′). Since the thickness of the obstacles is one, we have that dσ(x′)dy3=εdσ(y). Hence
which gives (23).
Now, let us give two results which will be useful for obtaining a priori estimates of the solution (˜uε,˜pε) of problem (8)-(9). These results are an extension of Cioranescu et al. (Proposition 5.3 and Corollary 5.4 in [15]) to the thin domain case.
Proposition 3. Let g∈L2(∂T′)3 and ˜φ∈H1(˜Ωε)3, extended by zero in outside of wε. Let ˆφε be given by (16). Then, there exists a positive constant C, independent of ε, such that
In particular, if g=1, there exists a positive constant C, independent of ε, such that
Proof. Due to density properties, it is enough to prove this estimate for functions in D(R3)3. Let ˜φ∈D(R3)3, one has
which implies (24). In particular, if g=1, proceeding as above, we have
which implies (25).
Corollary 1. Let g∈L2(∂T)3 be a Y′-periodic function. Then, for every ˜φ∈H1(˜Ωε)3, we have that there exists a positive constant C, independent of ε, such that
In particular, if g=1, there exists a positive constant C, independent of ε, such that
Proof. Since ˜φ∈H1(˜Ωε)3, then ˆφbε has similar properties as ˆφε. By using Proposition 2 with p=1 and Remark 3, we have
and by Proposition 3, we can deduce estimates (26) and (27).
Moreover, for the proof of the a priori estimates for the velocity, we need the following lemma due to Conca [17] generalized to a thin domain Ωε.
Lemma 4.1. There exists a constant C independent of ε, such that, for any function φ∈Hε, one has
Proof. We observe that the microscale of the porous medium ε is similar than the thickness of the domain ε, which lead us to divide the domain Ωε in small cubes of lateral length ε and vertical length ε. We consider the periodic cell Y. The function φ→(‖Dφ‖2L2(Yf)3×3+‖φ‖2L2(∂T)3)1/2 is a norm in H1(Yf)3, equivalent to the H1(Yf)3-norm (see Neˇcas [27]). Therefore, for any function φ(z)∈H1(Yf)3, we have
where the constant C depends only on Yf.
Then, for every k′∈Z2, by the change of variable
we rescale (29) from Yf to Qfk′,ε=Y′fk′,ε×(0,ε). This yields that, for any function φ(x)∈H1(Qfk′,ε)3, one has
with the same constant C as in (29). Summing the inequality (31) for all the periods Qfk′,ε and T′k′,ε×(0,ε), gives
In fact, we must consider separately the periods containing a portion of ∂ω, but they yield at a distance O(ε) of ∂ω, where φ is zero. Therefore, using Poincare's inequality one can easily verify that in this part (28) holds without considering the boundary term occuring in (28).
Considering the change of variables given in (7) and taking into account that dσ(x)=εdσ(x′)dy3, we obtain the following result for the domain ˜Ωε.
Corollary 2. There exists a constant C independent of ε, such that, for any function ˜φ∈˜H3ε, one has
The presence in (3) of the stress tensor in the boundary condition implies that the extension of the velocity is no longer obvious. If we consider the Stokes system with Dirichlet boundary condition on the obstacles, the velocity would be extended by zero in the obstacles. However, in this case, we need another kind of extension for the case in which the velocity is non-zero on the obstacles. Since in the extension required, the vertical variable is not concerned, therefore the proof of the required statement is basically the extension of the result given in Cioranescu and Saint-Jean Paulin [8,11] to the time-depending case given in Cioranescu and Donato [10], so we omit the proof. We remark that the extension is not divergence free, so we cannot expect the homogenized solution to be divergence free. Hence we cannot use test functions that are divergence free in the variational formulation, which implies that the pressure has to be included.
Lemma 4.2. There exists an extension operator Πε∈L(H3ε;H10(Λε)3) and a positive constant C, independent of ε, such that
Considering the change of variables given in (7), we obtain the following result for the domain ˜Ωε.
Corollary 3. There exists an extension operator ˜Πε∈L(˜H3ε;H10(Ω)3) and a positive constant C, independent of ε, such that
Using Corollary 3, we obtain a Poincaré inequality in ˜H3ε.
Corollary 4. There exists a constant C independent of ε, such that, for any function ˜φ∈˜H3ε, one has
Proof. We observe that
Since ˜Πε˜φ∈H10(Ω)3, we can apply the Poincaré inequality in H10(Ω) and then taking into account Corollary 3, we get
This together with (34) gives (33).
Now, for the proof of the a priori estimates for the pressure, we also need the following lemma due to Conca [17] generalized to a thin domain Ωε.
Lemma 4.3. There exists a constant C independent of ε, such that, for each q∈L2(Ωε), there exists φ=φ(q)∈Hε, such that
Proof. Let q∈L2(Ωε) be given. We extend q inside the cylinders by means of the function:
It is follows that Q∈L20(Λε)={p∈L2(Λε):∫Λεpdx=0} and
Since |Λε−Ωε| is bounded from below by a positive number, it follows from (37) and Cauchy-Schwartz inequality that
Besides that, since Q∈L20(Λε), it follows from Maruˇsić and Maruˇsić-Paloka (Lemma 20 in [26]) that we can find φ∈H10(Λε)3 such that
Let us consider φ|Ωε: it belongs to Hε. Moreover, (35) follows from (39) and the estimates (36) follows from (40) and (38).
Considering the change of variables given in (7), we obtain the following result for the domain ˜Ωε.
Corollary 5. There exists a constant C independent of ε, such that, for each ˜q∈L2(˜Ωε), there exists ˜φ=˜φ(˜q)∈˜Hε, such that
A priori estimates for (˜uε, ˜pε) in ˜Ωε: first, let us obtain some a priori estimates for ˜uε for different values of γ.
Lemma 4.4. We distinguish three cases:
i) for γ<−1, then there exists a constant C independent of ε, such that
ii) for −1≤γ<1, then there exists a constant C independent of ε, such that
iii) for γ≥1, then there exists a constant C independent of ε, such that
Proof. Taking ˜uε∈˜H3ε as function test in (10), we have
Using Cauchy-Schwarz's inequality and f′ε∈L2(Ω)2, we obtain that
and by using that g′∈L2(∂T)2 is a Y′-periodic function and estimate (26), we have
Putting these estimates in (44), we get
In particular, if we use the Poincaré inequality (33) in (45), we have
therefore (independently of γ∈R), using again (33), we get
These estimates can be refined following the different values of γ. To do so, observe that from estimate (32) we have
Using Young's inequality, we get
Consequently, from (45), we get
which applying in a suitable way the Young inequality gives
For the case when γ<−1, estimate (48) reads
Then, estimate (32) gives
since 1≤(1−γ)/2, and so, we have proved (41).
For γ≥−1, estimate (48) reads
Applying estimate (32), we get
since −γ≤(1−γ)/2. Then, we have proved (42) for −1≤γ<1. Observe that for γ≥1, the estimates (46)-(47) are the optimal ones, so we have (43).
We will prove now a priori estimates for the pressure ˜pε for different values of γ.
Lemma 4.5. We distinguish three cases:
i) for γ<−1, then there exists a constant C independent of ε, such that
ii) for −1≤γ<1, then there exists a constant C independent of ε, such that
iii) for γ≥1, then there exists a constant C independent of ε, such that
Proof. Let ˜Φ∈L2(˜Ωε). From Corollary 5, there exists ˜φ∈˜H3ε such that
Taking ˜φ∈˜H3ε as function test in (10), we have
By using that g∈L2(∂T)3 is a Y′-periodic function and estimate (26), we have
Analogously, using estimate (27) and the Cauchy- Schwarz inequality, a simple computation gives
Then, turning back to (53) and using (52), one has
The a priori estimates for the pressure follow now from (54) and estimates (41)-(42) and (43), corresponding to the different values of γ.
A priori estimates of the unfolding functions (ˆuε,ˆpε): let us obtain some a priori estimates for the sequences (ˆuε,ˆpε) where ˆuε and ˆpε are obtained by applying the change of variable (16) to (˜uε,˜pε).
Lemma 4.6. We distinguish three cases:
i) for γ<−1, then there exists a constant C independent of ε, such that
ii) for −1≤γ<1, then there exists a constant C independent of ε, such that
iii) for γ≥1, then there exists a constant C independent of ε, such that
Proof. Using properties (18) and (19) with p=2 and the a priori estimates given in Lemma 4.4 and Lemma 4.5, we have the desired result.
4.2. Some compactness results
Let us remember that, for the velocity, we denote by ˜Uε the zero extension of ˜uε to the whole Ω, and for the pressure we denote by ˜Pε the zero extension of ˜pε to the whole Ω. In this subsection we obtain some compactness results about the behavior of the sequences ˜Πε˜uε, where ˜Πε is given in Corollary 3, (˜Uε,˜Pε) and (ˆuε,ˆpε).
Lemma 4.7. There exists an extension operator ˜Πε, given in Corollary 3, such that
i) for γ<−1, then
Moreover, (ε−1˜Uε,ε−γ˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(Ω) and any weak-limit point (˜u,˜p) of this sequence satisfies
ii) for −1≤γ<1, then
Moreover, (εγ˜Uε,ε˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(Ω) and any weak-limit point (˜u,˜p) of this sequence satisfies
iii) for γ≥1, then
Moreover, (˜Uε,ε2˜Pε) is bounded in H1(0,1;L2(ω)3)×L2(Ω) and any weak-limit point (˜u,˜p) of this sequence satisfies
Proof. We proceed in three steps:
Step 1. For γ<−1: from estimates (41) and (49), we have immediately the convergences, after eventual extraction of subsequences, (62) and (63).
Moreover, we have
and we can apply Corollary 3 to ˜uε and we deduce the existence of u∗∈H10(Ω)3 such that ˜Πε˜uε converges weakly to u∗ in H10(Ω)3. Consequently, by Rellich theorem, ˜Πε˜uε converges strongly to u∗ in L2(Ω)3.
On the other side, we have the following indentity:
Due the periodicity of the domain ˜Ωε we have that χ˜Ωε converges weakly-⋆ to |Y′f||Y′| in L∞(Ω), and we can pass to the limit in the term of the left hand side. Thus, χ˜Ωε(˜Πε˜uε) converges weakly to |Y′f||Y′|u∗ in L2(Ω)3. In the right hand side, ˜Uε converges to zero, so we obtain (61).
Step 2. For −1≤γ<1: from the estimates (42) and (50), we deduce convergences (65) and (66).
Moreover, as −1≤γ<1, we have
and using Corollary 3, we have
Consequently,
and passing to the limit in the identity
we deduce that u∗=0, and so (64) is proved.
Step 3. For γ≥1: from estimate (43) and Dirichlet boundary condition, we deduce that
and we have immediately, after eventual extraction of subsequences, the convergence (68). From estimate (51), we have immediately, after eventual extraction of subsequences, the convergence (69).
Moreover, we can apply Corollary 3 to ˜uε and we deduce the existence of u∗∈H10(Ω)3 such that ε˜Πε˜uε converges weakly to u∗ in H10(Ω)3. Consequently, by Rellich theorem, ε˜Πε˜uε converges strongly to u∗ in L2(Ω)3.
On the other side, we have the following indentity:
We can pass to the limit in the term of the left hand side. Thus, χ˜Ωε(ε˜Πε˜uε) converges weakly to |Y′f||Y′|u∗ in L2(Ω)3. In the right hand side, ε˜Uε converges to zero, so we obtain (67).
Finally, we give a convergence result for ˆuε.
Lemma 4.8. We distinguish three cases:
i) for γ<−1, then for a subsequence of ε still denote by ε, there exists ˆu∈L2(R2;H1♯(Yf)3), such that
ii) for −1≤γ<1, then for a subsequence of ε still denote by ε, there exists there exists ˆu∈L2(R2;H1♯(Yf)3), independent of y, such that
iii) for γ≥1, then for a subsequence of ε still denote by ε, there exists there exists ˆu∈L2(R2;H1♯(Yf)3) such that
Proof. We proceed in three steps:
Step 1. For γ<−1, using (55), there exists ˆu:R2×Yf→R3, such that convergence (70) holds. Passing to the limit by semicontinuity and using estimates (55), we get
which, once we prove the Y′-periodicity of ˆu in y′, shows that ˆu∈L2(R2;H1♯(Yf)3).
It remains to prove the Y′-periodicity of ˆu in y′. To do this, we observe that by definition of ˆuε given by (16) applied to ˜uε, we have
a.e. (x′,y2,y3)∈R2×(−1/2,1/2)×(0,1). Multiplying by ε−1 and passing to the limit by (70), we get
Analogously, we can prove
These equalities prove that ˆu is periodic with respect to Y′. Convergence (71) is straightforward from the definition (22) and the Sobolev injections.
Finally, using Proposition 1, we can deduce
and multiplying by ε−1 and taking into account that ˜uε is extended by zero to the whole Ω, we have
Using convergences (62) and (70), we have (72).
Step 2. For −1≤γ<1, using (57) and taking into account that ε1−γ2≤ε−γ, then there exists ˆu:R2×Yf→R3, such that convergence (73) holds. Convergence (74) is straightforward from the definition (22) and the Sobolev injections.
On the other hand, since εγDyˆuε=εγ+12εγ−12Dyˆuε and εγ−12Dyˆuε is bounded in L2(R2×Yf)3×3, using (73) we can deduce that Dyˆu=0. This implies that ˆu is independent of y. Finally, (75) is obtained similarly to the Step 1.
Step 3. For γ≥1, using the second a priori estimate in (59) and the Poincaré-Wirtinger inequality
we deduce that there exists ˆu∈L2(R2;H1(Yf)3) such that
and (77) holds. Convergence (76) is straightforward from the definition (22) and the Sobolev injections.
It remains to prove the Y′-periodicity of ˆu in y′. To do this, we observe that by definition of ˆuε given by (16) applied to ˜uε, we have
a.e. (x′,y2,y3)∈R2×(−1/2,1/2)×(0,1), which implies
which tends to zero (see the proof of Proposition 2.8 in [15]), and so
Analogously, we can prove
These equalities prove that ˆu is periodic with respect to Y′.
Step 4. From the second variational formulation in (10), by Proposition 2, we have that
and using the extension of the velocity, we obtain
We remark that the second term in the left-hand side and the one in the right-hand side have the same order, so in every cases when passing to the limit after multiplying by a suitable power of ε and using that ˆψε converges strongly to ˜ψ in L2(ω×∂T) (see Proposition 2.6 in [15] for more details), it is not possible to find the usual incompressibility condition in thin domains given by
On the other hand, we focus in the third case. Thus, using Proposition 1 in the left-hand side of (80), we have
which, multiplying by ε|Y′| and since MYf[ˆuε] does not depend on the variable y, is equivalent to
Thus, passing to the limit using convergences (77), we get condition (79).
4.3. Proof of Theorem 3.1
In this section, we will multiply system (10) by a test function having the form of the limit ˆu (as explained in Lemma 4.8), and we will use the convergences given in the previous section in order to identify the homogenized model in every cases.
Proof of Theorem 3.1: We proceed in three steps:
Step 1. For γ<−1. Let ˜φ∈D(Ω)3 and ˜ψ∈D(Ω) be test functions in (10). By Proposition 2, one has
i.e.,
Next, we prove that ˜p does not depend on y3. Let ˜φ=(0,ε−γ+1˜φ3)∈D(Ω)3 be a test function in (83), we have
Taking into account that ˜Pε is zero extension of ˜pε to the whole Ω, we have
and by the second a priori estimate (41), the convergences (63) and (71), passing to the limit we have
so ˜p does not depend on y3.
Let ˜φ=(ε−γφ′(x′,y3),ε−γ˜φ3(x′))∈D(Ω)3 be a test function in (83), we have
and
Taking into account that ˜Pε is zero extension of ˜pε to the whole Ω, we have
Using that ˆφε converges strongly to ˜φ in L2(ω×∂T)3 (see Proposition 2.6 in [15] for more details) and by the second a priori estimate (41), the convergences (63) and (71), passing to the limit we have
and
which implies that M∂T′[ˆu3]=0.
Taking into account that
implies that
In order to obtain the homogenized system (12), we introduce the auxiliary problem
for a.e. (x′,y3)∈Ω, which has a unique solution in H1(Y′f) (see Chapter 2, Section 7.3 in Lions and Magenes [24]). Using this auxiliary problem, we conclude that
which together with (84) and M∂T′[ˆu3]=0 gives
and
which together with (72) gives
This together with the definition of θ and μ1, implies (12).
Step 2. For −1≤γ<1. First, we prove that ˜p does not depend on y3. Let ˜φ=(0,ε2˜φ3)∈D(Ω)3 be a test function in (83). Reasoning as Step 1 and by the second a priori estimate (42), the convergence (66) and (74), passing to the limit we deduce that ˜p does not depend on y3.
Let ˜φ=(εφ′(x′,y3),ε˜φ3(x′))∈D(Ω)3 be a test function in (83). Reasoning as Step 1 and by the second a priori estimate (42), the convergences (11), (66) and (74), passing to the limit we have
and
which implies that ˆu3=0.
Taking into account that
implies that
which together with (75) gives (13) after integrating the vertical variable y3 between 0 and 1.
Step 3. For γ≥1. For all ˆφ(x′,y)∈D(ω;C∞♯(Y)3), we choose ˆφε(x)=ˆφ(x′,x′/ε,y3) as test function in (83). Then we get the following variational formulation:
First, we remark that thanks to (60), there exists ˆp∈L2(ω×Yf) such that ε2ˆpε converges weakly to ˆp in L2(ω×Yf). Now, we prove that ˆp does not depend on y. For that, we consider ε3ˆφε in the previous formulation, and passing to the limit by (76) and (77), we get
which shows that ˆp does not depend on y.
Now, we consider ˆφ with divyˆφ=0 in ω×Yf (which is necessary because ˆu satisfies (79)), and similarly we define ˆφε. Then, taking ε2ˆφε, the variational formulation (86) is the following:
Reasoning as Step 1, and using the convergences (11), (76), (77) and the convergence of ˆpε, passing to the limit we have
By density, this equation holds for every function ˆφ(x′,y)∈L2(ω;H1♯(Y)3) such that divyˆφ=0. This implies that there exists ˆq(x′,y)∈L2♯(ω×Yf) such that (88) is equivalent to the following problem:
We remark that ˆp is already the pressure ˜p. This can be easily proved by multiplying equation (83) by a test function ε2φ′(x′,y3) and identifying limits.
Finally, we will eliminate the microscopic variable y in the effective problem. Observe that we can easily deduce that ˆu3=0 and ˆq=ˆq(x′,y′) and moreover, the derivation of (14) from the previous effective problem is an easy algebra exercise. In fact, we can write ∫10ˆu(x′,y)dy3=1μ∑2i=1∂xi˜p(x′)wi(y′) and ˆq(x′,y′)=1μ∑2i=1∂xi˜p(x′)qi(y′) with (wi,qi), i=1,2, the solutions of the local problems (15), and use property (78) which involves the functions ∫10ˆu(x′,y)dy3 and ∫10˜u(x′,y3)dy3. As well-known, the local problems (15) are well-posed with periodic boundary conditions, and it is easily checked, by integration by parts, that
By definition A is symmetric and positive definite.
5.
Conclusions
The behavior of the flow of Newtonian fluids through periodic arrays of cylinders has been studied extensively, mainly because of its importance in many applications in heat and mass transfer equipment. However, the literature on Newtonian thin film fluid flows through periodic arrays of cylinders is far less complete, although these problems have now become of great practical relevance because take place in a number of natural and industrial processes. This paper deals with the modelization by means of homogenization techniques of a thin film fluid flow governed by the Stokes system in a thin perforated domain Ωε which depends on a small parameter ε. More precisely, Ωε has thickness ε and is perforated by a periodic array of cylindrical obstacles of period ε.
The main novelty here are the combination of the mixed boundary condition considered on the obstacles and the thin thickness of the domain. Namely, a standard (no-slip) condition is imposed on the exterior boundary, whereas a non-standard boundary condition of Robin type which depends on a parameter γ is imposed on the interior boundary. This type of boundary condition is motivated by the phenomenon in which a motion of the fluid appears when a electrical field is applied on the boundary of a porous medium in equilibrium. The main mathematical difficulties of this work are to treat the surface integrals and extend the solution to a fixed domain in order to pass to the limit with respect to the parameter ε. We overcome the first difficulty by using a version of the unfolding method which let us treat the surface integrals quite easily. Moreover, we need to develop some extension abstract results and adapt them to the case of thin domain.
By means of a combination of homogenization and reduction of dimension techniques, depending on the parameter γ, we obtain three modified 2D Darcy type laws which model the behavior of the fluid and include the effect of the surface forces and the measure of the obstacles. We remark that we are not able to prove a divergence condition for the limit averaged fluid flow as obtained if we had considered Dirichlet boundary conditions, which from the mechanical point of view means that some fluid ``disappear" through the cylinders and so, it is represented by the motion of a compressible fluid. To conclude, it is our firm belief that our results will prove useful in the engineering practice, in particular in those industrial applications where the flow is affected by the effects of the surface forces, the fluid microstructure and the thickness of the domain.
Acknowledgments
We would like to thank the referees for their comments and suggestions.









 DownLoad:
DownLoad: