Control techniques of switched reluctance motors in electric vehicle applications: A review on torque ripple reduction strategies

1.   Introduction

Electric vehicles (EVs) have emerged as a revolutionary-changing alternative to reduce the negative consequences of fossil fuel consumption in a time characterized by growing concerns about environmental sustainability and the need for energy-efficient transportation ^[1]. The global automotive industry is constantly looking for novel, innovative technologies that promise improved effectiveness, lower emissions, and more energy economy. In the EV system, the electric motor holds paramount importance, and selecting the appropriate electric motor is essential to meet the specific requirements of EV applications. While permanent magnet synchronous motors (PMSMs) have gained attention in EVs due to their efficiency and high-power density, their reliance on rare-earth minerals for magnets presents challenges ^[2]. These include the high cost of extracting and processing these materials, limited global reserves, environmental effects, and the magnets' sensitivity to high temperatures, which can affect motor performance under demanding automotive conditions.

Consequently, a growing imperative is to develop motors without rare-earth elements for high-productivity electric vehicle (EV) applications ^[3]. As a result, motor development devoid of these substances is becoming more and more necessary for superior productivity EV applications. Within this framework, SRMs grow as powerful contenders to established electrical motors for EV applications by offering an expensive-earth-free choice. SRMs are distinguished by their simple double salient structure, low production and maintenance costs, and rotor built of electrical steel ^[4,5]. The machine has built-in fault tolerance since independent focused windings are installed on stator slots.

Furthermore, SRMs exhibit versatility and can operate under various temperature and speed circumstances. Because of these features, the switching reluctance machine is a compelling choice for variable speed applications and harsh conditions ^[6]. However, the performance of SRM is restricted by some limitations, such as torque ripples and the nonlinearity of magnetic characteristics imposed by the double salient structure and the current switching, which mitigates its dependability and restricts its spread ^[7]. Also, acquiring accurate control utilizing only conventional methods is challenging due to being influenced by the machine characteristics, the configuration of the converter, and feedback variables. Therefore, the researchers have focused on overcoming these drawbacks and enhancing the SRM performance by adopting many advanced control strategies proposed in the literature ^[1,5,8] that aim to address the inherent challenges of SRMs, such as high torque ripple and acoustic noise to enhance effectiveness and reliability in electric vehicle applications.

The main contribution includes an extensive overview and evaluation of advanced control strategies of SRMs, which encompasses a comprehensive analysis of existing strategies, including advanced control techniques and design optimizations, focusing on torque ripple mitigation strategies, which comprise torque and current control strategies, and a discussion of their benefits and drawbacks. The organization of this paper is as follows: Section 2 gives the SRM drive system, including SRM fundamentals, the nonlinear model of the SRM, and converter topologies for SRM Drives. Section 3 comprises control strategies of SRM Drive Systems. Furthermore, the torque ripple reduction technologies are introduced in section 4. Finally, section 5 is the conclusion.

2.   SRM drive system

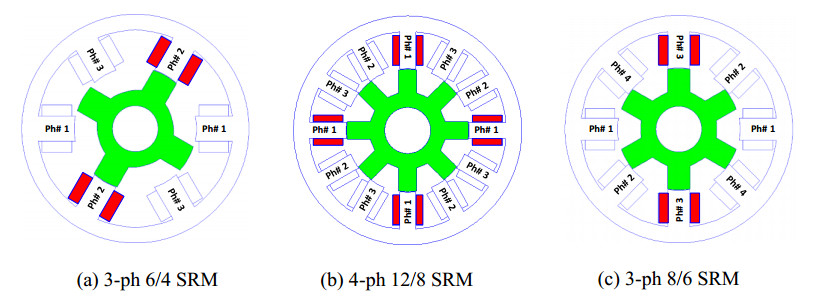
The SRM is a special kind of synchronous machine with double salient construction for both the stator and rotor and also no windings or permanent magnets on the rotor. This motor converts the reluctance torque into mechanical power. Where the alignment tendency of poles produces the torque, the rotor will move to a position where reluctance is lowest and, as a result, maximize the excited winding's inductance. Figure 1 depicts an illustration of common arrangements of SRM.

2.1.   Nonlinear model of the SRM

An SRM has highly nonlinear characteristics because of its doubly salient construction and the switching current excitation. Therefore, the nonlinear modelling of this motor is required to predict the dynamic performance and analyze its magnetization characteristics ^[9,10]. These characteristics can be computed by the function analysis approach ^[11,12], neural network approach ^[13], finite element method (FEM), and indirect measurements ^[14]. First, it is necessary to describe the SRM's mathematical model to calculate and analyze these characteristics. The voltage and flux linkage equations are as follows:

where $V$ denotes the phase voltage, $R$ is the winding resistance per phase, $\lambda (i, \theta)$ denotes the flux linkage, which is a highly nonlinear function of rotor position and phase current $i$ and can be given as:

where $L$ is phase inductance, the torque expression can be derived by substituting the flux linkage expression from Eq 3 into Eq 1, which yields:

The Simulink model of one phase of 8/6 SRM was built using finite-element methods (FEM) based on the magnetic flux linkage characteristic. Figure 2 shows the magnetic flux linkage, inductance, and torque characteristic curves at the aligned and unaligned rotor positions at 0° and 30°, respectively.

2.2.   Converter topologies for SRM drives

The power converter is a vital component of the SRM system because the SRM cannot operate without a converter. Also, the converter's performance greatly affects the drive's cost and efficiency. Since the stator's outer side and the rotor's inner side of the SRM contain salient poles. Therefore, the power converters for SRM are different from the other machines. Recent years have seen considerable advancements in the development of power converters and the commutation control circuit employed to feed SRM ^[15,16]. The power converters utilized for SRM can be divided into three main classifications: Half-bridge, self-commutating, and force-commutating, besides further commutation circuits ^[4]. Each type of SRM power converter has benefits and drawbacks. As a result, the best choice of converter configuration and control techniques is based on the nature of the load and the applications' specific demands ^[17,18]. The most typical and often utilized converter of SRMs is the asymmetric bridge converter due to its benefit of being ameliorated fault-tolerant, quick demagnetization and regenerative braking ability. Figure 3 depicts the overall schematic diagram for the SRM drive system with an asymmetric bridge converter and control circuit.

2.3.   Switching angles approaches

The excitation angles (θ_on, θ_off) significantly produce the SRM torque through the synchronous excitation with the rotor position. They immediately impact the current profile, the torque generation, and, consequently, the performance of SRM during the range of operating speeds. The excitation process generally involves three parameters: The switch-on angle, the switch-off angle and the reference current (I_ref) through a wide speed range ^[19]. To maximize the performance of the SRM, the switching angles (θ_on, θ_off) should be selected to excite the motor in the increasing inductance region (dL/dθ > 0) and de-energized before the negative inductance region (dL/dθ < 0) to prevent negative torque generation as shown in Figure 4. Therefore, the switching angles (θ_on, θ_off) are essential parameters for SRM control ^[20]. However, due to the highly nonlinear characteristics of SRMs, this process is not easy. Much research has been conducted to determine the optimal switching angle values for enhancing SRM performance.

Many techniques are used to obtain the appropriate excitation angles for phase current and rotor speed functions. In ^{[21,22,23,24]}, Analytical approaches have been employed to estimate the switching angles to increase motor efficiency at various speed ranges. A closed-loop switch-on angle (CL θ_on) is proposed in ^[25,26] without requiring motor parameters. In ^[27], an adaptive analytical determination for optimum excitation angles (θ_on and θ_off) of SRM drives along a broad range of operating speeds by taking into account the influence of back-emf voltage by optimal computation of the θ_on angle and avoiding the production of negative torque through the whole operating range by optimal the θ_off angle.

However, this suggestion does not consider a good solution for torque ripple reduction. In ^[28], a simple adaptive controller is introduced for online tuning of the switch-on angle depending on the nonlinear inductance profile of SRM, and offline tuning by a multi-task optimization function for optimized switch-off to mitigate the torque ripple and improving the efficiency of the motor. Also, the paper ^[29] presented an analytical method to estimate the optimal switch-on angle online based on the nonlinear inductance profile of SRM with consideration of back electromotive force. At the same time, the switch-off angle is optimized offline through a secondary objective function to minimize the torque ripple. To superior the performance of SRM with minimized torque ripple, intelligent control methods like fuzzy logic and neural networks are employed in order to optimize the switching angles ^{[30,31,32,33]}. A fuzzy adaptive control technique is proposed in ^[31] to automatically control switching angles in SRM. This approach optimizes the switch-on and switch-off angle timings depending on the online rotor position to produce high torque.

Recently, metaheuristics optimization algorithms have been suggested based on different objective functions like output torque, torque ripple, and motor efficiency to optimize the switching angles for better performance of SRM ^{[34,35,36,37,38,39]}. The Genetic algorithm (GA) has been utilized to find the optimal current excitation angles based on a multi-objective optimization function to enhance the output torque profile and decrease the torque ripple of the machine through various operating ranges ^[34]. In ^[36], a modified PSO algorithm based on velocity-controllable (VCPSO) is suggested for optimizing the switch-off angle of the SRM with the current chopping regulator strategy to increase the efficiency of real-time tracking. The Grey Wolf (GW) algorithm, another powerful optimization technique, achieved SRM's optimum performance ^[39].

3.   Control strategies of SRM drive systems

SRM is an excellent alternative for the growing traction motor applications such as E-bikes and Electric Vehicles due to its robustness, reliability, and broad constant power range of operation. In contrast, it suffers from drawbacks such as torque ripple and sound noise. The control of the SRM must be capable of considering operations under different operating conditions, which make the controller's design more challenging due to the nonlinearity of magnetic characteristics caused by the double salient structure ^[40]. These difficulties require highly accurate and sophisticated SRM controls on the part of the designer. SRM drives are operated and controlled by synchronizing the motor phase energization with the rotor position. The control method can be accomplished utilizing a position sensor feedback signal or a senseless method that estimates the rotor position based on the machine's magnetic properties ^[41,42,43]. Generally, numerous control schemes are suggested to enhance the SRM's performance in terms of increased efficiency, reduced torque ripple, consistent torque, and a wide speed range. Various well-known machine control systems exist depending on the applications, including position, speed, current, and torque control, as depicted in Figure 5 ^[44]. Due to its pole saliency and nonlinear magnetic characteristics, the SR machine differs from conventional DC and AC machine types. Moreover, the current control scheme in SRM is different from torque control despite these two being synonyms in DC drives.

4.   Torque ripple reduction technologies

Torque ripple is the primary restriction to the dependability of utilizing the SRM drives in high-performance applications such as electric vehicles (EVs). The torque ripple occurs because of the double salient structure, which causes extremely nonlinear magnetic characteristics and discontinuous current commutation ^[44], as shown in Figure 6. These reasons increase the torque ripple and complicate the control of SRM drives. The torque ripple can be mitigated by either enhancing the geometry of the machine design or by adopting different control techniques. Figure 7 demonstrates the classification of torque ripple reduction strategies used for SRM and the improvements made to each control approach ^[2,5,6]. The optimal performance of the SRM drive system depends on the machine characteristics, the control technique, the converter configuration, and feedback variables. However, the SRM drive system has a lot of feedback variables. At least one current sensor must be needed to measure the motor's current and a position sensor ^[41,42]. The motor's torque strongly depends on the rotor position and switching current angles; these variables can be stored in look-up tables for simpler control processing. In this context, we introduce a comprehensive categorization of control strategies to mitigate torque ripple and enhance the performance of SRM drives.

4.1.   Optimization design topology

SRMs are known for their simple and robust construction characterized by the absence of permanent magnets, and stator and rotor poles are normally symmetrically and evenly distributed around the motor's circumference ^[45,46]. This innovative design enables engineers to optimize the motor's performance by strategically shaping the stator and rotor poles. Optimization often employs sophisticated software programs and algorithm methods, such as finite element analysis (FEA) and PSO algorithms, to find the most effective pole designs, sizes, and configurations ^[47]. By carefully tuning these parameters, researchers can mitigate the torque ripple, maximize the torque average production, and improve the overall efficiency of this motor. An optimal topology design is essential to ensure that SRMs play a crucial role in EV applications ^[48]. Recently, there has been a trend by researchers to focus on the design optimization of SRM to fulfil the requirements of EVs, such as maximizing the output torque and reducing torque ripple ^[49]. In ^[50], the design and optimization of SRM are presented to produce a consistent output torque at high-speed operation. This paper focuses on the initial design of this motor and optimizes the electromagnetic design to achieve a high output power of 8 kW at a high speed of 100,000 rpm. A novel magnetic parameter design approach of SRM is presented in ^[51]. This methodology is based on the nonlinear characteristic of flux linkage, and the multi-objective optimization function is utilized to accurately calculate the design parameters without overly depending on the designer's experience. In ^[52], the SRM design optimization using the layered technique has been presented based on a multi-physical analytical model of SRM. Taguchi algorithm is employed to examine the level of effect of the primary geometric dimensions on the dynamic performance. In ^[53], A two-step design optimization procedure is proposed to reduce the torque ripple of the DSAFSRM without compromising its efficiency.

Additionally, the suggested DSAF-SRM is compared with a double-sided radial flux SRM in output torque, torque ripple, power density and efficiency. In ^[54], a 6/4 SRM with a misaligned segmental rotor is introduced in order to produce maximum torque with a low torque ripple. The segmental rotor has a 15-degree misalignment to achieve a one-layer 2D structure with a short flux path structure. In ^[55], a new geometry for SRM depending on the rotor pole skewing is presented to mitigate the torque ripple. This paper uses a differential evolutionary algorithm based on a multi-objective function to build an asymmetrical skew rotor-SRM. The optimization parameters are selected for an enhanced design with a lower torque ripple than a conventional structure. In ^[56], a comprehensive analysis of the advancements in the modelling and design optimization of SRMs using Machine Learning (ML) based Intelligent methods.

4.2.   Control strategy improvements

Today, control technology has become the most appropriate choice for reducing torque ripple due to the developments in semiconductors, Integrated circuits, and power electronics converters. This development has brought a significant revolution in the possibility of controlling and improving the performance of the SRM. According to the operational theory of the SRMs, the tiny gradients of inductance in the minimum and maximum inductance zones lead to low phase torque in these regions. Therefore, the torque falls in the region of phase commutation and produces a high torque ripple ^[44]. Control technique enhancements are simpler and more affordable than motor topology design to mitigate the torque ripple. The enhanced control strategies for reducing torque ripple can be categorized into two major techniques: Torque control and current control ^[5,6], as shown in Figure 7. To get a superior control strategy performance, the following techniques should be improved to be compatible with the overall drive system.

4.2.1.   Torque control strategy

Torque Control is essential for the electric propulsion system in EV applications. It should follow the torque reference fed by the torque controller unit with fast response to enhance the dynamic performance at different operating situations of the electric vehicle, such as accelerate, decelerate ^[57]. As for SRM, torque control can be categorized into direct, indirect, intelligent control, and other methods, which will be covered in more detail in the following subsections.

4.2.1.A.   Indirect torque control

1. Open loop current sharing

The open loop current control technique is utilized to acquire the average torque directly from the phase current of the SRM. The basic concept is computing the shape of phase current offline to achieve zero torque ripple, which depends on the capability to track the current profile ^[58], as shown in Figure 8. This approach directly utilizes the taken values of three currents from the lockup table I = f(T, θ), which is calculated according to the rising and falling capability of the current (as well as concerning minimizing torque ripple or another imposed requirement) for each operating case. This approach has the benefit of being able to achieve a minimum torque ripple that is restricted only by switching frequency. In addition, the motor's efficiency can be maximized in this method. However, this method suffers from some drawbacks, such as the sensitivity to any changes in the variables of this motor. Also, it needs a large memory space to store the current profile data ^[58]. In ^[59], the current sharing method uses the simulation to determine the inductance and the rate it varies with the rotor position for each motor phase involved in producing positive torque. The current magnitude is changed using the PWM approach following the rotor position to reduce torque ripple. Two positive generating phases are simultaneously turned on to minimize the torque during commutation with various PWM. In ^[60,61], an effective methodology is developed to reduce torque ripple through coupled simulations of finite element analysis and dynamic simulation. This coupled simulation is used to detect the required current profile and fine the tuning of the current shape. The suggested approach was built to operate from zero to maximum speed, as the application would allow. In ^[62], a new method for computing current profiles will reduce the torque ripple SRM produces under normal and one open-phase fault conditions. In addition, a new scheme to the current profile calculation offline for torque ripple mitigation is proposed. To suppress the torque ripple in SRM, ^[63] suggests five new optimization techniques. The phase-current profile has been optimized in these techniques using the simplex approach based on a genetic algorithm. These optimization processes are tailored to two optimization techniques: The simplex method and the genetic algorithm. The torque ripple during commutation is minimized in ^[64] using closed-loop control and the speed signal ripple. It is simpler and less expensive to utilize a speed sensor or estimator to get the speed signal than it is to use a torque sensor. This method can capture the torque ripple data using a signal processing approach from the speed signal.

The results demonstrate that the torque ripple reduced through the commutation period by finding the appropriate shaping of current. A comparative study was conducted for a different precomputed current profiling approach for torque ripple reduction ^[65]. Additionally, the suggested approach provides lower average currents and allows for applying a peak current restriction. Additionally, it aids in quantifying the variables affecting torque ripple that are problematic for other approaches. A hybrid speed ripple minimization solution for SRM is presented in ^[66], which combines current profiling, effective tracking error elimination, and excitation approaches. The suggested method can accomplish the decrease of stator vibration and the enhancement of torque generating capacity. A common sharing approach for current and flux-linkage control is presented in ^[67] for the high-performance control of SRM. This method shares current and flux linkage between the phases, significantly reducing the torque ripple. However, it also has the ability to mitigate the torque ripple drastically.

2. Torque sharing function (TSF)

TSF is one of the most effective and popular indirect control approaches for torque ripple mitigation in the SRM drive system. This strategy is performed by employing the static characteristics of this motor through TSF, which distributes the total torque among the motor phases utilizing TSF, as shown in Figure 9. The output of TSF is the reference torque for each phase, which is transformed into a reference phase current utilizing the torque inverse model (i-T-θ) of SRM. Then, a current controller is employed to control the feedback current to follow its reference current by hysteresis or PWM control. Moreover, to ensure that the produced torque from each phase is stable, the TSF employs the turn-on, turn-off, and overlap angles according to the rotor position to independently generate reference torque signals for each phase ^[68]. The TSF could be utilized in a linear or nonlinear function. Due to the nonlinear SRM features considered, the linear TSF is not quite effective because the torque ripple is extremely problematic according to the rotor position. In ^[69], a genetic algorithm is employed to identify the turn-on and overlap angles for various TSFs. This optimization algorithm tries to mitigate the torque ripple and cooper loss in SRMs running at a wide range of speeds. In ^[70], an offline optimized TSF based on a multi-objective function is proposed for minimizing torque ripple. The suggested TSFs with various Tikhonov factors are compared with the classical TSFs, such as linear, cubic, and exponential, considering efficiency and torque–speed characteristics. In ^[71], an off-line Optimization algorithm is used to identify the optimal switch-on and overlap angles of sinusoidal TSF for every operational point of SRM. An optimized TSF based on modified ant colony optimization (ACO) is presented in ^[72] to improve the output torque and minimize the RMS phase current of SRM during a broad range of operating speeds. An improved TSF was utilized in ^[73] to compensate for the torque error with the incoming motor phase due to its lower rate of change of flux linkage based on the absolute changing rate of flux linkage. The suggested method is compared with traditional TSFs (sinusoidal, cubic, and linear) to effectively investigate minimizing the torque ripple and enhancing performance during abroad range of speeds. An optimal current profile is achieved in ^[74] by utilizing a developed TSF. In addition, a robust current controller is derived using the Lyapunov stability theory to follow the current accurately. The suggested approach offers minimal torque ripple, higher efficiency, and enhanced anti-disturbance capabilities. In ^[75], a new TSF is presented to provide a lower current following error by adopting a new current reference generation approach and optimization algorithm. An offline calculation based on an optimization algorithm is employed to obtain the phase current reference from the torque command for minimizing the torque ripple and copper losses. Two-torque ripple mitigation control techniques based on TSF are presented in ^[76]. The first method uses the torque to minimize current ripple, and the other method is the direct instantaneous torque control method, which leads to a reduced torque ripple. A novel IITC approach based on hybrid TSF is introduced in ^[77]. The hybrid TSF originated to overcome the torque following error issue during phase demagnetization by re-profiling the reference torque section of the incoming phase to be the perfect mirroring of the measured torque of the outgoing phases. Thus, the torque profile is improved with less torque ripple due to excellent torque monitoring capabilities in this approach. The torque ripple and disturbance for an SRM drive are reduced by a piecewise TSF presented in ^[78] based on an enhanced linear active disturbance rejection control (LADRC) and modified coyote optimization algorithm (MCOA). First, the piecewise TSF is used with an enhanced linear extended state observer to minimize the torque ripple, which has minimal influence on the current peak value and the rate of change in the current value. Then, the MCOA is suggested to find the optimum switching angles and the coefficients in the piecewise function and LADRC to get better comprehensive performance.

3. Average torque control (ATC)

ATC is one of the most significant traditional torque control methods for SRM drive systems. The main benefit of this approach is that the reference phase current remains fixed throughout one excitation cycle. It can be utilized at a broad speed range and requires constant reference torque and discrete rotor position ^[79]. The drawbacks of this strategy are that it generates significant speed oscillations and fluctuations at low speeds due to torque ripples throughout the phase commutation. In this method, to produce a constant average torque, the torque of each phase can be obtained from the saved data using the torque sharing look-up table according to i_ref, θ_on, and θ_off, as depicted in Figure 10. The commended torque in this strategy can be divided into phases according to the reference current (i_ref) and motor speed (ω_m), where the current ripple should be minimized as low as possible to generate output torque with a low ripple. In addition, to achieve precise operating conditions, the control factors, including reference current, turn-on angle, and turn-off angle, can also be optimized.

The SRM for light electric vehicle (LEV) applications is accurately and dynamically controlled by a control method that combines offline pre-calculated control variable sets and closed-loop control ^[79,80]. The open loop control system is sensitive to changes in machine parameters, which are affected by operating conditions. The control variables that are estimated off-line usually diverge from the reference commands. To avoid the undesirable divergence between reference and actual torque, it becomes desirable to follow the average torque by altering the closed-loop control parameters with online computation. To determine the online average torque of an SRM, a new technique was developed in ^[80]. This new method of estimating the average torque and energy ratio can be applied to closed-loop torque control. In addition, this paper developed an approach to calculate the average torque by estimating the machine variables, such as phase current and phase voltage for one phase of the motor. This calculated torque can be utilized for on-line feedback control. In ^[81], a simple quadratic equation is utilized to determine the switching angles based on the motor's speed and phase current values to enhance the efficiency of low low-power SRM motor. An improvement of the ATC method was proposed in ^[82], based on a current-peak regulation approach to the control torque in low-speed chopping mode and high-speed single pulse control. This technique provides a smooth transition between two modes of operation. A speed control approach based on average torque control was proposed in ^[83]. The control parameters are determined according to multi-objective criteria to optimize the performance of SRM.

In ^[84,85], a search algorithm based on a multi-objective function was employed to optimize the excitation angles offline. This algorithm produces high-output torque and mitigates torque ripple using the ATC technique for electric scooters and EV applications. In ^[86], a new method of ATC strategy of SRM is proposed to get high operating performance for EVs. This method uses an online average torque estimator with Current chopping control-angle position control (CCC-APC) hybrid crossover control to improve performance over a broad speed range. In addition, a genetic algorithm (GA) is utilized to identify the optimal excitation angles to provide high efficiency and low torque ripple. In ^[87], a novel ATC technique of SRM based on a hybrid flux–current locus control strategy with a micro-stepping process is proposed. Despite its complexity, the benefit of the suggested ATC is that it generates the commended average torque over any given range of rotor angles.

4. Vector control (field‑oriented control)

The vector control strategy is widely utilized in AC machines to enhance torque control performance due to Park's transformation. Regretfully, there is no such transformation to isolate the position from the flux-linkage and torque of SRMs in the early development of SRM control techniques, even in the linear situation, as shown in Figure 11. However, in the last decades, the field‑oriented control was developed based on the average value of the first-order inductance and the relationship between the q-axis current and torque was derived, but only for the unsaturated SRM ^[88].

In the vector control method of SRM, a sinusoidal current is applied to each circuit along with a DC offset, constituting the unipolar excitation current. This excitation current comprises DC and AC components, generating the virtual rotor flux and a rotating stator field. Hence, the SRM can be operated similarly to traditional AC machines. Notably, it has been demonstrated that continuous current excitation can reduce the vibration and the acoustic noise of the SRM in the vector control. Nevertheless, it is essential to note that the application of vector control to SRMs operating in high-speed regions hasn't been fully utilized because of uncertainties surrounding factors such as bus voltage, switching frequency, and inverter specifications required to facilitate vector control in high-speed drives. In ^[89], vector control was proposed for the SRM drive. The drive conditions for the SRM drive system in high-speed regions, such as switching frequency and bus voltage, are established in the high-speed region and can realize low vibration. A complex rotating vector control strategy is suggested in ^[90] for estimating the air gap torque of an SRM. The Vector method can handle an arbitrary number of spatial harmonics of the inductance saliency and saturation for enhancing the air gap torque of the SRM. The d-q control method-based flux-weakening control for SRMs has been introduced in ^[91]. The d-q control of SM has been modified to operate with SRMs by eliminating negative aspects and nonlinearities. The suggested controller has a simple structure and effectively eliminates the requirement of switching angles controller from the SRM control structure. To mitigate the torque ripple by controlling torque within a specified hysteresis band, a vector control method of SRM is introduced in ^[92] that employs a combination of fuzzy logic and ANN controllers. Vector control for SRM drives with unipolar current excitation has been suggested in ^[93]. This method involves the application of a sinusoidal current with a DC offset to each circuit, resulting in an excitation current comprising both DC and AC components. A novel approach for torque ripple reduction based on vector control of SRM is presented in ^[94]. The proposed strategy used a non-sinusoidal dq transform and the derivatives of inductance as main variables to mitigate the torque ripple average current and enhance the efficiency while minimizing the copper losses.

4.2.1.B.   Direct torque control

1. Instantaneous Torque Control (ITC)

Recently, the algorithm of instantaneous torque control has made significant advancements and has been widely used to solve the issues of indirect torque control approaches. The important advantages of this approach are that instantaneous torque is taken into account as a control variable directly; torque to current conversion and closed-loop currents control is no longer necessary. Besides, ITC can rapidly eliminate errors instantly with an excellent dynamic response, as well as torque ripples, which will be minimized ^[95]. The ITC scheme has three approaches: indirect ITC (IITC) dependent on torque sharing function (TSF), direct torque flux control (DTFC), as well as direct ITC (DITC). Figure 12 depicts the schematic diagram of the DITC approach for the SRM drive system. The instantaneous torque is estimated online, and then the torque error (∆T) is utilized as a control variable input without any current loop to generate an appropriate switching signal for the SRM drive. An improved DITC-based adaptive commutation algorithm is suggested in ^[96] to enhance the average torque and efficiency of SRM by appropriately adjusting the switching angles in real-time. In ^[97], a modified ant colony optimization (ACO) is employed to precisely find the optimum excitation angles to enhance the performance of the DITC approach for SRMs. This strategy focuses on minimizing the torque ripple and improving the efficiency of the SRM. An enhanced DITC with adaptive switching angles is proposed in ^[98] for enhancing the SRM's performance. In this control approach, the switching angles are dynamically tuned to enhance the commutation interval so that the DITC can flexibly set this process. An enhanced DITC method of SRM is presented in ^[99]. The proposed scheme includes a torque error compensation and an uncomplicated online torque estimator. The switching angles are optimized to achieve high torque per ampere (MTPA), low torque ripple, and highest efficiency. Besides, this paper thoroughly compares the proposed DITC, IITC, and ATC strategies. The comparison results demonstrate that the proposed DITC performs better with a low torque ripple. In ^[100], the researchers suggest a TSF based on adaptive turn-on angle for improving a DITC strategy to mitigate the torque ripple in commutation overlap regions. This method presents TSF and provides the appropriate candidate voltage values for various sectors, where the working cycle is divided into six sectors in this method.

A modified PWM-DITC based on a fixed switching frequency is suggested to suppress the torque ripple ^[101]. The PWM is employed to modulate the torque deviation, and the optimum excitation angles are chosen according to the PWM modulation signal and the rotor sector position. This method provides an effective solution for the issue of shaft breaking in the starting and generating system of SRM. In ^[102], an optimized DITC approach for SRM and a new adaptive dynamic excitation technique is proposed. In terms of torque tracking during commutation areas, two operational modes have been established. Besides, the excitation angles are dynamically adopted by a phase current endpoint detector and a torque error regulator throughout each electrical cycle. This strategy generates full torque to mitigate the torque ripple and improve system efficiency. In ^[103], a new control strategy is suggested, which combines adopted hysteresis and PWM in DITC. This proposed approach accounts for the benefits of the PWM and the hysteresis methods. With this method, the torque error will be minimized by PWM in DITC. In ^[104], an improved IITC approach of SRMs for EVs is introduced to satisfy the vehicle's requirements, which include low torque ripple, maximum torque per ampere (MTPA), and excellent efficiency throughout the full speed range. An online analytical method is utilized to achieve the optimal torque production turn-on (θ_on) angle. In addition, an improved TSF is proposed to compensate for torque following errors.

2. Model predictive torque control (MPC)

Model predictive control (MPC) has been used successfully in industrial control applications and, recently, in industrial power electronic systems. The major goal of model predictive control in electric motor drives is to identify the converter's optimum switching state at each switching instant to satisfy specific constraints and meet the stated performance objectives using a system's predictive model. The MPC has been used in the SRM to predict the torque, current, and flux of the SRM, as shown in Figure 13 ^{[105,106,107]}. The MPC is considered an appropriate strategy to handle the nonlinearity of the magnetic characteristics of SRM and address the complicated switching rules. Different MPC techniques for SRM have been suggested ^[107]. An MPC strategy based on choosing candidate voltage vectors in six regions is presented in ^[108]. The cost function is established to find the optimal voltage vector from candidate voltage vectors to reduce the torque ripple and copper loss.

A model predictive control strategy is suggested in ^[109] to suppress torque ripple. This approach predicts the torque and current through the torque-current-position and the current-flux-position two-dimensional look-up tables, respectively. The cost function is based on torque and current and then optimized to acquire an ideal control signal. Authors in ^[110] employed the candidate voltage vectors (CVVs) algorithm based on the modified model predictive torque control (MPTC) method for SRM to minimize torque ripple and increase system efficiency successfully. This method of MPTC is modified in three ways. The first way, the flux linkage estimation, is omitted compared to traditional MPTC. Second, the commutation region of the SRM is redefined, and according to the optimal torque contribution profile, the motor's electric cycle is split into six sectors. The total number of CVVs is then minimized to 2 or 3 at each control period, and each sector's CVVs are adopted depending on phase torque characteristics. The cost function is established to minimize torque ripple and reduce copper loss by choosing the optimal voltage vector from CVVs.

A modified MPTC-based TSF approach for SRM is presented in ^[111]. This strategy distributes the torque reference to each phase through a sinusoidal TSF approach. Then, the predictive torque control strategy is employed to follow the phase torque reference and minimize the torque ripple. In ^[112], an online adaptive approach is presented to modify the excitation angles for SRM via the finite control set model predictive control (FCS-MPC) approach to decrease the negative torque generation. The proposed method uses a simple online scheme to modify the switch-off angle for a single prediction horizon FCS-MPC to eliminate negative torque generation. As discussed, the FCS-MPTC strategy is considered one of the most effective methods to minimize the commutation torque ripple. The limited voltage vectors lead to high-frequency torque ripples. To solve this problem and improve the torque control performance, a continuous control set (CCS) model predictive torque control (MPTC) approach with low torque ripple is presented in ^[113]. This approach is established based on the optimal torque references, which can be optimized by the Lagrange multiplier method. In ^[114], a four-quadrant operation strategy of SRM based on the PWM-MPC method with an online adaptive commutation angle was proposed. In this strategy, a composed of MPC and deadbeat predictive control (DPC) is utilized in the commutation region to improve the performance of SRM. A new indirect MPTC method is presented in ^[115] to suppress the torque ripple of SRM in EV applications. The proposed method is established by two aspects: Torque inverse model to provide an additional error compensator and robust predictive current controller seeks out all possible switching states and utilizes the switching state that minimizes cost function as the optimum output. The proposed IPTC technique, which is simple to implement as well as suitable for electric vehicle driving, indirectly achieves immediate torque control through accurate current following. In ^[116], two novel strategies are introduced based on TSF, DITC, and MPC to suppress the torque ripple of SRM further. The first method combines TSF with DITC strategy, and the second approach integrates MPC and TSF. According to the results, both strategies can successfully reduce torque ripple, but the TSF + MPC strategy can follow the reference torque more precisely and provide low torque ripple.

4.2.1.C.   Intelligent control

1. Iterative learning control

Iterative learning control (ILC) is particularly well suited to improve output tracking performance uncertain non-linear systems together with high-precision analysis without the requirement to determine the system's parameters ^[117]. The main concept is repeatedly applying a simple algorithm to the system or plant to obtain perfect tracking, as shown in Figure 14. Therefore, it is an iterative technique for determining the optimal system input to ensure the output is as near the required one as possible ^[118]. As a result, it is considered for SRMs' dynamic torque control to mitigate torque ripple. To enhance torque control performance SRM, a developed ILC is built in two stages ^[119], including determining optimal phase voltages for accurate waveform tracking and suitable phase current waveforms for the specified torques. In ^[120], a control system for SRM using a direct instantaneous torque controller called (DITC), which is based on the ILC method, is suggested.

Moreover, the ILC performs efficiently to reduce torque ripples in steady-state operations. Because ILC learning takes a limited time, performance loss will occur over transient periods. The proposed method employed a sliding mode controller (SMC) combined with ILC to get torque track and improve control response during transient periods. An adaptive ILC strategy based on the accurate magnetization characteristics of the SRM is suggested in ^[121]. The proposed method included torque ripple controller (TCIL) and energy conversion loss controller (ECIL) schemes to reduce the torque ripple and energy conversion loss. A novel direct torque controller based on a spatial ILC approach for SRM is suggested in ^[122] to emphasize torque ripple reduction. The ILC employed a linearized magnetization characteristic and a straightforward learning rule to produce the appropriate control signal. This approach is appropriate for applications needing ripple-free constant torque at low speeds. An optimal torque controller combining the TSF method and the current controller is presented in ^[123] for reducing the torque ripple along with the stator current-oriented approach. To optimize the TSF scheme, a current controller based ILC considers the mutual inductance with simultaneous two-phase commutation. An improved control method is presented to mitigate the torque ripple of SRM using the ILC approach ^[124]. In the proposed method, a feed-forward learning compensator is employed to control the torque pulsations produced in SRM due to the overlapping of phase currents by finding the appropriate current profile for a reference torque and then applying it to the phase winding.

2. Artificial intelligence techniques

Artificial intelligence techniques have recently been utilized to convert human knowledge into a form that computers can understand. The intelligent control can be utilized for offline or online current optimization to optimize the SRM problems further and minimize the torque ripple. It has significant self-learning and adaptive capabilities such as fuzzy logic, neural networks, neural-fuzzy networks, and evolutionary algorithms ^[125].

Fuzzy logic control

Fuzzy Logic control is a popular intelligent control method that deals with nonlinear or complex control systems for better performance because it has strong stability and flexibility. Besides, having an exact mathematical model of the controlled item is unnecessary when designing a fuzzy controller. Figure 15 depicts the fuzzy logic controller to control the torque of SRM. In ^[126], a fuzzy logic controller is presented to suppress the torque ripple and modify the performance of SRM. Then, a performance comparison between the fuzzy and PI controller is implemented to depict the validity of the suggested controller. In ^[127], a fuzzy logic control based on the current modulation approach for direct torque control of SRM. The proposed modulated reference phase current uses a fuzzy logic controller in order to address the system's nonlinearities so that the torque ripples are further reduced. A novel adaptive TSK fuzzy sliding mode controller based on DITC without a torque sensor is suggested in ^[128]. The sliding mode controller (SMC) executes fast responses to mitigate the impact of uncertainties and external disturbances. The coefficients of the adaptive method (AFC) are tuned online by Lyapunov stability theory to improve the performance of SRM. An enhanced fuzzy logic control based on the TSF strategy is suggested in ^[129] to mitigate the torque ripple and enhance the dynamic response of the speed controller of SRM. This approach employs a combination of fuzzy and PID control to adjust the proportion factor automatically. In fuzzy control, the scale factors for speed and torque are self-tuned by the output torque characteristics. In ^[130], a fuzzy controller based IITC strategy is proposed to minimize the torque ripple of SRM. First, a fuzzy controller is implemented to produce a compensation current in accordance with the torque error. Then, the input factor is reset by human experience, and the output factor is properly designed depending on the inductance deviation.

Artificial neural network

The artificial neural network (ANN) technique is inspired by the human brain model. Its benefits include self-repair capacity fault tolerance, organic learning, and linear data processing ^[131]. An artificial neural network (ANN) is introduced in ^[132] to mitigate the torque ripple of SRM. In this scheme, the ANN technique is employed to predict the stator current and flux to improve current and speed response regarding reduced torque ripple during a broad speed range. In ^[133], a genetic neural network controller-based DTC approach is suggested to minimize the torque ripple of SRM. In the proposed approach, suitable data are selected for training and testing, which leads to weight adjustment in the network. Therefore, the error is decreased, demonstrating the accuracy of the voltage vectors chosen from the vector table and producing improved torque response throughout a wider speed range. In ^[134], An improved TSF technique-based artificial neural network for four quadrants operation of the SRM is presented to mitigate the torque ripple as depicted in Figure 16. The ANN is employed to translate the torque reference to the appropriate current. An online reference torque neural network (RTNN) based on the TSF approach is proposed in ^[135] to modify the reference torque. The RTNN is constructed on the TSF approach as a single-input and single-output network. Then, the parameters of RTNN are trained according to the torque error to reduce the torque ripple. Last, the suggested approach is compared with the fuzzy torque compensation and PD current compensation methods to demonstrate the successfulness of the RTNN method. An intelligent torque control method based on the BP neural network is suggested in ^[136]. At first, the fitting generalization capability of the BP neural network is used to establish the nonlinear relationship between speed, load torque, and turn-on angle. After that, the control method can automatically tune the turn-on angle according to the operation conditions to reduce the torque ripple.

Fuzzy-neural network

The neuro-fuzzy inference system (ANFIS) incorporates the merits of both approaches, artificial neural networks and fuzzy logic systems ^[137]. The schematic diagram of the ANFIS controller for torque control is the same in Figure 15 or maybe in Figure 16, with replacing the control unit, depending on the suggested approach. To mitigate the torque ripple of SRM, a hybrid ANFIS method is presented in ^[138]. The proposed approach is employed to find the optimal switch-off angle while the switch-on angle is estimated analytically. Then, the ANFIS method is compared with the analytical method and fuzzy logic controller to depict the ANFIS controller's ability to decrease torque ripple. To enhance the torque control performance of SRM, a genetic neural network is integrated with a DTC approach is suggested in ^[33]. The proposed scheme chooses the appropriate data bits for GA training and testing. Also, the artificial network fuzzy inference system-based DTC strategy is presented in ^[139] to provide high torque with minimized torque ripple of SRM throughout a broad speed range. In ^[140], an improved intelligent control based on the Lyapunov stability theory controls SRM to improve the speed response and minimize the torque ripple. The suggested method is divided into two sections; the main section is the speed controller, and the other part is the torque controller. The speed controller uses an adaptive fuzzy controller based on the Hamilton–Jacobi–Bellman theory to optimize the controller's parameters. Moreover, the torque controller is implemented using an ANN for torque estimation, reducing the torque ripple. In ^[141], ANFIS based on space vector Modulation is utilized to choose voltage space vectors better. The SVM-DTC provides a fixed switching frequency, while the suggested ANFIS technique controls the torque and stator flux. This technique improves the torque profile with low torque ripple and flux ripple.

Machine learning

Machine learning is a modified generation of intelligent control systems with a high rate of automatic learning with a simple structure, making it ideal for use on an industrial scale ^[142]. In ^[143], a machine-learning approach is presented based on two pre-trained ANN models to minimize the torque ripple throughout a broad speed range of SRM. The proposed pre-trained ANN is utilized to predict the actual torque according to the motor's current and position and to compute the optimal reference currents for each phase to minimize the torque ripple. A novel intelligent technique based on a computational model of the mammalian limbic system and emotional processes (BELBIC) is suggested in ^[142] to control the speed of SRM with a focus on torque ripple mitigation. In this technique, simple and effective controls are achieved by employing machine learning without the requirement of any classical controllers and completely independent of the motor parameters. The suggested approach offers fast auto-learning and high tracking potency, which leads to improved speed response with reduced torque ripple. The same intelligent controller (BELBIC) method combined with the PI conventional controller is presented in ^[144] to control the torque of SRM indirectly. This technique is employed to modify the transient state and improve dynamic response.

4.2.1.D.   Other torque control strategies

There are many other strategies for reducing the torque ripple; a general overview of a few of these methods is covered in this section. The feedback linearization (FBL) technique applies state feedback to the nonlinear system in order to linearize the closed-loop system ^{[145,146,147]}, thereby compensating the motor's nonlinear properties. This approach has significant limitations, such as the need for a precise motor model that requires high currents during low-speed operation and the measurement of state variables (position, velocity, and stator currents). To overcome these disadvantages, an adaptive feedback linearization approach has been utilized based on multi-objective optimization by genetic algorithm ^[148] to identify the optimal coefficients of the feedback linearization control approach. Another method utilized to enhance the torque control strategy's performance is the non-linear control method ^[149,150]. A nonlinear internal model control (IMC), depending upon an appropriate commutation technique for SRM, is proposed in ^[151]. This control approach is robust for internal and external disturbances caused by modeling uncertainties. It can successfully offset the system's nonlinearity.

Also, researchers have utilized non-linear control methods called variable structure control methods for reducing the torque ripple ^{[152,153,154,155]}. In ^[155], the variable structure control strategy is utilized to mitigate the torque ripple of SRM with robust torque control. To enhance the performance of the structure control method to suppress the torque ripple, a combination of variable structure control theory and fuzzy logic control is suggested in ^[154]. In ^[156], a sliding mode control is used based on variable structure control, which has many features of fast response, insensitivity to adjusting parameters and disturbances, and strong robustness. Besides that, this method is not dependent on the parameters and disturbances. References ^{[157,158,159]} developed the sliding mode control as a torque control strategy to mitigate the torque ripple.

Comparison of torque control methods for torque ripple reduction

The torque control strategies discussed in this paper are categorized into four methods, including their sub-sections, as shown in Figure 4, and all these methods are utilized to minimize torque ripple with control of the average torque. The effectiveness of these strategies is assessed and compared through a list of some key aspects of each strategy, as shown in Table 1. The table offers a general comparison regarding advantages, disadvantages and complexity, but it does not specify the best way to mitigate torque ripple. Therefore, it is essential to carefully assess the application's specific requirements to select the most suitable control strategy. The choice of the torque control method of SRM application is based on the vehicle itself and factors such as the desired torque precision, speed range, cost constraints, and available computational resources.

4.2.2.   Current control strategy

The current control is the most popular scheme to mitigate the torque ripple acoustic noise and vibrations in SRMs. In addition, Torque control is greatly impacted by setting the current profile in each phase of SRM. The phase current is shaped according to several predetermined parameters to achieve various speed, torque, power, and efficiency goals across various operating conditions. A control stage usually tracks the current and demands excitation angles θ_on and θ_off. Where the output of the current controller is the reference voltage provided to the inverter via hysteresis current control (HCC) or a modulation stage in the form of PWM ^[160]. Generally, there are many major classifications of current control in SRM based on HHC or PWM techniques, which are detailed discussion in the following subsections in accordance with the block diagram in Figure 7.

4.2.2.A.   Model-Independent methods

1. Current chopping control (CCC)

Current chopping control is a common strategy employed for controlling the current of SRM due to its simplicity and independence on the machine parameters ^[161]. A hysteresis controller with a predefined hysteresis band is employed in the strategy. Hard and soft chopping methods are based on defining upper and lower boundaries and modifying the excitation signal to maintain the instantaneous current within the error band ^[162]. These techniques are characterized using positive, negative and zero voltage levels. The discrete number of possible duty cycles (1, 0 and ‒1) and the limited sampling frequency substantially impact this strategy's ability to track the reference current. Various approaches have been used in the literature to enhance the current tracking capabilities. Figure 17 depicts the general diagram of a hysteresis current control strategy. The CCC approach is presented in ^[163] to keep the current within a set hysteresis band, which leads to improved performance at low and medium speeds. The CCC strategy is improved in ^[164] to keep the SRM's torque within a set of hysteresis bands using an appropriate source voltage. To examine the effect of SRM's control settings on the dynamic response of the EV. A Fix angle current chopping control (FA-CCC) and adaptive variable angle current chopping control (AVA-CCC) is proposed in ^[165] to enhance the torque speed characteristics of SRM. To achieve high performance with minimal torque ripple at the low switching frequency, a current chopping controller based on fuzzy logic control is suggested in ^[30]. The proposed controller achieves this by altering the duty cycle of each interrupted period. In ^[166], a modified current chopping controller based on a segmented PWM variable duty cycle according to the inductance characteristic curve is used to mitigate the torque ripple.

2. Intelligent current control

The intelligent control method has been researched as an efficient candidate solution instead of the hysteresis controller while falling within model-independent methods ^[167]. These approaches commonly incorporate a learning mechanism to augment the controller's effectiveness. This may be achieved either online, with the controller modified using experimental measurements, or offline, using the results of consecutive simulations. These approaches offer several notable benefits, including their capability to handle highly nonlinear behaviors and adapt to parametric changes over time.

Furthermore, these methods can also be applied with PWM, leading to a consistent switching frequency. In contrast, these approaches' primary limitations are the slow learning rate, the requirement for training data, and their substantial complexity. In ^[168], a new current tracking strategy using ILC for SRM is proposed for tracking the reference current with fewer PWM cycles. The iterative learning current control approach utilizes real-time periodic learning at various rotor positions to calculate the optimal duty ratio to track the reference current. A hybrid torque controller that integrates optimal TSF and ILC approaches is presented in ^[169]. The TSF is used to optimize the torque and current profiles to mitigate the torque ripple. The iterative learning control (ILC) is used as a current controller to provide effective current tracking. An ANN-based algorithm is proposed in ^[170] for speed and current controllers to enhance the performance of SRM with lower torque ripple. The Levenberg–Marquardt algorithm is employed for optimizing the parameters of the ANN for both controllers, resulting in efficient and faster convergence during training and testing.

The reference ^[178] uses a novel compensation scheme-based fuzzy logic control and ANFIS to compensate for the phase current and produce the optimum possible phase current waveform. In the suggested method, the fuzzy logic and ANFIS controllers control the motor current to reduce the torque ripple, where a compensating signal is added as input to the current loop control. In ^[171], An improved ANFIS based on a Hybrid SSD-SFO algorithm for speed and current control of SRM to mitigate the torque ripple. In the proposed strategy, two ANFIS controllers control the speed and current. Additionally, the Hybrid SSD-SFO (social ski-diver-based sunflower optimization) algorithm was used to optimize the switching angles of SRM and the parameters of the ANFIS controller for both the current and speed controller. The simulation results demonstrate that the suggested approach performs effectively with less torque ripple.

Other intelligent control techniques offer adequate current tracking for SRMs based on machine learning presented in ^[172]. A new Q-learning scheduling strategy for controlling the current of SRM is proposed in this paper to minimize the torque ripple. The reference current path is followed using a table of Q-cores originating on an SRM model's nonlinear surface without including any model parameters data to schedule the infinite horizon linear quadratic trackers (LQT) handled by Q-learning algorithms, as illustrated in Figure 18.

4.2.2.B.   Model-Based methods

1. Linear current control (PI-PWM)

In this strategy, the current control of SRM can be accomplished by linear control theory (PI, PD, PID) to offer appropriate consideration. The PI(D) controller calculates a PWM signal's duty cycle based on the tracking current error. In this approach, the dynamics of the current loop are regulated by the sampling time and filtered to reduce the current ripple caused by the switching frequency ^[173]. This technique is simple to implement with both digital and analogue electronic circuits. However, the digital implementation is better for improving the performance of SRM. Figure 19 shows the schematic diagram of a linear current control method of SRM. Besides, the PWM technique has benefits like low current ripple and a consistent switching frequency than the hysteresis controller ^[174]. However, because of the nonlinear behavior of the SRM, constructing linear controllers is a difficult issue. To address this issue, researchers suggested a modified linear current controller to improve the response of this approach.

A digital PWM current controller is implemented in ^[175,176] to enhance the performance of SRM. The controller switches between two high and low states using a digital approach to achieve the desired speed. In ^[177], a linear controller is implemented for a small signal model of SRM. Two PI controllers are utilized for both speed and current loops. The machine's back-EMF is a disturbance that influences SRMs' current control. Therefore, some methods employ EMF compensation as a solution. A digital PI current controller based on an improved back-EMF decoupling scheme is suggested in ^[174]. This technique improved the performance of SRM by adjusting the PI parameters. In ^[178], a simple current control approach depending on narrow voltage pulse injection and a single threshold is presented for an SRM to achieve senseless control. A two PI-PWM closed-loop control is implemented to enhance the response of the suggested method. In ^[175], an adapted parameter of the PI-PWM current controller of SRM is introduced to achieve a fast dynamics response with a less current ripple of the proposed current controller. This method proposes a modified sampling scheme to avoid the control loop's PWM delay. To superior the performance of the linear current control, an adaptive PI-based current control is developed ^[179]. Two speed and current control loops are utilized to minimize the torque ripple.

2. Model predictive current control

Predictive current control is an excellent alternative to traditional current control strategies. It can deal with nonlinearities and constraints with many features such as online optimization, low current distortion, and effectiveness in dynamic response ^[180]. The MPC strategy consists of three paradigms, which include the estimation phase, prediction phase, and cost function design step, as shown in Figure 20. The states employed for estimation and prediction are chosen according to the designed cost function ^[106]. In ^[181], a predictive control approach is presented to track the current reference in an SRM accurately. The proposed technique tracks two reference currents to achieve a fast dynamic response through a broad range of torque-speed characteristics. In addition, it offers a better torque profile with a low torque ripple. In the variable switching frequency control, the inverter could be within the range of audibility, which results in acoustic noise issues. Therefore, a predictive current control strategy based on fixed switching frequency was suggested in ^[182]. The proposed method employed deadbeat predictive current control to predict the desired duty ratio of the PWM pulse for a certain reference current in each digital time step through a broad range of speeds. To enhance the performance with minimized torque ripple for the SRM, the incorporation of the predictive current control method with a TSF approach was presented in ^[183,184]. The proposed strategy in ^[183] tracks the reference current at a low switching frequency to minimize the pulsation torque ripple. In ^[184], An enhanced MPC strategy based on offline training and online adjustment for the phase current to avoid the model mismatch issue. The proposed approach utilized a radial basis function (RBF) neural network to adjust the model parameters, enhancing the tracking performance and minimizing the torque ripple. A new control approach based on the TSF utilizing predictive current control is suggested in ^[144] to mitigate the ripple of torque and current. In addition, an optimized PWM control is introduced by precisely predicting the duty ratio of the voltage using the data of the motor running parameter.

Moreover, an MPC method based on a fixed-switching frequency utilizing a multiplexed current sensor for SRM is presented in ^[185]. In this method, the only current sensor used in this system was time division multiplexing for phase current sampling, and the duty ratio of PWM was constrained to maintain an adequate sampling time for A/D conversion. This strategy aimed to reduce costs with guaranteed performance. In ^[186], A virtual-flux finite control set MPC (FCS-MPC) approach of SRM is developed to control the phase current through a flux linkage-tracking algorithm indirectly. This technique uses a discrete voltage equation to predict a virtual flux and determines the switching mode, resulting in the minimum error concerning the flux reference.

3. Sliding mode current controller

Sliding mode control (SMC) is one of the effective methods for addressing control of highly nonlinear dynamic systems because it has a good dynamic response and superior robustness in controlling power converters and motor drive systems ^[187]. Sliding mode control has been suggested as a good solution to control the SRM, especially the speed control approach. It is employed to control the current to minimize the torque ripple. Figure 21 illustrates the architecture of sliding mode current control of SRM. In ^[188], an SMC-PI current controller is introduced to mitigate the torque ripple and enhance the efficiency of SRM. A second-order sliding mode current controller based on the super twisting algorithm is proposed in ^[189] to achieve high performance and lower current ripples. In ^[190], a digital control scheme based on SMC is suggested to offer a carrier-less pulse width modulation. The proposed algorithm presents a good dynamic response with minimized torque ripple and a constant switching frequency. A fixed-switching-frequency SMC is proposed in ^[191,192]. In ^[191], an integral SMC is presented as an inner control loop of the TSF method to mitigate the torque ripple. In ^[192], an integral SMC is proposed to acquire a fixed switching rate and low sampling rate for mutually coupled SRM and asymmetric bridge converters. An adaptive SMC is suggested in ^[193] to improve the performance of SRM.

Additionally, a modified technique is adaptive to identify the combined uncertainties, enhancing the robustness against coefficient uncertainties and other external disturbances. Moreover, the suggested control employed the Lyapunov theory to investigate the stability. A PWM super-twisting SMC for SRM with a fixed-gain construction is presented in ^[194] to achieve appropriate reference tracking and torque ripple minimization. A digital SMC-based robust model-free PWM current control technique of SRM is presented in ^[195]. The suggested method enables the total reduction of the phase inductance or flux-linkage identification process. Besides, this method accurately tracks the reference phase current at a consistent switching frequency. It presents a powerful tracking response during a wide operating range of the SRM with low current ripple.

Comparison of current control methods for torque ripple reduction

The current control strategies for SRMs are developed to exploit their specific characteristics for EV applications. These strategies can be divided into two major sections with subsections that aim to mitigate the torque ripple of SRM, as depicted in Figure 7. Here is a comparison of several typical SRM current control strategies regarding advantages, limitations, model information, complexity, and switching frequency, as shown in Table 2. The model-independent methods like current hysteresis control are the most common due to their simplicity and effectiveness in tracking the current profile without the need for the model information. However, it provides variable switching frequency, may produce a high current ripple, and can present fixed switching frequency, but it requires data and extensive training. On the other hand, model-based methods like MPC and sliding mode control offer an optimal current profile, low torque ripple, and enhanced efficiency while considering nonlinearities. However, they require accurate motor models and involve higher computational demands.

5.   Conclusions

To fulfill the growing demand for effective and sustainable transportation solutions, electric vehicle (EV) propulsion systems have grown quickly. SRMs have captured significant attention for EV applications due to their inherent simplicity, robustness, high reliability, and rare-earth-free composition. However, the SRM encounters numerous challenges requiring the widespread adoption of innovative solutions. Among the primary issues is the torque ripple issue resulting from its inherent structure, which can lead to noise and vibration that affect the SRM performance for EV applications and constraints further developments. Therefore, to achieve the requirements of the propulsion system in the EV market, the performance of SRM must be outstanding with low torque ripple and high energy efficiency. As a result, the improvements in modeling and simulation techniques are crucial for accurately predicting motor performance and optimizing design parameters to minimize these effects. Furthermore, developing advanced control strategies is essential to mitigate torque ripple and improve the efficiency and reliability of SRMs. Additionally, the innovations in power converter topologies for SRMs in EVs can lead to more compact, efficient, and cost-effective solutions.

This review paper presented a comprehensively survey and analyzed torque ripple mitigation strategies in SRMs. It discusses the converter topologies' switching angle schemes and focus on control strategies to minimize the torque ripple. Each strategy's effectiveness, advantages, and limitations are critically assessed, considering factors such as torque ripple, efficiency, implementation, and computational complexity in real-world applicability. Besides that, it discusses methods developed by the researcher. It summarizes the research status and predict future research directions, aiming to guide for improving low-noise SRM drives in EV applications.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest in this paper.