Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review

1.   Introduction

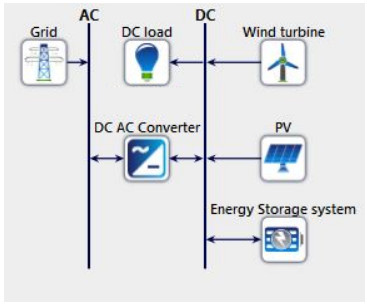
The concept of microgrid was proposed several years ago due to the integration of DERs ^[1]. In recent years, the DC microgrid has become more attractive compared to the AC microgrid for two reasons. Firstly, most residential and office loads are based on electronic DC loads such as televisions, computers, printers, laptops, phones, tablets, and LED lighting. Secondly, DERs such as photovoltaics, batteries, and small wind power have DC coupling. Therefore, using DC-DC converters in DC microgrids is a more efficient technique for connecting the DERs to the load directly instead of indirectly integrating the DERs to the load through an AC microgrid that utilizes AC-DC and DC-AC transformations ^[2,3,4,5]. The typical architecture of a DC microgrid is shown in Figure 1 ^[6]. Because the DERs are decentralized and connected to the point of common coupling in DC microgrids, several control issues of interfacing parallel-connected DC-DC converters with maximum power point tracking, voltage control, and load current sharing are encountered. Although utilizing parallel-connected converters in DC microgrids has several advantages such as power expandability, system reliability, efficiency, and ease of maintenance, the voltage regulation at the point of common coupling and load current sharing present challenging control issues ^[7,8].

Several control methods have been presented in the literature on current sharing between parallel-connected converters in a DC microgrid ^{[9,10,11,12,13,14,15,16,17,18,19,20]}. These methods can be classified into three types based on the circuit theoretic viewpoint. The first type is based on the structure of parallel-connected converters in which all parallel converters are represented by their Thevenin sources with their control based on the droop method.

In the second type, all parallel-connected converters are represented by one Thevenin source connected in parallel with Norton sources. The Thevenin source regulates the output voltage and generates a current reference for the current mode operation of the Norton sources. The second type is commonly known as master-slave current-sharing method. The third type has a structure in which Norton current sources represent the parallel-connected converters. In this structure, all converters follow a reference current signal, which is derived from an output voltage feedback loop ^[9]. In general, the first type is called a passive control method, while the second and third types are called active control methods. The second and third types need a communication link to achieve precise current sharing. A typical active current sharing method for controlling parallel-connected DC-DC converter, which uses a radio-frequency (RF) communication interface in a master-slave arrangement, is presented in ^[10,11]. One of the parallel modules, which is the master module, uses a voltage control loop to produce the reference current for all parallel converters. The reference current is sent through RF transmission. The delay due to the RF transmission on the stability is investigated to determine a satisfactory operation region. Most of the active current sharing methods for controlling parallel-connected DC-DC converters are based on a high-bandwidth communication network and are utilized in central control ^[12]. However, because the distributed energy resources in a DC microgrid are connected to the point of common coupling, it is better in terms of investment cost and data reliability to decentralize the primary control of voltage and current sharing. Therefore, the droop method has received more attention in DC microgrid due to the elimination of communication networks.

Although the conventional droop method decentralizes the parallel modules' control, its voltage regulation and current sharing are the main drawbacks ^[13]. Therefore, several improved droop methods have been presented in the literature to enhance the load current sharing and voltage regulation ^{[14,15,16,17,18,19,20,21]}. The most effective approach presented in the literature is based on updating the parallel-connected converters' droop gain. This approach generally is called adaptive droop control ^[14]. The adaptive droop control method requires knowledge of converter currents that are shared between the parallel-modules by a low bandwidth communication scheme.

Furthermore, low bandwidth communication is used as well to exchange information between parallel converters to improve load sharing and restore the voltage of the common DC bus ^[15]. The required voltage and current data are sent to the other control system of the other converters to achieve a precise load sharing current and voltage restoration. Virtual resistance (VR) droop methods have been presented in ^{[16,17,18,19,20]}. These methods are based on a communication network to determine the virtual droop gain, which improves load sharing and voltage regulation. A tertiary optimization control for parallel-connected DC-DC converter has been proposed in the literature to enhance the virtual resistance droop method's efficiency ^[16]. By varying the virtual resistance, adjustments in load current sharing between the converter can be made. Stability analysis is studied to demonstrate the effectiveness of varying VR on the dynamic performance of the system. The tertiary optimization control which is based on a hierarchical control system (centralized control) needs a communication network. Another virtual resistance method is presented in ^[17]. The virtual resistance method is based on the droop index algorithm to minimize the circulating current and improve the load current sharing differences between parallel-connected converters. For the droop index algorithm, a virtual resistance value is calculated based on the output voltage mismatch at the output of the converters and normalized current sharing. Minimization of circulating current is achieved, and the load current is improved during the transient and steady-state conditions. While the droop index is calculated instantaneously using the measurements of the output currents and voltage for each converter, a communication network is required. In ^[18], a low bandwidth communication network is used in a three-level hierarchical control algorithm. The three-level hierarchical control algorithm is used to minimize the mismatch in the output voltage of the parallel-connected converters due to the droop method. However, the effect of the cable resistance connecting the outputs of the converters to the DC bus is not considered. A decentralized controller is presented in ^[19], which is based on the droop controller. The voltage in DC microgrid varies due to changes in the load. Thus, achieving current sharing in the converters is challenging. The problem can be alleviated by using another control loop, which uses low bandwidth digital communication between the converters. Another virtual droop gain which is based on an adaptive droop control method is presented in ^[20]. The method uses instantaneous virtual resistance to eliminate the voltage difference and minimize the current sharing difference when a different cable resistance is presented. However, the instantaneous virtual droop gain is calculated using the normalized current sharing differences and the losses in the converters' output side, which are a function of the individual output voltage and current for both converters. This approach requires a communication link between parallel-connected converters. An offline approach based on optimal values of droop resistances is obtained from minimizing the total current sharing error using the particle swarm optimization (PSO) technique ^[21]. However, the approach is associated with a heavy mathematical burden and takes a long time to find the optimal values.

Approaches that use modified droop control methods without communication to control active and reactive power in AC microgrids are presented in ^{[22,23,24,25]}. However, an alternative droop without communication proposed in this paper is for DC microgrids. The proposed method is utilized to overcome the drawbacks of using communication network and offline optimal droop gain computation in DC microgrid. The alternative droop method overcomes the issues of current sharing and voltage regulation. The proposed method's implementation is based on developing the modified droop method, including the cable resistance and the control algorithm technique. The unequal current sharing, which is due to the cable resistance mismatches, is dynamically improved by implementing a virtual droop gain. The virtual droop gain compensates for the cable resistance mismatches, which connects the two converters to the point of common coupling. A proper load sharing in both transient and steady-state conditions is achieved. The common DC bus voltage is restored using an adaptive voltage gain that estimates the voltage at the common DC bus and shifts the droop gain up or down depending on the load condition to ensure a constant voltage at the load bus. The proposed method is compared with the modified droop method and the control algorithm technique. The comparative results show that the improvement in the system's dynamic responses and restore the voltage at the point of common coupling is achieved by the proposed method. Furthermore, precise load current sharing for the proposed method is achieved with a better dynamic response in comparison to the modified droop method and control algorithm technique. The dynamic performance of the proposed method is tested by using MATLAB simulation and validated using experimental results.

2.   Limitation of conventional droop control method in a DC microgrid

The load regulation characteristics of parallel-connected converters in a DC microgrid affect the voltage deviation of the point of common coupling and the load current sharing. To illustrate, a standalone DC microgrid is constructed by two parallel-connected converters, two cable resistances, and a load resistor, as shown in Figure 2. The two converters are simplified by Thevenin equivalent. They are connected to the common DC bus through cable resistances. The output voltage for each converter, which is based on the droop control method, is given by

where ${V}_{dcn}$ is the output voltage of converter$n$, ${V}_{NLn}$ is the no-load voltage of converter $n$, ${K}_{n}$ is the droop gain of converter $n$, and ${I}_{n}$ is the output current of converter $n$.

The voltage at the common DC bus based on Figure 2 can be derived as

It can be observed from Figure 3(a) that a small mismatch in the parameters of the parallel-connected converters causes unequal load current sharing between parallel modules. The mismatch in the parameters of the parallel module could result from manufacturing tolerance. Therefore, if the voltage at the common DC bus is ${V}_{bus}$, the current sharing for converter Ⅰ and converter Ⅱ are ${I}_{1}$ and ${I}_{2}$ respectively, which are unequal. Furthermore, the increase in loading changes the operating point from ${V}_{bus}$ to ${V‘}_{bus}$, and the load current sharing ${I‘}_{1}$ and ${I‘}_{2}$ are still unequal. Moreover, if the cable resistances that connect the parallel modules to the common DC bus are different, the load current sharing is degraded, as shown in Figure 3(b). If the cable resistance ${R}_{c2}$ is greater than the cable resistance ${R}_{c1}$, the load current sharing for converter Ⅰ and converter Ⅱ are degraded from ${I}_{1}$ and ${I}_{2}$ to ${I‘}_{1}$ and ${I‘}_{2}$ respectively. In other words, the differences in cable resistance worsen the load current sharing according to the load regulation characteristic of each converter. Furthermore, the third limitation of the droop method is the voltage deviation. According to (1)-(3), the droop gains for converter Ⅰ and Ⅱ cause the output voltage to decrease when the load current increases. Figure 3(c) shows the load regulation characteristics of two parallel modules with different droop gain ${K}_{1}$ and ${K}_{2}$. However, the voltage deviation increases when the droop gain is higher, as shown in Figure 3(c). Therefore, the droop gains ${K‘}_{1}$ and ${K‘}_{2}$, which are higher than ${K}_{1}$and ${K}_{2}$ for converter Ⅰ and converter Ⅱ, respectively, increase the voltage deviation for the same load currents.

3.   Droop control method

The main purpose of the droop control method is to control parallel-connected converters for achieving equal load current sharing and maintaining acceptable voltage at the point of common coupling. In DC microgrid, the point of common coupling makes the droop control method more attractive compared to the active current sharing methods. In this section, an overview of the modified droop method, including the cable resistance and control algorithm technique, is summarized ^[26,27]. Since the alternative droop strategy utilizes the modified droop method and control algorithm technique, it is presented and explained accordingly in this section.

3.1.   Modified droop control method

The modified droop method with cable resistance implementation is reported in ^[26]. The method is used to estimate the voltage set point for each controller according to the converters' droop characteristics. The first step for estimating the voltage set point uses the measurements of voltage and current at the common DC bus to determine the load resistance as

The modified droop method including cable resistances estimates the load current sharing, which determined by solving Eqs (2), (3), and (4) as

The voltage set-points for the parallel-connected converters are determined based on the estimated current sharing values and the common DC bus voltage. The set-point of the output voltage of each converter is determined locally without transmitting voltage and current data from one converter to the other as

The block diagram and flowchart for estimating current sharing and the output voltage set-point of the modified droop with cable resistance are shown in Figure 4 and Figure 5, respectively.

3.2.   Modified droop method with control algorithm technique

Another loop control that is added to the modified droop method is reported in ^[27]. The addition loop control is responsible for ensuring a precise current sharing when there is a mismatch in parallel modules' parameters. It compares the current sharing for each converter with the load current. If the percentage of current sharing for converter Ⅰ is lower than 50%, an additional $\mathit\Delta V$ is added to the converter's set point to increase its current sharing to the load current, and vice versa. A small value $\mathit\Delta V$ is chosen to prevent an oscillatory output current. Figure 6 shows the block diagram of the modified droop method along with the additional control algorithm.

3.3.   The alternative droop control method

In the proposed approach, two gains are added to the modified droop control method. These gains are a virtual droop gain VDG, and an adaptive voltage control gain AVCG. The virtual droop gain can improve the system's dynamic response for load current sharing between parallel modules and the adaptive voltage control gain can regulate the voltage. First of all, the virtual droop gain can be added to the droop Eqs (2) and (3) as

where ${K}_{v1}$ and ${K}_{v2}$ are the virtual droop gain for converter Ⅰ and Ⅱ, respectively. The virtual gains can be selected based on the differences in cable resistances. To illustrate, Figure 7(a) shows the load regulation characteristics for two parallel-connected converters. The cable resistances ${R}_{c1}$ and ${R}_{c2}$ connect converter Ⅰ and Ⅱ to the common DC bus, and ${R}_{c2}$ is greater than ${R}_{c1}$. Thus, according to the droop method, converter Ⅰ experiences higher current compared to converter Ⅱ.

Since the current sharing between the two parallel-connected converters is unequal, the values of ${K}_{v1}$ and ${K}_{v2}$ can be chosen based on the cable resistance compensation. To retrieve the original load regulation characteristics, the virtually gains ${K}_{v1}$ and ${K}_{v2}$ can compensate for ${R}_{c2}$ and ${R}_{c1}$ respectively as shown in Figure 7(b).

Secondly, the adaptive voltage control gain is determined based on the estimated voltage at the common DC bus, which is determined from the modified droop method and compared with its rated value. Thus, The AVCG can be determined as

For various load conditions, the voltage at the point of common coupling PCC is regulated by using its estimated value, as shown in Figure 8.

The steps that are used to regulate the voltage at the common DC bus by utilizing the AVCG are:

1-Measure the voltage at the PCC (${V}_{L}$) and the total load current (${I}_{L}$). The load resistor can be determined as given in Eq (5)

2-Based on the modified droop method with cable resistance implementation, the estimated output current for converter Ⅰ and converter Ⅱ can be determined by using Eqs (6) and (7).

3- The estimated voltage (${V}_{CC}$) at the common DC bus can be obtained as

The AVCG can be determined by using Eq (12). Thus, if the AVCG has a negative value, the droop method's load characteristic regulation is shifted up to a newer load characteristics regulation, as shown in Figure 8. Since the measurements are at the point of common coupling point, the AVCG has the same value for the two boost converters' local controller. Thus, the newer load characteristics regulations for both converters are shifted from the load regulation characteristics synchronously. The voltage position ensures that the voltage at the point of common coupling is at the rated value. However, suppose the AVCG has a positive value. In that case, the droop method's load characteristic regulations, for both converters, are shifted down to a newer load characteristics regulation, as shown in Figure 8. Therefore, the newer load characteristic regulation adjusts the voltage at the point of common coupling synchronously to the required value, which is the rated voltage for the DC microgrid. The block diagram for implementing the proposed approach, which improves the dynamic response of the unequal current sharing due to different cable resistances and voltage deviation, is shown in Figure 9.

4.   Simulation results

The Matlab/Simulink environment is used to demonstrate the effectiveness of the alternative droop method. The parameters of the system are given in Table 1. The boost converter parameters are determined based on the continuous current conduction mode of operation ^[28].

Furthermore, the voltage and current PI controllers in Figure 4, Figure 6, and Figure 9 are designed based on the state space averaging technique ^[29]. The SISOTOOL in MATLAB is used to determine the parameters of the PI controller, which are given in Table 2 ^[30].

The droop gains for converter Ⅰ and converter Ⅱ are determined based on two operating points, which are the no-load and full-load voltage and current ^[31,32]. The values for the droop gains ${K}_{1}$ and ${K}_{2}$, which are used in the simulated and experimental modules, are 0.8133 and 0.8182, respectively. In this paper, different cable resistances are selected: the values of ${R}_{c1}$ and ${R}_{c2}$ are equal to 0.2 Ω and 0.1 Ω, respectively to verify the effectiveness of the proposed method. Thus, the virtual gains are selected to compensate for the differences in the cable resistances ${R}_{c1}$ and ${R}_{c2}$. The values of virtual gains ${K}_{v1}$ and ${K}_{v2}$ are 0.1 and 0.2 respectively. Furthermore, two different values of load resistances are used to compare the performance of the proposed method compared to the modified droop method. However, in the Matlab simulation study, three cases are tested to demonstrate the feasibility of the proposed method. Case-1 presents the results of the modified droop method based on the block diagram of Figure 4. Case-2 presents the modified droop method with a control algorithm technique shown in Figure 6. Case-3 presents the results of the proposed method shown in Figure 9.

In Case-1, the voltage and current sharing responses between the two parallel-connected converters are tested with an increase in the load from 15.51 Ω and 13.804 Ω. The transient responses of the current sharing for converter Ⅰ and converter Ⅱ and the total load current are shown in Figure 10. The step increase in load occurs at 3 seconds. It can be noticed that the load current for the two parallel-connected boost converters is not shared equally.

Furthermore, the transient responses of the output voltage for converter Ⅰ and converter Ⅱ and the load voltage for the step increase in the load are shown in Figure 11. It can be observed that when the step increase in the load is placed, the voltage at the load or common DC bus decreases, which is the main drawback of the conventional droop method.

The steady-state values for the output voltage of converter Ⅰ and converter Ⅱ, the voltage at the common DC bus, load current sharing, and the percentage deviation of the current sharing for case-1 are shown in Table 3.

It can be observed from Table 3 that the voltage drops from 11.97 V to 11.925 V at the common DC bus when a step increase in the load is applied. Furthermore, the load current sharing is unequal due to the mismatches in the converters' parameters and the differences in cable resistances.

In Case-2, the control algorithm is implemented with the modified droop method. The block diagram in Figure 6 is simulated using MATLAB/Simulink environment. For the same load condition in Case-1, the output currents transient response for converter I, converter Ⅱ and the total load current are shown in Figure 12.

Although the load current is shared equally between the parallel-connected boost converters, as shown in Figure 12, the common DC bus's output voltage is dropped, as shown in Figure 13.

It can be observed from Figure 13, and the load voltage drops from 11.96 V to 11.92 V. The steady-state values for the output voltages and currents for converter Ⅰ and converter Ⅱ and common DC bus's voltage are given in Table 4.

From Table 4, the steady-state values of the output currents for converter Ⅰ and converter Ⅱ are equal, but the voltage at the common DC bus (load voltage) drops from 11.96 V to 11.92 V due to the droop action. Thus, including the control algorithm with the modified droop method can enhance the load sharing, but it does not restore the voltage at the common DC bus to its rated value (12 V).

To compare the proposed method with the modified droop control method and the modified droop method with control algorithm, the block diagram of the proposed method in Figure 9 is simulated using MATLAB/Simulink environment. The results are based on the same loading condition and cable resistances in Case-1 and Case-2. In Case-3, the cable resistances that connect each converter to the common DC bus are considered as 0.2 Ω and 0.1 Ω for ${R}_{c1}$ and ${R}_{c2}$ respectively. The values of the virtual droop gain are set at 0.1 and 0.2 for ${K}_{v1}$ and ${K}_{v2}$ respectively. Different load resistances are used to test the performance of the proposed method. The transient responses for the current sharing accuracy enhancement of converter I and converter II along with the load current are shown in Figure 14, where 15.51 Ω and 13.804 Ω load resistances are applied, respectively.

From Figure 14, it can be observed that the output currents of the parallel-connected converter are equal for different loading conditions. Furthermore, the proposed method restores the voltage at the common DC bus. The response of the output voltage for converter Ⅰ and converter Ⅱ and the common DC bus voltage are shown in Figure 15. The voltage at the common DC bus is restored when a step increase in the load demand is applied.

The steady-state values of the simulated results for the proposed method given in Table 5 show that the current sharing accuracy is enhanced, and the voltage at the common DC bus is restored to its rated value.

The comparison between the steady-state values of the load current sharing and the voltage at the common DC bus for the three cases indicates that the proposed alternative droop control method shows an improved performance over the modified droop method and the modified droop method with control algorithm. Although the modified droop method with control algorithm provides a precise load current sharing, it has poor voltage regulation at the common DC bus. The performance of the modified droop method with control algorithm degrades as the mismatches of the cable resistance increase. To illustrate, the block diagram of the modified droop method with the control algorithm, as shown in Figure 6 is simulated using MATLAB/Simulink environment for larger differences in the cable resistances compared to the used values of the previous cases. The cable resistance values of ${R}_{c1} = 0.4\mathrm{ }\mathrm{\Omega }$ and ${R}_{c2} = 0.1\mathrm{ }\mathrm{\Omega }$ are used to connect converter I and converter II respectively to the common DC bus. The results are compared with the proposed alternative droop method, which uses virtual droop gain of ${K}_{v1} = 0.1$ and ${K}_{v2} = 0.4$. The comparison considers the same load condition and the same value of $\mathit\Delta V$ for regulating the common DC bus. Figure 16 shows the dynamic response for the load current sharing of the control algorithm in comparison to the alternative droop method.

From Figure 16, it can be observed that the dynamic response of the alternative droop method is better than the modified droop with control algorithm. The required time to reach a precise load current sharing for the alternative droop method is 0.2 seconds compared to 2.3 seconds for the modified droop method with control algorithm. After a step increase in the load, the alternative droop method also tracks the operating point faster than the modified droop method with control algorithm. The main reason for improving the dynamic response of the proposed is the utilization of the virtual droop gains, which compensate for the large mismatches of the cable resistance. The virtual droop gain shortens the time to reach the desired operating point, which enhances the dynamic response of the parallel-connected converter system. From Figure 16, the output currents of converter Ⅰ and converter Ⅱ for the proposed method are slightly higher than the output currents of the modified droop method with control algorithm because the proposed method restores the voltage at the common DC bus to its rated value of 12 V.

5.   Experimental validation

To validate the proposed alternative droop method, a laboratory prototype of two boost converter is implemented, as shown in Figure 17. In real-time control, the simulated model is compiled by dSPACE 1104. The parameters of the two boost converters that are given in Table 1 are used. Furthermore, to test the proposed control method, different cable resistance of 0.2 Ω and 0.1 Ω are used to connect converter Ⅰ and Ⅱ respectively to the common DC bus. Two different load resistance of 15.51 Ω and 13.804 Ω are employed respectively, to compare the simulated MATLAB module with real-time implementation.

Since the signal applied to DSPACE 1104 A/D channel is limited to ± 10 V, the voltage and current sensors' measurements have a conversion ratio of 30-10 V and 10-1 V, respectively, and software protection in Matlab/Simulink is used to prevent signals greater than ±10V. Moreover, because the D/A channel of the dSPACE 1104 is limited to ±10 V, a gate driver is used to provide PWM of 15 V and isolate the dSPACE 1104 from the actual hardware. Initially, the load is set to 15.51 Ω. The output current for converter Ⅰ and converter Ⅱ and the load current is shown in Figure 18. When a step increase in the load from 15.51 Ω to 13.804 Ω is applied, the transient response for the proposed method validates the accuracy of current sharing between the two converters, as shown in Figure 18.

The output voltage waveforms of converter Ⅰ and converter Ⅱ and at the common DC bus are shown in Figure 19. It can be observed that the voltage at the common DC bus is kept at a rated value of 12 V during the step change in the load.

For the two load resistance values of 15.51 Ω to 13.804 Ω, the steady-state values of the load current sharing and the voltage at the common DC bus along with the estimated value of the voltage by the proposed method are given in Table 6. The percentages of current deviation that is carried out from the real-time implementation validate the proposed method.

Furthermore, the estimated voltage by the proposed method is observed as shown in Table 6. The value is used to adjust the regulation characteristics of the droop method. Therefore, the voltage at the common DC bus or load is maintained at its rated value during different load conditions.

6.   Conclusion

The alternative droop method for controlling parallel-connected converters is presented. The proposed method enhances current sharing by implementing the virtual droop gain, which modifies the regulation characteristics of the droop method. Furthermore, the adaptive voltage control gain restores the voltage at the common DC bus at its rated value. The adaptive voltage control gain used the estimated voltage at the common DC bus to shift the droop method's regulation characteristics. The alternative droop method is compared with the modified droop method and the modified droop method with control algorithm. The results show that the alternative droop method is better than the modified droop method in terms of voltage restoration and precise load current sharing. The proposed method's performance is also better than the modified droop method with control algorithm in terms of the voltage restoration and the dynamic response of reaching precise load current sharing. The alternative droop method is verified using MATLAB/Simulink, and the experimental validation of the simulated method is proved.

Acknowledgments

The authors would like to thank the Libyan government for funding this research.

Conflict of interest

All authors declare no conflicts of interest in this paper.