1.
Introduction
The fundamental assumption underlying the dynamics of stock markets is the stochastic behavior of traders, which determines the market values of equities in the same manner. Bachelier was the pioneer to model the Brownian processes in 1900 even before Einstein (1905), and applied it to study financial systems (Davis and Etheridge, 2006). He proposed that the price of assets can be described as a stochastic process, he used Brownian motion for valuing stock options, but, his work was forgotten until rediscovered in 1950s. After him, the random walk mathematics was made more rigorous by Wiener, and since then it has been quite often used to explain numerous physical processes.
The financial mathematics is essentially based on the stochastic behavior of stock markets, and probability theory is quite often used to make computations and future estimates. By the same token, the various types of applications of the Boltzmann-Liouville theory of statistical mechanics, the Langevin equation, the Fokker-Planck equation, Markovian process, Lévy flight process, and the Chapman-Kolmogorov equation finds applications in mathematical finance. In fact, the famous Black-Sholes equation is derived using the analogy with the Fourier's heat-transfer equation and the Fokker-Planck equation (Richmond et al., 2013, Neftçi, 2000). Brownian motion does not permit the incorporation of jumps in stock markets, and the models which include Lévy processes offer a better description of such sharp changes (Courtois and Walter, 2014).
The fractal theory and scaling introduced by Mandelbrot opened a new door in financial systems as well as in all natural and social systems to recognize chaos as a kind of hyper order (Mandelbrot, 1983; Mandelbrot, 1997). There have been efforts in the past to use chaos theory and fractal structure in conjunction with other theories to analyze financial systems (Yu, 2013). Besides the chaos theories some other methods like path integrals and different entropy concepts imply that some basic physical principles are needed to explain the stock price dynamics (Montagna and Nicrosini, 2002; Matteo, 2007; Jiang and Gu, 2016; Hattori and Abea, 2016; Ya, 2010). The "econophysics" coined by Stanley now has been a new discipline to use physical concepts and methods to study financial systems (Mantegna and Stanley, 2000).
Assuming that stochastic processes are fundamental facts of markets the question then arises on how we can explain the Elliott waves in a variety of markets. Elliott's descriptions are empirically-derived sets of rules to interpret market dynamics, which, essentially fluctuate due to a number of reasons, and traders' psychology to optimize their benefits create some kind of well-defined patterns. The description depends on some assumptions which are difficult to analyze (Gehm, 1983). The behavior of people swings through trends and reverses, no matter whether it takes place in ten-minutes or ten-years interval of time, and exhibits some patterns which are called Elliott waves. There occur cycles, super-cycles, and grand super-cycles in the market. Cycles are composed of two major components, one "impulse wave" which can be subdivide into five waves (shown by 1-2-3-4-5) and the other the "corrective wave" subdivided into three waves (shown by a-b-c) (Frost and Prechter, 1999; Greenblatt, 2013; Kirkpatrick and Dahlquist, 2010). There are severe attempts to use Elliott wave patterns to make future forecasting through the tools of fuzzy logic, neural network, artificial intelligence, etc. (Chen et al., 2007; Magazzino et al., 2012; Tirea et al., 2012; Kotyrba et al., 2013; Volna et al., 2013; Wang et al., 2013; D'Angelo and Grimaldi, 2017, Marañon and Kumral, 2018; Patel and Modi, 2018). It was shown that Elliott waves could be generated as the trajectories of fractional Brownian motion, such that the generator has a Hurst parameter close to zero (Ilalan, 2016).
Elliott waves are intrinsically related to Fibonacci numbers and golden ratio (Frost and Prechter, 1999; Casti, 2002; Chatterjee et al., 2002; Atsalakis et al., 2011; Glover et al., 2013). Elliott waves are commonly used as technical analysis tools to make future predictions (Vishvaksenan et al., 2016; Tirea and Negru, 2016; Kyal, 2017, 2018; Chendroyaperumal, 2011; Ribeiro, 2019; Sattari, 2020). It could also be combined with other methods for more advanced predictions (Reich, 2017; Goodman, 2017; Duan et al., 2018; Ramli, 2018; Ivanova, 2019). In technical analysis the terms "support/resistance" are used to mean that asset price tends to cease and reverse its trend to decrease or increase, respectively. Fibonacci numbers describe the sequential growth of living organisms, historically, to calculate the growth of rabbit populations in the wild. The population growth occurs through autocatalysis, i.e., the present number multiplies itself. Autocatalysis in financial systems was described in the past in relation to graph theory and especially on the formation of networks, but not in relation to the physical dynamics (Jain and Krischna, 2003; Caetano and Yoneyama, 2015).
Autocatalytic behavior in asset prices originates both from the nature of asset and the self-oriented behavior of customers. The people would naturally think of their daily and future endeavors and plan their investments accordingly. They would like to buy those assets of which price tends to increase due to any reason such as technological, climatic, home or international political situation, etc. Autocatalysis occurs in different manners in different systems. In living organisms, the off-springs contribute to the multiplication of population, i.e., the organisms multiply themselves; in saving account the amount of interest gain turns out to be the amount of multiplication by the end of the term; in forest fire it is the exothermic energy which is multiplied as a greater number of trees are burnt per unit time. In finance, autocatalysis first occurs at the customers' profit stage. Everybody wants to get more by selecting out certain type of assets. It then occurs at the asset value stage as its price increases due to demand, that is, the value of the asset increases in time. Thus, the collective behavior of customers for massive buys and sells results in massive fluctuations which creates a kind of wave in financial systems. The wave generation is common in competitive systems. For instance, in the autocatalytic Lotka-Volterra system having "grass-rabbit-fox" as the system elements the timely change of rabbit and fox populations follows oscillating curves with a time lag in between. The increase of the number of preys and predators in the system results in further cycles and so new additional periodicities. The system may even go to chaos depending on the system parameters, mainly the initial populations, birth rates, etc. The chaotic behavior in financial systems and the related scaling relations also indicate that there might be a kind of order originating from the dynamical structure. In fact, even Brownian motion has scaling relations (Peitgen et al., 1992). The competition among multi component systems produces mixed wave-like and chaotic behavior. In the limit, the strong turbulence or chaos in the system enhances the Brownian behavior which then becomes highly dominant while wave-like behavior is depressed.
In all studies done in the past the financial systems were considered to be a stochastic system and statistical methods were heavily used to analyze them. The use of statistical mechanics and chaos theories naturally introduced a new impact in the field, but yet the hard-core physical concepts like energy is not an issue in scientific research. The use of entropy in financial systems is related to the statistical properties and not to the time dependent dynamical behavior. The physical and mathematical basis of the of Elliott waves in financial systems also has not yet been understood. The stability and instability issue in stochastic systems cannot be easily grasped without using the thermodynamic concepts. To address all these hard-core physics approach has been used here. First the theoretical basis of wave behavior was established. Then the dynamic energy and entropy changes were discussed by using the theory of viscoelasticity. The randomness and the wave-like behavior in financial systems was studied on equal footing, and their interplay on the stability and instability was discussed by tracking the states which can be expressed in terms of golden ratio. Finally, the physical and the mathematical grounds of Elliott waves and golden ratio was established.
2.
Fluctuations
The price of an asset may change up and down at varying magnitudes, and let us show the distribution of fluctuations by f. It changes with time t, current price μ per share, and also with velocity v, i.e., with the velocity of the change of price. The distribution f(t,μ,v) at time t goes to f(t+dt,μ+dμ,v+dv) at time t+dt. New shares are not frequently issued in stock markets. Assume the number of shares is constant in dt, one can write,
The Taylor expansion of the right-hand side about dt=0, and its truncation gives,
If new shares are issued anytime this equation need to modified as,
For simplicity we can drop the new issues and go with Equation 2.
There are a vast number of assets in the market and correspondingly there are too much fluctuations in their values due to the activities of traders. Let us consider a target asset and show its distribution function at time t by ˉf(t). At time t+dt its distribution becomes f as it is traded, and its market value either increased or decreased depending on in what direction it is traded on the average. If we show the extent of fluctuation (i.e., the change in dt) by f′ we can simply write that f=ˉf+f′. Let us define an averaging operator A; when it operated on f it gives (Weinstock, 1969; Dupree, 1966; Gündüz, 1979; Gündüz, 1996),
It is clear that, Af′=0, and (1−A)f′=f′. Equation 2 can now be split into two equations by operating on Equation 2 by A and (1-A), such that,
In these equations L is a linear operator defined by,
where v=∂μ/∂t represents the velocity of the change of asset value, and φ is a unit force term as ∂v/∂t denotes acceleration. The ˉf(t) and f′(t) terms keep changing in time, the values of ˉf(t+δt) and f′(t+δt) depend on ˉf(t) and f′(t), respectively. Therefore, we can define a time propagator U(t,t0) to be a solution of,
Dupree originally introduced this type of propagator to elucidate strong turbulence problems in plasma physics, and Weinstock further improved this technique (Dupree, 1966; Weinstock, 1969; Gündüz, 1979). We can use Equation 9 to solve Equation 7, and after a few steps one gets,
The substitution of Equation 11 in 6 yields,
We now operate on L(t) by A and (1−A), and get,
Equation 12 can be put into a more useful form, and this was done in Appendix-A. The new form is (Equation (A-9)),
This equation is of non-Markovian nature, because, the last term depends on t1 rather than the running time t. U(t,t1) propagates μ and v backwards in time over the trajectories of Equation 9; and the system owns has a kind of memory. The substitution of Equation 15 in Equation 16 gives,
where the first term on the right-hand side was omitted as it denotes the very initial state. Meanwhile A before the integral sign was also dropped as it operates on ˉf(t1). Defining,
one can rewrite Equation 17 as,
Equation 17 entails that ˉf(t) picks up the fluctuations and grows in time when it has tendency to grow. It may also go in the opposite direction if an instability breaks up in the system.
For a while, let us assume a very short interval of time such that the system variables do not change significantly. Then, we have near-equilibrium state, so that ∂ˉf(t)/∂t→0. Let us also assume that the change of ˉf with respect to μ is very small or negligible. By the same token, ∂v(t1)≈∂v(t), and also U(t,t1)≈1. Thus, we get only the last term on the right-hand side, and it denotes the contribution of fluctuations. This is a time independent case, and so we have D=φ2. Since U(t,t1) propagates μ and v backwards in time, the integration of the last term of Equation 19 yields,
where k is a constant. The solution of this equation is simply,
where ω=k/φ. It is seen that an oscillatory trigonometric function (i.e., cosine function) can describe the distribution function of a fluctuating system at its equilibrium state (or steady-state). What actually happens is that our target asset picks up the small fluctuating waves persistently occurring in the market and its value changes accordingly. In case if its value decreases then if feeds back other assets, i.e., traders go and buy the other assets. That is, ˉf changes by f′ in positive or negative direction depending on the activities of traders.
3.
Force, energy, and entropy
3.1. Conservative and dissipative energies
In this section the change in asset values will be studied not by distributional or statistical methods but by using the concepts like viscoelasticity, thermodynamic energy etc., and the distributional properties will be treated back in the next section. Hence, the way how distributional dynamics consolidates macro dynamics will be explained.
Since φ is a unit force term there is a direct relation between the force and the asset value. However, the essential question here is to define the force in financial systems. Whatever affects the stock markets something like industrial or agricultural productions and sales, climatic conditions, domestic or international policies, strikes, wars, political crises, etc. their overall effects show up as the change in the price of asset values. All these effects in the large scale are reflected as the change in stock market index. Thus, the effect of force term is somehow embedded in the change of asset values or in the change of stock market index. In this research S & P-500 stock market index was used as case study.
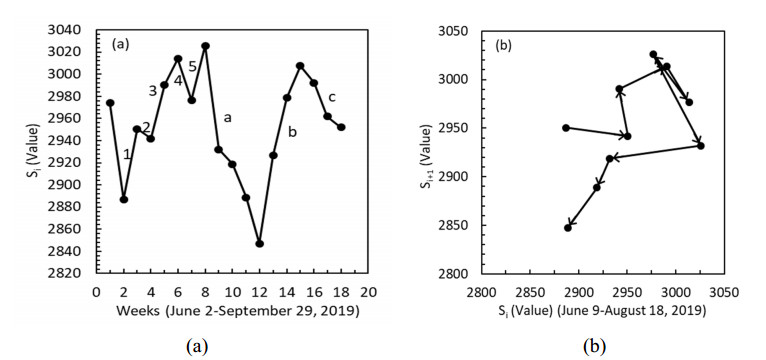
Figure 1a shows randomly scattered data, but we may also think of its pattern to imply the existence of Elliott wave even though we need a larger picture for a correct decision. The numbers 1 to 5 may represent the motive phase while the letters "a" to "c" may represent the corrective phase. Anyway, the discussion on Elliott waves will be considered in Section 4 & 5. We now consider only the scattered aspects of data.
Whatever affect the markets are reflected as the magnitudes of data. However, there is not one-to-one correlation between the magnitude of cause and the magnitude of its outcome. For instance, consider a terrifying volcanic eruption or decision to cut the crude oil production world-wide by some percent. The repetitions of these actions by the same magnitude do not influence the affected asset prices or the market index by the same repeating ratio of magnitude. However, since the index is influenced from the events, the effects of consecutive cumulative events can be observed from the consecutive values of market index. Two consecutive index values (i.e., Si and Si+1) can be simply related to each other by a simple equation,
where G is a constant.
In physics, if there is a change then there exists a flux associated with it. For instance, heat flow (Fourier's law), mass flow (Fick's law), chemical reaction (Gibbs' law), electric current (Ohm's law), and deformation (stress-strain equation) all have the same mathematical structure which can be simply expressed as,
where J denotes the flux, X the driving force, and 1/L is a phenomenological constant relating force to flux (or current). This mathematical form has its roots in the discourse of ancient philosophers Heraclitus and Aristotle. Heraclitus' nature is very dynamic and keeps changing indefinitely as expressed by his famous statement "everything in nature is in flux (i.e., flows)". Aristotle introduced the concept of "potentiality" which is an a priori need for the events to occur in nature, and said "today's actuality is the potential of tomorrow's actuality".
Potentiality-to-actuality relation somehow looks like cause-and-effect principle, but it is much more general than that. Because, it is possible to cast even non-physical parameters into this expression. For instance, G in Equation 22 is a phenomenological constant, and if G=1 the whatever goes in comes out (i.e.Si=Si+1); the asset value or index does not change. If G>1 the output Si+1 comes out to be less than the input Si because of the loss due to several reasons. When G<1 the output Si+1 comes out to be more than the input Si because of some other additional positive inputs during the process. Aristotle's principle can be phrased for this special case as; "now" (orSi) influences "next" (orSi+1) by a proportion G. Therefore, if we plot Si+1 vs Si we can study the changes in the system more quantitatively. The scattering diagram of Fig. 1a was given in Figure 1b where less data was used for clarity.
The series data of Figure 1a is connected by arrows in Figure 1b, and thus each arrow connecting consecutive data gives information about what happened in causality domain. We have a graph diagram in Figure 1b and each vector of the graph can be associated with force and energy. Now let us consider two consecutive vectors given in Figure 2.
Since "loss" and "gain" is somehow determined by the magnitude of G in Equation 22, or by the relative magnitudes of Si and Si+1, the length of vectors and the angles between two consecutive vectors can give us information about the force and the energy involved. Note that vector AB in Figure 2 is changed or deformed into vector BC with a new length and angle between them. Therefore, we need to use the type of physics of deformable objects, that is, we need to use viscoelastic theory to evaluate the behavior displayed in scattering diagram. In viscoelastic theory, the slope of BC gives the ratio G″/G′ i.e.,
According to vector properties we may write,
Hence, by using Equation 22 one can find out the numerical value of G first, and then by using Equations 24 and 25 one can determine the numerical values of G′ and G″.
Once G′ and G″ were determined one can then compute the thermodynamic work-like and heat-like energies. The energy of the in-line motion (i.e., horizontal direction) gives work-like energy, and the one along the out-of-line direction (i.e., vertical direction) gives heat-like energy. Note that the work-like energy is conservative but the heat-like energy is dissipative. The work-like energy (w), and the heat-like energy (q) expressions can be obtained from the definitions of these energies in viscoelastic theory. The energy is defined as "energy~(stress)2/modulus" (Rosen, 19930). Hence, we can write,
In former studies the patterns of G′ and G″ depending on the magnitude of Wiener noise were studied in full detail by using produced data at varying drift and volatility and also by using the daily data for DJI, Nasdaq-100, Nasdaq-Composite, and S & P 500 for 30 years from 1986 to 2015 (Gündüz and Gündüz, 2016; Gündüz and Gündüz, 2017). In a recent article, lethargy concept which substitutes Wiener noise in the general sense was used to elucidate the pattern formations not only in stock markets (Nasdaq-100) but also in some other time series systems like uniform distribution (i.e., white noise), normal distribution (i.e., brown noise) and music (Gündüz, 2018).
Since viscoelastic theory involves deformations it is crucial to compute the extent of deformations associated with the vectors given in scattering diagram (i.e., Figure 1b). In Figure 3 several vectors with different slopes are shown, where grids were used to grasp deformation pattern visually. The gray unit cells are those through which a vector passes through. Since momentum and energy are used in the general sense to characterize the changes in the physical world, the unit cells which characterize the surface shape of vectors of Figure 3 can be studied by utilizing the surface energy of a crystal subjected to shear force.
In Appendix-B the computation of the surface energy because of deformation was given (i.e., Equation B-4). It is,
where "ℓ'" is the length of vector, "d" is the length of each side of unit cell, and "ε" is the energy of the free (or broken) surface of unit cell. This equation denotes a circle with a diameter of E=εℓ/√2d. The energy attains its maximum value of Emax=εℓ/√2d when θ=π/4=45°, because, cos(θ−π/4)=1. This is the case for "f" vector in Figure 3. When θ=0°, we get the minimum energy, i.e. Emin=εℓ/2d, and this is the case for vector "f" in Figure 3.
Vector "a" has similar energy like "f" and vector "b" like "e". We can visualize "b" as "e" provided the horizontal and vertical axes are interchanged. In other words, instead of considering the slope "m" we need to consider its inverse "1/m" when θ>45o. Then we get the right surface energy for "b" vector equal to that of "e". The same thing holds also for "a" and "f". Since slope is equal to G″/G′ according to Equation 24, we can say that the maximum dissipative situation occurs when G″=G′ (or when θ=45°, tanθ=1); vector "c" represents this case.
In scattering diagram, the vectors are connected to each other like segments in a polymer chain. An impact on a chain disturbs the closest segments, but it fades away as one gets far away from that point. A similar situation also occurs in the vectors of scattering diagram, where the consecutive ones have a strong memory while as one moves further the memory of the vectors left far behind fades out. In this respect, in the scattering diagram, we do not have short-term memory as in Markovian systems but weakened memory of the past. The calculations for the conservative work-like energy and the dissipative heat-like energy were carried out for S & P-500 daily index data from January-1-1986 to December-31-2019, and shown in Figure 4. Figure 4a shows the change of index, Figure 4b, and Figure 4c show the changes of w, and q, respectively.
The w and q values were displayed both with positive and negative signs. A vector in scattering diagram absorbs energy in the thermodynamic sense as it goes away from the origin and so the value of w increases and a positive sign is assigned, and if it moves in the reverse direction negative sign is assigned. In fact, the directional change along horizontal axis(i.e. in Δx) tells us what to be used. In the same manner, if the change in vertical axis(i.e. in Δy) is positive the vector goes upward and gains heat-like energy, and the sign is positive, and when Δy is negative the vector goes downward and loses heat-like energy and the sign is negative. However, care is needed when m>1 and negative in sign. In this case, the sign of q and w will be reversed as the coordinates are exchanged. When m>1 but positive there occurs no sign effect.
There occurs more or less a smooth increase until 2600th day from the beginning and then a peak develops in between 2600th–4353th days (Figure 4a). The change of w until 2600th day is pretty much smooth while q shows considerable fluctuations (Figures 4a and 4c). In the 2600th–4353th days interval we have serious fluctuations in w, and q shows highly turbulent fluctuations in this interval. The magnitude of fluctuations in w decreased within 4353th–5203th days and the system has the similar behavior of the first zone (i.e. 0-2600th day) but with more severe fluctuations. As seen from Figure 4b high turbulence is observed again after 5203th day till 5775th day. Therefore, the beginning of this second peak is not 4353th day but 5203th day. In other words, the extent of fluctuations tells us where the peak starts and where it ends. In fact, we have very severe change in w at 5775th day, and it is not just before minimum at 5847th day.
The change of w follows the same behavior and as seen from the remaining part of Figure 4b large magnitude of fluctuations occur whenever there occurs a sharp change in the index value. Sharp changes actually occur due to Levy flight behavior, not due to Brownian motion, but they both coexist in financial systems. The behavior of q also follows the same pattern of w with higher degree of turbulence.
3.2. Configurational entropy of vectors
The configuration of vectors on scattering diagram as mentioned earlier looks like the configurations of polymer chains. The configurational entropy of the chains is computed from the statistical distribution of the end-to-end distance. However, in a scattering diagram each vector attaches once at a time and it is an evolving system with continuously increasing number of vectors of different lengths. Therefore, the configurational entropy can be calculated in a similar manner but with a slight modification. The beginning point of the first vector can be taken as the starting point, and the end-to-end distance at each attachment of a new vector can be found out with respect to this point.
The probability distribution function of the end points at each step can be in general expressed by,
where p denotes the probability distribution, and r denotes the average end-to-end distance between the origin and the end point of the last vector. From the definition of entropy (Sent), one gets,
where k is the Boltzmann constant, and κ takes care of the first term which is a constant. Now consider only two-vector case as in Figure 2. Let r(x,y) be the distance of point C to the origin, i.e., point A. Thus r(x0,y0) denotes the coordinate points of B. We can relate r(x0,y0) to r(x,y) through the deformation matrix (λ1,λ2), such that,
Now Equation 31 is substituted into Equation 30 to express x and y in terms of x0 and y0. Equation 30 can also be expressed in terms of x0 and y0. The difference between these two gives us the change of entropy (ΔSent) as r(x0,y0)→r(x,y). Hence, one gets,
The computed values of ΔSent for each sequential change of vectors is given in Figure 5 together with the change of the index values in time.
The entropy change is given in Figure 5 where the second vertical axis denotes the index values.
Most of the entropy values are very close to 0.5 which is the most probable case when there occurs extremely high randomness in the system. In order words, Brownian motion is highly dominant as expected in S & P-500 index. The large magnitude entropy changes occur whenever the index value goes to minimum as seen from Figure 5. This is due to the reason that the w and q values also were very large as the index rolled down to minimum (Figure 4). The large difference in w and q values naturally entails large changes in entropy.
4.
Instability
Stock markets are very dynamic and fluctuating systems exhibiting instantaneous changes. In other words, persistent instability prevails because of both frequently low and infrequently high magnitude fluctuations. The energy and entropy computations were carried out above without taking into consideration the magnitudes of fluctuations.
In energy calculations, we needed only two parameters, one is the vector length and the other is the modulus which are related to the slope or to the angle θ (Figure 2). The vector length and θ are intimately related to each other. In entropy calculations, the vector length has some considerable effect but the dominant parameter is the angle θ, because, the end-to-end distance is predominantly dependent on how vectors move forward or backward through a series of bending at varying angles. Therefore, the statistical distribution of θ can give important clues about the dynamical behavior of the system.
4.1. The Elliott waves and θ
As we know the Elliott waves refer to a kind of pattern or to a kind of order in the system. The Elliott waves are dictated by the Fibonacci numbers which represent a special kind of growth rate or refer to the growth through autocatalysis. The ratio of consecutive Fibonacci numbers in a few steps gets close to the limiting value which is the golden ratio ϕ, and it is given by the following series expansion.
The unique property of this series system is that all the numbers used are "1", therefore, it is the least convergent series. In other words, if the inner dynamics of a system is described by ϕ, then it is in a state which is the closest to instability. Therefore, the golden number or the Elliott waves represent the states where randomness is a bit lowered such that a kind of stability at minimality is achieved.
Since G′ and G″ are the modulus of the in-line and out-of-line components of a vector, respectively, the G′ and G″ components of vectors in a scattering diagram can be shown by a representative picture given in Figure 6.
Figure 7 has the same structure of the series and parallel connected resistors in an electrical circuit. The equivalent G value (Geq) can be found out using the method of computing equivalent resistor for this system. It is given by the following equation.
In the case when all moduli are equal, i.e., when G′1=G″1=G′2=G″2=G′3=G″3.... or in an alternative saying when θ=45° for all cases, one gets,
Hence,
If we had only G′1, G′2, and G″2 in Figure 7 we would have Geq=G′1(3/2); adding G′2 to this group would give Geq=G′1(5/3); and then adding G′3 would give Geq=G′1(8/5), and so on. Note that these ratios are the ratio of consecutive Fibonacci numbers. What happens here is an interesting feature of such autocatalytic systems which are subject also to fluctuations. Such systems have quite large instabilities and the stability state to be achieved will be something definable or expressible in terms of golden ratio which represents the least stable state or least convergent state mathematically. Other states which are a bit more stable can be then be expressed by Fibonacci numbers. This is what we observe in Elliott waves, they represent the fairly stable or quasi-stable states very close to instability either in the motive phase or corrective phase. The Elliott pattern can be destroyed easily, because, the Brownian motion prevails in the medium, and the Elliott waves form on a knife-edge. The segments of long-term patterns include many fluctuating zones. There is a "continuous destruction and generation" phenomenon in the medium, and the Elliot patterns may show up in the short and long terms.
Due to coexistence of both Elliott waves and Brownian motion there exists a mutual energy transfer between the two. If energy is transferred from Brownian particles (i.e., independently behaving traders) to Elliott waves (i.e., traders behaving according to a kind of common or group motion) then Elliott waves gain more energy. It first speeds up (i.e., motive phase), then tries to stabilize itself (i.e., corrective phase). As high energy states traders start to sell their shares to make profit out it, which, in turn, leads to instability, i.e., the wave is damped and energy is transferred from the wave to Brownian particles. It means, the people go and buy shares of other assets in the market. The Elliott wave may reborn sooner or later as it may pick up again the fluctuating tiny waves prevailing in the medium all the time.
4.2. The distribution of θ
The percent distribution of θ is given in Figure 8 where θ angle was changed by 1°. That is, the number of the data between say −90° and −89° is summed up and its percentage was reported at −89.5°.
There are two major minima in Figure 6, one at around −45° and the other at around 45°. The distribution strip more or less has an oscillatory dependence on angle. It clearly indicates that some angles occur more frequently and some less frequently. The fluctuations create a band rather than an oscillating curve.
Since stability conditions are achieved at certain proportions of Fibonacci numbers we must expect some anomalies in the trend of the distribution of some system parameters, and in more pronounced manner in the distribution of θ values. The question then arises as how the golden ratio can be related to θ. It was shown by Equation 21 that the steady part of the distribution function oscillates by a trigonometric relation (i.e., cosine function relation) when it is at equilibrium state. The oscillation frequency ω is inversely proportional to the force expressed by φ. In Equations 26 and 27 the vector −BC refers to a kind of force which is expressed by both φ and Si. In fact, Figure 8 implies that the distribution of θ also shows similar behavior. There should be some preferred angles and the associated changes in the stock markets accordingly. The next question is then the cosine of what angle is related to golden ratio. We know from trigonometry that,
where, π=180°, and so, cos36°=ϕ/2. Using the cosine law (i.e.cos2Θ=2cos2Θ−1) it is possible to find out other angles which involve ϕ in some form. For instance, by writing 2Θ=36° one can express 18° in terms of ϕ such that cos18°=(1/2)√2+ϕ. Using the same procedure one can also express 9° in terms ϕ. By using the above expression in the general form (i.e.cos(Θ+β)=cosΘcosβ−sinΘsinβ) one can express all angles which are multiple of 9° in terms of ϕ. Some of these expressions can be quite simple, such as sin18°=cos72°=1/2ϕ, and sin54°=ϕ/2.
The percent distribution data was summed in an interval of 3° (i.e.±1.5°) rather than 1°, and the distribution in percent is given in Figure 9 where the vertical grid lines pass through 9° multiple of θ values.
In Figure 9 the angles which are the multiples of 9° are designated by black circles while the others are designated by open circles. In Figure 9a the arrows indicate the relative position of a peculiar black circle between the two white neighbors. The down-arrow says that the black circle is at a position lower than the two white circles on its left and right. Similarly, the up-arrow says that the black circle is at a position higher than the white circles on its left and right. Out of 19 black circles 9 of them are down-arrows, 6 of them are up-arrows, and 4 of them are in alignment with the white circles. This indicates that black circles which are expressed in terms of ϕ are in the further lower positions (i.e., down-arrows) or in the further upper positions (i.e., up-arrows) than the white circles. They have higher influence on the dynamics of stability and instability in the system.
In Figure 9 the angles which are the multiples of 9° are designated by black circles while the others are designated by open circles. In Figure 9a the arrows indicate the relative position of a peculiar black circle between the two white neighbors. The down-arrow says that the black circle is at a position lower than the two white circles on its left and right. Similarly, the up-arrow says that the black circle is at a position higher than the white circles on its left and right. Out of 19 black circles 9 of them are down-arrows, 6 of them are up-arrows, and 4 of them are in alignment with the white circles. This indicates that black circles which are expressed in terms of ϕ are in the further lower positions (i.e., down-arrows) or in the further upper positions (i.e., up-arrows) than the white circles. They have higher influence on the dynamics of stability and instability in the system.
There seem to be two different patterns of the distribution as seen from Figure 9b where the broken curves somehow pass through the appropriate points. The down-arrow points are mainly aligned on or below the lower curve whereas all upper arrow circles are above the upper curve. In addition, all upper-arrow points are either in the minimum or maximum zones of Figure 9b.
The lower curve includes relatively less frequency of occurrence of angles and the upper curve the relatively more frequently occurring angles. The angles with higher percentage of occurrence represent the more preferable dynamical behavior in the system. These points are aligned in the upper zone of Figure 9 along the horizontal grid line passing through 2%. The dynamical changes corresponding to the minimal zones (i.e. around ±45°) are relatively fewer occurring cases. However, in these zones up-arrows have relatively higher percentages and play more predominant role to influence the dynamical changes. Another point is that at θ=0° the up-arrow also plays a major role to change the behavior.
The minimal zones around ±45° correspond to an important physical fact. At 45° we have G′=G″, that is, the elastic (i.e., conservative) and viscous (i.e., dissipative) components are of equal magnitude. In order words, the system is neither elastic nor viscous, and in viscoelastic theory this state is called "gel" state; it is a kind of transition state. This state is minimal as seen from Figures 8 and 9. The dynamics of asset values or stock market index reflect the behavior of traders. They don't like to stay at the insecure (i.e., unstable) gel state, rather they take decisive actions which make them more deterministic in their behavior.
4.3. The change of Si and θ
In order to have a feeling about how θ angles of multiples of 9° appear in the time series data of S & P-500 two different cases were displayed in Figure 10. In the first case a small segment (between December 7, 1994 and April 3, 1995) where there occurs a smooth increase was considered, while in the second case the data around a minimum (between January 13, 2009 and June 22, 2009) was considered. They are shown in Figures 10a and 10b, respectively.
As observed from Figure 10a in several cases the next white circle after the black one exhibits a jump in value, which represents actually a kind of excited state compared to the back one; these are the cases at 2264th, 2269th, 2298th, and 2323th days data points. The smooth increase of the points ends with a black circle in some cases, such as 2264th, 2287th, and 2298th days data points. In some cases, black circles appear at the minimum which represent the most stable states; these are 2269th, 2290th, 2296th, 2321th, and 2339th day data points. These observations clearly show that the black circles represent the relatively stable cases in financial dynamics. It does not mean that stability occurs only in these points, but it rather says that in a turbulent media where there exists Brownian dominated motion, the stability close by to instability is achieved at states where dynamics can be expressible in terms of golden ratio or terms which involve golden ratio of some form.
In Figure 10b we observe similar behaviors as in Figure 10a. What is interesting is that the downward peak region with a minimum behaves in a different way than the case in Figure 10a. The peak between two vertical broken lines starts with a black circle at the 5832th day with an Si value of 826.84 and ends with another black circle at the 5865th day with an Si value of 834.38; both values are of similar magnitude. On the left leg we have 9 black and 10 white circles while we have 10 black and 9 white circles. The ratio of blacks to whites is almost one. This is not the situation in Figure 10a where we have 26 black and 55 white circles; the ratio of black to white is less than one half. This ratio is very close to "1 black-2 white" distribution displayed in Figure 9.
There are two important points here; the first point is related to the dynamics in the peak. The almost equal number of blacks and whites in this peak shows that traders make such decisions which ensure them to stabilize their positions, i.e., they take very careful actions. They take more courageous decisions if the things go as in Fig. 10a, where positions represented by black circles are less preferred.
The second important conclusion is that even in very smoothly rising market as in Figure 10a blacks and whites are half and half. However, the way the points in Figure 9a are arranged so that for every one black circle we have two white circles, because, the intervals were arranged by 3o, and there are two whites for any 9° of change in θ angle. If the system were completely random the percent distribution of blacks and white circle wouldn't be at half and half ratio.
4.4. Entropy and θ
The stability and instability issues are related to entropy. The entropy is calculated by using two consecutive index values as seen from Equations 31 and 32. The quite low or quite high entropy values occur when the difference between two consecutive index values is high. This situation is clearly observed in Figure 5 where we observe larger entropy change in the zone of minimal regions. We can investigate the change of entropy at the peculiar angles which are multiples of 9°. This can be done by matching the black symbols of Figures 10a and 10b with their corresponding entropies.
The matching of the index values of the peak between two vertical broken lines of Figure 10b with the entropy values of the same region is given in Figure 12.
In the peak region of Figure 12b the percent distribution of white squares is 22.2% for case "i", 33.3% for case "ii", and 44.5% for case "iii". In case of black squares, the distribution is 29.4% for case "i", 47.1% for case "ii", and 23.5% for case "iii".
The percentage of white squares in Figure 12b for the case "iii" is 44.5% which is larger than the case in Figure 11b where it is 32.7%. The white squares are somehow pushed out from the maximal and minimal regions in Figure 12b. These regions are occupied at a relatively higher percentage by black squares. In Figure 11b the percentage of black squares in "i" and "ii" regions add up to 58.6% whereas it is 76.5% in Figure 12b. In Figure 11b the black squares in the minimal regions is 34.5% whereas it is 47.1% in Figure 12b. In a peak severe change occurs while descending down or rising up. The motion is quite directed and up and down fluctuations of similar magnitude are quite reduced. The decrease in the index value is due to degradation of the wave (i.e.ˉf), into smaller waves (i.e.f′), and the index value increases as the reverse happens. In the peak region, the traders are much more precautious and their attitudes are conservative, and they are represented by the increased number of black circles or black squares.
5.
Elliott waves and peculiar angles
The connection between the Elliott waves and the golden ratio can be better understood in terms of the changes of angles derived from golden ratio, i.e., in terms of the multiples of 9°. The physics behind such changes is the gel state which occurs at 45°. The gel state is expressed in term of a geometric term which is the angle that provides equality between the two opponent forces due to conservative and dissipative actions. There are five steps (i.e., 0°, 9°, 18°, 27°, 36°) between 0° and 45°, and also another five steps between 45° and 90°. Here we exclude 45° as the gel state is a quasi-state, it is neither elastic nor viscous. Other states reveal from the decomposition of this quasi-state. We may say that the real states (or new forms) reveal from this quasi-state as in the case of spinodal decomposition. In case of θ angle we have four such regions between −90° and 90°, and also four regions for α angle (Figure 2) between 0° and 180°.
The θ or α angle is actually connected to the oscillation frequency ω according to equation 21. Therefore, the fluctuations with tiny amplitudes result in tiny waves according to equation 21, and these waves combine and decompose perpetually. Besides the main frequencies the harmonic frequencies are also generated. Can small fluctuations add up and give big fluctuations? The answer is positive according to equation 19–21.
The major motive Elliott wave is denoted by the numbers (1) to (5), and the corrective wave by (A) to (C) which has relatively smaller amplitude in Figure 13. The golden ratio found out from the heights between the horizontal broken lines was indicated outside the diagram on the right-hand side.
Here we must keep in mind that whenever we have an Elliott wave, we have a collective motion and therefore we have an ordered structure. As the golden ratio denotes the closest stable state to randomness or in other words the least stable state (see Equation 36–37) we may question how Elliott waves and golden ratio are bound to each other.
As mentioned before the least stable states can be achieved when the angles between the consecutive vectors are multiples of 9°, and there are only five stages which allows this possibility between 0°−45°. A wave designates a collective motion, and collective motion can be thought of as the commonly exercised behavior of a large group of dealers in the market. Their behavior turns into wave behavior, i.e., creates wave in the physical sense, and the most durable surviving waves can be achieved when the angles between the consecutive vectors have five choices. The waves not structured in five consecutive branches are naturally short-lived waves and they are difficult to recognize.
Now let us consider autocatalysis here once more. Every growing system has two major groups of parameters; the ones which increase the growth, and the ones which control (i.e., pulls down) the growth. Similarly, a commodity, asset, and so forth may have increasing value or its value is dragged down depending on conditions. The logistic equation is used to formulate this phenomenon.
where xn denotes the situation at the nth step and xn+1 denotes it at the (n+1)th step. xn refers to the growth and (1−xn) to the control variable. Inside the parenthesis "1" means that every change is expressed in terms of fractions. r is a constant and tells us at what proportion xn is transformed into xn+1. Another well-known autocatalytic system is the Lotka-Volterra problem in ecology where xn denotes the prey population and (1−xn) the predator population. It is a time dependent continuous function and we have dx/dt on the left-hand side instead of xn+1. If we consider the increase of predator population then the sign of the term on the right-hand side of Equation 39 changes. In the increasing step of an asset price the asset functions as predator, it pulls (or attracts) the investors, and adversely influences the price of the other assets. Hence, we can change Equation 39 into the form,
where we set also r=1 for simplicity. It can now be expressed as,
In Figure 13 the points (1), (2), (3), (4), (5), (A), (B), and (C) are connected by dotted lines, and each line has a kind of memory of what happened in between the two connected points. In Equation 22 we had related two consecutive values with each other, and using a similar logic we can relate two consecutive lines also. The angle between the two lines gives information about the dynamics in the range covered by the lines. We can ask if the angles produced by the dotted lines passing through (1)−(2)−(3) and through (2)−(3)−(4) have a kind of connected property. A more general question is that if the autocatalytic behavior has a kind of deterministic effect can we see this effect in the angles between the lines of the subsequent points (1), (2), (3), (4), (5), (A), (B), and (C)? If so, then the angles must also exhibit a kind of behavior of which underlying dynamics base on Equation 41. Thus, we can set xn to denote the angle function between the lines. Since oscillations are given by the cosine of an angle by Equation 21, we can set φ for ωt in Equation 21. That is, we can set xn=cosφn. Equation 41 now becomes,
The angles which are the multiples of 9° were said to be related to golden ratio because of Equation 38. Starting with 9° we can obtain other angles for instance 18° from the cosine relation (i.e.cos2φ=2cos2φ−1). For a special case let us set, φn+1=2φn, then we can write Equation 42 as,
Hence, by substituting Equation 43 in 42 we easily get,
The solution gives cosφn=0.618=1/ϕ. This surprising result is due to the fact that if we set xn+1=1 in Equation 41 we get the algebraic relation x2+x−1=0, which is also the algebraic relation to obtain the golden ratio. The autocatalytic systems (or logistic equation) and the golden ratio have common mathematical basis. Therefore, we may expect that the angles between any two connecting lines in an Elliott wave may be the multiple of 9°.
It was also mentioned above that the growth of a wave expressed by Equation 17 or Equation 19 also represents a kind of autocatalytic mechanism; the more it peaks up smaller waves, the greater it gets in time. However, the bigger it becomes the larger the probability that it breaks up into smaller waves. This mechanism is the underlying logic of Equation 39.
Now we can calculate the φ values in degrees between the consecutive lines connecting the points (1), (2), (3), (4), and (5) in Figure 13 by using geometric relations. The calculated values were given in Table 1. The numbers in parenthesis in the first row are the associated corner numbers. The φ refers to the calculated degrees, and φ′ is the best fitting degree which is the multiple of 9°.
The agreement between φ and φ′ is very good. The lines were drawn between the first and the last points in each case. The angle is very case sensitive, and even a small change in the second decimal of Si value is directly reflected as a significant change in the value of φ. As mentioned before φ′ values were determined with 3° (±1.5°) precision. The largest difference occurs in (1) by 2.94°.
Now we can make local analysis for the Elliott waves. Figure 14 shows a magnified view of the first two major branches (i.e., line #1 & #2) of Figure 13.
The apex of the first peak of Figure 13 is shown by 5 in Figure 14. In the rising branch we have a motive phase designated by the numbers from 1 to 5 also marked by the dotted lines, and we also have a corrective phase which is shown by the letters from A to C. There could be more fine structured waves for instance between 2 and 4, but the analysis will not be further carried out for such detailed states. In Table 2 we see the angles between two consecutive intersecting dotted lines; and the numbers or letters denote the appropriate corners.
It is seen that each φ has a degree which is very close to one of the peculiar degrees. In fact, the dotted lines were drawn by using only two data points excluding all others in between. In a fluctuating system a point at minimum or at maximum may not represent the real minimum or maximum, because, the data represents only the closing value by the end of a day, and it is not meaningful to take the daily average. Anyway, Table 2 clearly indicates that the calculated φ degrees are strongly associated with the peculiar degrees φ′, i.e., the multiples of 9°.
On the descending branch we have a motive phase from 1′ to 5′, and two corrective phases which are from A′ to C′, and from A″ to C″, respectively. The angles of the motive phase are shown in Table 3 and those of corrective phases in Table 4.
Here we see again a nice correspondence between φ and φ′ values in both Table 3 & 4.
In order to investigate it further the descending #4 and the ascending #5 branches of major Elliott wave (Figure 13) were also analyzed. These two cases were shown in detail in Figure 15.
In Figure 15a the corrective phase reveals within the motive phase, whereas in Figure 15b it reveals after the motive wave. The angles are given in Table 5, and Table 6, respectively.
We also see in Tables 5 and 6 that there is a close correspondence between the values of φ and the values of φ′.
In Figure 13 there are two regions where the amplitudes of fluctuations are quite low. One them is the third branch of the major Elliott wave, and the second is the very early smooth region where the amplitudes are really minute. The magnified views of these regions were shown in Figure 16.
The angles for Figure 16a were given in Table 7, and the angles for Figure 16b were given in Table 8.
There is also a very good correspondence between φ with φ′ when we have small amplitude fluctuations.
We always observe consistency in all cases from Table 1 to Table 8.
6.
Conclusions
Asset values and stock market index values cannot be fully described by Brownian motion, but rather by a mixed Brownian and wave-like dynamics. Fluctuations create small waves which are picked up by a rising asset, commodity, or so forth. By the same way the high asset value is partly degraded to produce small fluctuating waves which are picked up by other assets. This behavior can be elucidated at macro level using scattering diagram technique and the theory of viscoelasticity, such that, a vector in scattering diagram can be split into its conservative and dissipative components. The distribution of angles between the consecutive vectors do not have uniformity but rather have some peculiar preferences. These angles are those which can be expressed in terms of golden ratio and they actually correspond to relatively higher stability states.
The entropy values corresponding to the states associated with these peculiar angles also support that the stability and instability issues in stock markets are closely related to the occurrence of these angles. The traders in financial systems always look for secure positions, and they are more precautions while there were sharp falls and rises, where, we see these peculiar angles more frequently.
The Elliot waves represent an ordered pattern which forms in a manner that its structure has a stability state closest to instability. The angles between the lines of Elliott waves come out to be those which are obtained from golden ratio. In other words, we observe the relations involving golden ratio in the time dependent spectrum of asset values because of the formation mechanism of the Elliott waves. In this study, the formation principles of Elliott waves were established on physical and mathematical grounds.
Acknowledgements
I am grateful to Dr. Yalın Gündüz, Bundesbank in Frankfurt, for his enlightening help on Elliott waves and on stock markets in all aspects. My gratitude is extended to Dr. Merih Şengönül, Atılım Üniversitesi in Ankara for his permanent interest, encouragements, and providing some important documents in the literature. The author deeply appreciates the leading recommendations of the anonymous reviewer.
Conflicts of interest
The author declares no conflict of interest.
Appendix A
The multiplication of both sides of Equation 11 by AˉL(t) gives,
We have the following conditions,
Now Equation (A-1) takes the form,
The second term of Equation 12 simply reduces to the following equation, because, AL′(t)ˉf(t)=0.
The third term of Equation12 can be expressed as,
The substitution of Equation (A-4) in Equation (A-6) yields,
Then the substitution of Equation (A-5) and Equation (A-7) in Equation 12 gives,
Using Equation 13 in the last term, and doing some simplifications yields,
Appendix B
A typical broken surface of a crystal is shown in Figure B-1.
The surface has two dimensions but only the side view is shown in Figure B-1, the other dimension may be assumed to be unity. We will consider the edge with length l in Figure B-1.
The ticks on the unit cells indicate new unit cell surfaces created, and "d" denotes the length of each side of unit cell. Let's assign a unit energy of ε/2 to each bond, i.e., to each newly created unit cell surface both along the horizontal (i.e., x-) and vertical (i.e., y-) axis. The surface energy can be calculated by taking into consideration the horizontal and vertical axes.
The total number of bonds along both directions is,
The total energy of created surfaces can be given by,
This equation denotes a circle with a diameter of εl/√2d.









 DownLoad:
DownLoad:


















