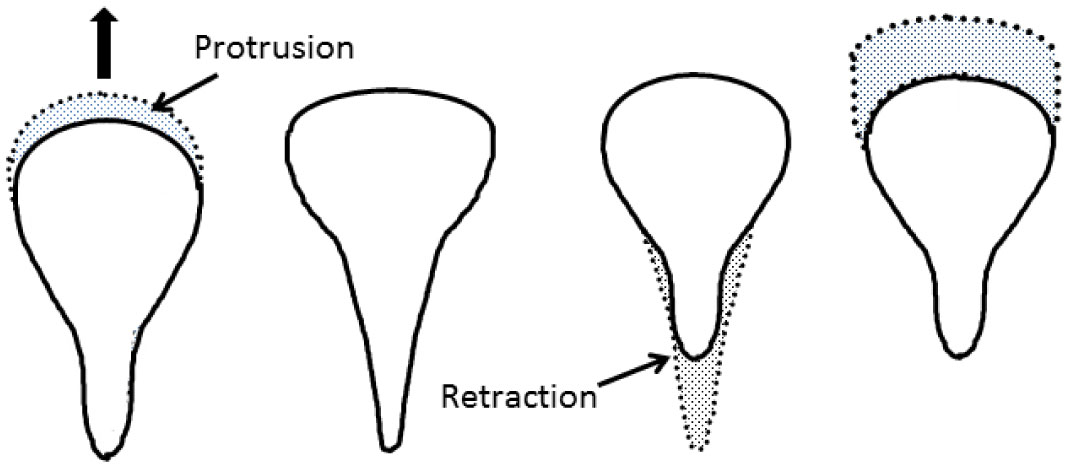
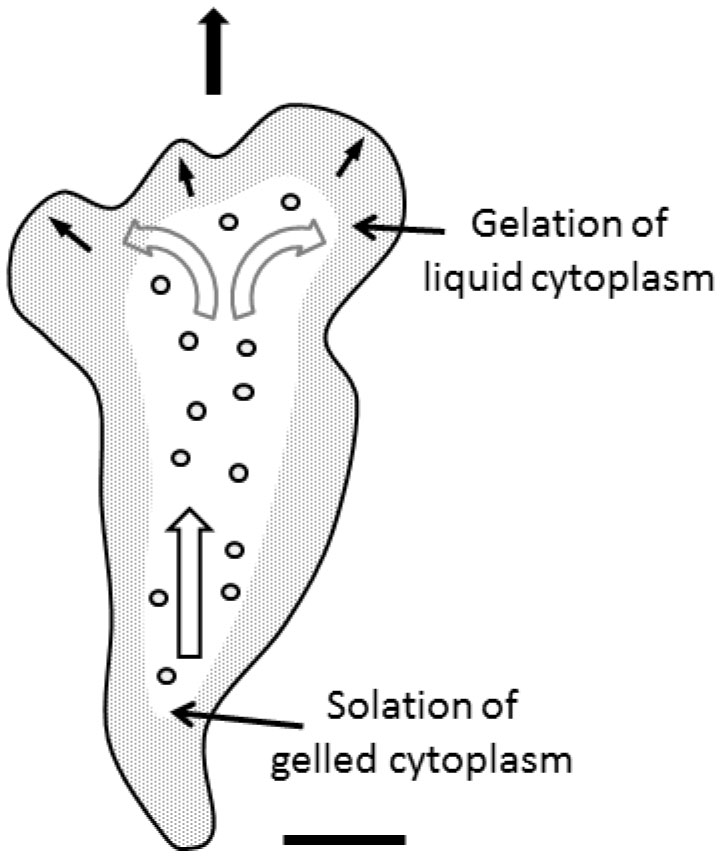
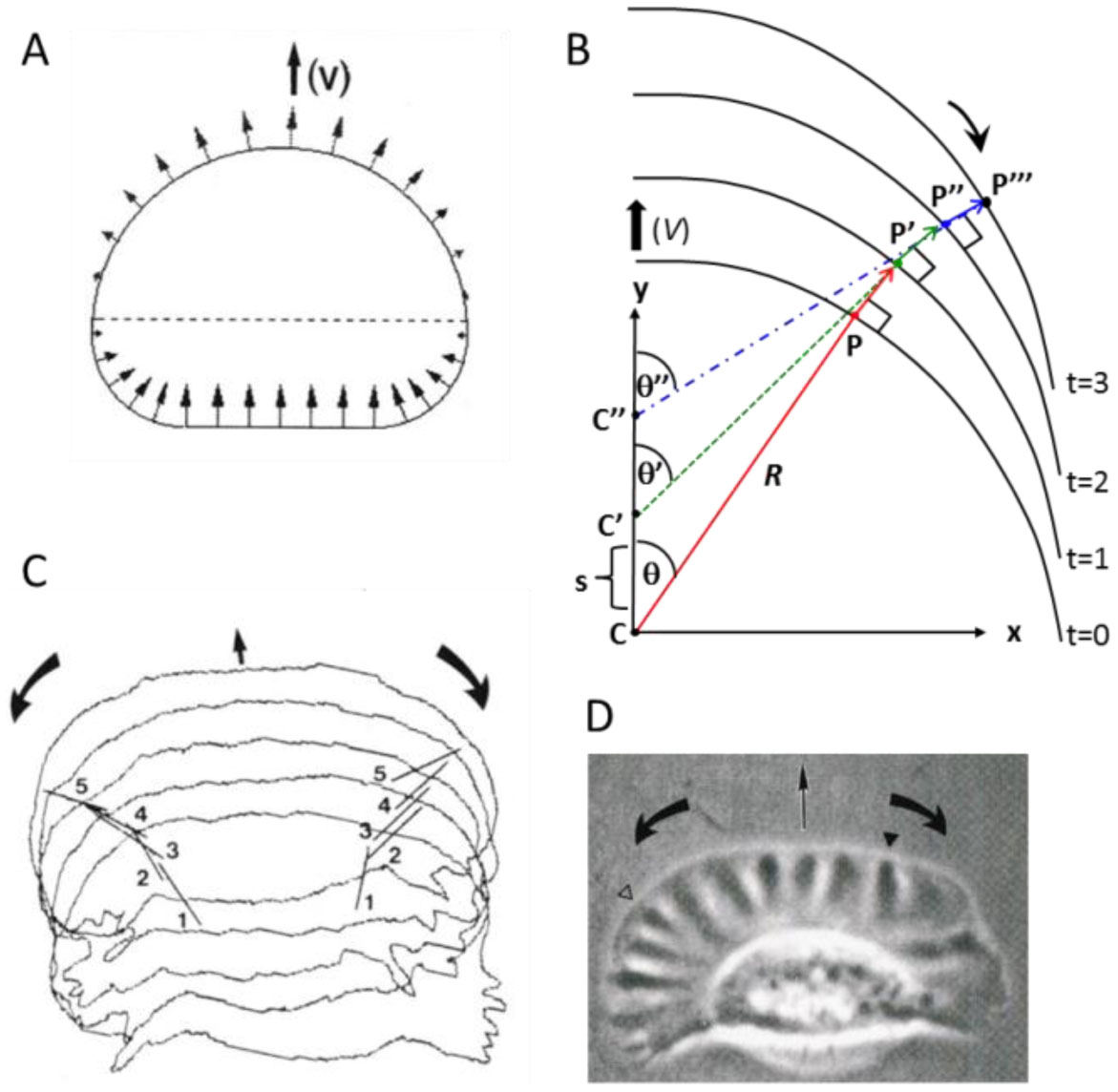
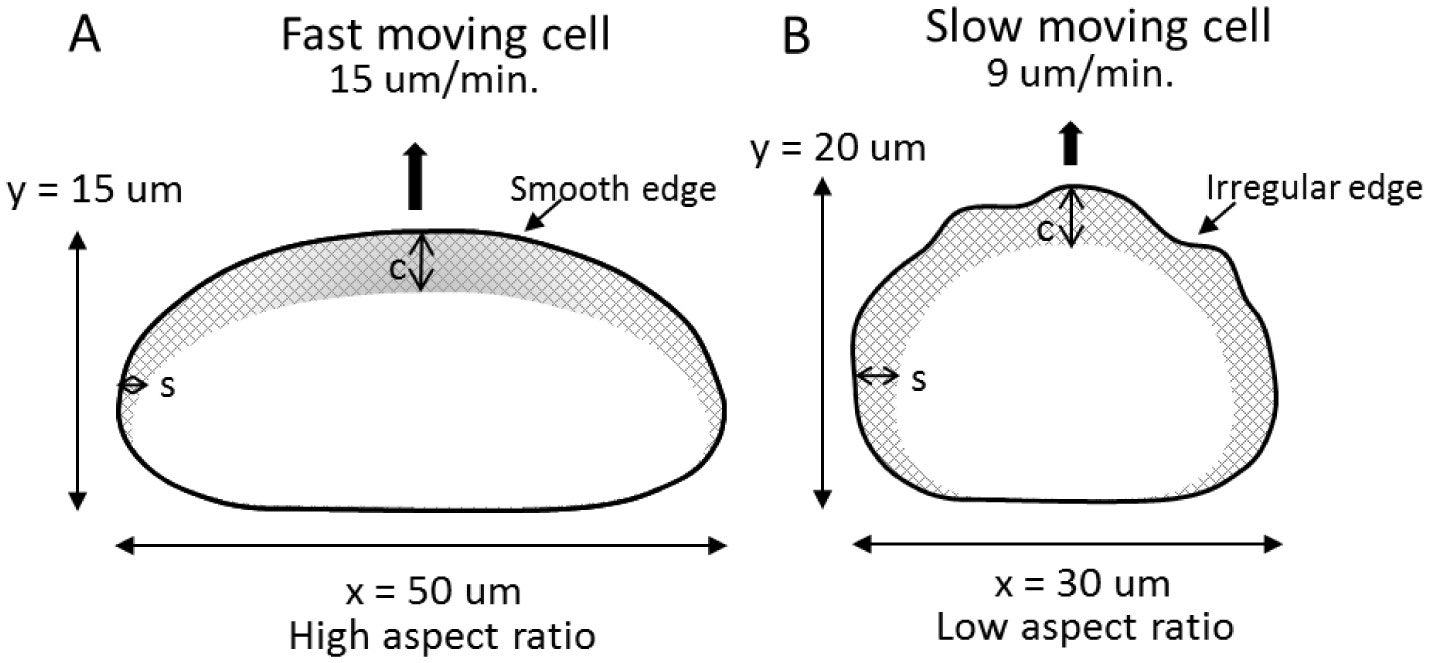
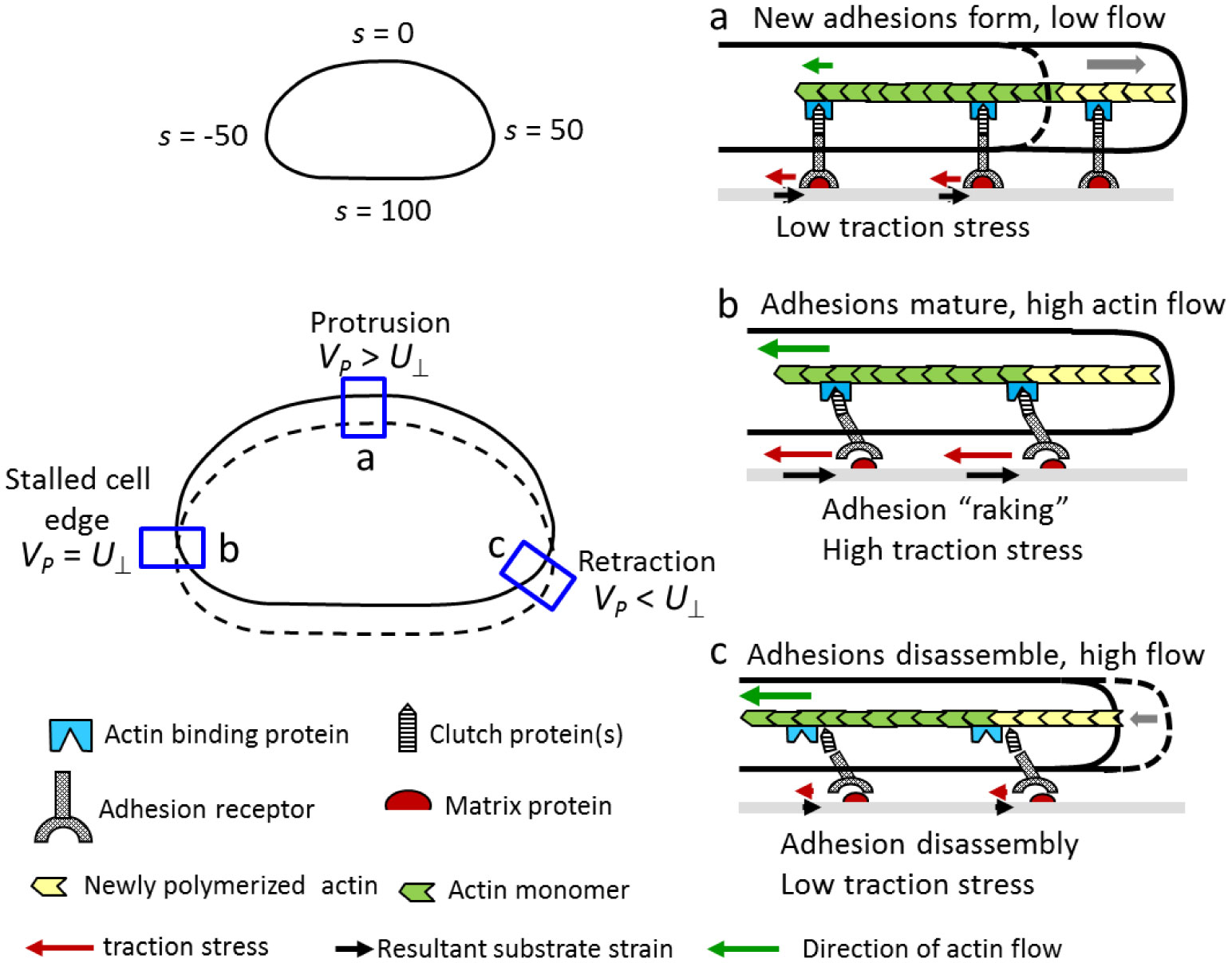
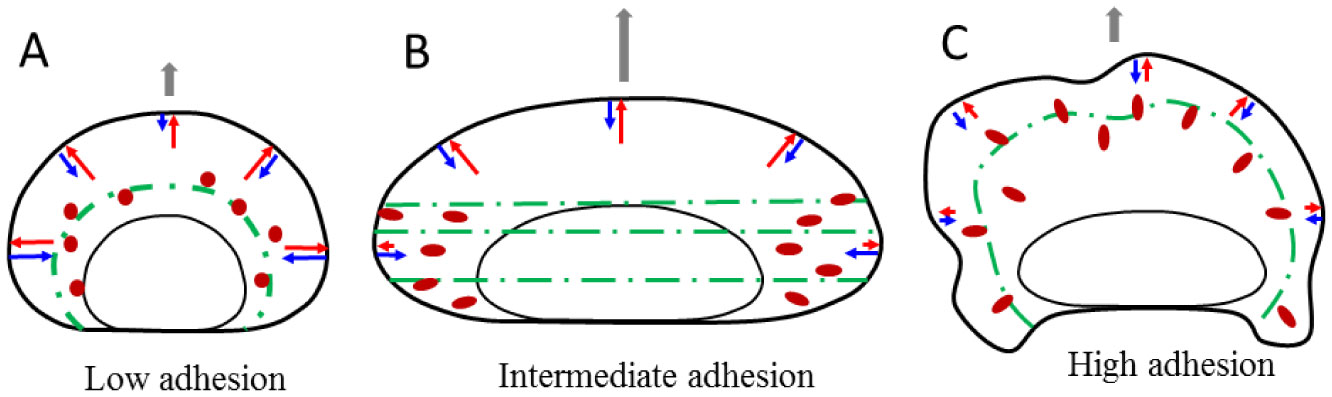
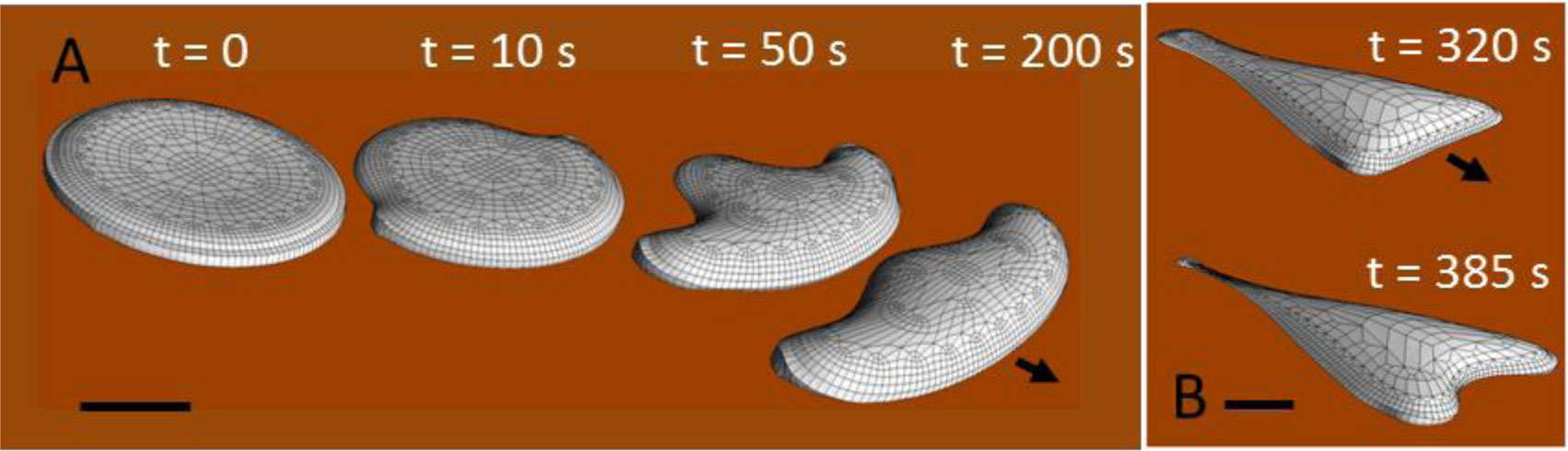
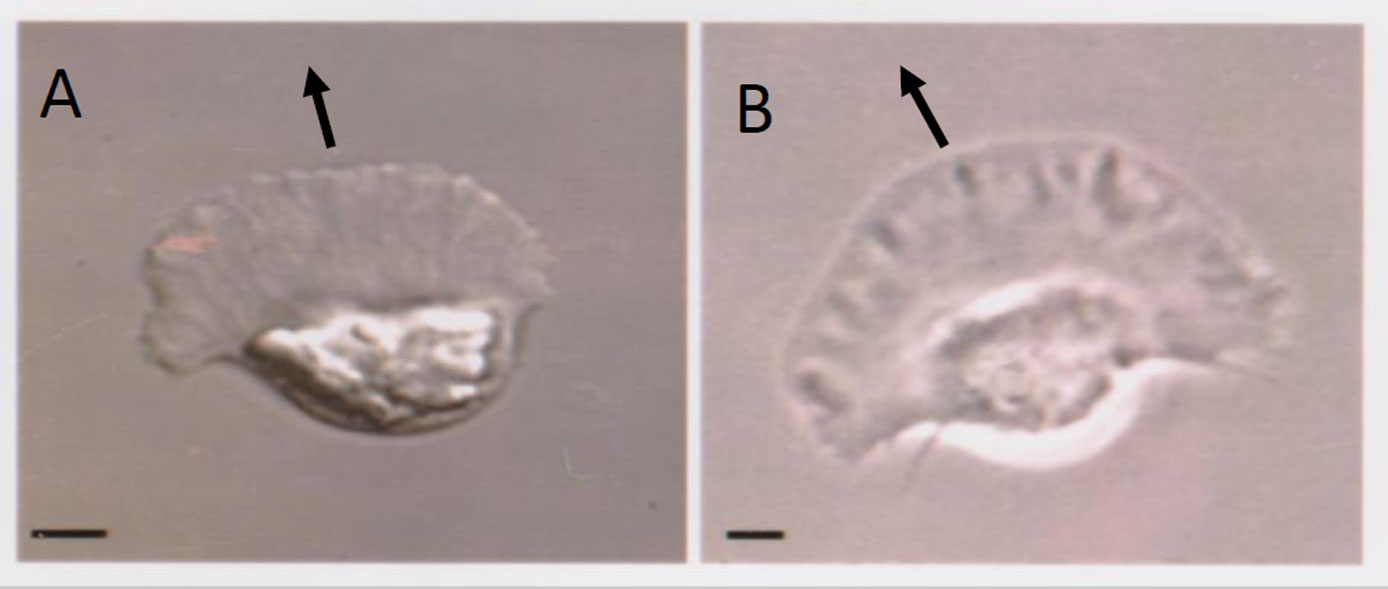
Cell movement is a complex phenomenon that is fundamental to many physiological and disease processes. It has been the subject of study for more than 200 years, and yet we still do not fully understand this process. Cell movement consists of four steps; protrusion and adhesion formation at the front followed by contractile force generation and detachment at the rear. Much is known about the molecular mechanisms underlying these steps however, it is not clear how they are integrated at the cellular level. Part of the problem is the incorporation of a vast amount of molecular and biophysical data into a basic working model of motility. A promising solution to this problem is the combined approach of mathematical modeling and experimentation, using the fish epithelial keratocyte as a model system. The goal of this review is to illustrate, using examples, how the reciprocity between experimentation and modeling can provide new insights into the mechanism of cell motility. Several modeling approaches are described including: conceptual models, “bottom-up” models based on molecular dynamics, and “top-down” models that consider cell shape and movement. The Graded Radial Extension (GRE) model forms the basis of a several mathematical models, from a simpler 1D model that links actin filament dynamics to cell shape, to more complex 2D and 3D simulations of keratocyte movement. Together these models suggest that cell movement emerges from the mechanical interaction between different sub-processes of motility, namely, the treadmilling actin meshwork, the plasma membrane, adhesion turnover and contractile force generation. In addition, the feedback regulation between these sub-processes is important for the robust, self-organizing nature of movement.
1.
Introduction
The effect of disease on eco-epidemiology system is a significant topic from both mathematical and ecological perspectives. The disease factor usually leads to a more complex and diverting dynamics than those in the disease-free system [1,2]. Within the interactions between predator and prey, the disease could only spread in prey or predator population, also could spread between prey and predator [3,4,5]. Birds (particularly pelicans) infect vibrio and die by preying on vibrio-infected fish (particularly tilapia) at the Salton Sea in the desert of Southern California [3], which is an example of disease spreads amongst the prey. For the disease in predator, taking fox rabies as an example, foxes (Vulpis) infect rabies and transmit to other foxes or their prey rabbits by biting in Europe and North America [6]. More relevant examples could be found in [7]. From the mathematical epidemiology point of view, one needs much more attention in the dynamics of infected predator to observe whether the presence of the prey allows the survival of a part of the predator population [8].
A variety of diseased predator models have been proposed to study the complex interaction between prey and predator with infected diseases [2,9,10] and the reference therein. Most common epidemic model applied in predator-prey interactions is the $ SI $-type, i.e., the predator population $ Y(t) $ is divided into two sub-classes, namely susceptible predator $ S(t) $ and infected predator $ I(t) $, respectively [10,11,12]. The infection term could be mass-action term (bilinear form) $ \beta S I $ or saturation form $ \frac{\beta S I}{S+I} $ [4]. The infected predators usually behave differently with susceptible ones, and suffer an additional death rate. In a epidemic model, the global dynamics are usually determined by the basic reproduction number $ \mathcal{R}_0 $, i.e., the disease will dies out in the population when $ \mathcal{R}_0\leq 1 $, and the disease will persist in the population when $ \mathcal{R}_0 > 1 $. However, the basic reproduction number is no longer a threshold parameter determining the global dynamics in diseased predator models, on the contrary, the dynamics are relatively comprehensive and unexpected.
Predation is the key force in a prey-predator interaction, which could affect the size of prey population by direct hunting [9,13,14,15], and elicit a variety of anti-predator responses [16,17,18]. Consequently, prey tends to alter behaviors in a certain extent, such as change of habitat, foraging activity, vigilance, physiological changes. This anti-predator behaviors accelerate the extinction, evolution and development of prey population in the long run. Under the risk of predation, prey may reduce its foraging activity in order to stay alert, leading to starvation which impacts on population growth [19,20]. Therefore, an immediately result of anti-predator behaviors is the reduction of prey growth rate, which is the cost for prey in prey defense [19,21,22,23,24,25,26].
Consider a simple birth-death process of the prey $ X(t) $ with the cost of anti-predator behaviors [27]:
where $ X, Y $ represent the density of the prey and predator, respectively. $ a $ is the birth rate of prey, $ d $ is the natural death rate of prey. $ F(k, Y) $ accounts for the cost of anti-predator defence due to fear, the parameter $ k $ reflects the level of fear which drives anti-predator behaviors of prey. The fear factor $ F(k, Y) $ has some specific assumptions under the ecological motions, for details see [20,27].
To derive a simple diseased predator model incorporating the anti-predator defence due to fear, we adopted the following fear effect term $ F(k, Y) $:
Based on the results in [4,9,11], we can obtain the eco-epidemiological system with cost of anti-predator behaviors as following system of nonlinear differential equations:
where $ X, S, I $ represent the density of prey, susceptible predator and infected predator at time $ t $, respectively. $ r $ is the intrinsic growth rate of prey, $ K $ is the carrying capacity of the prey, $ a $ is the predation coefficient, $ b $ is the predators handling time of a prey, $ e $ is the biomass conversion constant, $ \beta $ is the transmissibility coefficient. $ d_1 $ and $ d_2 $ are the mortality rates of the susceptible predator and infected predator, and naturally $ d_1 < d_2 $.
This paper consists of six sections. In the next section, we prove the positivity and boundedness of the solution of system (1.1). In Section 3, we provide the existence conditions of the equilibria of the model. We analyze the stability of equilibria and show the occurrence of Hopf bifurcation in Section 4. In Section 5, the correctness of the theoretical proof is illustrated by numerical simulation. Finally, we summarize our results with ecological interpretations in Section 6.
2.
Positivity and boundedness
In view of the ecological significance, we only consider the solutions $ (X(t), S(t), I(t)) $ of system (1.1) on
Theorem 2.1. Each solution of system (1.1) with initial value $ (X(0), S(0), I(0))\in {\mathbb R}^{3}_{+} $ is positive and ultimately bounded.
Proof. Since the right-hand side of system (1.1) is completely continuous and locally Lipschitzian on $ {\mathbb R}^{3}_{+} $, the solution $ (X(t), S(t), I(t)) $ with initial condition $ (X(0), S(0), I(0))\in {\mathbb R}^{3}_{+} $ exists and is unique on $ {\mathbb R}^{3}_{+} $.
By integrating, it follows from system (1.1) that
Hence, the solution $ (X(t), S(t), I(t)) $ of system (1.1) with the initial condition $ (X(0), S(0), I(0))\in {\mathbb R}^{3}_{+} $ remains positive.
From the first equation of (1.1), we can obtain
then
Let $ N(t) = eX(t)+S(t)+I(t) $, we can get
then
This ends the proof.
Remark 2.2. From Theorem 2.1, we know that all positive solutions of system (1.1) with initial conditions $ (X(0), S(0), I(0))\in \mathbb{R}_+^3 $ are defined in the following positive bounded invariant:
3.
Existence of the equilibria
System (1.1) possesses at most three boundary equilibria:
(i) Trivial equilibrium: $ E_0 = (0, 0, 0); $
(ii) Axial equilibrium: $ E_1 = (K, 0, 0); $
(iii) Planar equilibrium: $ E_2 = (X_2, S_2, 0) $ exists if $ ea-bd_1 > 0 $ and $ K > \frac{d_1}{ea-bd_1} $, where
For epidemic models, the most critical problem is the threshold property for the extinction and persistence of the disease, which is generally governed by the basic reproduction number $ \mathcal{R}_0 $. The basic reproduction number can be interpreted as the expected number of secondary cases produced, in a completely susceptible population, by a typical infected individual during its entire period of infectiousness. Following [28], we define the basic reproduction number for the predator population in the system (1.1) by
where $ S_2 $ is given by (3.1).
Next, we mainly focus on the existence of positive equilibrium $ E_3 = (X_3, S_3, I_3) $ of system (1.1). The coordinates $ X_3, S_3, I_3 $ are positive solutions to the following system of equilibrium equations:
Thus,
and $ X_3 $ is the positive root of (3.2) in $ \left(X_2, +\infty\right) $:
where
If $ ea-bd_1 > 0 $ and $ r > \dfrac{ad_2(\beta+k(d_2-d_1))}{\beta^2} $, we have
By Descartes' rule of signs, system (1.1) has at least one positive equilibrium $ E_3. $
Hence, we have the following results on the existence of the positive equilibrium. It is worthy to note that the positive equilibrium is not unique due to the impact of fear effect $ k $.
Theorem 3.1. If $ ea-bd_1 > 0 $ and $ r > \frac{ad_2(\beta+k(d_2-d_1))}{\beta^2} $, then system (1.1) has at least one positive equilibrium $ E_3 = (X_3, S_3, I_3), $ where $ S_3 = \frac{S_2}{\mathcal{R}_0} $, $ I_3 = {\frac {X_3(ea-bd_{{1}})-d_{{1}}}{ \left(bX_3+1 \right) \beta}} $ and $ X_3 $ is the positive root of (3.2) in $ \left(X_2, +\infty\right) $.
4.
Stability analysis
4.1. Local stability
Regarding the local stability of trivial equilibrium $ E_0 $ and axial equilibrium $ E_1 $, we have the following results. The proof is standard, so we omit it here.
Theorem 4.1. For system (1.1),
(i) The trivial equilibrium $ E_0 = (0, 0, 0) $ is unstable;
(ii) If one of the following inequalities holds:
(ii-1) $ ea-bd_1 < 0 $;
(ii-2) $ ea-bd_1 > 0 $ and $ K < \frac{d_1}{ea-bd_1} $,
then the axial equilibrium $ E_1 = (K, 0, 0) $ is stable; while $ E_1 = (K, 0, 0) $ is unstable if $ ea-bd_1 > 0 $ and $ K > \frac{d_1}{ea-bd_1} $.
Secondly, we will show the local stability of the planar equilibrium $ E_2 $ of system (1.1). For convenience, set
Theorem 4.2. For system (1.1), assume that $ ea-bd_{{1}} > 0 $. If one of the following inequalities holds:
(Ⅰ) $ r\leq r_1 $ and one of the following inequalities holds:
(Ⅰ-1) $ \frac{d_1}{ea-bd_1} < K\leq K_1 $;
(Ⅰ-2) $ K > K_1 $ and $ k > k_1 $;
(Ⅱ) $ r_1 < r < r_2 $ and one of the following inequalities holds:
(Ⅱ-1) $ \frac{d_1}{ea-bd_1} < K\leq K_1 $;
(Ⅱ-2) $ K_1 < K $ and $ k > \max\{k_1, k_2\} $;
(Ⅲ) $ r > r_2 $ and one of the following inequalities holds:
(Ⅲ-1) $ \frac{d_1}{ea-bd_1} < K\leq K_2 $;
(Ⅲ-2) $ K_2 < K $ and $ k > \max\{k_1, k_2\} $,
then equilibrium $ E_2 $ is stable; otherwise, it is unstable.
Proof. The Jacobian matrix of system (1.1) at $ E_2 $ is given by
where
Hence, the characteristic equation of $ J_2 $ is given as
where
Clearly, one can see that $ J_2 $ has three eigenvalues $ \lambda_1 $, $ \lambda_2 $ and $ \lambda_3 = \beta S_2-d_2. $ Since $ a_{12} < 0, a_{21} > 0 $, then $ -a_{12}a_{21} > 0 $.
From (3.1), we can obtain
where
Note that the sign of $ \Phi $ depends on
where
One can obtain that $ P(k) $ is decreasing with respect to $ k $. If $ K\leq{\frac {ea+bd_{{1}}}{b \left(ea-bd_{{1}} \right) }} $ holds, we have $ P(0)\leq0 $, which means that $ P(k) < 0 $ for all $ k > 0 $; if $ K > {\frac {ea+bd_{{1}}}{b \left(ea-bd_{{1}} \right) }} $ and $ k > k_1 $ hold, we can get $ P(k) < 0 $. Therefore, when one of the following inequalities holds:
(i) $ K\leq{\frac {ea+bd_{{1}}}{b \left(ea-bd_{{1}} \right) }} $;
(ii) $ K > {\frac {ea+bd_{{1}}}{b \left(ea-bd_{{1}} \right) }} $ and $ k > k_1 $,
we can obtain $ a_{11} < 0 $, which implies that the real parts of $ \lambda_1 $ and $ \lambda_2 $ are all negative.
It follows from system (3.1) that
where
Note that the sign of $ \Theta $ depends on
Then if one of the following inequalities holds:
(Ⅰ) $ ea-bd_{{1}} > 0 $ and $ r\leq\frac{d_2(ea-bd_1)}{\beta e} $;
(Ⅱ) $ ea-bd_{{1}} > 0 $, $ r > \frac{d_2(ea-bd_1)}{\beta e} $ and one of the following inequalities:
(Ⅱ-1) $ K\leq\frac{\beta erd_1}{(ea-bd_1)(\beta er-d_2(ea-bd_1))} $;
(Ⅱ-2) $ K > \frac{\beta erd_1}{(ea-bd_1)(\beta er-d_2(ea-bd_1))} $ and $ k > k_2: = -\frac{\beta((ea-bd_1)(d_2(ea-bd_1)-\beta er)K+\beta erd_1)}{(Kd_2(ea-bd_1)^2+\beta erd_1)d_2} $,
we have $ \lambda_3 = \beta S_2-d_2 < 0. $
Thus, we can arrive at the conclusion.
It should be pointed out that another way to state Theorem 4.2 is as follows.
Remark 4.3. For system (1.1), assume that $ ea-bd_1 > 0 $ and $ \mathcal{R}_0 < 1 $. If one of the following inequalities:
(Ⅰ) $ \dfrac{d_1}{ea-bd_1} < K\leq K_1; $
(Ⅱ) $ K > K_1 $ and $ k > k_1 $
holds, then the planar equilibrium $ E_2 $ is stable; otherwise, it is unstable.
Next, we will show the local stability of the positive equilibrium $ E_3 $ of system (1.1).
The Jacobian matrix of system (1.1) at $ E_3 $ is given by
where
The characteristic equation of $ J_3 $ is given as
where
Note that if $ A_1 > 0 $ holds, then $ b_{11} < 0 $, which means that $ A_3 > 0. $ According to Routh-Hurwitz criterion, the positive equilibrium $ E_3 $ is locally asymptotically stable when $ A_1 > 0 $ and $ A_1A_2-A_3 > 0 $.
Therefore, we can establish the following statement.
Theorem 4.4. Assume that $ ea-bd_1 > 0 $ and $ r > \frac{ad_2(\beta+k(d_2-d_1))}{\beta^2} $ hold. The positive equilibrium $ E_3 $ of system (1.1) is locally asymptotically stable if $ A_1 > 0 $ and $ A_1A_2-A_3 > 0 $, where $ A_i, i = 1, 2, 3 $ is defined as in (4.5). Otherwise, it is unstable.
Remark 4.5. Theorem 4.4 gives a sufficient condition about the stability of the positive equilibrium $ E_3 $ for system (1.1). However, the complexity of model (1.1) leads to the failure to theoretically demonstrate how the fear factor affects the stability of the positive equilibrium. This will be discussed later through numerical simulations.
4.2. Hopf bifurcation
In this subsection, we take $ k $ as the bifurcation parameter. The characteristic equation of system (1.1) at $ E_3 $ is (4.4), and $ A_i(k), i = 1, 2, 3 $ are defined as (4.5).
Theorem 4.6. Hopf bifurcation near the positive equilibrium $ E_3 $ for system (1.1) occurs whenever the critical parameter $ k $ attains the value $ k = k_h $ in the domain:
Proof. If $ k = k_h $, the characteristic Eq (4.4) equals
then (4.6) can be factorized as
Clearly, (4.7) has three roots: $ \lambda_1 = i\sqrt{A_2(k_h)} $, $ \lambda_2 = -i\sqrt{A_2(k_h)} $ and $ \lambda_3 = -A_1(k_h) $. The roots are of the form $ \lambda_1 = p_1(k)+ip_2(k) $, $ \lambda_2 = p_1(k)-ip_2(k) $ and $ \lambda_3 = -p_3(k) $, where $ p_i(k) (i = 1, 2, 3) $ are real numbers.
From the characteristic Eq (4.4), we can get
where $ ' = \frac{{\mathrm{d}}}{{\mathrm{d}}k} $. Substituting $ \lambda = i\sqrt{A_2} $ into (4.8), we obtain that
which implies that
By using monotonicity condition in the real part of the complex root $ \frac{{\mathrm{d}} {\mathrm{Re}}(\lambda)}{{\mathrm{d}}k}|_{k = k_h}\neq0 $, the transversality condition $ \frac{{\mathrm{d}}\Delta(k)}{{\mathrm{d}}k}|_{k = k_h}\neq0 $ can be obtained to ensure the existence of Hopf bifurcation.
5.
Numerical simulations
Results from numerical simulations are provided in this section to demonstrate our theoretical results. As we will show, the observations shed lights on the impact of fear factor. We choose the parameters of system (1.1) as follows:
Then we have
Example 5.1 (The stability of $ E_1 $).
We adopt $ K = 0.2, k = 0.01 $, then system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $ and axial equilibrium $ E_1 = (0.2, 0, 0) $. In this case, one can know that the conditions of Theorem 4.1 are satisfied, which means that $ E_1 $ is locally asymptotically stable. The numerical results are shown in Figure 1.
Example 5.2 (The impacts of $ K $ and $ k $ on the stability of $ E_2 $).
In this example, we will choose three values of carrying capacity $ K $ for numerical experiments. We conclude that the carrying capacity and fear effect are other key factors related to the extinction of infected predators, in addition to the basic reproduction number $ \mathcal{R}_0 $.
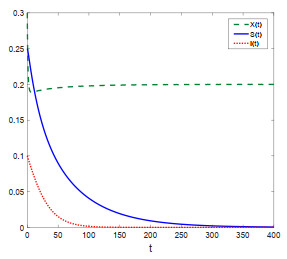
Firstly, we take $ K = 0.3 < K_2 $, then we have $ k = 0.1 $ which yields that $ \mathcal{R}_0 = 0.263 < 1 $. In this case, system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (0.3, 0, 0) $, and planar equilibrium $ E_2 = (0.286, 0.139, 0) $. By Theorem 4.5, $ E_2 $ is locally asymptotically stable, see Figure 2(a). Thus, when the carrying capacity of the prey $ K $ is small, no matter what the level of fear $ k $ is, the small size of prey population will lead to the extinction of infected predators.
Secondly, for comparison, we take $ K_2 < K = 15 $, then
Choosing $ k = 0.1 < \max\{k_1, k_2\} $ which yields $ \mathcal{R}_0 = 5.792 > 1 $, then we have
In this case, system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (15, 0, 0) $, planar equilibrium $ E_2 = (0.286, 3.070, 0) $, and positive equilibrium $ E_3 = (7.351, 0.530, 7.125) $. By Theorem 4.5, $ E_2 = (0.286, 3.070, 0) $ is unstable. On the contrary, $ E_3 = (7.351, 0.530, 7.125) $ is locally asymptotically stable. The numerical simulation is shown in Figure 2(b).
Finally, we take $ K_2 < K = 60 $, then we have
Choosing $ k = 30 > \max\{k_1, k_2\} $ which yields that $ \mathcal{R}_0 = 0.649 < 1 $, system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (60, 0, 0) $, and planar equilibrium $ E_2 = (0.286, 0.344, 0) $. By Theorem 4.5, $ E_2 $ is locally asymptotically stable, see Figure 2(c). Thus, when the carrying capacity of the prey $ K $ is relatively large, a high level of fear $ k $ will lead to the extinction of infected predators.
Example 5.3 (The impact of $ k $ on the stability of $ E_3 $). We adopt $ K = 60 $, then we have $ k_h = 0.26 $. In the next, we will choose three values of $ k $, corresponding to the local stability of $ E_3 $, Hopf bifurcation, and instability of $ E_3 $, to illustrate the impact of fear factor on the population dynamics.
Firstly, we take $ k = 0.1 < k_h $ which yields that $ \mathcal{R}_0 = 5.881 > 1 $, then system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (60, 0, 0) $, planar equilibrium $ E_2 = (0.286, 3.117, 0) $ and a unique positive equilibrium $ E_3 = (24.047, 0.530, 12.213) $. In this case, we obtain that
which means that $ E_3 $ is local asymptotically stable. The numerical results are shown in Figure 3.
Secondly, we take $ k = 0.26 = k_h $ which yields that $ \mathcal{R}_0 = 4.682 > 1 $, then system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (60, 0, 0) $, planar equilibrium $ E_2 = (0.286, 2.481, 0) $ and a unique positive equilibrium $ E_3 = (12.975, 0.530, 9.665) $. In this case, we obtain that
which means that system (1.1) undergoes a Hopf bifurcation and there is a limit cycle around $ E_3 $. The numerical results and the bifurcation diagrams of system (1.1) with respect to the parameter $ k $ are shown in Figures 4 and 5, respectively. Comparing Figures 3 and 4(a), one can see that there are two different implications induced by the fear factor $ k $: the first is that the stability of $ E_3 $ converts from stable into unstable, and the second is the decrease of values of $ X_3 $ and $ I_3 $ of $ E_3 $.
Finally, we take $ k = 0.5 > k_h $ which yields that $ \mathcal{R}_0 = 3.821 > 1 $, then system (1.1) has trivial equilibrium $ E_0 = (0, 0, 0) $, axial equilibrium $ E_1 = (60, 0, 0) $, planar equilibrium $ E_2 = (0.286, 2.025, 0) $ and a unique positive equilibrium $ E_3 = (7.685, 0.530, 7.322) $. In this case, we can obtain that
which means that $ E_3 $ is unstable. The numerical results are shown in Figure 6. One can find that the difference between Figures 4 and 6 is the decrease of values of $ E_3 $ from $ (12.975, 0.530, 9.665) $ to $ (7.685, 0.530, 7.322), $ which is induced by the impact of the feat factor.
6.
Conclusions
In this paper, we explored a predator-prey model that incorporates infectious disease in predator population and the cost of anti-predator behaviors. The cost of anti-predator behaviors is measured by a fear effect $ k $ leading to an reduction of prey's birth rate. We fulfill a complete stability analysis of equilibria for system (1.1) and show that the system (1.1) exhibits the Hopf bifurcation. Biologically, we focus on the impact of fear effect on the population dynamics. As we will see later, the cost of a high level of fear effect is disastrously. The main findings are summarized in the following.
$ 1) $ Small size of prey population leads to the extinction of infected predators.
If the carrying capacity $ K $ is relatively small, the planar equilibrium $ E_2 $ is stable, see Figure 2(a). Thus, no matter what the level of fear effect $ k $ is, a small size of prey population will lead to the extinction of infected predators.
$ 2) $ Low level of the fear effect doesn't impact on the population dynamics.
If the level of fear effect $ k < k_h $, the positive (coexistence) equilibrium $ E_3 $ is stable, see Figure 3. Hence, we conclude that a small fear effect $ k $ is not the key disturbance and does not change the coexistence dynamics of system (1.1). However, the densities of the prey and infected predator gradually decrease as $ k $ increasing.
$ 3) $ Certain medium level of the fear effect lead to periodic oscillation.
If $ k = k_h $, the fear effect can destabilize the stability of $ E_3 $ and will benefit the occurrence of periodic oscillation. In other words, system (1.1)undergoes a limit cycle, see Figures 4 and 5.
$ 4) $ High level of the fear effect leads to complex dynamics and the infected predator can go to extinction.
If $ k > k_h $, $ E_3 $ is unstable, see Figure 6. Therefore, a large fear effect $ k $ persistently and dramatically influence the population dynamics of prey and predator. Furthermore, if the level of the fear factor $ k $ is extremely high, the planar equilibrium $ E_2 $ is stable, see Figure 2(c). The prey will respond to perceived predation risk and show a variety of anti-predator responses, dramatically decreasing the recruitment of susceptible predator, which will lead to an extinction of infected predator.
Acknowledgements
The authors would like to thank the editor and the referees for their helpful comments. This research was supported by the National Natural Science Foundation of China (Grant No. 12171192, 12031020 and 12071173), the Science and Technology Research Projects of the Education Office of Jilin Province, China (JJKH20211033KJ), the Technology Development Program of Jilin Province, China (20210508024RQ) and Huaian Key Laboratory for Infectious Diseases Control and Prevention, China (HAP201704).
Conflicts of interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.









 DownLoad:
DownLoad: