Novel insights into the function of the conserved domain of the CAP superfamily of proteins

Nick K. Olrichs; J. Bernd Helms; Nick K. Olrichs; J. Bernd Helms

doi:10.3934/biophy.2016.2.232

AIMS Biophysics

2016, Volume 3, Issue 2: 232-246. doi: 10.3934/biophy.2016.2.232

Previous Article Next Article

Review Topical Sections

Novel insights into the function of the conserved domain of the CAP superfamily of proteins

Nick K. Olrichs ,
J. Bernd Helms ^,

Department of Biochemistry & Cell Biology and Institute of Biomembranes, Utrecht University, Utrecht, The Netherlands

Received: 16 March 2016 Accepted: 18 April 2016 Published: 21 April 2016

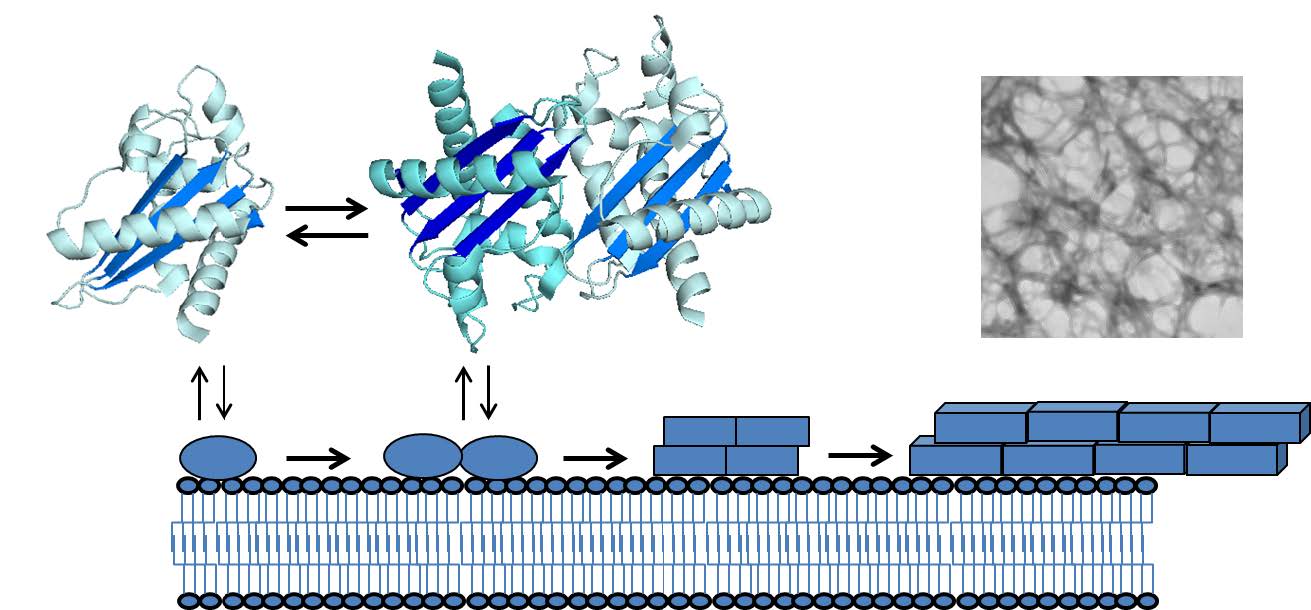
Members of the Cysteine-rich secretory proteins, Antigen 5, and Pathogenesis-related 1 proteins (CAP) superfamily are found in a remarkable variety of biological species. The presence of a highly conserved CAP domain defines the CAP family members, which in many cases is linked to other functional protein domains. As a result, this superfamily of proteins is involved in a large variety of biological processes such as reproduction, tumor suppression, and immune regulation. The role of the CAP domain and its conserved structure throughout evolution in relation to the diverse functions of CAP proteins is, however, poorly understood. Recent studies on the mammalian Golgi-Associated plant Pathogenesis Related protein 1 (GAPR-1), which consists almost exclusively of a CAP domain, may shed new light on the function of the CAP domain. GAPR-1 was shown to form amyloid fibrils but also to possess anti-amyloidogenic properties against other amyloid forming peptides. Amyloid prediction analysis reveals the presence of potentially amyloidogenic sequences within the highly conserved sequence motifs of the CAP domain. This review will address the structural properties of GAPR-1 in combination with existing knowledge on CAP protein structure-function relationships. We propose that the CAP domain is a structural domain, which can regulate protein-protein interactions of CAP family members using its amyloidogenic properties.

Keywords:

Citation: Nick K. Olrichs, J. Bernd Helms. Novel insights into the function of the conserved domain of the CAP superfamily of proteins[J]. AIMS Biophysics, 2016, 3(2): 232-246. doi: 10.3934/biophy.2016.2.232

Related Papers:

[1]	Martin Heida, Benedikt Jahnel, Anh Duc Vu . Regularized homogenization on irregularly perforated domains. Networks and Heterogeneous Media, 2025, 20(1): 165-212. doi: 10.3934/nhm.2025010
[2]	Hakima Bessaih, Yalchin Efendiev, Florin Maris . Homogenization of the evolution Stokes equation in a perforated domain with a stochastic Fourier boundary condition. Networks and Heterogeneous Media, 2015, 10(2): 343-367. doi: 10.3934/nhm.2015.10.343
[3]	Martin Heida . Stochastic homogenization on perforated domains III–General estimates for stationary ergodic random connected Lipschitz domains. Networks and Heterogeneous Media, 2023, 18(4): 1410-1433. doi: 10.3934/nhm.2023062
[4]	Nils Svanstedt . Multiscale stochastic homogenization of monotone operators. Networks and Heterogeneous Media, 2007, 2(1): 181-192. doi: 10.3934/nhm.2007.2.181
[5]	Patrick Henning . Convergence of MsFEM approximations for elliptic, non-periodic homogenization problems. Networks and Heterogeneous Media, 2012, 7(3): 503-524. doi: 10.3934/nhm.2012.7.503
[6]	Mogtaba Mohammed, Mamadou Sango . Homogenization of nonlinear hyperbolic stochastic partial differential equations with nonlinear damping and forcing. Networks and Heterogeneous Media, 2019, 14(2): 341-369. doi: 10.3934/nhm.2019014
[7]	Valeria Chiado Piat, Sergey S. Nazarov, Andrey Piatnitski . Steklov problems in perforated domains with a coefficient of indefinite sign. Networks and Heterogeneous Media, 2012, 7(1): 151-178. doi: 10.3934/nhm.2012.7.151
[8]	Luca Lussardi, Stefano Marini, Marco Veneroni . Stochastic homogenization of maximal monotone relations and applications. Networks and Heterogeneous Media, 2018, 13(1): 27-45. doi: 10.3934/nhm.2018002
[9]	Brahim Amaziane, Leonid Pankratov, Andrey Piatnitski . Homogenization of variational functionals with nonstandard growth in perforated domains. Networks and Heterogeneous Media, 2010, 5(2): 189-215. doi: 10.3934/nhm.2010.5.189
[10]	Luis Caffarelli, Antoine Mellet . Random homogenization of fractional obstacle problems. Networks and Heterogeneous Media, 2008, 3(3): 523-554. doi: 10.3934/nhm.2008.3.523

Abstract

1. Introduction

The microstructure of portable artificial kidneys is responsible for the blood filtration and urine formation (mechanical process of biofluid) which acts as a micromachine due to very small size but do the complex process of reabsorption, filtration, excretion and secretion in its different parts. Kidneys contain renal speck and renal tubule; renal speck is further split into glomerulus and Bowman's capsule where blood is filtered through the glomerulus circulates and filtered blood then comes to the renal tubule where reabsorption takes place. Within the nephron, glomerular purification comprises on reflexive movement of blood plasma from glomerulus capillaries to the Bowman's capsule that is easily permeable to H₂O, small solutes like urea, sodium ion, and glucose but not porous to hemoglobin and platelets. The next part of the renal tubule is the proximal convoluted tubule (PCT) where effective and reactive transport take place to reabsorb glucose, sodium chloride, and water from the glomerular filtrate. The current model describes biomechanics of plasma having variable viscosity depending upon the distance from centre to the proximal tube wall that is the main segment of kidneys where constant reabsorption and filtration take place.

Different studies of viscous flow through renal tubule having permeable wall property with constant, linear and nonlinear rate of reabsorption have been discussed. Burgen et. al. [1] introduced a study of viscous flow through kidney with glucose reabsorption and developed mathematical equations for solute reabsorption and used the results to check the high affinity of glucose. The dynamics of biofluid through renal tubule and flow behavior in the presence of constant reabsorption on the wall has been discussed by Macey et. al. [2]. He analysed the viscous flow through infinite cylinder using the Navier Stokes equations with constant and linear reabsorption on the walls of cylinder and noticed the Poiseuille flow for constant reabsorption and for the linear reabsorption the flow lines become flattens instead of curve lines. The dynamical properties of the viscous flow through a permeable tube had been examined by Marshall et. al. [3] and found the exact solution with the help of Navier-Stokes equation for velocity and pressure using the Darcy's law also, the approximate solution for the leakage flux has calculated for the proximal renal tubule. Berkstresser et. al. [4], Tewarson et. al. [5] and Gupta et. al. [6] introduced the numerical and analytic techniques for the solution of mathematical model of viscous flow through renal tubule. Ahmad et al. [7] discussed the exact solution of viscous flow through the renal tube and showed the periodic flow in radial direction of the tube. Muthu et al. [8] presented the finite difference method to find the viscous flow through the cross section of tube with permeable boundary, he found the axial velocity and mean pressure generated by the reabsorption on the wall and flux on the axial direction. Koplik et al. [9], Pozrikidis et al. [10], Kropinski et al. [11] and Haroon et al [12] obtained the results for volume flow rate, glucose reabsorption, velocity and shear stress for Newtonian flow through permeable tube and slit by different methods. They found the slip and no slip effect on the velocity, leakage flux, flow rate and used the resulting formulas to find the reabsorption rate and mean pressure against the fractional reabsorption.

The viscosity of plasma filtered in kidney is not a fixed quantity, but it changes according to the diameter of proximal tubule, also flow resistance in renal tube decreases strongly with reduced diameter of the tube which is less than 0.3mm as mentioned in the study of Gilmer et. al. [13]. The flow resistance of the fluid to be filtered in proximal tube is considerably the case of Poiseuille flow because of pressure gradient which describes that resistance in the flow is low at the centre of tube and high near the tube wall. Few studies have been presented the effect of viscosity on the blood flow through kidney (Lamport et. al. [14],[15], Gaylor et. al. [16] and Omori et. al. [17], Halfenstein et. al. [18], Mukhopadhyay et. al. [19],[20]) but in all these studies only theoretical and experimental data has been used. Recently, Mehboob et. al. [21] presented the effect of variable viscosity and constant reabsorption on the slow viscous flow through narrow straight tubule and found the formulas for the leakage flux, mean pressure drop and flow rate but this problem was formulated in cylindrical coordinate system. There is not a single study available in literature which describes the mathematical formulas of creeping flow having varying viscosity across the height of channel with uniform absorption on the permeable walls of the channel in rectangular coordinate system.

Keeping above studies in mind, it has been assumed that the viscosity is an exponential function of distance from the centre to the boundary and reabsorption on the wall is constant. In this paper to study the effect of exponential type of viscosity for the viscous flow through a kidney, authors have considered the uniform reabsorption on the wall and discussed the problem formulation in section 2, methodology of complex system is included in section 3, mathematical results are presented in fourth section, application of the problem is in section 5, discussion is in section 6 and conclusion is included in section 7.

2. Materials and methods

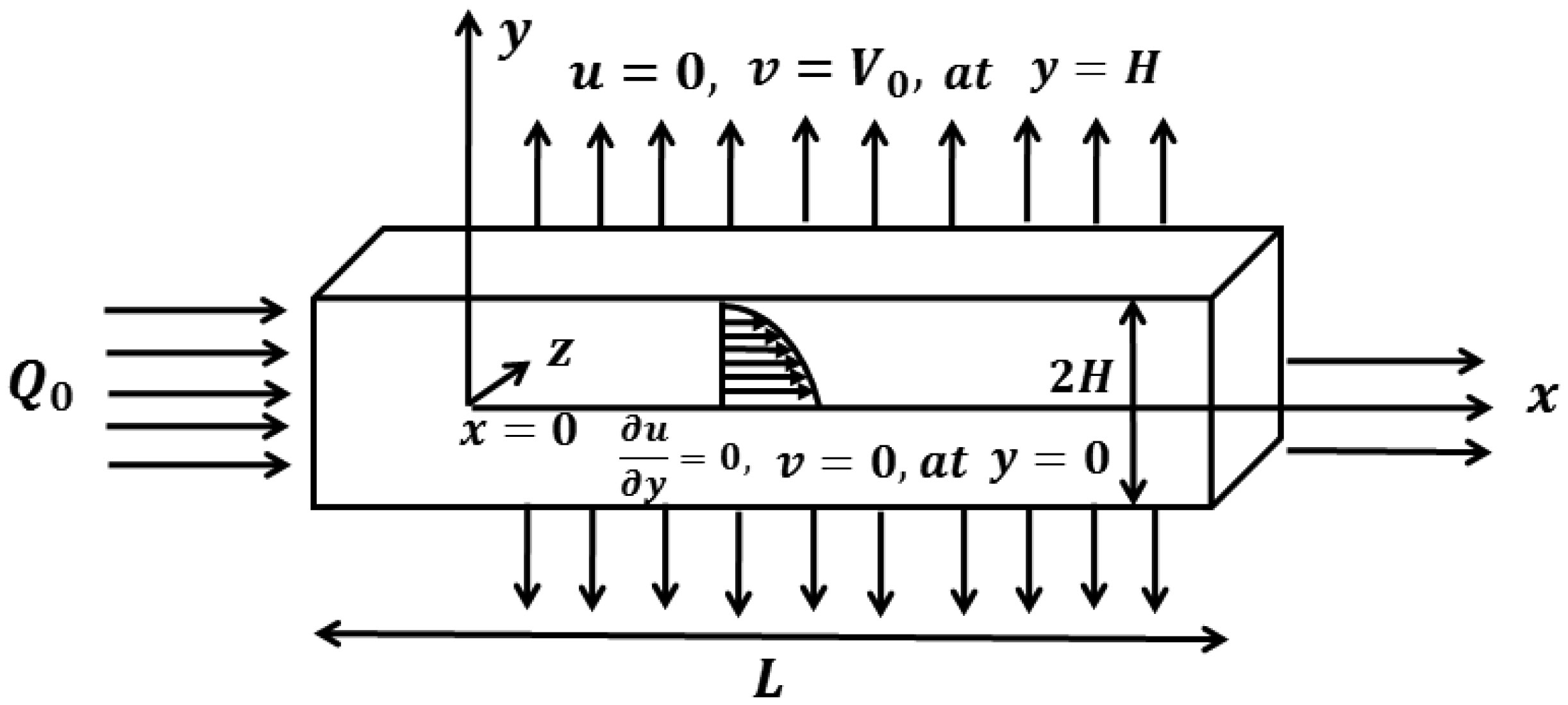
The present mathematical model suggests that a viscous fluid across a rectangular cross section is flowing under the effect of constant flux applied at the entrance of slit. The -axis locating at the middle of rectangular slit and -axis in the vertical direction of centre line as mentioned in Figure 1, due to symmetric behaviour, the upper half of a rectangular slit has considered to reduce the calculations.

Since the kidney contains the proximal renal tube and movement in this tube is of Poiseuille type Layton et al [22] which requires that axial velocity is highest at the middle of slit that is stated in Eq (7). Since boundaries of renal tubule are permeable and reabsorption takes place through these boundaries at a constant rate which is stated in Eq (8). These hypotheses support to assume that thickness is a decreasing function of distance from base to the boundary, therefore in the current research authors have assumed the Navier-Stokes equation with non-constant viscosity. The current problem of two-dimension, incompressible steady state creeping flow through slit become complicated due to non-constant viscosity.

Figure 1. Schematic diagram of the problem.

DownLoad: Full-Size Img PowerPoint

The suggested model recommends that movement of fluid through a slit satisfy the following flow field.

$V = [u (x, y), v (x, y), 0],$ (1)

where u and v represents horizontal and transverse velocity components.

The fluid flow through the nephron is incompressible i.e density is constant throughout the flow field and satisfy the following continuity equation

$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0.$ (2)

The creeping viscous flow across a slit suggests that in the absence of inertia term NSE's with variable viscosity satisfy the following set of equations.

$\frac{\partial p}{\partial x} = \frac{\partial}{\partial x} (2 µ (y) \frac{\partial u}{\partial x}) + \frac{\partial}{\partial y} {µ (y) (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x})},$ (3)

$\frac{\partial p}{\partial y} = \frac{\partial}{\partial x} {µ (y) (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x})} + \frac{\partial}{\partial y} (2 µ (y) \frac{\partial v}{\partial y}) .$ (4)

2.1. Exponential viscosity

Case I: $µ (y) = e^{- β y}$

Since the viscosity is a decreasing function of radius of tube which is mentioned in Ref. (Gilmer et al [13]& Tripathi et al [23]) therefore, the variable viscosity in the following form has chosen

$µ (y) = e^{- β y}, β > 0.$ (5)

The assumptions of plasma flow through renal proximal tube and constant reabsorption on the permeable boundary satisfy the following boundary conditions

$\frac{\partial u}{\partial y} = 0, v = 0, a t y = 0,$ (6)

$u = 0, v = V_{0}, a t y = H,$ (7)

$Q_{0} = 2 W \int_{0}^{H} u (0, y) d y .$ (8)

Stream function and velocity profile are associated by the following expressions

$u = \frac{\partial ψ}{\partial y}, v = - \frac{\partial ψ}{\partial x} .$ (9)

The above expressions of stream function and Eqs (3,4) give the following form

$\frac{\partial p}{\partial x} = 2 e^{- β y} \frac{\partial^{3} ψ}{\partial x^{2} \partial y} + \frac{\partial}{\partial y} {e^{- β y} (\frac{\partial^{2} ψ}{\partial y^{2}} - \frac{\partial^{2} ψ}{\partial x^{2}})},$ (10)

$\frac{\partial p}{\partial y} = e^{- β y} \frac{\partial}{\partial x} (\frac{\partial^{2} ψ}{\partial y^{2}} - \frac{\partial^{2} ψ}{\partial x^{2}}) + 2 \frac{\partial}{\partial y} {e^{- β y} (- \frac{\partial^{2} ψ}{\partial x \partial y})} .$ (11)

Eliminating pressure gradient from Eqs (10,11), one can write the following expression.

$\nabla^{4} ψ - β^{2} E^{2} ψ - 2 β \frac{\partial}{\partial y} (\nabla^{2} ψ) = 0,$ (12)

where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}$ a and $E^{2} = \frac{\partial^{2}}{\partial x^{2}} - \frac{\partial^{2}}{\partial y^{2}}$ .

Boundary conditions in terms of stream function are given as follows

$\frac{\partial^{2} ψ}{\partial y^{2}} = 0, \frac{\partial ψ}{\partial x} = 0, a t y = 0,$ (13)

$\frac{\partial ψ}{\partial y} = 0, \frac{\partial ψ}{\partial x} = - V_{0}, a t y = H,$ (14)

$ψ (0, 0) = 0, a n d ψ (0, H) = \frac{Q_{0}}{2 W} .$ (15)

The non-dimensional quantities are chosen from Ref. [12]

$\begin{array}{l} x^{*} = \frac{x}{L}, y^{*} = \frac{y}{L}, V_{0}^{*} = \frac{V_{0}}{U_{0}}, ψ^{*} = \frac{ψ}{U_{0} L}, β^{*} = β L, \\ Q_{0}^{*} = \frac{Q_{0}}{U_{0} W L}, τ_{w}^{*} = \frac{τ_{w}}{µ (y) U_{0} / L}, u^{*} = \frac{u}{U_{0}}, v^{*} = \frac{v}{U_{0}}, H^{*} = \frac{H}{L}, \end{array}$ (16)

where U₀ is reference velocity, L is the length of slit, H is the height and W is the width of slit. Nondimensional form of Eqs (12-15) after releasing “*” take the following form

$\nabla^{4} ψ - β^{2} E^{2} ψ - 2 β \frac{\partial}{\partial y} (\nabla^{2} ψ) = 0,$ (17)

$\frac{\partial^{2} ψ}{\partial y^{2}} = 0, \frac{\partial ψ}{\partial x} = 0, a t y = 0,$ (18)

$\frac{\partial ψ}{\partial y} = 0, \frac{\partial ψ}{\partial x} = - V_{0}, a t y = H,$ (19)

$ψ (0, 0) = 0, a n d ψ (0, H) = \frac{Q_{0}}{2 W} .$ (20)

2.1.1. Solution of the problem

To get the solution of problem given in Eqs (17-20), Inverse method [12] is used which requires the following function.

$ψ (x, y) = x R (y) + T (y),$ (21)

where R(y) and T(y) represent unknown functions.

Invoking Eq (21) in Eqs (17-20), one can obtain the following set of equations

$\frac{d^{4} R}{d y^{4}} - 2 β \frac{d^{3} R}{d y^{3}} + β^{2} \frac{d^{2} R}{d y^{2}} = 0,$ (22)

$\frac{d^{4} T}{d y^{4}} - 2 β \frac{d^{3} T}{d y^{3}} + β^{2} \frac{d^{2} T}{d y^{2}} = 0,$ (23)

and boundary conditions are

$R (0) = 0, \frac{d^{2} R (0)}{d y^{2}} = 0,$ (24)

$R (H) = - V_{0}, \frac{d R (H)}{d y} = 0,$ (25)

$T (0) = 0, \frac{d^{2} T (0)}{d y^{2}} = 0,$ (26)

$T (H) = \frac{Q_{0}}{2}, \frac{d T (H)}{d y} = 0.$ (27)

Solving Eqs (22,23) under the boundary conditions (24-27), one can obtained the following expressions for R(y) and T(y)

$(y) = \frac{V_{0} (2 + e^{H β} y β (1 - H β) - e^{y β} (2 - y β))}{- 2 + e^{H β} (2 - H β (2 - H β))},$ (28)

and

$(y) = \frac{Q_{0} (- 2 - e^{H β} y β (1 - H β) + e^{y β} (2 - y β))}{- 4 + e^{H β} (4 - 2 H β (2 - H β))} .$ (29)

Following stream function can be found after using R(y) and T(y) in Eq. (21)

$ψ (x, y) = \frac{(Q_{0} - 2 V_{0} x) (- 2 - e^{H β} y β (1 - H β) + e^{y β} (2 - y β))}{- 4 + e^{H β} (4 - 2 H β (2 - H β))}$ (30)

2.1.2. Velocity distribution

With the aid of above stream function and Eq (9), one can get the next components of velocity

$u (x, y) = \frac{- (Q_{0} - 2 V_{0} x) β (1 - H β - e^{- (H - y) β} (1 - y β))}{4 - 4 e^{- H β} - 2 H β (2 - H β)},$ (31)

and

$v (x, y) = \frac{V_{0} (- 2 - e^{H β} y β (1 - H β) + e^{y β} (2 - y β))}{- 2 + e^{H β} (2 - H β (2 - H β))} .$ (32)

Above equations show that horizontal velocity u(x, y) depends upon x and y, also horizontal velocity is maximum at y = 0 i.e.

$u_{m a x} = \frac{- (Q_{0} - 2 V_{0} x) β (1 - H β - e^{- H β})}{4 - 4 e^{- H β} - 2 H β (2 - H β)},$ (33)

and v(x, y) is maximum at y = H.

$v_{m a x} = V_{0} .$ (34)

Flow rate across the slit can be calculated by the following formula

$Q (x) = 2 \int_{0}^{H} u (x, y) d y,$ (35)

$Q (x) = Q_{0} - 2 V_{0} x,$ (36)

which results from the inlet to the outlet of rectangular cross section.

2.1.3. Pressure

In biological movements pressure performs an important role therefore to find the pressure, Eqs. (9-10) with the help of Eq (31) and Eq (32) are reduced into the following form

$\frac{\partial p}{\partial x} = - β e^{- β y} (x \frac{d^{2} R}{d y^{2}} + \frac{d^{2} T}{d y^{2}}) + e^{- β y} (x \frac{d^{3} R}{d y^{3}} + \frac{d^{3} T}{d y^{3}}),$ (37)

$\frac{\partial p}{\partial y} = - e^{- β y} (\frac{d^{2} R}{d y^{2}} - 2 β \frac{d R}{d y}) .$ (38)

Using R(y) and T(y), Eqs (37,38) take the following form

$\frac{\partial p}{\partial x} = \frac{- (Q_{0} - 2 V_{0} x) β^{3}}{- 4 + e^{H β} (4 - 2 H β (2 - H β))},$ (39)

$\frac{\partial p}{\partial y} = \frac{V_{0} β^{2} (2 e^{- y β} (1 - H β) - e^{- H β} (2 - y β))}{2 - 2 e^{- H β} - H β (2 - H β)} .$ (40)

Integration of above expressions yield the following form

$p (x, y) = \frac{- V_{0} β (4 e^{- y β} (1 - H β) + e^{- H β} y β (4 - y β))}{4 - 4 e^{- H β} - 2 H β (2 - H β)} + f (x),$ (41)

where f(x) i is given by as follows

$f (x) = \frac{- x (Q_{0} - V_{0} x) β^{3}}{- 4 + e^{H β} (4 - 2 H β (2 - H β))} + C,$ (42)

where C is an arbitrary factor. Inserting Eq (42) in Eq (41), we can compose the subsequent form of pressure

$p (x, y) - p (0, 0) = \frac{- β (4 (- 1 + e^{- y β}) V_{0} (1 - H β) + e^{- H β} β (4 V_{0} y + Q_{0} x β - V_{0} (x^{2} + y^{2}) β))}{4 - 4 e^{- H β} - 2 H β (2 - H β)},$ (43)

where p(0, 0) shows pressure at creek of rectangular cross section.

The average pressure drop is defined as follows

$\overset{̅}{p} (x) = \frac{1}{H} \int_{0}^{H} (p (x, y) - p (0, 0)) d y .$ (44)

After inserting value of p(x, y) − p(0, 0) from Eq (43), the above equation takes the following form.

$\overset{̅}{p} (x) = \frac{12 V_{0} {(1 - H β)}^{2} + e^{- H β} (3 H Q_{0} x β^{3} + V_{0} (- 12 - H β (- 12 - 6 H β + (H^{2} + 3 x^{2}) β^{2})))}{12 e^{- H β} - 6 (2 - H β (2 - H β))} .$ (45)

Pressure drops over the length of rectangular cross section is given by the following formula

$Δ \bar{p} (L) = \bar{p} (0) - \bar{p} (L),$ (46)

which reduces to

$Δ \bar{p} (L) = \frac{- e^{- H β} L (- Q_{0} + L V_{0}) β^{3}}{4 - 4 e^{- H β} - 2 H β (2 - H β)} .$ (47)

2.1.4. Wall shear stress

Shear forces are very crucial in the viscous flow with variable viscosity and support to find the resistance on plane which are penned as follows

${τ_{w} |}_{y = H} = - µ (y) {(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x})}_{y = H},$ (48)

Invoking Eqs (31,32) in above equation, we attained

${τ_{w} |}_{y = H} = \frac{H (Q_{0} - 2 V_{0} x) β^{3}}{4 - 4 e^{- H β} - 2 H β (2 - H β)} .$ (49)

2.1.5. Fractional reabsorption and leakage flux

The ratio of reabsorption to filtration rate can be measured by the following formula

$F A = \frac{Q (0) - Q (L)}{Q (0)} = \frac{2 V_{0} L}{Q_{0}}$ (50)

Leakage flux is given by the following formula

$q (x) = - \frac{d Q (x)}{d x} = 2 V_{0} .$ (51)

2.2. Linear viscosity

Case II: $µ (y) = 1 - β y$

In this case we will take the following viscosity

$µ (y) = 1 - β y, β > 0,$ (52)

After injecting Eq (52) and Eq (9) in Eqs (2,3), we get

$\frac{\partial p}{\partial x} = 2 (1 - β y) \frac{\partial^{3} ψ}{\partial x^{2} \partial y} + \frac{\partial}{\partial y} {(1 - β y) (\frac{\partial^{2} ψ}{\partial y^{2}} - \frac{\partial^{2} ψ}{\partial x^{2}})},$ (53)

$\frac{\partial p}{\partial y} = (1 - β y) \frac{\partial}{\partial x} (\frac{\partial^{2} ψ}{\partial y^{2}} - \frac{\partial^{2} ψ}{\partial x^{2}}) + 2 \frac{\partial}{\partial y} {(1 - β y) (- \frac{\partial^{2} ψ}{\partial x \partial y})} .$ (54)

Reducing pressure gradient from Eqs (53,54), one can obtain the compatibility equation in terms of stream function

$(1 - β y) \nabla^{4} ψ - 2 β \frac{\partial}{\partial y} (\nabla^{2} ψ) = 0,$ (55)

where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}$ .

There will be no change in Eq (55) after using non-dimensional quantities given in Eq (16)

2.2.1. Solution of the problem

Substituting Eq (21) into the Eq (55) to get

$(1 - β y) \frac{d^{4} R}{d y^{4}} - 2 β \frac{d^{3} R}{d y^{3}} = 0,$ (56)

$(1 - β y) \frac{d^{4} T}{d y^{4}} - 2 β \frac{d^{3} T}{d y^{3}} = 0.$ (57)

On solving Eqs (56,57) under the boundary conditions (24-27), we get the solution

$R (y) = \frac{V_{0} (- 2 y β \ln (- β + H β^{2}) - 2 \ln (1 - y β) - y β (2 + 2 H β - y β - 2 \ln (- β + y β^{2})))}{- H β (- 2 - H β) + 2 \ln (1 - H β)},$ (58)

and

$T (y) = \frac{Q_{0} (2 y β \ln (- β + H β^{2}) + 2 \ln (1 - y β) - y β (- 2 - 2 H β + y β + 2 \ln (- β + y β^{2})))}{- 2 H β (- 2 - H β) + 4 \ln (1 - H β)},$ (59)

Invoking R(y) and T(y) into Eq. (21) to get the following stream function

$ψ (x, y) = \frac{(2 y β \ln (- β + H β^{2}) + 2 \ln (1 - y β) - y β (- 2 - 2 H β + y β + 2 \ln (- β + y β^{2})))}{2 H β (2 + H β) + 4 \ln (1 - H β)} (Q_{0} - 2 V_{0} x) .$ (60)

2.2.2. Velocity field

With the aid of Eq (9) and Eq (60), flow field in axial and vertical direction are found as follows

$u (x, y) = \frac{- (Q_{0} - 2 V_{0} x) β (- (H - y) β - \ln (- β + H β^{2}) + \ln (- β + y β^{2}))}{H β (2 + H β) + 2 ln (1 - H β)},$ (61)

and

$v (x, y) = \frac{V_{0} (2 y β \ln (- β + H β^{2}) + 2 \ln (1 - y β) - y β (- 2 - 2 H β + y β + 2 \ln (- β + y β^{2})))}{H β (2 + H β) + 2 ln (1 - H β)} .$ (62)

Horizontal velocity is maximum at y = 0.

$u_{m a x} = \frac{- (Q_{0} - 2 V_{0} x) β (- H β + ln (- β) - \ln (- β + H β^{2}))}{H β (2 + H β) + 2 ln (1 - H β)},$ (63)

and v(x, y) is maximum at y = H.

$v_{m a x} = V_{0} .$ (64)

Flow rate within the four-sided slit is attained by using Eq (61) in Eq (35).

$Q (x) = Q_{0} - 2 V_{0} x .$ (65)

2.2.3. Pressure distribution

To find pressure, Eqs (53,54) can be composed in following manner

$\frac{\partial p}{\partial x} = - β (x \frac{d^{2} R}{d y^{2}} + \frac{d^{2} T}{d y^{2}}) + (1 - β y) (x \frac{d^{3} R}{d y^{3}} + \frac{d^{3} T}{d y^{3}}),$ (66)

$\frac{\partial p}{\partial y} = - (1 - β y) \frac{d^{2} R}{d y^{2}} + 2 β \frac{d R}{d y} .$ (67)

By using Eqs (58,59) in Eqs (66,67) to get

$\frac{\partial p}{\partial x} = \frac{(Q_{0} - 2 V_{0} x) β^{3}}{H β (2 + H β) + 2 \ln (1 - H β)},$ (68)

$\frac{\partial p}{\partial y} = \frac{2 V_{0} β^{2} (- 2 H β + 3 y β - 2 \ln (- β + H β^{2}) + 2 \ln (- β + y β^{2}))}{H β (2 + H β) + 2 \ln (1 - H β)} .$ (69)

Integrating Eq (69) yields

$p (x, y) = \frac{(Q_{0} - V_{0} x) x β^{3}}{H β (2 + H β) + 2 \ln (1 - H β)} + H (y),$ (70)

where H(y) is given by as follows

$H (y) = \frac{- V_{0} β (4 y β \ln (- β + H β^{2}) + 4 \ln (1 - y β) - y β (- 4 - 4 H β + 3 y β + 4 \ln (- β + y β^{2})))}{H β (2 + H β) + 2 \ln (1 - H β)} + C,$ (71)

where C is an arbitrary factor. Using Eq (71) in Eq (70), we can write the subsequent form of pressure

$p (x, y) - p (0, 0) = - β (- β (Q_{0} x β + V_{0} (- x^{2} β + y (- 4 - 4 H β + 3 y β))) + 4 V_{0} (\ln (1 - y β) - y β (- \ln (- β + H β^{2}) + \ln (- β + y β^{2})))) / H β (2 + H β) + 2 ln (1 - H β),$ (72)

where p(0, 0) shows the pressure at entrance of the slit.

Mean pressure drop can be find by substituting the value of p(x, y) − p(0, 0) in Eq (44) as follows

$\overset{̅}{p} (x) = V_{0} (\frac{1}{H} - 2 β) + \frac{(H^{2} V_{0} + x (Q_{0} - V_{0} x)) β^{3}}{H β (2 + H β) + 2 \ln (1 - H β)} .$ (73)

To get the pressure drop over the length L, invoke the values of p(0) and p(L) in Eq (47).

$Δ \bar{p} (L) = - \frac{L (Q_{0} - L V_{0}) β^{3}}{H β (2 + H β) + 2 ln (1 - H β)} .$ (74)

2.2.4. Wall shear stress

Invoking Eqs (61,62) in Eq (48) to attain wall shear stress

${τ_{w} |}_{y = H} = - \frac{H (Q_{0} - 2 V_{0} x) β^{3}}{(1 - H β) (H β (2 + H β) + 2 \ln (1 - H β))} .$ (75)

3. Constant viscosity

Case III: If we apply the limit β → 0 on Eq 31, 32 and 43 and solving the resulting expressions by the L' Hospital rule, one can attain the results of constant viscosity µ which are same as mentioned in Ref. [12].

$ψ (x, y) = \frac{1}{2} (\frac{Q_{0}}{2} - V_{0} x) \frac{y}{H} (3 - {(\frac{y}{H})}^{2}),$ (76)

$u (x, y) = \frac{3 (Q_{0} - 2 V_{0} x)}{4 H} (1 - {(\frac{y}{H})}^{2}),$ (77)

$v (x, y) = \frac{V_{0}}{2} \frac{y}{H} (3 - {(\frac{y}{H})}^{2}),$ (78)

$p (x, y) - p (0, 0) = - \frac{3 µ (Q_{0} - V_{0} x) x}{2 H^{3}} - \frac{3 µ V_{0} y^{2}}{2 H^{3}} .$ (79)

4. Application to kidneys flow

We have utilized biological data of mammalian kidneys to find the values of V₀ and Δp in artificial renal tubule which is assumed to be the permeable channel. In this study length of artificial renal tubule (slit) is chosen to be L = 0.12cm and height of slit has considered as H = 0.0005cm, average viscosity µ = 6.9×10⁻³dynsec/cm², Q₀ = 1.25×10⁻⁴cm³/sec, β = 2.5×10⁻³/cm and W = 0.1 cm (as $H ≪ W$ ) from Zhang et al [24]. Table 1 shows the calculated values of mean pressure and reabsorption rate for the constant and variable viscosity. As cited in Refs. (Mehboob et. al. [21], Layton et al [22], Korkmaz et al [25], Herranz et al [26] and Tortora et al [27] in usual conditions glomerulus pressure is assumed to be about $45 m m H g (59995.07433675 d y n / c m^{2})$ which is above the average pressure than that observed in tubes elsewhere in the body. It has stated in Table 1 the reducing values of reabsorption rate causes to lower the fractional reabsorption, but the average pressure drop in the renal tubule enhances with the falling values of reabsorption rate, also the assumption of variable viscosity indicate that average pressure drop is elevated as matched with the case of constant viscosity.

The results of this study are beneficial to measure the change in pressure compared to the fractional reabsorption because the viscosity of the liquid decay near the boundary which is the consequence of lubricating nature of permeable wall. The numerical values given in table 1 indicate that the various rate of reabsorption requires the different mean pressure which may be supportive for the patients of nephrotic disorder. The present data from table 1 also support the person that how much intake of fluid is needed to generate the mean pressure next to the filtration rate which has examined by the blood CP and urine test.

Table 1. Fractional reabsorption, reabsorption rate of fluid and pressure variation for persistent (constant) viscosity and variable viscosity in a renal tubule.

Viscosity	FA	90%	80%	70%	60%
	V₀cm/sec	4.7×10⁻³	4.2×10⁻³	3.6×10⁻³	3.1×10⁻³
Constant	Δp(0.12)dyn/cm²	1212.19	2404.51	3835.3	5027.62
Variable	Δp(0.12)dyn/cm²	6460.62	7025.69	7703.78	8268.84

| Show Table

DownLoad: CSV

5. Results

Figure 2. Effect of V₀ at entrance region (x = 0.1).

DownLoad: Full-Size Img PowerPoint

Figure 3. Effect of β at entrance region (x = 0.1).

DownLoad: Full-Size Img PowerPoint

Figure 4. Effect of V₀ at middle region (x = 0.5).

DownLoad: Full-Size Img PowerPoint

Figure 5. Effect of β at middle region (x = 0.5).

DownLoad: Full-Size Img PowerPoint

Figure 6. Effect of V₀ at exit region (x = 0.9).

DownLoad: Full-Size Img PowerPoint

Figure 7. Effect of β at exit region (x = 0.9).

DownLoad: Full-Size Img PowerPoint

Figure 8. Effect of V₀ in the tranverse direction of flow.

DownLoad: Full-Size Img PowerPoint

Figure 9. Effect of β in the transverse direction of flow.

DownLoad: Full-Size Img PowerPoint

Figure 10. Effect of V₀ on pressure difference.

DownLoad: Full-Size Img PowerPoint

Figure 11. Effect of β on pressure difference.

DownLoad: Full-Size Img PowerPoint

Figure 12. Effect of V₀ on wall shear stress.

DownLoad: Full-Size Img PowerPoint

Figure 13. Effect of β on wall shear stress.

DownLoad: Full-Size Img PowerPoint

Figure 14. (a) V₀ = 0.4, (b) V₀ = 1.2, (c) V₀ = 1.5.

DownLoad: Full-Size Img PowerPoint

Figure 15. (a) β = 0.1, (b) β = 0.2, (c) β = 0.65.

DownLoad: Full-Size Img PowerPoint

6. Discussion

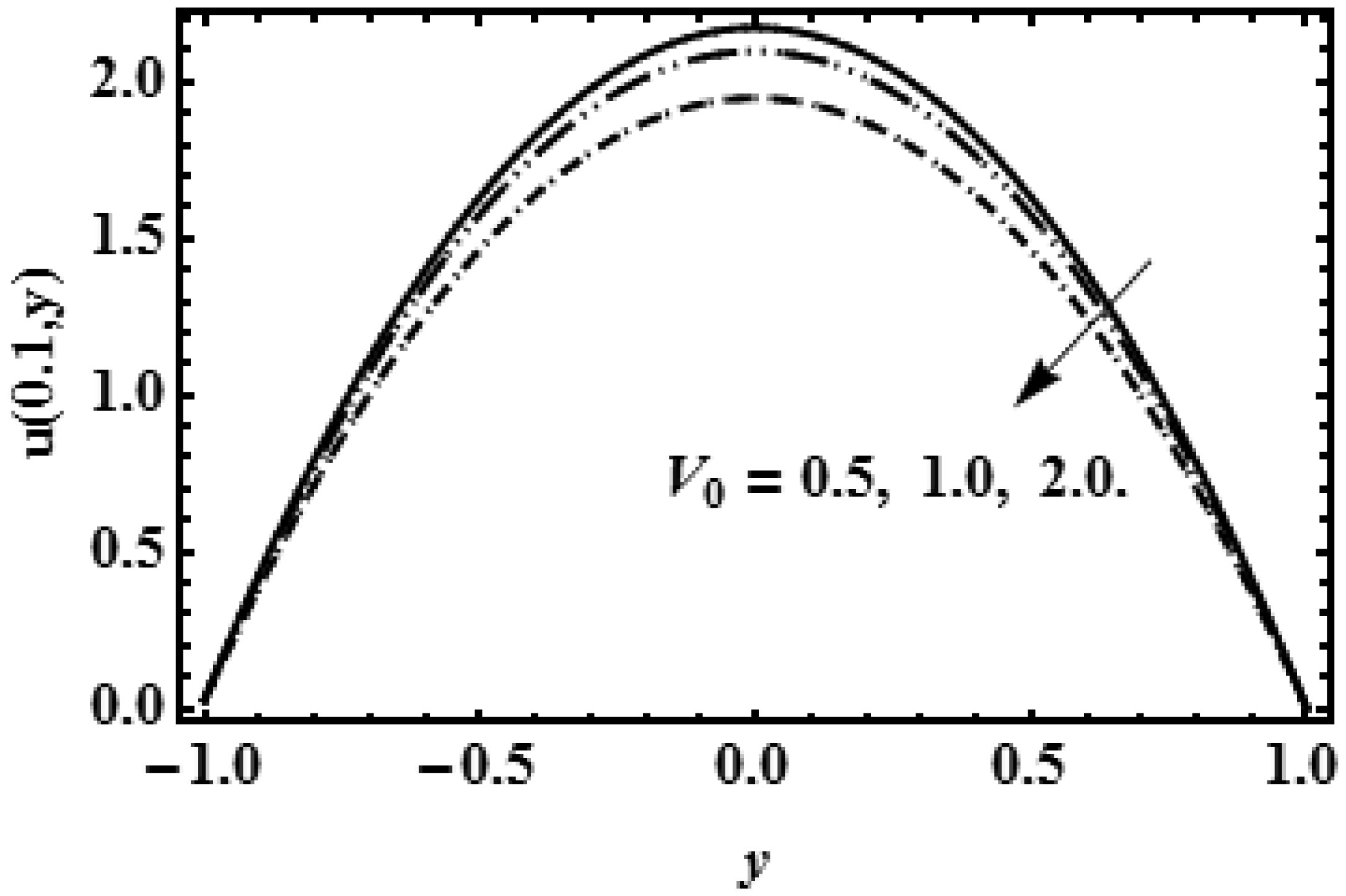
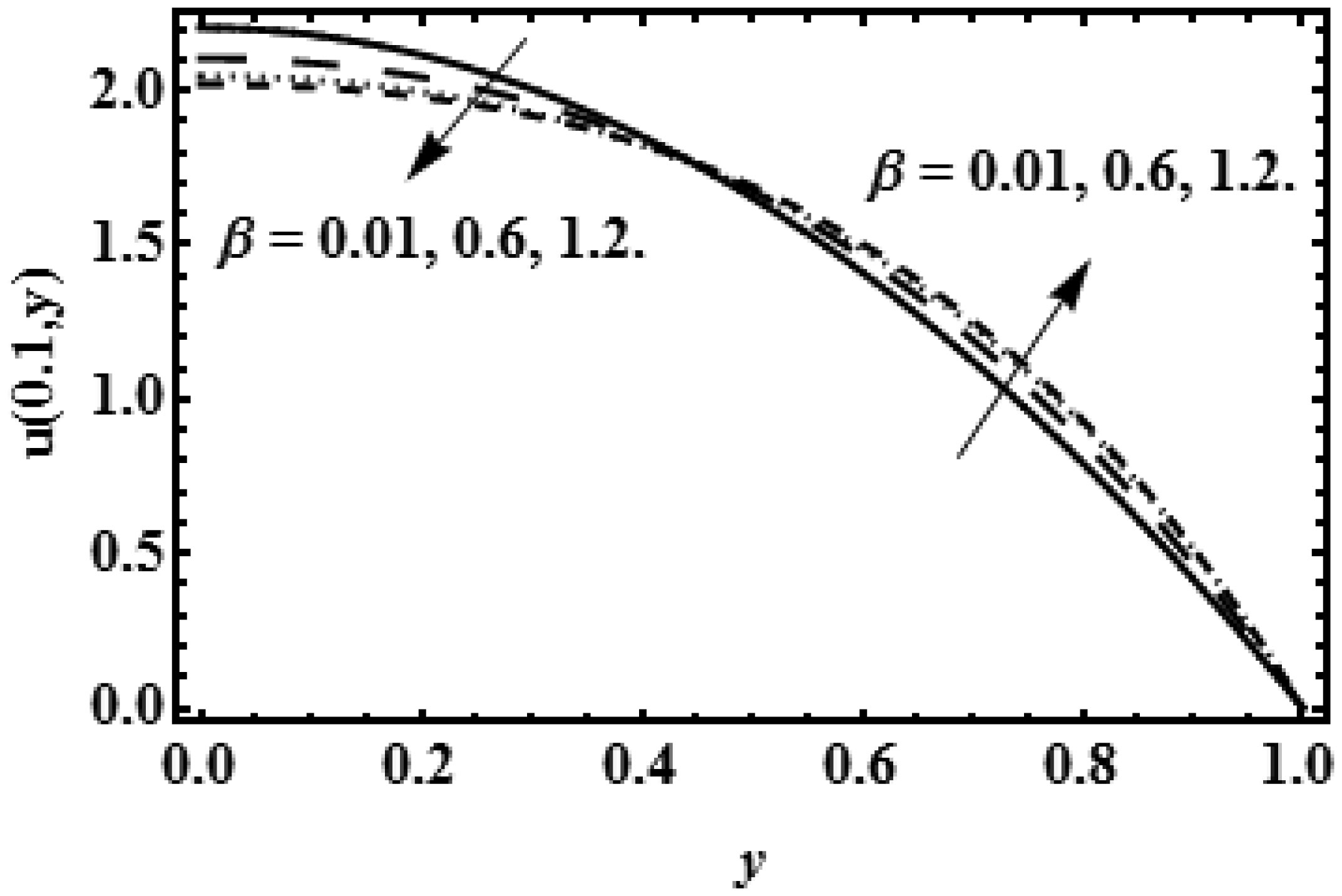
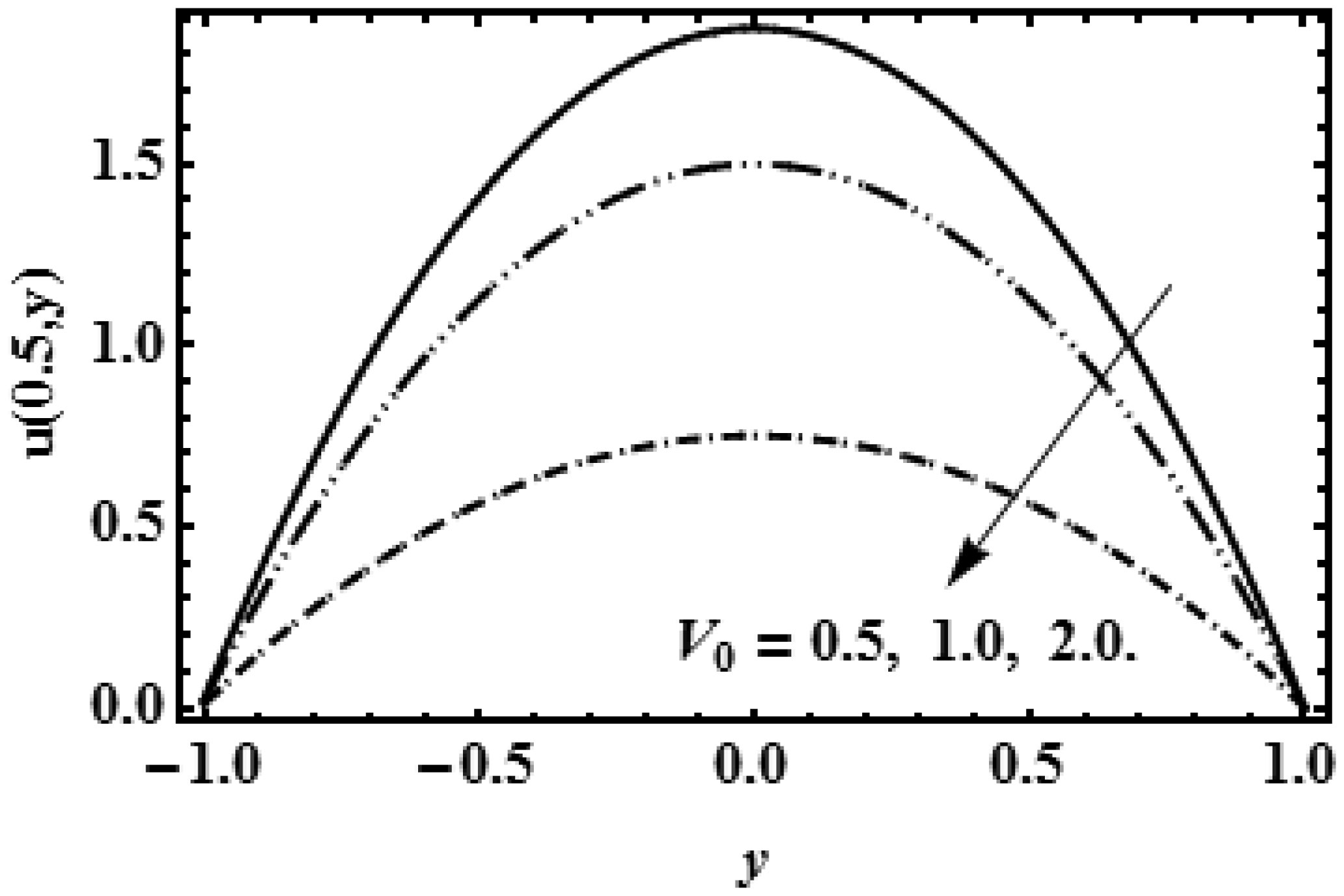
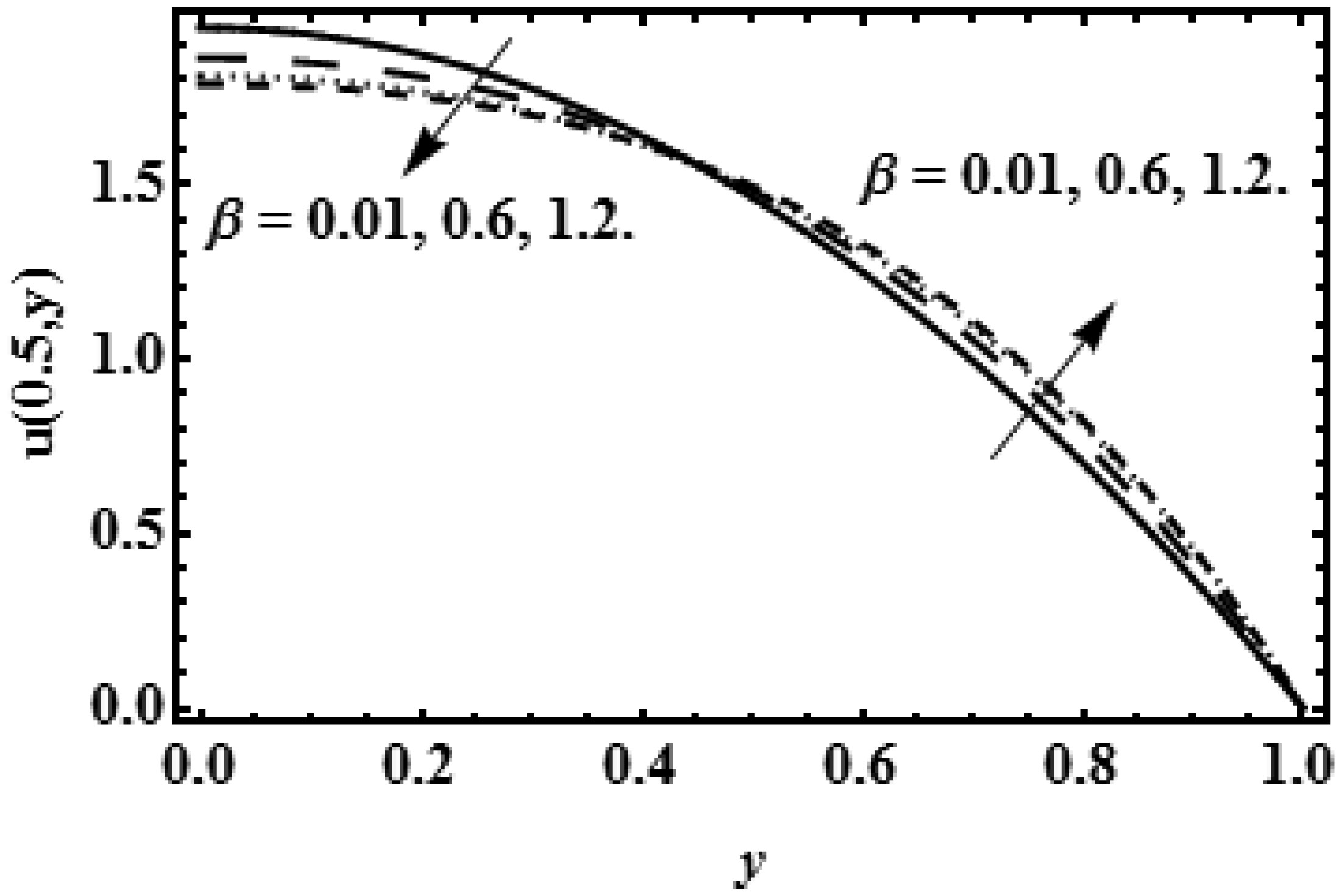
In this research the mathematical results of flow speed, flow pattern, pressure and shearing force are presented by the graphs which are plotted in software Mathematica under the effect of different values of reabsorption velocity V₀ and viscosity parameter β at x = 0.1, x = 0.5, x = 0.9, which are entry, central and leaving points of the rectangular cross section respectively.

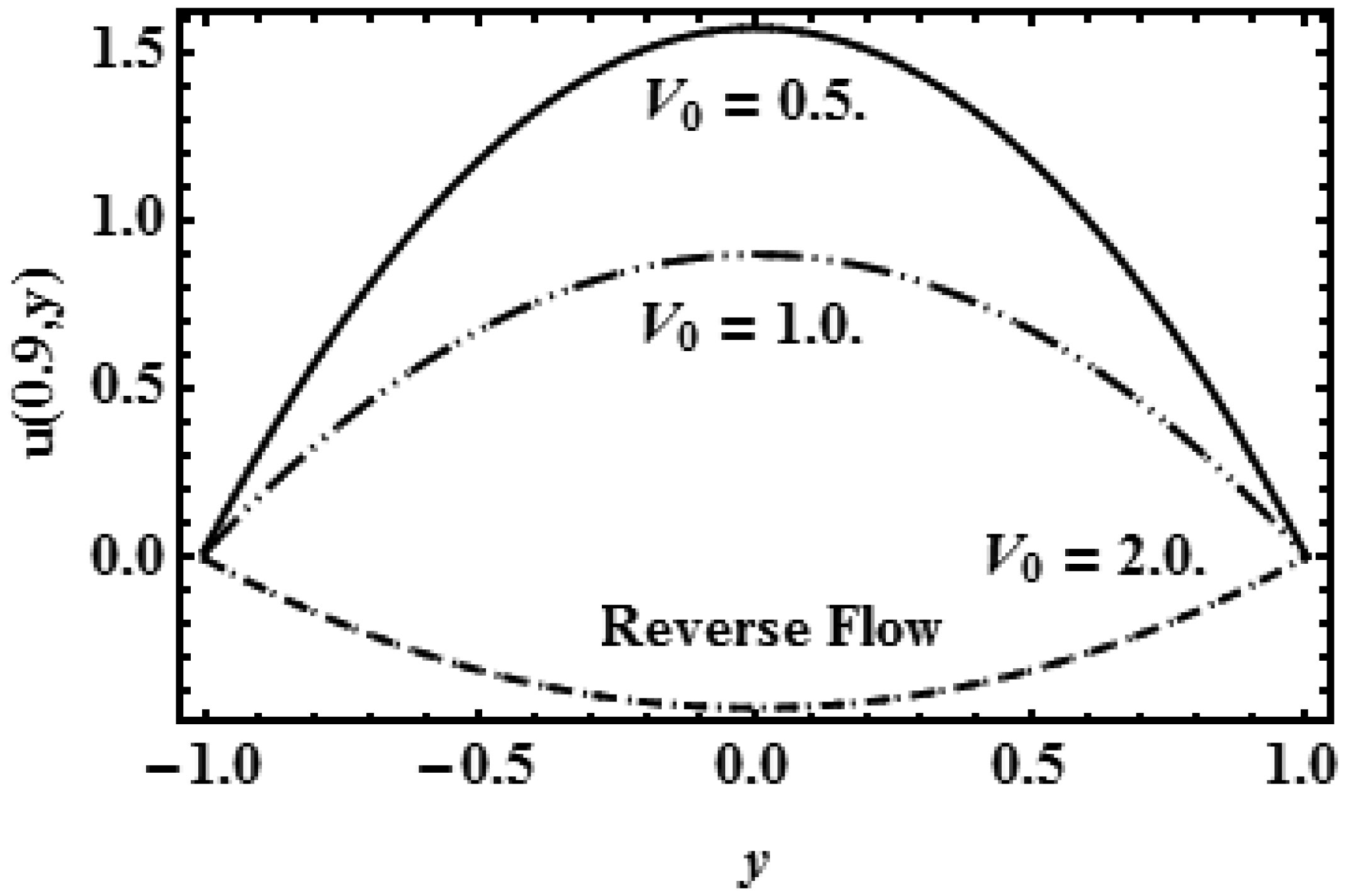
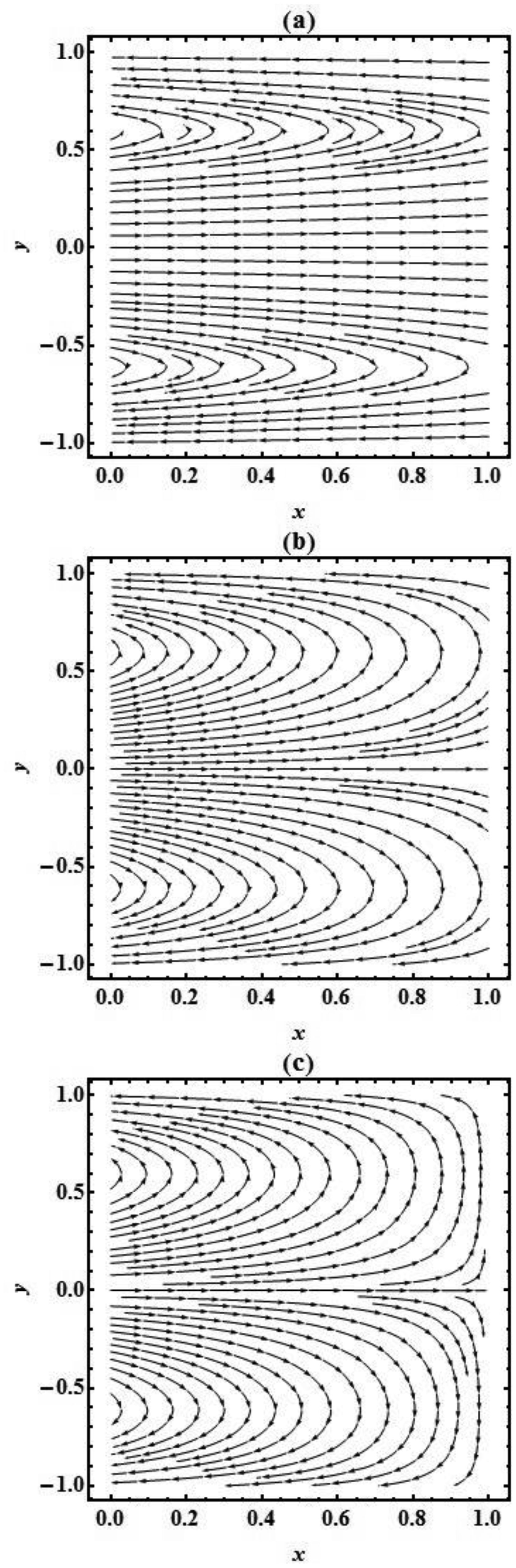
Figures (2), (4) and (6) show the decaying effect of reabsorption rate V₀ on axial velocity at the points x = 0.1, 0.5, 0.9 on the slit and observe that decay is swifter near the center region (x = 0.5) but near the departure region (x = 0.9) back flow has been examined. It has been noted that near the centre of slit drift is highest due to change in pressure and near the borders of slit (y = h) the fluid movement become motionless due to deposition of the particles (reabsorption V₀).

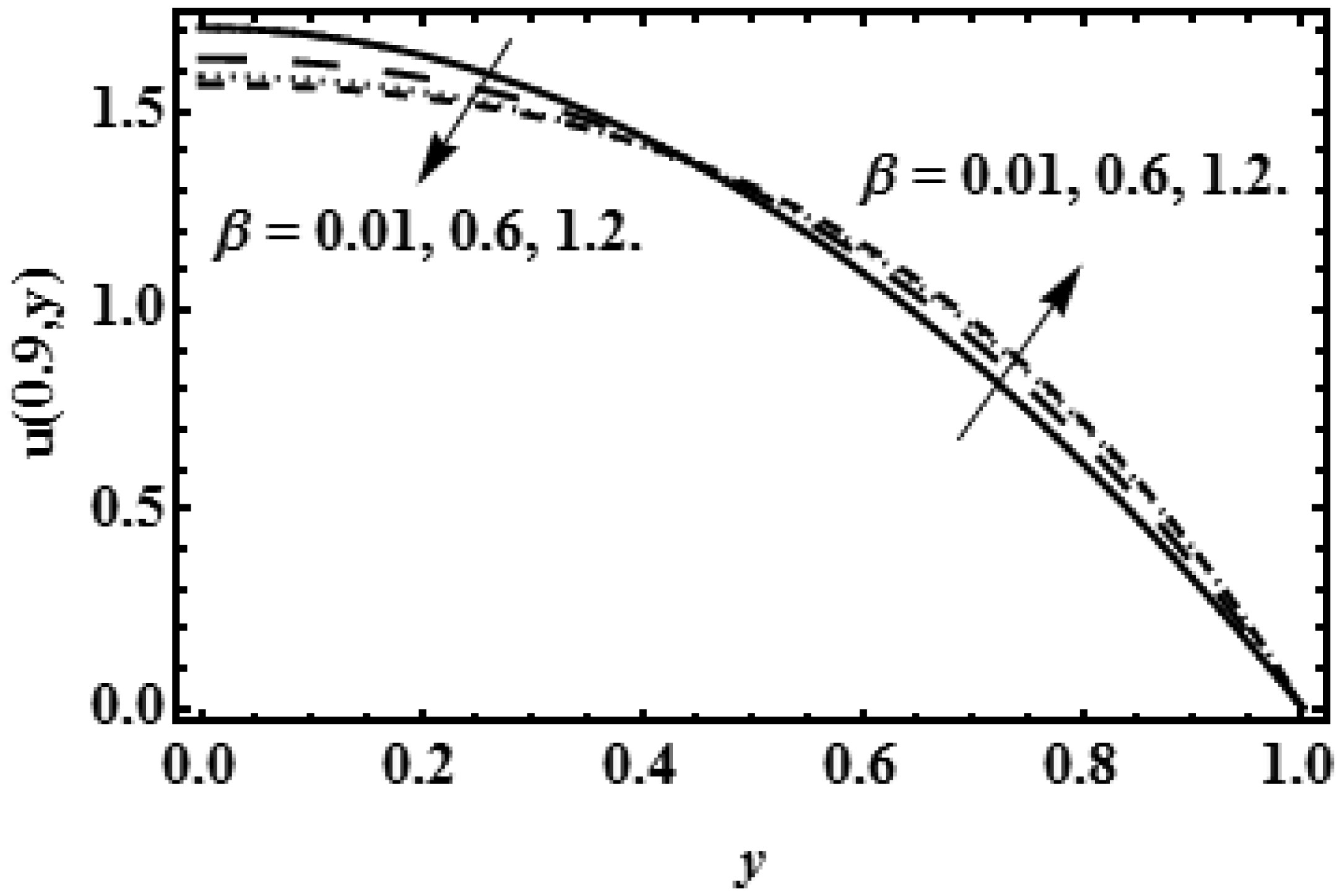
Figures (3), (5) and (7) explain the decelerating impact of viscosity parameter β on axial rate near the center of the slit at the points x = 0.1, 0.5, 0.9 of the slit. The axial flow rises away from the centre (y = h) and decays near the centre line (y = 0) due to the growing values of viscosity parameter β, because resistance at the boundary wall (y = h) makes the motionless flow at the boundary but the resistive forces become stronger near the centre of slit (y = 0) due to pressure gradient $\frac{d p}{d x}$ which helps to make the decreasing effect on axial velocity.

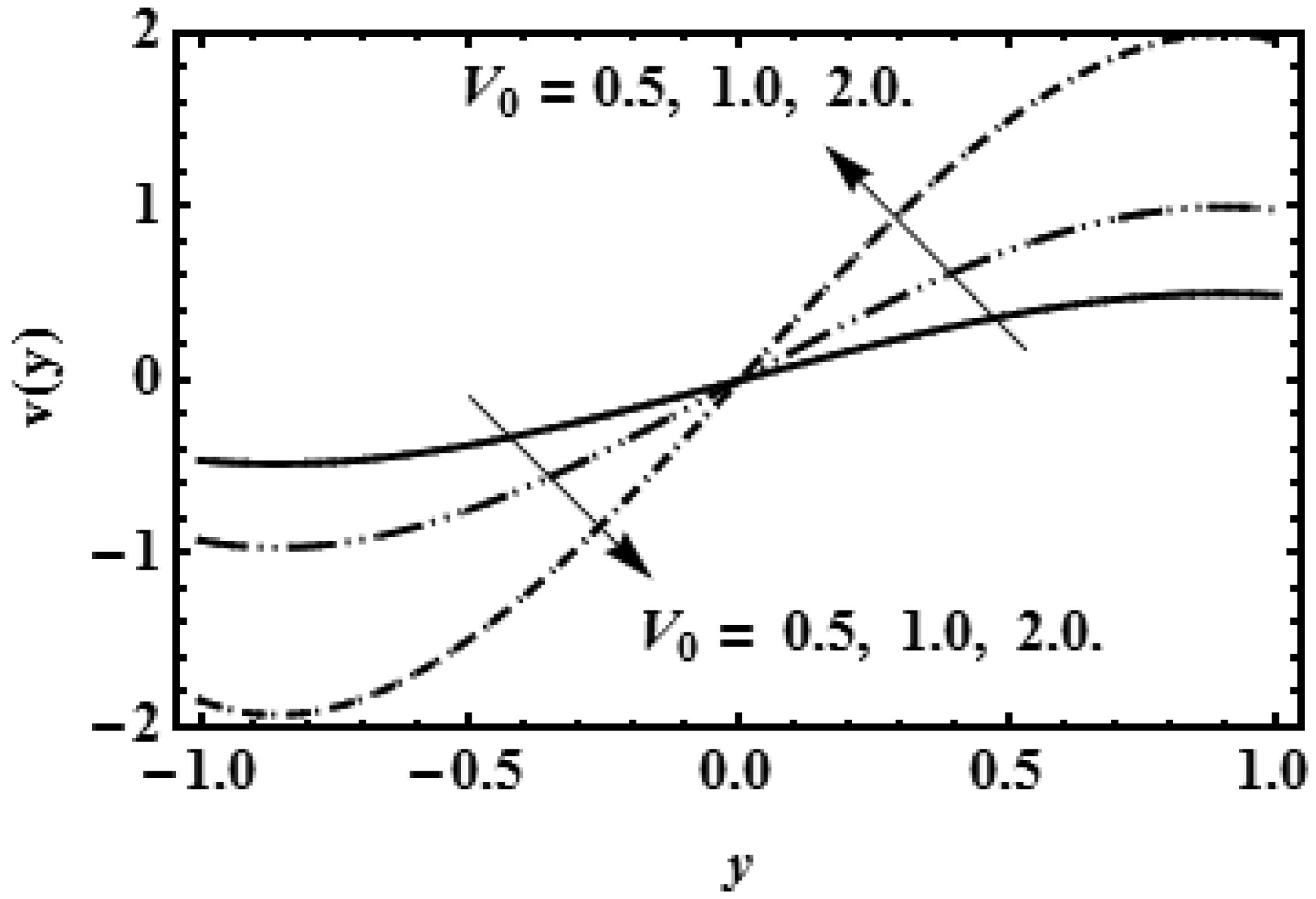
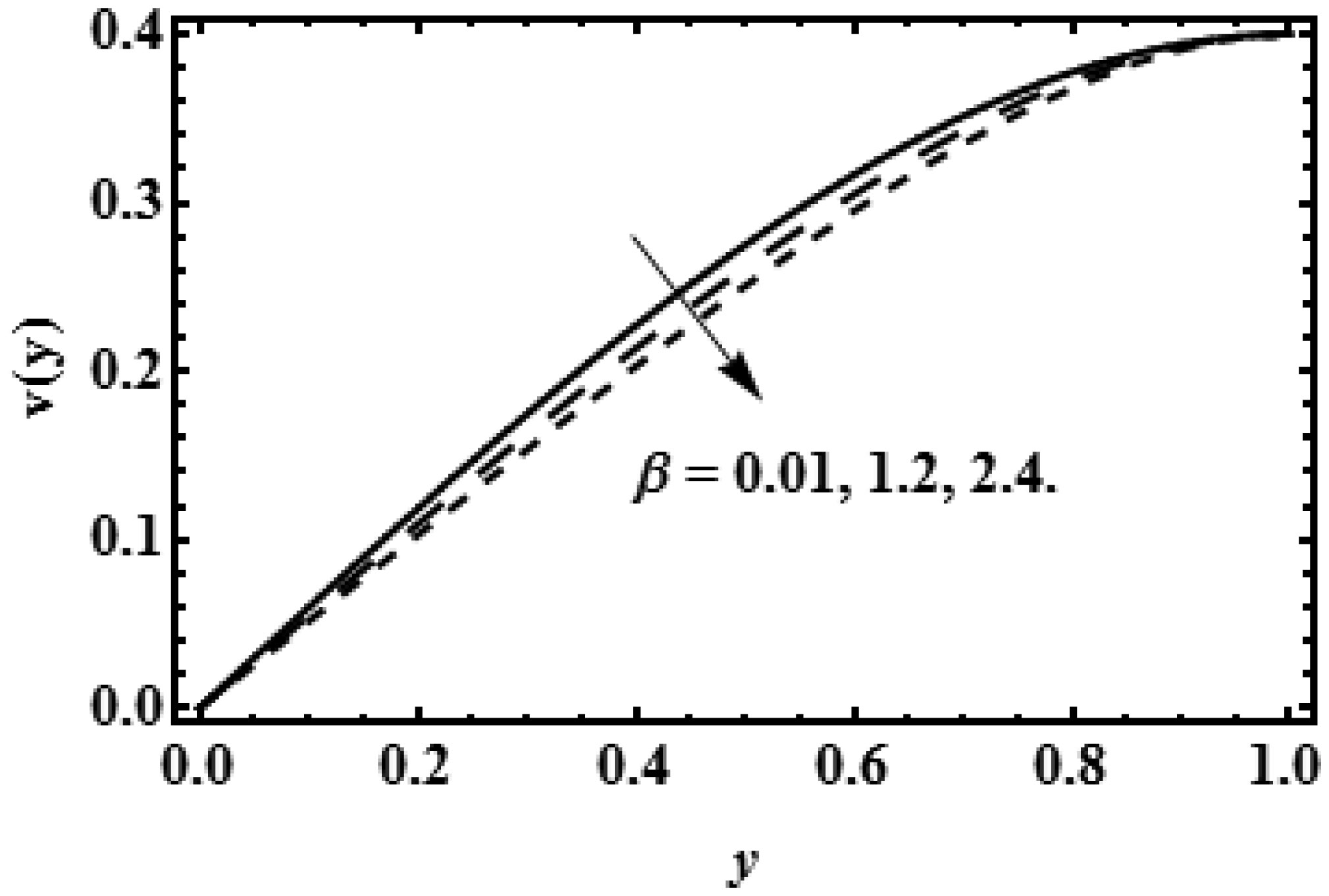
Figure 8 illustrates the variation of reabsorption rate V₀ at the vertical direction of flow field, which displays the symmetry about the centre line (y = 0). The presence of reabsorption V₀ indicates the growing effect on the transverse flow near the permeable membrane of renal tube. Decaying effect of viscosity parameter β on the vertical flow is displayed through the Figure 9, it is observed that the resistive force retards the movement of the fluid molecules in vertical direction.

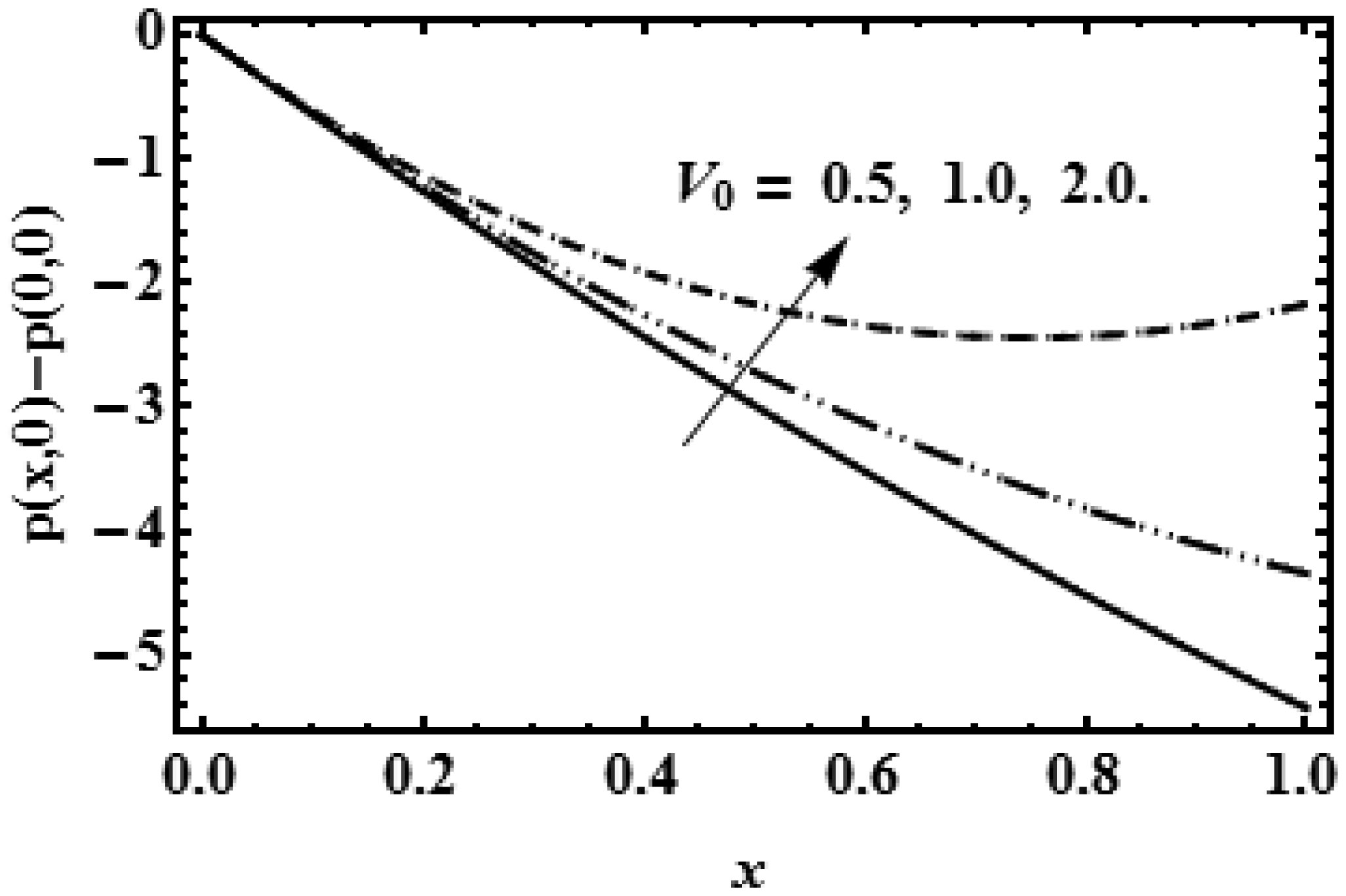
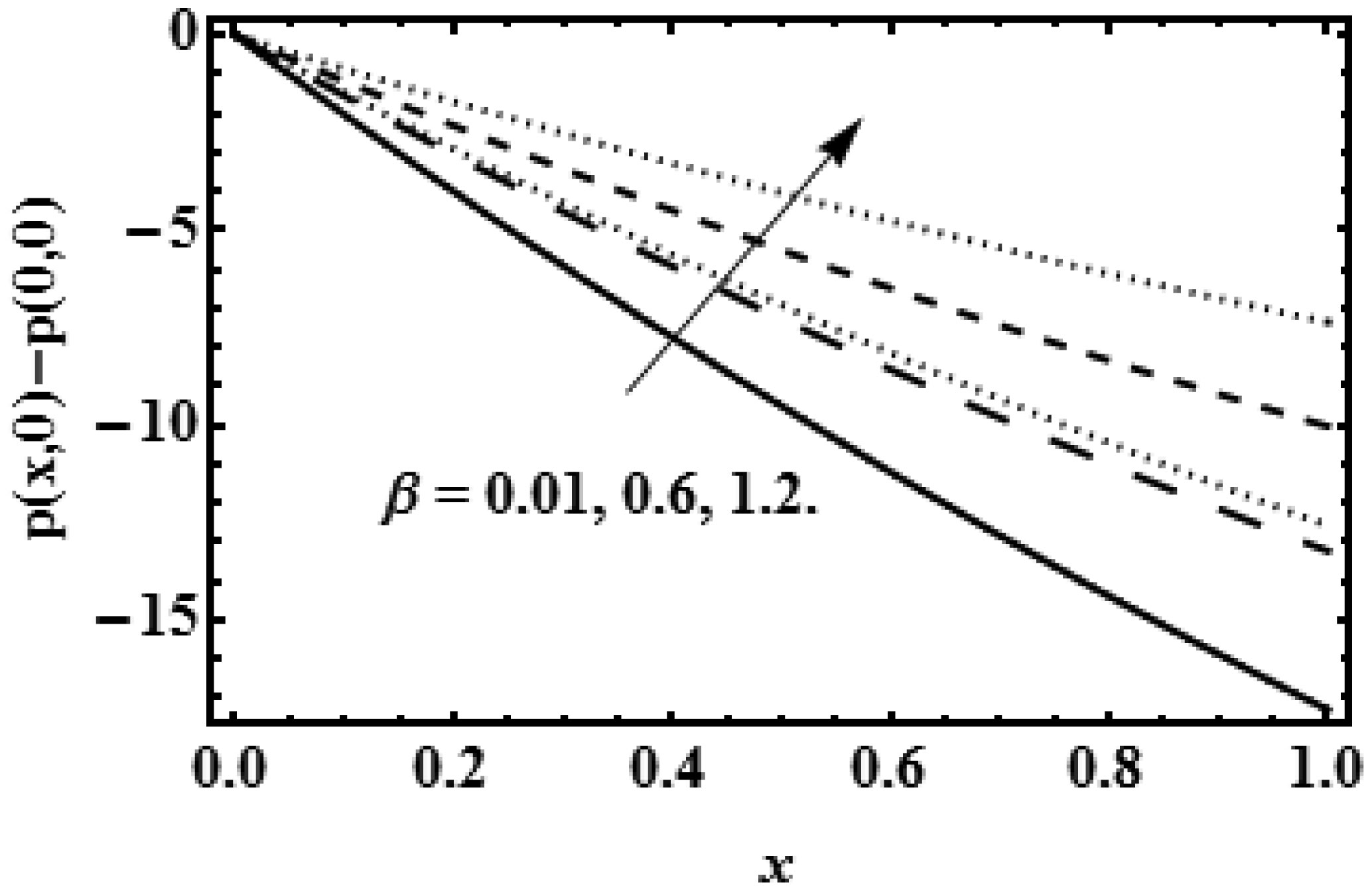
The pressure p plays a vital role for the flow of viscous fluid, therefore graphical results for pressure p are displayed in Figure 10 and Figure 11. The decreasing effect of reabsorption velocity V₀ on pressure difference is displayed in Figure 10 which shows that presence of reabsorption V₀ on the membrane require the low change in pressure for the viscous flow through permeable channel and the pressure at the entrance x = 0.1 is high as compared with the other region x = 0.9 of the slit. Figure 11 indicates that rising values of β help to reduce the pressure difference from entry point x = 0.1 to the centre line y = 0, which is evidenced that decreasing viscosity β help to reduce the pressure for the viscous fluid flow.

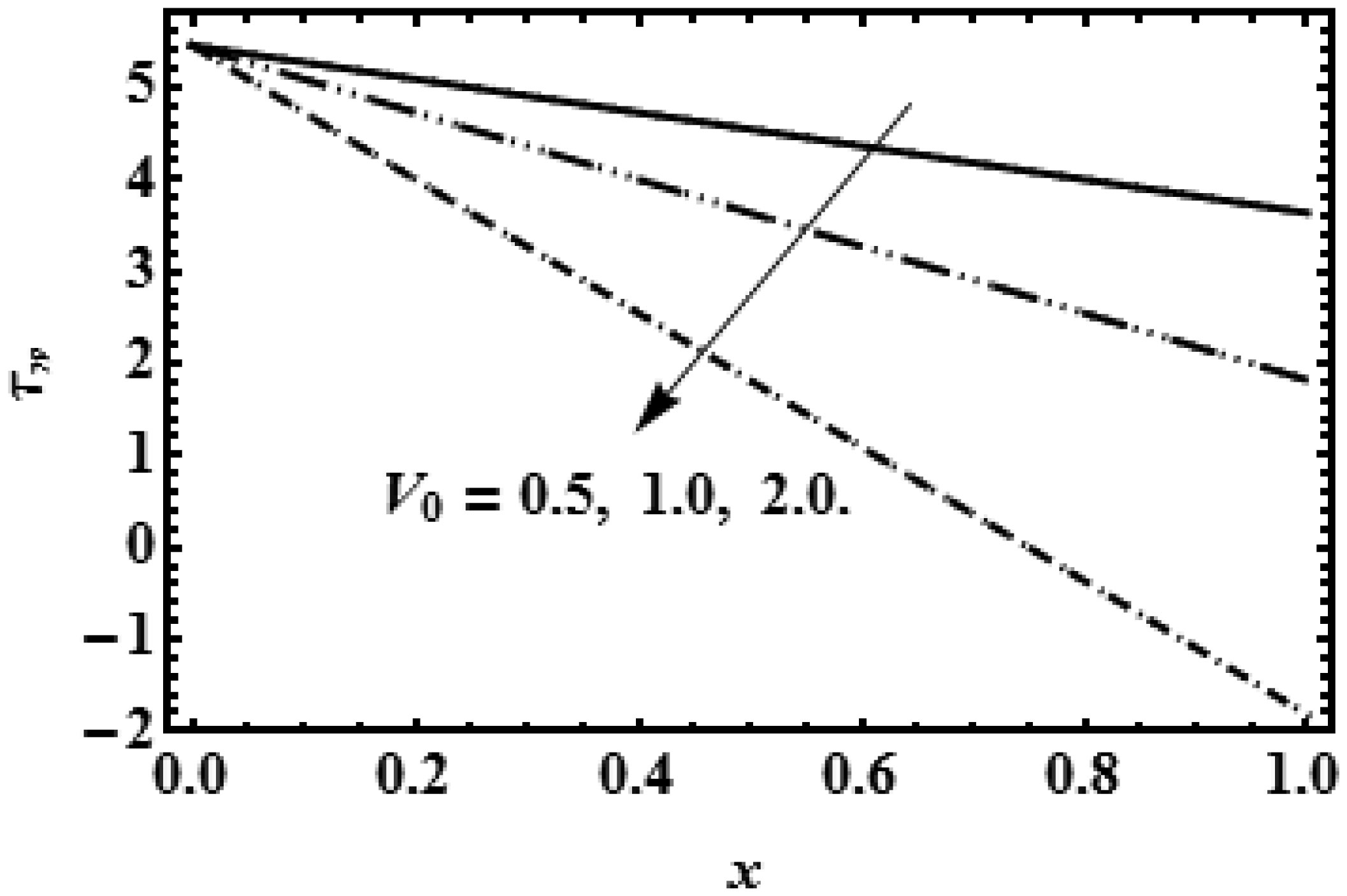
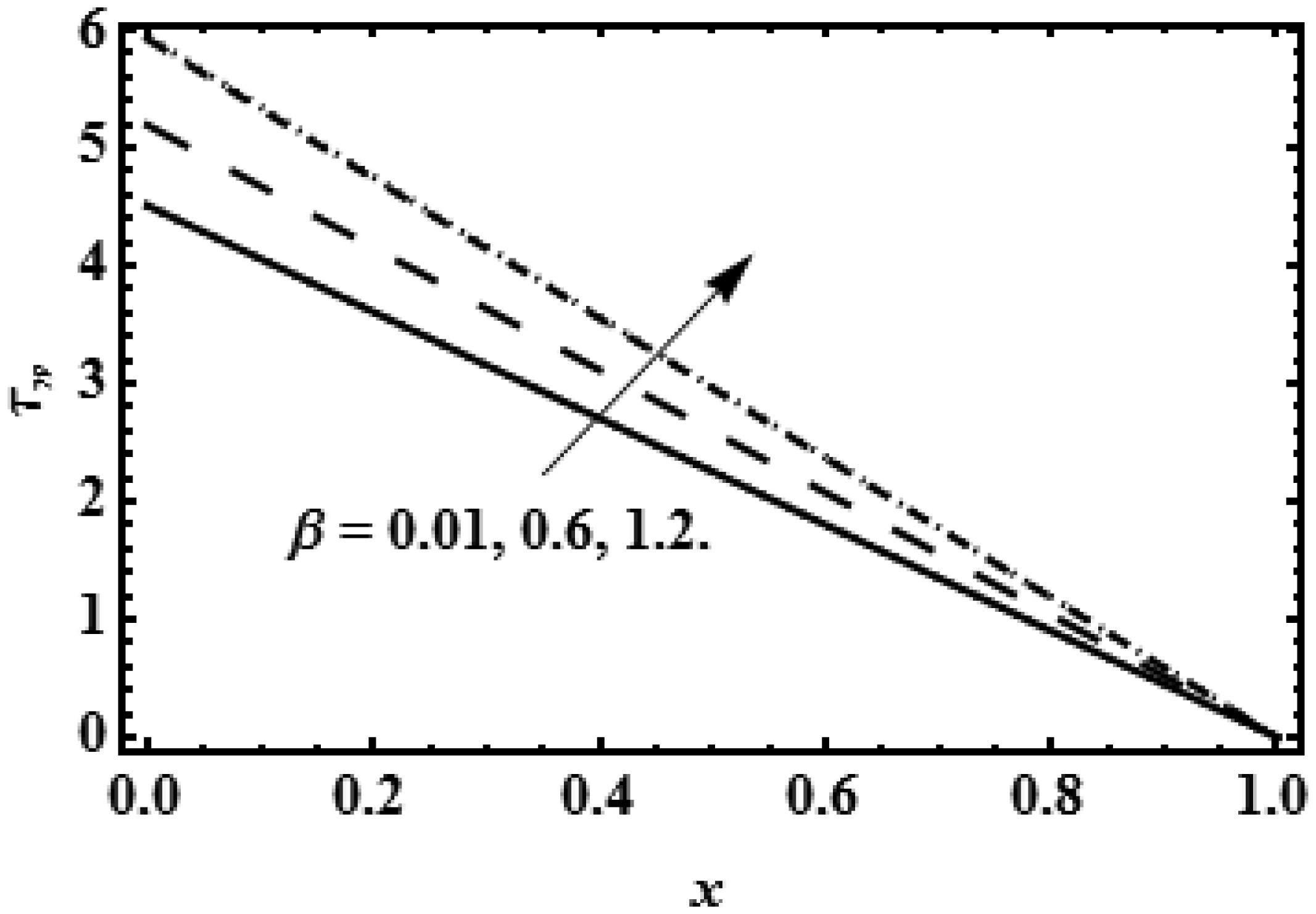
When the fluid is in contact with the surface then wall shear stress is an important phenomenon on the boundary surface. The variation in wall shear stress against V₀ is described in Figure 12 which shows the reduction in the shear stress on the wall with the mounting values of reabsorption V₀. The constant reabsorption V₀ on the wall helps to reduce the shearing forces on the permeable wall, which indicates that flow across the tube move easily without the large load. The rising values of parameter β results to improve the shearing forces on the wall because the growing values of β increases the resistance near the boundary wall which requires the high load for the fluid flow near the boundary.

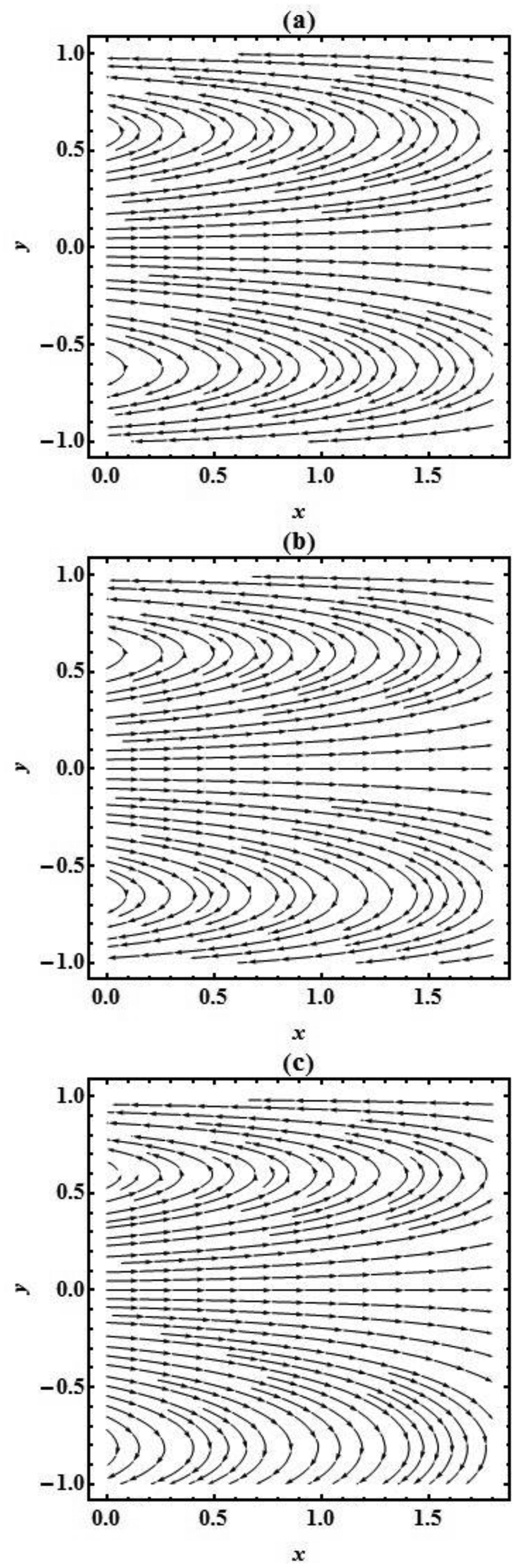
The pattern of the flow field can be observed by the streamlines which are plotted in Figure 14 (a-c) and Figure 15 (a-c). It is examined that addition in reabsorption velocity V₀ triggers the number of lines which indicates that the fluid is becoming thin in the presence of reabsorption V₀, but the number of streamlines reduces with the mounting values of viscosity parameter β which indicates that fluid is going to be thin, and it contains more resistance for the fluid flow.

7. Conclusions

This research presents the mathematical modelling of plasma flow through the renal tube, the two-dimensional slit in rectangular coordinate is considered in the analogy of proximal renal tube and viscous fluid is assumed as a plasma with variable viscosity from centre line to the boundary surface due to reabsorption on the permeable wall. The complex mathematical model is solved by the inverse method and exact expression for flow speed, load, shear force and filtration are calculated. The application of the present study is presented with the numerical data present in the literature. The special cases for the linear and constant reabsorption are also obtained and observed that results of constant reabsorptions match with the existing results (Haroon et al. [12]) which validates the current research. The impact of reabsorption and viscosity parameter on the physical quantities of the flow field are observed through graphs. The numerical results of mean pressure and constant reabsorption against filtration rate show that constant viscosity of the plasma in slit requires less amount of average pressure but the biofluid having variable viscosity along the slit requires high average pressure for the fluid flow.

References

[1]	Gibbs GM, Roelants K, O'Bryan MK (2008) The CAP superfamily: cysteine-rich secretory proteins, antigen 5, and pathogenesis-related 1 proteins--roles in reproduction, cancer, and immune defense. Endocr Rev 29: 865–897.
[2]	Gibbs GM, O'Bryan MK (2007) Cysteine rich secretory proteins in reproduction and venom. Soc Reprod Fertil Suppl 65: 261–267.
[3]	Yamazaki Y, Morita T (2004) Structure and function of snake venom cysteine-rich secretory proteins. Toxicon 44: 227–231.
[4]	Choudhary V, Schneiter R (2012) Pathogen-Related Yeast (PRY) proteins and members of the CAP superfamily are secreted sterol-binding proteins. Proc Natl Acad Sci USA 109: 16882–16887.
[5]	Xu X, Francischetti IM, Lai R, et al. (2012) Structure of protein having inhibitory disintegrin and leukotriene scavenging functions contained in single domain. J Biol Chem 287: 10967–10976.
[6]	Kelleher A, Darwiche R, Rezende WC, et al. (2014) Schistosoma mansoni venom allergen-like protein 4 (SmVAL4) is a novel lipid-binding SCP/TAPS protein that lacks the prototypical CAP motifs. Acta Crystallogr D Biol Crystallogr 70: 2186–2196.
[7]	Milne TJ, Abbenante G, Tyndall JD, et al. (2003) Isolation and characterization of a cone snail protease with homology to CRISP proteins of the pathogenesis-related protein superfamily. J Biol Chem 278: 31105–31110.
[8]	Eberle HB, Serrano RL, Fullekrug J, et al. (2002) Identification and characterization of a novel human plant pathogenesis-related protein that localizes to lipid-enriched microdomains in the Golgi complex. J Cell Sci 115: 827–838.
[9]	Serrano RL, Kuhn A, Hendricks A, et al. (2004) Structural analysis of the human Golgi-associated plant pathogenesis related protein GAPR-1 implicates dimerization as a regulatory mechanism. J Mol Biol 339: 173–183.
[10]	Shoji-Kawata S, Sumpter R, Leveno M, et al. (2013) Identification of a candidate therapeutic autophagy-inducing peptide. Nature 494: 201–206.
[11]	Kuballa P, Nolte WM, Castoreno AB, et al. (2012) Autophagy and the immune system. Annu Rev Immunol 30: 611–646.
[12]	Eberle HB, Serrano RL, Fullekrug J, et al. (2002) Identification and characterization of a novel human plant pathogenesis-related protein that localizes to lipid-enriched microdomains in the Golgi complex. J Cell Sci 115: 827–838.
[13]	Zhou Q, Hao L, Huang W, et al. (2016) The Golgi-Associated Plant Pathogenesis-Related Protein GAPR-1 Enhances Type I Interferon Signaling Pathway in Response to Toll-Like Receptor 4. Inflammation 39: 706–717.
[14]	Baxter RM, Crowell TP, George JA, et al. (2007) The plant pathogenesis related protein GLIPR-2 is highly expressed in fibrotic kidney and promotes epithelial to mesenchymal transition in vitro. Matrix Biol 26: 20–29.
[15]	Aalberts M, van Dissel-Emiliani FM, van Adrichem NP, et al. (2012) Identification of distinct populations of prostasomes that differentially express prostate stem cell antigen, annexin A1, and GLIPR2 in humans. Biol Reprod 86: 82:1–8.
[16]	Van Galen J, Van Balkom BW, Serrano RL, et al. (2010) Binding of GAPR-1 to negatively charged phospholipid membranes: unusual binding characteristics to phosphatidylinositol. Mol Membr Biol 27: 81–91.
[17]	van Galen J, Olrichs NK, Schouten A, et al. (2012) Interaction of GAPR-1 with lipid bilayers is regulated by alternative homodimerization. Biochim Biophys Acta 1818: 2175–2183.
[18]	Olrichs NK, Mahalka AK, Kaloyanova D, et al. (2014) Golgi-Associated plant Pathogenesis Related protein 1 (GAPR-1) forms amyloid-like fibrils by interaction with acidic phospholipids and inhibits Abeta aggregation. Amyloid 21: 88–96.
[19]	Yoshiike Y, Minai R, Matsuo Y, et al. (2008) Amyloid oligomer conformation in a group of natively folded proteins. PLoS One 3: e3235.
[20]	Schwarzman AL, Gregori L, Vitek MP, et al. (1994) Transthyretin sequesters amyloid beta protein and prevents amyloid formation. Proc Natl Acad Sci USA 91: 8368–8372.
[21]	Chen J, Yagi H, Sormanni P, et al. (2012) Fibrillogenic propensity of the GroEL apical domain: a Janus-faced minichaperone. FEBS Lett 586: 1120–1127.
[22]	Rekas A, Ahn KJ, Kim J, et al. (2012) The chaperone activity of alpha-synuclein: Utilizing deletion mutants to map its interaction with target proteins. Proteins 80: 1316–1325.
[23]	Ofengeim D, Ito Y, Najafov A, et al. (2015) Activation of necroptosis in multiple sclerosis. Cell Rep 10: 1836–1849.
[24]	Zhang L, Qu S, Liang A, et al. (2015) Gene expression microarray analysis of the sciatic nerve of mice with diabetic neuropathy. Int J Mol Med 35: 333–339.
[25]	Karlsson O, Berg AL, Hanrieder J, et al. (2015) Intracellular fibril formation, calcification, and enrichment of chaperones, cytoskeletal, and intermediate filament proteins in the adult hippocampus CA1 following neonatal exposure to the nonprotein amino acid BMAA. Arch Toxicol 89: 423–436.
[26]	Nishi H, Hashimoto K, Madej T, et al. (2013) Evolutionary, physicochemical, and functional mechanisms of protein homooligomerization. Prog Mol Biol Transl Sci 117: 3–24.
[27]	Marianayagam NJ, Sunde M, Matthews JM (2004) The power of two: protein dimerization in biology. Trends Biochem Sci 29: 618–625.
[28]	Ali MH, Imperiali B (2005) Protein oligomerization: how and why. Bioorg Med Chem 13: 5013–5020.
[29]	Wang X, Sharp JS, Handel TM, et al. (2013) Chemokine oligomerization in cell signaling and migration. Prog Mol Biol Transl Sci 117: 531–578.
[30]	Zimmerberg J, Kozlov MM (2006) How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol 7: 9–19.
[31]	Park PS, Filipek S, Wells JW, et al. (2004) Oligomerization of G protein-coupled receptors: past, present, and future. Biochemistry 43: 15643–15656.
[32]	Adi-Harel S, Erlich S, Schmukler E, et al. (2010) Beclin 1 self-association is independent of autophagy induction by amino acid deprivation and rapamycin treatment. J Cell Biochem 110: 1262–1271.
[33]	Ku B, Woo JS, Liang C, et al. (2008) An insight into the mechanistic role of Beclin 1 and its inhibition by prosurvival Bcl-2 family proteins. Autophagy 4: 519–520.
[34]	Chiti F, Dobson CM (2006) Protein misfolding, functional amyloid, and human disease. Annu Rev Biochem 75: 333–366.
[35]	Dobson CM (2003) Protein folding and misfolding. Nature 426: 884–890.
[36]	Iannuzzi C, Irace G, Sirangelo I (2015) The effect of glycosaminoglycans (GAGs) on amyloid aggregation and toxicity. Molecules 20: 2510–2528.
[37]	Oskarsson ME, Singh K, Wang J, et al. (2015) Heparan Sulfate Proteoglycans Are Important for Islet Amyloid Formation and Islet Amyloid Polypeptide-induced Apoptosis. J Biol Chem 290: 15121–15132.
[38]	Kinnunen PK (2009) Amyloid Formation on Lipid Membrane Surfaces. The Open Biology Journal 2: 163–175.
[39]	Burke KA, Yates EA, Legleiter J (2013) Biophysical insights into how surfaces, including lipid membranes, modulate protein aggregation related to neurodegeneration. Front Neurol 4: 17.
[40]	Sunde M, Serpell LC, Bartlam M, et al. (1997) Common core structure of amyloid fibrils by synchrotron X-ray diffraction. J Mol Biol 273: 729–739.
[41]	Glabe CG (2008) Structural classification of toxic amyloid oligomers. J Biol Chem 283: 29639–29643.
[42]	Kayed R, Lasagna-Reeves CA (2013) Molecular mechanisms of amyloid oligomers toxicity. J Alzheimers Dis 33 Suppl 1: S67–78.
[43]	Breydo L, Uversky VN (2015) Structural, morphological, and functional diversity of amyloid oligomers. FEBS Lett 589: 2640–2648.
[44]	Haass C, Selkoe DJ (2007) Soluble protein oligomers in neurodegeneration: lessons from the Alzheimer's amyloid beta-peptide. Nat Rev Mol Cell Biol 8: 101–112.
[45]	Kagan BL, Jang H, Capone R, et al. (2012) Antimicrobial properties of amyloid peptides. Mol Pharm 9: 708–717.
[46]	Greenwald J, Riek R (2012) On the possible amyloid origin of protein folds. J Mol Biol 421: 417–426.
[47]	Gsponer J, Babu MM (2012) Cellular strategies for regulating functional and nonfunctional protein aggregation. Cell Rep 2: 1425–1437.
[48]	Fowler DM, Koulov AV, Balch WE, et al. (2007) Functional amyloid--from bacteria to humans. Trends Biochem Sci 32: 217–224.
[49]	Maji SK, Perrin MH, Sawaya MR, et al. (2009) Functional amyloids as natural storage of peptide hormones in pituitary secretory granules. Science 325: 328–332.
[50]	Puzzo D, Arancio O (2013) Amyloid-beta peptide: Dr. Jekyll or Mr. Hyde? J Alzheimers Dis 33 Suppl 1: S111–20.
[51]	Hervas R, Li L, Majumdar A, et al. (2016) Molecular Basis of Orb2 Amyloidogenesis and Blockade of Memory Consolidation. PLoS Biol 14: e1002361.
[52]	Jacob RS, George E, Singh PK, et al. (2016) Cell Adhesion on Amyloid Fibrils Lacking Integrin Recognition Motif. J Biol Chem .
[53]	Halfmann R, Jarosz DF, Jones SK, et al. (2012) Prions are a common mechanism for phenotypic inheritance in wild yeasts. Nature 482: 363–368.
[54]	Li J, McQuade T, Siemer AB, et al. (2012) The RIP1/RIP3 necrosome forms a functional amyloid signaling complex required for programmed necrosis. Cell 150: 339–350.
[55]	Parry TL, Melehani JH, Ranek MJ, et al. (2015) Functional Amyloid Signaling via the Inflammasome, Necrosome, and Signalosome: New Therapeutic Targets in Heart Failure. Front Cardiovasc Med 2: 25.
[56]	Rapsinski GJ, Wynosky-Dolfi MA, Oppong GO, et al. (2015) Toll-like receptor 2 and NLRP3 cooperate to recognize a functional bacterial amyloid, curli. Infect Immun 83: 693–701.
[57]	Heneka MT, Kummer MP, Latz E (2014) Innate immune activation in neurodegenerative disease. Nat Rev Immunol 14: 463–477.
[58]	Maldera JA, Vasen G, Ernesto JI, et al. (2011) Evidence for the involvement of zinc in the association of CRISP1 with rat sperm during epididymal maturation. Biol Reprod 85: 503–510.
[59]	Lu S, Faris JD, Sherwood R, et al. (2014) A dimeric PR-1-type pathogenesis-related protein interacts with ToxA and potentially mediates ToxA-induced necrosis in sensitive wheat. Mol Plant Pathol 15: 650–663.
[60]	Borloo J, Geldhof P, Peelaers I, et al. (2013) Structure of Ostertagia ostertagi ASP-1: insights into disulfide-mediated cyclization and dimerization. Acta Crystallogr D Biol Crystallogr 69: 493–503.
[61]	Prados-Rosales RC, Roldan-Rodriguez R, Serena C, et al. (2012) A PR-1-like protein of Fusarium oxysporum functions in virulence on mammalian hosts. J Biol Chem 287: 21970–21979.
[62]	Sugiyama H, Burnett L, Xiang X, et al. (2009) Purification and multimer formation of allurin, a sperm chemoattractant from Xenopus laevis egg jelly. Mol Reprod Dev 76: 527–536.
[63]	Asojo OA, Goud G, Dhar K, et al. (2005) X-ray structure of Na-ASP-2, a pathogenesis-related-1 protein from the nematode parasite, Necator americanus, and a vaccine antigen for human hookworm infection. J Mol Biol 346: 801–814.
[64]	Ma D, Francischetti IM, Ribeiro JM, et al. (2015) The structure of hookworm platelet inhibitor (HPI), a CAP superfamily member from Ancylostoma caninum. Acta Crystallogr F Struct Biol Commun 71: 643–649.
[65]	Tsolis AC, Papandreou NC, Iconomidou VA, et al. (2013) A consensus method for the prediction of 'aggregation-prone' peptides in globular proteins. PLoS One 8: e54175.
[66]	Egge N, Muthusubramanian A, Cornwall GA (2015) Amyloid properties of the mouse egg zona pellucida. PLoS One 10: e0129907.
[67]	Guyonnet B, Egge N, Cornwall GA (2014) Functional amyloids in the mouse sperm acrosome. Mol Cell Biol 34: 2624–2634.
[68]	Swanson WJ, Aagaard JE, Vacquier VD, et al. (2011) The molecular basis of sex: linking yeast to human. Mol Biol Evol 28: 1963–1966.
[69]	Garcia MC, Lee JT, Ramsook CB, et al. (2011) A role for amyloid in cell aggregation and biofilm formation. PLoS One 6: e17632.
[70]	Da Ros VG, Munoz MW, Battistone MA, et al. (2015) From the epididymis to the egg: participation of CRISP proteins in mammalian fertilization. Asian J Androl 17: 711–715.
[71]	Caballero J, Frenette G, D'Amours O, et al. (2012) Bovine sperm raft membrane associated Glioma Pathogenesis-Related 1-like protein 1 (GliPr1L1) is modified during the epididymal transit and is potentially involved in sperm binding to the zona pellucida. J Cell Physiol 227: 3876–3886.
[72]	Busso D, Goldweic NM, Hayashi M, et al. (2007) Evidence for the involvement of testicular protein CRISP2 in mouse sperm-egg fusion. Biol Reprod 76: 701–708.
[73]	Doty A, Buhi WC, Benson S, et al. (2011) Equine CRISP3 modulates interaction between spermatozoa and polymorphonuclear neutrophils. Biol Reprod 85: 157–164.
[74]	Ernesto JI, Weigel Munoz M, Battistone MA, et al. (2015) CRISP1 as a novel CatSper regulator that modulates sperm motility and orientation during fertilization. J Cell Biol 210: 1213–1224.
[75]	Burnett LA, Xiang X, Bieber AL, et al. (2008) Crisp proteins and sperm chemotaxis: discovery in amphibians and explorations in mammals. Int J Dev Biol 52: 489–501.
[76]	Burnett LA, Anderson DM, Rawls A, et al. (2011) Mouse sperm exhibit chemotaxis to allurin, a truncated member of the cysteine-rich secretory protein family. Dev Biol 360: 318–328.
[77]	Usmani SM, Zirafi O, Muller JA, et al. (2014) Direct visualization of HIV-enhancing endogenous amyloid fibrils in human semen. Nat Commun 5: 3508.
[78]	Castellano LM, Shorter J (2012) The Surprising Role of Amyloid Fibrils in HIV Infection. Biology (Basel) 1: 58–80.
[79]	Doncel GF (2006) Exploiting common targets in human fertilization and HIV infection: development of novel contraceptive microbicides. Hum Reprod Update 12: 103–117.
[80]	Gebbink MF, Claessen D, Bouma B, et al. (2005) Amyloids--a functional coat for microorganisms. Nat Rev Microbiol 3: 333–341.
[81]	Garcia-Sherman MC, Lundberg T, Sobonya RE, et al. (2015) A unique biofilm in human deep mycoses: fungal amyloid is bound by host serum amyloid P component. NPJ Biofilms Microbiomes 1: 15009.
[82]	Syed AK, Boles BR (2014) Fold modulating function: bacterial toxins to functional amyloids. Front Microbiol 5: 401.
[83]	Pisa D, Alonso R, Rabano A, et al. (2015) Different Brain Regions are Infected with Fungi in Alzheimer's Disease. Sci Rep 5: 15015.
[84]	Oh J, Kim JG, Jeon E, et al. (2007) Amyloidogenesis of type III-dependent harpins from plant pathogenic bacteria. J Biol Chem 282: 13601–13609.
[85]	van Loon LC, Rep M, Pieterse CM (2006) Significance of inducible defense-related proteins in infected plants. Annu Rev Phytopathol 44: 135–162.
[86]	Van Loon LC, Van Strien EA (1999) The families of pathogenesis-related proteins, their activities, and comparative analysis of PR-1 type proteins. Physiol Mol Plant Pathol 55: 85–97.
[87]	Niderman T, Genetet I, Bruyere T, et al. (1995) Pathogenesis-related PR-1 proteins are antifungal. Isolation and characterization of three 14-kilodalton proteins of tomato and of a basic PR-1 of tobacco with inhibitory activity against Phytophthora infestans. Plant Physiol 108: 17–27.
[88]	Rauscher M, Adam AL, Wirtz S, et al. (1999) PR-1 protein inhibits the differentiation of rust infection hyphae in leaves of acquired resistant broad bean. Plant J 19: 625–633.
[89]	Benhamou N (1995) Immunocytochemistry of plant defense mechanisms induced upon microbial attack. Microsc Res Tech 31: 63–78.
[90]	Lee YK, Hippe-Sanwald S, Lee SC, et al. (2000) In situ localization of PR-1 mRNA and PR-1 protein in compatible and incompatible interactions of pepper stems with Phytophthora capsici. Protoplasma 211: 64–75.
[91]	Santén K, Marttila S, Liljeroth E, et al. (2005) Immunocytochemical localization of the pathogenesis-related PR-1 protein in barley leaves after infection by Bipolaris sorokiniana. Physiol Mol Plant Pathol 66: 45–54.
[92]	Teixeira PJ, Costa GG, Fiorin GL, et al. (2013) Novel receptor-like kinases in cacao contain PR-1 extracellular domains. Mol Plant Pathol 14: 602–609.
[93]	Jiang G, Hunter T (1999) Receptor signaling: when dimerization is not enough. Curr Biol 9: R568–71.
[94]	Chen YL, Lee CY, Cheng KT, et al. (2014) Quantitative peptidomics study reveals that a wound-induced peptide from PR-1 regulates immune signaling in tomato. Plant Cell 26: 4135–4148.
[95]	Chien PS, Nam HG, Chen YR (2015) A salt-regulated peptide derived from the CAP superfamily protein negatively regulates salt-stress tolerance in Arabidopsis. J Exp Bot 66: 5301–5313.
[96]	Buch F, Pauchet Y, Rott M, et al. (2014) Characterization and heterologous expression of a PR-1 protein from traps of the carnivorous plant Nepenthes mirabilis. Phytochemistry 100: 43–50.
[97]	Osman A, Wang CK, Winter A, et al. (2012) Hookworm SCP/TAPS protein structure--A key to understanding host-parasite interactions and developing new interventions. Biotechnol Adv 30: 652–657.
[98]	Moyle M, Foster DL, McGrath DE, et al. (1994) A hookworm glycoprotein that inhibits neutrophil function is a ligand of the integrin CD11b/CD18. J Biol Chem 269: 10008–10015.
[99]	Asojo OA (2011) Structure of a two-CAP-domain protein from the human hookworm parasite Necator americanus. Acta Crystallogr D Biol Crystallogr 67: 455–462.
[100]	Del Valle A, Jones BF, Harrison LM, et al. (2003) Isolation and molecular cloning of a secreted hookworm platelet inhibitor from adult Ancylostoma caninum. Mol Biochem Parasitol 129: 167–177.
[101]	Horn M, Bertling A, Brodde MF, et al. (2012) Human neutrophil alpha-defensins induce formation of fibrinogen and thrombospondin-1 amyloid-like structures and activate platelets via glycoprotein IIb/IIIa. J Thromb Haemost 10: 647–661.
[102]	Canobbio I, Abubaker AA, Visconte C, et al. (2015) Role of amyloid peptides in vascular dysfunction and platelet dysregulation in Alzheimer's disease. Front Cell Neurosci 9: 65.
[103]	Wang YL, Kuo JH, Lee SC, et al. (2010) Cobra CRISP functions as an inflammatory modulator via a novel Zn2+- and heparan sulfate-dependent transcriptional regulation of endothelial cell adhesion molecules. J Biol Chem 285: 37872–37883.
[104]	Alexandrescu AT (2005) Amyloid accomplices and enforcers. Protein Sci 14: 1–12.
[105]	Hughes AJ, Hussain R, Cosentino C, et al. (2012) A zinc complex of heparan sulfate destabilises lysozyme and alters its conformation. Biochem Biophys Res Commun 425: 794–799.
[106]	Berthelot K, Lecomte S, Coulary-Salin B, et al. (2016) Hevea brasiliensis prohevein possesses a conserved C-terminal domain with amyloid-like properties in vitro. Biochim Biophys Acta 1864: 388–399.
[107]	Lay FT, Mills GD, Poon IK, et al. (2012) Dimerization of plant defensin NaD1 enhances its antifungal activity. J Biol Chem 287: 19961–19972.
[108]	Poon IK, Baxter AA, Lay FT, et al. (2014) Phosphoinositide-mediated oligomerization of a defensin induces cell lysis. Elife 3: e01808.
[109]	Garvey M, Meehan S, Gras SL, et al. (2013) A radish seed antifungal peptide with a high amyloid fibril-forming propensity. Biochim Biophys Acta 1834: 1615–1623.
[110]	Marangon M, Van Sluyter SC, Waters EJ, et al. (2014) Structure of haze forming proteins in white wines: Vitis vinifera thaumatin-like proteins. PLoS One 9: e113757.
[111]	Yu XM, Griffith M (1999) Antifreeze proteins in winter rye leaves form oligomeric complexes. Plant Physiol 119: 1361–1370.

This article has been cited by:

1.	Martin Heida, Benedikt Jahnel, Anh Duc Vu, An ergodic and isotropic zero-conductance model with arbitrarily strong local connectivity, 2024, 29, 1083-589X, 10.1214/24-ECP633
2.	Martin Heida, Benedikt Jahnel, Anh Duc Vu, Regularized homogenization on irregularly perforated domains, 2025, 20, 1556-1801, 165, 10.3934/nhm.2025010

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Biophysics

1.1 2.4

Metrics

Article views(7405) PDF downloads(1523) Cited by(13)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Biophysics

Novel insights into the function of the conserved domain of the CAP superfamily of proteins

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. Exponential viscosity

2.1.1. Solution of the problem

2.1.2. Velocity distribution

2.1.3. Pressure

2.1.4. Wall shear stress

2.1.5. Fractional reabsorption and leakage flux

2.2. Linear viscosity

2.2.1. Solution of the problem

2.2.2. Velocity field

2.2.3. Pressure distribution

2.2.4. Wall shear stress

3. Constant viscosity

4. Application to kidneys flow

5. Results

6. Discussion

7. Conclusions

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Materials and methods

2.1. Exponential viscosity

2.1.1. Solution of the problem

2.1.2. Velocity distribution

2.1.3. Pressure

2.1.4. Wall shear stress

2.1.5. Fractional reabsorption and leakage flux

2.2. Linear viscosity

2.2.1. Solution of the problem

2.2.2. Velocity field

2.2.3. Pressure distribution

2.2.4. Wall shear stress

3. Constant viscosity

4. Application to kidneys flow

5. Results

6. Discussion

7. Conclusions

References