Skin dose enhancement from the application of skin-care creams using FF and FFF photon beams in radiotherapy: A Monte Carlo phantom evaluation

1.   Introduction

We study the following first-order coupled nonlinear system,

with $t\in \left[0, T\right]$ $(T > 0)$ and $f, g:\left[0, T\right] \times \mathbb{R}^{2}\rightarrow \mathbb{R}$ $L^{1}$-Carathéodory functions, together with the boundary conditions

The motivation for the study of systems (1.1) and (1.2) arise from the application of nonlinear models to several phenomena in different domains of life, namely population dynamics ^[1], neuroscience ^[2], biological systems ^[3], ecology ^[4], electronic circuits ^[5], celestial mechanics ^[6], among others.

Periodic solutions are usually found in differential equations. For example:

In ^[7], the authors present sufficient conditions for the solvability of a class of singular Sturm-Liouville equations with periodic boundary value conditions. The problem describes the periodic oscillations of the axis of a satellite in the plane of the elliptic orbit around its center of mass.

In ^[8], the authors study the stability of two coupled Andronov oscillators sharing a mutual discrete periodic interaction. The study was motivated by the phenomenon of synchronization observed in Huygens' clocks ^[9].

In ^[10], the authors prove the existence of positive periodic solutions in a generalized Nicholson's blowflies model, using Krasnoselskii cone fixed point theorem.

In ^[11], it is considered the dynamics of hematopoietic stem cell populations under some external periodic regulatory factors at the cellular cycle level. The existence of periodic solutions in the respective nonautonomous differential system is typically associated to the presence of some hematological disease.

However, nonlinear systems with non-oscillatory nonlinearities can hamper the search for periodic solutions.

To overcome that difficulty, in ^[12] the authors use well-ordered lower and upper solutions to guarantee the existence of solutions of a first-order fully coupled system. In ^[13], the authors introduce the idea of well-ordered coupled lower and upper solutions, to obtain an existence and localization result for periodic solutions of first-order coupled non-linear systems of $n$ ordinary differential equations.

Motivated by these works, in this paper we present some novelties: A new translation technique to deal with lower and upper solutions, not necessarily well-ordered; A method to provide sufficient conditions to obtain existence and localization results, combining the adequate coupled lower and upper solutions definition with the monotonicity of the nonlinearities.

This work is organized as follows. In Section 2 we present the definitions and the solvability conditions for problems (1.1) and (1.2). In Section 3, we present the main results regarding the existence and localization of solutions for the problem, using the lower and upper solutions technique, together with Schauder's fixed point theorem, and a numerical example. In Section 4 we adapt the solvability conditions of Section 2 to the lack of monotonicity criteria in the nonlinearities. We find coupled lower and upper solutions for the original problem. Finally, in Section 5, we present an application to a real case scenario of population dynamics.

2.   Definitions

In this work we consider the space of continuous functions in $[0, T],$ $\left(C[0, T]\right)^2,$ with the norm $\left\Vert (z, w) \right\Vert = \max \left\{ \left\Vert z \right\Vert, \left\Vert w \right\Vert \right\}$, with $\left\Vert u \right\Vert = \max_{t\in \lbrack 0, T]}\left\vert u (t) \right\vert$.

So, $(C[0, T])^2$ is a Banach space.

The nonlinearities assumed will be $L^{1}-$Carathéodory functions, that is:

Definition 2.1. The function $h:[0, T]\times \mathbb{R}^{2}\rightarrow \mathbb{R},$ is a $L^{1}-$Carathéodory if it verifies

$(i)$ for each $\left(y_{1}, y_{2}\right) \in \mathbb{R}^{2}$, $t\mapsto h(t, y_{1}, y_{2})$ is measurable in $[0, T];$

$(ii)$ for almost every $t\in \lbrack 0, T],$ $\left(y_{1}, y_{2}\right) \mapsto h(t, y_{1}, y_{2})$ is continuous in $\mathbb{R} ^{2};$

$(iii)$ for each $L > 0$, there exists a positive function $\psi _{L}\in L^{1}[0, T],$ such that, for $\max \left\{ \left\Vert y_{i}\right\Vert, i = 1, 2\right\} < L$,

A key argument in this work is the lower and upper solutions method, but not necessarily well-ordered as it is standard in the literature. This issue is overcome by a new type of lower and upper solutions' definition with some adequate translations:

Definition 2.2. Consider $C^{1}$-functions $\alpha _{i}, \beta _{i}:[0, T]\rightarrow \mathbb{R},$ $i = 1, 2.$ The functions $\left(\alpha _{1}, \alpha _{2}\right)$ are lower solutions of the periodic problems (1.1) and (1.2) if

with

and

The functions $\left(\beta _{1}, \beta _{2}\right)$ are upper solutions of the periodic problems (1.1) and (1.2) if

with

and

By solution we mean $(C^1[0, T])^2$ functions verifying (1.1) and (1.2). The existence tool is the Schauder's fixed-point theorem (Theorem 2.A of ^[14]):

Theorem 2.1. Let $Y$ be a nonempty, closed, bounded and convex subset of a Banach space $X$, and suppose that $P:Y\rightarrow Y$ is a compact operator. Then $P$ has at least one fixed point in $Y$.

3.   Existence and localization theorem

This method allows to obtain an existence and localization result for periodic non-trivial solutions in presence of well ordered lower and upper solutions:

Theorem 3.1. Let $\left(\alpha _{1}, \alpha _{2}\right)$ and $\left(\beta _{1}, \beta _{2}\right)$ be lower and upper solutions of (1.1) and (1.2), respectively$.$ Assume that $f$ is a $L^{1}$-Carathéodory function in the set

$g$ is a $L^{1}$-Carathéodory function in

with

for fixed $t\in \lbrack 0, T]$ and $y_{1}\in \mathbb{R}$, and

for fixed $t\in \lbrack 0, T]$ and $y_{2}\in \mathbb{R}$. Then problems (1.1) and (1.2) has, at least, a solution $(z, w)\in \left(C^1[0, T]\right) ^{2}$ such that

Proof. For $i = 1, 2,$ define the continuous functions $\delta_i^0:[0, T]\times \mathbb{R} \rightarrow \mathbb{R}$, given by

and

and consider the auxiliary problem composed by

together with the periodic boundary conditions (1.2).

Step 1. Integral form of (3.3) and (1.2).

The general solution of (3.3) and (1.2) is

with

and, by (1.2),

Therefore, the integral form of (3.3) and (1.2) is

Define the operator $T:(C[0, T])^{2}\rightarrow (C[0, T])^{2}$ such that

with

Following Definition 2.1, the norm of the operator $T$, defined in (3.6), is given by

Step 2. $T$ has a fixed point.

The conditions for Theorem 2.1 require the existence of a nonempty, bounded, closed and convex subset $D\subset \left(C\left[0, T \right] \right) ^{2}$ such that $TD\subset D$.

As $f,$ $g$ are $L^{1}$-Carathéodory functions, by Definition 2.1, there are positive $L^{1}[0, T]$ functions $\psi _{iL}, i = 1, 2$, such that

with

Consider the closed ball of radius $K$,

with $K$ given by

For $t\in \lbrack 0, T]$,

Similarly,

Since $T_{1}$ and $T_{2}$ are uniformly bounded, so is $T$.

Consider $t_{1}, t_{2}\in \lbrack 0, T]$ and $t_{1} < t_{2}$, without loss of generality. Then,

proving that $T_{1}$ is equicontinuous.

In the same way, it can be proved that $\big\lvert T_{2}(z(t_{1}), w(t_{1}))-T_{2}(z(t_{2}), w(t_{2}))\big\rvert \xrightarrow[t_1 \rightarrow t_2]{}0.$

Therefore, $T$ is equicontinuous.

By (3.12), it is clear that $TD\subset D$, then, by Schauder's Fixed Point Theorem, $T$ has a fixed point $(z^{\ast }(t), w^{\ast }(t))\in (C[0, T])^{2}$, which is a solution of (3.3) and (1.2).

Step 3. The pair $(z^{\ast }(t), w^{\ast }(t))$, solutions of (3.3) and (1.2), is a solution of the initial problems (1.1) and (1.2).

To prove that $(z^{\ast }, w^{\ast })\in (C[0, T])^{2}$ is a solution of the original problem (1.1), (1.2), it is enough to prove that

In the first case, suppose, by contradiction, that there exists some $t\in \lbrack 0, T]$ such that

and define

If $t_{0}\in]0, T[$, then

and, by (3.17) and (3.1) and Definition 2.2, the following contradiction with (3.18) holds:

If $t_{0} = 0$, then, by (1.2) and Definition 2.2,

Then, by (3.17),

and

Therefore, by (3.17) and (3.1) and Definition 2.2,

which contradicts (3.19).

Therefore, $z^{\ast }(t)\geq \alpha _{1}^{0}(t), \forall t\in \lbrack 0, T]$. The same arguments can be used to prove the other inequalities of (3.16).

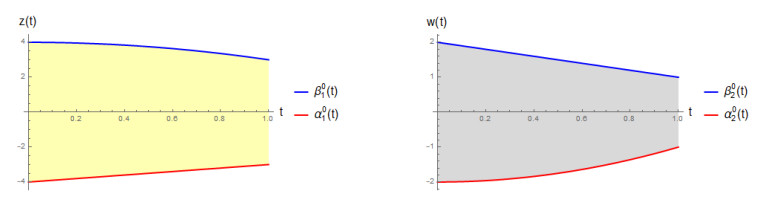
Example 3.1. Consider the following system, for $t\in \lbrack 0, 1],$

together with the periodic boundary conditions (1.2).

The functions $\alpha _{i}, \beta _{i}:\left[0, 1\right] \rightarrow \mathbb{R},$ $i = 1, 2,$ given by

are, respectively, lower and upper solutions of problems (3.20) and (1.2), according to Definition 2.2, with

and

The above problem is a particular case of (1.1) and (1.2), where

and

As the assumptions of Theorem 3.1 are verified, then the system (3.20), (1.2) has, at least, a solution $(z^*, w^*)\in (C[0, 1])^{2}$ such that

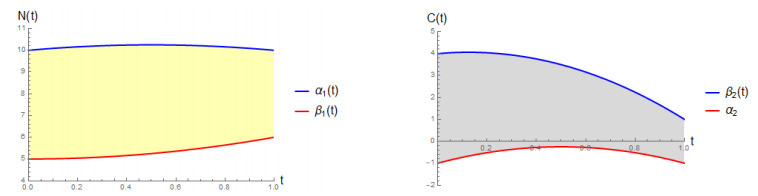
as shown in Figure 1.

Moreover, this solution is not trivial, since constants are not solutions of (3.20).

4.   Ordered lower and upper-solutions and monotonicity

In this section we present a technique to deal with the lack of monotonicity requirements in Theorem 3.1 on the nonlinearities, by defining coupled lower and upper solutions $\alpha _{i}$ and $\beta _{i},$ conveniently, as in the next definition:

Definition 4.1. Consider the $C^{1}$-functions $\alpha _{i}, \beta _{i}:[0, T]\rightarrow \mathbb{R},$ $i = 1, 2.$ The functions $\left(\alpha _{1}, \alpha _{2}\right)$ are coupled lower solutions of the periodic problems (1.1) and (1.2) if

and

The functions $\left(\beta _{1}, \beta _{2}\right)$ are coupled upper solutions of the periodic problems (1.1) and (1.2) if

and

Theorem 4.1. Let $\left(\alpha _{1}, \alpha _{2}\right)$ and $\left(\beta _{1}, \beta _{2}\right)$ be lower and upper solutions of (1.1) and (1.2), respectively, according to Definition 4.1, such that

Assume that $f$ is a $L^{1}$-Carathéodory function in the set

$g$ is a $L^{1}$-Carathéodory function in

with

for $t\in \lbrack 0, T]$, $y_1 \in \mathbb{R}$, and

for $t\in \lbrack 0, T]$, $y_2 \in \mathbb{R}$. Then problems (1.1) and (1.2) has, at least, a solution $(z, w)\in \left(C^1[0, T]\right) ^{2}$ such that

Remark 4.1. This method relating the definition of coupled lower and upper-solutions, and the monotonicity properties of the nonlinearities, can be applied to other types of monotonicity.

Proof. For $i = 1, 2,$ define the continuous functions $\delta_i:[0, T]\times \mathbb{R} \rightarrow \mathbb{R}$, given by

and

and consider the auxiliary problem composed by

together with the periodic boundary conditions (1.2).

Problems (4.4) and (1.2) can be addressed using the arguments for the proof of Theorem 3.1. The corresponding operator has a fixed point $(\bar{z}, \bar{w})$.

The delicate step, however, is to show that $(\bar{z}, \bar{w})$ is a solution of (1.1) and (1.2), such that

To prove the case for $\beta_1(t)\leq \bar{z}(t), \forall t \in [0, T]$, we suppose, by contradiction, that there exists some $t\in \lbrack 0, T]$ such that

and define

If $t_{0}\in]0, T[$, then

and, by (4.6), (4.1) and Definition 4.1, the following contradiction with (4.7) holds:

If $t_{0} = 0$, then, by (1.2) and Definition 4.1,

Then, by (4.6),

and

But by (4.6), (4.1) and Definition 4.1,

which contradicts (4.8).

Therefore, $\bar{z}(t)\geq \beta_1(t), \forall t\in [0, T]$. The same arguments can be applied to prove the inequality $\bar{z}(t)\leq \alpha_1(t)$.

Using the same technique, one can prove that

5.   Application to a criminal vs non-criminal population dynamics

In ^[15], the authors present an analysis of the dynamics of the interaction between criminal and non-criminal populations based on the pray-predator Lotka-Volterra models. Motivated by this work, we consider a variant of the constructed model with a logistic growth of the non-criminal population and a law enforcement term, that is,

where $C$ and $N$ are, respectively, the criminal and non-criminal population as functions of time, $\mu$ is the growth rate of $N$ in the absence of $C$, $a$ and $b$ are the variation rates of $N$ and $C$, respectively, due to their interaction, $\gamma$ is the natural mortality rate of $C$, $K$ is the carrying capacity for $N$ in the absence of $C$, and $l_{c}$ is the measure of enforced law on $C$.

We note that the interaction term could have different effects in each of the populations, hence, the, eventually, different multiplying factors $a$ and $b$.

As a numerical example, we consider the parameter set:

We choose a normalized period $T = 1$, representing the evolution dynamics in one year, and the periodic boundary conditions

Notice that the problem (5.1) and (5.3), with (5.2), is a particular case of (1.1) and (1.2) with

and the quadratic functions

are, respectively, coupled lower and upper solutions of (5.1) and (5.3), for the parameters (5.2), according to Definition 4.1.

As all the assumptions of Theorem 4.1 are verified, then there is at least a solution $(N, C)$ of (5.1), moreover,

and

The only constant solutions $(N, C)$ admissible by problem (5.1) are $(0, 0)$, $(750, 0)$, $(0, -2318.75)$ and $(750, -2318.75)$, which are beyond the lower and upper bounds $\alpha_i, \beta_i$. Hence, the region of solutions shown in Figure 2 contains only non-trivial solutions.

6.   Discussion

The existence of periodic solutions for problems where the nonlinearities have no periodicity at all is scarce in the literature, not only on differential equations but also on coupled systems of differential equations. This work aims to contribute towards fulfilling this gap, by presenting sufficient conditions to guarantee the existence of periodic solutions in the presence of lower and upper solutions and some adequate monotonicity properties on the nonlinearities.

The localization ensured by the lower and upper solutions method has been undervalued, as well as the estimation and some qualitative properties that it provides for the oscillation and variation of the solutions. The introduction of a practical example, and an application to a real social phenomenon, was intended to stress the potentialities of this technique.

7.   Conclusions

In the literature, in general, the lower and upper solutions method requires the well-ordered case, that is, the lower function below the upper one, and a specific local monotonicity on the nonlinearity. This work suggests techniques to overcome both restrictions, so that the search for functions that verify lower and upper solutions properties becomes easier.

For the first issue, we apply a translation, such that, regardless of the order relation between the lower and upper solutions, the shifted functions are always well-ordered.

Section 4 presents a technique that combines the definition of coupled lower and upper-solutions (Definition 4.1) with the monotonicity properties verified by the nonlinearities. In this way, this method can be applied to other problems where the different types of monotonicity hold.

Acknowledgments

This work research was supported by national funds through the Fundação para a Ciência e Tecnologia, FCT, under the project UIDB/04674/2020.

Conflict of interest

The authors declare no conflicts of interest.