Using huge amounts of road sensor data for official statistics

1.   Introduction

Childhood infections are among the highly prevalent types of infectious diseases. Influenza, hepatitis, chickenpox, malaria, rubella and tetanus are illustrations of infections. Vaccination of children is recommended by healthcare personnel to prevent them from contracting such infections. Vaccination has had a crucial effect in diminishing the prevalence of contagious illnesses in children. On the other hand, preventable diseases constitute a significant global health hazard. Vaccination has a considerable influence on the prevention of infectious illnesses in infants. Therefore, among the most vital aspects of preventative health initiatives is childhood diseases (CHD). Numerous physicians and mathematicians are interested in the dynamics of diseases such as Haq et al. ^[1], Koca ^[2], Khan et al. ^[3], Ullah et al. ^[4] and Singh et al. ^[5].

Vaccinations are the more efficient way to prevent illnesses in babies. As a result, developing a framework that anticipates the strongest performance of vaccine effectiveness needed is critical to preventing the development of such illnesses. In 1974, the World Health Organization's (WHO) "Extensive Immunization Program (EPI)" was established to expand vaccine availability for all children. Mathematical simulations are frequently employed to acquire a clearer and more comprehensive knowledge of the mechanisms of illness dissemination in children and to assess preventive approaches ^[6,7,8].

The scientists employed nonlinear systems to solve real-world challenges in a variety of fields. For physicians, the concept of dynamical problems is well-known. It is gaining popularity in a variety of professions and is exploring various facets of the aforementioned domain ^{[9,10,11,12,13,14,15]}. Several experts produced fractional-order differential equations throughout the past three decades. It was widely used to overcome significant challenges in a variety of disciplines; see ^{[16,17,18,19,20,21,22,23,24,25,26,27,28]}. Existence, stability analysis, simulation and optimal approaches are some of the noted features that have lately been introduced. The fractional derivative operators were proposed by several researchers, such as Caputo ^[29], Podlubny ^[30], Hilfer ^[31], Baleanu et al. ^[32], Singh et al. ^[33], Kumar et al. ^[34] and henceforth. Atangana-Baleanu ^[35] recently proposed a new concept of a fractional order derivative incorporating Mittag-Leffler as a non-singular kernel, and the authors ^[33] highlighted the further attributes. Employing fractional derivatives and implementing them into the CHD model has resulted in a variety of scientific findings.

All of the research aforementioned constructed a mechanistic and chaotic mathematical framework of CHD spread mechanisms, but none of them explored the fractional order feature of the paradigm. Unfortunately, no progress has been made in investigating the fractional-order behaviour of the CHD model, which correlates with the ABC fractional derivative operator up to this point.

Our aim is that we split the disease-affected community into three epidemiological categories in the paradigm described in this article: a susceptible category (S), an infected category (I), and a removed category (R) designating inoculated as well as healed individuals having persistent immunization.

In 2012, Arafa and other academics resurrected the classical childhood illness transmission dynamics ^[36]. The model is described as follows:

where ${\bf{S}} = \mathfrak{s}/N, \; {\bf{I}} = \iota/N, \; {\bf{R}} = \mathfrak{r}/N, \; \; N = \mathfrak{s}+\iota+\mathfrak{r}$. The vaccine's efficiency is $100$ percent in this scenario, and N assumed to be variable. Thus, $\nu$ represents the birth rate, $\beta$ reflects the general contact rate of a vulnerable individual with an infectious person, $\gamma$ represents the infected individual's recover-ability and readmission into the eliminated class, and ${\bf{P}}$ represents the immunized population at birth (with $0 < {\bf{P}} < 1$). Recently, Haq et al. ^[37] established the numerical solutions of fractional CHDs, Baleanu et al. ^[38] projected the exhibiting of prevalent CHDs via Caputo-Fabrizio in the frame of the Laplace transform, and Singh et al. ^[39] investigated vaccination of the SIR model.

In 1980, Adomian first proposed the Adomian decomposition method (ADM). This approach is useful for solving systems of differential equations numerically and analytically ^[40,41]. The Adomian approach handles nonlinear DEs and the system of fractional DEs without requiring a Lagrange multiplier, intricate integrals, or any more variables.

Adopting the above propensity, we use a recently developed arbitrary order derivative in the CHD model. The fundamental objective of this paper is to examine the CHD model by applying a revolutionary ABC fractional derivative operator and to describe the intricacies of the uniqueness and existence of the aforesaid model solution by aiding a fixed point postulate and the Picard–Lindelöf technique.

The following is a summary of the considerations in the design of this article: The ABC derivative of arbitrary order is investigated in Section 2. Furthermore, the existence theory of the mechanism is presented in Section 3. An algorithm is established with the correlation of the Elzaki transform and ADM. By employing the contraction mapping theorem and the Picard–Lindelöf technique, the uniqueness and existence of the solutions to the system are analyzed in Section 4. Some simulation and tabulation consequences are debated in Section 5. Finally, in Section 6, we summarise the concluding remarks and future directions.

2.   Preliminaries

The study of hypotheses and the use of derivatives and integrals of contested mappings is known as fractional calculus. In the subsequent ongoing area, we use essential terminology and findings obtained from fractional calculus theory.

Definition 2.1. (^[30]) The Caputo fractional derivative structure is stated as

Definition 2.2. (^[35]) For ${\bf{f}}\in\mathcal{H}_{1}(\check{\alpha}, \check{\beta}), \; \check{\alpha} < \check{\beta}, \alpha\in[0, 1]$ and The ABC fractional derivative is stated as follows:

where $\mathbb{B}(\alpha)$ in (2.2) is the normalization function with $\mathbb{B}(\alpha) = \mathbb{B}(0) = \mathbb{B}(1) = 1.$

Definition 2.3. (^[35]) Let $\alpha\in[0, 1]$, then the integral of fractional order $\alpha$ of the function ${\bf{f}}$ of the ABC-operator is defined as

Definition 2.4. (^[42]) A set $\mathcal{M}$ involving exponential function is defined as

where $z$ is a finite number, but $l_{1}, l_{2}$ may be finite or infinite.

Definition 2.5. (^[42,43]) A mapping ${\bf{f}}(\varrho)$ having Elzaki transform is described as

Theorem 2.6. (^[44])(Convolution property). The subsequent consequence holds true for Elzaki transform:

Definition 2.7. (^[44]) The CFD form of Elzaki transform is described as:

Definition 2.8. (^[45]) The ABC fractional derivative formation of Elzaki transform is described as

where $\mathbb{E}\big\{{\bf{f}}(\varrho)\big\}(\omega) = \mathfrak{U}(\omega).$

3.   A fractional CHDs model

It is necessary to modify the integer-order form to arbitrary setting in order to numerically investigate the effect of biological components and to approximate the emergence and spread of CHDs. As a result, in this study, we deduce the paradigm (1.1) for the Atangana-Baleanu derivative operator supplied as

where $\, ^{ABC}{\bf{D}}_{\varrho}^{\alpha}$ signifies the ABC fractional derivative operator having fractional order $\alpha,$ i.e., $0 < \alpha\leq1$ and the ICs ${\bf{S}}_{0}(\varrho) = {\bf{S}}(0), \; {\bf{I}}_{0}(\varrho) = {\bf{I}}(0), \; {\bf{R}}_{0}(\varrho) = {\bf{R}}(0).$

3.1.   Existence and uniqueness of fractional CHDs model

In what follows, we demonstrate that (3.1) has a fixed point. To do this, we utilize (3.1) as follows:

Taking into consideration the Definition 2.3 in the aforesaid system, we have

Furthermore, we show that the kernels $\Theta_{1}, \Theta_{2}, \Theta_{3}$ satisfy both the Lipschitz and contraction assumptions.

Theorem 3.1. The kernel $\Theta_1(\varrho, {\bf{S}}(\varrho))$ preserves the Lipschitz assumptions as well as contraction if the inequality

is satisfied.

Proof. Assume that $\Theta_{1}(\varrho, {\bf{S}}(\varrho)) = (1-{\bf{P}})\nu-\beta {\bf{S}}(\varrho){\bf{I}}(\varrho)-\nu {\bf{S}}(\varrho).$

For ${\bf{S}}$ and $\widehat{{\bf{S}}},$ we attain

where $K_{1} = \beta \chi_{1}+\nu,$ and $\big\|{\bf{I}}(\varrho)\big\| = \max_{\varrho\in J_{1}}\|{\bf{I}}(\varrho)\|\leq \chi_{1}$ is a bounded mapping.

Thus, (3.5) holds the Lipschitz assumption for $\Theta_{1}$ and also $0\leq\beta \chi+\nu < 1,$ shows that $\Theta_{1}$ is a contraction.

Analogously, the Lipschitz assumption for $\Theta_{2}$ and $\Theta_{3}$ are presented as follows:

where $K_{2} = \beta \chi_{2}+\gamma+\nu$ and $K_{3} = \nu$ and $\big\|{\bf{S}}(\varrho)\big\| = \max_{\varrho\in J_{1}}\|{\bf{S}}(\varrho)\|\leq \chi_{2}$ is a bounded mapping. Moreover, if $0\leq\beta \chi_{2}+\gamma+\nu < 1$ and $0\leq\nu < 1,$ then $\Theta_{2}$ and $\Theta_{3}$ are contraction.

Therefore, in view of kernels, (3.3) can be written in a recursive manner as follows:

supplemented by the initial conditions ${\bf{S}}_{0}(\varrho) = {\bf{S}}(0), \; {\bf{I}}_{0}(\varrho) = {\bf{I}}(0)$ and ${\bf{R}}_{0}(\varrho) = {\bf{R}}(0).$ Applying the norm on (3.7), then we have

In view of Lipschitz assumption (3.6), we obtain

Thus, we attain

Analogously, we attain

Also, we can express that

Next, to find the existence result, we surmise the subsequent theorem.

Theorem 3.2. The CHDs model $(3.1)$ has a solution, if there exists $T^{*}$ such that

Proof. Since the mappings ${\bf{S}}(\varrho), \; {\bf{I}}(\varrho)$ and ${\bf{R}}(\varrho)$ are bounded. Also, the kernels satisfies Lipschitz assumptions. Applying recursive technique on (3.10) and (3.11), we attain

As a result, the mappings $\Omega_{1n}(\varrho), \Omega_{2n}(\varrho)$ and $\Omega_{3n}(\varrho)$ presented in (3.13) have a solution that is continuous. Furthermore, we show that the mappings presented in (3.13) enable the solutions of (3.1), we surmise that

where $\mathcal{S}_{n}(\varrho), \; \mathcal{I}_{n}(\varrho)$ and $\mathcal{R}_{n}(\varrho)$ denotes the remainder terms of the solution.

Therefore, we have

After a recursive process, we attain

where $\alpha = \big\|{\bf{S}}-{\bf{S}}_{n-1}\big\|.$ Applying limit on obtaining equation as $n$ tends to $\infty,$ we find $\big\|\mathcal{S}_{n}(\varrho)\big\|\mapsto 0.$ In a similar fashion, one can evaluate that $\big\|\mathcal{I}_{n}(\varrho)\big\|\mapsto 0$ and $\big\|\mathcal{R}_{n}(\varrho)\big\|\mapsto 0.$ The existense result is illustrated.

To demonstrate the uniqueness of the solutions, we surmise that the system (3.1) has different solution such that ${\bf{S}}_{1}(\varrho), \; {\bf{I}}_{1}(\varrho)$ and ${\bf{R}}_{1}(\varrho),$ then we have the following:

Applying norm on above equation, we have

In view of Lipschitz assumptions (3.6), we have

This yields, we have

Theorem 3.3. The system of $(3.1)$ has a unique solution if the subsequent assumption satisfy

Proof. Assume that the hypothesis of (3.17) satisfy

which shows that $\Big\|{\bf{S}}(\varrho)-{\bf{S}}_{1}(\varrho) \Big\| = 0.$ Hence, we conclude ${\bf{S}}(\varrho) = {\bf{S}}_{1}(\varrho).$ Analogously, we can continue the same procedure for ${\bf{I}}$ and ${\bf{R}}.$

4.   Approximation technique and solution

4.1.   Configuration of Elzaki Adomian decomposition method

In order to find the solution of the system (3.1), employing the Elzaki transform

It follows that

Now, supplementing the initial conditions and employing the inverse Elzaki transform on the aforesaid system of equations, we have

Suppose that the infinite series formulation of ${\bf{S}}(\varrho), {\bf{I}}(\varrho)$ and ${\bf{R}}(\varrho)$ are represented as

whilst the nonlinear term

are dealt by the Adomian polynomial stated as

The first three polynomials are presented as

plugging (4.2)–(4.4) into (4.1), we attain

Comparing both sides of (4.5) presents the subsequent recursive algorithm, we have

By employing the inverse Elzaki transform, we attain the iterative terms as follows:

Analogously, one can achieve the additional components. Hence, the infinite series solution of (3.1) is presented as:

4.2.   Numerical solution and discussion

In this analysis, we utilize ${\bf{S}}_{0} = 1, {\bf{I}}_{0} = 0.5, \; {\bf{R}}_{0} = 0, \; \nu = 0.4, \; \beta = 0.8, \; \gamma = 0.03, P_{1} = 0.9$ and the EADM yields an approximate solution in the form of an infinite series. Thus, we compute the first four terms of (4.8) as follows:

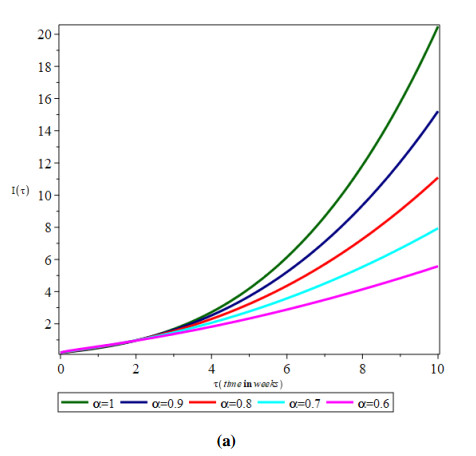
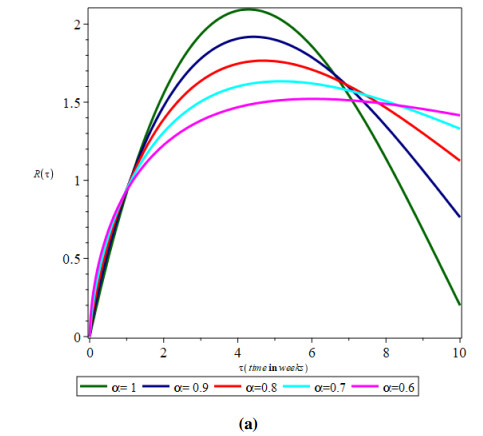
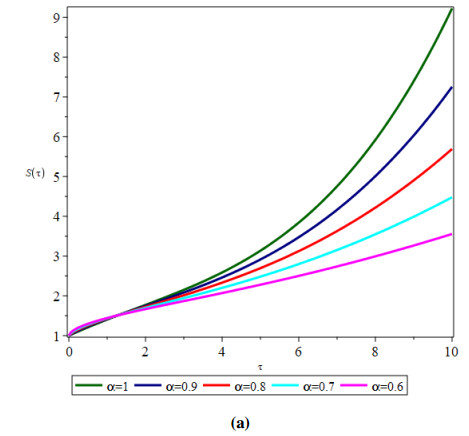
In Figure 1, the estimated solutions of several segments versus the provided data and pertaining to various fractional orders have been shown. Furthermore, the outcomes reveal that the response is constantly contingent on the time-fractional derivative and parametric settings. According to inoculation, the prevalence of the cured group progressively improves as the number of the vulnerable group diminishes. As shown in Figure 1, for a short period of time, responsiveness diminishes, resulting in a reduction in infection, as illustrated in Figure 2. Figure 3 depicts a typical case of glucose intolerance. This can be seen in the graphs for excessive plasma concentrations, where despite considerable increases in adjusted glucose metabolism concentrations in the liver, glycogen synthesis generation could be completely inhibited. The fractional-order derivative corresponds to the growth and contraction of distinct components. For a short period of time, the involved procedure is rapid on a small fractional order, but subsequently it reverses and remains sluggish on the identical lesser fractional order. As a result, in biological models, the fractional calculus depicts systemic mechanisms of deterioration and regeneration. The diffraction peaks and their associated vibrational frequencies are identical across scenarios; however, the timeframe of these peaks varies. Within fractional orders, the investigated model's transitory vibrations are considerably more spread out than those of its integer-order counterpart, whereby responses have prolonged interepidemic intervals. As a consequence, we arrived at the conclusion that, relying on the attribute values, the fractional-order framework simultaneously cumulates to the classical model and matches statistics equally, or incorporates data more accurately and excels the conventional paradigm.

Tables 1–3 exhibit the findings of the model of epidemic CHDs using Caputo, Caputo-Fabrizio, and ABC fractional derivatives for the susceptible class(${\bf{S}}$), infected class(${\bf{I}}$), and removed class(${\bf{R}}$), respectively. The summary statistics of the local stability investigations are supported by exisiting results provided by Haq et al. ^[37] and Baleanu et al. ^[38]. We proceeded by presenting several standard stability conclusions for a simplistic formula, as well as their application to a scenario in which the framework was reinforced substantially feasible by including a category of incubating persons and a group of biologically protective children.

5.   Some mathematical aspects of CHD model

5.1.   Existence approach by Picard–Lindelöf technique

Theorem 5.1. System of Eq $(3.1)$ has a solutions by employing the Picard–Lindelöf technique.

Proof. By means of kernels defined in (3.2), we have

where $\Theta_{1}(\varrho, {\bf{S}}(\varrho)), \; \Theta_{2}(\varrho, {\bf{I}}(\varrho))$ and $\Theta_{3}(\varrho, {\bf{R}}(\varrho))$ are contraction mappings according to (3.6), respectively.

Assume that

where

Taking the Picard operator, we have

presented as follows:

where $\Xi(\varrho) = \big\{{\bf{S}}(\varrho), {\bf{I}}(\varrho), {\bf{R}}(\varrho)\big\}, \; \Xi_{0}(\varrho) = \big\{\zeta_{1}, \zeta_{2}, \zeta_{3}\big\}$ and $\Delta(\varrho, \Theta(\varrho)) = \big\{\Theta_{1}(\varrho, {\bf{S}}(\varrho)), \Theta_{2}(\varrho, {\bf{I}}(\varrho)), \Theta_{3}(\varrho, {\bf{R}}(\varrho))\big\}.$

Next, we surmise that the solutions of the fractional CHD model are bounded in a specified time domain,

then we have

Taking into account the fixed point postulate via the Banach space with the metric, we get

Now we have

Since $\Xi$ is a contraction and $\rho\zeta < 1.$ Also, the introduced operator, $\Phi$ is contraction. Thus, the CHD model concerning the ABC derivative presented in (3.1) has a fixed point.

5.2.   Stability analysis

Assume that $(\varphi, \|.\|)$ denotes a Banach space and $\mathcal{U}$ signifies a self-map of $\varphi.$ Also, suppose that $\hbar_{n+1} = \Psi(\mathcal{U}, \hbar_{n})$ be a recursive scheme. Surmise that a fixed point set $\aleph(\mathcal{U})$ of $\mathcal{U}$ has at least one element. Suppose that $\hbar_{n}$ is convergent and tends to $z_{1}\in\aleph(\mathcal{U}).$ If $\{\hbar_{n}\}\subseteq\varphi$ and introducing $a_{n} = \|\hbar_{n+1}-\Psi(\mathcal{U}, \hbar_{n})\|$ and if $\lim_{n\mapsto\infty}a_{1}^{n} = 0$ gives the outcome $\lim_{n\mapsto\infty}\hbar^{n} = z_{1},$ then the recursive approach $\hbar_{n+1} = \Psi(\mathcal{U}, \hbar_{n})$ is said to be $\mathcal{U}$-stable.

Theorem 5.2. (^[46]) Assume that a Banach space $(\varphi, \|.\|)$ and $\mathcal{U}$ be a self-map of the Banach space $\varphi$ yields the outcome

where $\widetilde{H}$ and $\hbar$ such that $\hbar\in[0, 1], \widetilde{H}\geq0.$ Also, surmise that $\mathcal{U}$ is Picard $\mathcal{U}$-stable.

We surmise that the following recursive formulae have an association with the fractional CHD model (3.1)

The term $\frac{\omega^{\alpha}+1-\alpha}{\mathbb{B}(\alpha)}$ considered to be the Lagrange multiplier in the aforesaid system.

In the next result, we present the following theorem.

Theorem 5.3. Assume that the self-map $\mathcal{G}$ is represented as follows:

then the recursive system are $\mathcal{G}$ stable in $L^{2}\in(a_{1}, \mathbb{B})$ if $(1-{\bf{P}})\nu-\beta \varphi_{4}(\varrho)-\nu \varphi_{1}(\varrho) < 1, \; \beta \varphi_{4}(\varrho)-(\gamma+\nu)\varphi_{2}(\varrho) < 1$ and ${\bf{P}}\nu+\gamma \varphi_{2}(\varrho)-\nu \varphi_{3}(\varrho) < 1.$

Proof. Initially, we prove that $\mathcal{G}$ has a fixed point. To prove the above consequence, we obtain the outcome presented below for $(n, m)\in\mathbb{B}\times\mathbb{B}.$

and

Also, we have that

By plugging (5.11) in (5.9) and (5.10), we have

and

where $\varphi_{i}, \; i = 1, ...., 4,$ are mappings arising from $\mathbb{E}^{-1}\big[\frac{\omega^{\alpha}+1-\alpha}{\mathbb{B}(\alpha)}\mathbb{E}(\dot)\big]$ along with $\Big((1-{\bf{P}})\nu-\beta \varphi_{4}(\varrho)-\nu \varphi_{1}(\varrho)\Big) < 1, \; \Big(\beta \varphi_{4}(\varrho)-(\gamma+\nu)\varphi_{2}(\varrho)\Big) < 1$ and $\Big({\bf{P}}\nu+\gamma \varphi_{2}(\varrho)-\nu \varphi_{3}(\varrho)\Big) < 1.$

As a result, the self-map $\mathcal{G}$ has a fixed point. Moreover, the assumptions connected with the Theorem 5.2 are satisfied by $\mathcal{G}.$ Now, suppose that (5.12) and (5.13) hold, thus we have

It is noteworthy that in map $\mathcal{G}$ the supposition concerned with Theorem 5.2 satisfied. Thus, for the supposed map, $\mathcal{G}$ and the hypothesis relating to Theorem 5.2 are satisfied, hence $\mathcal{G}$ is Picard-stable. This completes the proof.

6.   Conclusions

In this study, the generalized fractional derivative is implemented to examine the mathematical model of CHDs. Also, with the assistance of the contraction mapping theorem, we demonstrated that the response of the proposed model (3.1) exists and has at least one solution. The Picard–Lindelöf approach with the self-map $\mathcal{U}$ used to validate the solution's stability. Furthermore, using the EADM algorithm, we comprehended the approximate results for various fractional-orders using the Matlab/Maple application, and we concluded that the results of the projected model (3.1) approach the classical solution when $\alpha\mapsto1.$ As a result, it can be concluded that EADM is a controllable, simplistic, and more powerful analytical process for analyzing linear/non-linear phenomena. The findings of this research are extremely beneficial to healthcare professionals who interact with peditric and associated concerns. Consequently, we deduce that the ABC derivative can be used to investigate the physical, pharmacological, physiological, medicinal, sociological, and economic systems.

Acknowledgments

This research was supported by Taif University Research Supporting Project Number (TURSP-2020/164), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare that they have no competing interests.