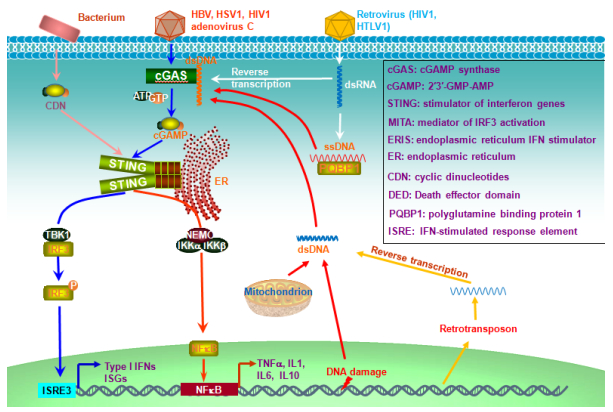
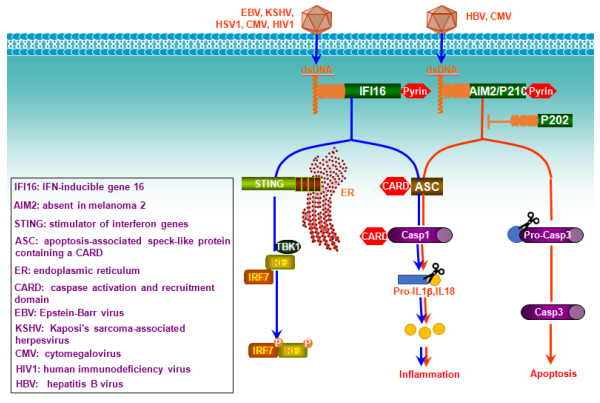
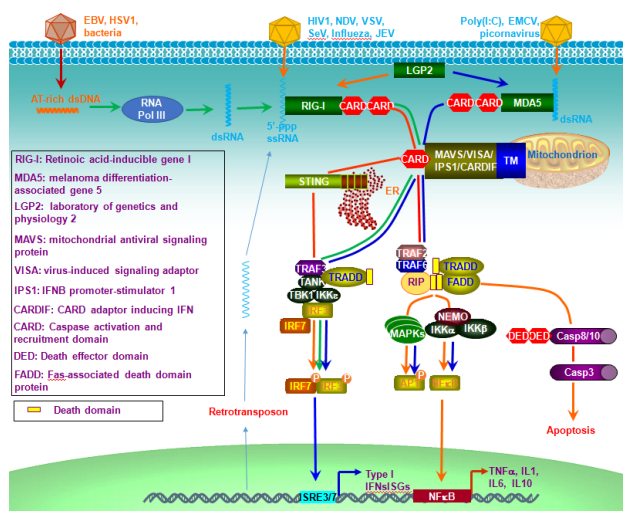
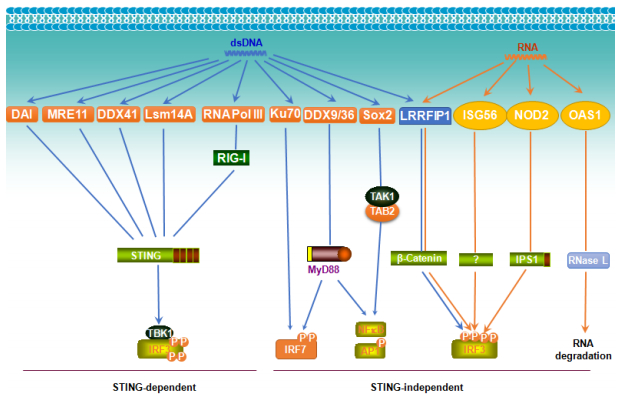
Pathogen-associated molecular patterns (PAMPs) and damage-associated molecular patterns (DAMPs) are recognized by different cellular pathogen recognition receptors (PRRs), which are expressed on cell membrane or in the cytoplasm of cells of the innate immune system. Nucleic acids derived from pathogens or from certain cellular conditions represent a large category of PAMPs/DAMPs that trigger production of type I interferons (IFN-I) in addition to pro-inflammatory cytokines, by specifically binding to intracellular Toll-like receptors or cytosolic receptors. These cytosolic receptors, which are not related to TLRs and we call them “Toll-free” receptors, include the RNA-sensing RIG-I like receptors (RLRs), the DNA-sensing HIN200 family, and cGAS, amongst others. Viruses have evolved myriad strategies to evoke both host cellular and viral factors to evade IFN-I-mediated innate immune responses, to facilitate their infection, replication, and establishment of latency. This review outlines these “Toll-free” innate immune pathways and recent updates on their regulation, with focus on cellular and viral factors with enzyme activities.
1.
Introduction
In this article, we investigate the following Kirchhoff-Schrödinger-Poisson type systems on the Heisenberg group:
where a,b are positive real numbers, Ω⊂HN is a bounded region with smooth boundary, 1<p<Q, Q=2N+2 is the homogeneous dimension of the Heisenberg group HN, Q∗=pQQ−p, q∈(2p,Q∗), ΔH,pu=div(|∇Hu|p−2∇Hu) is known as the p-horizontal Laplacian, and μ and λ are some positive real parameters.
In recent years, geometrical analysis of the Heisenberg group has found significant applications in quantum mechanics, partial differential equations and other fields, which has attracted the attention of many scholars who tried to establish the existence and multiplicity of solutions of partial differential equations on the Heisenberg group. For instance, in the subcase of problem (1.1), when p=2 and b=μ=0, the existence of solutions for some nonlinear elliptic problems in bounded domains has been established. Tyagi [1] studied a class of singular boundary value problem on the Heisenberg group:
and under appropriate conditions, obtained some existence results using Bonanno's three critical point theorem. Goel and Sreenadh [2] dealt with a class of Choquard type equation on the Heisenberg group, and they established regularity of solutions and nonexistence of solutions invoking the mountain pass theorem, the linking theorem and iteration techniques and boot-strap method.
In the case b≠0 and μ=0, problem (1.1) becomes the Kirchhoff problem, which has also been widely studied. For example, Sun et al. [3] dealt with the following Choquard-Kirchhoff problem with critical growth:
where f is a Carathéodory function, M is the Kirchhoff function, ΔH is the Kohn Laplacian on the Heisenberg group HN, μ>0 is a parameter and Q∗λ=2Q−λQ−2 is the critical exponent. In their paper, a new version of the concentration-compactness principle on the Heisenberg group was established for the first time. Moreover, the existence of nontrivial solutions was obtained even under nondegenerate and degenerate conditions. Zhou et al. [4] proved the existence of solutions of Kirchhoff type nonlocal integral-differential operators with homogeneous Dirichlet boundary conditions on the Heisenberg group using the variational method and the mountain pass theorem. Deng and Xian [5] obtained the existence of solutions for Kirchhoff type systems involving the Q-Laplacian operator on the Heisenberg group with the help of the Trudinger-Moser inequality and the mountain pass theorem. For more related results, see [6,7,8,9,10,11,12,13].
When b=0, p=2 and μ≠0, problem (1.1) becomes the Schrödinger-Poisson system. This is a very interesting subject and has recently witnessed very profound results. For example, An and Liu [14] dealt with the following forms of Schrödinger-Poisson type system on the Heisenberg group:
where μ∈R and λ>0 are some real parameters and 1<q<2. By applying the concentration compactness and the critical point theory, they found at least two positive solutions and a positive ground state solution.
Liang and Pucci [15] studied the following critical Kirchhoff-Poisson system on the Heisenberg group:
where Ω⊂H1 is a smooth bounded domain, ΔH is the Kohn-Laplacian on the first Heisenberg group H1 and 1<q<2. By applying the symmetric mountain pass lemma, they obtained the multiplicity of solutions with λ sufficiently small.
The Kirchhoff-Poisson system on the Heisenberg group with logarithmic and critical nonlinearity was considered by Pucci and Ye [13]:
Under suitable assumptions on the Kirchhoff function M covering the degenerate case, they showed that for a sufficiently large λ>0, there exists a nontrivial solution to the above problem.
When p≠2 and μ≠0, as far as we know, for Kirchhoff-Schrodinger-Poisson systems (1.1) with critical nonlinearities on the Heisenberg group, existence and multiplicity results are not yet available. In the Euclidean case, Du et al. [16] first studied the existence results for the Kirchhoff-Poisson systems with p-Laplacian under the subcritical case using the mountain pass theorem. Later, Du et al. [17] studied quasilinear Schrödinger-Poisson systems. For the critical case, Du et al. [18] also obtained the existence of ground state solutions with the variational approach.
Inspired by the above achievements, we aim to establish some results on the existence and multiplicity of nontrivial solutions of the Kirchhoff-Schrödinger-Poisson systems (1.1). The major difficulties in dealing with problem (1.1) are the presence of a nonlocal term and critical nonlinearities making the study of this problem very challenging.
Before presenting the main results of this article, we first present some concepts of the Heisenberg group. The Heisenberg group is represented by HN. If ξ=(x,y,t)∈HN, then the definition of this group operation is
ξ−1=−ξ is the inverse, and therefore (ξ′)−1∘ξ−1=(ξ∘ξ′)−1.
The definition of a natural group of dilations on HN is δs(ξ)=(sx,sy,s2t), for every s>0. Hence, δs(ξ0∘ξ)=δs(ξ0)∘δs(ξ). It can be easily proved that the Jacobian determinant of dilatations δs:HN→HN is constant and equal to sQ, for every ξ=(x,y,t)∈HN. The critical exponent is Q∗:=pQQ−p, where the natural number Q=2N+2 is called the homogeneous dimension of HN. We define the Korányi norm as follows
and we derive this norm from the Heisenberg group's anisotropic dilation. Hence, the homogeneous degree of the Korányi norm is equal to 1, in terms of dilations
The set
denotes the Korányi open ball of radius r centered at ξ0. For the sake of simplicity, we shall denote Br=Br(O), where O=(0,0) is the natural origin of HN.
The following vector fields
generate the real Lie algebra of left invariant vector fields for j=1,⋯,n, which forms a basis satisfying the Heisenberg regular commutation relation on HN. This means that
The so-called horizontal vector field is just a vector field with the span of [Xj,Yj]nj=1.
The Heisenberg gradient on HN is
and the Kohn Laplacian on HN is given by
The Haar measure is invariant under the left translations of the Heisenberg group and is Q-homogeneous in terms of dilations. More precisely, it is consistent with the (2n+1)-dimensional Lebesgue measure. Hence, as shown Leonardi and Masnou [19], the topological dimension 2N+1 of HN is strictly less than its Hausdorff dimension Q=2N+2. Next, |Ω| denotes the (2N + 1)-dimensional Lebesgue measure of any measurable set Ω⊆HN. Hence,
Now, we can state the main result of the paper.
Theorem 1.1. Let q∈(2p,Q∗). Then there exist positive constants μ1 and λ1 such that for every μ∈(0,μ1) and λ∈(λ1,+∞), the following assertions hold:
(I) Problem (1.1) has a nontrivial weak solution;
(II) Problem (1.1) has infinitely many nontrivial weak solutions if parameter a is large enough.
We can give the following example for problem (1.1) with p=3 and Ω⊂H1:
In this case, N=1, p=3 and q=8, then Q=2N+2=4, Q∗=12. If positive parameters μ small enough and λ large enough, by Theorem 1.1, we know that problem (1.1) has a nontrivial weak solution. Moreover, if in addition the parameter a is large enough, problem (1.1) has infinitely many nontrivial weak solutions. It should be noted that the methods in An and Liu [14] and Liang and Pucci [15] do not seem to apply to problem (1.1).
Remark 1.1. Compared with previous results, this paper has the following key new features:
1) The presence of the nonlocal term ϕ|u|p−2u;
2) The lack of compactness caused by critical index;
3) The presence of the p-Laplacian makes this problem more complex and interesting.
It is worth stressing that the nonlocal term and the critical exponent lead to the lack of compactness condition, and we use the concentration-compactness principle to overcome this difficulty. Moreover, we shall use some more refined estimates to overcome the presence of the p-Laplacian.
We need to emphasize here that despite the similarity of some properties between the classical Laplacian Δ and Kohn Laplacian ΔH, similarities can be misleading (see Garofalo and Lanconelli [20]), so there are still many properties that deserve further study. Moreover, for the case p≠2, it is difficult to prove the boundedness of Palais-Smale sequences. In order to overcome these difficulties, we use some more accurate estimates of relevant expression. Additionally, we use the concentration-compactness principle on the Heisenberg group to prove the compactness condition.
The paper is organized as follows. In Section 2, we introduce some notations and known facts. Moreover, we introduce some key estimates. In addition, we define the corresponding energy functional Iλ and its derivative at u, that is, I′λ(u). In Section 3, we prove Theorem 1.1.
2.
Preliminaries and (PS)c condition
2.1. Preliminaries
First of all, we collected some known facts, useful in the sequel. For additional background material, readers are advised to refer to Papageorgiou et al. [21].
Let
represent the usual Ls-norm.
Following Folland and Stein [22], we define the space ˚S21(Ω) as the closure of C∞0(Ω) in S21(HN). Then ˚S21(Ω) is a Hilbert space with the norm
We define the Folland-Stein space S1,p(Ω) as the closure of C∞0(Ω) with the norm
Then the embedding
is compact. However, if s=Q∗, the embedding is only continuous (see Vassiliev [23]).
Additionally, we say that (u,ϕ)∈S1,p(Ω)×S1,p(Ω) is a solution of problem (1.1) if and only if
and
for every v,ω∈S1,p(Ω)×S1,p(Ω). Moreover, (u,ϕ)∈S1,p(Ω)×S1,p(Ω) is a positive solution of problem (1.1) if u and ϕ are both positive. Therefore, in order to apply the critical point theory, we need to define the functional J(u,ϕ):S1,p(Ω)×S1,p(Ω)→R as follows
for every (u,ϕ)∈S1,p(Ω)×S1,p(Ω). Then J is C1 on S1,p(Ω)×S1,p(Ω) and its critical points are the solutions of problem (1.1). Indeed, the partial derivatives of J at (u,ϕ) are denoted by J′u(u,ϕ), J′ϕ(u,ϕ), namely for every v,ω∈S1,p(Ω)×S1,p(Ω),
and
Standard computations show that J′u (respectively J′ϕ) continuously maps S1,p(Ω)×S1,p(Ω) into the dual of S1,p(Ω). Moreover, the functional J is C1 on S1,p(Ω)×S1,p(Ω) and
if and only if (u,ϕ) is a solution of problem (1.1).
Lemma 2.1. Let u∈S1,p(Ω). Then there is a unique nonnegative function ϕu∈˚S21(Ω) such that
Furthermore, ϕu≥0 and ϕu>0 if u≠0. Also,
(i) ϕtu=tpϕu, for every t>0;
(ii) ‖ϕu‖˚S21(Ω)≤ˆC‖u‖p, where ˆC>0;
(iii) Let un⇀u in S1,p(Ω). Then, ϕun⇀ϕu in ˚S21(Ω), and
Proof. For any u∈˚S21(Ω), we define W:˚S21(Ω)→R,
Let vn→v∈˚S21(Ω), as n→∞. It follows by the Hölder inequality that
where
is the best Sobolev constant. This implies that W is a continuous linear functional. Using the Lax-Milgram theorem, we see that there is a unique ϕu∈˚S21(Ω) satisfying
Thus, ϕu∈˚S21(Ω) is the unique solution of problem (2.1). Moreover, applying the maximum principle, one has ϕu≥0 and ϕu>0 if u≠0. Indeed, for every t>0, one has
Hence ϕtu=tpϕu due to the uniqueness of ϕu.
Furthermore, since ϕu∈S1,p(Ω), we can view it as a text function in problem (2.1). Then by (2.4), the Sobolev inequality and the Hölder inequality, we have (henceforth C0, C1, C2 will denote positive constants)
Therefore, we get ‖ϕu‖˚S21(Ω)≤C1‖u‖p.
Since un⇀u in S1,p(Ω), we can conclude that un→u a.e. in Ω and {|un|p} is bounded in L2(Ω). Moreover, we have |un|p⇀|u|p in L2(Ω). Then for every v∈˚S21(Ω), it follows that
Therefore, ϕun⇀ϕu in ˚S21(Ω). By the Hölder inequality, the Sobolev inequality and (ⅱ), one has
Hence, {ϕun|un|p−2un} is bounded in L2p2p−1(Ω). Since
we get
The proof of Lemma 2.1 is complete.
By similar arguments as in An and Liu [14], we can get the following result.
Lemma 2.2. Let Ψ(u)=ϕu for every u∈S1,p(Ω), where ϕu is as in Lemma 2.1, and let
Then Ψ is C1 and Υ is the graph of Ψ.
We define the corresponding energy functional Iλ(u)=J(u,ϕu) of problem (1.1) by
Based on the definition of J and Lemma 2.2, we can conclude that Iλ is of C1.
Lemma 2.3. (see An and Liu [14]) Let (u,ϕ)∈S1,p(Ω)×S1,p(Ω). Then (u,ϕ) is a critical point of J if and only if u is a critical point of Iλ and ϕ=Ψ(u), where Ψ was defined in Lemma 2.2.
According to Lemma 2.3, we know that a solution (u,ϕu) of problem (1.1) corresponds to a critical point u of the functional Iλ with ϕ=Ψ(u) and
Therefore, based on the above arguments, we shall strive to use critical point theory and some analytical techniques to prove the existence of critical points of functional Iλ.
2.2. (PS)c condition
In this subsection, our main focus will be on proving that the functional Iλ satisfies the Palais-Smale condition.
Lemma 2.4. Let q∈(2p,Q∗). Then there exists μ1>0 such that for any μ<μ1, the energy functional Iλ satisfies (PS)c condition, where
and S is the best Sobolev constant given by (2.3).
Proof. Let us assume that {un}n⊂S1,p(Ω) is a (PS)c sequence related to the functional Iλ, that is,
It follows that
where ˆC is a positive constant given by Lemma 2.1(ⅱ). Let μ1=bˆC. By (2.9), we know that (PS)c sequence {un}n⊂S1,p(Ω) is bounded for every μ<μ1. Thus, we may assume that un⇀u weakly in S1,p(Ω), and un→u in Ls(Ω) with 1<s<Q∗. Furthermore, since Iλ(un)=Iλ(|un|), we may also assume that un≥0 and u≥0. Therefore, invoking the concentration compactness principle on the Heisenberg group (see Vassiliev [23, Lemma 3.5]), we obtain
where {xj}j∈Λ⊂Ω is the most a countable set of distinct points, ω and ν in HN are two positive Radon measures, and {ωj}j∈Λ, {νj}j∈Λ are nonnegative numbers. Moreover, we have
Next, we shall show that Λ=∅. Indeed, assume that the hypothesis ωj≠0 holds for some j∈Λ. Then when ε>0 is sufficiently small, we can find 0≤ψε,j≤1 satisfying the following
where ψε,j∈C∞0(BH(ξj,ε)) is a cut-off function. Clearly, (unψε,j)n is bounded in S1,p(Ω). It follows from (2.8) and the boundedness of (unψε,j)n that
that is,
It follows from the dominated convergence theorem that
Hence, letting ε→0, we get
By Lemma 2.1,
and since un→u in Ls(Ω) with 1<s<Q∗, one has
Combining (2.15) with (2.16), we obtain that
thus
Since
applying the Hölder inequality, we obtain
By (2.10), we have
and
Therefore, by (2.13)–(2.19), one gets νj≥aωj. It follows from (2.11) that
In fact, if νj≥(aS)Qp holds, therefore by (2.8) and (2.10), for every μ<μ1, we have
which contradicts (2.7). Thus, Λ=∅. By (2.10) and Λ=∅, we have
Let
If A=0, then un→0 in S1,p(Ω). So assume now that A>0. By (2.8), we get
Let v=u in (2.22). Then
By (2.8), (2.10), (2.21) and Lemma 2.1, one also has
Thus, combining (2.23) and (2.24), we get limn→∞‖un‖p=‖u‖p. Thus, we see that un→u in S1,p(Ω) by the uniform convexity of S1,p(Ω). This completes the proof of Lemma 2.4.
3.
Proof of Theorem 1.1
3.1. Existence of a nontrivial weak solutions
We need the following auxiliary lemmas to prove our main result.
Lemma 3.1. Let q∈(2p,Q∗) and μ∈(0,μ1). Then functional Iλ satisfies the mountain pass geometry, that is,
(i) There exist constants ρ,α>0 satisfying Iλ(u)|∂Bρ≥α, for every u∈S1,p(Ω);
(ii) There exists e∈S1,p(Ω)∖¯Bρ satisfying Iλ(e)<0.
Proof. First, applying the Hölder inequality, we get
Let
We now show that there exists a constant ρ>0 satisfying f(ρ)≥ap. We see that f is a continuous function on [0,+∞) and limt→0+f(t)=ap. Hence there exists ρ such that f(t)≥ap−ε1, for every 0≤t≤ρ, where ρ is small enough such that ‖u‖=ρ. If we choose ε1=a2p, we have f(t)≥a2p, for every 0≤t≤ρ. In particular, f(ρ)≥a2p and we obtain Iλ(u)≥a2pρp=α for ‖u‖=ρ. Hence assertion (i) of Lemma 3.1 holds.
Next, we shall show that assertion (ⅱ) of Lemma 3.1 also holds:
Thus, we can deduce that Iλ(s0u)<0 and s0‖u‖>ρ, for every s0 large enough. Let e=s0u. Then e is the desired function and the proof of (ⅱ) of Lemma 3.1 is complete.
Proof of Theorem 1.1(I). We claim that
where
Indeed, we can choose v1∈S1,p(Ω)∖{0} with ‖v1‖=1. From (3.2), we have lims→+∞Iλ(sv1)=−∞. Then
So sλ satisfies
Next, we shall prove that {sλ}μ>0 is bounded. In fact, suppose that the following hypothesis sλ≥1 is satisfied for every λ>0. Then it follows from (3.4) that
Since 2p<q<Q∗, we can deduce that {sλ}λ>0 is bounded.
Next, we shall demonstrate that sλ→0, as λ→∞. Suppose to the contrary, that there exist sλ>0 and a sequence (λn)n with λn→∞, as n→∞, satisfying sλn→sλ, as n→∞. Invoking the Lebesgue dominated convergence theorem, we see that
It now follows that
Thus, invoking (3.4), we can show that this cannot happen. Therefore, sλ→0, as λ→∞.
Furthermore, (3.4) implies that
and
Hence based on the definition of Iλ and sλ→0, as λ→∞, we get that
So, there is λ1>0, satisfying for every λ>λ1,
Letting e=t1v1 with t1 large enough for Iλ(e)<0, we get
Therefore
for λ large enough. This completes the proof of Theorem 1.1(Ⅰ).
3.2. Existence of infinitely many nontrivial weak solutions
In this subsection, we shall use the Krasnoselskii genus theory to prove Theorem 1.1(Ⅱ). To this end, let E be a Banach space and denote by Λ the class of all closed subsets A⊂E∖{0} that are symmetric with respect to the origin, that is, u∈E implies −u∈E. Moreover, suppose that X is k-dimensional and X=span{z1,⋯,zk}. For every n≥k, inductively select zn+1∉Xn=span{z1,⋯,zn}. Let Rn=R(Zn) and Υn=BRn⋂Zn. Define
and
where γ(V) is the Krasnoselskii genus of V.
Theorem 3.1. (see Rabinowitz [24, Theorem 9.12]) Let I∈C1(E,R) be even with I(0)=0 and let E be an infinite-dimensional Banach space. Assume that X is a finite-dimensional space, E=X⊕Y and that I satisfies the following properties:
(i) There exists θ>0 such that I satisfies (PS)c condition, for every c∈(0,θ);
(ii) There exist ρ,α>0 satifying I(u)≥α, for every u∈∂Bρ⋂Y;
(iii) For every finite-dimensional subspace ˜E⊂E, there exists R=R(˜E)>ρ such that I(u)≤0 on ˜E∖BR.
For every i∈N, let ci=infX∈Γimaxu∈ZI(u), hence, 0≤ci≤ci+1 and ci<θ, for every i>k. Then every ci is a critical value of I. Moreover, if ci=ci+1=⋯=ci+p=c<θ for i>k, then γ(Kc)≥p+1, where
Lemma 3.2. There is a nondecreasing sequence {sn} of positive real numbers, independent of λ, such that for every λ>0, we have
where Γn was defined in Theorem 3.1.
Proof. By the definition of Γn, one has
therefore sn<∞ and sn≤sn+1.
Proof of Theorem 1.1(II). We note that Iλ satisfies Iλ(0)=0 and Iλ(−u)=Iλ(u). In the sequel, we shall divide the proof into the following three steps:
Step 1. We shall prove that Iλ satisfies hypothesis (ⅱ) of Theorem 3.1. Indeed, similar to the proof of (ⅰ) in Lemma 3.1, we can easily prove that the energy functional Iλ satisfies the hypothesis (ii) of Theorem 3.1.
Step 2. We shall prove that Iλ satisfies hypothesis (ⅲ) of Theorem 3.1. Indeed, let Y be a finite-dimensional subspace of S1,p(Ω). Since all norms in finite-dimensional space are equivalent, it follows that for every u∈Y, we have
for some positive constant C>0. Also, because of 2p<Q∗, we can choose a large R>0 such that Iλ(u)≤0 on S1,p(Ω)∖BR. This fact implies that the energy functional Iλ satisfies the hypothesis (iii) of Theorem 3.1.
Step 3. We shall prove that problem (1.1) has infinitely many nontrivial weak solutions. Indeed, applying the argument in Wei and Wu [25], we can choose a1 large enough so that for every a>a1,
that is,
Thus, one has
From Lemma 2.4, we know that Iλ satisfies (PS)cλi(i=1,2,⋯,n) condition. This fact implies that the levels cλ1≤cλ2≤⋯≤cλn are critical values of Iλ, which be guaranteed by an application of the Rabinowitz result [24, Proposition 9.30].
If cλi=cλi+1 where i=1,2,⋯,k−1, then applying the Ambrosetti and Rabinowitz result [26, Remark 2.12 and Theorem 4.2], we see that the set Kcλi consists of infinite number of different points, so problem (1.1) has infinite number of weak solutions. Hence, problem (1.1) has at least k pairs of solutions. Since k is arbitrary, we can conclude that problem (1.1) has infinitely many solutions. This completes the proof of Theorem 1.1(Ⅱ).
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Song was supported by the National Natural Science Foundation of China (No. 12001061), the Science and Technology Development Plan Project of Jilin Province, China (No. 20230101287JC) and Innovation and Entrepreneurship Talent Funding Project of Jilin Province (No. 2023QN21). Repovš was supported by the Slovenian Research Agency program No. P1-0292 and grants Nos. J1-4031, J1-4001, N1-0278, N1-0114 and N1-0083.
Conflict of interest
The authors declare there is no conflict of interest.













 DownLoad:
DownLoad: