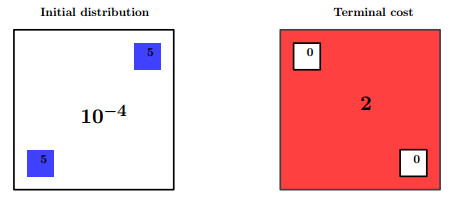
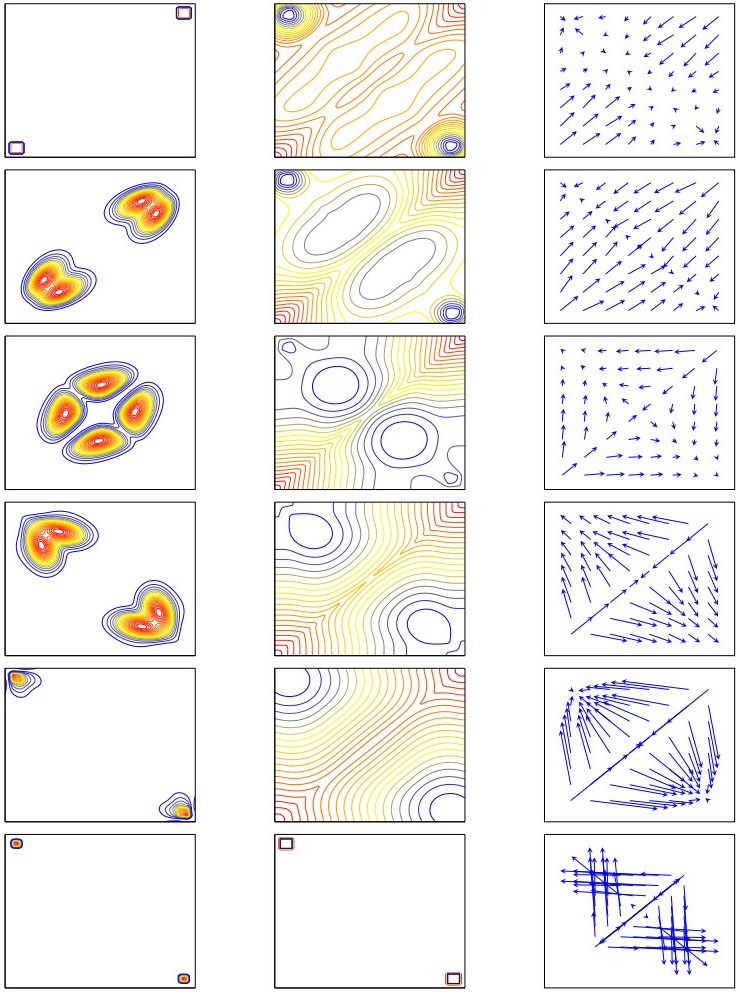
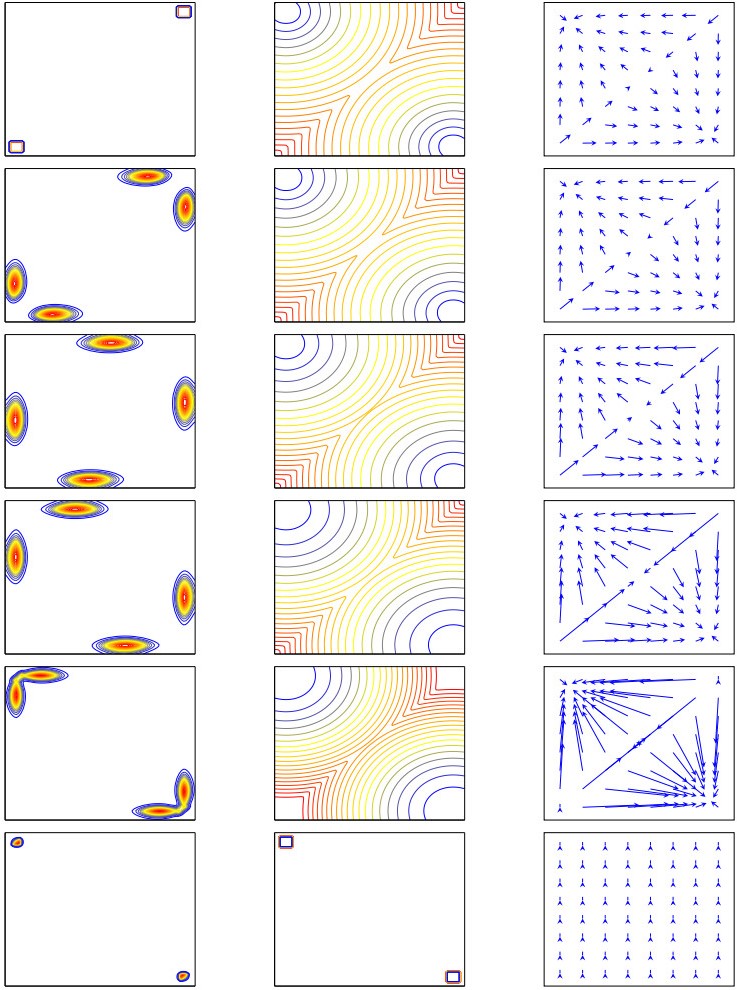
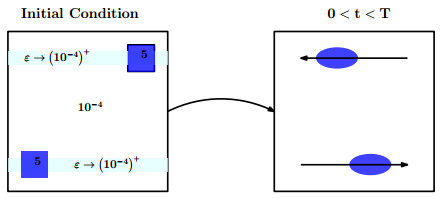
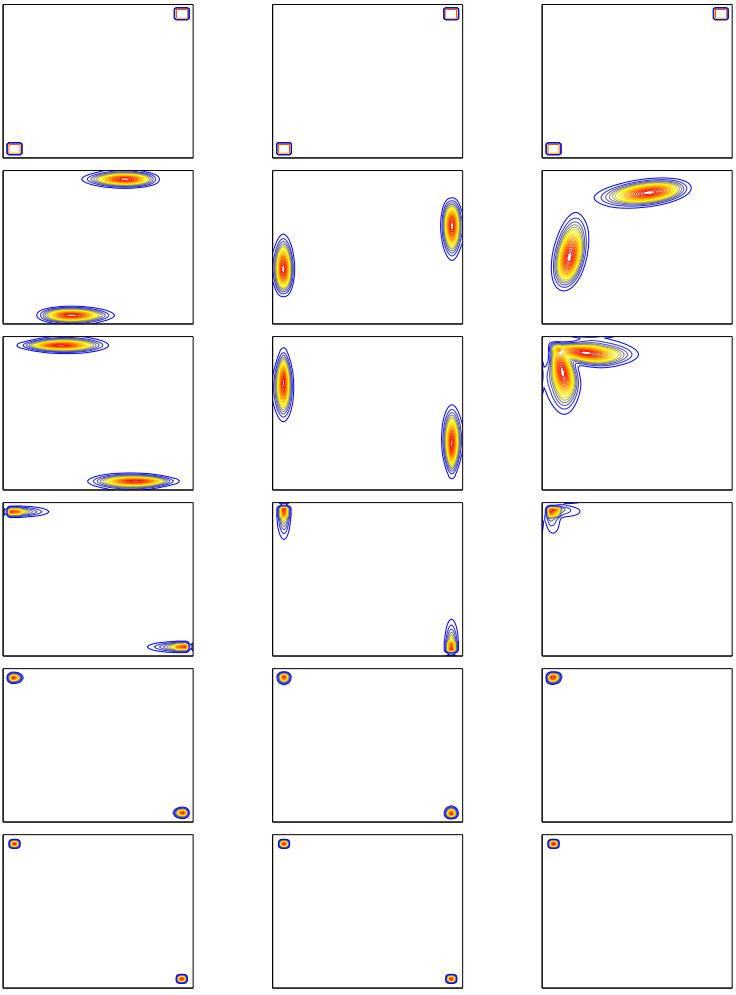
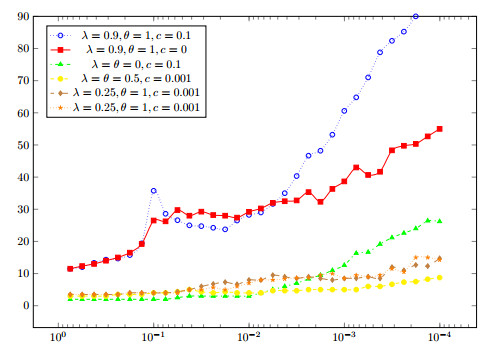
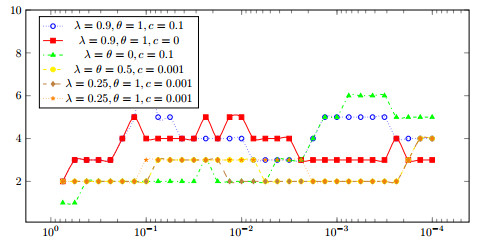
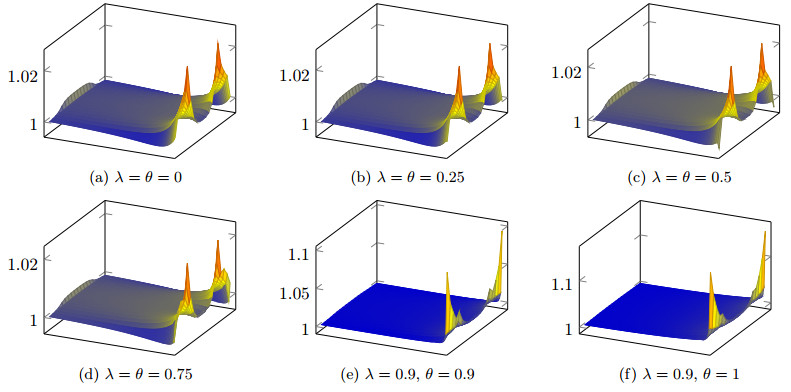
We consider a class of mean field games in which the agents interact through both their states and controls, and we focus on situations in which a generic agent tries to adjust her speed (control) to an average speed (the average is made in a neighborhood in the state space). In such cases, the monotonicity assumptions that are frequently made in the theory of mean field games do not hold, and uniqueness cannot be expected in general. Such model lead to systems of forward-backward nonlinear nonlocal parabolic equations; the latter are supplemented with various kinds of boundary conditions, in particular Neumann-like boundary conditions stemming from reflection conditions on the underlying controled stochastic processes. The present work deals with numerical approximations of the above megntioned systems. After describing the finite difference scheme, we propose an iterative method for solving the systems of nonlinear equations that arise in the discrete setting; it combines a continuation method, Newton iterations and inner loops of a bigradient like solver. The numerical method is used for simulating two examples. We also make experiments on the behaviour of the iterative algorithm when the parameters of the model vary.
Author summary
Traumatic brain injury effects millions of Americans each year. In addition to the immediate injury concerns, patients afflicted with a TBI have the potential for long term debilitating damage. We construct a dynamic, three dimensional model that has the ability to investigate the patient physiology and vessel structure beyond the millisecond time scale. Increased experimental work done recently make clear that therapeutic interventions over the course of days to weeks may create significant long term positive outcomes in a patients recovery. We create a mathematical model that is able to simulate the patient angiogenesis over these time scales. We explore the role that protein interactions have on global microvascular growth and overall restoration of blood flow to the damaged tissue region.
1.
Introduction
Traumatic brain injury (TBI) has symptoms that are persistent, debilitating and possibly chronic. TBI usually occurs from a violent blow or acute movement to the head or body with moderate to severe occurrences resulting in symptoms that may persist from days, weeks and even years. TBI in the United States annually accounts for an estimated 1.7 million injuries and are attributed to a third of all injury-related deaths. In addition, they are a major cause of disability and cognitive disorders in young adults [1]. Within 24 hours of the causing event, reduced global cerebral blood flow (CBF) is associated with poor overall outcome and rehabilitation of the individual [2]. In addition, secondary damage caused by ischemia related to hypotension and hypoxia can cause further damage to the brain post TBI [3]. There is also evidence that the reduction in CBF caused by a TBI along with other neuropathologic parallels lead to an increased incidence of Alzheimer's disease [4]. CBF changes immediately after the injury and continues to have prolonged effects over the following days/weeks as the angiogenesis process occurs. Reduced CBF and associated vasculature damage is a hallmark of poor neurologic outcome after TBI [5,6] and significantly contributes to the overall pathogensis of the injury.
Beyond cellular and biological processes, TBI recovery and vasculature angiogenesis has recently been shown to be a function of mechanical and locational variables. Studies have shown that the severity of the TBI on animals creates distinct patterns related to the depth of deformation and velocity of impact [7]. Other experimental studies have examined regional changes during the TBI recover process. These include: differences in CBF between ipsilateral and contralateral regions surrounding the injury site [4], oxygen partial pressure recovery differences [3], and cerebrovascular resistance and perfusion pressure changes [8]. Due to the non-symmetric and location specific differences of TBI recovery, further investigations are still required.
A combination of several secondary reactions to a TBI initiates an inflammatory cascade within minutes of the injury that has been shown to contributing to complications during the healing process. Evidence suggests that it may be necessary to dampen maladaptive inflammatory responses in order to promote wound healing [9]. In addition, the inflammatory response may create more secondary damage than the primary injury for mild TBI cases [10]. The activation of vascular endothelial growth factor (VEGF) in the cerebral tissue following a TBI happens within hours of the injury [11]. There is evidence of VEGF protein in 40% of capillaries as early as 4 hours-post impact that is shown to drive vascular density. There has been shown a difference between hypoxia driven vascular reconstruction and TBI driven reconstruction. Not only is the vascular density increased by the sprouting of capillaries that occurs during VEGF stemmed angiogenesis, but the existing vessels must adapt to meet the new blood flow requirements. Cancer research has shown that inflammatory cytokines induce VEGF production, which is a major component of tumor angiogenesis [12].
Under hypoxic conditions, cells will release VEGF. The binding of VEGF to VEGFR on the endothelial cell surface initiates a biochemical cascade that leads to sprouting angiogenesis. Although there are multiple isoforms of VEGF and its receptor, experimental studies suggest VEGF165 and VEGFR2 to be the most relevant and strongest at stimulating angiogenesis in the human brain, compared to other isoforms and VEGFR1 [11,13]. The goal of angiogenesis is to re-establish a vessel network that sufficiently meets metabolic demands, and eliminates hypoxia. One endothelial cell that binds VEGF to its receptor will become the "tip cell." This cell is the leader of the new vessel that is sprouting from the existing vasculature. Through Dll4-Notch lateral inhibition the tip cell signals its neighboring cells to become non-tip cells, or stalk cells [14]. In this way, not all the endothelial cells that bind VEGF will become tip cells.
VEGF is well known to instantiate angiogenesis [15] and is the subject of several tumor models [16,17,18,19,20]. These models are generally structured as either a continuous or discrete model in which the vascular growth is modeled through conservation equations for endothelial-cell density [21] or probabilistic reinforced random-walk models (cellular automota models) [22]. These formulations capture capillary growth branching from a primary root vessel due to endothelial-cell flux due to chemosensory stimulus through tumor induced angiogenesis. Concentrations of VEGF are represented through tumor angiogenic factors, secreted into the surrounding tissues. Other models of angiogenesis include: partial differential equation model to account for diffusion and ligand-receptor binding with two different VEGF isoforms, VEGF121 and VEGF165, stimulating and inhibiting VEGF signals on angiogenesis, and reinforced random walks and Michaelis-Menten kinetics to model the interactions and influence of growth factors, fibronectin, and movements and densities of endothelial cells [23,24,25]. VEGF models have also been leveraged to study capillary growth in the retina due to oxygen deficiencies [26].
The interaction of ligands and receptors involved in the angiogenesis process have been modeled stochastically and deterministically. Monte Carlo simulations are particularly useful for very small scale interactions where the stochastic component of ligand movement and binding dominates [27]. When modeling on a larger spatial scale, looking at the bulk characteristics, greater collective concentration of a ligand is accurate and saves computational complexity. It has been shown that when modeling a sufficiently large area and with ligand and receptor concentrations/densities of VEGF and its receptors at typical values, stochastic and deterministic models give similar results. Deterministic models include those that employ reaction-diffusion equations and differential equations to describe ligand-receptor interactions governed by reaction rate constants that are proportional to ligand and receptor concentrations. The reaction rate constants are specific to which molecules are interacting. Studies that have employed this model for studying VEGF kinetics, often using rate constants that are self-determined or those found in literature, include [23,24,28]. Apart from association and dissociation, other dynamics are modeled, such as: insertion, decay, and internalization [29]. To model the entire angeogenic, process connections between the VEGF interactions and vessel growth are required and are a unique extension to these models that this work will demonstrate.
Fractals are utilized to examine vasculature networks and phenomena in a variety of models. It has been shown that the fractal dimensions of tumor vasculature can be closely represented by an invasion percolation model where the angiogenesis follows a random, locally determined process that is unlike the global process found in healthy tissue [30]. Creation of the vascular bed as a bifurcating or trifurcating tree is more than reasonable due to the physical resemblance and branching found in blood vessels and lung airways [31]. A Space filling tree has also been used to determine biological principals that can influence a generated network [32]. This model generally mapped well to the overall blood microvascular structure. Tissue structure and entry points of the largest arteries have also been used to develop vascular trees in silico [33]. This type of model can be generalized to several tissue types and may be used alongside the design and development of artificial tissue [34]. For this work, we combine a three dimensional fractal model with an lumped model of the VEGF protein receptor interactions. To achieve this result we rely upon open source medical image data as an input to the model.
With increasing availability and granularity of medical image data, it has become easier to develop more accurate vascular models. Medical image data and computer vision algorithms have been utilized to extract vessel structure from retina images (a 2-dimensional model) and of mouse cerebral vasculature [35,36,37]. Medical images and mathematical algorithms can be used in tandem to approximate the entire cerebral vessel structure using experimental data and tree generation algorithms [38]. Generation of a cerebral vascular structure using medical images can be automated, although it still may require manual attention [39] and manual segmentation is still used to validate the more automated procedures [40].
Despite the breadth of angiogenesis mathematical models and advances in imaging, work still must be done to understand the relationship between vessel restructuring during a TBI injury outside of the milisecond to second timescales. In addition, computational models may be used to address how regional variations in injury patterns effect recovery. We develop a multi-scale model of changes in VEGF after TBI by connecting the dynamics of the angiogenic process to fractal models of the arteriole and capillaries. In this way, we are able to determine global vessel structure outcomes in patients in the days and weeks post injury. We investigate how the location of the TBI effects the volume recovered in the damaged tissue and how VEGF and VEGFR interactions influence this recovery. We also develop a model to couple VEGF to a generic inhibitory drugs to answer whether specific amounts of drug can be applied to optimize recovery as a function of TBI location.
2.
Materials and methods
2.1. Cerebral vascular architecture
We construct our baseline vascular model by manually extracting vessel data from medical images. Computationally, we represent this as a non-perfect binary tree of "Fiducial Nodes, " as fiducials were used to mark the medical images to trace the vasculature. The tree is non-perfect because there may be multiple consecutive nodes in which each node only has one child node. When the vasculature branches, these are the cases in which a node will have two children. We restrict our vessel growth model by limiting fiducial nodes to no more than two children. In our model, we focus on the larger arterial and arteriole vessels, and do not model those smaller in diameter than approximately 0.2mm.
The cerebral vascular architecture was constructed solely with the use of open source available data and software. Magnetic resonance angiography (MRA) images from healthy volunteers were obtained from the CASILab at the University of North Carolina, Chapel Hill [41]. MRA images were loaded into 3D Slicer4 (subsequently referred to as Slicer) [42,43]. We manually filtered the network using the Vascular Modeling Toolkit module which aided in identifying blood vessels. Vessels were mapped by manually placing fiducials at vessel bending and branching points and noting their connectivity to other fiducials. Focus was on mapping arterial vessels with fiducial markers. Fiducials were placed until the granularity of the medical image prevented further tracking the path of a vessel (usually at about 0.4 mm), or appeared to anastomose with another vessel.
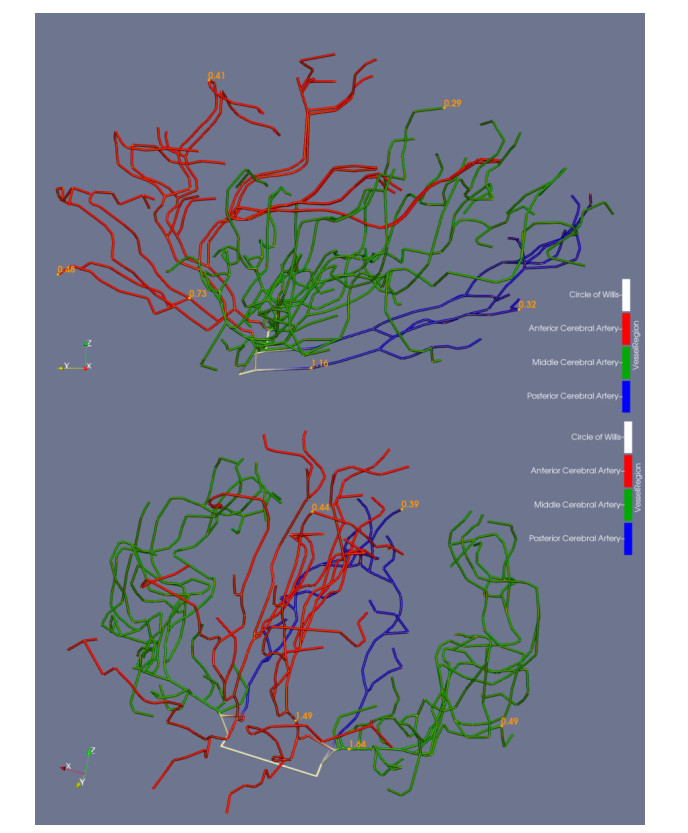
The measurement tool in Slicer was used to measure vessel diameters at branching and vessel terminus fiducial nodes. Slicer was also used to exclude the skull from the MRA data. The diameters of fiducial nodes marking vessel bending points were set via linear interpolation between the diameters measured at nearest-neighbor branching and terminal nodes. Figure 1 displays the extracted vessel architecture and segments the major regions of the brain. The fiducial list was exported from Slicer in a.vtk format and served as input to our blood flow and protein model to create the vessel architecture.
Due to the image resolution, only major vessels to a minimum of about 0.2 mm were mapped and extracted from the volunteer MRA. Thus, arterioles and capillaries are not included in the model. Veins are excluded as well. The major cerebral arteries mapped include: the anterior cerebral arteries and the middle cerebral arteries, which arise from the internal carotid arteries, and the posterior cerebral arteries, which arise from the basilar artery [44]. Although, both blood supplies from the carotid arteries and basilar artery are connected at the circle of Willis. The anterior, middle, and posterior cerebral arteries are seen in the three groupings of vessels on either side of the hemisphere, Figure 1.
It stands out that the model cerebral vasculature is not evenly distributed across the entire brain's volume. The brain is composed of gray and white matter. The white matter is home to neuronal axons and the gray matter to neuronal cell bodies, which require an approximately five times greater oxygen supply [45]. Thus, the gray matter gets the majority of the blood supply to the brain and the model's vessels are prominent in gray matter regions [46].
2.2. Injury model and angiogenesis
Traumatic brain injury can tear cerebral blood vessels, causing bleeding and preventing vessels from effectively delivering and removing metabolic nutrients and wastes [47]. We model TBI damage on the cerebral vasculature by reducing blood vessel radius after the impact, effectively simulating the bulk outcomes of edema and hematoma. In the model, the TBI is inflicted to a spherical region of the brain, Figure 2. Iterating through each of the fiducial nodes, the vessel radius of nodes in the TBI region are decreased by 50%. We note, that we are not considering the effects of TBI impact to all fluid located in the damaged region, only the vessels located therein. Due to only large vessels being modeled, the volume lost to TBI is calculated not as the volume lost by reducing vessel radii in the TBI region, but instead by multiplying a factor to the TBI region volume. We compute the lost volume in the damaged region by approximating the volume of the microvessels that occupy up to 1.86% of the damaged tissue, by volume [48]. To calculate our vascular volume, we multiply the volume of the spherical TBI region by 0.01 and by the damage factor (50% in the case of this study).
We then model sprouting angiogenesis by creating new vessels off of the existing vasculature. To determine whether a new vessel will form, three conditions must be satisfied. First, we compute the probability of VEGF causing a sprout by evaluating the probability density function of VEGF at that vessel node (dependent upon the distance from the TBI region and the simulation time). Second, we weight the probability of diffusion with the concentration of bound ligand-receptor ([LR] = [VEGFR-VEGF]). The dynamics of this bound complex are defined by equations 14-16 and more detail can be found in section 2.4. The concentration of the bound VEGFR-VEGF, scaled by the diffusion term, must be greater than a random number generated between 0 and 1 times a multiplier in order for a sprout to form. In this study, we set the random number multiplier (RNM) to 150 to spread out new sprout formation over time and to try and capture logarithmic vessel bifurcations assuming that the angiogenesis process has exhausted itself after two weeks. Lastly, we check if there are any other vessel nodes nearby that have already formed a sprout to represent an upscaling of Dll4 notch lateral inhibition, where adjacent endothelial cells won't both be the tip cell in sprout formation. These checks are applied to each of the vessel nodes a part of the original vasculature every hour after injury.
We estimate the availability of VEGF near each vessel node by leveraging a solution of the diffusion equation for the VEGF, the diffusing species. This provides concentration over time for a distance outside of the damaged tissue region. For a given diffusing species, VEGF, we can denote the concentration at a given distance and time from the TBI region and initial impact time by:
Here P(→x,t) denotes the probability that a node will sprout at time t after the injury and a distance →x from TBI region in three dimensional space. D is the diffusivity of VEGF, taken to be 1×10−6cm2/s and σ denotes the diffusion constant given the diffusivity of the tissue. Because VEGF is released from the damaged tissue during a TBI, we scale the probability to consider the entire damaged region not just a single point source release, effectively smoothing the probability function to be a distance of 3mm from the center point of the TBI. We choose to do this to account for the small distance that VEGF released from the tissue has to diffuse to the endothelial cells. We then apply this smoothing distance to each vessel node when computing the probability that a node will bifurcate. Algorithmically, we shift each of the node's distances by the radius of the spherical TBI region less 3mm, such that →x is the distance from the edge of the TBI region plus 3mm to a vessel node that is outside of the TBI region. Δ→x=L/3, where L is the vessel node length. Computationally, for each labeled node point, we store its associated length and name this value the vessel node length. We normalize the distance by 3 which is the most common vessel length amongst the initial fiducial nodes, Figure 3.
Otherwise satisfying diffusion and [VEGFR-VEGF] requirements, nodes that are not marked as already having a nearby sprout are allowed to form a sprout. Nodes within the minimum distance to sprout, determined by ascending and descending the vasuclature from the node in question, are then marked as having a nearby sprouting node and are not allowed to sprout. The minimum sprout distance for this study is set to 10mm because we assume each sprouting vessel is a lumped vessel that includes vasculature within a 10mm distance. Since our model places a maximum of one parent node and two child nodes restriction on each vessel node, our model accounts for a node that already has two child nodes passing the sprout formation checks by bisecting the vessel node in the middle of its length with a new placeholder node, termed the bisecting node. This new bisecting node's two child nodes are set to the node that was bisected and a new sprouting vessel node. These checks for new sprout initiation are applied every hour.
2.3. Vessel growth and orientation
Once sprouts have formed they are either grown in length or bifurcated, forming two sprout child nodes at each time step, minus a growth cutoff that prevents vessels from crossing the center of the TBI. This cutoff is defined as a plane, which contains the point of the center of the TBI, and whose normal is parallel to the direction that the first sprout to form off of the original vessel network grows in. Sprouts grow in length towards the center of the TBI region in proportion to the bound ligand-receptor concentration ([VEGFR-VEGF] = [LR]) and that sprouts radius, r. We are assuming that the new sprout has an initial radius, r, neglecting the time needed to generate a functional radius. The change in length is given by:
Using dL, we calculate dx, dy, dy, and dz with the following rotation equations, Figure 6 :
We can then add these contributions to the x, y, and z coordinates of the sprouting node to get an update at each timestep dt. Once reaching their max length defined by the length-to-radius ratio (LRR), the sprout will stop growing and bifurcate into two child sprouts, Figure 4.
Numerous values have been proposed for the LRR for different vascular trees [49]. Research has supported an LRR of about 50 [50], maximum LRR's of about 70 (centered around 20) [51], and other research supporting a range from 10 to 60 [49]. Validating against the vascular density, Figure 8, we take the LRR to be ≈13. We assume only the size of terminal child vessels increase in length, and the diameters of other non-terminal sprouts that were previously increasing in length before they bisected do not change. This is in contrast to [52]'s review of neovascularization after TBI, which suggested vessels increase in diameter and is something we plan on investigating in the future.
As suggested by previous work, for physiological resemblance, we utilize an asymmetrical fractal, in which each blood vessel branches into two asymmetrical daughter vessels, where the parameters associated with vessel length and radii will vary at different locations in the arterial tree. Although blood vessels exhibit a variety of branching styles, including trifurcation, they most often bifurcate. We follow a previously derived principle of minimum work [53], by proposing a cubic relationship between blood vessel radius and blood flow. We apply this with conservation of mass to define the equations governing the relationship between parent and daughter blood vessels involved with vessel bifurcation to be:
Integrating previous work, [54], we optimize the bifurcation angles θ2 and θ1 (Figure 5) to derive the following equations:
Our choice of k is based off previous work that has shown shown this value to fluctuate between 2 in larger arterial vessels to 3 in the microvasculature [34,55,56]. We use the power law with k=3 for the sprouting angiogenesis within the microvasculature, in line with previous results.
Arterial trees posses asymmetry [50,51], with proposed asymmetry ratio, γ, between daughter vessels given by:
Given Eq 2.7, k, and γ, a direct relationship between each daughter and parent vessel radius can be determined by:
α defines the relationship between R2 and R0. β defines the relationship between R1 and R0.
Substituting α and β into 2.7 we can determine α and β just in terms of γ:
Using the equations defined above, once a sprouting node reaches it's LRR, we create two child sprouting nodes with a specific radius. Initially they have a length of zero, and at each time step they will grow in length. The direction they grow in is determined by subtracting θ1 from the parent X, Y, and Z angles for the sprout with radius R1, and by adding θ2 from the parent X, Y, and Z angles (θx, θy, and θz) for the sprout with radius R2. Additionally, to help fill 3D space, each of the child vessels is rotated ϕ=π/6 about the parent vessel's axis using a rotational matrix given by:
We can then get a the new direction of growth for the child vessels by multiplying the rotation matrix to the parent vessels unit vector, ^uparent=(ux,uy,uz). The resulting angle of growth for the child vector can be defined by θx, θy, and θz, see Figure 6 and stored by the sprout child. After this, the angle of growth is set, and sprouting nodes will grow in length.
We use Eq (2.3) and Eq (2.7) to investigate how rapidly sprouts grow across generations. The following proof shows that the rate of parent growth dVdt is the same for the parent as for the cumulative children.
Proof. r0, r1, and r2 are the radii of the parent, and two child sprouts respectively. dV and dL are the change in volume and in length of the vessel in one growth increment. dt is the time step. [LR] is the relative concentration.
Since parent growth stops as soon as child sprouts form it, given a constant bound VEGFR-VEGF concentration ([LR]), growth will continue at the same rate in the children. Thus, if [LR] is constant, the only way to speed up overall return of blood volume is for additional sprouting node fractal trees to form, as existing ones will continue to restore volume at the same rate, even when they branch. We note that for this simulation, the [LR] is non-constant and so vessel growth is scales non-linearly as a function of the bound ligand, which is itself a function of VEGF production and diffusion. Important to note is that the ability of sprouting node fractal trees to return blood volume could be limited by the plane perpendicular to the most ancestral sprouting node that is used as a stopper for sprout growth not to continue to the opposite side of the TBI region. All code is implemented in C++ with a modern object oriented programming architecture. This allows for massive vascular tree generation and long running simulations. Investigations into multi-day recovery and implications for vascular healing are investigated.
2.4. Protein-receptor kinetics
We iterate on previous work [23,24,29] to construct a system of ordinary differential equations (ODE) to model the temporal profiles VEGF, VEGFR, and the bound complex, VEGFR-VEGF. These equations account for the protein kinetics associated with formation/insertion, degradation/removal, association and dissociation of the VEGF protein and its receptor and are given by:
α, β, kon, and koff are rate constants representing formation/insertion, degradation/removal, association, and dissociation of VEGF and VEGFR, respectively. Except for α, each term is formed by multiplying the rate constant with its associated ligand/receptor/bound complex concentration. Specific kinetics on VEGFRs, or their coupling to NRP1, is not modeled and is assumed to be appropriately upscaled into modeling VEGFR potent as a monomer. We couple the bound concentration, [LR] to a probability density equation, Eq 2.1, to determine if a node will have a vessel sprout from it, see subsection 2.2. Computationally, we solve these equations with a forward euler differencing scheme and a time step of 1 minute.
We also include terms representing the cardiovascular changes after TBI, such as hypoxia induced VEGF production and VEGFR expression [57,58,59]. Thus, we determine αL as a variable dependent on lost blood volume, where lost blood volume is taken to be the immediate result of TBI, proportional to extent of TBI injury and correlated to hypoxia. We model these terms with piecewise logistic functions, where αL is a dependent variable of blood volume lost and αR a dependent variable of VEGF concentration:
Here the independent variable, x, that determines αL and αR, represents blood volume (still) lost by TBI in mm3 at each simulation time step. At x=x0=0, the αL generation term is set to the steady state production rate, P0=5×10−15M/s. For x>x0, Pmax=5×10−14M/s, k=0.07mm−3, and x1=32. For αR, x represents [VEGF] in Molar, x0=1.2×10−11M, P0=2.4×10−13M/s, Pmax=7.5×10−13M/s, k=1.3×10111/M, x1=3×10−11M.
Rate constants were chosen to be within an order of magnitude of those that had values reported in literature (Table 1), and are set as follows: degradation/internalization of ligand and of receptor βL=βR=8×10−5, internalization of bound ligand-receptor βLR=5×10−5, association constant of ligand and receptor kon=1×106, and dissociation constant of bound ligand-receptor is koff=1.5×10−3. See Table 1 for a compilation of rate constants/coefficients from literature and our model.
Initial conditions in our model are [L]=[VEGF]=12pM, [R]=[VEGFR]=3nM, and [LR]=[VEGFR−VEGF]=20pM. These initial conditions were chosen to be close to those values reported in other studies and that also would create a relatively smooth profile of VEGF protein interactions if suddenly greater growth factor was applied due to TBI [48]. We take experimental data for free VEGF in the human vastus lateralis at rest and in breast cancer tissue, measured at around 1pM. For VEGFR2, we start with reported values of about 0.3pmol/cm3 per tissue of VEGFR2 in the vastus lateralis tissue model. We then Convert the VEGFR2 tissue model value to Molar, yielding 0.3pmolcm3VEGFR2×1M/6.2×107pmolcm3=5×10−9M=5nM. Other reported data on breast cancer tissue show a value for VEGFR2 = 0.33nM. Bound receptor-ligand complex was chosen to be an approximation of [VEGF].
To validate this model, we compiled literature that reported temporal changes in VEGF after brain injury. Work by [63] and [64] report on human VEGF found in cerebral spinal fluid and intracerebrally while work by [11,65,66,67,68,69] reported data on murine and rat subjects, Figure 7. We note that there was no control protocols on the human subject data and that all data collected in these studies were collected from cerebral spinal fluid. This differs from our model in that we assume [VEGF] is located in the microvasculture and tissues surrounding the injury site. In addition, the TBI is only classified as severe, but imaging data was not used to quantify the lesion. It is clear that additional validation studies are needed. Our model produces a maximal VEGF concentration of about 4 times baseline 12-24 hours post-injury. This compares well with the averaged the maximal [VEGF] across all collected studies for the first 24 hours post-injury, which is about 4.1 times baseline concentration. Although the averaged value is generally in line with experimental data, the general dynamics of the model are slower to resolve than is to be expected. We aim to improve upon the tail dynamics in future studies by including additional molecular interaction pathways for VEGF during the injury period. In addition, more data is required to classify the receptor expression and binding during angiogenesis. Studies suggest a secondary peak days after the initial injury which would speed up the tail dynamics of our model but is not included in this analysis [11].
Because we struggled to find high quality human data to validate our model, we chose not to fit the VEGF dynamics to the available data. We instead chose to keep our rate constants in line with experimental in vitro data which was generally collected in a highly controlled environment, Table 1. This still yielded good results for the dynamics of VEGF in the first 24 hours post-injury but did slow the uptake and metabolism of VEGF in later portion of the simulation. In addition, the vascular density, Figure 8, struggles to meet validation data. We do note that experimental data obtained for vascular density varied with respect to the subject, experimental design, and type of injury. Subjects were murine and rat and the studies used a variety of injury types and models, including weight drop, fluid perfusion, cold lesion, and stroke. Data was collected either through imaging or measured post-mortem. Since the vasculature changes to such a degree during angiogenesis, more experimental data is needed to validate the vessel growth models in this computational model. We also note that to properly quanity density of the microvascularture we will need to refine our spouting model to consider the venous return growth, which we omit for this study.
3.
Results
We used our model to simulate VEGF kinetics and sprouting angiogenesis returning lost blood volume with the TBI region at different locations: frontal, lateral, superior, and posterior (Figure 2), and with different scaling factors that either increase or decrease the VEGF growth rate or association rate relative to their normal values. Normal values were arbitrarily set to values that give an approximate complete return of lost blood volume to a TBI at Location 0, after 14 days, as recovery by the 7-14 day mark has been shown to complete the initial angiogenic recovery period [9]. We investigated the effects of different VEGF generation and association rates and their effects on location specific recovery profiles. This was done by multiplying the VEGF generation rate, αL, and the association rate of VEGF with VEGFR, kon, factors we will denote as γL and γon respectively, and setting these new values as the new αL and kon rates used in Eq (2.14). There are many steps in the angiogenesis pathway [78] and the γ scaling factors represent ways the model can be customized or adjusted to allow for individualized, or patient specific, simulations, in vitro experimental conditions, or account for drug interaction.
3.1. Location dependant recovery
We position the TBI location to cover each major vessel region of the cerebral vasculature, denoted here as L0-L5. We then simulate our model over a 14 day recovery period and report on volume restored to the damaged region over time, Figure 10. We show that our model displays strong dependence on location of the injury site and the overall progression to recovery of the lost volume. This is consistent with experimental studies showing varying patient recoveries as a function of TBI lesion location [79]. Volume recovered in the regions L0 and L1, which are vessel regions supplied by the anterior and middle cerebral arteries, respectively, are almost able to reach baseline values over the fourteen day period without intervention. Location L3, which denotes vessels supplied by the posterior cerebral artery, was not able to recover as readily. This could be due to the fact that the vascular density in this area is reduced, restricting the number of sprouts able to be formed during the recovery period. This theory is justified by Figure 9 showing that the number of bisectors produced is prolonged over the recovery period, compared to L0. Additionally, the total bisectors produced is reduced by about half, comparing the two locations. This is contrast to the volume restored over the 14 day simulation window with L0 restoring around 80% of baseline and L3 only restoring around 20%.
To better understand how the the influence of [VEGF] has on bisector and sprout generation we note that there is a strong dependence on the VEGF release as a function of volume lost. We note that as γL changes, for the same location, there is a strong response in vessel geometry, Figure 11. This seems natural according to our model construction since our random distribution function is itself a function of VEGF release. As VEGF release is increased, the probability for a sprout to form off a given node will also increase. [VEGFR] also increases within hours but did not reach the peak until 48 hours post injury, similar to [VEGF] protein which has been shown to peak around 24 hours post injury. Similarly, it has also been shown that VEGF isoforms near the location of the experimental TBI were significantly increased when compared to other regions of the brain [80,81], similar to our model results. We can also see that location plays a strong role in the vessel architecture 14 days after the injury, since a TBI occurring in a location near a number of large vessels, the VEGF will have more nodes available to sprout. Location of the TBI certainly has a strong effect on the recover profile of the patient. The density of the microvasculature generated during the angiogenesis process has been reported experimentally and we show good validation with experimental results, Figure 8.
3.2. Protein-receptor association and binding
Using our model, we can investigate how the role of association and production affects recovery at each of the simulated injury locations, Figure 2. If we can get an understanding of how these parameters may influence patient recovery in each location, over a 14 day recovery window, it may be possible to tailor treatment of a patient depending on the type, location, and severity of the TBI. We begin by reporting on bisectors generated and volume restored as a function of γon and γL which denote the binding of VEGF to the receptor VEGFR and the release of VEGF in the tissue as a response to the TBI injury, respectively. For this investigation we hold the location of the TBI constant at L0, Figure 2, and report total volume restored and bisectors produced over a 14 day simulation. For this location it is clear that the number of bisectors produced and volume resorted is a non-linear function of each of these parameters, Figure 12. Each γ produces a strong early positive response in number of bisectors and volume restoration over the simulation period. The association rate γon, has a strong early effect with little effects beyond the initial adjustments of the parameter between 0 and 1. The generation rate shows a quadratic response early on, with a more linear increase as it is increased beyond 2. Total bisectors and volume restoration are influenced more as a function of γL in total. Physiologically, as more VEGF is dispersed from the injured tissue, a stronger angiogenic response from the cerebral vasculature is seen, with volume restored beyond what the initial damage (≈70 mL) generated.
We investigate these responses as a function of each TBI location to determine influence of these parameters to overall volume recovery. We choose four different injury locations that cover the major regions of the brain. For each location we iterate each parameter from 0.2 up to 2.0 in increments of 0.2. We then report the volume restored, in total, after a 14 day simulation time, Figure 13. At Location 1 and 4, the least amount of volume is concentrated at the tip of where γL and γon are at a minimum, and more volume is able to be restored along the front edges of the graph, so long as γL and γon are not both at a small value. In contrast, for Location 2 and Location 3, very little volume is returned, if at all, for elevated levels of either parameter so long as either γL or γon is a small value. For location 3, to sustain a significant volume restoration, both parameters must be elevated, to promote not only binding affinity but also an increase VEGF response to the TBI. As long as the TBI location is in close contact with other large vessels, restoring volume to baseline has a much higher probability during a 14 day simulation, than for TBI locations that are not near larger arterioles.
For each location, we investigate the number of bisectors generated and the associated volume restoration after a 14 day simulation, while iterating over various γL values. These values correspond to VEGF production in the damaged tissue and influence the probability of bisector generation. Although connected, there isn't a one-to-one correspondence between bisector generation and volume restoration, Figure 14. Early increase in VEGF release create steep response in vessel sprouting (bisectors) of the vasculature. Once saturated, the location seems to play the strongest role on long term vessel architecture, seemingly having a strong influence on the plateau seen in the data. Once the bisectors reach a maximum for the region, even additional VEGF protein does not seem to be able to increase that total number. A more refined input cerebral vessel architecture could possibly display more nuanced results of the sprout formations. In contrast, the VEGF release plays a strong role in volume restoration regardless of location. There is no apparent maximum reached and dynamics of the response transition from quadratic to linear as γL reaches ≈0.8, Figure 14.
In Figure 13, it is seen that different locations are capable of restoring more or less volume than others, and different locations are more / less sensitive to different values of γL or γon. We looked at possible ways to adjust, in combination, γL and γon for different locations in order to restore blood volume to baseline, See Figure 15. These results show that it is possible to adjust the production and binding rate of VEGF in the brain vascular tissue in order to generate a similar outcome as a function of lesion location. In this sense, this simulation would be able to determine the needs of each patient specifically as a function of their injury profile, by adjusting the physiological response to the injury by manipulating VEGF. We investigate this possibility by making the parameter values that govern VEGF dynamics a function of time, creating the possibility for pharmacological interventions.
3.3. Protein-receptor drug effects
To investigate potential therapeutics involving VEGF, perhaps drugs that promote or hinder the production of VEGF, we apply the γL and γon parameter changes at specific times after TBI, effectively creating a delay to onset of a pharmaceutical agent. Obviously, more structure can be applied to problem, we are merely delaying the influence of a particular parameter as a set time after injury. We are not fully modeling the absorption, transport and update of a pharmaceutical to the site of action in the brain tissue. Efforts towards a more complete drug model may be future extensions to this work. We can use this analysis to investigate how to keep VEGF concentration from over compensating for the injury, in order to mitigate its negative effects, like vessel permeability.
We look at how altering the dynamical system parameters at varying times after TBI could interplay with its protein interactions and on its overall effect on sprouting angiogenesis and return of the lost blood volume. We begin by outputting the full profile of the dynamical system for a normal simulation and one where we perturb γL by increasing it to 1.8, 3 days after the injury, Figure 16. This parameter effects the tissue release of VEGF, and is shown here 3 days into the simulation to create a large spike in available VEGF protein in the tissue. This spike increases the slope of the response of volume restoration during the simulation, leading to more volume restored over a 14 day period. The number of bisectors produced seems to remain unchanged, or be little effected.
To investigate the broader impacts on recovery for the delayed drug administration we iterate over values of γL and report total volume lost and bound concentration [VEGF-VEGFR] at the end of a 14 day simulation, Figure 17. The delayed adjustments to the VEGF production rate greatly reduces the maximum bound concentration area on the contour plot. Showing a tightening and increasing how rapid the bound concentrations are being converted into bisectors. There is an expected shift to the right of the dynamics of the bound complex, but an unexpected tightening of the temporal progress of the angiogenesis process. Maximum uptake, occurring along the gradient of the valleys in the contour, is shifted up, denoting different γL for the most rapid healing dynamics over the simulation time. The minimum dynamics of the protein complex have similarly shifted upward and tightened along the peak, γL≈0.8. Change in the overall dynamics show promise in the ability of a pharmaceutical to influence the healing process over a prolonged time line. The volume restoration is less interesting with a clear shift right in the overall dynamics. Although there does appear to be a tightening of the maximum and minimum gradient between parameter values for parameter shift after 3 days. This could potentially add some instability towards designing an in-silico treatment plan for a given patient vasculature and injury.
4.
Discussion
We present a dynamic, three dimensional model of vascular angiogenesis due to TBI lesion. Our model is able to report values for bulk blood flow restoration to the injury region over weeks of the recovery process. This model is unique in the sense that we strive to answer questions on timescales that are inhibitory for most traditional three dimensional models developed in the past. Compute times for full resolution of the forcing, growth, and fluid dynamics of a TBI injury are too prohibitive to answer questions on the time scales described in this paper. We introduce several approximations such as fractal growth, diffusion equation approximations, and a simplified VEGF model in order to couple many different processes that exist on very different time and spacial scales. From this, we are able to investigate changes in the healing dynamics (including volume restoration and vessel architecture) due to lesion location and adjustments to the VEGF protein dynamics. These results give us the first look at the healing process for a given injury and brain vessel structure but still need more validation and submodel investigations to be considered a viable pre-treatment patient analysis for clinicians.
We present results that agree well with the first 24 hours for [VEGF] but that struggle to capture the dynamics of the full 7-14 days. Simulated vessel density data is even further out of line with experimental results, although the authors note that these results vary more extensively than those reported for [VEGF]. For [VEGF], most experimental data agrees that after 14 days, values have returned to baseline levels but our model is still elevated at around 2 times baseline concentrations at the end of the simulation. We note that there is generally not enough high quality, controlled, TBI data for human subjects but that this data does exist in animal models. Because we use, as an input, the healthy vasculature of a human, we chose not to fit our simulation to murine or rat data but to instead keep our rate constants in line with experimental values, Table 1. In general, more work is needed to fit this model to available data and a number of future studies will aid in this regard. Particularly the secondary peak of [VEGFR] that is seen in some experimental data could contribute, notably, to the late stage [VEGF] model dynamics. To improve upon vessel density, we must match our model vaculature to murine brain data, and include more complexity to the three dimensional vessel growth models. We do hope to improve the model in these areas and believe that questions pertaining to agiogenesis over longer time scales is relevant to the overall understanding of the healing process.
As created, this model is able to test our hypothesis that location of the TBI plays a pronounced role in VEGF release and vessel restructuring. It should not be interpreted as a one for one representation of the angiogenesis process for a given MR image as there is still additional work that must be completed for this model to accurately replicate experimental results. To properly test VEGF concentration during a TBI we will need to include cerebral spinal fluid, the brains ventricular system and the VEGF diffusion dynamics into that fluid space. These additions would be valid inclusions and more extensive validation of the model is required. Future work may also target vessel density, post injury, by developing a model of the veins, return flow, and represent the micro vaculature on a much smaller spacial scale.
It is important to note, that we are trying to simulate large scale, system level, processes, from a model of the small scale physiology. Additionally, we only model sprouting angiogenesis by generating smaller vessels off the larger arteries and arterioles that we were able to capture from the manual segmentation process. In this sense, you can think of each bisector sprout in the model as a lumped representation of many sprouts that may form physiologically. With more refinement to the vessel structure this approximation should no longer be necessary and is an area of future work. Integration with a machine learning segmentation algorithm could potentially create a more rapid pipeline to the model simulation. Full automation of generating the input vessel structure could lead to rapid, first pass patient injury models.
Only major vessels to a minimum of about 0.2 mm were mapped from the volunteer MRA, due to the image resolution. Thus, arterioles and capillaries are not included in the model. Veins are excluded as well and could be an obvious area of improvement. Venous return flow and the implications of hypoxia on downstream regions of the brain from the lesion location is not considered in this study but could be a possible area of investigation in the future. Other iterations of the model may account for vessels changing in diameter and length, and the direction of sprout growth can be better adapted to local conditions, as opposed to the lumped VEGF condition for which concentrations of VEGF and related proteins are assumed to be the same in the entire TBI injury region. Tissue resistance and force approximations and how each influence the growth trajectory could be investigated in future model studies.
Other possible future model iterations and updates may include: oxygen reduction and associated ischemia, edema, a more refined model of the microvasculature and relation of VEGF with vessel leakage and intracranial pressure (ICP). A simulation of the blood flow along the vessel model generated, using a 1D approximation could allow us to compare ICP to cerebral perfusion pressure (CPP) and see its effect on cerebral blood flow and hypoxia. There tends to be high quality experimental data associated with these parameters and including these models would be an excellent means of further validating the model in the future.
5.
Conclusions
We present a multiscale model of the TBI injury and angiogenesis process for given three dimensional MR images of the brain vasculature. We couple four major models including: vessel sprouting, bisection and growth, probabilistic sprouting formation, and a VEGF interaction ODE model. We computationally implement this model in C++ to ensure computational speed and the ability to handle very large vessel structures over a 14 day simulation window. We validate VEGF, VEGFR, and vessel density over the simulation period and note improvements required to meet experimental results. We are able to use this model to test the relationship between volumetric flow restoration and vessel architecture and use this model to show volumetric restoration varies significantly as a function of location of injury. We then show that the model can be used to change outcomes for different locations by influencing the protein interaction parameters. These parameters are investigated over a range of different time administrations and we note that the volume restoration dynamics display significant differences as a function of delayed onset of VEGF generation and association parameters. We conclude that this model is an excellent first step in understanding the long term dynamics of healing during angiogenesis by coupling three dimensional vessel architecture and traditional VEGF ODE models. As an input to this model, we conclude that different vessel MR generations can be used to get a more refined understanding of the small vessel dynamics.
Acknowledgments
Funding generously provided by Army Research Lab contract number W911NF-17-1-0572. We'd also like to thank Dr. Virginia Pasour for her continued guidance and support of the project. The MR brain images from healthy volunteers used in this paper were collected and made available by the CASILab at The University of North Carolina at Chapel Hill and were distributed by the MIDAS Data Server at Kitware, Inc.
Data Availability
All data that support the findings of this study are available (and reproducible) through the public TBISimulator repository: https://github.com/ajbaird/TBISimulator. This includes all input files and a compiled executable of the code base that may be used to reproduce all findings. The executable may be used for other TBI related studies by altering input configuration files and MR data.
Conflict of interest
The authors declare that there are no competing interests.









 DownLoad:
DownLoad: