The stochastic extinction and stability conditions for nonlinear malaria epidemics

1.   Introduction

Despite all technological advances to control malaria, the disease continues to exhibit an alarming high mortality rate. In fact, the latest WHO-World Malaria Report 2017 ^[1] estimates a total of 216 million cases of malaria from 91 countries in 2016, which constitutes a 5 million increase in the total malaria cases from the malaria statistics obtained previously in 2015. Moreover, the total death count was 445000, and sub-Saharan Africa accounts for 90% of the total estimated malaria cases. This rising prevalence trend in the malaria data continues to signal a need for more learning about the disease, improvement of the existing control strategies and equipment, and also a need for more advanced resources etc. to fight and eradicate, or ameliorate the burdens of the malaria.

The following facts about malaria given in ^[2] are recalled. Malaria like other mosquito-borne diseases such as dengue fever, yellow fever, zika fever, lymphatic filariasis, and the different types of encephalitis etc. exhibits some unique biological characteristics. For instance, the incubation of the disease requires two hosts - the mosquito vector and human hosts.Therefore, the total latent time lapse of disease incubation extends over two segments of delay incubation times namely:- (1) the incubation period of the malaria plasmodium (or the half-life cycle) inside the vector, and (2) the incubation period of the plasmodium (or the other half-life cycle) inside the human being. See references ^[3,4].

In particular, the malaria plasmodium undergoes the first developmental half-life cycle called the sporogonic cycle inside the female Anopheles mosquito lasting approximately 10–18 days, following a successful blood meal obtained from an infectious human being through a mosquito bite. Moreover, the mosquito becomes infectious. The parasite completes the second developmental half-life cycle called the exo-erythrocytic cycle lasting about 7–30 days inside the exposed human being, whenever the parasite is transferred to the human being in the process of the infectious mosquito foraging for another blood meal. See the references^[3,4,5].

The exposure and successful recovery from a malaria parasite, for example, falciparum vivae induces natural immunity against the disease which can protect against subsequent severe outbreaks of the disease. Moreover, the effectiveness and duration of the naturally acquired immunity against malaria is determined by several factors such as the species and the frequency of exposure to the parasites. Furthermore, it has been determined that other biological factors such as the genetics of the human being, for instance, sickle-cell anaemia, duffy negative blood types have bearings on the naturally acquired immunity against different species of malaria. See the references^[4,6,7].

Compartmental mathematical epidemic dynamic models play a vital role to understand the dynamics of infectious diseases (cf. ^{[8,9,10,11,12,13,14,15,16,17,18,19,20,21]}). Moreover, mathematical modeling is one special way of understanding malaria, and malaria models go as far back as 1911 with Ross^[22] who studied mosquito control. Several other authors such as ^{[2,23,24,25,26,27,28,29,30]} have also made strides in the understanding of malaria mathematically.

Some studies have shown the presence of noise in the dynamics of malaria. Noise can be seen in seasonal variations of the malaria incidence over yearly data, and over spatial disparities. In fact, some authors such as ^[31] studying the seasonality of P. falciparum transmission have shown that there are several climatic drivers responsible for the temporal variation and spatial distribution of malaria transmission rates, for instance, temperature, rainfall, and vegetation indices etc. The randomness in the malaria incidence over time, and spatially is a good reason to consider stochastic representations of the disease dynamics.

From global malaria data (cf.^[1,32]), there are also apparent disparities in the geographical prevalence rates of malaria, in association to the economic growth, wealth and modern infrastructure of countries in the world etc. In fact, several studies (cf. ^[32]) show the association between poverty and malaria prevalence rates, modern infrastructure and malaria endemicity or eradication, across the same population in a country, the world, and also over calendar years etc. For instance, the poorest Sub-Sahara countries also exhibit the highest malaria prevalence rates (cf. ^[1,32]), and within a single malaria endemic region, the poorer are predisposed to live in naturally unhealthy, and malaria vulnerable conditions compared to the rich. Thus, using natural death rate as indicator for living standards, there is evident temporal and spatial variability in the natural death rate of populations in which malaria is prevalent. Therefore, there is also good reason to consider the stochastic perturbations in the malaria dynamics owing to the natural death rates in the populations.

There are several different ways to introduce white noise into infectious dynamic systems, for example, as random perturbation of the driving parameters of the infectious system known as environmental white noise (see ^[20,21,33]), or perturbation of the density of the system also known demographic white noise (see ^[34]). Some other authors such as ^[35,36] have suggested a mean-reverting process technique to include white noise processes. Also, some stochastic models for malaria involving white noise perturbations include ^[37,38,39].

An important investigation in the study of infectious population dynamic systems influenced by white noise is the extinction of the disease, and the asymptotic stability of the disease-free population over sufficiently long time. Several papers in the literature^{[40,41,42,43,44,45]} have addressed these topics. Investigations about the extinction of disease from the population seek to find conditions that favor the extinction of the disease-related classes such as the exposed and infectious classes in the population, and consequently lead to the survival of the susceptible and infection-free population classes over sufficiently long time. The techniques used to investigate extinction of the disease in stochastic systems include examining the sample paths of the system near a disease-free steady state, and computing the sample Lyapunov exponent of the trajectories of the system^{[40,41,42,43,44,45]}.

Cooke ^[46] presented a deterministic epidemic dynamic model for vector-borne diseases, where the bilinear incidence rate defined as $\beta S(t)I(t-T)$ represents the number of new infections occurring per unit time during the disease transmission process. It is assumed in the formulation of this incidence rate that the number of infectious vectors $V_{i}(t)$ at time $t$ interacting and effectively transmitting infection to susceptible human beings, $S(t)$, after $\beta$ number of effective contacts per unit time per infective is proportional to the infectious human population, $I(t-T)$, at earlier time $t-T$. Cook's method of studying the dynamics of a vector-borne disease in a human population without directly including the vector population dynamics has been utilized by several other authors, for example ^{[2,14,20,47,48]}. Some criticism of the Cooke model concerns the absence of a rationale for the assumption about the proportionality between $V_{i}(t)$ and $I(t-T)$ used as an approximation for the force of infection. Furthermore, there is the question whether the Cooke model emerges from the combined vector-host dynamics. Takeuchi et. al. ^[48] answered this question and presented an extension of the Cooke model, with a joint dynamics for the vector-host populations, and under the assumption of a large constant vector population present, the proportionality between the states $V_{i}(t)$ and $I(t-T)$ is justified.

Recently, applying similar reasoning of the Cooke model, Wanduku^[2] developed and studied a novel family of SEIRS dynamic models for malaria with three distributed delays, structured similarly as (1.1)–(1.4) below.

The malaria model in ^[2] was simplified by omitting the mosquito dynamics, and applying other assumptions about the death rates of mosquitoes and humans. Moreover, timescales to measure model parameters were not well-specified, and the model was not applied to reliable malaria data. Furthermore, as earlier highlighted above, the temporal and spatial variabilities in the malaria transmission and natural death rates, suggest that the deterministic model in ^[2] cannot effectively fit and describe most realistic malaria scenarios, where environmental variability is inevitable. Thus, to improve the applicability of ^[2], it is essential to add more epidemiologically sound assumptions, and define timescales for the model parameters in (1.1)–(1.4), and also derive the malaria model from the mosquito vs. human dynamics perspective. Moreover, a stochastic dynamical model should be considered, incorporating the noises from the disease transmission and natural death rates. The modified family of malaria SEIRS dynamic models (in ^[2]) is given as follows:

where the initial conditions are given in the following: let $h = h_{1}+ h_{2}$ and define

where $\mathcal{C}((-\infty, t_{0}], \mathbb{R}_{+})$ is the space of continuous functions with the supremum norm

Also, the function $G$ satisfies the conditions of Assumption 1.1. The epidemiologically sound assumptions for the model (1.1)–(1.4), and the full derivation of the malaria dynamics from the mosquito vs. human interaction is given in the A.

In the malaria dynamics (1.1)–(1.4), the disease spreads in the normalized human population of total size $N(t) = S(t)+ E(t)+ I(t)+ R(t)\in (0, 1]$, where $S(t)$, $E(t)$, $I(t)$ and $R(t)$ represent the susceptible, exposed, infectious and naturally acquired immunity classes at time $t$, respectively. The positive constants $B$, and $\mu$ represent the constant birth and natural death rates, respectively. Furthermore, the disease related deathrate is denoted $d$. The rate $\beta$ is the average effective contact rate per infected mosquito per unit time. The recovery rate from malaria with acquired immunity is $\alpha$.

Also, the incubation delays inside the mosquito and human hosts are denoted $T_{1}$ and $T_{2}$, respectively, and the period of effective naturally acquired immunity is denoted $T_{3}$. Moreover, the delays $T_{1}, T_{2}$ and $T_{3}$, are random variables with arbitrary densities denoted $f_{T_{1}}(s)$, $f_{T_{2}}(u)$ and $f_{T_{3}}(r)$, and their supports given as $s\in [t_{0}, h_{1}]$, $u\in [t_{0}, h_{1}]$ and $r\in [t_{0}, +\infty)$, respectively. All parameters in (1.1)–(1.4) are dimensionless, and defined in (A.42). The nonlinear incidence function $G$ which signifies the response to disease transmission by the susceptible class as malaria increases in the population, satisfies the following assumptions

Assumption 1.1. $A1$ $G(0) = 0$; $A2$: $G(I)$ is strictly monotonic on $[0, \infty)$; $A3$: $G''(I) < 0$; $A4$. $\lim_{I\rightarrow \infty}G(I) = C, 0\leq C < \infty$; and $A5$: $G(I)\leq I, \forall I > 0$.

Note, in this paper, the derivation of (1.1)–(1.4) in A applies similar reasoning in ^[48]. Furthermore, the malaria model (1.1)–(1.4) is extended by incorporating the independent white noise perturbations of the disease transmission rate $\beta$, and the natural deathrates of the susceptible, exposed, infectious and removal populations.

The primary focus of this study is to investigate the extinction of malaria over time in a class of stochastic models for vector-borne diseases in a very noisy environment comprising of variability from the disease transmission and natural death rates.

This work is presented as follows:- in A, a proper malaria model is derived. In Section 1, the stochastic extended dynamic model is derived. In Section 4, the model validation results are presented. In Section 5, the extinction conditions for the disease are presented for the case where the noise stems jointly from the disease transmission and natural death rates. In Section 6, the extinction conditions for the disease are presented for the case where the noise stems only from the disease transmission rate. Moreover, the asymptotic stability in the mean of the disease-free equilibrium is also presented. Finally, in Section 7, numerical simulation results are given.

2.   Validation results for (1.1)–(1.4) and some model properties

Since the system (1.1)–(1.4) is structured similarly as ^[2], some ideas from ^[2] can be applied. The following result presents model validation results.

Theorem 2.1. Given the initial conditions in (1.5)–(1.6), there exists a unique positive solution $Y(t) = (S(t), E(t), I(t), R(t))^{T}$ for the system (1.1)–(1.4), for all $t\geq t_{0}$. Moreover, the solution lies in the closed ball in $\mathbb{R}^{4}_{+}$ centered at zero and radius $\frac{B}{\mu} = 1$, whenever $N(t_{0})\leq \frac{B}{\mu} = 1$. That is, for $N(t_{0})\leq \frac{B}{\mu} = 1$, the solution $Y(t)\in \bar{B}_{\mathbb{R}^{4}_{+}}(0, \frac{B}{\mu} = 1)$, where

Furthermore, the unit closed ball (subspace) $\bar{B}_{\mathbb{R}^{4}_{+}}(0, \frac{B}{\mu} = 1)$ is self-invariant with respect to the system (1.1)–(1.4).

Proof: See [Theorem 3.1, [2]] and apply the dimensionless parameters in (A.42).

The disease-free equilibrium of the system is given in the following result.

Theorem 2.2. The system (1.1)–(1.4) has a disease-free equilibrium $E_{0} = (S^{*}_{0}, E^{*}_{0}, I^{*}_{0}) = (S^{*}_{0}, 0, 0)$, where $S^{*}_{0} = \frac{B}{\mu} = 1$, and $E^{*}_{0} = I^{*}_{0} = 0$.

From the analysis of the malaria model (1.1)–(1.4) with initial conditions in (1.5)–(1.6) in ^[2], the threshold values for disease eradication such as the basic reproduction number for the disease dynamics when the system is in steady state are obtained in both cases where the delays in the system $T_{1}, T_{2}$ and $T_{3}$ are constant, and also arbitrarily distributed.

From [Lemma 6.2.3 and Theorem 4.2, ^[2]], for $S^{*}_{0} = \frac{B}{\mu} = 1$, when the delays in the system are all constant, the basic reproduction number of the disease is given by

Furthermore, the threshold condition $\hat{R}^{*}_{0} < 1$ is required for the disease-free equilibrium $E_{0} = (S^{*}_{0}, 0, 0)$ in Theorem 2.2 to be asymptotically stable, and for the disease to be eradicated from the steady state human population.

On the other hand, from [Lemma 6.2.3 and Theorem 4.2, [2]], when the delays in the system $T_{i}, i = 1, 2, 3$ are random, and arbitrarily distributed, the basic reproduction number is given by

where, $\hat{K}_{0} > 0$ is a constant that depends only on $S^{*}_{0}$ (in fact, $\hat{K}_{0} = 4+ S^{*}_{0}$). In addition, malaria is eradicated from the system in the steady state, whenever $R_{0}\leq 1$.

The results in [Theorem 5.1, [2]] also show that when $R_{0} > 1$, and the expected survival probability rate $E(e^{-\mu(T_{1}+ T_{2})})$ of the parasites over their complete life cycle is significant, the deterministic system (1.1)–(1.4) establishes a unique endemic equilibrium state denoted by $E_{1} = (S^{*}_{1}, E^{*}_{1}, I^{*}_{1})$.

3.   Derivation of the stochastic model

As mentioned earlier in the introduction, there are several different techniques to introduce gaussian noise processes into a dynamic system. The approach in ^[39] is applied to model the environmental fluctuations in the disease transmission rate $\beta$, and the natural death rates $\mu$ of the different states $S(t)$, $E(t)$, $I(t)$ and $R(t)$ of the human population. This approach entails the construction of a random walk process for the rates $\beta$, and $\mu$ over an infinitesimally small interval $[t, t+dt]$ and applying the central limit theorem. In the book chapter ^[49], the author has illustrated in details the derivation of the noise in the disease transmission and natural death rates $\beta$, and $\mu$, respectively, for the system (1.1)–(1.4). Therefore, only the basics expressions are given in this section, and the reader is directed to [[49], pp 12-13] for a full development of the stochastic model from the random walk approximation perspective.

For $t\geq t_{0}$, let $(\Omega, \mathfrak{F}, P)$ be a complete probability space, and $\mathfrak{F}_{t}$ be a filtration (that is, sub $\sigma$- algebra $\mathfrak{F}_{t}$ that satisfies the following: given $t_{1}\leq t_{2} \Rightarrow \mathfrak{F}_{t_{1}}\subset \mathfrak{F}_{t_{2}}; E\in \mathfrak{F}_{t}$ and $P(E) = 0 \Rightarrow E\in \mathfrak{F}_{0}$). The variability in the disease transmission and natural death rates are represented by independent white noise or Wiener processes with drifts, and the rates are expressed as follows:

where $\xi_{i}(t)$ and $w_{i}(t)$ represent the standard white noise and normalized wiener processes for the $i^{th}$ state at time $t$, with the following properties: $w(0) = 0, E(w(t)) = 0, var(w(t)) = t$. Furthermore, $\sigma_{i}, i = S, E, I, R$, represents the intensity of the white noise process due to the random natural death rate of the $i^{th}$ state, and $\sigma_{\beta}$ is the intensity of the white noise process due to the random disease transmission rate. Moreover, the $w_{i}(t), i = S, E, I, R, \beta, \forall t\geq t_{0}$, are all independent. In this study the words ``strength" and ``intensity" of the white noise are used synonymously. Also, the constructions ``strong noise" and ``weak noise" are used to refer to white noise with high and low intensities, respectively.

Substituting (3.1) into the deterministic system (1.1)–(1.4) leads to the following generalized system of Ito-Doob stochastic differential equations describing the dynamics of malaria in the human population.

where the initial conditions are given in the following: Let $h = h_{1}+ h_{2}$ and define

where $\mathcal{C}((-\infty, t_{0}], \mathbb{R}_{+})$ is the space of continuous functions with the supremum norm

Furthermore, the random continuous functions $\varphi_{k}, k = 1, 2, 3, 4$ are $\mathfrak{F}_{0}-measurable$, or independent of $w(t)$ for all $t\geq t_{0}$.

It can be observed that (3.3) and (3.5) decouple from the other equations for $S$ and $I$ in the system (3.2)–(3.5). It is customary to show the results for this kind of decoupled system using the simplified system containing only the non-decoupled system equations for $S$ and $I$, and then infer the results to the states $E$ and $R$, since these states depend exclusively on $S$ and $I$. Nevertheless, for convenience, the existence results of the system (3.2)–(3.5) will be shown for the vector $X(t) = (S(t), E(t), I(t))$, and the extinction results presented for the decoupled system $(S(t), I(t))$. The following notations will be used throughout this study:

4.   Stochastic model validation results

The existence and uniqueness of solution of the stochastic system (3.2)–(3.5) is exhibited in the following theorem. Moreover, the feasibility region of the the solution process $\{X(t), t\geq t_{0}\}$ of the system (3.2)–(3.5) is defined. The standard methods utilized in the earlier studies^{[20,33,50,51]} are applied to establish the results.

It should be noted that the existence and qualitative behavior of the positive solution process of the system (3.2)–(3.5) depend on the sources (natural death or disease transmission rates) of variability in the system. As it is shown below, certain sources of variability lead to very complex uncontrolled behavior of the sample paths of the system. In the book chapter ^[49], the detailed proof of the existence, and uniqueness of the solution process $\{X(t), t\geq t_{0}\}$ of the system (3.2)–(3.5) is given. Thus, only the results are presented below:

The following Lemma describes the behavior of the positive local solutions for the system (3.2)–(3.5). This result will be useful in establishing the existence and uniqueness results for the global solutions of the stochastic system (3.2)–(3.5).

Lemma 4.1. Suppose for some $\tau_{e} > t_{0}\geq 0$ the system (3.2)–(3.5) with initial condition in (3.6) has a unique positive solution $Y(t)\in \mathbb{R}^{4}_{+}$, for all $t\in (-\infty, \tau_{e}]$, then if $N(t_{0})\leq \frac{B}{\mu} = 1$, it follows that

(a.) if the intensities of the independent white noise processes in the system satisfy $\sigma_{i} = 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$, then $N(t)\leq \frac{B}{\mu} = 1$, and in addition, the set denoted by

is locally self-invariant with respect to the system (3.2)-(3.5), where $\bar{B}^{(-\infty, \tau_{e}]}_{\mathbb{R}^{4}_{+}, }\left(0, \frac{B}{\mu}\right)$ is the closed ball in $\mathbb{R}^{4}_{+}$ centered at the origin with radius $\frac{B}{\mu}$ containing the local positive solutions defined over $(-\infty, \tau_{e}]$.

(b.) If the intensities of the independent white noise processes in the system satisfy $\sigma_{i} > 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$, then $N(t)\geq 0$, for all $t\in (-\infty, \tau_{e}]$.

Proof:

It follows directly from (3.2)–(3.5) that when $\sigma_{i} = 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$, then

The result in (a.) follows easily by observing that for $Y(t)\in \mathbb{R}^{4}_{+}$, the equation (4.2) leads to $N(t)\leq \frac{B}{\mu}-\frac{B}{\mu}e^{-\mu(t-t_{0})}+N(t_{0})e^{-\mu(t-t_{0})}$. And under the assumption that $N(t_{0})\leq \frac{B}{\mu}$, the result follows immediately. The result in (b.) follows directly from Theorem 4.1. The following theorem presents the existence and uniqueness results for the global solutions of the stochastic system (3.2)–(3.5).

Theorem 4.1. Given the initial conditions (3.6) and (3.7), there exists a unique solution process $X(t, w) = (S(t, w), E(t, w), I(t, w))^{T}$ satisfying (3.2)–(3.5), for all $t\geq t_{0}$. Moreover,

(a.) the solution process is positive for all $t\geq t_{0}$ a.s. and lies in $D(\infty)$, whenever the intensities of the independent white noise processes in the system satisfy $\sigma_{i} = 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$. That is, $S(t, w) > 0, E(t, w) > 0, I(t, w) > 0, \forall t\geq t_{0}$ a.s. and $X(t, w)\in D(\infty) = \bar{B}^{(-\infty, \infty)}_{\mathbb{R}^{4}_{+}, }\left(0, \frac{B}{\mu}\right)$, where $D(\infty)$ is defined in Lemma 4.1, (4.1).

(b.) Also, the solution process is positive for all $t\geq t_{0}$ a.s. and lies in $\mathbb{R}^{4}_{+}$, whenever the intensities of the independent white noise processes in the system satisfy $\sigma_{i} > 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$. That is, $S(t, w) > 0, E(t, w) > 0, I(t, w) > 0, \forall t\geq t_{0}$ a.s. and $X(t, w)\in \mathbb{R}^{4}_{+}$.

Proof: See [Theorem 2, [49]].

Remark 4.1. Theorem 4.1 signify that the stochastic system (3.2)–(3.5) has a unique positive solution $Y(t)\in \mathbb{R}^{4}_{+}$ globally for all $t\in (-\infty, \infty)$. Furthermore, it follows that a positive solution of the stochastic system that starts in the closed ball centered at the origin with a radius of $\frac{B}{\mu}$, $D(\infty) = \bar{B}^{(-\infty, \infty)}_{\mathbb{R}^{4}_{+}, }\left(0, \frac{B}{\mu}\right)$, will continue to oscillate and remain bounded in the closed ball for all time $t\geq t_{0}$, whenever the intensities of the independent white noise processes in the system satisfy $\sigma_{i} = 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$. Hence, the set $D(\infty) = \bar{B}^{(-\infty, \infty)}_{\mathbb{R}^{4}_{+}, }\left(0, \frac{B}{\mu}\right)$ is a positive self-invariant set for the stochastic system (3.2)–(3.5). In the case where the intensities of the independent white noise processes in the system satisfy $\sigma_{i} > 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$, the solution are positive and unique, and continue to oscillate in the unbounded space of positive real numbers $\mathbb{R}^{4}_{+}$. In other words, the positive solutions of the system are bounded, whenever $\sigma_{i} = 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$ and unbounded, whenever $\sigma_{i} > 0$, $i\in \{S, E, I\}$ and $\sigma_{\beta}\geq 0$.

The implication of this result to the disease dynamics represented by (3.2)–(3.5) is that the occurrence of noise exclusively from the disease transmission rate allows a controlled situation for the disease dynamics, since the positive solutions exist within a positive self invariant space. The additional source of variability from the natural death rate can lead to more complex and uncontrolled situations for the disease dynamics, since it is obvious that the intensities of the white noise processes from the natural death rates of the different states in the system are driving the positive solutions of the system unbounded. Some examples of uncontrolled disease situations that can occur when the positive solutions are unbounded include:- (1) extinction of the population, (2) failure to find an infection-free steady population state, wherein the disease be controlled by bringing the population into that state, and (3) a sudden significant random flip of a given state such as the infectious state from a low to high value, or vice versa over a short time interval etc. These facts become more apparent in the subsequent sections where conditions for disease eradication are derived.

5.   Extinction of disease with noise from both disease transmission and natural death rates

The extinction of the vector-borne disease from the population described by the stochastic epidemic dynamic model (3.2)–(3.5) is exhibited in this section. Noting that (3.3) and (3.5) decouple from the system (3.2)–(3.5), it follows that the two other equations for $S(t)$ and $I(t)$ in (3.2) and (3.4), respectively, depend only on the states $(S(t), I(t))$. Therefore, it suffices to show extinction of the disease from the population by showing the extinction of the infectious population $I(t)$.

Recall Theorem 4.1(b), asserts that the system (3.2)–(3.5) has a unique solution process $\{Y(t), t\geq t_{0}\}$ with positive solution paths for the malaria dynamics. Furthermore, all paths that start in $\mathbb{R}^{4}_{+}$ continue to oscillate in the space $\mathbb{R}^{4}_{+}$. Moreover, it was remarked in Remark 4.1 that the solution paths are potentially liable to become unbounded in the space $\mathbb{R}^{4}_{+}$, whenever the strength of the noise from the natural death rates is strong.

In this section, the threshold conditions for the intensities $\sigma_{i}, i\in\{S, E, I, R\}$, and other parameters of the disease dynamics in (3.2)–(3.5), which are sufficient for extinction are presented. Recall ^[52,53], the following definition of the extinction of a species denoted by the process $Z(t), t\geq t_{0}$ in a stochastic dynamic system:

Definition 5.1.

(1.) $Z(t)$ is said to be extinct if $\lim_{t\rightarrow \infty}{Z(t)} = 0$, a.s.

(2.) $Z(t)$ is said to be stable in the mean if $\lim_{t\rightarrow \infty}{\frac{1}{t}\int^{t}_{t_{0}}Z(s)}ds = c > 0$, a.s.

(3.) $Z(t)$ is said to be strongly persistent in the mean if $\liminf_{t\rightarrow \infty}{\frac{1}{t}\int^{t}_{t_{0}}Z(s)}ds > 0$, a.s.

That is, the species is extinct if every path for the process $Z(t), t\geq t_{0}$ converges to zero with probability one, and stable in the mean, if every path converges in the mean asymptotically to a constant, with probability one. Note that if the species is stable in the mean, then it is also strongly persistent, but the converse is not always true.

Also, the following lemma from ^[54] known as the exponential martingale inequality will be used to establish the extinction results, whenever Theorem 4.1(b) holds.

Lemma 5.1. Let $g = (g_{1}, g_{2}, \ldots, g_{m})\in L^{2}(\mathbb{R}_{+}, \mathbb{R}^{1\times m})$, and $T, c, \theta$ be any positive numbers. Then

Proof: See ^[54]

Theorem 5.1. Let $\sigma_{i} > 0, \forall i\in \{S, E, I, R, \beta\}$, and let $(S(t), I(t))$ be the solution of the decoupled system (3.2) and (3.4) with initial conditions in (3.6) and (3.7), that satisfies Theorem 4.1(b). Suppose further that the following relationship holds

Then it follows that the solution of the decoupled system (3.2) and (3.4) satisfies

That is, $I(t)$ tends to zero exponentially almost surely. In other words, the infectious population is extinct and the disease dies out with probability one.

Proof:

The differential operator $dV$ applied to the function

with respect to the system (3.2) and (3.4) leads to the following

where,

Define the following

It is easy to see that $M_{2}(t)$ is a local martingale with a quadratic variation given by

Furthermore, utilizing the exponential martingale inequality in Lemma 5.1, it follows that for any random integer $k\equiv k(w), w\in \Omega$, and constant $0 < c < 1$, the probability of the event $A_{k}$ defined below

The sequence of events $\left\{A_{k}\right\}_{k = 0}^{\infty}$ satisfies $\sum_{k}{P(A_{k})} < \infty$, and consequently by Borel-Cantelli Lemma^[54], there exists a random integer $k_{0}\equiv k_{0}(w) > t_{0}$ such that

whenever $k > k_{0}$. And (5.12) further leads to

Now, integrating both sides of (5.5) over the interval $[t_{0}, t]$, it follows from (5.6)–(5.13) and some algebraic manipulations and simplifications that for any $t\in [t_{0}, k]$,

Moreover, (5.14) simplifies to

Diving both sides of (5.15) by $t$, it follows that for $k-1\leq t\leq k$, one obtains the following inequality

It follows further that for sufficiently large $k$ (i.e. $k\rightarrow \infty$), then $t\rightarrow\infty$, and consequently, taking the limit supremum of (5.16) as $t\rightarrow\infty$, it is easy to see that (5.16) reduces to

But, it is easy to see from the strong law of large numbers for local martingales (see, e.g. ^[54]) that

Consequently, (5.16) reduces to

Thus, for $c$ infinitesimally small, that is, $c\rightarrow 0$, (5.3) follows immediately from (5.19).

Remark 5.1 Theorem 5.1 and Theorem 4.1[b] signify that when the intensities of the disease transmission and natural death rates, $\sigma_{\beta}$ and $\sigma_{I}$, respectively, are positive, then all sample paths of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5) that start in $\mathbb{R}^{2}_{+}$ continue to oscillate in $\mathbb{R}^{2}_{+}$. Moreover, the sample paths of the infectious state $I(t), t\geq t_{0}$ of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ ultimately turn to zero exponentially, almost surely, whenever the intensities of the disease transmission and natural death rates, $\sigma_{\beta}$ and $\sigma_{I}$, respectively, are related as shown in (5.2). Furthermore, the sample Lyapunov exponent from (5.3) is estimated by the term $Q$, expressed as a function of $\sigma_{\beta}$ and $\sigma_{I}$ as follows

where

It follows from (5.20)–(5.21) that when the condition (5.2) holds, then the infectious population $I(t)$ dies out exponentially, almost surely, whenever the function $Q$ in (5.21) is positive, that is, $Q > 0$. In addition, the rate of the exponential decay of each sample path of the infectious population $I(t)$ is given by the estimate $Q(\sigma^{2}_{\beta}, \sigma^{2}_{I})$ of the sample Lyapunov exponent in (5.20).

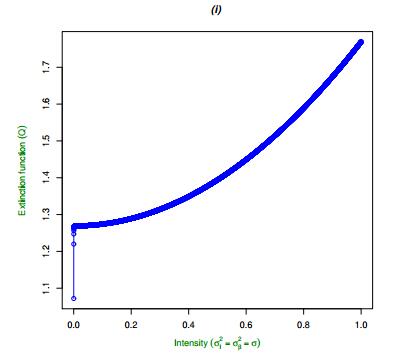
The function $Q$ can be used to evaluate the qualitative effects of the intensities $\sigma_{\beta}$ and $\sigma_{I}$ on the rate of extinction of the disease from the system. Indeed, observe that the function $Q$ increases monotonically with respect to continuous changes in each intensity $\sigma_{\beta}$ and $\sigma_{I}$. This observation suggests that larger values of the intensities $\sigma_{\beta}$ and $\sigma_{I}$, lead to larger values of $Q$, and consequently lead to a larger rate of extinction of the disease from the population. Figure 1 illustrates the behavior of the decay rate $Q$, as the intensities $\sigma_{\beta}$ and $\sigma_{I}$ of the independent white noise processes in the system continuously increase in value.

The following assumptions hold for the example exhibited in Figure 1: (1) the intensities of the random fluctuations in the disease transmission rate and natural death rate of infectious individuals, $\sigma_{\beta}$ and $\sigma_{I}$, respectively, continuously change equally, that is, $\sigma_{\beta} = \sigma_{I}$ , (2) the other parameters of the system (3.2)–(3.5) are selected conveniently as follows: the expected effective disease transmission rate $\beta = 6.277E-5$, recovery rate $\alpha = 0.55067$, average natural death rate of human beings $\mu = 0.6$, and disease related death rate $d = 0.11838$.

6.   Extinction and stability of equilibrium with noise from disease transmission rate

Recall Theorem 4.1(a), asserts that the system (3.2)–(3.5) has a unique solution process $\{Y(t), t\geq t_{0}\}$ with positive solution paths for the malaria dynamics. In addition, all paths that start in $D(\infty)$ continue to oscillate in the space $D(\infty)$. Also, it was remarked earlier in Remark 4.1 that with noise in the disease dynamics exclusively from the disease transmission rate, that is, $\sigma_{\beta} > 0$ and $\sigma_{i} = 0, i\in \{S, E, I, R\}$, the unique solution paths are relatively more "well-behaved" with lesser tendency to drift outside of the self-invariant space $D(\infty)$, regardless whether the noise in the disease dynamics from the disease transmission rate is strong.

In this section, it will be shown that the conditions for the extinction of the disease from the population have no bearings on the intensity $\sigma_{\beta}$ of the noise in the disease transmission rate. In fact, it will is shown that the extinction of the disease from the population depends only on the basic reproduction number $R^{*}_{0}$ in (2.2) and (2.3), or on the survival probability rate of the malaria parasites. The following lemmas will be used to establish the extinction results, whenever Theorem 4.1(a) holds.

Lemma 6.1. Suppose Theorem 4.1(a) holds, then the unique solution process $Y(t)\in D(\infty), t\geq t_{0}$ of the stochastic system (3.2)-(3.5) also lies in the space

where $D^{expl}(\infty)\subset D(\infty)$. Moreover, the space $D^{expl}(\infty)$ is also self-invariant with respect to the stochastic system (3.2)–(3.5).

Proof:

Suppose Theorem 4.1(a) holds, then it follows from (4.2) that the total population $N(t) = S(t)+E(t)+I(t)+R(t)$ satisfies the following inequality

It is easy to see from (6.2) that

and (6.1) follows immediately.

Lemma 6.2. Let Theorem 4.1(a) hold, and define the following Lyapunov functional in $D^{expl}(\infty)$,

where $V(t)$ is defined in (5.4). It follows that

Proof:

The differential operator $dV$ applied to the Lyapunov functional $\tilde{V}(t)$ with respect to the system (3.2)-(3.5) leads to the following

where,

Since $S(t), I(t)\in D^{expl}(\infty)$, and $G$ satisfies the conditions of Assumption 1.1, it follows easily that

Now, integrating both sides of (6.6) over the interval $[t_{0}, t]$, it follows from (5.9) and (6.4) that

where $M_{2}(t)$ is defined in (5.9). Diving both sides of (6.9) by $t$, and taking the limit supremum as $t\rightarrow\infty$, it is easy to see that (6.9) reduces to

But, from (5.10), applying Assumption 1.1 and $H\ddot{o}lder$ inequality to the quadratic variation of $M_{2}(t)$, it is easy to see that

Furthermore, in $D^{expl}(\infty)$,

Thus, from (6.11), the quadratic variation of $M_{2}(t)$ satisfies

Therefore, it is easy to see by the strong law of large numbers for local martingales (see, e.g. ^[54]) that

And the result (6.5) follows immediately from (6.14) and (6.10).

The conditions for extinction of the infectious population over time can be expressed in terms of two important parameters for the disease dynamics namely - (1) the basic reproduction number $R^{*}_{0}$ in (2.2), and (2) the expected survival probability rate of the parasites $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$, defined in [Theorem 5.1, Wanduku^[2]].

Theorem 6.1. Suppose the conditions for Lemma 6.2 are satisfied, and let the basic reproduction number $R^{*}_{0}$ be defined as in (2.2). In addition, let one of the following conditions hold

1. $R^{*}_{0}\geq 1$ and $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, or

2.$R^{*}_{0} < 1$.

Then

where $\lambda > 0$ is some positive constant. In other words, $I(t)$ converges to zero exponentially, almost surely.

Proof:

Suppose Theorem 6.1 [1.] holds, then from (6.5),

where the positive constant $\lambda > 0$ is taken to be as follows

Also, suppose Theorem 6.1 [2.] holds, then from (6.5),

where the positive constant $\lambda > 0$ is taken to be as follows

Remark 6.1. Theorem 6.1, Theorem 4.1[a] and Lemma 6.1 signify that when the intensity of the noise from the disease transmission rate $\sigma_{\beta}$ is positive, and the intensities of the noises from the natural death rates satisfy $\sigma_{i} = 0, i\in \{S, E, I, R\}$, then all sample paths of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5) that start in $D^{expl}(\infty)\subset D(\infty)$ continue to oscillate in $D^{expl}(\infty)$. Moreover, the sample paths of the infectious state $I(t), t\geq t_{0}$ of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ ultimately turn to zero exponentially, almost surely, whenever either the expected survival probability rate of the malaria parasites satisfy $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, or whenever the basic production number of the disease satisfy $R^{*}_{0} < 1$. Furthermore, the sample Lyapunov exponent from (6.15) is estimated by the term $\lambda$, defined in (6.17) and (6.19).

It follows from (6.15) that when either of the conditions in Theorem 6.1[1.-2.] hold, then the infectious population $I(t)$ dies out exponentially, almost surely, whenever $\lambda$ in (6.17) and (6.19) is positive, that is, $\lambda > 0$. In addition, the rate of the exponential decay of each sample path of the infectious population $I(t)$ in each scenario of Theorem 6.1[1.-2.] is given by the estimate $\lambda > 0$ of the sample Lyapunov exponent in (6.17) and (6.19).

The conditions in Theorem 6.1[1.-2.] can also be interpreted as follows. Recall [^[2], Remark 6.2.2], the basic reproduction number $R^{*}_{0}$ in (2.2) (similarly in (2.3)) represents the expected number of secondary malaria cases that result from one infective placed in the steady state disease free population $S^{*}_{0} = \frac{B}{\mu}$. Thus, $\frac{1}{R^{*}_{0}} = \frac{(\mu+d+\alpha)}{\beta S^{*}_{0}}$, for $R^{*}_{0}\geq 1$, represents the probability rate of infectious persons in the secondary infectious population $\beta S^{*}_{0}$ leaving the infectious state either through natural death $\mu$, diseases related death $d$, or recovery and acquiring natural immunity at the rate $\alpha$. Thus, $\frac{1}{R^{*}_{0}}$ is the effective probability rate of surviving infectiousness until recovery with acquisition of natural immunity. Moreover, $\frac{1}{R^{*}_{0}}$ is a probability measure provided $R^{*}_{0}\geq 1$.

In addition, recall [^[2], Theorem 5.1 & 5.2] asserts that when $R^{*}_{0}\geq 1$, and the expected survival probability $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$ is significantly large, then the outbreak of malaria establishes a malaria endemic steady state population $E_{1}$. The conditions for extinction of disease in Theorem 6.1[1.], that is $R^{*}_{0}\geq 1$ and $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$ suggest that in the event where $R^{*}_{0}\geq 1$, and the disease is agammaessive, and likely to establish an endemic steady state population, if the expected survival probability rate $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$ of the malaria parasites over their complete life cycle of length $T_{1}+T_{2}$, is less than $\frac{1}{R^{*}_{0}}$- the effective probability rate of surviving infectiousness until recovery with natural immunity, then the malaria epidemic fails to establish an endemic steady state, and as a result, the disease ultimately dies out at an exponential rate $\lambda$ in (6.17). This result suggests that, malaria control policies should embark on vector control strategies such as genetic modification techniques in order to reduce the chances of survival of the malaria parasites inside the mosquitos, and in the human beings.

In the event where $R^{*}_{0} < 1$ in Theorem 6.1[2.], extinction of disease occurs exponentially over sufficiently long time, regardless of the survival of the parasites. Moreover, the rate of extinction is $\lambda$ in (6.19). Also observe that the conditions in Theorem 6.1[1.-2.] for extinction of the infectious population $I(t)$ in the case of noise originating exclusively from the disease transmission rate $\beta$ has no bearings on the intensity of the noise from the disease transmission rate $\sigma_{\beta}$. That is, the size of $\sigma_{\beta}$ is not likely to reverse the extinction of malaria from the population, provided that $R^{*}_{0} < 1$. This implies that the condition for extinction $R^{*}_{0} < 1$ is robust to external influence from perturbations in the malaria transmission rate. This fact is also exhibited in Figure 3.

As it can be observed from several simulation studies involving white noise processes, in many occasions, the extinction of the infectious population over time coincides with extinction of the susceptible population, if the intensity of the noise in the epidemic dynamic system is high. And this suggests that the extinction of the disease from the population does not always imply the survival of the disease free population over time.

The following result describes the average behavior of the trajectories of the susceptible population over sufficiently long time in the phase plane of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5), and also states conditions for the asymptotic stability in the mean of the trajectories (see Definition 5.1(2)), in the event where the conditions of Theorem 6.1 are satisfied.

Theorem 6.2. Suppose any of the conditions in the hypothesis of Theorem 6.1[1.-2.] are satisfied. It follows that in $D^{expl}(\infty)$, the paths of the susceptible population in the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5) satisfy

That is, the susceptible population is strongly persistent over long-time in the mean, and almost sure asymptotically stable on average. Moreover, the average value of the susceptible population over sufficiently long time is the disease-free equilibrium $S^{*}_{0} = \frac{B}{\mu}$.

Proof:

Suppose either of the conditions in Theorem 6.1[1.-2.] hold, then if we further let

then it follows clearly from Theorem 6.1 that $P(\Omega_{1}) = 1$. That is, for every $\epsilon > 0$, there is a positive constant $K_{1}(w, \epsilon)\equiv K_{1} > 0$, such that

It follows from (6.22) that

In $D^{expl}(\infty)$, define

The differential operator $dV_{1}$ applied to the Lyapunov functional $V_{1}(t)$ in (6.24) leads to the following

where

Estimating the right-hand-side of (6.25) in $D^{expl}(\infty)$, and integrating over $[t_{0}, t]$, it follows from (6.22)-(6.23) that

where

Observe that similarly to (6.11)-(6.14), it is easy to see by the strong law of large numbers for local martingales (see, e.g. [54]) that

Thus, dividing both sides of (6.27) by $t$ and taking the limit supremum as $t\rightarrow \infty$, it follows that

On the other hand, estimating $g(S, I)$ in (6.26) from below and using the conditions of Assumption 1.1 and (6.23), it is easy to see that in $D^{expl}(\infty)$,

Moreover, for $t\in[t_{0}, K_{1}+h_{1}]$, then

Therefore, applying (6.31)–(6.32) into (6.25), then integrating both sides of (6.25) over $[t_{0}, t]$, and diving the result by $t$, it is easy to see from (6.25) that

Observe that in $D^{expl}(\infty)$, $\lim_{t\rightarrow \infty}\frac{1}{t}V_{1}(t) = 0$, a.s., and $\lim_{t\rightarrow \infty}\frac{1}{t}V_{1}(t_{0}) = 0$. Moreover, from (6.29), $\lim_{t\rightarrow \infty}{\frac{1}{t}M_{3}(t)} = 0, \quad a.s$. Therefore, rearranging (6.33), and taking the limit infinimum of both sides as $t\rightarrow \infty$, it is easy to see that

It follows from (6.30) and (6.34) that

Hence, for $\epsilon$ arbitrarily small, the result in (6.20) follows immediately from (6.35).

Remark 6.2. Theorem 6.2, Theorem 6.1, Theorem 4.1[a] and Lemma 6.1 signify that when the intensity of the noise from the disease transmission rate $\sigma_{\beta}$ is positive, and the intensities of the noises from the natural death rates satisfy $\sigma_{i} = 0, i\in \{S, E, I, R\}$, then all sample paths of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5) that start in $D^{expl}(\infty)\subset D(\infty)$ continue to oscillate in $D^{expl}(\infty)$. Moreover, the sample paths of the infectious state $I(t), t\geq t_{0}$ of the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ ultimately turn to zero exponentially, almost surely, whenever either the expected survival probability rate the malaria parasite satisfy $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, for $R^{*}_{0}\geq 1$, or whenever the basic production number satisfy $R^{*}_{0} < 1$. Furthermore, the rate of the exponential decrease of the infectious population from (6.15) is estimated by the term $\lambda$, defined in (6.17) and (6.19).

In addition, Theorem 6.2 asserts that when either the expected survival probability rate the malaria parasites satisfy $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, for $R^{*}_{0}\geq 1$, or whenever the basic production number satisfy $R^{*}_{0} < 1$, the susceptible population remains persistent in the mean over sufficiently large time, moreover, every sample path of the susceptible population $S(t)$ that starts in $D^{expl}(\infty)$ continues to oscillate in $D^{expl}(\infty)$, and on average all sample paths converge to the disease free steady state population $S^{*}_{0} = \frac{B}{\mu} = 1$.

In other words, over sufficiently long time, the population that remains will be all susceptible malaria-free people, and the population size will be equal to the disease free steady state population $S^{*}_{0} = \frac{B}{\mu} = 1$ of the system (3.2)-(3.5).

6.1.   Sensitivity of the extinction results to the probability densities $f_{T_{i}}, i=1, 2$

Recall Remark 6.1 explains that the fraction $\frac{1}{R^{*}_{0}}$ is a probability measure, whenever $R^{*}_{0}\geq 1$. Observe that various types of lifetime probability densities $f_{T_{i}}, i = 1, 2$ will model different behaviors of the malaria plasmodium during the incubation periods $T_{i}, i = 1, 2$, and lead to different interpretations of the expected survival probability rate $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$.

For instance, consider a hypothetical scenario, where the exposed mosquitoes incubating the parasites in the sporogonic cycle, independently survive natural death, and attain the full maturation period of the parasites over the sporogonic cycle (between 10–18 days[3]), at a constant arrival rate of $\gamma_{1}$ mosquitoes/day, and the exposed human beings incubating the parasites undergoing the exo-erythrocytic cycle (over 7-30 days[3]), also survive natural death, and independently attain the full maturation period of the parasites in the exo-erythrocytic cycle, with constant arrival rate of $\gamma_{2}$ humans/day. Then, it follows that the independent Poisson processes $\{M_{i}(t), t\geq t_{0}\}, i = 1, 2$, respectively, describe the number of mosquitoes and humans, respectively, incubating the parasites, which attain maturity at any time $t\geq t_{0}$, from the onset of the sporogonic cycle, where susceptible mosquitos $\hat{V}_{s}$ bite and obtain infected blood meal from an infectious human ${I}(t)$, and the onset of the exo-erythrocytic cycle, where the mosquitos in the infectious state $\hat{V}_{i}(t)$, bite and transmit the plasmodium into a susceptible human ${S}(t)$, respectively. Moreover, $\hat{V}_{i}(t), \hat{V}_{s}(t), {S}(t)$ and ${I}(t)$ are defined in A.

Thus, the random variables $T_{i}, i = 1, 2$ indicating the time until the parasites in the different developmental stages in the two separate half-life cycles attain maturity (equivalently, $T_{1}$ is time until an exposed mosquito attains maturity of the parasites in the sporogonic cycle, and $T_{2}$ is time until an exposed human being attains the maturity point of the parasites in the exo-erythrocytic cycle), follow independent exponential distributions with means $\frac{1}{\gamma_{i}}, i = 1, 2$, respectively. Recall ^[2] gives justification for independence between $T_{1}$ and $T_{2}$, and implying that the Poisson processes $\{M_{i}(t), t\geq t_{0}\}, i = 1, 2$ are independent.

For the given scenario of the incubating malaria parasites above, the expected survival probability

can be interpreted as a probability of two independent events inside the exposed mosquitos and inside the exposed human beings.

Indeed, the term $\frac{\gamma_{1}}{\mu_{v}}$ represents the total exposed mosquitoes incubating malaria parasites in the sporogonic cycle, that survive natural death, and attain maturity stage of the parasites called sporozoites, inside the mosquitos, and totaled over the average life span of a mosquito $\frac{1}{\mu_{v}}$. The denominator

represents the total mosquitoes that survive natural death, $\frac{\gamma_{1}}{\mu_{v}}$, until maturation of the parasites, and the total mosquitoes that die naturally, $\frac{\mu_{v}}{\mu_{v}}$, over the average life span of a mosquito $\frac{1}{\mu_{v}}$. Thus, $\left(\frac{\frac{\gamma_{1}}{\mu_{v}}}{\frac{\gamma_{1}}{\mu_{v}}+1}\right)$ is the probability that an exposed mosquito, survives natural death, and attains the full maturation period of the parasites in the sporogonic cycle.

Applying similar reasoning above, the term $\left(\frac{\frac{\gamma_{2}}{\mu}}{\frac{\gamma_{2}}{\mu}+1}\right)$ is the probability that an exposed human being incubating the plasmodium, survives natural death, and attains the full maturation period of the parasites in the exo-erythrocytic cycle. Therefore, the expected survival probability (6.36) is interpreted as the probability that the parasites will survive in the exposed mosquitoes attaining their half-life cycle(sporogonic cycle), and survive in the exposed human beings, completing their second half-life cycle (exo-erythrocytic cycle).

Since the distribution of the delays $T_{i}, i = 1, 2$ is not unique, it follows that every lifetime distribution, e.g. Weibull, Gamma, Beta, Lindley distributions, with completely different set of parameters, will lead to different interpretations of the expected survival probability $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$, and the extinction conditions $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, for $R^{*}_{0}\geq 1$, in Theorem 6.1[1.].

Based on the observations from Theorem 6.2, the following proposition is made, which asserts that the average behavior of the sample paths of (3.2)-(3.5) near the disease-free equilibrium, leads to Lyapunov stability in probability. The proof appears in ^[55].

Proposition 6.3. Suppose the assumptions of Theorem 6.2 are satisfied, then the disease-free equilibrium $E_{0} = (S^{*}_{0}, 0) = (\frac{B}{\mu}, 0)$ of the decoupled system (3.3) and (3.5) is stochastically stable in probability. In other words, if either the basic reproduction number $R^{*}_{0}$, or the expected survival probability of the malaria plasmodium $E(e^{-(\mu_{v}T_{1}+\mu T_{2})})$, satisfy $R^{*}_{0} < 1$, or $E(e^{-(\mu_{v}T_{1}+\mu T_{2})}) < \frac{1}{R^{*}_{0}}$, whenever $R^{*}_{0}\geq 1$, respectively, then every trajectory for the solution process $\{(S(t), I(t)), t\geq t_{0}\}$ of the decoupled system (3.3) and (3.5) that starts near $E_{0}$, tends to remains near $E_{0}$.

7.   Example: Application to P. vivax malaria

In this example, using ideas from the malaria model and data in ^[56], the stochastic extinction results of this study are exhibited. This is accomplished by examining the sample paths of the decoupled system (3.2) and (3.4) relative to the disease-free equilibrium $E_{0}$ over sufficiently long time.

(a.) The model (3.2)–(3.5) is applied to P. vivax malaria, and the data in ^[56] for P. vivax will be used. Also, since in A (B) it is assumed that $V_{0} > > \hat{N}((t), t\geq t_{0}$, it is assumed that the sizes of the total vector and human populations are consistent with one of the following countries Brazil, India, Myanmar, or Papua New Guinea which experienced the highest P.vivax prevalence in 2010 (cf. [57]). It is assumed that high P. vivax prevalence reflects high infestation by mosquitoes. In the absence of Anopheles mosquito population data for Brazil, and to minimize unrealism, some useful information about realistic sizes of other species of mosquitoes ``unleashed" in a city of Brazil is used to simulate the hypothetical Anopheles mosquito population size. In 2015-2016, Oxitex conducted a project themed ``Friendly Aedes aegypti Project" for dengue fever control in Piracicaba, Brazil(cf. ^[58]). It is reported that ``friendly mosquitoes" were tried on an area of the city consisting of 12 neighborhoods, and a total of 65,000 residents. The Oxitex mosquito production facility produced about 60 million ``Friendly Mosquitoes" per week. It is assumed in this example that the hypothetical human and vector populations are comparable in features to those in Piracicaba, and the human population is infested daily by $V_{0} = (60/7)million$ anopheles mosquitoes. Moreover, the initial human population size $\hat{N}(t_{0}) = 65000$. In addition, the per capita mortality rate $\hat{\mu}_{v}$ of mosquitos given in ^[56] lies in $\hat{\mu}_{v}\in [0.2, 0.5]$, and here selected to be $\hat{\mu}_{v} = 0.5$ per day.

(b.) The 2010 average lifespan for human beings in Piracicaba was $75.9$ years or $27703.5$ days (cf. ^[59]). Thus, in this example, the natural deathrate of humans is assumed as $\hat{\mu} = 1/27703.5$ per day. The 2010 estimated birthrate for Brazil was $\hat{B} = \rm{18.43 births}/ \rm{1,000 population}$ per day (cf. ^[60]), and this value is used for the hypothetical human population in this example. The 2010 malaria related deathrate $\hat{d}$ is estimated using data from 2011 WHO malaria ^[61] for Brazil. Indeed, the time-series graph for Brazil death cases over years from 2000-2010 shows the normalized malaria deathrate for 2010 was approximately $75/100,000$^*. Thus, daily malaria related deathrate here is estimated as $\hat{d} = 75/100,000/365/day$.

^*The malaria deathrate is calculated as number of cases reported, divided by the total population $\times 100,000$. (cf.^[61])

(c.) Using ideas from ^[56], the effective transmission rate from infectious human to mosquito $\Lambda$ in (A.2)-(A.3) can be expressed as $\Lambda = \frac{a}{\left(\frac{\hat{B}}{\hat{\mu}}\right)}b$, where $a\in [0.2, 0.5]$ (cf.^[56]) is rate of biting on humans per mosquito per day, so that $\frac{a}{\left(\frac{\hat{B}}{\hat{\mu}}\right)}$ - the smallest possible biting rate per human per day is assumed fixed for the human population $\hat{N}(t)\in (0, \frac{\hat{B}}{\hat{\mu}}], \forall t\geq t_{0}$. The term $b$ is the fraction of bites on humans that result to infection in mosquito per day. In this example, it is assumed $a = 0.2/day$ and the fraction $b = 500000/V_0$ of bites result in infection of the mosquito.

(d.) Furthermore, using ideas in ^[56] the effective transmission rate from infectious mosquitoes to susceptible humans $\hat{\beta}$ in (A.14)–(A.17) can be expressed as $\hat{\beta} = \frac{a}{\left(\frac{\hat{B}}{\hat{\mu}}\right)}c$, where $c$ is the fraction of mosquito bites on humans that result to infection in humans per day. Moreover, it is assumed for Subsections 7.1, 7.2 that the fraction $c = 10000/V_0$ of bites lead to infection of humans.

(e.) The range of values for the recovery rate $\hat{\alpha}$ is given in ^[56], and here selected as $\hat{\alpha} = 0.01/day$. (f.) Range of values for the incubation period for P.vivax in humans $T_{2}\in [10,100]$ days is given in ^[56], and here selected as $T_{2} = 15$ days. Also, since the incubation period $T_{1}$ for P.vivax in mosquitoes varies with temperature, similar to ^[56], it is assumed to be $T_{1} = 9$ days. Furthermore, the naturally acquired immunity (NAI) against malaria is determined by exposure to parasites, age and other biological factors, and it is not clear how NAI affects the duration of blood-stage malaria infections (cf.^[62]). Since a plausible assumption in the instance of repeated malaria infections is that $T_{3}\geq T_{1}+T_{2}$, it will be assumed that repeated malaria infections in the population results in constant effective NAI lasting approximately $T_{3} = 182.5$ days (or approximately 6 months).

The dimensional estimates for the parameters of the malaria model given in (a.)-(e.) are applied to (A.42) to find the dimensionless parameters for the model (3.2)-(3.5) given in Table 1.

Moreover, the Euler-Maruyamas stochastic approximation scheme is used to generate paths for the different states $S(t), E(t), I(t), R(t)$ over the time interval $[0, 1000]$ days. The special nonlinear incidence functions $G(I) = \frac{a_{1}I}{1+I}, a_{1} = 0.05$ in ^[63] is utilized to generate the numeric results. Furthermore, the following initial fractions of susceptible, exposed, infectious and removed individuals in the initial population size $\hat{N}(t_{0}) = 65000$ are used:

For the given set of dimensionless parameter estimates in Table 1, where $\beta = 0.02146383$, the disease-free equilibrium is $E_{0} = (S^{*}_{0}, 0, 0) = (1, 0, 0)$, and from (2.2), the basic reproduction number is $\hat{R}^{*}_{0} = 0.2498732 < 1$.

7.1.   Example 1: The joint effect of the intensity of white noise from disease transmission and natural deathrates

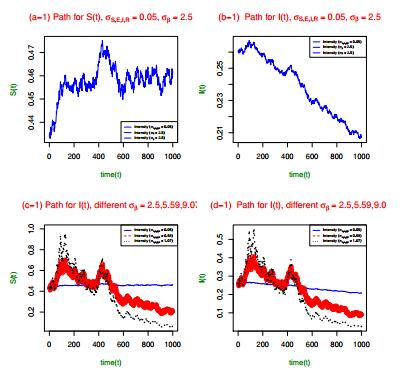
Figure 2 can be used to verify the results about the extinction of the infectious population in Theorem 5.1. Indeed, it can be observed that for the malaria data in Table 1, and the initial conditions for the system (3.2)-(3.5) in (7.1), and also the intensity conditions exhibited in Figure 2, that is, (1) solid blue line $(\sigma_{i} = 0.05, \sigma_{\beta} = 2.5), \forall i\in\{S, E, I, R\}$, (2) red solid-and-dotted line $(\sigma_{i} = 0.59, \sigma_{\beta} = 5.59), \forall i\in\{S, E, I, R\}$, and (3) black dotted line $(\sigma_{i} = 1.07, \sigma_{\beta} = 9.07), \forall i\in\{S, E, I, R\}$, it follows from (5.20) that the estimates of the rate of extinction of the malaria population $I(t)$ are respectively, (1) $Q = 0.08711203 > 0$, (2) $Q = 0.2599415 > 0$, and (3) $Q = 0.6583461 > 0$. That is,

The Figure 2(b-1) and (d-1) confirm that over sufficiently large time, when $Q > 0$, then the infectious population becomes extinct. Moreover, as the intensities increase across from $(\sigma_{i} = 0.05, \sigma_{\beta} = 2.5), \forall i\in\{S, E, I, R\}$ to $(\sigma_{i} = 1.07, \sigma_{\beta} = 9.07), \forall i\in\{S, E, I, R\}$, the value of $Q$ increases, and the infectious population is extinct more rapidly. Furthermore, note that the basic reproduction number in (2.2) for this scenario is $\hat{R}^{*}_{0} = 0.2498732 < 1$, which signifies that the disease is getting eradicated from the population over time, leading to the small rise in the susceptible population seen in Figure 2(a-1) over sufficiently long time. Nevertheless, the general decrease in the paths of the susceptible population $S(t)$ in Figure 2(c-1) over time is accounted for by the presence and rise in the intensity of the noise in the natural death rate across from $(\sigma_{i} = 0.05, \sigma_{\beta} = 2.5), \forall i\in\{S, E, I, R\}$ to $(\sigma_{i} = 1.07, \sigma_{\beta} = 9.07), \forall i\in\{S, E, I, R\}$, respectively.

7.2.   Example 2: The effect of the intensity of white noise from disease transmission rate and stochastic stability

The list of parameter values in Table 1 are also used to examine the paths of the different states of the stochastic system (3.2)–(3.5), whenever the conditions of Theorem 6.1 and Theorem 6.2 are satisfied.

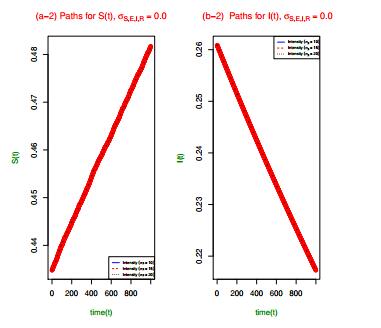
Figure 3 is used to verify the results about the extinction of the infectious population over time in Theorem 6.1, and the long-term behavior of the susceptible population $S(t)$ in Theorem 6.2. Indeed, it can be observed that for the given malaria data in Table 1, and the initial conditions for the system (3.2)-(3.5) in (7.1), and also the intensities of the white noise processes in the system- (1) solid blue line $(\sigma_{i} = 0.0, \sigma_{\beta} = 10), \forall i\in\{S, E, I, R\}$, (2) red solid-and-dotted line $(\sigma_{i} = 0.0, \sigma_{\beta} = 15), \forall i\in\{S, E, I, R\}$, and (3) black dotted line $(\sigma_{i} = 0, \sigma_{\beta} = 20), \forall i\in\{S, E, I, R\}$, it follows that the basic reproduction number in (2.2) in each scenario is $\hat{R}^{*}_{0} = 0.2498732 < 1$. Therefore, the condition of Theorem 6.1(a.) is satisfied, and from (6.19), the estimates for the rate of extinction of the malaria population $I(t)$, for the given lines (1)–(3) above, are respectively, (1) $\lambda = 0.08589658 > 0$, (2) $\lambda = 0.08589786 > 0$, and (3) $\lambda = 0.08589831 > 0$. That is,

The Figure 3(b-2) confirms that over sufficiently large time, when $\lambda > 0$, then the infectious population becomes extinct. Furthermore, note that the basic reproduction number in (2.2) in these scenarios is $\hat{R}^{*}_{0} = 0.2498732 < 1$, which signifies that the disease is getting eradicated from the population over time, and the susceptible population seen in Figure 3(a-2) oscillates slightly over sufficiently long time, and approaches the disease-free equilibrium state $S^{*}_{0} = \frac{B}{\mu} = 1$.

Indeed, clearly, the three sample paths of $S(t)$ in Figure 3(a-2) are monotonic increasing functions over long time, and approach $S^{*}_{0} = \frac{B}{\mu} = 1$ asymptotically, almost surely. This, suggests that the susceptible population is almost surely path-wise stable on average over sufficiently long time near $S^{*}_{0} = \frac{B}{\mu} = 1$ as shown in Theorem 6.2.

The Figure 3 also confirms Theorem 6.1 that the extinction of the infectious population $I(t)$ over sufficiently large time has no bearing on the size of the intensity $\sigma_{\beta}$, or the strength of the noise from the disease transmission rate, provided that the basic reproduction number $\hat{R}^{*}_{0} < 1$. For all sample paths depicted in Figure 3(a-2), the basic reproduction number remains the same value $\hat{R}^{*}_{0} = 0.2498732 < 1$. Moreover, the estimates of the rate of extinction are also approximately the same values for the lines (1)-(3), that is, (1) $\lambda = 0.08589658 > 0$, (2) $\lambda = 0.08589786 > 0$, and (3) $\lambda = 0.08589831 > 0$, respectively. Thus, the extinction conditions of Theorem 6.1 are robust, to external influence of noise in disease transmission rate, as remarked early in Remark 6.1.

In addition, since clearly every path of the susceptible population in Figure 3(a-1) almost surely approaches the disease-free equilibrium state $S^{*}_{0} = \frac{B}{\mu} = 1$, regardless of the size of the intensity of the noise $(\sigma_{\beta})$ in disease transmission rate, there is numerical evidence that the disease-free steady state $E_{0} = (S^{*}_{0}, 0) = (\frac{B}{\mu}, 0) = (1, 0)$, is stochastically asymptotically stable, whenever the basic reproduction number $R^{*}_{0} < 1$, as proposed in Proposition 6.3.

8.   Conclusion

A stochastic family of SEIRS models for malaria is derived and studied, where the noises in the system represent the variability in the disease dynamics from the disease transmission and natural death rates. The threshold conditions for the extinction of malaria in the population over sufficiently long time are presented for both cases of (1) noises in the system from both the disease transmission and natural death rates, and (2) noise exclusively from the disease transmission rate.

The analytic results show that the dynamics of the disease in the case of noise exclusively from the disease transmission rate exhibits more profound characteristics such as (a) stability in the mean of the disease free steady state population asymptotically, (b) the threshold conditions for the extinction of malaria, and consequently for the asymptotic stability in the mean of the malaria-free population, are robust to the intensity of the noise from the disease transmission rate. Finally, numerical simulation results are presented to justify the analytical results of the study.

Acknowledgments

I express sincere gratitude to the editor and associate editors for inviting my contribution to this special issue and for the constructive feedback from all reviewers.

Conflict of interest

There is no conflict of interest in this paper.

Appendix

A.   Derivation of the Model (1.1)–(1.4) from the vector-host dynamics

The assumptions for the family of malaria models in ^[2] are adopted and modified in the following. (A) The delays represent the incubation period of the infectious agents (plasmodium or dengue fever virus etc.) in the vector $T_{1}$, and in the human host $T_{2}$. The third delay represents the naturally acquired immunity period of the disease $T_{3}$, where the delays are random variables with density functions $f_{T_{1}}, t_{0}\leq T_{1}\leq h_{1}, h_{1} > 0$, and $f_{T_{2}}, t_{0}\leq T_{2}\leq h_{2}, h_{2} > 0$ and $f_{T_{3}}, t_{0}\leq T_{3} < \infty$. All other assumptions for $T_{1}, T_{2}$ and $T_{3}$ are similar to the study ^[2].

(B) The vector (e.g. mosquito) population consists of two main classes namely: the susceptible vectors $V_{s}$ and the infectious vectors $V_{i}$. Moreover, it is assumed that the total vector population denoted $V_{0}$ is constant at any time, that is, $V_{s}(t)+V_{i}(t) = V_{0}, \forall t\geq t_{0}$, where $V_{0} > 0$ is a positive constant. The susceptible vector population $V_{s}$ are infected by infectious human beings $\hat{I}$, and after the incubation period $T_{1}$ of the infectious agent, the exposed vector become infectious $V_{i}$. Moreover, it is assumed that there is homogenous mixing between the vector-host population. Therefore, the birth rate and death rate of the vectors must be equal, and denoted $\hat{\mu}_{v}$. It is further assumed that the turnover of the vector population is very high, and the total number of vectors $V_{0}$ at any time $t$, is very large, and as a consequence, $\hat{\mu}_{v}$ is sufficiently large number. In addition, it is assumed that the total number of vectors $V_{0}$ is exceedingly larger than the total human population present at any time $t$, denoted $\hat{N}((t), t\geq t_{0}$. That is, $V_{0} > > \hat{N}((t), t\geq t_{0}$.

(C) The human population is similarly defined as in Wanduku^[2], and consists of susceptible $(\hat{S})$, Exposed $(\hat{E})$, Infectious $(\hat{I})$ and removed $(\hat{R})$ classes. The susceptible humans are infected by the infectious vectors $V_{i}$, and become exposed (E). The infectious agent incubates for $T_{2}$ time units, and the exposed individuals become infectious $\hat{I}$. The infectious class recovers from the disease with temporary or sufficiently long natural immunity and become $(\hat{R})$. Therefore, the total population present at time $t$, $\hat{N}(t) = \hat{S}(t)+\hat{E}(t)+\hat{I}(t)+\hat{R}(t), \forall t\geq t_{0}$.

Furthermore, it is assumed that the interaction between the infectious vectors $V_{i}$ and susceptible humans $\hat{S}$ exhibits nonlinear behavior, due to the overcrowding of the vectors as described in (B), and resulting in psychological effects on the susceptible individuals which leads to change of behavior that limits the disease transmission rate, and consequently in a nonlinear character for the incidence rate characterized by the nonlinear incidence function $G$. $G$ satisfies the conditions of Assumption 1.1.

(D) There is constant birthrate of human beings $\hat{B}$ in the population, and all births are susceptible individuals. It is also assumed that the natural deathrate of human beings in the population is $\hat{\mu}$ and individuals die additionally due to disease related causes at the rate $\hat{d}$. From a biological point of view, the average lifespan of vectors $\frac{1}{\hat{\mu}_{v}}$, is much less than the average lifespan of a human being in the absence of disease $\frac{1}{\hat{\mu}}$. It follows very easily that assuming exponential lifetime for all individuals (both vector and host) in the population, then the survival probability over the time intervals of length $T_{1} = s\in [t_{0}, h_{1}]$, and $T_{2} = s\in [t_{0}, h_{2}]$, satisfy

That is, (A.1) signifies that the survival chance of the mosquitoes, and consequently the parasites or virus inside the mosquitoes over the complete life cycle of the parasites lasting for $T_{1}+T_{2}$ time units, is less than the survival chance of human beings over the same period of time. Furthermore, recall [Theorem 5.1, ^[2]] asserts that it is necessary for the expected survival rate $E(e^{-\hat{\mu}_{v}T_{1}-\hat{\mu} T_{2}})$ to be significant for the disease to establish a steady endemic population. All other assumptions for the malaria model (1.1)-(1.4) remain the same as in ^[2].

Applying similar ideas in ^[48], the vector dynamics from (A)-(D) follows the system

where $\Lambda$ is the effective disease transmission rate from an infectious human being to a susceptible vector. Observe that the incidence rate of the disease into the vector population $\Lambda e^{-\hat{\mu}_{v}T_{1}}\hat{I}(t-T_{1})V_{s}(t-T_{1})$ represents the rate of new infectious vectors occurring at time $t$, which became exposed at earlier time $t-T_{1}$ after obtaining an infected blood meal from an infectious person, and surviving over the incubation period $T_{1}$, with the exponential survival probability rate $e^{-\hat{\mu}_{v}T_{1}}$, the vectors become infectious at time $t$. The detailed host population dynamics is derived as follows.

At time $t$, it follows from (C) that when susceptible humans $\hat{S}$ and infectious vectors $V_{i}$ interact with $\hat{\beta}$ effective contacts per vector, per unit time, then under the assumption of homogenous mixing, the incidence rate of the disease into the human population is given by the term $\hat{\beta}\hat{S}(t)V_{i}(t)$. With the assumption of crowding effects of the vector population, it follows from (C) that the incidence rate of the disease can be written as

where $G$ is the nonlinear incidence function satisfying the conditions in Assumption 1.1.

The susceptible individuals $\hat{S}$ who have acquired infection from infectious vectors $V_{i}$, but are non infectious form the exposed class $\hat{E}$. The population of exposed individuals at time $t$ is denoted $\hat{E}(t)$. After the incubation period, $T_{2} = u\in [t_{0}, h_{2}]$, of the infectious agent in the exposed human host, the individual becomes infectious, $\hat{I}(t)$, at time $t$. Applying similar reasoning in ^[64], the exposed population, $\hat{E}(t)$, at time $t$ can be written as follows

where

represents the probability that an individual remains exposed over the time interval $[0, t]$. It is easy to see from (A.6) that under the assumption that the disease has been in the population for at least a time $t > \max_{t_{0}\leq T_{1}\leq h_{1}, t_{0}\leq T_{2}\leq h_{2}} {(T_{1}+ T_{2})}$, in fact, $t > h_{1}+h_{2}$, so that all initial perturbations have died out, the number of exposed individuals at time $t$ is given by

Moreover, since $T_{2} = u\in [t_{0}, h_{2}]$ is a random variable, it follows from (A.8) that the expected number of exposed individuals at time $t$ is given by

Similarly, for the removal population, $\hat{R}(t)$, at time $t$, individuals recover from the infectious state $\hat{I}(t)$ at the per capita rate $\hat{\alpha}$ and acquire natural immunity. The natural immunity wanes after the varying immunity period $T_{3} = r\in [t_{0}, \infty]$, and removed individuals become susceptible again to the disease. Therefore, at time $t$, individuals leave the infectious state at the rate $\hat{\alpha} \hat{I}(t)$ and become part of the removal population $\hat{R}(t)$. Thus, at time $t$ the removed population is given by the following equation

where

represents the probability that an individual remains naturally immune to the disease over the time interval $[0, t]$. But it follows from (A.10) that under the assumption that the disease has been in the population for at least a time $t > \max_{t_{0}\leq T_{1}\leq h_{1}, t_{0}\leq T_{2}\leq h_{2}, T_{3}\geq t_{0}}{(T_{1}+ T_{2}, T_{3})} = T_{max}\geq \max_{ T_{3}\geq t_{0}}{(T_{3})}$, in fact, the disease has been in the population for sufficiently large amount of time so that all initial perturbations have died out, then the number of removed individuals present at time $t$ from (A.10), is given by

Since $T_{3}$ is distributed, the expected number of removal individuals at time $t$ can be written as

It follows from the assumptions (A)-(D), (A.5), (A.8), (A.9), and (A.13) that for $T_{j}, j = 1, 2, 3$ fixed in the population, the dynamics of malaria in the human population is given by the system

Furthermore, the incidence function $G$ satisfies the conditions in Assumption 1.1. And the initial conditions are given in the following:-

where $\mathcal{C}((-T_{max}, t_{0}], \mathbb{R}_{+})$ is the space of continuous functions with the supremum norm

It is shown in the following that the vector-host dynamics in (A.2)-(A.4) and (A.14)-(A.18) lead to the model (1.1)-(1.4), which omits the dynamics of the vector population, under the assumptions (A)-(D).

Firstly, observe that the system (A.14)-(A.18) satisfies [Theorem 3.1, [2]], and the total human population $\hat{N}(t) = \hat{S}(t)+\hat{E}(t)+\hat{I}(t)+\hat{R}(t), \forall t\geq t_{0}$ obtained from system (A.14)-(A.18) with initially condition that satisfies $N(t_{0})\leq \frac{\hat{B}}{\hat{\mu}}$, must satisfy

Therefore, the assumption (B) above, interpreted as $\frac{\hat{N}(t)}{V_{0}} < < 1, \forall t\geq t_{0}$ implies that

Define

then from (A.21)–(A.22), it follows that $\epsilon = \frac{\left(\frac{\hat{B}}{\hat{\mu}}\right)}{V_{0}} < < 1$.

Employing similar reason in ^[48], define two natural dimensionless time scales $\eta$ and $\varrho$ for the joint vector-host dynamics (A.2)–(A.4) and (A.14)-(A.18) in the following.

Note that since the total vector population $V_{0}$ from (B) above is constant, that is, $V_{s}(t)+V_{i}(t) = V_{0}, \forall t \geq t_{0}$, and from (A.20) and [Theorem 3.1, ^[2]] the total human $0 < \hat{N}(t)\leq \frac{\hat{B}}{\hat{\mu}}, \forall t \geq t_{0}$, whenever $\hat{N}(t_{0})\leq \frac{\hat{B}}{\hat{\mu}}$, then the time scales $\eta$ and $\varrho$ arise naturally to rescale the total vector and maximum total human populations $V_{0}$ and $\left(\frac{\hat{B}}{\hat{\mu}}\right)$, respectively, at any time.

The time scales (A.23)-(A.24) can be distinguished as "fast" and "slow" using the following example. A particle's movement on the $\varrho$ time scale covers one unit of time $\varrho = 1$ at much early time $t_{\varrho} = \frac{1}{V_{0}\Lambda}$ on the $t$ time scale, compared to the particle's movement on the $\eta$ time scale, where the particle overs one unit of time $\eta = 1$ at much later time $t_{\eta} = \frac{1}{\left(\frac{B}{\mu}\right)\Lambda} > > t_{\varrho}$, since (A.21) holds. Thus, movement on the time scale $\varrho$ is "fast", and on $\eta$ is "slow". See ^[48] for more information.

Therefore, from above, let

be the dimensionless vector variables, and

be the dimensionless human variables. And since $0 < \hat{N}(t)\leq \frac{\hat{B}}{\hat{\mu}}, \forall t \geq t_{0}$, whenever $\hat{N}(t_{0})\leq \frac{\hat{B}}{\hat{\mu}}$, it follows from (A.26) that

Applying (A.25)-(A.26) to (A.2)-(A.4) leads to the following

Observe from (A.27)-(A.30) that for nonnegative values for the vector variables $\hat{V}_{i}(t)\geq 0, \hat{V}_{s}(t)\geq 0, \forall t\geq t_{0}$, and positive values for the human variables ${S}(t), {E}(t), {I}(t), {R}(t) > 0, \forall t\geq t_{0}$, it is follows that

Thus, on the time scale $\varrho$ which is "fast", it is easy to see from (A.28)-(A.31), that under the assumption that $\epsilon$ from (A.22) is infinitesimally small, that is $\epsilon\rightarrow 0$, then

which implies that the dynamics of $\hat{V}_{i}$ and $\hat{V}_{s}$ behaves as in steady state. And thus, it follows from (A.28)-(A.32) that

It follows further from (A.33), and $\hat{V}_{s}$ in steady state (i.e. $\hat{V}_{s}(t-T_{1}) = \hat{V}_{s}(t)$) that

For sufficiently large value of the birth-death rate $\hat{\mu}_{v}$ (see assumption (B)), such that $\hat{\mu}_{v}e^{\hat{\mu}_{v}T_{1}} > > \Lambda \left(\frac{\hat{B}}{\hat{\mu}}\right)$, then it follows from (A.34) that $\hat{V}_{s}(t)\approx 1$, and consequently from (A.30) and (A.25), $V_{s}(t)\approx V_{0}$. Moreover, it follows further from (A.33) that

and equivalently from (A.25)-(A.26) that (A.35) can be rewritten as follows

While on the fast scale $\varrho$ the term $\hat{I}(t-T_{1})$ behaves as the steady state, on the slow scale $\eta$, it is expected to still be evolving. In the following, using (A.25)-(A.26), the dynamics for the human population in (A.14)-(A.18) is nondimensionalized with respect to the slow time scale $\eta$ in (A.23).

Without loss of generality(as it is usually the case), it is assumed that on the $\eta$ timescale, the nonlinear term $G(V_{i}(t))$ expressed as $G(V_{0}\hat{V}_{i}(\eta))$, can be rewritten from (A.36) as

by factoring a constant term $\frac{\Lambda V_{0}\left(\frac{\hat{B}}{\hat{\mu}}\right)}{\hat{\mu}_{v}}$, and the function $\hat{G}$ carries all the properties of Assumption 1.1. Thus, from the above and (A.36), the system (A.14)-(A.18) is rewritten in dimensionless form as follows:

where

The system (A.38)-(A.41) describes the dynamics of malaria on the slow scale $\eta$. Furthermore, moving forward, the analysis of the model (A.38)-(A.41) is considered only on the $\eta$ timescale. To reduce heavy notation, the following substitutions are made. Substitute $t$ for $\eta$, and the delays $T_{j}, \forall j = 1, 2, 3$ will substitute $T_{j\eta}, \forall j = 1, 2, 3$. Moreover, since the delays are are distributed with density functions $f_{T_{j}}, \forall j = 1, 2, 3$, it follows from (A)-(D), (A.6)-(A.13), (A.38)-(A.41) and (A.18) that the expected SEIRS model for malaria is given as follows:

where the initial conditions are given in the following: let $h = h_{1}+ h_{2}$ and define

where $\mathcal{C}((-\infty, t_{0}], \mathbb{R}_{+})$ is the space of continuous functions with the supremum norm

Also, the function $G$ satisfies the conditions of Assumption 1.1.