1. Introduction
Titanium dioxide has been extensively investigated for applications ranging from water splitting, dye-sensitized solar cells, degradation of pollutants, and destruction of bacteria to bio-medical applications [1,2,3,4,5]. Titania has been widely used because it is inexpensive to synthesize, benign, and photostable. A porous structured titanium dioxide can improve photocatalytic activity due to improved mass transport properties. In this regard, mesoporous materials offer promise. In recent years, several methods have been attempted to prepare porous TiO2 nanomaterials [6,7,8]. These include supercritical, hydrothermal, hard templating, and Evaporation-Induced Self-Assembly (EISA) methods. The high temperature supercritical method minimizes the collapse of pores, but requires expensive instrumentation, is energy intensive, and has challenges in scaling up due to the requirements of relatively high pressures and temperatures [8]. Hydrothermal method requires the use of autoclaves and relatively high pressures and temperatures [9]. The hard templating method is laborious, requires multiple steps of impregnation and long processing times [10,11]. In comparison to the above methods, EISA seems to be a facile and simple method, and it has the added benefit that the materials can be prepared and processed at mild conditions [12,13]. Another main advantage of the EISA method is that the material can be recovered as a powder or as a film. Several parameters such as pH, water content, nature and concentration of precursor(s) and surfactant, humidity, temperature etc. affect the quality and nature of the final mesostructured material, and these have been investigated previously [6]. The common precursor(s) for the synthesis of titania by EISA include TiCl4 and/or Ti(OCH(CH3)2)4. TiCl4 is highly reactive, toxic, and hazardous and hence titanium alkoxides are preferable. The EISA method involves the use of non-ionic (e.g. pluronic polymers such as P123) or cationic (e.g. cetyltrimethylammonium bromide (CTAB)) surfactants. An advantage of CTAB is that its critical micelle concentration is higher than that of P123. Also, the cloud point is a major issue with P123. Thus, a clear micellar solutions can be readily prepared at room temperature using CTAB. In addition, CTAB can be used at both low and high pH values. Thus, in the present study, Ti(OCH(CH3)2)4 and CTAB were used in the preparation of TiO2. Although several factors have been investigated, surprisingly, a systematic study of aging time has not been explored using the EISA method. This is important because the composition of the solution changes during the evaporation process, and this has profound effect on the nature of the final phase(s) formed.
It has been reported that mixedphases of titania exhibit higher activities in comparison to pure phases [14,15]. This has been the reason for the high activity of Degussa P25 for several photocatalytic reactions. Li et al. reported that the presence of small rutile crystallites in close contact with anatase created catalytic “hot spots” and this was responsible for high photocatalytic activity [16]. Thus, it is important to explore effective methods to prepare mixed-phase titania in a facile manner. Previous attempts to prepare TiO2 with mixed phases using surfactants required calcination (typically at relatively high temperatures in the range of 600 to 1200 oC) [9], use of highly reactive TiCl4 in addition to Ti(OR)4 [17], or hydrothermal treatment [18]. In addition, microemulsion method [19], flame pyrolysis, [20], or physical vapor deposition [21] methods have also led to the formation of mixed phases of anatase and rutile. In comparison to these methods of synthesis, the EISA method seems to relatively easy.
The anatase-to-rutile phase transformation as a function of aging time for the preparation of TiO2 mesostructured materials by the EISA method has not been investigated carefully and provides the impetus for this work. The mesostructured materials were evaluated for solar hydrogen production. The material with anatase (95%) and rutile (5%) exhibited high activity even in the absence of Pt as a co-catalyst. Our results suggest that mixed phases of TiO2 with varying compositions can be obtained by aging using the EISA method and by calcination at moderate temperatures in contrast to previous literature attempts to prepare mixed phases of anatase and rutile. Thus, this synthetic protocol is simple, and the composition of the titania phase(s) can be varied by simply varying the aging time. This study provides an ideal opportunity for making both powders and thin films of mixed phases for various applications in a facile manner.
2. Materials and Methods
2.1. Materials
Commercially available cetyltrimethylammonium bromide (CTAB, Alfa Aesar, 98+%), titanium isopropoxide (Ti(OCH(CH3)2)4, Acros, 98+%), conc. hydrochloric acid (Fisher-Scientific, ACS grade), ethanol (Pharmco-AAPER, ACS/USP grade, 200 proof) were used as received. Deionized water was used throughout the experiments.
2.2. Synthesis
The EISA method was used for preparing mesoporous TiO2 materials [12,13,22]. In a typical synthesis, 0.468 g of cetyltrimethylammonium bromide (CTAB) was dissolved in 5 mL of ethanol in a beaker. The solution was heated slowly to 50 °C and the beaker was covered with parafilm to prevent evaporation of ethanol. In another beaker, 4.4 mL of ethanol, 2.4 mL of Ti(OCH(CH3)2)4, and 0.93 mL of conc. HCl were mixed. These two solutions were combined and stirred. Then, 2.46 mL of deionized water was added drop wise and the mixture was stirred. The resulting solution was poured into petri dishes and then placed in an oven and heated to 60 °C and aged for various times. The materials were removed after 0.25,1, and 6 days. Finally, the materials were calcined at 500 °C for 6 h in static air at a heating rate of 3 oC/min to remove the template and named as TiO2-0.25d, TiO2-1d, and TiO2-6d.
Thermogravimetric analysis of the calcined mesostructured material indicates a weight loss of only 0.55 wt.% between 200 and 550 oC. This weight loss corresponds to loss of surface hydroxyl groups from titania, and this indicates that the cationic surfactant was removed after calcination.
2.3. Characterization and photocatalytic studies
TiO2 materials were characterized extensively by a variety of techniques. The powder X-ray diffraction studies of the mesostructured materials were recorded at room temperature using a Rigaku Ultima IV instrument with Cu Kα radiation (λ = 1.5408 Å). The accelerating voltage used was 40 kV, and the emission current was maintained at 44 mA. The samples were scanned with a step size of 0.02°, in the 2θ range from 10 to 80°. The ratios of the mixed phases present in the samples were determined by performing quantitative analysis using the Reference Intensity Ratio (RIR) method in the PDXL software (version 2) provided by Rigaku. Raman spectra were collected using a Horiba Jobin Yvon Labram Aramis Raman spectrometer with a He-Ne laser (532 nm) as the light source. The unfiltered beam of scattered laser radiation was focused onto the materials using a microscope objective (×50) for an acquisition time of typically 10 s. Transmission Electron Microscopic (TEM) images were obtained using a Tecnai G2 instrument operating at 120 kV. Prior to the analysis, the materials were dispersed in ethanol and the suspensions were sonicated for 30 min. Then, one drop of the suspension was placed on a copper grid coated with carbon film, and allowed to dry overnight before conducting the TEM studies. The textural properties, such as surface area, pore volume, and pore size distribution of the materials were analyzed using N2 physisorption measurements. After the samples were dried overnight at 80 °C and degassed at 100 °C extensively, N2 isotherms were obtained at −196 °C using a NOVA 2200e (Quantachrome Instruments) surface area analyzer. The specific surface area was calculated by applying the Brunauer-Emmett-Teller (BET) equation to the relative pressure range (P/P0) of 0.05-0.30. The pore volume was determined from the amount of N2 adsorbed at the highest relative pressure of P/P0 ≈ 0.99. The average pore diameter was calculated by using the formula, average pore diameter = 4 (pore volume) / (specific surface area). The UV-Vis diffuse reflectance spectra were recorded using a Cary 100 Bio UV-Visible spectrophotometer equipped with a praying mantis diffuse reflection accessory (Harrick Scientific). The band gaps of the materials were calculated extrapolating the high slope region to the X-axis in the Tauc plot obtained by transforming the absorbance plot using the Kubelka-Munk function.
The photocatalytic experiments were carried out as follows. A known amount of the photocatalyst (1 g/L) was suspended in a solution of H2O and methanol (molar ratio of [H2O]/[CH3OH] = 8). The suspension was degassed for 30 min. with high-purity argon prior to irradiation. The suspensions were continuously stirred throughout the course of the experiment. A 300 W Xenon lamp (Oriel light source) with an appropriate filter was used as the source of UV radiation. The amount of H2 produced was measured by gas chromatography (SRI 8610 C) equipped with a molecular sieve column and a TCD detector, and by using a calibration curve prepared previously. Photoluminescence (PL) measurements were carried out on a Horiba Jobin Yvon-Fluoromax 4 instrument. The excitation wavelength used was 300 nm, and the emission spectra were monitored in the range of 375-500 nm.
3. Results and Discussion
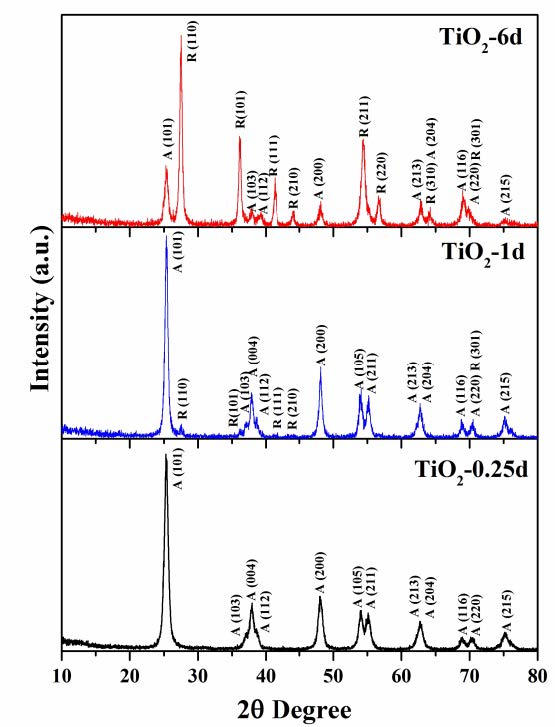
The powder X-ray diffractograms of the titania materials as a function on aging is shown in Figure 1. After aging for 0.25 day, peaks due to (101), (103), (004), (112), (200), (105), (211), (213), (204), (116), (220), and (215) diffraction planes of the anatase phase only are observed.
After aging for 1 day, a small peak appears at 2θ = 27.7o that is due to (110) diffraction plane of the rutile phase. In addition, anatase phase which is predominant in this material can also be clearly seen. However, after 6 days of aging, the percentage of rutile increases significantly, and peaks due to (110), (101), (111), (210), (211), (220), (310), and (301) diffraction planes of rutile can be observed in addition to the anatase phase. The variation in the phase of titania can be explained as follows.
A typical EISA synthesis involves multiple steps, and the choice of the solvent, acid, amount of water, titania precursor, and surfactant is critical, apart from the aging temperature and time [7]. In the present work, the molar ratio of [water]/[titanium isopropoxide] used was relatively high, i.e. ~17. At such high ratios, both hydrolysis and condensation of the titania precursor occur rapidly. This leads to the formation of titania oxo clusters first, prior to self-assembly. As evaporation of the most volatile component (ethanol) takes place initially, there is an increase in the concentration of the titania oligomers and the non-volatile surfactant. This triggers the self-assembly process and leads to the formation of a titania-surfactant hybrid phase. The hybrid “titaniatropic” phase consists of pre-formed titania nanobuilding blocks that are self-assembled around the surfactant molecules. These interactions are of the type, Ti-OH+…X−…CTAB+, where X represents bromide ions from CTAB, or chloride ions from HCl used in the synthesis. In the next steps, equilibration of water and solvent between the hybrid phase and the environment takes place. The continued evaporation of the solvent (ethanol and water) promotes the formation of a mesostructure. As the aging time is increased, the solution is progressively enriched with acid. Even though, most of the HCl eventually evaporates, some amount of residual Cl− ions persist leading to a condensed mesoporous network of the type TiO2-x/2(OH, Cl)x [23]. It has been reported that as the acid concentration increases, the edge shared bonds between the titania octahedral clusters and oxygen atoms decreases and the corner shared bonds between the titania oxo clusters and oxygen increases [24,25]. In the rutile structure, each titania octahedron is linked to two edge shared and eight corner shared oxygen atoms, respectively. On the other hand, in the anatase structure, the titania octahedron are connected to four edge and four corner sharing oxygen pairs. The reorientation of the TiO6 clusters due to the increase in the localized concentration of acid with aging time results in the formation of rutile phase. Hence, by changing the aging time, one can modulate the phase(s) of titania. In this study, the amount of rutile content continues to progressively increase with increase in aging time. For example, with an aging time of 6 h (TiO2-0.25d), the rutile content was found to be 0% whereas after 6 days of aging (TiO2-6d), a predominantly rutile phase (71%) was obtained. Further increase in aging time does not seem to increase the amount of rutile phase. For sake of briefness, we are discussing results pertaining to aging times of 6 h (TiO2-0.25d), 1 day (TiO2-1d), and 6 days (TiO2-6d) in this study.
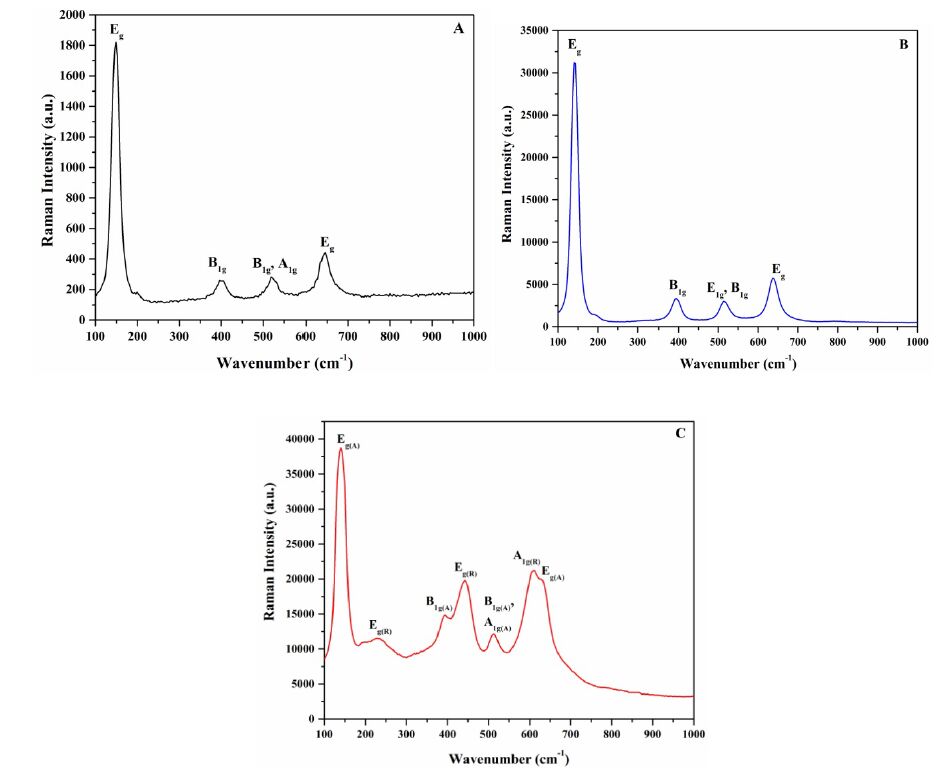
Raman studies indicate the presence of only anatase in TiO2-0.25d (Figure 2A) and is consistent with powder XRD studies. Peaks at 148 cm−1 (Eg), 393 cm−1 (B1g),519 cm−1 (A1g and B1g), and 643 cm−1 (Eg) attributed to the anatase phase can be clearly seen. Figure 2B shows the Raman spectra of TiO2-1d. The highest intense peak seems to be slightly shifted to 143 cm−1 (Eg), whereas the other peaks appear at wavenumbers similar to those observed in TiO2-0.25d. However, the Raman spectra of TiO2-1d show phonon modes due to the anatase phase only. This may be due to the relatively low amounts of rutile (5%) and sensitivity of the instrument that preclude the observation of phonon modes of rutile. However, the material aged after 6 days, TiO2-6d show peaks due to both anatase and rutile phases. In addition to the phonon modes of anatase described previously for TiO2-0.25d and TiO2-1d, peaks at 230 cm−1 (Eg), 442 cm−1 (Eg), and 610 cm−1 (A1g) that may be ascribed to the rutile phase can also be seen as indicated in Figure 2C. Thus, the Raman studies confirm the findings of the powder XRD studies.
Transmission electron microscopic (TEM) studies were also conducted to discern the morphology and phase. The TEM image of TiO2-0.25d shown in Figure 3A,indicate the presence of irregularly shaped titania particles that are fairly compact in nature, i.e. less porous in nature. The high resolution TEM images are shown in the inset in Figure 3A. Lattice fringes with d spacing values of 3.50 Å can be seen. This value is close to the d spacing (3.52 Å) of the (101) plane that is predominant in anatase. The TEM of TiO2-6d (Figure 3B) indicate a more open porous structure. The inset in Figure 3B shows the presence of both anatase (due to d (101) with a value of 3.50 Å) and rutile (due to d (110) with a value of 3.23 Å) phases, and is consistent with powder XRD and Raman studies. In summary, powder XRD, Raman, and TEM studies indicate the presence of a mixed phase in the sample aged for 6 days, whereas only anatase phase is present after 6 hours of aging. Aging for 1 day results in the presence of small amounts (5 wt.%) of rutile phase, which can be discerned from powder XRD studies only.
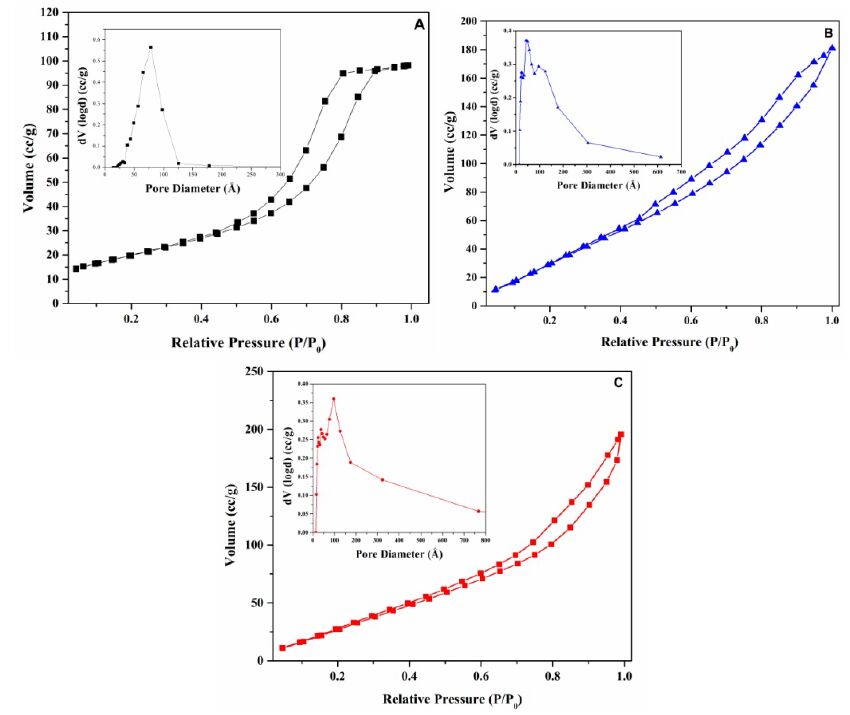
The textural properties of the mesostructured materials were investigated, and the results are shown in Figure 4. The materials exhibit type IV (IUPAC classification) isotherms, which are typical of mesoporous materials.
Figure 4A shows the nitrogen isotherm for TiO2-0.25d. At low values of relative pressures (P/P0), monolayer adsorption of N2 takes place. This is followed by multilayer adsorption and capillary condensation at higher relative pressures. Owing to the differences in pressures at which capillary evaporation and condensation take place, the isotherms display hysteresis. The hysteresis observed in this material, can be classified as H1 type. This type of hysteresis loop is typical of materials that contain aggregates that are fairly compact and having high degree of pore uniformity [26]. The pore volume (0.15 cm3/g) and specific surface area (72 m2/g) of this material is relatively low. The inset in Figure 4A shows the pore size distribution. As can be seen in the inset, the pore size is fairly uniform and centered near 80 Å. On increasing the aging time to 1 day, the specific surface area increases dramatically from 72 m2/g (for the sample, TiO2-0.25d) to 161 m2/g in TiO2-1d. The isotherm (Figure 4B) indicates that the hysteresis loops do not level off at relative pressures close to the saturation vapor pressure, suggesting that the materials are composed of loose assemblies of irregular shaped plate-like particles forming slit-like pores of broad pore size distribution. The broad pore size distribution can be seen in the inset in Figure 4B. A hierarchical set of pores centered near 50 Å and 100 Å, and extending into the upper range of mesopore (500 Å) can be observed. Increasing the aging time to 6 days, preserves the mesoporosity and the specific surface area drops slightly to 145 m2/g. However, the pore volume is still large. The isotherm and the pore size distribution for TiO2-6d is shown in
Figure 4C. The results are similar to that observed for the sample aged for 1 day,i.e., TiO2-1d. The textural properties of the mesostructured materials are listed in Table 1. In summary, the textural properties of the mesostructured materials indicate that extending the aging time facilitates in creating more open and porous mesostructures with higher specific surface area and larger pore volumes.
Table 1. Physico-chemical properties of titanium dioxide prepared at various aging times.
|
Material
|
Anatase Crystallite Size (nm)a
|
Anatase (%)b
|
Rutile (%)b
|
Specific
Surface Area (m2/g)c
|
Pore Volume (cc/g)d
|
Average Pore Diameter (Å)
|
Bandgap (eV)f
|
H2
(mmole /g TiO2)
|
|
TiO2-0.25d
|
10
|
100
|
0
|
72
|
0.15
|
84
|
3.22
|
0.27
|
|
TiO2-1d
|
16
|
95
|
5
|
161
|
0.28
|
70
|
3.09
|
0.51
|
|
TiO2-6d
|
13
|
29
|
71
|
145
|
0.30
|
83
|
3.04
|
0.09
|
a. Crystallite size was calculated using the Debye-Scherrer method by selecting the highest intense peak for anatase at 2θ = 25.36° (d101).
b. TiO2 phase percentages were calculated using reference intensity ratio (RIR) using the Rigaku PDXL software.
c. Specific surface area was determined by applying the Brunauer-Emmett-Teller (BET) equation to the relative pressure range of P/P0 = 0.05-0.30.
d. The pore volume was determined from the amount of N2 adsorbed at the highest relative pressure (P/P0) of approximately 0.99.
e. The bandgap was estimated by extrapolation of the high slope value from the Kubelka-Munk plot on the X-axis. |
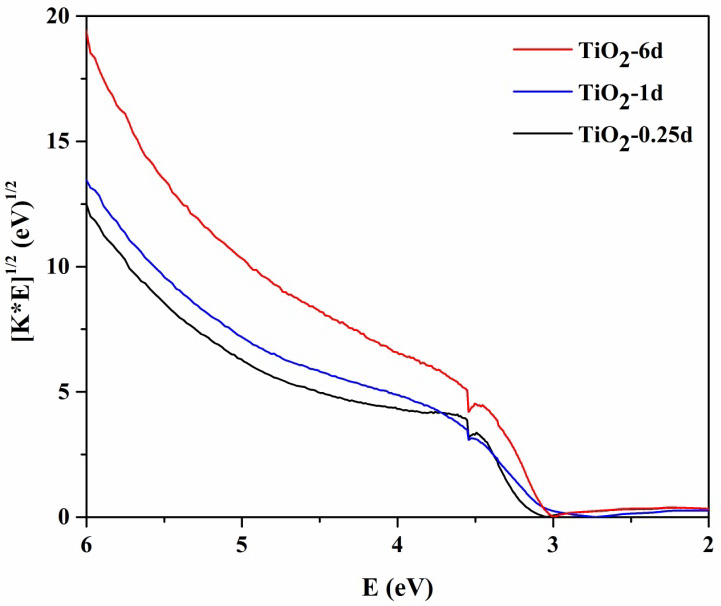
Diffuse reflectance (DR) spectral studies were carried out in order to discern the band gap. The absorption edge was calculated by plotting the Kubelka-Munk function, [KE] 1/2 against the photon energy, E, measured in eV (Figure 5). The band gap energy (Eg) was estimated by extrapolating the linear portion of the spectra to [KE]1/2 = 0. The DRS studies indicate that the band gap decreases as the rutile content increases, as indicated in Table 1. This is consistent with the fact that the band gap of anatase and rutile are ~3.2 and ~3.0 eV, respectively. Increase in the aging time increases the amount of rutile, and the DRS results obtained in this study are consistent with the expected trend.
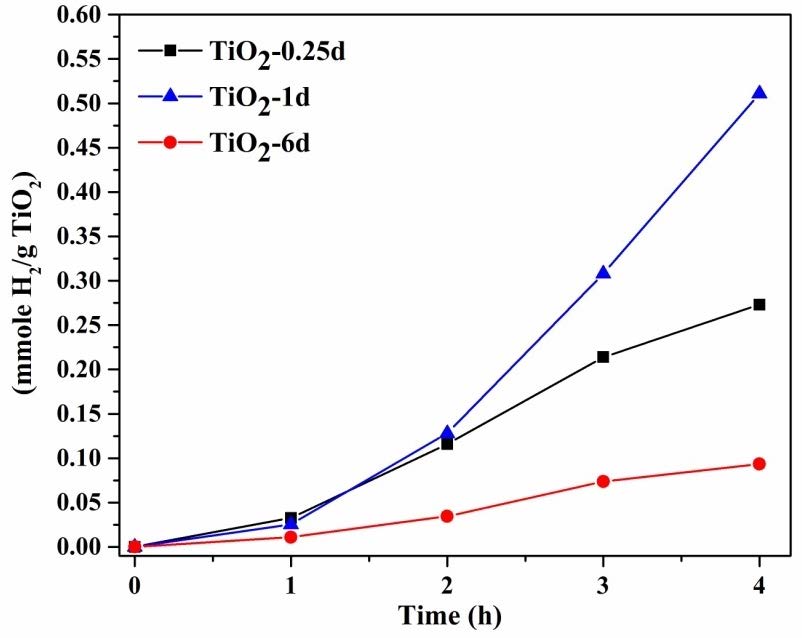
The photocatalytic activity of the materials was investigated, and the results are shown in Figure 6. After four hours of irradiation, the activity is found to be in the order TiO2-1d > TiO2-0.25d > TiO2-6d.
TiO2-1d has 95% anatase and 5% rutile phases, whereas TiO2-0.25d has only anatase phase. TiO2-6d showed 29% anatase and 71% rutile. The conduction band edge of rutile is relatively more positive as compared to anatase, and the presence of excess rutile content is detrimental to photocatalytic activity [14]. These results suggest an optimal amount of rutile is conducive to enhanced activity.
The photocatalytic activity of TiO2 is dependent on the crystallinity, crystallite size, surface area, porosity, phase etc. Even though the crystallinity of TiO2-0.25d is higher than that of other materials prepared in this study, its activity is lower in comparison to the material, TiO2-1d. This may be due to its relatively low surface area. The crystallite sizes of the materials lie in a narrow range and cannot account for the differences in activity. The high activity of TiO2-1d may be attributed to its high specific surface area and most importantly because of the presence of an optimal amount of mixed phases of anatase and rutile that minimizes electron-hole recombination. The presence of mixed phases of titania has been shown to have important implications in photocatalysis. The synergistic effect in the material, TiO2-1d is due to the effective trapping and separation of the charge-carriers across the two different crystallite phases [14]. This has been observed previously and our results are consistent with prior observations.
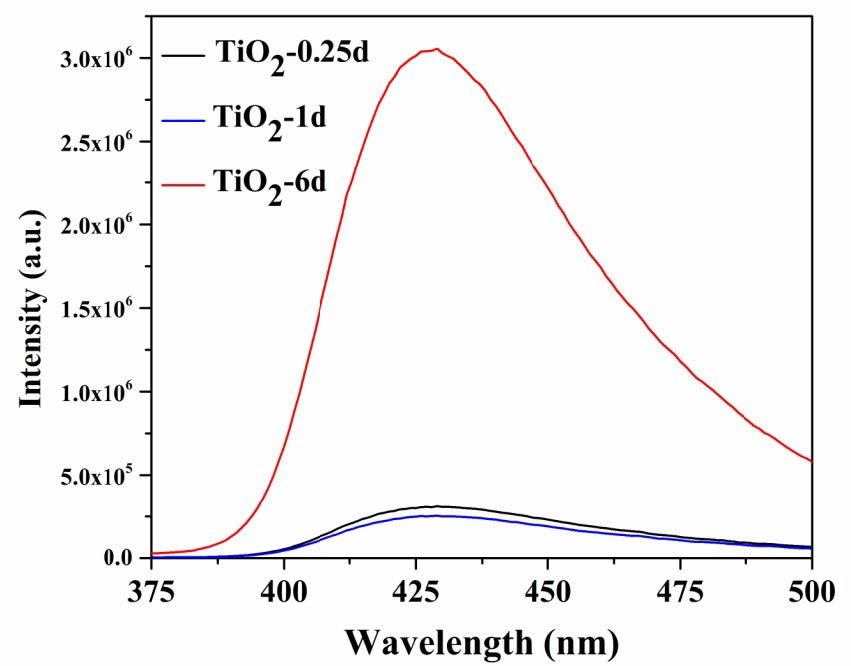
In order to understand the trends in photocatalytic activities, photoluminescence (PL) studies were carried out. PL experiments (Figure 7) confirm the trends in photocatalytic activities. TiO2-1d shows the least emission indicating that the recombination of electron-hole pairs are minimized the most in this material.
TiO2-6d show higher emission indicating enhanced recombination of the charge-carriers. The high rate of recombination of the charge-carriers results in low activity and the presence of large amounts of rutile is detrimental to its activity because its conduction band is located at relatively more positive values to the H+/H2 redox couple. The emission observed in the mesostructured titania materials are the characteristic emissions due to the recombination of free and bound excitons.
4. Conclusion
EISA is a versatile method for the preparation of hierarchical mesostructured TiO2. By changing the aging time, one can successfully prepare controlled amounts of mixed phases by using a convenient titania precursor and a readily available surfactant. A mixed mesostructured titania consisting of anatase (95%) and rutile (5%) showed high photocatalytic activity due to minimized electron-hole recombination and enhanced specific surface area. This facile method paves the way for the fabrication of hierarchical porous TiO2 for other applications such as degradation of dyes.
Acknowledgments
This work was supported by DE-EE-0000270, NSF-CHE-0722632, NSF-CHE-0840507, NSF-DGE-0903685, NSF-EPS-0903804, and SD NASA-EPSCOR NNX12AB17G. We are thankful to Dr. C.Y. Jiang for Raman studies.
Conflict of Interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: