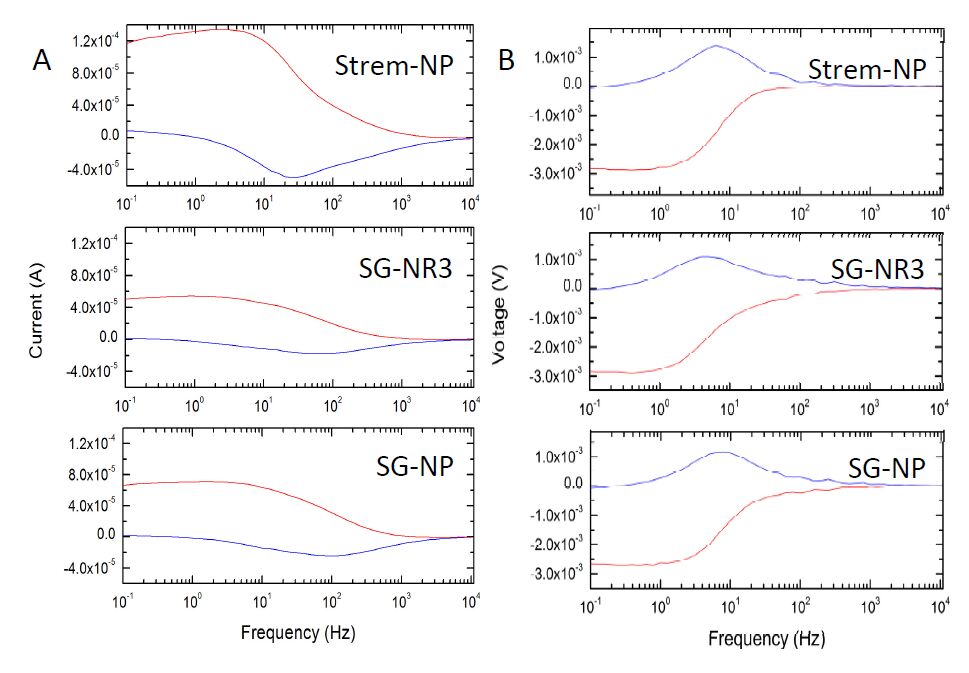
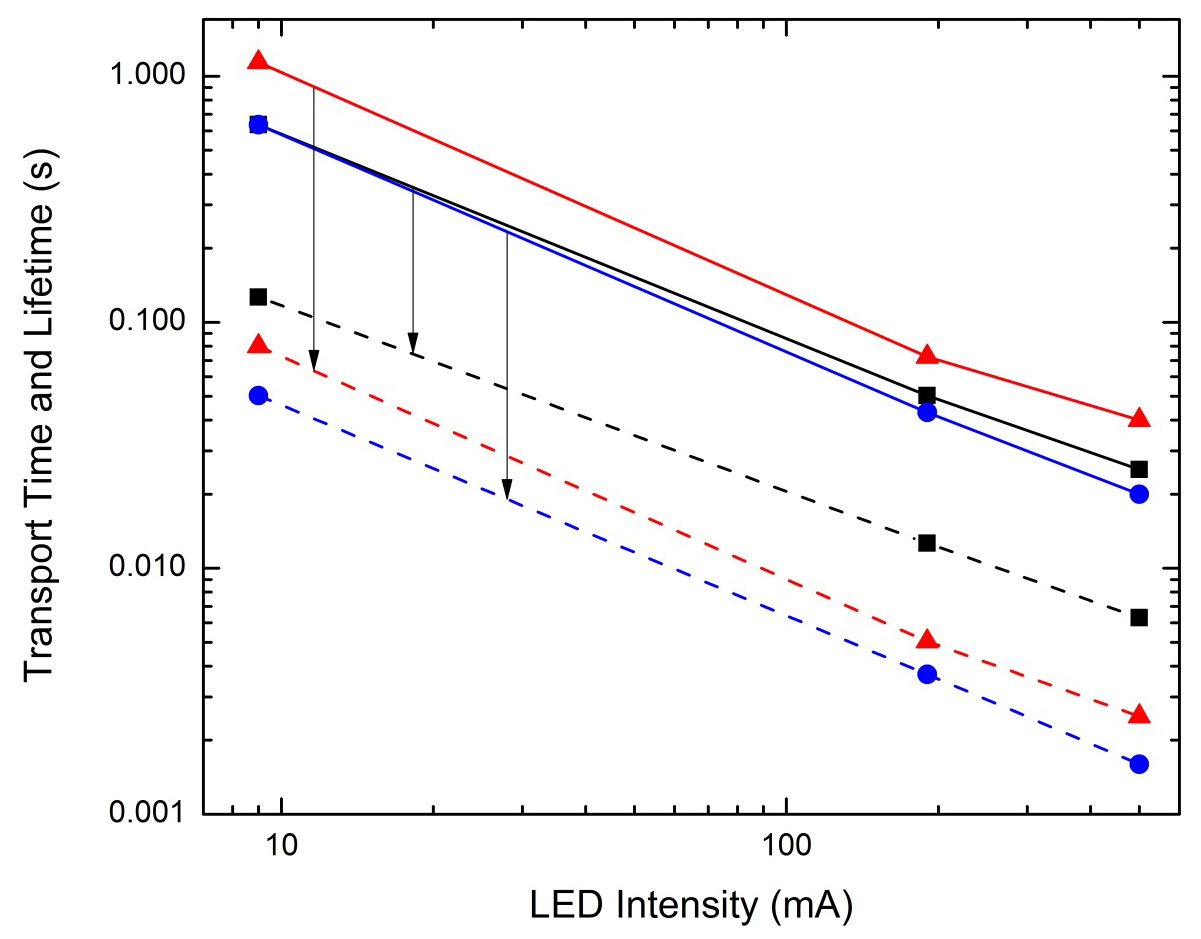
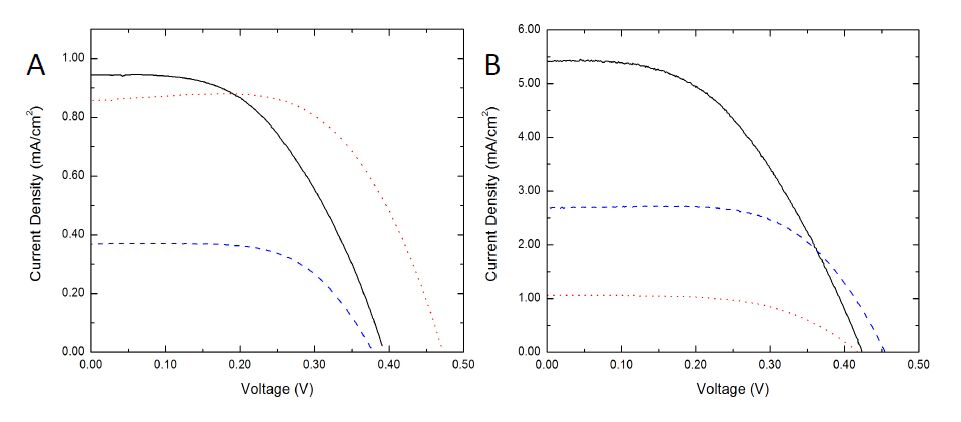
Owing to its high electron mobility, zinc oxide represents a promising alternative to titanium dioxide as the working electrode material in dye-sensitized solar cells (DSCs). When zinc oxide is grown into 1-D nanowire arrays and incorporated into the working electrode of DSCs, enhanced electron dynamics and even a decoupling of electron transport (τd) and electron lifetime (τn) have been observed. In this work, DSCs with working electrodes composed of solution-grown, unarrayed ZnO nanorods are investigated. In order to determine whether such devices give rise to similar decoupling, intensity modulated photocurrent and photovoltage spectroscopies are used to measure τd and τn, while varying the illumination intensity. In addition, ZnO nanorod-based DSCs are compared with ZnO nanoparticle-based DSCs and nanomaterial shape is shown to affect electron dynamics. Nanorod-based DSCs exhibit shorter electron transport times, longer electron lifetimes, and a higher τn/τd ratio than nanoparticle-based DSCs.
1.
Introduction
An important tool for describing the natural process is a system of fractional differential equations [1,2]. An ordinary system of fractional differential equations (FDEs) is described by
where $ a\in \mathbb{R}, $ $ \bf{q}:[0, a] \rightarrow \mathbb{R}^\nu $ is a $ \nu $-dimensional vector function and $ \bf{p}:[0, a]\times \mathbb{R}^\nu\rightarrow \mathbb{R}^\nu. $ Here, $ {^C_0D_t^{\alpha}} $ is the Caputo fractional derivative of order $ \alpha > 0. $
FDEs of the form (1.1) are used in an extensive amount of published papers for describing diverse evolutionary processes. Pollution model for lake [3], dynamical models of happiness [4] and Irving-Mullineux oscillaton [5] are among them.
A system of type (1.1) has at least $ n = \lceil \alpha\rceil $ (ceil of $ \alpha $) degree of freedom due to the presence of $ n $ the integer-order derivative. To have a unique solution more information of the system's states is required. In most applied problems this information on the boundary is known. These problems are referred to as boundary value problems. Initial value problems, terminal value problems (TVPs) and Sturm-Liouville problems are among boundary value problems. For initial value problems, the states of the system in the beginning time of the model are known. These states may include derivatives or more complex operators of the modeled process in the initial time. For initial value problems, the states of the system in the beginning time/point of the model are known. These states may include derivatives or more complex operators of the modeled process in the initial time. For terminal value problems, the system's states are known at the end terminal. However, for Sturm-Liouville problems states of the system are known in both initial and end boundaries. These systems have completely different dynamics and behaviors [6].
Adding boundaries information is not the only way to reduce the degree of freedom. For example, the information in the intermediate point/time can be used [7] for such a reduction. Such problems are known as intermediate value problems.
Recently, TVPs for fractional systems of the order less than one ($ 0 < \alpha < 1 $) have received some extensive attention and interest [8,9,10,11,12,13,14]. These problems can be described by
where $ D^{\alpha} $ is fractional derivative and $ \bf{q}_a $ is a given $ \nu $-dimensional vector. At the first glance, these systems seem to be well-posed with regular source functions [15,16]. Surprisingly, Cong and Tuan [17] revealed some counterexamples. The papers [14,18] pointed out that the well-posedness depends on the terminal value $ a. $ For larger $ a $ we may not obtain a unique solution.
Surprisingly, TVPs for fractional differential equations of higher-order derivatives $ \alpha\geq 1 $ are not well-studied. An order $ \alpha\in(1, 2] $ problem on an infinite interval have been studied in [19]. These problems have the form
where $ \bf{q}'(\infty)\in\mathbb{R} $ is a given number and $ {^C_{0}D_t^{\alpha}} $ stands for Caputo derivative.
This paper's important aim is to study the existence results and regularity of the higher-order terminal value problem for systems of FDEs. The other important aim of this paper is to introduce an analyzed high-order numerical method for solving such problems. Thus, the piecewise polynomial collocation method (PPCM) as a numerical solver is introduced and analyzed in detail.
The PPCMs have some superior advantages in solving differential or integral equations. For example, if we use polynomials collocation methods (known as spectral methods) we may encounter Runge-phenomena. The piecewise characteristic of the PPCMs avoids such probable divergence. In comparison with Runge-Kutta methods, the coefficient and parameters of the given methods are obtained constructively. It is remarkable to mention that for ordinary differential equations PPCMs, for some piecewise polynomial spaces are equivalent to Runge-Kutta methods. Conclusively, having more parameters (collocation parameters, degree of polynomial space, step size, meshing method) for controlling error, complexity and order of convergence makes the PPCMs competitively superior category of methods.
This paper is organized as follows: In Sections 2 and 3 we obtain the existence and uniqueness of a mild solution for higher-order FDEs. The regularity for the linear case is studied in Section 4. A numerical method is introduced in Section 5 and analysand in Section 6. Supportive numerical experiments are given in Section 7.
2.
Higher order terminal value problem
Consider the system (1.1) with terminal values
where $ n-1 < \alpha < n $ and $ n\in\mathbb{N}. $ The $ \nu $-dimensional vector function $ \bf{q} = [q_1, \ldots, q_\nu] $ is an unknown vector and $ \bf{q}^{(i)}_{a}\in\mathbb{R}^{\nu} $ ($ i = 0, \ldots, n-1 $) are known vectors.
Further, we impose the Lipschitz condition on components of the function $ \bf{p}:[0, a]\times \mathbb{R}^{\nu}\rightarrow \mathbb{R}^{\nu}. $ Thus, we suppose
where $ L_i $ ($ i = 0, \ldots, \nu $) are constants and are not depend on $ t. $ Let $ \bf{z} = \bf{q}^{(n-1)}, $ ($ \bf{z}' = \bf{q}^{(n)} $). Taking repeatedly integrals and using terminal values, we obtain
By definition of Caputo derivative, we have
Acting Riemann-Liouville integral $ {_0J^{\alpha-n+1}_t} $ on both sides of Eq (1.1), we obtain
Finally, putting $ t = a $ and using terminal conditions, we obtain
Remark 1. The solution of the coupled system of (2.2) and (2.4) can be regarded as a mild solution of the system (2.1).
3.
Existence of a unique solution
Since we use vector functions, we need a norm combined with vector norm and function norm. This combinations brings us to face complexity in calculating induced norm. In this respect, the max norm defined by
seems to be more easier. We establish well-posedness of the inverse problems (1.1) and (2.1). We define the operators $ \mathcal{P} $ and $ \mathcal{Q}:(\mathcal{C}[0, a])^{2\nu} \rightarrow (\mathcal{C}[0, a])^\nu $ by the right hand sides of systems (2.2) and (2.4), i. e.,
and
Let $ \mathcal{P}_i $ and $ \mathcal{Q}_i:(\mathcal{C}[0, a])^{2\nu} \rightarrow \mathcal{C}[0, a] $ be the $ i $th component of the operator $ \mathcal{P} $ and $ \mathcal{Q}, $ respectively. Setting $ \bf{w} = [\bf{q}, \bf{z}] $ and defining the operator $ \mathcal{T}:\mathbb{R}^{2\times \nu}\rightarrow \mathbb{R}^{2\times \nu} $ by
the Eqs (2.2) and (2.4) can be compactly written as
It is straightforward to show that for $ \bf{w}_1 $ and $ \bf{w}_2\in (\mathcal{C}[0, a])^{2\nu}. $ We can write
and
where $ L_M = \max_{i = 1, \ldots, \nu} L_i. $ Now, the Eqs (3.4) and (3.5) give
Conclusively, we can estate the following theorem.
Theorem 3.1. Let each component of the continuous function $ \bf{p}:[0, a]\times \mathbb{R}^{\nu}\rightarrow \mathbb{R}^{\nu} $ ($ \nu\in \mathbb{N} $) satisfy the Lipschitz condition with the Lipschitz constant $ L_i $ and let
Then, the problem (1.1) with terminal conditions (2.1) has a unique mild solution on $ (\mathcal{C}[0, a])^{2\nu} $ if
Proof. Suppose $ \bf{w}\in (\mathcal{C}[0, a])^{2\nu}. $ Since all integral operators involving in the definition of $ \mathcal{T} $ transform a continuous functions into a continuous functions, therefore, $ \mathcal{T}(\bf{w})\in (\mathcal{C}[0, a])^{2\nu}. $ The operator $ \mathcal{T} $ is contractor by (3.6) and the space $ (\mathcal{C}[0, a])^{2\nu} $ is a Banach space by the norm $ \|.\|_{\infty}. $ Thus, by contraction mapping theorem $ \bf{w} = \mathcal{T}(\bf{w}) $ has a unique solution which completes the proof.
The next corollary is an important result of Theorem 3.1 which shows the regularity of the solution on more smooth spaces.
Corollary 1. Suppose the hypotheses of Theorem 3.1 are satisfied. Then, the mild solution $ \bf{q} $ obtained from solving systems (2.2) and (2.4) satisfies the system (1.1) with terminal conditions (2.1). Moreover,
Proof. Taking derivative from Eq (2.2) and using Theorem 3.1 results $ \bf{q}^{(n-1)} = \bf{z}\in (\mathcal{C}[0, a])^{\nu}. $ Thus, $ \bf{q}\in (\mathcal{C}^{n-1}[0, a])^{\nu}. $ Similarly, putting $ t = a $ in Eq (2.2) and its derivatives, proves that $ \bf{q} $ satisfies terminal conditions. Replacing $ \bf{z} = \bf{q}^{(n-1)} $ in (2.2) we obtain
where $ {_a \mathcal{J}_t^{\alpha-n+1}} $ is the Riemann-Liouville fractional integral. Noting that $ \alpha-n+1 > 0 $, we can take a fractional derivative of order $ \alpha-n+1 $ from (3.8) to obtain
which shows that the component $ \bf{q} $ of the mild solutions satisfies (1.1).
4.
Regularity for linear FDEs
The regularity of the solution is important for analyzing numerical methods, especially finite difference methods and methods based on projection [20]. The regularity speaks about the order of differentiability of solutions. Usually, the regularity is investigated in the space $ \mathcal{C}^m[a, b], $ (see Corollary 1). But, some good functions such as $ \sqrt{t}\in \mathcal{C}[a, b] $ do not belong to $ \mathcal{C}^m[a, b]. $ The space $ \mathcal{C}^m(a, b]\cap \mathcal{C}[a, b] $ contains such functions. This space is not Banach or complete. Therefore, we need to introduce another Banach space such that
In this paper, we study regularity on the following weighted space $ {\mathcal{C}}^{m, \alpha}(0, a] $ introduced in [13].
Definition 4.1. [13] Let $ 0\leq \alpha < 1 $ and $ m\in \mathbb{N}. $ Then $ q\in {\mathcal{C}}^{m, \alpha}(0, a] $ if there exist functions $ q_i\in {\mathcal{C}}[0, a] $ for $ i = 0, \cdots, m+1 $ such that $ q = t^{\alpha} q_0+q_1 $ and
Theorem 4.2. The space $ {\mathcal{C}}^{m, \alpha}(0, a] $ with the norm
is a Banach space.
Proof. Let $ {q_{n}}\in {\mathcal{C}}^{m, \alpha}(0, a], $ $ n\in\mathcal{N} $ be a Cauchy sequence with norm $ \|.\|_{\alpha, m}. $ Thus, by the definition of $ {\mathcal{C}}^{m, \alpha}(0, a] $ there exists functions $ q_{n, i} $ in $ \mathcal{C}[0, a] $ for $ i = 0, \cdots, m+1 $ such that $ q_{n}(t) = t^{\alpha} q_{n, 0}(t)+q_{n, 1}(t) $ and
From the definition of the norm $ \|.\|_{\alpha, m}, $ the sequences $ q_{n, i} $ for a fixed $ i $ are Cauchy sequence in the Banach space $ \mathcal{C}[0, a] $ and thus have a unique limit say $ q_{i}. $ Let $ q $ defined by $ q(t) = t^{\alpha} q_0(t)+q_1(t) $ on $ [0, a]. $ Following items show that $ q\in {\mathcal{C}}^{m, \alpha}(0, a]. $
● $ \lim_{n\rightarrow \infty} q_n(t) = \lim_{n\rightarrow \infty} t^{\alpha} q_{n, 0}(t)+q_{n, 1}(t) = t^{\alpha} q_0(t)+q_1(t) = q $ for all $ t\in [a, b]; $
● $ q\in \mathcal{C}[0, a], $ since $ q_0\in \mathcal{C}[0, a] $ and $ q_1\in \mathcal{C}[0, a]; $
● $ \lim_{n\rightarrow \infty} D^{i}q_n(t) = \lim_{n\rightarrow \infty} t^{\alpha-i}q_{n, i+1}(t) = t^{\alpha-i}q_{i+1}(t). $ For each $ t\in(a, b] $ we can find $ \epsilon > 0 $ such that $ D_{\epsilon} = [t-\epsilon, t]\subset (a, b]. $ It is trivial that $ D^{i}q_n(t) $ converges uniformly to $ t^{\alpha-i}q_{i+1}(t) $ on $ D_{\epsilon} $. According to Theorem 7.17 of [21] $ D^{i}q(t) = \lim_{n\rightarrow \infty} D^{i}q_n(t) $ on $ D_{\epsilon}. $ Thus $ D^{i}q(t) = t^{\alpha-i}q_{i+1}(t) $ for all $ t\in D_\epsilon $ and hence for all $ t\in (a, b]. $
Let $ \nu\in \mathbb{N}. $ For a $ \nu $ dimensional vector functions, $ \bf{p} = [f_1, \ldots, f_{\nu}] $ in $ ({\mathcal{C}}^{m, \alpha}(0, a]\subset ({\mathcal{C}}^{m}(0, a])^{r}, $ we use the max norm defined by
The system (1.1) with
is a system of linear FDEs. Here $ A $ is a given $ \nu\times \nu $ dimensional matrix function and $ \bf{b}\in (\mathcal{C}[0, a])^\nu $ is a given source function. To study linear systems we introduce the operators $ \mathcal{W}_1 $ and $ \mathcal{W}_2:(\mathcal{C}[0, a])^{2\nu} \rightarrow (\mathcal{C}[0, a])^\nu $ by
and
Let us also define the vector valued functions $ \mathcal{G}_2 $ and $ \mathcal{G}_1:[0, a] \rightarrow \mathbb{R}^\nu $ by
and
Let $ \bf{T} = [\mathcal{W}_1, \mathcal{W}_2]^T $ and $ \mathcal{G} = [\mathcal{G}_1, \mathcal{G}_2]^T $. Then, the Eqs (2.2) and (2.4) can be written as an inhomogeneous system
where $ \bf{w} = [\bf{q}, \bf{z}]^T. $
Theorem 4.3. Let $ a\in\mathbb{R} $ and $ \alpha > 0. $ Assume each component of $ A $ and $ b $ are in $ {\mathcal{C}}^{m, \alpha}(0, a]) $ and the hypotheses of Theorem 3.1 are satisfied for related $ \bf{p}:[0, a]\times \mathbb{R}^{\nu}\rightarrow \mathbb{R}^{\nu} $ ($ \nu\in \mathbb{N} $).Then, the problem (1.1) with terminal conditions (2.1) has a unique mild solution on $ ({\mathcal{C}}^{m, \alpha}(0, a])^{2\nu}. $
Proof. Since $ \bf{T} $ is a combination of weakly singular integral operators, it is a compact linear operator on $ (\mathcal{C}[0, a])^{2\nu} $ and $ ({\mathcal{C}}^{m, \alpha}(0, a])^{2\nu} $. Also, it is clear that
System (25) has a unique solution on $ (\mathcal{C}[0, a])^{2\nu} $ by Theorem 3.1. Therefore, the homogeneous system $ \bf{w}-\bf{T}(\bf{w}) = 0 $ has the trivial null space in $ (\mathcal{C}[0, a])^{2\nu} $ and thus $ ({\mathcal{C}}^{m, \alpha}(0, a])^{2\nu}. $ Conclusively, alternative Fredholm theorem asserts that the system (4.7) has a unique solution on $ ({\mathcal{C}}^{m, \alpha}(0, a])^{2\nu}. $
Remark 2. Regularity of the nonlinear case needs further investigations.
Example 1. Consider the system (1.1) with $ a = 0.5, $ $ \alpha = 2.5 $ and $ \bf{p} $ defined by (4.2)
Obviously, $ L_1 = 0.5, $ $ L_2 = 0.5. $ and thus $ L_M = 0.5. $ Therefore,
and Condition (3.7) holds. By Theorem 3.1 the terminal value problem (1.1) with arbitrary terminal value (2.1) has a unique solution on $ \mathcal{C}[0, a] $. Since all components of $ A $ and $ \bf{b} $ belong to $ {\mathcal{C}}^{m, \alpha}(0, a], $ ($ m\in\mathbb{N} $) the mild solution belongs to $ ({\mathcal{C}}^{m, \alpha}(0, a])^4, $ by Theorem 4.3. Furthermore, we obtain the regularity of the solution of the system (1.1) on the closed interval $ [0, a] $ by Corollary 1 and we have
5.
Numerical method
Considering the memory, one of the best methods for solving the coupled systems (2.2)–(2.4) is to use collocation methods on piecewise polynomial spaces. To implement such methods we partition the solution interval $ [0, a] $ into sub-intervals $ \sigma_i = [t_{i}, t_{i+1}], $ $ i = 0, \ldots, N-1, $ with length $ h_i: = t_{i+1}-t_i $ where $ 0 = t_0 < \ldots < t_{N} = a $ are nodes of a chosen mesh (uniform or graded mesh) and $ N\in \mathbb{N}. $ A graded mesh with exponent $ r\geq1 $ is described by
Let $ 0 < c_1 < \ldots < c_m\leq 1 $ ($ m\in\mathbb{N} $) be collocation parameters, $ t_{n, i} = t_n+c_ih_n $ ($ n = 0, \ldots, N-1 $) be collocation points and let $ \hat{\bf{q}}_N(t) $ and $ \hat{\bf{z}}_N(t) $ be approximate solutions. The restriction of approximate functions to the $ \sigma_k $ is fully determined by Lagrange polynomials interpolation formula
and
where $ Q_{k, j} = \hat{\bf{q}}_N(t_{n, j}), $ $ Z_{k, j} = \hat{\bf{z}}_N(t_{k, j}), $ $ t_{k, j} = t_k+hc_j $ and $ L_j $ ($ j = 1, \ldots, m $) are Lagrange polynomials of degree $ m-1. $ The integrals in the operators $ \mathcal{P} $ and $ \mathcal{Q} $ of systems (3.1) and (3.2) can be discretized as:
where
For $ t\in [t_k, t_{k+1}] $ ($ k = 0, \ldots, N-1 $) we have
where
and
Similarly, we discretize integrals of the operator $ \mathcal{Q}. $ We have
By interpolating $ \bf{p}(t_l+sh_l, \bf{q}(t_l+sh_l)) $ on $ c_i $ we obtain
and thus
where
and finally
where
The discretized mappings $ \mathcal{P}_N $ and $ \mathcal{Q}_N:(\mathcal{C}[0, a])^{2\nu} \rightarrow (PC[0, a])^\nu $ ($ PC $ stands for piecewise continuous space) related to systems (3.1) and (3.2) can be defined by
and
on $ \sigma_k. $ Setting $ \mathcal{T}_N = [\mathcal{P}_N, \mathcal{Q}_N], $ unknowns vectors $ Q_{l, j} $ and $ Z_{l, j} $ can be obtained by solving the nonlinear system
for $ k = 0, \ldots, N-1 $ and $ o = 1, \ldots, m. $ Taking into account that
the dense solution can be evaluated in all points of the desired interval by Eqs (5.1) and (5.2). We note that the six parameters $ \gamma_{n, i, l, j}, $ $ \eta_{n, l, j}, $ $ \bar{\eta}_{n, k, j}, $ $ \varrho_{n, l, j}, $ $ \zeta_{n, l, j} $ and $ \bar{\zeta}_{n, k, j} $ fully determines the method for each $ m $. The equations of these six parameters for $ m = 1 $ and $ m = 2 $ are provided in Tables 1 and 2, respectively.
6.
Numerical analysis
For simplifying our analysis we recall some notations. Let $ S_{m-1}^{-1}(I_h) $ be the space of piecewise polynomials of degree less than $ m, $ ($ m\in \mathbb{N} $) on the mesh partitioning $ I_h = \{t_i:\; i = 0, \cdots, N\}. $ The projection operator $ \Pi_{m-1, N}:({\mathcal{C}}[0, a])^{2\nu}\rightarrow \left(S_{m-1}^{-1}(I_h)\right)^{2\nu} $ is uniquely determined by interpolation on collocation points such that
Since $ \hat{\bf{w}}_N(t): = [\hat{\bf{q}}_N(t), \hat{\bf{z}}_N(t)]\in \left(S_{m-1}^{-1}(I_h)\right)^{2\nu} $ we have
Thus, Eq (5.10) can be written as
A useful theorem regarding $ \Pi_{m-1, N} $ that simplifies existence and convergence analysis is the following theorem.
Theorem 6.1. Let $ m, N\in\mathbb{N}. $ Then, $ \Pi_{m-1, N} $ is a bounded linear operator. Let
be induced norm of $ \Pi_{m-1, N} $ and
Then, $ \Lambda\leq \Lambda_1 $ and
Proof. In each sub-interval $ \sigma_n $ of $ [0, a] $ by Lagrange interpolation formula, we have
The rest of the proof is straightforward by taking the max norm.
6.1. Existence results for the proposed numerical method
One of the most fundamental questions is whether the system (6.1) has a unique solution? The answer is affirmative. For $ \hat{\bf{w}}_N(t) $ in $ \left(S_{m-1}^{-1}(I_h)\right)^{2\nu} $ the operators $ \mathcal{P}_N $ of (5.8) and $ \mathcal{P} $ of (3.1) are equivalent and we have
Thus, the inequality (3.4) holds for $ \mathcal{P}_N $ and
for all $ \bf{w}_1, \bf{w}_2\in\left(S_{m-1}^{-1}(I_h)\right)^{2\nu}. $ However, $ \mathcal{Q}_N $ is different from $ \mathcal{Q} $ in this space and we need further computing. Actually, $ \mathcal{Q}_N $ can be described by
where $ \bf{q} $ is the first $ \nu $ element of $ \bf{w}. $ More precisely
Therefore,
Theorem 6.2. Let
Then, the numerical solution of system (1.1) obtained by (6.1) exists and is unique.
Proof. The operator $ \Pi_{m-1, N} \mathcal{T}_N:\left(S_{m-1}^{-1}(I_h)\right)^{2\nu}\rightarrow \left(S_{m-1}^{-1}(I_h)\right)^{2\nu} $ is a contractor by (6.7). Thus, by using contraction mapping theorem, $ \Pi_{m-1, N} \mathcal{T}_N $ admits a unique fixed-point.
Remark 3. Obviously, if
holds, then Eq (6.8) holds too. For $ m = 1 $ we have $ \Lambda_1 = 1, $ and Eq (3) matches with Eq (3.7). However, our estimate may not be optimal for higher degrees of approximations. Also, we guess using the convergence properties of $ \Pi_{m-1, N} $ when $ N\rightarrow \infty, $ we may obtain a convergence result without dependency on $ \Lambda_1. $
6.2. Detailed implementation: Solving nonlinear system
An important question is how to solve the nonlinear Eq (6.1). There are many methods available in literature that we can employ. The Newton iteration method is one of them [14]. The advantage is that it is fast. The disadvantage is that it needs computation of Jacoby as well as a good initial value for an iteration. It increases competition cost for higher dimension (computation of $ \nu^2 $ function for each iteration) and complexity of the implementation. However, strict restriction of $ \lambda_\Lambda $ and analytic discussion of the previous section is constructive and suggests the use of an iterative method. Since the operator $ \Pi_{m-1, N} \mathcal{T}_N $ is a contractor operator, beginning with an arbitrary initial value grantees the convergence of the related iterative method. In our algorithm, we initialize the iteration by
Then, we estimate the solution by the recursive formula
The computation of iteration (6.10) continues with the smallest $ \kappa $ such that
where $ Tol $ is a desired user tolerance. We report such $ \kappa $ as a number of iteration to achieve the given tolerance.
6.3. Convergence analysis
Theorem 6.3. Suppose $ \hat{\bf{w}}_N = [\hat{\bf{w}}_N, \hat{\bf{w}}_N] $ ($ N\in\mathbb{N} $) be a discretized collocation solution of (2.2) and (2.4) described by (6.1). Let the conditions of Theorems 3.1 and 6.2 be fulfilled. Then, the coupled systems (2.2) and (2.4) have a unique solution $ \bf{w} $ on $ (\mathcal{C}[0, a])^{2\nu} $ and the $ \hat{\bf{w}}_N $ converges to the $ \bf{w}. $ Furthermore, supposing $ \bf{w}\in ({\mathcal{C}}^{m, \alpha}(0, a])^{2\nu} $ implies
Proof. Let $ \bf{w} $ be the solution of the coupled systems (2.2) and (2.4). Define the residue operator by
and let $ \bf{e} = \hat{\bf{w}}_N-\bf{w}. $ Subtracting Eq (3.3) from (6.1), we obtain
Taking maximum norm, we obtain
Applying Eq (6.8), we obtain
and finally
This is a good news since we can obtain the asymptotic behavior of $ \|R(\bf{w})\|_{\infty} $ for the known $ \bf{w}. $ Thanks to Theorem 8 of [20], one can easily prove that
which completes the proof.
7.
Examples
All numerical experiments is implemented in MATLAB software. The tolerance number for solving related nonlinear equations is $ Tol = 10^{-14}. $ This tolerance is close to the floating-point relative accuracy $ 2.2204e-16 $ for data type of double-precision (64 bit) in standard machine. The numerical examples show theoretically the obtained order of convergence is sharp and can not be improved more.
Example 2. Let $ 1 < \alpha\leq 2 $ and
on $ [0, 0.15]. $ We note that $ \bf{p}(t, .)\in (\mathcal{C}[0, 0.25])^{2} $ but $ \bf{p}(t, .)\notin (\mathcal{C}^1[0, 0.25])^{2}. $ Since $ L_M = 0.1, $ one can check that the conditions of Theorem 3.1 for $ a = 0.25 $ hold and the system (2.1) with boundary condition
and
has a unique solution on $ [0, a]. $ The solution by Corollary 1 belongs to $ (\mathcal{C}^1[0, a])^2. $ We apply a numerical method based on collocation parameter $ c = [0.5, 1]. $ Thus, the dense solution on each sub-interval $ \sigma_k $ ($ k = 0, \cdots, N-1 $) of a given partition can be described by
An estimated norm of the given method can be determined by (6.2) and we have
Taking into account (6.8), we obtain
Consequently, by using Theorem 6.2 the nonlinear Eq (6.1) has a unique solution and the iteration process (6.10) converges to that solution. Theorem 6.3 implies the numerical solution converges to the exact solution by following order ($ \mathrm{O} $)
In Tables 3 and 4, we provided the maximum error
estimated order of proposed method ($ O_N $) and the number of iteration for required tolerance. As we see $ O_N = 0.5, 1, 1.5, 2 $ for $ r = 1, 2, 3, 4 $ respectively, which is in agreement with theoretical result (see Eq (7.2)).
Remark 4. Theorem 1 provides a sharp result when we consider all the components of the state of the system 1 ($ \bf{w} = [\bf{q}, \bf{z}] $). However, it can be improved for the desired state of the solution $ \bf{q}. $ According to Corollary 1, $ \bf{q} $ has better regularity for $ n\geq 1. $ Thus, we guess that the order of convergence for $ \bf{q} $ component with uniform mesh $ r = 1, $ can be greater than or equal to $ n-1. $ Thus, for that component, a greater graded mesh exponent is not necessary. The error $ E_{\bf{q}}(r, N) = \|\hat{\bf{q}}_N-\bf{q}\|_{\infty} $ and the estimated order of convergence of Example 2 is reported in Table 5. The order $ 2 $ is achieved with $ r = 1.5 $.
To show the sharpness of theoretical results, we add numerical experiments for the case $ m = 1 $ with $ c = 0.5 $ (for other choice of $ c $ on $ [0, 1] $ we have similar results). The dense solution on each sub-interval $ \sigma_k $ can be described by
In this case $ \Lambda_1 = 1 $ and by (6.8)
Consequently, by using Theorem 6.2 the nonlinear Eq (6.1) related to $ m = 1 $ has a unique solution and the iteration process (6.10) converges to the exact solution. By Theorem 6.3 we expect
The sharpness of this result can be seen in Table 6.
Remark 5. The low order method have the advantage of supporting larger class of terminal value problem with large value of $ a $. The reason is that with $ m = 1, $ we have $ \Lambda_1 = 1 $ which is three times smaller than $ \Lambda_1 $ for the case $ m = 2. $
8.
Conclusions
TVPs for higher-order (greater than one) fractional differential equations are rarely studied in the literature. In this paper, we tried to have a comprehensive study with a simple analysis to cover all general interests. Many questions in this topic deserve to study with more scrutiny. The regularity of nonlinear cases as well as optimal bound for obtaining well-posed problems are among them. We think the terminal value problem is important in applied since it monitors the past evolution of a dynamical system. Also, it can be regarded as a control problem for having the desired future by finding suitable initial value. We think this topic will catch more interest similar to the initial value problem.
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: