We consider a model for a disease with
two competing strains and vaccination.
The vaccine provides complete protection against one of the strains
(strain 2) but only
partial protection
against the other (strain 1). The partial protection leads to
existence of subthreshold equilibria of strain 1. If the first strain
mutates into the second, there are subthreshold coexistence equilibria
when both vaccine-dependent reproduction numbers are below one.
Thus, a vaccine that is specific toward the second strain
and that, in absence of other strains, should be able to eliminate
the second strain
by reducing its reproduction number below one,
cannot do so because it provides only
partial protection to another strain that mutates into the second strain.
1.
Introduction
Pancreatic cancer is a malignancy with a very poor prognosis, as the number of its new cases almost equals to related deaths [1]. The major type of pancreatic tumors is pancreatic ductal adenocarcinoma (PDAC), where metastasis is present in most cases, leading to an extremely low 5-year survival rate [2]. PDAC samples can be classified into four major molecular subtypes including squamous, pancreatic progenitor, immunogenic, and aberrantly differentiated endocrine exocrine (ADEX) subtypes, and squamous subtype had the worse prognosis [3]. Meanwhile, it has been demonstrated that PDAC patient with isolated liver metastases exhibited worse overall survival when compared to those with other sites of metastases [4]. Thus, for patients with PDAC, it is of great importance to investigate molecular mechanism behind liver-metastatic behaviors and identify markers to assess the risks of metastasis.
So far, several researches have focused on demonstrating the genomic changes behind metastatic PDAC. Unique gene expression profiles were uncovered between liver and peritoneal metastatic PDAC cell lines, suggesting that different mechanisms were involved when site-specific metastases were present [5]. Aberrant expression of Zeb1, EphA2, DPC4 and MKK4 was found to be associated with metastatic pancreatic cancers [6,7], and dysregulated PRDM14 expression was confirmed to affect liver metastasis in mice [8]. Notably, Zeb1 is a key transcription factor promoting epithelial-mesenchymal transition (EMT) in pancreatic cancer [9]. Moreover, metastatic PDAC is often accompanied with an immunosuppressive tumor microenvironment (TME), and evidences suggest that stemness and differentiation of pancreatic ductal epithelial cells were associated with inflammatory cytokines in the hepatic microenvironment [10]. For example, interleukin (IL)-1α, a cytokine that mostly secreted by macrophages, were found to induce metastasis in PDAC, while a recent study has reported an association between macrophage-derived granulin and CD8+ T cell infiltration in PDAC metastatic tumors [11]. Pharmacological depletion of macrophages was deemed effective in reducing metastatic behavior in mice with pancreatic cancer [12]. However, molecular mechanisms possibly underlying altered macrophage secretion and infiltration are seldom addressed, thus it is of great necessity to explore significantly dysregulated genes in varied types of immune cells in the metastatic TME of PDAC patients [13]. In the present study, we focused on exploring the RNA signatures of liver metastasis in PDAC, anticipated to identify a set of liver metastasis-related genes, evaluate their prognostic values, and reveal key cell types involved in liver metastasis of PDAC.
2.
Materials and methods
2.1. Data acquisition
We collected four gene expression datasets including The Cancer Genome Atlas [14] (TCGA), GSE151580, GSE71729 [15] and E-MTAB-6134 [16] from UCSC Xena (https://xena.ucsc.edu/), Gene Expression Omnibus (GEO, https://www.ncbi.nlm.nih.gov/geo/), and ArrayExpress (https://www.ebi.ac.uk/arrayexpress/), for the systematic data analysis, respectively. The detailed clinical characteristics of the PDAC samples were summarized in Table 1. The first two gene expression datasets were used to identify liver metastasis-related genes. The RNA-seq data were normalized to FPKM or TPM, and the microarray data were pre-normalized by previous studies. Moreover, we also collected the cell types and their specific marker genes from previous study [17].
2.2. Differential expression analysis
The two-sample comparison was conducted to identify differentially expressed genes, and the differential gene expression levels were test by t test and fold changes. The thresholds of P-value and log2 (fold change) were selected at 0.01 and 0.25.
2.3. Gene set overrepresentation and enrichment analysis
The Gene set overrepresentation enrichment analysis was used to test the degree of overlapping genes between two gene sets. The gene set enrichment analysis was employed to test whether the gene set of interest was expressed at the lowest or highest order of all the genes ranked by a specified statistic. The two analyses were implemented in R clusterProfiler [18] package.
2.4. Calculation of liver metastasis score using single-sample gene set enrichment analysis (ssGSEA)
The liver metastasis score was calculated using single-sample gene set enrichment analysis (ssGSEA) [19], which defines an enrichment score that represents the degree of absolute enrichment of a gene set in each sample within a given data set. The enrichment score, a variant of Kolmogorov-Smirnov statistic, was proposed by the previous study [20]. The ssGSEA was implemented in R GSVA [21] package.
2.5. Cox proportional hazard regression analysis
The overall survival time and status, and the liver metastasis score were used as the response and predictor variables for the Cox proportional hazard regression model. The Cox model was fitted using R survival [22] package (https://cran.r-project.org/web/packages/survival/index.html), and visualized by R survminer package (https://cran.r-project.org/web/packages/survminer/index.html). The log-rank test was employed to test the difference of survival time between the two groups.
2.6. Statistical analyses
The statistical analysis was implemented in R-4.0.2. The two-sample comparisons were performed by Wilcoxon rank-sum test or student-t test. Multiple-sample comparisons were performed by analysis of variance (ANOVA) or Kruskal-Wallis test. P-value of 0.05 was indicated as statistical significance.
3.
Results
3.1. Identification of liver metastasis-related genes in pancreatic ductal adenocarcinoma (PDAC)
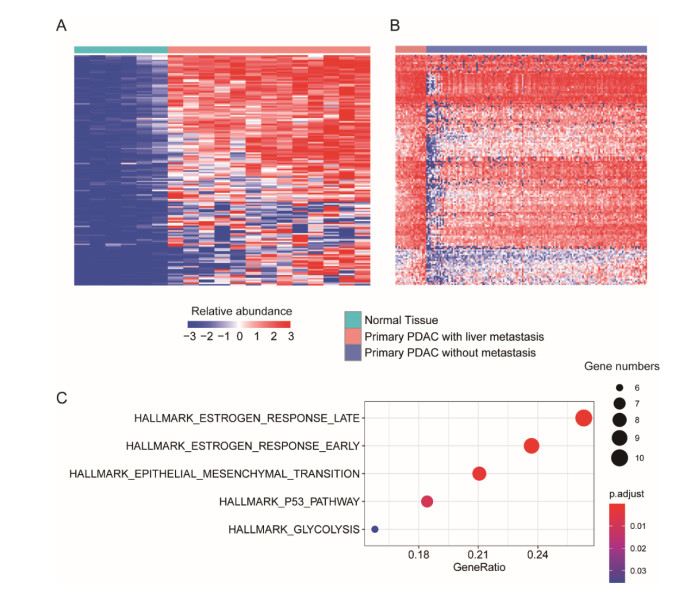
To identify the liver metastasis-related genes in PDAC, we conducted a systematic analysis of two gene expression datasets. Specifically, we compared the primary tissues of liver-metastatic PDAC patients with those of PDAC without liver metastasis using TCGA cohort [14] (n = 182). Moreover, the primary tissues of liver-metastatic PDAC patients were also compared with their adjacent normal tissues using GSE151580 cohort (n = 19). Totally, we identified 154 genes upregulated in primary tissues of liver-metastatic PDAC patients as compared with both primary tissues of PDAC patients without liver metastasis and adjacent normal tissues (P-value < 0.01 and log2 (fold change) > 0.25, Supplementary Table S1).
As shown in Figure 1A and 1B, the 154 genes had significantly different expression profiles between those tissues, and were termed as liver metastasis-related genes. Furthermore, the gene set enrichment analysis was conducted to characterize the biological function of those liver metastasis-related genes, and epithelia mesenchymal transition (EMT) was significantly enriched by those genes (Figure 1C, Supplementary Table S2), indicating that EMT was significantly associated with liver metastasis in PDAC. In addition, estrogen response, p53, and glycolysis pathways were also enriched by those genes, further suggesting their potential roles in the liver metastasis of PDAC.
3.2. A large proportion of liver metastasis-related genes was primarily regulated at epigenetic level
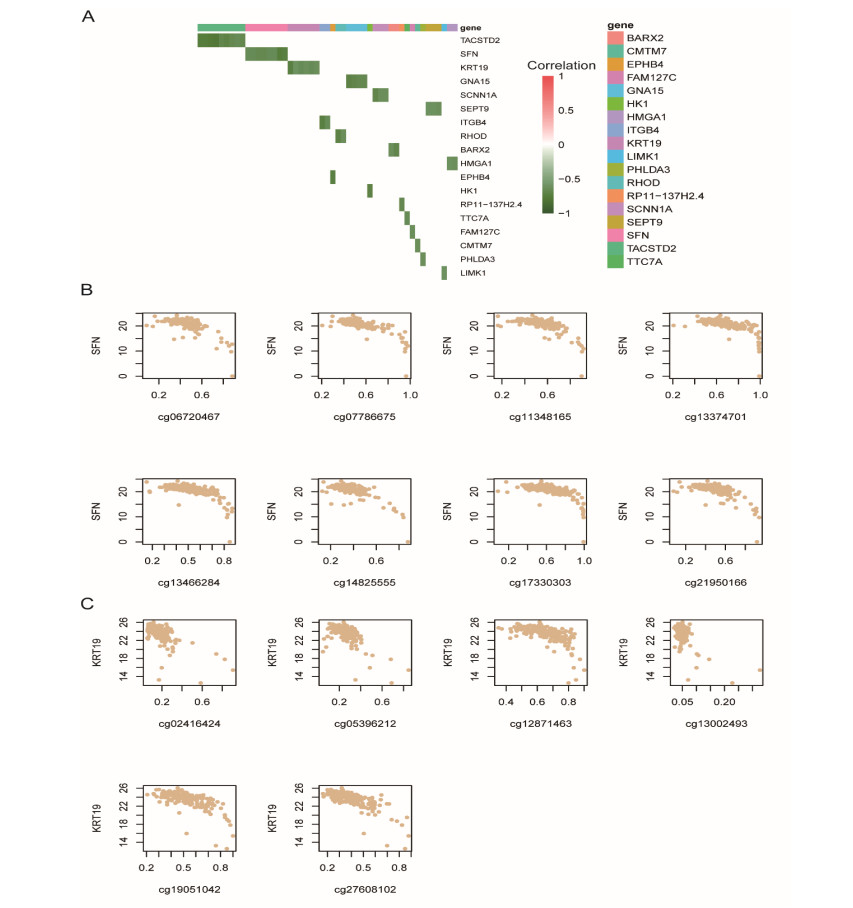
To further investigate whether the liver metastasis-related genes were regulated at epigenetic level, we conducted correlation analysis between the DNA methylation level within promoter regions and their corresponding target genes using TCGA cohort. Among the liver metastasis-related genes, 18 were predicted to be epigenetically regulated by their promoter DNA methylation at a stringent threshold (Figure 2A, correlation test, FDR < 0.05, n = 182). Notably, SFN (Stratifin), a gene encoding a cell cycle checkpoint protein [23], was reversely correlated with the DNA methylation levels of 8 sites, including cg06720467, cg07786675, cg11348165, cg13374701, cg13466284, cg14825555, cg17330303, and cg21950166, within the promoter (Figure 2B). Moreover, KRT19 (Keratin-19), a well-known marker for ductal cell [24], was also negatively correlated with its DNA methylation levels of 6 sites. These results suggested that DNA methylation acted as a pivotal role in the regulation of the liver metastasis-related genes.
3.3. The clinical significance of the liver metastasis-related genes in PDAC
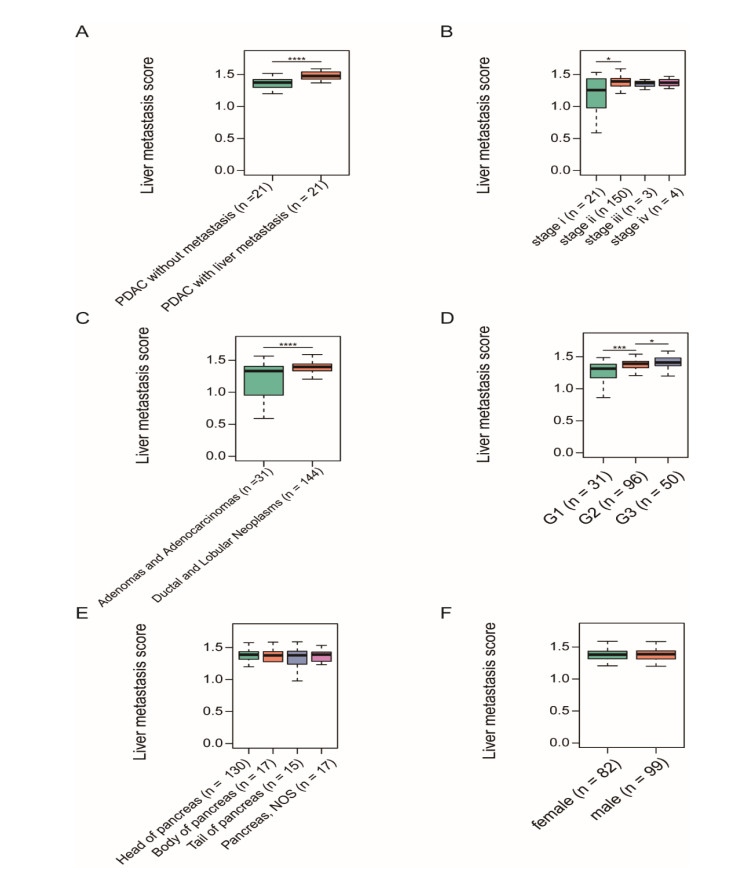
To reveal the association of the liver metastasis-related genes with the clinical characteristics of PDAC, we derived a liver metastasis score (LMS) based on the liver metastasis-related genes for TCGA PDAC patients. Specifically, the LMS of each PDAC patient was estimated by single-sample gene set enrichment analysis (ssGSEA). The PDAC patients with liver metastasis had significantly higher LMS than those without liver metastasis (Figure 3A, t test, P-value < 0.0001). Moreover, the LMS was observed lower in patients with stage I as compared with those with stage II (Figure 3B, P-value < 0.05). Furthermore, the comparative analysis of the disease types and tumor grades revealed that the ductal and lobular type had a higher liver metastasis score than adenomas and adenocarcinoma (Figure 3C, P-value < 0.0001), and higher LMS was observed in PDAC patients with higher grade (Figure 3D, P-value < 0.05), suggesting that patients with ductal and lobular type or higher grade might have a higher risk of liver metastasis. In addition, there were no significant associations of LMS with tumor sites and gender (Figure 3E, F). These results demonstrated that the LMS derived from liver metastasis-related genes was closely associated with the clinical characteristics of disease type and tumor grade in PDAC.
3.4. The prognostic significance of the liver metastasis-related genes in PDAC
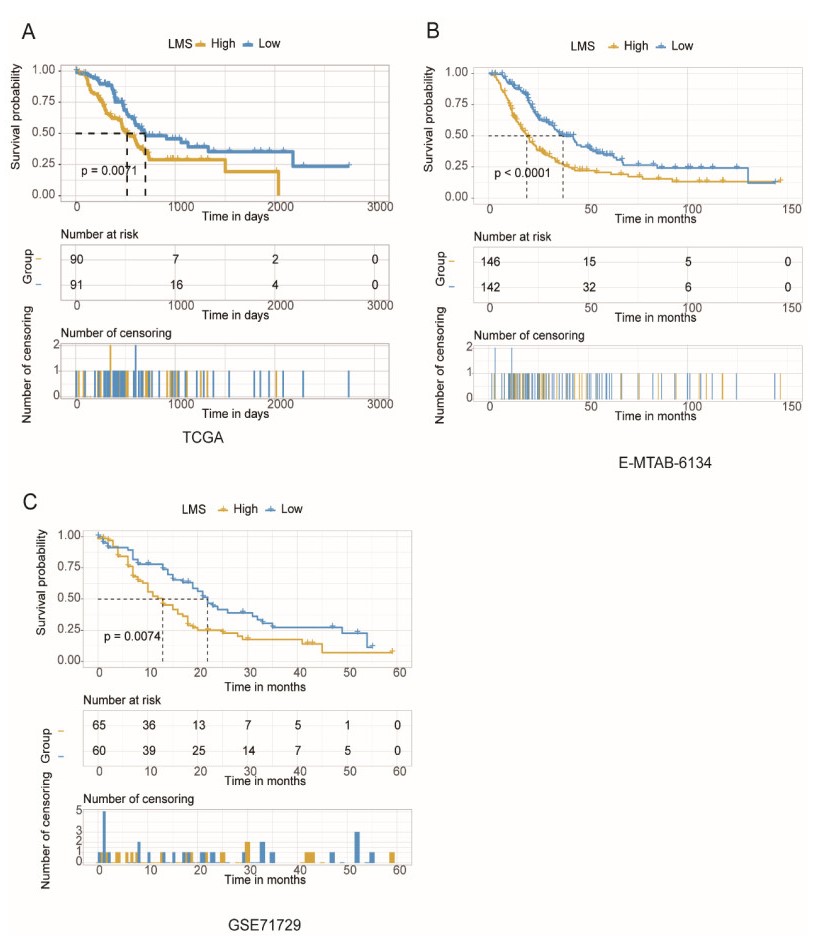
To evaluate the prognostic significance of the liver metastasis-related genes in PDAC, we built a Cox proportional hazard regression model based on the liver metastasis score (LMS). The samples in The Cancer Genome Atlas (TCGA) cohort were divided into high and low LMS groups by the LMS median. Specifically, the high LMS group showed significantly shorter overall survival than low LMS group (Figure 4A, log-rank test, P-value < 0.05). To further confirm the prognostic value of LMS, we also divided the samples from two public datasets, termed as GSE71729 [15] (n = 145) and E-MTAB-6134 [16] (n = 309), into high and low LMS groups, respectively. Consistently, the prognostic differences were also observed in the two datasets (Figure 4B, C, Table 2, P-value < 0.05). Collectively, these results indicated that the LMS might be a prognostic predictor for PDAC.
3.5. The cell types potentially confer liver metastasis in PDAC
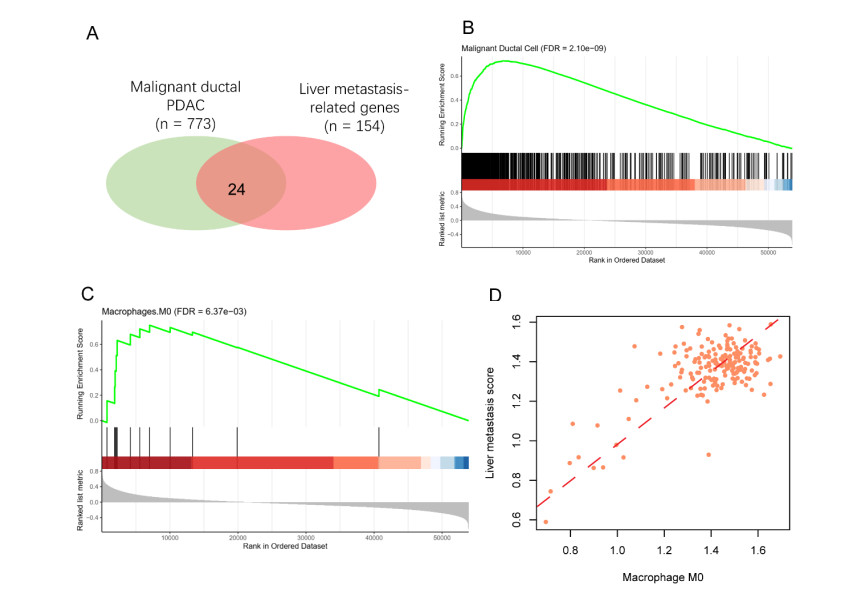
As the tumor metastasis was regulated by the cell types infiltrating into the tumor microenvironment and some specific tumor cells, we then investigated whether some specific cell types were responsible for liver metastasis in PDAC. Firstly, we collected the marker genes of cell types in PDAC tissues from earlier study [17]. The overrepresentation test of the liver metastasis-related genes revealed that those genes were highly enriched in the marker genes of malignant ductal cell (Figure 5A). Specifically, some metastasis-related genes such as MET (MET Proto-Oncogene), KRT19 (Keratin-19), KRT7 (Keratin-7), AGRN (Agrin), SDC4 (Syndecan-4), and SFN (Stratifin) were found to be specifically expressed in malignant ductal cell, indicating that the liver metastasis-related genes might be expressed in malignant ductal cells, which might be responsible for the liver metastasis in PDAC. Moreover, we also conducted correlation analysis between LMS and gene expression levels. Gene set enrichment analysis (GSEA) revealed that most of the marker genes in malignant ductal cell were positively correlated with LMS (Figure 5B, FDR < 0.05), further suggesting that malignant ductal cells were responsible for liver metastasis via expressing the liver metastasis-related genes. Furthermore, marker genes of M0 macrophage were also highly positively correlated with LMS (Figure 5C, FDR < 0.05). In addition, as motivated by previous study [25], we also estimated the relative abundance of macrophage M0 in PDAC tissues using gene expression and macrophage M0-specific genes by ssGSEA method. Consistently, the LMS was highly positively correlated with the relative activity of macrophage M0 (Figure 5D, Spearman correlation: 0.784). Therefore, the positive correlation between LMS and malignant ductal cell or macrophage M0 specific genes indicated that the two cell types might have the potential to promote liver metastasis of PDAC.
4.
Discussion
Pancreatic ductal adenocarcinoma (PDAC) is one of the most lethal malignancies worldwide [26]. Liver metastasis accounts for the high mortality rate and confers poor prognosis in PDAC [27]. Therefore, a better understanding of the mechanisms underlying the acquisition of the metastatic potential in PDAC is highly desirable.
In this study, we conducted a systematic analysis of gene expression data to identify liver metastasis-related genes in PDAC. Specifically, a total of 154 genes were identified to be upregulated in primary tissues of PDAC with liver metastasis. These liver metastasis-related genes were involved in signaling pathways such as EMT, estrogen response, p53, and glycolysis. EMT, a developmental program that enables stationary epithelial cells to gain the ability to migrate and invade, has been implicated in carcinogenesis and cancer metastasis by enhancing mobility and invasion [28]. Consistently, EMT was also found as the key players in PDAC metastasis [29]. Particularly, glycolysis was also identified as a key pathway involved in liver metastasis of PDAC. The metabolic reprogramming from oxidative phosphorylation to glycolysis in pancreatic cancer cells, has been found to enhance the invasion-metastasis cascade by promoting EMT, angiogenesis and metastatic colonization of distant organs [30]. Combined with the result in this study, the liver metastasis-related genes were functionally relevant to liver metastasis in PDAC.
The integrative analysis of DNA methylation and gene expression data revealed that the liver metastasis-related genes were primarily regulated at epigenetic level. Particularly, SFN, a cell cycle checkpoint protein, and KRT19, a marker gene for ductal cells, were predicted to be regulated by multiple methylation sites at the promoter. It should be noted that the two genes have been found as novel biomarkers of poor prognosis in PDAC [31,32]. We thus speculated that the overexpression of SFN might be associated with uncontrolled cell cycle progression and stemness maintenance, while the high expression of KRT19 gave us a hint that ductal cells might play key roles in liver metastasis in PDAC. In addition, some other DNA methylation-associated genes were also reported to be associated with tumor initiation or progression. For example, TACSTD2 (tumor associated calcium signal transducer 2) encoded a carcinoma-associated antigen [33], suggesting that it might be a potential diagnostic marker in PDAC.
Clinically, we found that liver metastasis score (LMS), derived from liver metastasis-related genes, was found to be closely associated with clinical characteristics associated with prognostic outcomes [34], such as disease type and tumor grade, in PDAC. Furthermore, we also divided the samples from TCGA, GSE71729 and E-MTAB-6134 cohorts into high and low LMS groups, and the two groups exhibited significantly different prognostic outcomes across the three cohorts, suggesting that the LMS might be a promising biomarker for risk stratification in PDAC. However, as the liver metastasis-related genes used to derive LMS were mainly enriched in glycolysis and EMT pathway, which were altered in many other cancers, the LMS might not be the PDAC-specific prognostic marker.
Furthermore, we also found that the liver metastasis-related genes were primarily expressed in malignant ductal cells by integrative analysis of the bulk and single-cell gene expression data. An earlier study [17] reported that the malignant ductal cells might be transited from ductal cells with abnormal gene expression profiles to malignant ductal cells by trajectory analysis. The malignant ductal cells were characterized to have highly proliferative and migratory subpopulations [17]. Moreover, the high correlation between LMS and M0 macrophage indicated that M0 macrophage might promote liver metastasis of PDAC. The macrophage cell subpopulations in tumors commonly refer to M2 macrophage, exhibiting anti-inflammatory and pro-tumoral effects [35], however, the role of unpolarized macrophage (M0) in tumor tissues was rarely reported. In accordance with our finding, low expression of M0 macrophage is associated with better clinical prognosis in bladder cancer patients [36]. Collectively, the malignant ductal cells and M0 macrophage might function as tumor-promoting cells in PDAC.
However, this study still has some limitations. First, the biological function of some novel liver metastasis-related genes has not been validated by experiments. Second, the clinical significance of malignant ductal cells needs to be evaluated by clinical specimens. In addition, the protein expression levels of some important liver metastasis-related genes need to be evaluated. In summary, the systematic analysis greatly improves our understanding of the critical cell types and genes expressed by these cell types in the process of liver metastasis in PDAC.
Acknowledgements
This project is supported by the Lead project of Western medicine of the Shanghai Science Committee (No. 16411967200), the PLA's youth training program of the medical science and technology (No. 16QNP095), and National Natural Science Foundation of China (No. 81871992).
Conflicts of interests
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad: