For HIV-infected individuals, cancer remains a significant burden. Gaining insight into the epidemiology and mechanisms that underlie
AIDS-related cancers can provide us with a better understanding of cancer immunity and viral oncogenesis. In this paper, an HIV-1 dynamical
model incorporating the AIDS-related cancer cells was studied. The model consists of three components, cancer cells, healthy CD4+ T lymphocytes
and infected CD4+ T lymphocytes, and can have six steady states. We discuss the existence, the stability properties and the biological meanings
of these steady states, in particular for the positive one: cancer-HIV-healthy cells steady state. We find conditions for Hopf bifurcation of
the positive steady state, leading to periodic solutions, sequences of period doubling bifurcations and appearance of chaos. Further, chaos and
periodic behavior alternate. Our results are consistent with some clinical and experimental observations.
1.
Introduction
Renal cell carcinoma (RCC) is a genitourinary type of carcinoma, accounting for more than 2% of cancer-associated deaths worldwide [1,2]. KIRC is the most common subtype of RCC [3]. Presently, surgical resection is the major therapy of KIRC patients, after which patients with KIRC still have a quite large risk of cancer recurrence and metastasis [4]. In fact, more than 30% of patients who are diagnosed with KIRC experience metastasis, leading to a poor five-year survival rate [5]. It is commonly recognized that the patients with metastatic KIRC have a very dismal prognosis mainly due to the failure of early diagnosis and resistance to chemoradiotherapy [6]. it is urgently needed to find sensitive and reliable biomarkers for individualized prediction of KIRC patients.
Previous studies have reported that specific molecules could serve as survival-associated KIRC hallmarks. For example, Chen et al. suggested that a 3-mRNA predictor was proved to be a useful model for prognostic evaluation and could improve personalized management of KIRC patients [7]. Guan et al. identified a biomarker in KIRC based on miRNA-seq and digital gene expression-seq data [8]. A study revealed the prognostic value of a long non-coding RNA signature in localized clear cell renal cell carcinoma [9]. A previous research reported that fibroblast activation protein predicted prognosis in KIRC [10]. In the process of exploring prognostic markers of cancer, accumulating studies reported that epigenetic modification could affect key cancer-related genes, which implied its significant role in carcinogenesis. For instance, a study suggested that epigenetic therapeutics served as a new weapon in the war against cancer [11]. A previous research revealed their study in the cancer epigenome for therapy [12]. A research reported the interacting cancer machineries: cell signaling, lipid metabolism, and epigenetics [13]. Presently, DNA methylation is significantly involved in epigenetic regulatory mechanism which is intensively studied. Alters in DNA methylation may impact gene expression and interplay with numerous feedback mechanisms [14]. Thus, DNA methylation is a key factor for cancer development and various studies has suggested that DNA methylation may function as a predictor for diagnosis and prognosis of cancer. For instance, Brock et al. revealed DNA methylation markers in stage I lung cancer [15]. Shen et al. suggested that seven-DNA methylation CpG-based prognostic signature coupled with gene expression may predict survival of oral squamous cell carcinoma [16]. Gündert et al. indicated that genome-wide DNA methylation analysis revealed a prognostic classifier for non-metastatic colorectal cancer [17]. It has been reported that DNA methylation profiling is highly accurate and reproducible even using small specimens and poor quality material [18]. Therefore, the analysis of DNA methylation is promising to uncover novel biomarkers for predicting prognosis of cancer. However, few studies have explored the ability of DNA methylation for prognostic prediction in patients with KIRC. It's very promising to build a methylomics-related signature for predicting prognosis of KIRC.
In present study, an integrative analysis was carried out for the prediction of KIRC patients' prognosis and a 9 DNA methylation signature-based classifier was developed using univariate, LASSO, and multivariate Cox regression model. Next, we used Kaplan-Meier analysis, ROC analysis to assess and validate the prediction accuracy of the classifier in internal validation set, external validation set and entire TCGA set. In addition, a high prognostic predicted power of our nomogram was proved based on the training set and internal validation set.
2.
Materials and methods
2.1. DNA methylation information of KIRC patients
The KIRC DNA methylation information and relevant clinical information was downloaded from TCGA database by using R TCGAbiolinks package [19]. The KIRC DNA methylation data was measured by using Illumina Infinium HumanMethylation450 BeadChip (450 k) arrays based on the manufacturer's instructions. E-MTAB-3274 was retrieved from ArrayExpress database using ArrayExpress package [20]. The DNA methylation levels were set as β values, computed as M / (M + U + 100), with U standing for an unmethylated signal and M standing for a methylated signal. After removing the patients without survival data, the remaining 282 patients with complete DNA methylation data and clinical information were used for constructing prognostic model. The 282 patients were grouped into a training group (70%, n = 198 samples) to identify a prognostic classifier and an internal validation group (30%, n = 84) to validate the predictive performance of the classifier. On the other hand, the 102 KIRC patients of E-MTAB-3274 from ArrayExpress database were employed as an external validation dataset. LASSO COX regression analysis was employed to further determine the candidate methylation sites involved in KIRC patients' RFS. In addition, LASSO analysis was executed by using 1000 iterations on the basis of a publicly available R package "glmnet" [21].
2.2. Data processing, normalization and determination of differentially expressed methylation sites
Pre-processing of the raw data was implemented for the determination of a prognostic classifier of KIRC. First of all, Raw methylation data was filtered for selecting the probes in at least one sample. After that, the normalization of the data was executed with "betaqn" function of wateRmelon package [22]. Subsequently, the total KIRC samples were divided into two cohorts (recurrence and no recurrence cohort) in accordance to recurrence status. The standardized beta was transformed to M value on the basis of the formulation: M = log (β/(1-β)). M value was applied for the elimination of the variance which resulted from multiple probes. Finally, M value was exploited for the determination of the differentially expressed methylation sites between recurrence and no recurrence cluster according to "dmpFinder" function of minfi package [23].
2.3. Generation of methylomics-related signature
In the training set, the differentially expressed methylation sites were analyzed by a univariate Cox proportional hazards regression analysis to screen the promising sites that were importantly associated with RFS of KIRC patients. Then, those sites with p-values < 0.05 in the univariate Cox proportional hazards regression model were used for the LASSO Cox regression analysis to extract candidate sites tightly related to KIRC patients' RFS. Finally, the multivariate Cox regression analysis was performed by the candidate sites for selecting the methylome-based predictor of KIRC patients' RFS. As a result, 9 DNA methylation sites were employed to develop the methylation-based prognostic predictor. Then a risk-score model was constructed by using the 9-DNA methylation signature to compute risk scores of all of the KIRC patients. According to this risk score tool, we separated patients into high and low-risk groups by using a cutoff risk score of the median risk score. We conducted ROC analysis to assess the power of the 9-DNA methylation signature. AUC value was calculated in ROC analysis to weigh the predicted accuracy of methylome-based predictor for KIRC patients' RFS with the "survivalROC" package [24], the larger of the AUC value, the better for the predicted accuracy of the signature. Kaplan–Meier survival was exploited to compare differences in RFS between high- and low-risk clusters and Kaplan–Meier curves were obtained across the "survival" package [25].
2.4. Gene set variation analysis (GSVA)
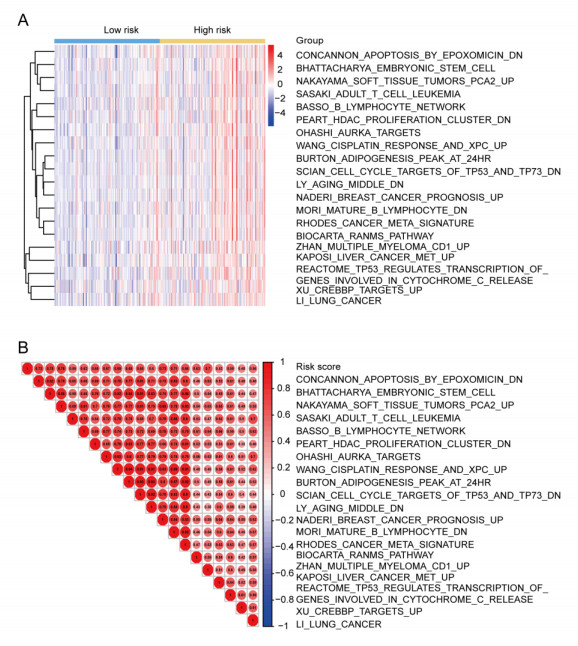
Single sample gene sets enrichment analysis (ssGSEA) was conducted based on TCGA KIRC mRNA dataset with GSVA package [26] to assess the 9-DNA methylation signature-relevant signaling pathways. The most important pathway positively correlated with risk score was measured. According to this risk score model, we separated patients into high and low-risk groups by using a cutoff risk score of the median risk score. A p value of < 0.05 was considered as statistically significant.
2.5. Construction of the nomogram
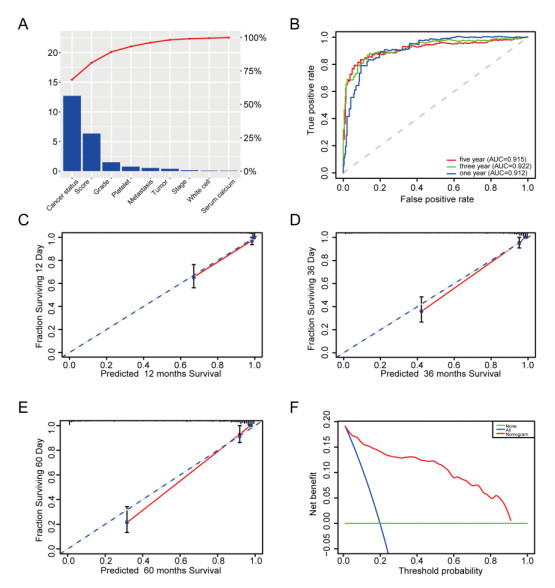
The univariate and multivariate Cox proportional hazard analysis were conducted via the methylation risk score and other clinic-related variables. Cox proportional hazard models was exploited to measure hazard ratios (HR) and corresponding 95% confidence interval (CI) of variables. Factors that were significant (P < 0.05) from the multivariate Cox proportional hazard analysis were applied for constructing a nomogram by using the 'rms' R package. The prognostic nomogram was developed in TCGA-KIRC dataset for predicting 1, 3, 5-year's RFS of KIRC patients, respectively. C-index, ROC and calibration plot and decision curve analysis (DCA) were applied to evaluate prognostic nomogram performance. The results of the nomogram were presented in the calibrate curve, and the 45° line refers to the ideal prediction.
3.
Results
3.1. Clinical characteristics of the study populations
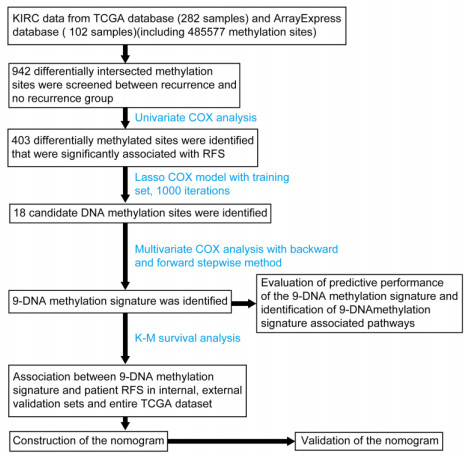
Totally, 282 TCGA patients and 102 ArrayExpress database patients who were clinically and pathologically diagnosed as KIRC were included in this study. A flow chart of the study procedure was developed to summarize our study (Figure 1). The clinical feature of KIRC patients from TCGA dataset and ArrayExpress dataset was summarized in Table 1.
3.2. Determination of 9 methylation sites signature
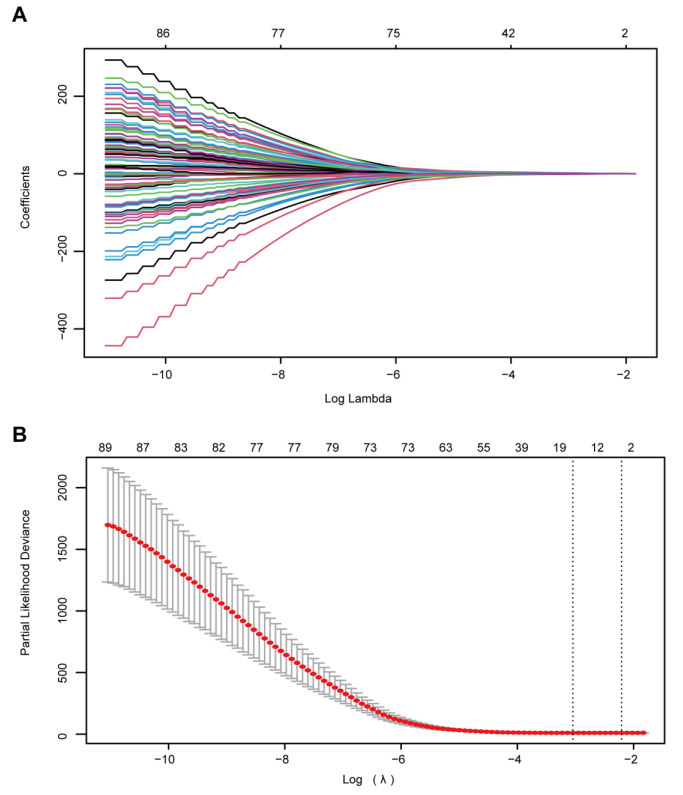
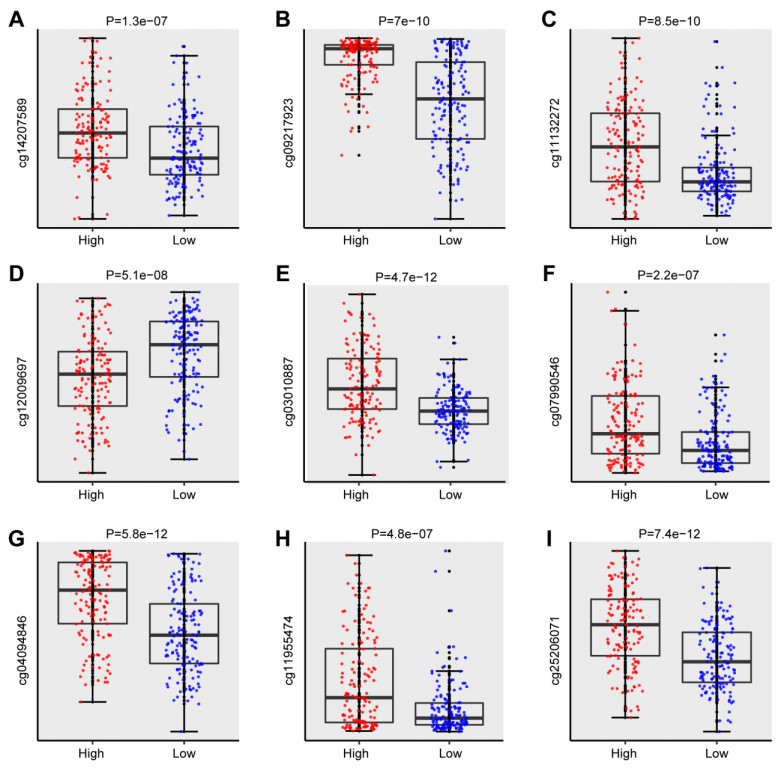
We selected 942 differentially methylated sites between recurrence and no recurrence cohorts for univariate Cox proportional hazard regression analysis. As a result, 403 DNA methylation sites were proved to be strongly involved in KIRC patients' RFS (P < 0.05) (Table S1). After that the above 403 KIRC DNA methylation sites were projected to LASSO Cox regression model and 18 methylation sites were screened as the candidate prognostic sites (Figure 2) which were significantly related to RFS of KIRC patients. Those 18 candidate methylation sites were further analyzed by multivariable Cox analysis in the training set. Finally, 9 methylation sites (P < 0.05) were identified as the independent risk factors tightly associated with RFS of KIRC patients, including cg12009697, cg14207589, cg07990546, cg04094846, cg11132272, ca11955474, cg03010887, cg09217923, cg25206071. These 9 methylation sites were used for building a DNA methylation-based signature to predict the RFS of KIRC patients. Therefore, we constructed the risk score formula as follows: risk score = 2.625*cg14207589 + 4.519*cg09217923 + 2.615*cg11132272 - 2.373*cg12009697 + 2.751*cg03010887 + 1.568*cg07990546 + 1.344*cg04094846 + 1.507*cg11955474 + 2.065*cg25206071. We discovered that, the hypermethylation levels of cg14207589, cg09217923, cg11132272, cg03010887, cg07990546, cg04094846, cg11955474, cg25206071 tended to have poor survival rates. Whereas the hypomethylation levels of cg12009697 tended to have poor survival rates. (Figures 3 and S1).
3.3. Interplays between 9 DNA methylation signature and KIRC patients' RFS in the internal validation, external validation and entire TCGA set
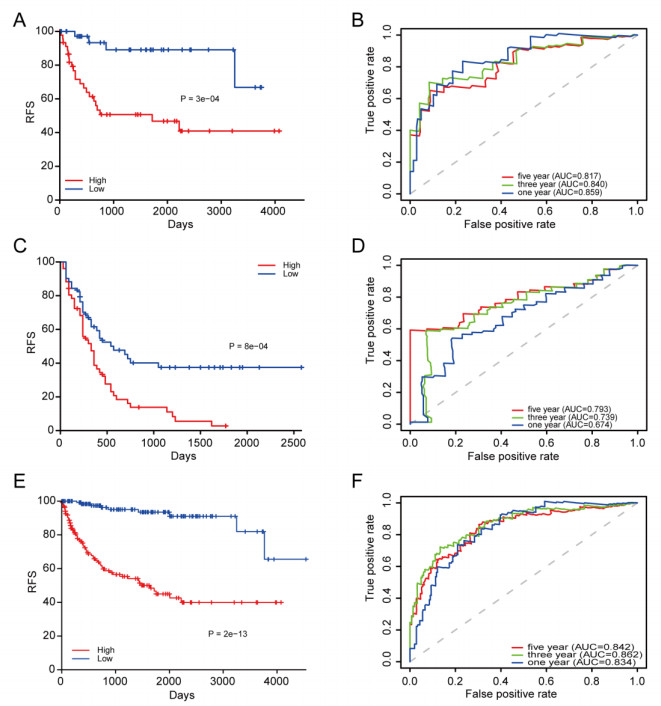
In order to analyze the predictive capability of this 9 DNA methylation-based signature, we divided the patients in each set into high and low-risk cohorts based on the median risk score. Kaplan–Meier survival analysis was exploited to examine the difference in RFS between the two cohorts. The patients in high- risk cohort generated a significantly unfavorable RFS in internal validation set (p = 3e-04) (Figure 4A), similar results were obtained in external validation set (p = 8e-04) (Figure 4C) and entire TCGA set (p = 2e-13) (Figure 4E). After that, the power of the 9-DNA methylation signature-based indicator for KIRC patients' RFS was explored by using a time-dependent ROC curve. The AUC of the biomarker at 1, 3, 5 years in internal set were 0.859, 0.840, 0.817, respectively (Figure 4B), in external validation set (0.674, 0.739, 0.793, respectively) (Figure 4D) and entire TCGA set (0.834, 0.862, 0.842, respectively) (Figure 4F). We concluded that the 9-DNA methylation signature-related indicator yielded a great power for the prediction of KIRC patients' RFS.
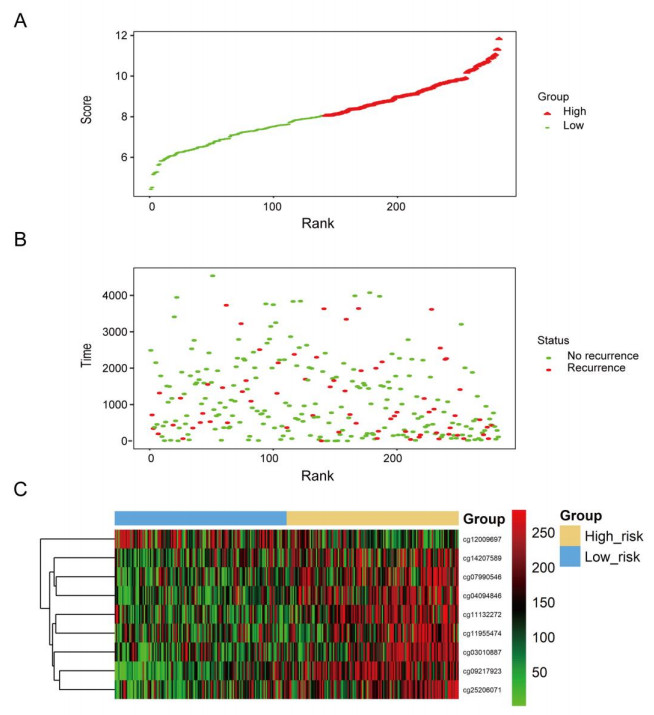
Subsequently, the rank of the patients from entire TCGA set was carried out according to the risk scores (Figure 5A), and the dotplot of the total patients was performed according to their survival status (Figure 5B). We noted that the high-risk cohort generated a worse survival than that in the low-risk cohort. Figure 5C showed the heatmap of 9 methylation sites distribution according to risk score, which supported the previous observation (Figure S2). Then, we performed subgroup analysis by using a few clinical variables containing age, gender, anatomic site, grade and stage. The majority of sub-groups showed a good predictive power of the 9-DNA methylation signature for KIRC patients' RFS (Figures S3–S7).
3.4. Determination of the 9-DNA methylation signature-related biological pathways
We separated patients into high and low-risk groups by using a cutoff risk score of the median risk score. Figure 6A showed the top 20 enriched pathways that were more activated in the high-risk cases than that in low-risk cases. The same trend between the enriched pathways and risk score was further addressed in Figure 6B, which proved a good correlation between the pathways and the risk score (Table S2).
3.5. Nomogram development
We first performed univariate and multivariate Cox tool according to a few clinic-related covariates. Hazard ratios (HRs) manifested that the 9-DNA methylation-related classifier was tightly related to KIRC patients' RFS (P < 0.001, HR 1.47, 95% CI 1.13–1.92) (Table 2 and Figure S8), manifesting that the 9-DNA methylation signature was an independent predictor of KIRC patients' RFS in the entire TCGA set. To further reinforce the prognostic value of the 9-DNA methylation-based signature for KIRC in a quantitative strategy. We developed a nomogram (Figure 7) that integrated the 9-DNA methylation-associated signature and the conventional clinic-associated covariates containing cancer status, grade. The significance between the 9-DNA methylation-based factor and the conventional clinic-associated covariates was described in Figure 8A. The value of the nomogram was weighed on the basis of C-index (0.802, 95%CI: 0.768-0.828), AUC (1, 3, 5-year: 0.912, 0.922, 0.915) (Figure 8B) and calibration plot (Figure 8C–E), proving a good value of the tool. In addition, DCA manifested that the nomogram created more crucial value of clinical utilization as predictor of KIRC patients' RFS than that in treat all or treat none group. Net benefit was available for KIRC patients in 3-year recurrent risks (Figure 8F). We concluded that our nomogram had a great value and may have potential for clinical application.
4.
Discussion
The KIRC DNA methylation information and relevant clinical information from TCGA database was analyzed to unearth the predictor of KIRC patients' RFS. Eventually, 9 DNA methylation sites (cg12009697, cg14207589, cg07990546, cg04094846, cg11132272, ca11955474, cg03010887, cg09217923, cg25206071) were found to be strongly associated with RFS of KIRC patients. The above 9 DNA methylation sites were mapped to 4 genes (TLX2, OSBP, TAAR2, IL19). It is interesting to note that, previous researches suggested that most of these 4 genes were correlated with cancer, respectively. For instance, Liu et al. found that methylated COL4A1, COL4A2, TLX2, and ITGA4 demonstrated high accuracy for the detection of colorectal neoplasms in stool and they may be potentially valuable biomarkers for the detection of colorectal cancer [27]. Liao et al. demonstrated that TAT-OSBP-MKK6(E) was a novel artificially designed molecule, which induced apoptosis and selectively targeted human ovarian carcinoma HO8910 cells. Their study provided novel insights that may aid in the development of a new generation of anticancer drugs, which implied the importance of OSBP in cancer [28]. Hsing et al. suggested that upregulated IL-19 in breast cancer promoted tumor progression and affected clinical result [29]. The result manifested that the 3 of the 4 genes involved in the 9 sites played important roles in progression of cancer.
Multiple studies indicated that nomograms may strengthen prognostic predictive accuracy for cancer by integrating several clinical variables in a quantitative method. For example, Wang et al. constructed a nomogram to predict gleason sum upgrading of clinically diagnosed localized prostate cancer among Chinese patients [30]. Lee et al. built a prognostic nomogram to predict progression-free survival in patients with platinum-sensitive recurrent ovarian cancer [31]. Taşkın et al. found a nomogram with potential clinical application to predict lymph node metastasis in endometrial cancer patients diagnosed incidentally by postoperative pathological assessment [32]. However, nomograms for improving predictive ability of KIRC patients' RFS have been rarely reported. In this study, we aimed to develop a nomogram using both methylation risk score and several clinic-associated covariates for predicting 1, 3, 5-year RFS for KIRC patient from the entire TCGA set. The indicators of the C-index, AUC, DCA and calibration curve from the entire TCGA set exhibited that our nomogram had discriminative accuracy and was adopted as the preferred predictive model. Furthermore, we developed the nomogram as a predicator in a quantitative method for the prognosis of KIRC patient, which could predict the accruate survival percentage of KIRC patients. In addition, the key virtues of the nomogram contained clinical applicability and convenient factors, which was readily available according to historical records. On the other hand, DNA methylation profiling is highly accurate and reproducible even using small specimens and poor quality material [18], suggesting that this methylomics-correlated nomogram method had a great advantage to predict prognosis of cancer patients in comparison to other signatures.
Growing researches manifested that LASSO Cox regression model can be employed to unearth markers of multiple cancers, For example, Connell et al. found a four-group urine risk classifier for predicting outcome in prostate cancer patients based on LASSO Cox regression analysis [33]. Zhang et al. identified a new eight-long noncoding RNA molecular signature for breast cancer survival prediction according to the LASSO method, univariate and multivariate Cox analyses [34]. Liu et al. identified an eight-lncRNA prognostic model for breast cancer using WGCNA network analysis and a Cox‑proportional hazards model based on LASSO Cox regression model [35]. Du et al. constructed a diagnostic nomogram of platelet-based score models for hepatic alveolar echinococcosis and atypical liver cancer using LASSO Cox regression model [36]. A significant merit of LASSO is that it has sparse estimates of the regression coefficients which suggests that various components are precisely 0. In other words, LASSO can automatically remove unnecessary variables. LASSO has various preferred properties for regression models with numerous variables, and multiple efficient optimization algorithms are available for linear regression and generalized linear models [37]. To our knowledge, fewer studies have used LASSO regression model for the determination of a prognostic predictor of KIRC. We performed LASSO Cox regression analysis to select candidate methylation sites tightly related to KIRC patients' RFS for filtering the variables between univariate and multivariate Cox analysis, further improving prognostic predicted ability of 9-DNA methylation-associated signature.
There are still a few limitations of this study. Firstly, our study is a retrospective one and the prospective studies including a larger number of samples of various medical centers are needed to verify the outcomes. Secondly, more factors should be mapped into our external validation set to improve the predicted accuracy of the nomogram. Thirdly, the nomograms were developed by using retrospective data from TCGA database, which may be correlated with the potential hazard of selection bias.
5.
Conclusions
We successfully identified a 9-DNA methylation-based signature, which was a useful prognostic predictor for KIRC patients' RFS. A nomogram combining methylation risk score and the conventional clinic-related covariates was helpful in improving the predicted ability of clinical prognosis for KIRC patients.
Acknowledgements
This work was supported by the National Nature Science Foundation of China (Grant Nos. 82073324).
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: