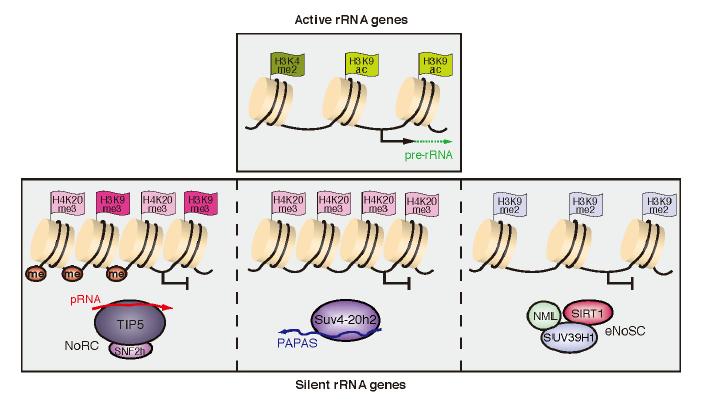
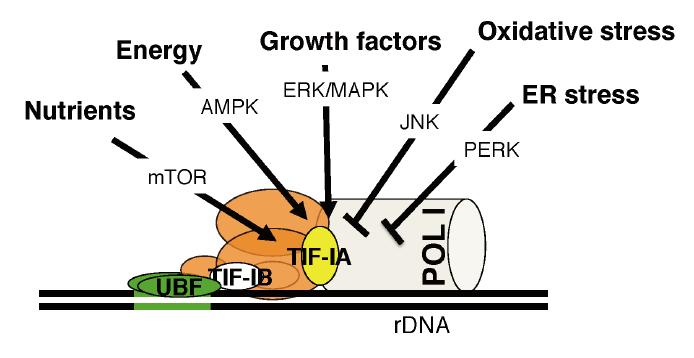
Within the cell nucleus the nucleolus is the site of rRNA transcription and ribosome biogenesis and its activity is clearly essential for a correct cell function, however its specific role in neuronal homeostasis remains mainly unknown. Here we review recent evidence that impaired nucleolar activity is a common mechanism in different neurodegenerative disorders. We focus on the specific causes and consequences of impaired nucleolar activity to better understand the pathogenesis of neurodegenerative disorders, such as Alzheimer's disease (AD), Parkinson's disease (PD), Huntington's disease (HD) and amyotrophic lateral sclerosis/frontotemporal dementia (ALS/FTD). In particular, we discuss the genetic and epigenetic factors that might regulate nucleolar function in these diseases. In addition, we describe novel animal models enabling the dissection of the context-specific series of events triggered by nucleolar disruption, also known as nucleolar stress. Finally, we suggest how this novel mechanism could help to identify strategies to treat these still incurable disorders.
1.
Introduction and main result
Existing methods and algorithms appeared in some literatures assume that variables are independent, but it is not plausible. In many stochastic models and statistical applications, those variables involved are dependent. Hence, it is important and meaningful to extend the results of independent variables to dependent cases. One of these dependence structures is weakly dependent (i.e., $ {{\rho }^{*}} $-mixing or $ \tilde{\rho} $-mixing), which has attracted the concern by many researchers.
Definition 1.1. Let $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ be a sequence of random variables defined on a probability space $ \left(\Omega, \mathcal{F}, P \right) $. For any $ S\subset \text{N = }\left\{ 1, 2, \ldots \right\} $, define $ {{\mathcal{F}}_{S}} = \sigma \left({{X}_{i}}, i\in S \right) $. The set $ {{L}_{2}}\left({{\mathcal{F}}_{S}} \right) $ is the class of all $ \mathcal{F} $-measureable random variables with the finite second moment. For some integer $ s\ge 1 $, denote the mixing coefficient by
where
Noting that the above fact $ \text{dist}\left(S, T \right)\ge s $ denotes $ \text{dist}\left(S, T \right) = \inf \left\{ \left| i-j \right|:i\in S, j\in T \right\}\ge s $. Obviously, $ 0\le {{\rho }^{*}}\left(s+1 \right)\le {{\rho }^{*}}\left(s \right)\le 1 $ and $ {{\rho }^{*}}\left(0 \right) = 1 $. The sequence $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ is called $ {{\rho }^{*}} $-mixing if there exists $ s\in \text{N} $ such that $ {{\rho }^{*}}\left(s \right) < 1 $. Clearly, if $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ is a sequence of independent random variables, then $ {{\rho }^{*}}\left(s \right) = 0 $ for all $ s\ge 1 $.
$ {{\rho }^{*}} $-mixing seems similarly to another dependent structure: $ \rho $-mixing, but they are quite different from each other. $ {{\rho }^{*}} $-mixing is also a wide range class of dependent structures, which was firstly introduced to the limit theorems by Bradley [4]. From then on, many scholars investigated the limit theory for $ {{\rho }^{*}} $-mixing random variables, and a number of important applications for $ {{\rho }^{*}} $-mixing have been established. For more details, we refer to [12,16,18,19,21,23,24] among others.
The concept of complete convergence was firstly given by Hsu and Robbins[9] as follows: A sequence of random variables $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ converges completely to a constant $ \lambda $ if $ \sum\limits_{n = 1}^{\infty }{P\left(\left| {{X}_{n}}-\lambda \right| > \varepsilon \right)} < \infty $ for all $ \varepsilon > 0 $. By the Borel-Cantelli lemma, the above result implies that $ {{X}_{n}}\to \lambda $ almost surely (a.s.). Thus, the complete convergence plays a crucial role in investigating the limit theory for summation of random variables as well as weighted sums.
Chow [8] introduced the following notion of complete moment convergence: Let $ \left\{ {{Z}_{n}}; n\ge 1 \right\} $ be a sequence of random variables, and $ {{a}_{n}} > 0 $, $ {{b}_{n}} > 0 $, $ q > 0 $. If $ \sum\limits_{n = 1}^{\infty }{{{a}_{n}}E\left(b_{n}^{-1}\left| {{Z}_{n}} \right|-\varepsilon \right)_{+}^{q}} < \infty $ for all $ \varepsilon \ge 0 $, then the sequence $ \left\{ {{Z}_{n}}; n\ge 1 \right\} $ is called to be the complete $ q $-th moment convergence. It will be shown that the complete moment convergence is the more general version of the complete convergence, and is also much stronger than the latter (see Remark 2.1).
According to the related statements of Rosalsky and Thành[14] as well as that of Thành[17], we recall the definition of stochastic domination as follows.
Definition 1.2. A sequence of random variables $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ is said to be stochastically dominated by a random variable $ X $ if for all $ x\ge 0 $ and $ n\ge 1 $,
The concept of stochastic domination is a slight generalization of identical distribution. It is clearly seen that stochastic dominance of $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ by the random variable $ X $ implies $ E{{\left| {{X}_{n}} \right|}^{p}}\le E{{\left| X \right|}^{p}} $ if the $ p $-th moment of $ \left| X \right| $ exists, i.e. $ E{{\left| X \right|}^{p}} < \infty $.
As is known to us all, the weighted sums of random variables are used widely in some important linear statistics (such as least squares estimators, nonparametric regression function estimators and jackknife estimates). Based on this respect, many probability statisticians devote to investigate the probability limiting behaviors for weighted sums of random variables. For example, Bai and Cheng[3], Cai[5], Chen and Sung[6], Cheng et al.[7], Lang et al.[11], Peng et al.[13], Sung[15,16] and Wu[20] among others.
Recently, Li et al.[12] extended the corresponding result of Chen and Sung[6] from negatively associated random variables to $ {{\rho }^{*}} $-mixing cases by a total different method, and obtained the following theorem.
Theorem A. Let $ \left\{ X, {{X}_{n}}; n\ge 1 \right\} $ be a sequence of identically distributed $ {{\rho }^{*}} $-mixing random variables with $ E{{X}_{n}} = 0 $, and let $ \left\{ {{a}_{ni}}; 1\le i\le n, n\ge 1 \right\} $ be an array of real constants such that $ \sum\limits_{i = 1}^{n}{{{\left| {{a}_{ni}} \right|}^{\alpha }}} = O\left(n \right) $ for some $ 1 < \alpha \le 2 $. Set $ {{b}_{n}} = {{n}^{1/\alpha }}{{\left(\log n \right)}^{1/\gamma }} $ for $ 0 < \gamma < \alpha $. If $ E{{{\left| X \right|}^{\alpha }}}/{{{\left(\log \left(1+\left| X \right| \right) \right)}^{\alpha /\gamma -1}}}\; < \infty $, then
In addition, Huang et al.[10] proved the following complete $ \alpha $-th moment convergence theorem for weighted sums of $ {{\rho }^{*}} $-mixing random variables under some moment conditions.
Theorem B. Let $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ be a sequence of $ {{\rho }^{*}} $-mixing random variables, which is stochastically dominated by a random variable $ X $, let $ \left\{ {{a}_{ni}}; 1\le i\le n, n\ge 1 \right\} $ be an array of real constants such that $ \sum\limits_{i = 1}^{n}{{{\left| {{a}_{ni}} \right|}^{\alpha }}} = O\left(n \right) $ for some $ 0 < \alpha \le 2 $. Set $ {{b}_{n}} = {{n}^{1/\alpha }}{{\left(\log n \right)}^{1/\gamma }} $ for some $ \gamma > 0 $. Assume further that $ E{{X}_{n}} = 0 $ when $ 1 < \alpha \le 2 $. If
then
It is interesting to find the optimal moment conditions for (1.5). Huang et al.[10] also posed a worth pondering problem whether the result (1.5) holds for the case $ \alpha > \gamma $ under the almost optimal moment condition $ E{{{\left| X \right|}^{\alpha }}}/{{{\left(\log \left(1+\left| X \right| \right) \right)}^{\alpha /\gamma -1}}}\; < \infty $?
Mainly inspired by the related results of Li et al.[12], Chen and Sung[6] and Huang et al.[10], the authors will further study the convergence rate for weighted sums of $ {{\rho }^{*}} $-mixing random variables without assumptions of identical distribution. Under the almost optimal moment condition $ E{{{\left| X \right|}^{\alpha }}}/{{{\left(\log \left(1+\left| X \right| \right) \right)}^{\alpha /\gamma -1}}}\; < \infty $ for $ 0 < \gamma < \alpha $ with $ 1 < \alpha \le 2 $, a version of the complete $ \alpha $-th moment convergence theorem for weighted sums of $ {{\rho }^{*}} $-mixing random variables is established. The main result not only improves the corresponding ones of Li et al.[12], Chen and Sung[6], but also partially settles the open problem posed by Huang et al.[10].
Now, we state the main result as follows. Some important auxiliary lemmas and the proof of the theorem will be detailed in the next section.
Theorem 1.1. Let $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ be a sequence of $ {{\rho }^{*}} $-mixing random variables with $ E{{X}_{n}} = 0 $, which is stochastically dominated by a random variable $ X $, let $ \left\{ {{a}_{ni}}; 1\le i\le n, n\ge 1 \right\} $ be an array of real constants such that $ \sum\limits_{i = 1}^{n}{{{\left| {{a}_{ni}} \right|}^{\alpha }}} = O\left(n \right) $ for some $ 0 < \alpha \le 2 $. Set $ {{b}_{n}} = {{n}^{1/\alpha }}{{\left(\log n \right)}^{1/\gamma }} $ for $ \gamma > 0 $. If $ E{{{\left| X \right|}^{\alpha }}}/{{{\left(\log \left(1+\left| X \right| \right) \right)}^{\alpha /\gamma -1}}}\; < \infty $ for $ \alpha > \gamma $ with $ 1 < \alpha \le 2 $, then (1.5) holds.
Throughout this paper, let $ I\left(A \right) $ be the indicator function of the event $ A $ and $ I(A, B) = I(A\bigcap B) $. The symbol $ C $ always presents a positive constant, which may be different in various places, and $ {{a}_{n}} = O\left({{b}_{n}} \right) $ stands for $ {{a}_{n}}\le C{{b}_{n}} $.
2.
Lemmas and proofs
To prove our main result of this paper, we need the following important lemmas.
Lemma 2.1. (Utev and Peligrad[18]) Let $ p\ge 2 $, $ \left\{ {{X}_{n}}; n\ge 1 \right\} $ be a sequence of $ {{\rho }^{*}} $-mixing random variables with $ E{{X}_{n}} = 0 $ and $ E{{\left| {{X}_{n}} \right|}^{p}} < \infty $ for all $ n\ge 1 $. Then there exists a positive constant $ C $ depending only on $ p $, $ s $ and $ {{\rho }^{*}}\left(s \right) $ such that
In particular, if $ p = 2 $,
The following one is a basic property for stochastic domination. For the details, one refers to Adler and Rosalsky[1] and Adler et al.[2], or Wu[22]. In fact, we can remove the constant $ C $ in those of Adler and Rosalsky[1] and Adler et al.[2], or Wu[22], since it was proved in Reference [[14], Theorem 2.4] (or [[17], Corollary 2.3]) that this is indeed equivalent to $ C = 1 $.
Lemma 2.2. Let $ \left\{ {{X}_{n}}, n\ge 1 \right\} $ be a sequence of random variables which is stochastically dominated by a random variable $ X $. For all $ \beta > 0 $ and $ b > 0 $, the following statements hold:
Consequently, $ E{{\left| {{X}_{n}} \right|}^{\beta }}\le E{{\left| X \right|}^{\beta }} $.
Lemma 2.3. Under the conditions of Theorem 1.1, if $ E{{{\left| X \right|}^{\alpha }}}/{{{\left(\log \left(1+\left| X \right| \right) \right)}^{\alpha /\gamma -1}}}\; < \infty $ for $ 0 < \gamma < \alpha $ with $ 0 < \alpha \le 2 $, then
Proof. By Definition 1.2, noting that
It is easy to show that
and
Hence, (2.5) holds by (2.6)–(2.8).
Proof of Theorem 1.1. For any given $ \varepsilon > 0 $, observing that
By Theorem A of Li et al.[12] declared in the first section, we get directly $ I < \infty $. In order to prove (1.5), it suffices to show that $ J < \infty $.
Without loss of generality, assume that $ {{a}_{ni}}\ge 0 $. For all $ t\ge 1 $ and $ 1\le i\le n $, $ n\in \text{N} $, define
It is easy to check that
which implies
To prove $ J < \infty $, we need only to show that
Since
it follows from Lemma 2.3 that
Next, we prove that
By $ E{{X}_{n}} = 0 $ and (2.4) of Lemma 2.2, it follows that
Observe that,
For $ 0 < \gamma < \alpha $ and $ 1 < \alpha \le 2 $, it is clearly shown that
and
Thus,
and
Then, (2.11) holds by the argumentation of (2.12)–(2.16).
Hence, for $ n $ sufficiently large, we have that $ {\mathop {\max }\limits_{1 \le j \le n} }\, \left| \sum\limits_{i = 1}^{j}{E{{Y}_{i}}} \right|\le \frac{{{b}_{n}}{{t}^{1/\alpha }}}{2} $ holds uniformly for all $ t\ge 1 $. Therefore,
By the Markov's inequality, (2.2) of Lemma 2.1 and (2.3) of Lemma 2.2, we get that
Based on the formula (2.2) of Lemma 2.2 in Li et al.[10], we get that
Denoting $ t = {{x}^{\alpha }} $, by (2.3) of Lemma 2.2, the Markov's inequality and Lemma 2.3, we also get that
Analogous to the argumentation of Lemma 2.3, it is easy to show that
Hence, the desired result $ {{J}_{1}} < \infty $ holds by the above statements. The proof of Theorem 1.1 is completed.
Remark 2.1. Under the conditions of Theorem 1.1, noting that
Since $ \varepsilon > 0 $ is arbitrary, it follows from (2.22) that the complete moment convergence is much stronger than the complete convergence. Compared with the corresponding results of Li et al.[12], Chen and Sung[6], it is worth pointing out that Theorem 1.1 of this paper is an extension and improvement of those of Li et al.[12], Chen and Sung[6] under the same moment condition. In addition, the main result partially settles the open problem posed by Huang et al.[10] for the case $ 0 < \gamma < \alpha $ with $ 1 < \alpha \le 2 $.
3.
Conclusions
In this work, we consider the problem of complete moment convergence for weighted sums of weakly dependent (or $ {{\rho }^{*}} $-mixing) random variables. The main results of this paper are presented in the form of the main theorem and a remark as well as Lemma 2.3, which plays a vital role to prove the main theorem. The presented main theorem improves and generalizes the corresponding complete convergence results of Li et al.[12] and Chen and Sung[6].
Acknowledgments
The authors are most grateful to the Editor as well as the anonymous referees for carefully reading the manuscript and for offering some valuable suggestions and comments, which greatly enabled them to improve this paper. This paper is supported by the Doctor and Professor Natural Science Foundation of Guilin University of Aerospace Technology.
Conflict of interest
All authors declare no conflicts of interest in this paper.













 DownLoad:
DownLoad: