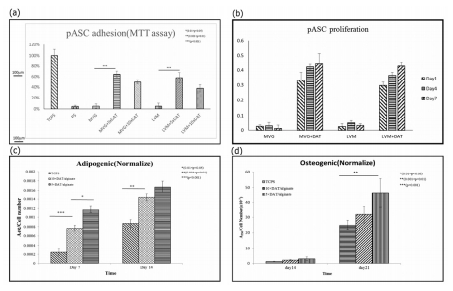
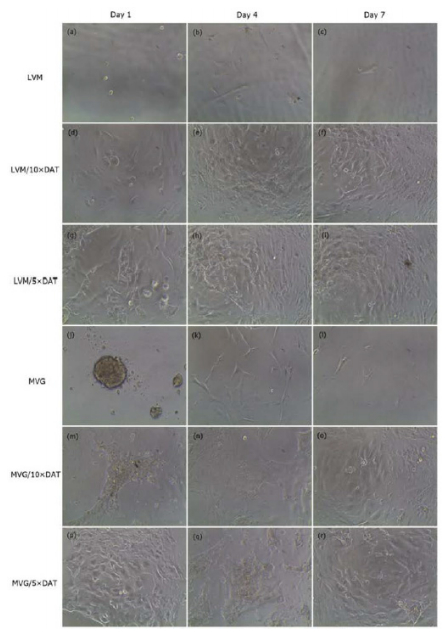
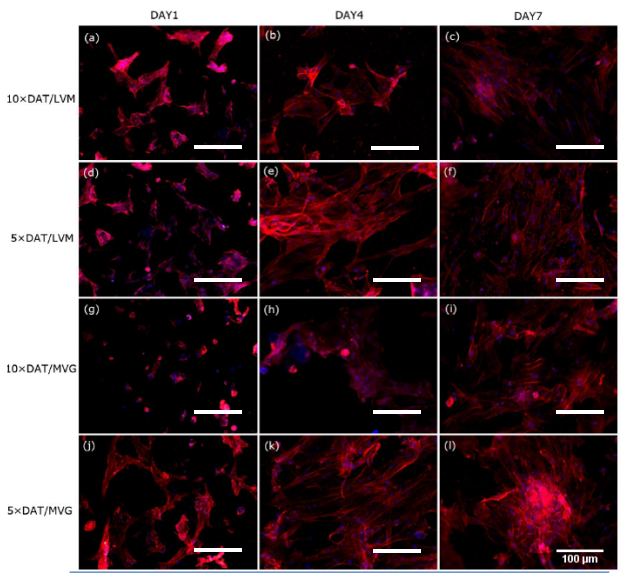
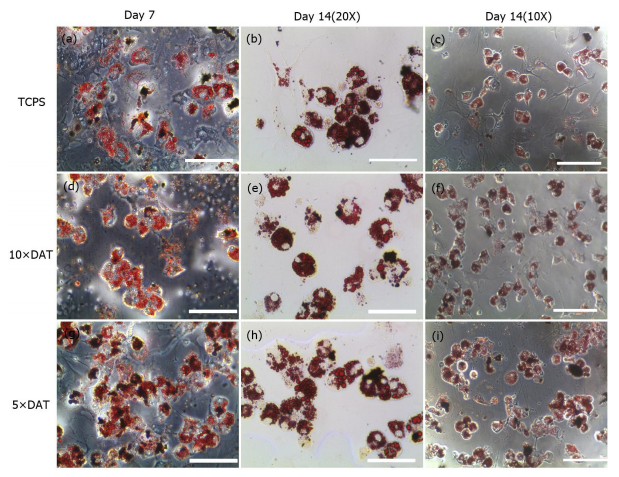
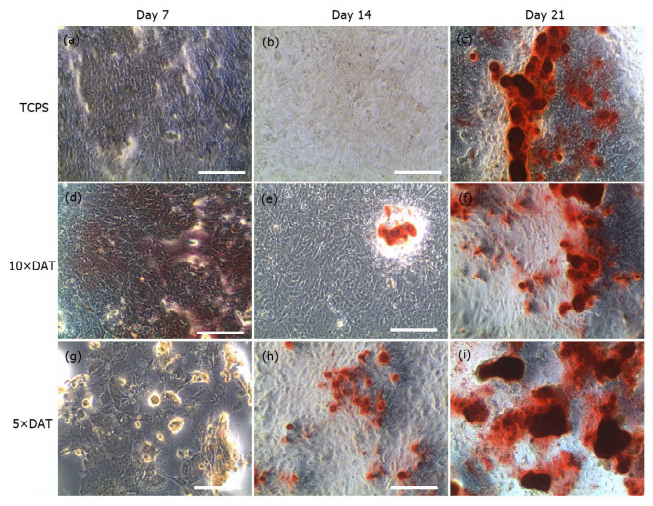
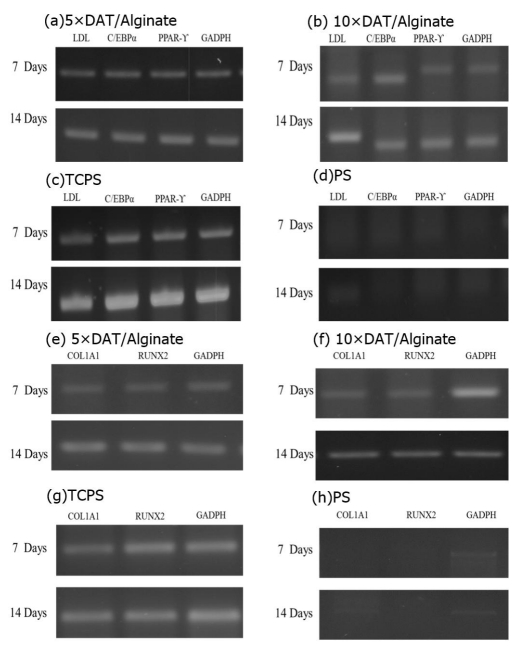
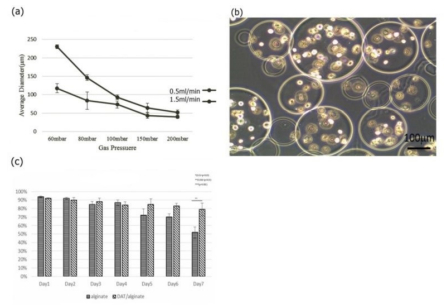
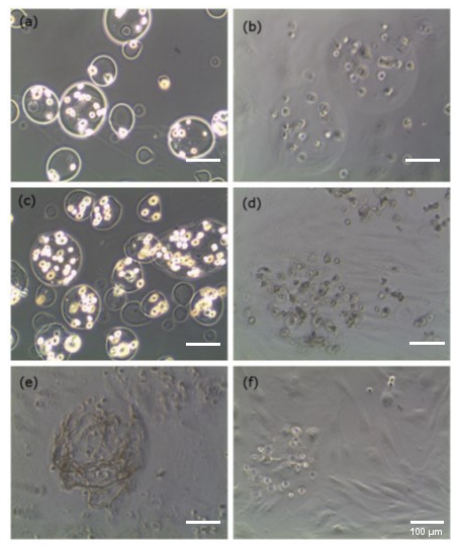
Stem cells are utilized to create living and functional tissues to regenerate and repair tissue or organs in the body in cell based and regenerative treatments. It has been demonstrated that stem cell treatments can improve perfusion and stimulate neovascularization in peripheral arterial disease. However, such treatments usually suffer from some deficiencies, such as immune rejection and limited proliferation of implanted cells.In this study, we focused on the application of the decellularized adipose tissue (DAT), which is a native extracellular matrix (ECM), in cell based therapies. Biomaterials extracted from the organism itself possesses great potential as scaffold materials for stem cell culture as well as new tissue construct formation, especially if the ECM and cell are from the same source (in our case, the adipose tissue). Therefore, DAT solution (DATsol) was combined with alginate in our study to culture adipose stem cells (ASCs).We investigated the mixture of DATsol and high or low molecular weight alginate. The 2-D in vitro study of DATsol/alginate was found to promote cell adhesion and differentiation. ASCs, immobilized in DATsol/alginate microspheres, demonstrated metabolic activity which with an overall viability higher than 80%. The results suggested that the use of DATsol and alginate possesses great potential for application in cell based therapies in ischemia patients which facilitates the development of new mature and stable capillaries.
1.
Introduction
In calculus and mathematical analysis, integration and differentiation are two fundamental operations. In actuality, these are the infinitesimal forms of the operations on numbers for subtraction and addition, respectively.
New definitions of differentiation and integration in which the roles of addition and subtraction move to multiplication and division and a new form of calculus is introduced is called multiplicative calculus. This is also called non-Newtonian calculus. Despite answering all of the conditions expected from calculus, multiplicative calculus is not as popular as the Newton and Leibnitz conditions, unfortunately.
The applications of multiplicative calculus are more limited than the calculus of Newton and Leibnitz. Therefore a well-developed tool with a wider scope has already been made and the question of whether it is fair to design a new tool with a limited scope arises. The solution is comparable to the question of why mathematicians use a polar coordinate system when a rectangular coordinate system that better describes points on a plane exists. We believe that the mathematical instrument of multiplicative calculus can be particularly helpful for the study of economics and finance.
Assume for motivation's sake that by depositing $σ, one will receive $ς after a year. The original number then fluctuates ς/σ times. How frequently does it change each month? Assume that the change over a month is p times for this. The total then becomes ς=σp12 for a year. The formula for computing p is now p=(ς/σ)112. Assume that deposits fluctuate daily, hourly, by minute, by second, etc. and that the function φ indicating its value at various time points, is the formula
The above formula shows that how the value of φ(ω) varies at moment ω. For comparison with Definition (1.1), the definition of derivative is
We observe that the difference in (1.2) is replaced by division, and that the division by Δω is replaced by raising it to the reciprocal power 1/Δω. The limit (1.1) is a called multiplicative derivative.
Mathematical analysis has long been the dominant area of mathematics, and inequalities play a major role in mathematical analysis. The significance of inequalities has long been recognized in the field of mathematics. The mathematical roots of the theory of inequality were set by eminent mathematicians in the 18th and 19th centuries. The impact of inequalities was significant in the years that followed, and many well-known mathematicians were drawn to the subject. In the 20th century, it was the ground breaking work of Hardy, Littlewoods, and Polya which was published in 1934 that sparked the development of the field as a subfield of modern mathematics.
The Hermite-Hadamard inequality, named after Charles Hermite and Jacques Hadamard and commonly known as Hadamard's inequality, says that if a function φ:[σ,ς]→R is convex, the following double inequality holds:
If φ is a concave mapping, the above inequality holds in the opposite direction. The inequality (1.3) can be proved by using the Jensen inequality. There has been much research done in the direction of Hermite-Hadamard for different kinds of convexities. For example, in [1,2,3,4], the authors established some inequalities linked with midpoint and trapezoid formulas of numerical integration for convex functions. For some more inequalities and their applications, one can consult [5,6].
Very recently, Ali et al. [7] proved the Hermite-Hadamard type inequality in the framework of multiplicative calculus and stated it as follows:
Theorem 1.1. Let φ:[σ,ς]→R+ be a multiplicative convex function then, the following inequality holds:
After the work of Ali et al. [7], many researchers started work in this directions and proved different variants of integral inequalities in the setting of multiplicative calculus. For example, the Hermite-Hadamard-type inequalities for general multiplicative convex functions were proved in [8] and Özcan used the multiplicative preinvexity and established Hermite-Hadamard-type inequalities in [9]. For multiplicative s -convex and multiplicative s-preinvex functions, the Hermite-Hadamard-type inequalities were found in [10,11], which, for h-preinvex functions, were proved in [12]. Ali et al. [13] established some Ostrowski's and Simpson's type of inequalities for multiplicative convex functions and gave their applications. Budak and Özcelik [14] used multiplicative fractional integrals and established Hermite-Hadamard type inequalities. In [15], Fu et al. introduced multiplicative tempered fractional integrals and established some new fractional Hermite-Hadamard type inequalities for multiplicative convex functions. Ali et al. [16] introduced the notions of multiplicative interval-valued integrals and established some new Hermite-Hadamard type inequalities for interval-valued multiplicative convex functions. For some conclusions on the sequence spaces with respect to non-newtonian calculus, fractional calculus and its applications and investigation of some characteristic features of complex numbers and functions in terms of non-Newtonian calculus together with some fundamental theorems and concepts of the classical calculus in the sense of non-Newtonian calculus, one can consult [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Inspired by the ongoing studies, we establish some new Simpson's and Newton's type of inequalities for multiplicative convex functions in the setting of multiplicative calculus. The main advantage of these inequalities is that they can be used to find the error bounds for Simpson's and Newton's formulas in the sense of multiplicative calculus. Since multiplicative calculus is modern calculus with lot of applications in banking and finance, the study about multiplicative calculus is valuable.
2.
Preliminaries
In this section, we recall some concepts of multiplicative calculus and convexity.
Definition 2.1. [34] For the positive real valued function φ, the multiplicative derivative is stated as:
Remark 2.2. The following expression gives us the relation between multiplicative and ordinary derivatives (see, [34]):
Theorem 2.3. [34] For multiplicative differentiable functions φ, G and a constant c, we have the following relations:
(1) (cφ)∗(τ)=φ∗(τ),
(2) (φG)∗(τ)=φ∗(τ)G∗(τ),
(3) (φ+G)∗(τ)=φ∗(τ)φ(τ)φ(τ)+G(τ)G∗(τ)G(τ)φ(τ)+G(τ),
(4) (φG)∗(τ)=φ∗(τ)G∗(τ),
(5) (φG)∗(τ)=φ∗(τ)G(τ)φ(τ)G′(τ).
Definition 2.4. [34] For the positive real valued and Riemann integrable function φ, the definite multiplicative integral over [σ,ς] is stated as
Proposition 2.5. [34] For multiplicative integrable functions φ and G, we have the following relations:
(i) ς∫σ((φ(ω))p)dω=(ς∫σ(φ(ω))dω)p,
(ii) ς∫σ(φ(ω)G(ω))dω=ς∫σ(φ(ω))dω.ς∫σ(G(ω))dω,
(iii) ς∫σ(φ(ω)G(ω))dω=ς∫σ(φ(ω))dως∫σ(G(ω))dω,
(iv) ς∫σ(φ(ω))dω=c∫σ(φ(ω))dω.ς∫c(φ(ω))dω, σ≤c≤ς,
(v) σ∫σ(φ(ω))dω=1 and ς∫σ(φ(ω))dω=(σ∫ς(φ(ω))dω )−1.
Lemma 2.6. [13] Let φ:[σ,ς]→R be multiplicative differentiable, and let G:[σ,ς]→R and h:J⊂R→[σ,ς] be two differentiable functions. Then we have
Definition 2.7. [35] A convex function φ:[σ,ς]→R is defined as
for all ω,y∈[σ,ς] and τ∈[0,1].
Definition 2.8. [35] A multiplicative or log convex function φ:[σ,ς]→R is defined as
for all ω,y∈[σ,ς] and τ∈[0,1].
3.
Multiplicative integral identities
In this section, we prove two integral identities in the framework of multiplicative calculus.
Let us start with the following lemmas.
Lemma 3.1. Let φ:[σ,ς]→R be a multiplicative differentiable function over (σ,ς). If φ∗ is an integrable function, then the following equality holds:
Proof. From Lemma 2.6, we have
and
After multiplying (3.2) and (3.3), using integration by the change of variables, we have
Thus, the proof is completed.
Lemma 3.2. Let φ:[σ,ς]→R be a multiplicative differentiable function over (σ,ς). If φ∗ is an integrable function, then the following equality holds:
Proof. This lemma can be proved in a similar way as that used to prove Lemma 3.1.
4.
Simpson's inequalities
In this section, we establish some new Simpson's inequalities for differentiable multiplicative convex functions by using Lemma 3.1.
Theorem 4.1. Under the assumptions of Lemma 3.1, if φ∗ is a multiplicative convex function, then the following inequality holds:
Proof. From the equality given by (3.1) and the multiplicative convexity of φ∗, we have
Theorem 4.2. Under the assumptions of Lemma 3.1, if (ln(φ∗))q, q>1 is a convex function, then the following inequality holds:
where 1p+1q=1.
Proof. From Lemma 3.1 and Hölder's inequality, we have
Applying the convexity of (ln(φ∗))q, we have
Thus, the proof is completed.
5.
Newton's inequalities
In this section, we establish some new Newton's inequalities for differentiable multiplicative convex functions by using Lemma 3.2.
Theorem 5.1. Under the assumptions of Lemma 3.2, if φ∗ is multiplicative convex function, then the following inequality holds:
Proof. This theorem can be proved in a similar way as that used to prove Theorem 4.1.
Theorem 5.2. Under the assumptions of Lemma 3.2, if (ln(φ∗))q, q>1 is a convex function, then the following inequality holds:
Proof. This theorem can be proved in a similar way as that used to prove Theorem 4.2.
6.
Examples
In this section, we assume some particular functions and give mathematical examples to show the validation of the newly established inequalities.
Example 6.1. We consider the function f(ω)=ω2 and from Theorem 4.1 for the interval [σ,ς]=[1,2], we have
and for the left hand side of the inequality (4.1), we have
Now, one can easily observe that
Thus, the inequality (4.1) is valid.
Example 6.2. We consider the function f(ω)=ω2 and from Theorem 4.2 for the interval [σ,ς]=[1,2], p=2 and q=2, we have
From (6.1) and (6.2), we can see that Theorem 4.2 is valid.
Example 6.3. We consider the function f(ω)=ω2 and from Theorem 5.1 for the interval [σ,ς]=[1,2], we have
and
Thus, from (6.3) and (6.4) the inequality (5.1) is valid.
Example 6.4. We consider the function f(ω)=ω2 and from Theorem 5.2 for the interval [σ,ς]=[1,2], we have
From (6.3) and (6.5), it is clear that the inequality (5.2) is true.
7.
Conclusions
In this paper, we established some new Simpson's type of inequalities for multiplicative differentiable log convex functions in the framework of multiplicative calculus. Moreover, we proved Simpson's second type of inequalities for multiplicative differentiable log convex functions in multiplicative calculus. The inequalities presented in the paper can be helpful in finding the bounds for Simpson's and Newton's formulas in the framework of multiplicative calculus. It is an interesting and new problem that the upcoming researchers can use to obtain similar inequalities for different kinds of convexities and coordinated convexities.
Acknowledgments
This research was funded by the National Science, Research and Innovation Fund (NSRF), and King Mongkut's University of Technology North Bangkok under grant no. KMUTNB-FF-65-49.
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: